Creating Coherence-Based Nurse Planning in the Perinatology Care System
Abstract
:1. Background
1.1. Nurse Capacity Planning and Control in Hospitals
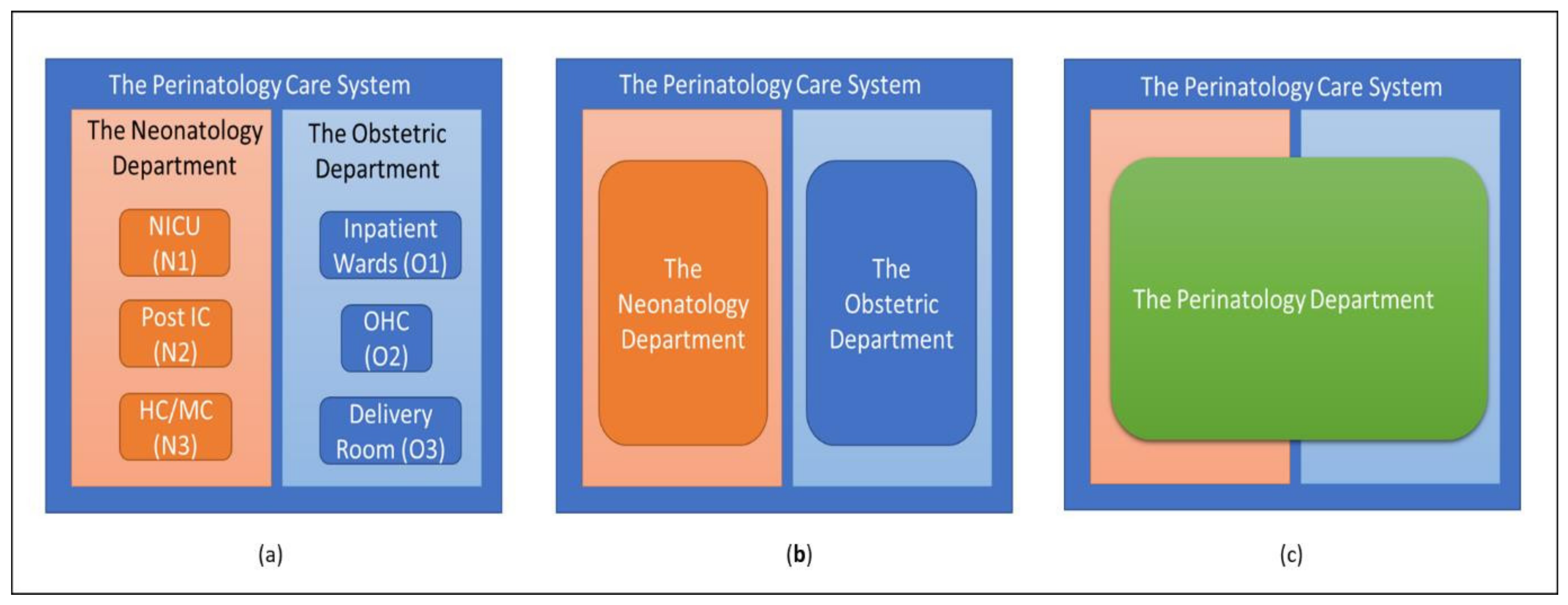
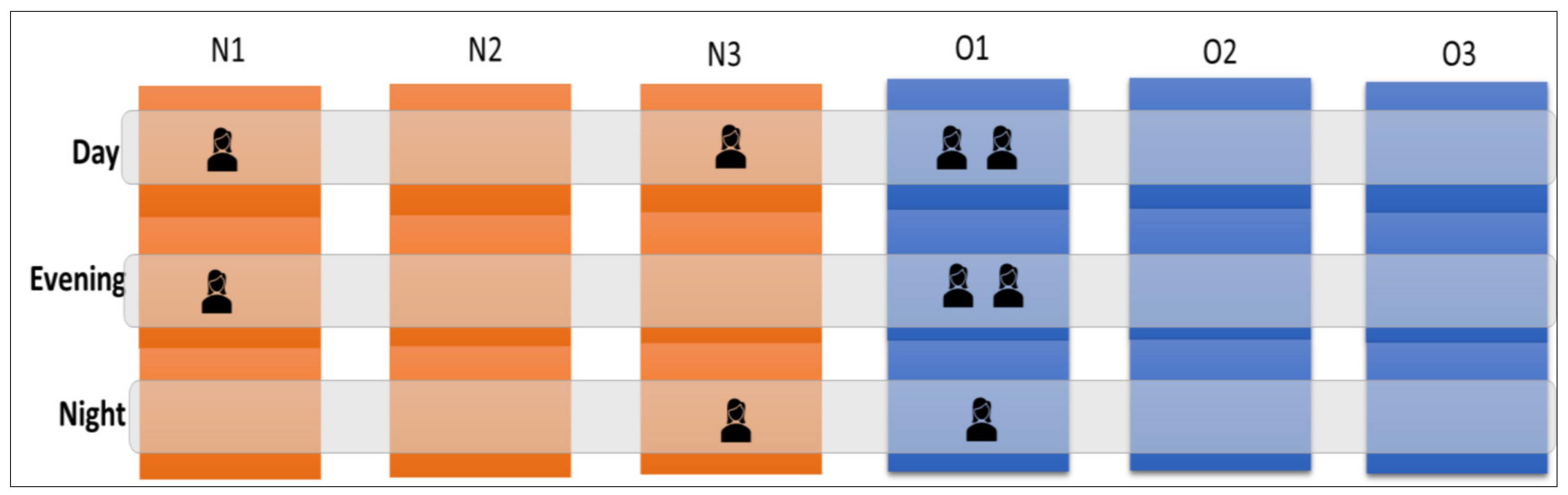
1.2. The Perinatology Care System at Radboudumc
1.3. What This Article Contributes
- What is the optimal care system configuration for minimizing under-/overstaffing at the real-time level?
- What is the best nurse flexibility strategy for minimizing under-/overstaffing at the real-time level?
- What would the minimum limit of flexibility needed by the system to minimize under-/overstaffing be?
- How can nurses be reallocated to a shift to minimize under-/overstaffing?
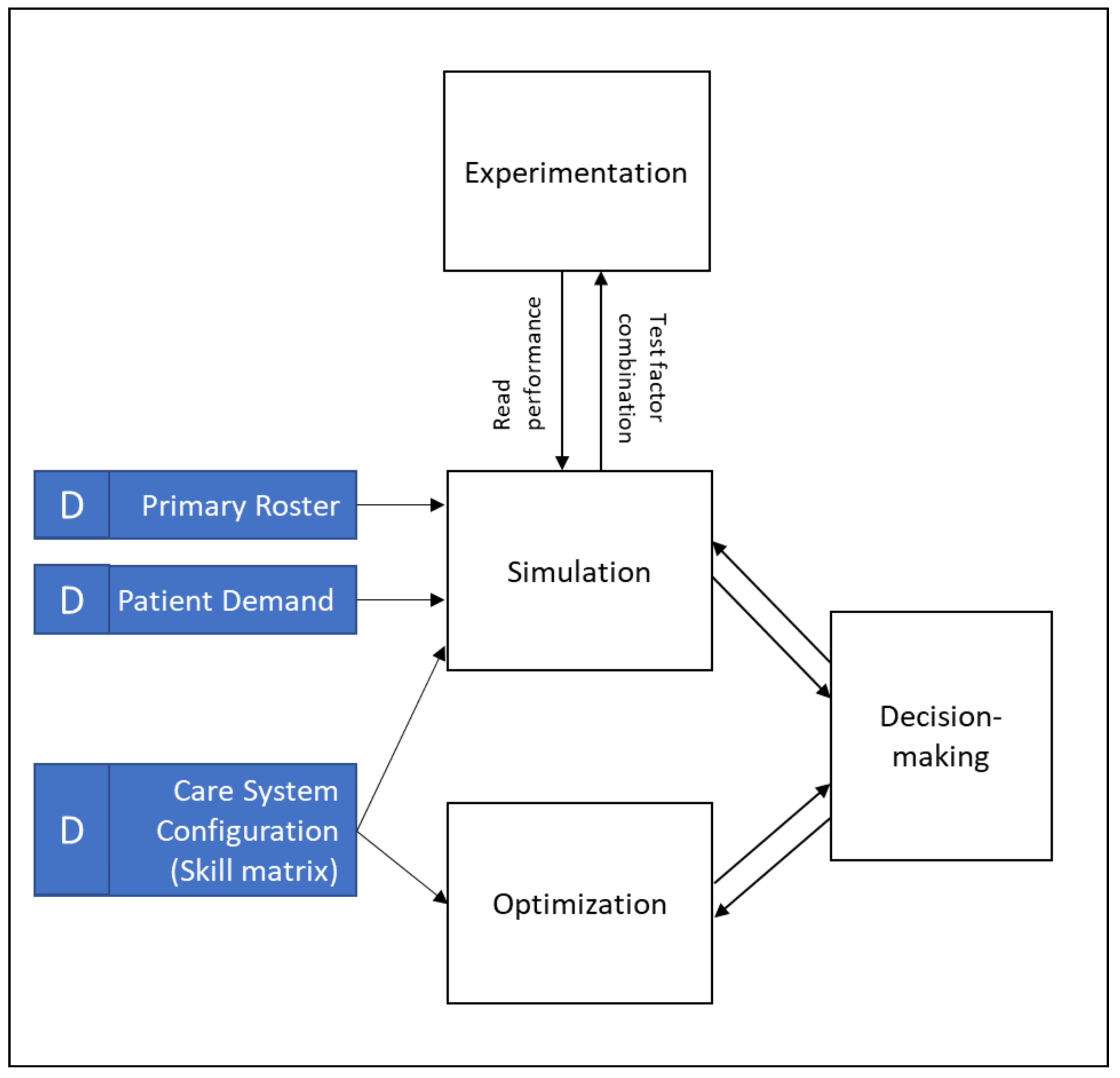
2. Method
2.1. Defining Flexibility: The Skill Matrix and the Planning Horizon
2.2. Nurse Flexibility Strategies
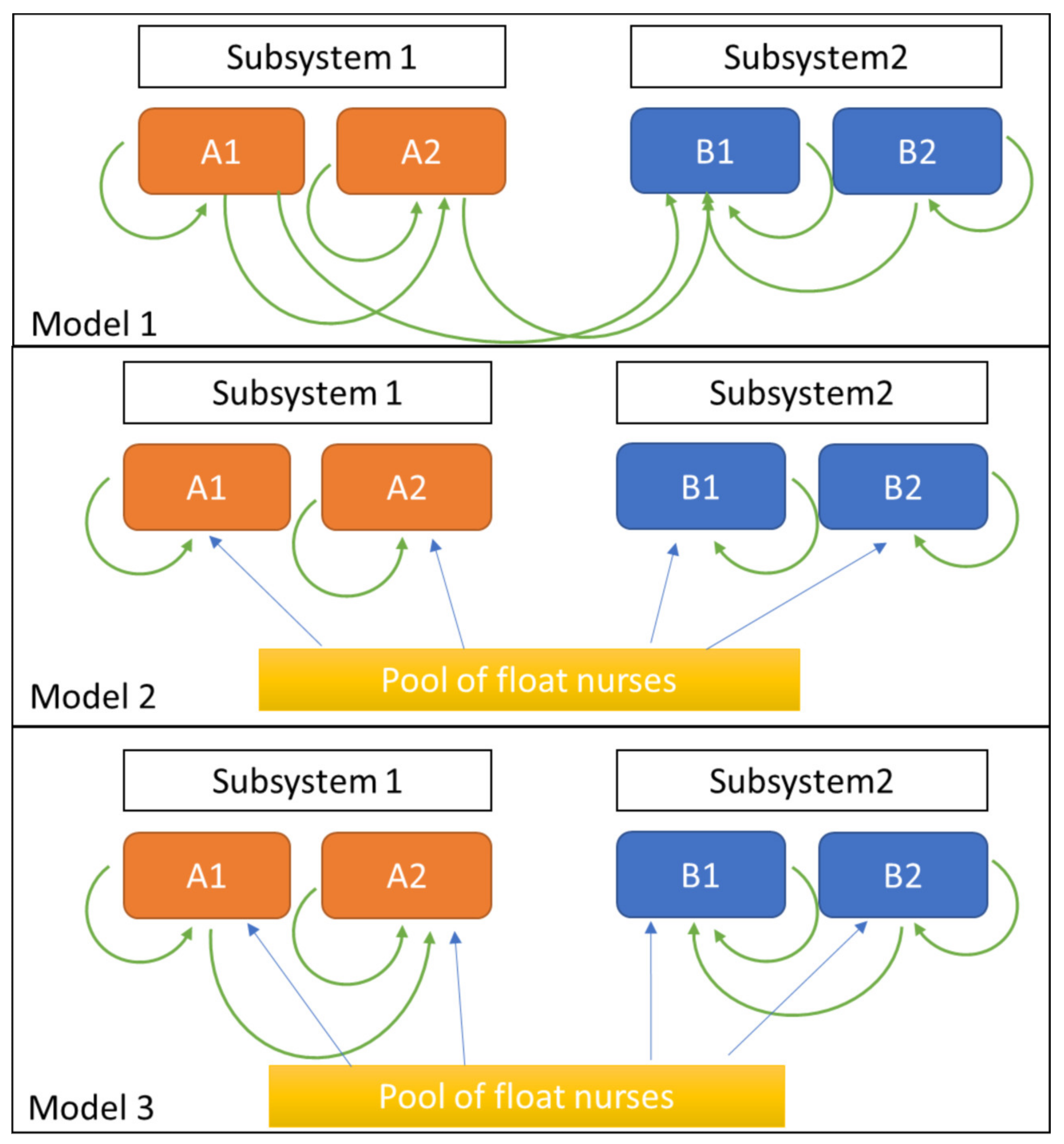
2.3. Model 1: Nurse Flexibility Based on Skill Requirements
2.4. Model 2: Nurse Flexibility with a Centralized Float Pool
2.5. Model 3: Combination of Models 1 and 2
2.6. The Best Flexibility Strategy
2.7. Reallocation Process at the Real-Time Level
2.8. The Optimal Care System Configuration
- The first criterion is the configuration that can minimize the average of under-/overstaffed nurses per shift, which are and , with or without the use of a flexibility strategy.
- The second criterion pertains to the regret that arises from having made a decision [43]. When a decision is made with the information that is currently available, it still might be wrong, given the uncertainty of several variables. This consequence of decision making under uncertain conditions is referred to as decision regret [43]. As explored in Bell [43], “regret” is quantified as the difference in the value between the real outcomes and the best outcomes produced by other alternatives. This definition allows there to be both positive and negative values of regret. In this study, we focused on the negative values of expected understaffing, given different demand conditions.
- The third criterion is the configuration that requires the lowest training cost to implement. We define the cost of the training nurses need to acquire the skills required to be able to adopt the flexibility strategy in Model r (whereas r = {1, 2, … s}). If we refer to the model that requires the lowest cost as =, then the optimal configuration is defined as . This configuration results in the minimum number of under-/overstaffed nurses per shift and is also the one that costs the least to implement.
2.9. Study Design
2.9.1. Simulation and Optimization
- Which nurse flexibility strategy is the best for minimizing under-/overstaffing occurrences;
- How to reallocate nurses to a shift at the real-time level;
- Which care system configuration is optimal for the Perinatology Care System.
2.9.2. Data Analysis
3. Numerical Results
3.1. Data Analysis of the Perinatology Care System Radboudumc
3.2. Reallocation Process at the Real-Time Level
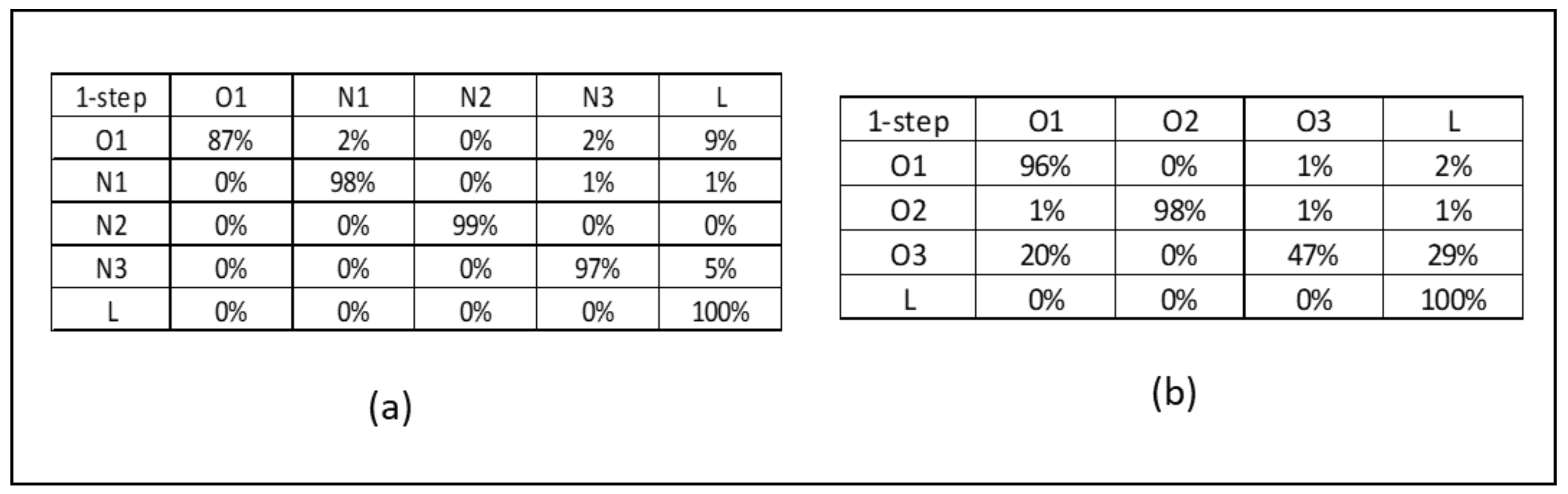
3.2.1. Step 1. Coherence-Based Demand
3.2.2. Step 2. Nurse Reallocation Policies
3.3. The Optimal Care System Configuration
3.3.1. What Is the Optimal Care System Configuration?
3.3.2. Reflection on the Size of Minimum Flexibility at the Current Perinatology Care System
- Size of Flexible Nurses in the Perinatology Care System
- Size of Flexible Beds in the Perinatology Care System
4. Discussion
4.1. Which Nurse Flexibility Strategy Is Best?
4.2. How Can Nurses Be Reallocated to a Shift to Minimize Under-/Overstaffing?
4.3. Which Care System Configuration Is Optimal for the Perinatology Care System?
4.4. What Are the Critical Success Factors for Applying the Proposed Method?
5. Conclusions
5.1. Practical Implications
5.2. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Updated Skill Matrix
| From/To | N1 | N2 | N3 | O1 Newborns | O1 Adults | O2 | O3 |
|---|---|---|---|---|---|---|---|
| N1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| O1 Newborns | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| O1 Adults | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| O2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| O3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| From/To | N1 | N2 | N3 | O1 Newborns | O1 Adults | O2 | O3 |
|---|---|---|---|---|---|---|---|
| N1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| O1 Newborns | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| O1 Adults | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| O2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| O3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Float Pool | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Appendix A.2. The Reallocation Algorithm Based on the Chosen Flexibility Strategy
- Model 1: Prioritization-Based Nurse Reallocation
- Model 2: Cross-Trained Float Nurses
- Model 3: Cross-Trained Float Nurses and Nurse Reallocation with Priority
References
- Dall, T.M.; Gallo, P.D.; Chakrabarti, R.; West, T.; Semilla, A.P.; Storm, M.V. An Aging Population and Growing Disease Burden Will Require A Large And Specialized Health Care Workforce By 2025. Health Aff. 2013, 32, 2013–2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, L. Managed Care and Technology Adoption in Health Care: Evidence from Magnetic Resonance Imaging. J. Health Econ. 2000, 20, 395–421. [Google Scholar] [CrossRef] [Green Version]
- Buchan, J.; Aiken, L. Solving nursing shortages: A common priority. J. Clin. Nurs. 2008, 17, 3262–3268. [Google Scholar] [CrossRef] [Green Version]
- McClean, S.I.; Millard, P.H. A three compartment model of the patient flows in a geriatric department: A decision support approach. Health Care Manag. Sci. 1998, 1, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Hopp, W.J.; Lovejoy, W.S. Hospital Operations: Principles of High Efficiency Health Care; Pearson Education: London, UK, 2014. [Google Scholar]
- Hall, R.; Belson, D.; Murali, P.; Dessouky, M. Modeling patient flows through the healthcare system. In Patient Flow: Reducing Delay in Healthcare Delivery; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–42. [Google Scholar]
- Driscoll, M.; Tobis, K.; Gurka, D.; Serafin, F.; Carlson, E. Breaking Down the Silos to Decrease Internal Diversions and Patient Flow Delays. Nurs. Adm. Q. 2015, 39, E1–E8. [Google Scholar] [CrossRef]
- Kolker, A. Interdependency of hospital departments and hospital-wide patient flows. In Patient Flow: Reducing Delay in Healthcare Delivery; Springer: Boston, MA, USA, 2013; pp. 43–63. [Google Scholar] [CrossRef]
- Winasti, W.; Elkhuizen, S.; Berrevoets, L.; van Merode, G.; Berden, H. Inpatient flow management: A systematic review. Int. J. Health Care Qual. Assur. 2018, 31, 718–734. [Google Scholar] [CrossRef]
- Khanna, S.; Boyle, J.; Good, N.; Lind, J. Unravelling relationships: Hospital occupancy levels, discharge timing and emergency department access block. Emerg. Med. Australas. 2012, 24, 510–517. [Google Scholar] [CrossRef]
- Resar, R.; Nolan, K.; Kaczynski, D.; Jensen, K. Using Real-Time Demand Capacity Management to Improve Hospitalwide Patient Flow. Jt. Comm. J. Qual. Patient Saf. 2011, 37, 217–227. [Google Scholar] [CrossRef]
- Inman, R.R.; Blumenfeld, D.E.; Ko, A. Cross-Training Hospital Nurses to Reduce Staffing Costs. Health Care Manag. Rev. 2005, 30, 116–125. [Google Scholar] [CrossRef]
- Griffin, J.; Xia, S.; Peng, S.; Keskinocak, P. Improving patient flow in an obstetric unit. Health Care Manag. Sci. 2011, 15, 1–14. [Google Scholar] [CrossRef]
- Hans, E.W.; van Houdenhoven, M.; Hulshof, P.J.H. A framework for healthcare planning and control. In Handbook of Healthcare System Scheduling; Springer: Boston, MA, USA, 2011; pp. 303–320. [Google Scholar] [CrossRef]
- Hulshof, P.J.H.; Kortbeek, N.; Boucherie, R.J.; Hans, E.W.; Bakker, P.J.M. Taxonomic classification of planning decisions in health care: A structured review of the state of the art in OR/OM. Health Sci. 2012, 1, 129–175. [Google Scholar] [CrossRef]
- Burke, E.K.; de Causmaecker, P.; Berghe, G.V.; van Landeghem, H. The State of the Art of Nurse Rostering. J. Sched. 2004, 7, 441–499. [Google Scholar] [CrossRef]
- Vanberkel, P.T.; Boucherie, R.J.; Hans, E.W.; Hurink, J.L.; Litvak, N. Efficiency evaluation for pooling resources in healthcare. OR Spectrum 2012, 34, 371–390. [Google Scholar] [CrossRef] [Green Version]
- Gnanlet, A.; Giland, W.G. Sequential and simultaneous decision making for optimizing health care resource flexibilities. Decis. Sci. 2009, 40, 295–326. [Google Scholar] [CrossRef]
- Li, L.L.X.; King, B.E. A healthcare staff decision model considering the effects of staff cross-training. Health Care Manag. Sci. 1999, 2, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, V.M.; Warner, D.M. A Branch and Bound Algorithm for Optimum Allocation of Float Nurses. Manag. Sci. 1976, 22, 972–981. [Google Scholar] [CrossRef]
- Munavalli, J.R.; Rao, S.V.; Srinivasan, A.; van Merode, G. Integral patient scheduling in outpatient clinics under demand uncertainty to minimize patient waiting times. Health Inform. J. 2019, 26, 435–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Munavalli, J.R.; Rao, S.V.; Srinivasan, A.; Manjunath, U.; van Merode, G.G. A Robust Predictive Resource Planning under Demand Uncertainty to Improve Waiting Times in Outpatient Clinics. J. Health Manag. 2017, 19, 563–583. [Google Scholar] [CrossRef] [Green Version]
- Bard, J.F.; Purnomo, H.W. Short-Term Nurse Scheduling in Response to Daily Fluctuations in Supply and Demand. Health Care Manag. Sci. 2005, 8, 315–324. [Google Scholar] [CrossRef]
- De Bruin, A.M.; van Rossum, A.C.; Visser, M.C.; Koole, G.M. Modeling the emergency cardiac in-patient flow: An application of queuing theory. Health Care Manag. Sci. 2007, 10, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Van Merode, F. Capaciteitsmanagement in relatie tot de besturing en organisatie van zorg. In Capaciteitsplanning in De Zorg; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3–22. [Google Scholar] [CrossRef]
- Cochran, J.K.; Bharti, A. Stochastic bed balancing of an obstetrics hospital. Health Care Manag. Sci. 2006, 9, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Asaduzzaman, M.; Chaussalet, T.; Robertson, N.J. A loss network model with overflow for capacity planning of a neonatal unit. Ann. Oper. Res. 2009, 178, 67–76. [Google Scholar] [CrossRef] [Green Version]
- Bittencourt, O.; Verter, V.; Yalovsky, M. Hospital capacity management based on the queueing theory. Int. J. Product. Perform. Manag. 2018, 67, 224–238. [Google Scholar] [CrossRef] [Green Version]
- Larson, N.; Sendelbach, S.; Missal, B.; Fliss, J.; Gaillard, P. Staffing Patterns of Scheduled Unit Staff Nurses vs. Float Pool Nurses: A Pilot Study. Medsurg Nurs. 2012, 21, 27–32. [Google Scholar] [PubMed]
- Vanberkel, P.T.; Boucherie, R.J.; Hans, E.W.; Hurink, J.L.; van Lent, W.A.M.; van Harten, W.H. Accounting for Inpatient Wards When Developing Master Surgical Schedules. Anesth. Analg. 2011, 112, 1472–1479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffiths, P.; Saville, C.; Ball, J.; Jones, J.; Pattison, N.; Monks, T. Nursing workload, nurse staffing methodologies and tools: A systematic scoping review and discussion. Int. J. Nurs. Stud. 2019, 103, 103487. [Google Scholar] [CrossRef]
- Wynendaele, H.; Willems, R.; Trybou, J. Systematic review: Association between the patient–nurse ratio and nurse outcomes in acute care hospitals. J. Nurs. Manag. 2019, 27, 896–917. [Google Scholar] [CrossRef]
- Legrain, A.; Bouarab, H.; Lahrichi, N. The Nurse Scheduling Problem in Real-Life. J. Med Syst. 2014, 39, 1–11. [Google Scholar] [CrossRef]
- Abdalkareem, Z.A.; Amir, A.; Al-Betar, M.A.; Ekhan, P.; Hammouri, A.I. Healthcare scheduling in optimization context: A review. Health Technol. 2021, 11, 445–469. [Google Scholar] [CrossRef]
- Takagi, H.; Kanai, Y.; Misue, K. Queueing network model for obstetric patient flow in a hospital. Health Care Manag. Sci. 2016, 20, 433–451. [Google Scholar] [CrossRef]
- Ferraro, N.M.; Reamer, C.B.; Reynolds, T.A.; Howell, L.J.; Moldenhauer, J.S.; Day, T.E. Capacity Planning for Maternal–Fetal Medicine Using Discrete Event Simulation. Am. J. Perinatol. 2014, 32, 761–770. [Google Scholar] [CrossRef] [PubMed]
- MacLean, L.; Hassmiller, S.; Shaffer, F.; Rohrbaugh, K.; Collier, T.; Fairman, J. Scale, Causes, and Implications of the Primary Care Nursing Shortage. Annu. Rev. Public Health 2014, 35, 443–457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ward, M.J.; Ferrand, Y.B.; Laker, L.F.; Froehle, C.M.; Vogus, T.J.; Dittus, R.S.; Kripalani, S.; Pines, J.M. The Nature and Necessity of Operational Flexibility in the Emergency Department. Ann. Emerg. Med. 2014, 65, 156–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dziuba-Ellis, J. Float Pools and Resource Teams: A Review of the Literature. J. Nurs. Care Qual. 2006, 21, 352–359. [Google Scholar] [CrossRef]
- Van Merode, G.G.; Groothuis, S.; Hasman, A. Enterprise Resource Planning for Hospitals. Int. J. Med. Inform. 2004, 73, 493–501. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Ray, P.K. Patient flow modelling and performance analysis of healthcare delivery processes in hospitals: A review and reflections. Comput. Ind. Eng. 2014, 78, 299–312. [Google Scholar] [CrossRef]
- Natarajan, G. Analysis of Queues: Methods and Applications; CRC Press Taylor & Francis Group: Abingdon, UK, 2012. [Google Scholar]
- Bell, D.E. Regret in Decision Making under Uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Van Merode, G.; Hasman, A.; Derks, J.; Goldschmidt, H.; Schoenmaker, B.; Oosten, M. Decision support for clinical laboratory capacity planning. Int. J. Bio-Med. Comput. 1995, 38, 75–87. [Google Scholar] [CrossRef] [Green Version]
- Elkhuizen, S.G.; Bor, G.; Smeenk, M.; Klazinga, N.S.; Bakker, P.J.M. Capacity Management of Nursing Staff as a Vehicle for Organizational Improvement in an Academic Hospital. BioMed Cent. Health Serv. Res. 2007, 7, 196. [Google Scholar] [CrossRef] [Green Version]
- Jordan, W.C.; Inman, R.R.; Blumenfeld, D.E. Chained cross-training of workers for robust performance. IIE Trans. 2004, 36, 953–967. [Google Scholar] [CrossRef]
- Van der Ham, A.; van Raak, A.; Ruwaard, D.; van Merode, F. Exploring changes in integration, differentiation, rules, coordination and performance following the introduction of a hospital planning centre: A case study. J. Health Organ. Manag. 2022, 36, 158–178. [Google Scholar] [CrossRef] [PubMed]
- Vos, L.; la Dückers, M.; Wagner, C.; van Merode, G.G. Applying the quality improvement collaborative method to process redesign: A multiple case study. Implement. Sci. 2010, 5, 19. [Google Scholar] [CrossRef] [Green Version]
- Kidner, M.C. How to keep float nurses from sinking. RN 1999, 62, 35. [Google Scholar] [PubMed]
- Larsson, A.; Fredriksson, A. Tactical capacity planning in hospital departments. Int. J. Health Care Qual. Assur. 2019, 26, 2019. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Care System Configuration | Controllable Variable (Name of Intervention) | Dependent Variable |
|---|---|---|
| Current configuration (6 separate units) | No flexibility intervention | R0 |
| Model 1 | R1 | |
| Model 2 Model 2 modifications in the size of the float pool to 20% and 40% of the total nurses in the system | R2 R2_20%, R2_40% | |
| Model 3 | R3 | |
| Configuration 1 (2 departments) | No flexibility intervention | R4 |
| Model 1 | R5 | |
| Model 2 | R6 | |
| Model 3 | R7 | |
| Configuration 2 (1 department) | No flexibility intervention | R8 |
| Unit | N1 | N2 | N3 | O1 | O2 | O3 | Total |
|---|---|---|---|---|---|---|---|
| #Beds | 14 | 4 | 11 | 32 (incl. 7 newborns beds) | 3 | 6 | 70 |
| % of total | 20% | 6% | 16% | 46% | 4% | 8% | 100% |
| Shifts | N1 | N2 | N3 | O1 | O2 | O3 | Total |
|---|---|---|---|---|---|---|---|
| Day | 12 | 2 | 4 | 6 | 1 | 3 | 28 |
| Night | 8 | 2 | 2 | 5 | 1 | 3 | 21 |
| Evening | 7 | 2 | 2 | 2 | 1 | 3 | 17 |
| Total | 27 | 6 | 8 | 13 | 3 | 9 | 66 |
| Shifts | N1 | N2 | N3 | O1 | O2 | O3 |
|---|---|---|---|---|---|---|
| Day | 1:1 | 1:2 | 1:3 | 1:5 | 1:3 | 1:2 |
| Evening | 1:2 | 1:2 | 1:6 | 1:6 | 1:3 | 1:2 |
| Night | 1:2 | 1:2 | 1:6 | 1:16 | 1:3 | 1:2 |
| Unit | Number of Nurses |
|---|---|
| N1 | 59 |
| N2 | 40 |
| N3 | 14 |
| Total for the Neonatology Department | 113 |
| O1, O2, and O3 | 53 |
| O1 and O2 | 5 |
| O1 | 5 |
| Total for the Obstetrics Department | 63 |
| Total for the Perinatology Care System | 176 |
| From/To | N1 | N2 | N3 | O1 Newborns | O1 Adults | O2 | O3 |
|---|---|---|---|---|---|---|---|
| N1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| O1 Newborns | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| O1 Adults | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| O2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| O3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| From/To | N1 | N2 | N3 | O1 Newborns | O1 Adults | O2 | O3 |
|---|---|---|---|---|---|---|---|
| N1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| O1 Newborns | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| O1 Adults | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| O2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| O3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Float Pool | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Configuration | Response | Actual Demand (CI = 31%) | Variable Demand (CI = 49%) | ||
|---|---|---|---|---|---|
| Average Understaffed (±SD) | Average Overstaffed (±SD) | Average Understaffed (±SD) | Average Overstaffed (±SD) | ||
| Current Configuration | R0 No flex | −1.6 (0.7) | 4.5 (1.9) | −2.4 (1.1) | 5.7 (2.4) |
| R1 Model 1 | −0.3 (0.6) | 2.8 (2.1) | −0.5 (0.9) | 3.5 (2.6) | |
| R2 Model 2 | −1.2 (1.1) | 3.7 (1.8) | −1.6 (1.4) | 4.5 (2.4) | |
| R3 Model 3 | −0.3 (0.6) | 2.8 (2.1) | −0.5 (0.9) | 3.5 (2.6) | |
| Configuration | Response | Average Understaffed (Rounded) | Average Overstaffed (Rounded) | Cost of Training |
|---|---|---|---|---|
| Current Configuration (a) | R0 No flex | −2.0 | 5.0 | EUR 0 |
| R1 Model 1 | 0.0 | 3.0 | EUR 0 | |
| R2 Model 2 | −1.0 | 4.0 | EUR 240,000 | |
| R2_20% | 0.0 | 3.0 | EUR 700,000 | |
| R2_40% | 0.0 | 3.0 | EUR 1,400,000 | |
| R3 Model 3 | 0.0 | 3.0 | EUR 240,000 | |
| R0 No flex_Variable demand | −2.0 | 6.0 | EUR 0 | |
| R1 Model 1_Variable demand | −1.0 | 4.0 | EUR 0 | |
| R2 Model 2_Variable demand | −2.0 | 5.0 | EUR 240,000 | |
| R2_20%_Variable demand | −1.0 | 4.0 | EUR 700,000 | |
| R2_40%_Variable demand | 0.0 | 4.0 | EUR 1,400,000 | |
| R3 Model 3_Variable demand | −1.0 | 4.0 | EUR 240,000 | |
| Configuration 1 (b) | R4 No flex | 0.0 | 3.0 | EUR 1,280,000 |
| R5 Model 1 | 0.0 | 3.0 | EUR 1,280,000 | |
| R6 Model 2 | 0.0 | 3.0 | EUR 1,280,000 | |
| R7 Model 3 | 0.0 | 3.0 | EUR 1,280,000 | |
| Configuration 2 (c) | R8 No flex | 0.0 | 3.0 | EUR 3,520,000 |
| Actual Demand (CI = 31%) | ||
|---|---|---|
| Flexibility Rate % | Frequency | Cumulative % |
| 0 | 3 | 0.82% |
| 2 | 8 | 3.01% |
| 4 | 20 | 8.49% |
| 5 | 96 | 34.79% |
| 7 | 71 | 54.25% |
| 9 | 114 | 85.48% |
| 11 | 26 | 92.60% |
| 13 | 12 | 95.89% |
| 15 | 7 | 97.81% |
| 16 | 5 | 99.18% |
| 18 | 3 | 100.00% |
| More | 0 | 100.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winasti, W.; Elkhuizen, S.G.; van Merode, F.; Berden, H. Creating Coherence-Based Nurse Planning in the Perinatology Care System. Healthcare 2022, 10, 925. https://doi.org/10.3390/healthcare10050925
Winasti W, Elkhuizen SG, van Merode F, Berden H. Creating Coherence-Based Nurse Planning in the Perinatology Care System. Healthcare. 2022; 10(5):925. https://doi.org/10.3390/healthcare10050925
Chicago/Turabian StyleWinasti, Windi, Sylvia G. Elkhuizen, Frits van Merode, and Hubert Berden. 2022. "Creating Coherence-Based Nurse Planning in the Perinatology Care System" Healthcare 10, no. 5: 925. https://doi.org/10.3390/healthcare10050925
APA StyleWinasti, W., Elkhuizen, S. G., van Merode, F., & Berden, H. (2022). Creating Coherence-Based Nurse Planning in the Perinatology Care System. Healthcare, 10(5), 925. https://doi.org/10.3390/healthcare10050925






