Crosswalk between Charlson Comorbidity Index and the American Society of Anesthesiologists Physical Status Score for Geriatric Trauma Assessment
Abstract
1. Introduction
2. Materials and Methods
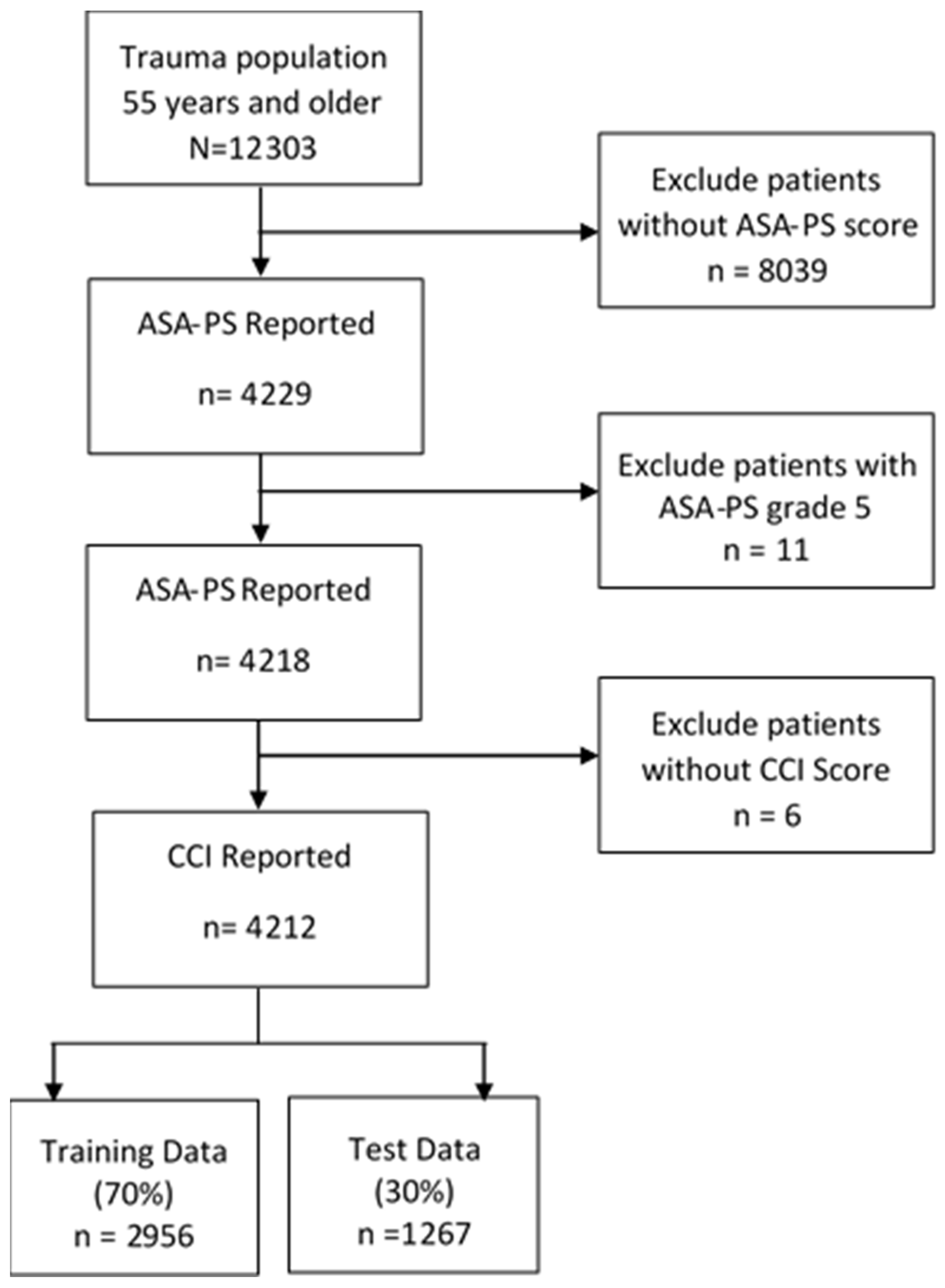
2.1. Study Design, Setting, and Patients
2.2. Inclusion and Exclusion Criteria
2.3. Variable Definitions
2.4. Data Analysis
2.5. Model Testing and Internal Validation
2.6. ASA-PS and CCI Crosswalk
3. Results
3.1. Population Characteristics
3.2. Univariate Regression Analysis
3.3. Multivariate Binary Logistic Regression: Prediction of ASA-PS Categories
3.4. Discriminant Properties
3.5. Multivariate Ordinal Logistic Regression: Prediction Probabilities
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Southern, A.; Lopez, R.; Jwayyed, S. Geriatric Trauma. Available online: https://www.ncbi.nlm.nih.gov/books/NBK442020/ (accessed on 4 January 2023).
- Colwell, C.; Moreira, M.; Grayzel, J. Geriatric Trauma: Initial Evaluation and Management. Available online: https://www.uptodate.com/contents/geriatric-trauma-initial-evaluation-and-management (accessed on 4 January 2023).
- Harbrecht, B.G.; Peitzman, A.B.; Rivera, L.; Heil, B.; Croce, M.; Morris, J.A., Jr.; Enderson, B.L.; Kurek, S.; Pasquale, M.; Frykberg, E.R.; et al. Contribution of age and gender to outcome of blunt splenic injury in adults: Multicenter study of the eastern association for the surgery of trauma. J. Trauma. 2001, 51, 887–895. [Google Scholar] [CrossRef]
- Fakhry, S.M.; Morse, J.L.; Garland, J.M.; Wilson, N.Y.; Shen, Y.; Wyse, R.J.; Watts, D.D. Redefining geriatric trauma: 55 is the new 65. J. Trauma. Acute Care Surg. 2021, 90, 738–743. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Zheng, Z.; Zhang, M. The incidence of geriatric trauma is increasing and comparison of different scoring tools for the prediction of in-hospital mortality in geriatric trauma patients. World J. Emerg. Surg. 2020, 15, 59. [Google Scholar] [CrossRef] [PubMed]
- Alshibani, A.; Alharbi, M.; Conroy, S. Under-triage of older trauma patients in prehospital care: A systematic review. Eur. Geriatr. Med. 2021, 12, 903–919. [Google Scholar] [CrossRef]
- Blomaard, L.C.; Speksnijder, C.; Lucke, J.A.; de Gelder, J.; Anten, S.; Schuit, S.C.E.; Steyerberg, E.W.; Gussekloo, J.; de Groot, B.; Mooijaart, S.P. Geriatric Screening, Triage Urgency, and 30-Day Mortality in Older Emergency Department Patients. J. Am. Geriatr. Soc. 2020, 68, 1755–1762. [Google Scholar] [CrossRef]
- Chu, I.; Vaca, F.; Stratton, S.; Chakravarthy, B.; Hoonpongsimanont, W.; Lotfipour, S. Geriatric trauma care: Challenges facing emergency medical services. Calif. J. Emerg. Med. 2007, 8, 51–55. [Google Scholar]
- Konda, S.R.; Lott, A.; Mandel, J.; Lyon, T.R.; Robitsek, J.; Ganta, A.; Egol, K.A. Who Is the Geriatric Trauma Patient? An Analysis of Patient Characteristics, Hospital Quality Measures, and Inpatient Cost. Geriatr. Orthop. Surg. Rehabil. 2020, 11, 2151459320955087. [Google Scholar] [CrossRef]
- Iles, K.A.; Duchesneau, E.; Strassle, P.D.; Chrisco, L.; Howell, T.C.; King, B.; Williams, F.N.; Nizamani, R. Higher Admission Frailty Scores Predict Increased Mortality, Morbidity, and Healthcare Utilization in the Elderly Burn Population. J. Burn. Care Res. 2022, 43, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.S.; Watts, J.N.; Peel, N.M.; Hubbard, R.E. Frailty and post-operative outcomes in older surgical patients: A systematic review. BMC Geriatr. 2016, 16, 157. [Google Scholar] [CrossRef] [PubMed]
- Anantha, R.V.; Painter, M.D.; Diaz-Garelli, F.; Nunn, A.M.; Miller, P.R.; Chang, M.C.; Jason Hoth, J. Undertriage Despite Use of Geriatric-Specific Trauma Team Activation Guidelines: Who Are We Missing? Am. Surg. 2020, 87, 419–426. [Google Scholar] [CrossRef]
- Boulton, A.J.; Peel, D.; Rahman, U.; Cole, E. Evaluation of elderly specific pre-hospital trauma triage criteria: A systematic review. Scand. J. Trauma. Resusc. Emerg. Med. 2021, 29, 127. [Google Scholar] [CrossRef] [PubMed]
- AARP. The Aging Readiness & Competitiveness Report: UNITED STATES; AARP: Washington, DC, USA, 2020. [Google Scholar]
- American College of Surgeons. Trauma Quality Improvement Program. In Geriatric Trauma Management Guidelines; American College of Surgeons: Chicago, IL, USA, 2012. [Google Scholar]
- American College of Surgeons. Trauma Quality Improvement Program. Available online: https://www.facs.org/quality-programs/trauma/quality/trauma-quality-improvement-program/ (accessed on 26 June 2022).
- Haugan, K.; Klaksvik, J.; Foss, O.A. 30-day mortality in patients after hip fracture surgery: A comparison of the Charlson Comorbidity Index score and ASA score used in two prediction models. Injury 2021, 52, 2379–2383. [Google Scholar] [CrossRef]
- Kim, E.M.; Li, G.; Kim, M. Development of a Risk Score to Predict Postoperative Delirium in Patients With Hip Fracture. Anesth. Analg. 2020, 130, 79–86. [Google Scholar] [CrossRef]
- McConaghy, K.M.; Orr, M.N.; Emara, A.K.; Sinclair, S.T.; Klika, A.K.; Piuzzi, N.S. Can extant comorbidity indices identify patients who experience poor outcomes following total joint arthroplasty? Arch. Orthop. Trauma. Surg. 2021. [Google Scholar] [CrossRef]
- Mulvey, H.E.; Haslam, R.D.; Laytin, A.D.; Diamond, C.A.; Sims, C.A. Unplanned ICU Admission Is Associated With Worse Clinical Outcomes in Geriatric Trauma Patients. J. Surg. Res. 2020, 245, 13–21. [Google Scholar] [CrossRef]
- Whitmore, R.G.; Stephen, J.H.; Vernick, C.; Campbell, P.G.; Yadla, S.; Ghobrial, G.M.; Maltenfort, M.G.; Ratliff, J.K. ASA grade and Charlson Comorbidity Index of spinal surgery patients: Correlation with complications and societal costs. Spine J. 2014, 14, 31–38. [Google Scholar] [CrossRef]
- Mannion, A.F.; Bianchi, G.; Mariaux, F.; Fekete, T.F.; Reitmeir, R.; Moser, B.; Whitmore, R.G.; Ratliff, J.; Haschtmann, D. Can the Charlson Comorbidity Index be used to predict the ASA grade in patients undergoing spine surgery? Eur. Spine J. 2020, 29, 2941–2952. [Google Scholar] [CrossRef]
- Mannion, A.F.; Fekete, T.F.; Porchet, F.; Haschtmann, D.; Jeszenszky, D.; Kleinstück, F.S. The influence of comorbidity on the risks and benefits of spine surgery for degenerative lumbar disorders. Eur. Spine J. 2014, 23, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Charlson, M.E.; Pompei, P.; Ales, K.L.; MacKenzie, C.R. A new method of classifying prognostic comorbidity in longitudinal studies: Development and validation. J. Chronic Dis. 1987, 40, 373–383. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.; Li, B.; Couris, C.M.; Fushimi, K.; Graham, P.; Hider, P.; Januel, J.M.; Sundararajan, V. Updating and validating the Charlson comorbidity index and score for risk adjustment in hospital discharge abstracts using data from 6 countries. Am. J. Epidemiol. 2011, 173, 676–682. [Google Scholar] [CrossRef]
- Charlson, M.E.; Carrozzino, D.; Guidi, J.; Patierno, C. Charlson Comorbidity Index: A Critical Review of Clinimetric Properties. Psychother. Psychosom. 2022, 91, 8–35. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, W.J.; Jongerius, E.J.; Mandjes-van Uitert, M.J.; van Munster, B.C.; de Rooij, S.E. Validation of the Charlson Comorbidity Index in acutely hospitalized elderly adults: A prospective cohort study. J. Am. Geriatr. Soc. 2014, 62, 342–346. [Google Scholar] [CrossRef]
- Quach, L.H.; Jayamaha, S.; Whitehouse, S.L.; Crawford, R.; Pulle, C.R.; Bell, J.J. Comparison of the Charlson Comorbidity Index with the ASA score for predicting 12-month mortality in acute hip fracture. Injury 2020, 51, 1004–1010. [Google Scholar] [CrossRef]
- Tran, A.; Mai, T.; El-Haddad, J.; Lampron, J.; Yelle, J.D.; Pagliarello, G.; Matar, M. Preinjury ASA score as an independent predictor of readmission after major traumatic injury. Trauma. Surg. Acute Care Open. 2017, 2, e000128. [Google Scholar] [CrossRef] [PubMed]
- Konda, S.R.; Lott, A.; Egol, K.A. Development of a Value-based Algorithm for Inpatient Triage of Elderly Hip Fracture Patients. J. Am. Acad. Orthop. Surg. 2020, 28, e566–e572. [Google Scholar] [CrossRef]
- Konda, S.R.; Lott, A.; Saleh, H.; Gales, J.; Egol, K.A. Use of the STTGMA Tool to Risk Stratify 1-Year Functional Outcomes and Mortality in Geriatric Trauma Patients. J. Orthop. Trauma. 2018, 32, 461–466. [Google Scholar] [CrossRef]
- Konda, S.R.; Lott, A.; Saleh, H.; Lyon, T.; Egol, K.A. Using Trauma Triage Score to Risk-Stratify Inpatient Triage, Hospital Quality Measures, and Cost in Middle-Aged and Geriatric Orthopaedic Trauma Patients. J. Orthop. Trauma. 2019, 33, 525–530. [Google Scholar] [CrossRef] [PubMed]
- Konda, S.R.; Parola, R.; Perskin, C.; Egol, K.A. ASA Physical Status Classification Improves Predictive Ability of a Validated Trauma Risk Score. Geriatr. Orthop. Surg. Rehabil. 2021, 12, 2151459321989534. [Google Scholar] [CrossRef]
- Chien, S.-H.; Yao, M.; Li, C.-C.; Chang, P.-Y.; Yu, M.-S.; Huang, C.-E.; Tan, T.-D.; Lin, C.-H.; Yeh, S.-P.; Li, S.-s.; et al. Charlson comorbidity index predicts outcomes of elderly after allogeneic hematopoietic stem cell transplantation for acute myeloid leukemia and myelodysplastic syndrome. J. Formos. Med. Assoc. 2021, 120, 2144–2152. [Google Scholar] [CrossRef]
- Setter, N.W.; Peres, M.L.; de Almeida, B.M.M.; Petterle, R.R.; Raboni, S.M. Charlson comorbidity index scores and in-hospital prognosis of patients with severe acute respiratory infections. Intern. Med. J. 2020, 50, 691–697. [Google Scholar] [CrossRef]
- Shebeshi, D.S.; Dolja-Gore, X.; Byles, J. Charlson Comorbidity Index as a predictor of repeated hospital admission and mortality among older women diagnosed with cardiovascular disease. Aging Clin. Exp. Res. 2021, 33, 2873–2878. [Google Scholar] [CrossRef] [PubMed]
- Shinonara, K.; Ugawa, R.; Arataki, S.; Nakahara, S.; Takeuchi, K. Charlson comorbidity index is predictive of postoperative clinical outcome after single-level posterior lumbar interbody fusion surgery. J. Orthop. Surg. Res. 2021, 16, 235. [Google Scholar] [CrossRef] [PubMed]
- Bhaskaran, K.; Smeeth, L. What is the difference between missing completely at random and missing at random? Int. J. Epidemiol. 2014, 43, 1336–1339. [Google Scholar] [CrossRef] [PubMed]
- Little, R.J. A Test of Missing Completely at Random for Multivariate Data with Missing Values. Available online: https://www.jstor.org/stable/pdf/2290157.pdf (accessed on 24 February 2022).
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef]
- Bodner, T.E. What Improves with Increased Missing Data Imputations? Struct. Equ. Modeling 2008, 15, 651–675. [Google Scholar] [CrossRef]
- Nassiri, V.; Lovik, A.; Molenberghs, G.; Verbeke, G. On using multiple imputation for exploratory factor analysis of incomplete data. Behav. Res. Methods 2018, 50, 501–517. [Google Scholar] [CrossRef]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef]
- Ruopp, M.D.; Perkins, N.J.; Whitcomb, B.W.; Schisterman, E.F. Youden Index and optimal cut-point estimated from observations affected by a lower limit of detection. Biom. J. 2008, 50, 419–430. [Google Scholar] [CrossRef]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Series B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tibshirani, R. The lasso method for variable selection in the Cox model. Stat. Med. 1997, 16, 385–395. [Google Scholar] [CrossRef]
- Brant, R. Assessing proportionality in the proportional odds model for ordinal logistic regression. Biometrics 1990, 46, 1171–1178. [Google Scholar] [CrossRef]
- StataCorp. Stata Statistical Software: Release 1; StataCorp LLC: College Station, TX, USA, 2020. [Google Scholar]
- Ringdal, K.G.; Skaga, N.O.; Steen, P.A.; Hestnes, M.; Laake, P.; Jones, J.M.; Lossius, H.M. Classification of comorbidity in trauma: The reliability of pre-injury ASA physical status classification. Injury 2013, 44, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Elixhauser, A.; Steiner, C.; Harris, D.R.; Coffey, R.M. Comorbidity measures for use with administrative data. Med. Care 1998, 36, 8–27. [Google Scholar] [CrossRef]
- American Society of Anesthesiologists. ASA Physical Status Classification System. Available online: https://www.asahq.org/standards-and-guidelines/asa-physical-status-classification-system (accessed on 6 June 2022).
- Wolters, U.; Wolf, T.; Stützer, H.; Schröder, T.; Pichlmaier, H. Risk factors, complications, and outcome in surgery: A multivariate analysis. Eur. J. Surg. 1997, 163, 563–568. [Google Scholar] [PubMed]
- Parenti, N.; Reggiani, M.L.; Percudani, D.; Melotti, R.M. Reliability of American Society of Anesthesiologists physical status classification. Indian. J. Anaesth. 2016, 60, 208–214. [Google Scholar] [CrossRef]

| Variables | Training Data (n = 2946) (70%) | Test Data (n = 1266) (30%) |
|---|---|---|
| Age (Mean (SD)) [years] | 76.7 (12.7) | 77.3 (12.8) |
| Sex | ||
| Male | 854 (29.0) | 383 (30.0) |
| Female | 2092 (71.0) | 883 (70.0) |
| Marital Status | ||
| Single | 739 (25.1) | 278 (21.9) |
| Married | 1252 (42.5) | 559 (44.2) |
| Divorced | 300 (10.2) | 134 (10.6) |
| Widowed | 655 (22.2) | 295 (23.3) |
| Body Mass Index | ||
| Normal Body Mass Index | 1220 (41.4) | 524 (41.4) |
| Underweight | 138 (4.7) | 65 (5.1) |
| Overweight | 1179 (40.0) | 505 (39.9) |
| Obese | 409 (13.9) | 172 (13.6) |
| CCI (Categorical Measure) | ||
| 0 | 1284 (43.4) | 554 (43.8) |
| 1 | 769 (26.1) | 324 (25.6) |
| 2 | 391 (13.3) | 183 (14.4) |
| 3 | 226 (7.7) | 92 (7.3) |
| 4+ | 280 (9.5) | 113 (8.9) |
| CCI (Continuous Measure) | ||
| Mean (SD) * | 1 (2) | 1 (2) |
| Median (Q1, Q3) | 1 (0, 2) | 1 (0, 2) |
| ASA-PS Grade | ||
| 1 | 77 (2.6) | 41 (3.2) |
| 2 | 979 (33.2) | 410 (32.4) |
| 3 | 1473 (50.0) | 656 (51.8) |
| 4 | 417 (14.2) | 159 (12.6) |
| ASA-PS Grade (Binary) | ||
| 1 and 2 (Low-risk) | 1056 (35.8) | 451 (35.6) |
| 3 and 4 (High-risk) | 1890 (64.2) | 815 (64.4) |
| Variables | ASA-PS 1 (%) | ASA-PS 2 (%) | ASA-PS 3 (%) | ASA-PS 4 (%) | Total |
|---|---|---|---|---|---|
| CCI—0 | 68 (88.3) | 659 (67.3) | 496 (33.7) | 57 (13.7) | 1280 (43.4) |
| CCI—1 | 3 (3.9) | 197 (20.1) | 463 (31.4) | 106 (25.4) | 769 (26.1) |
| CCI—2 | 1 (1.3) | 62 (6.3) | 243 (16.5) | 85 (20.4) | 391 (13.3) |
| CCI—3 | 5 (6.5) | 33 (3.4) | 123 (8.3) | 65 (15.6) | 226 (7.7) |
| CCI—4+ | 0 (0.0) | 28 (2.9) | 148 (10.1) | 104 (24.9) | 280 (9.5) |
| Total | 77 (100.0) | 979 (100.0) | 1473 (100.0) | 417 (100.0) | 2946 (100.0) |
| Variables | ASA-PS Grade 1 (95% CI) | ASA-PS Grade 2 (95% CI) | ASA-PS Grade 3 (95% CI) | ASA-PS Grade 4 (95% CI) | ASA-PS Grades 3 or 4 (Binary) (95% CI) |
|---|---|---|---|---|---|
| Age (in years) | 0.91 (0.89–0.94) | 0.95 (0.94–0.96) | 1.03 (1.02–1.04) | 1.04 (1.03–1.05) | 1.06 (1.05–1.07) |
| Sex | |||||
| Male | Ref | Ref | Ref | Ref | Ref |
| Female | 1.71 (0.97–3.02) | 1.33 (1.12–1.59) | 0.84 (0.71–0.98) | 0.79 (0.63–0.98) | 0.72 (0.61–0.85) |
| Marital Status | |||||
| Single | Ref | Ref | Ref | Ref | Ref |
| Married | 1.00 (0.59–1.69) | 1.26 (1.05–1.53) | 0.85 (0.71–1.02) | 0.88 (0.66–1.16) | 0.80 (0.66–0.96) |
| Divorced | 1.07 (0.50–2.28) | 1.15 (0.87–1.52) | 0.82 (0.63–1.07) | 1.14 (0.77–1.70) | 0.86 (0.66–1.14) |
| Widowed | 0.24 (0.09–0.63) | 0.43 (0.34–0.56) | 1.42 (1.14–1.75) | 1.98 (1.49–2.64) | 2.51 (1.97–3.21) |
| Body Mass Index | |||||
| Normal Weight | Ref | Ref | Ref | Ref | Ref |
| Underweight | 2.27 (0.97–5.31) | 0.67 (0.45–0.99) | 1.07 (0.75–1.52) | 1.36 (0.85–2.17) | 1.28 (0.88–1.88) |
| Overweight | 1.46 (0.89–2.38) | 1.05 (0.88–1.24) | 0.87 (0.74–1.02) | 1.13 (0.90–1.42) | 0.92 (0.78–1.08) |
| Obese | 0.31 (0.10–1.04) | 0.86 (0.67–1.09) | 1.24 (0.99–1.56) | 0.96 (0.69–1.34) | 1.25 (0.98–1.59) |
| CCI (Categorical Measure) | |||||
| 0 | Ref | Ref | Ref | Ref | Ref |
| 1 | 0.07 (0.02–0.22) | 0.32 (0.27–0.39) | 2.39 (1.99–2.87) | 3.43 (2.45–4.80) | 3.74 (3.08–4.55) |
| 2 | 0.05 (0.01–0.33) | 0.18 (0.13–0.24) | 2.60 (2.06–3.28) | 5.96 (4.17–8.53) | 6.84 (5.11–9.16) |
| 3 | 0.40 (0.16–1.01) | 0.16 (0.11–0.24) | 1.89 (1.42–2.51) | 8.66 (5.85–12.82) | 6.50 (4.51–9.38) |
| 4+ | No Data | 0.10 (0.07–0.16) | 1.77 (1.37–2.30) | 12.68 (8.85–18.17) | 11.83 (7.89–17.75) |
| CCI (Continuous Measure) | |||||
| CCI | 0.35 (0.24–0.53) | 0.55 (0.51–0.59) | 1.12 (1.07–1.17) | 1.52 (1.44–1.61) | 1.94 (1.79–2.10) |
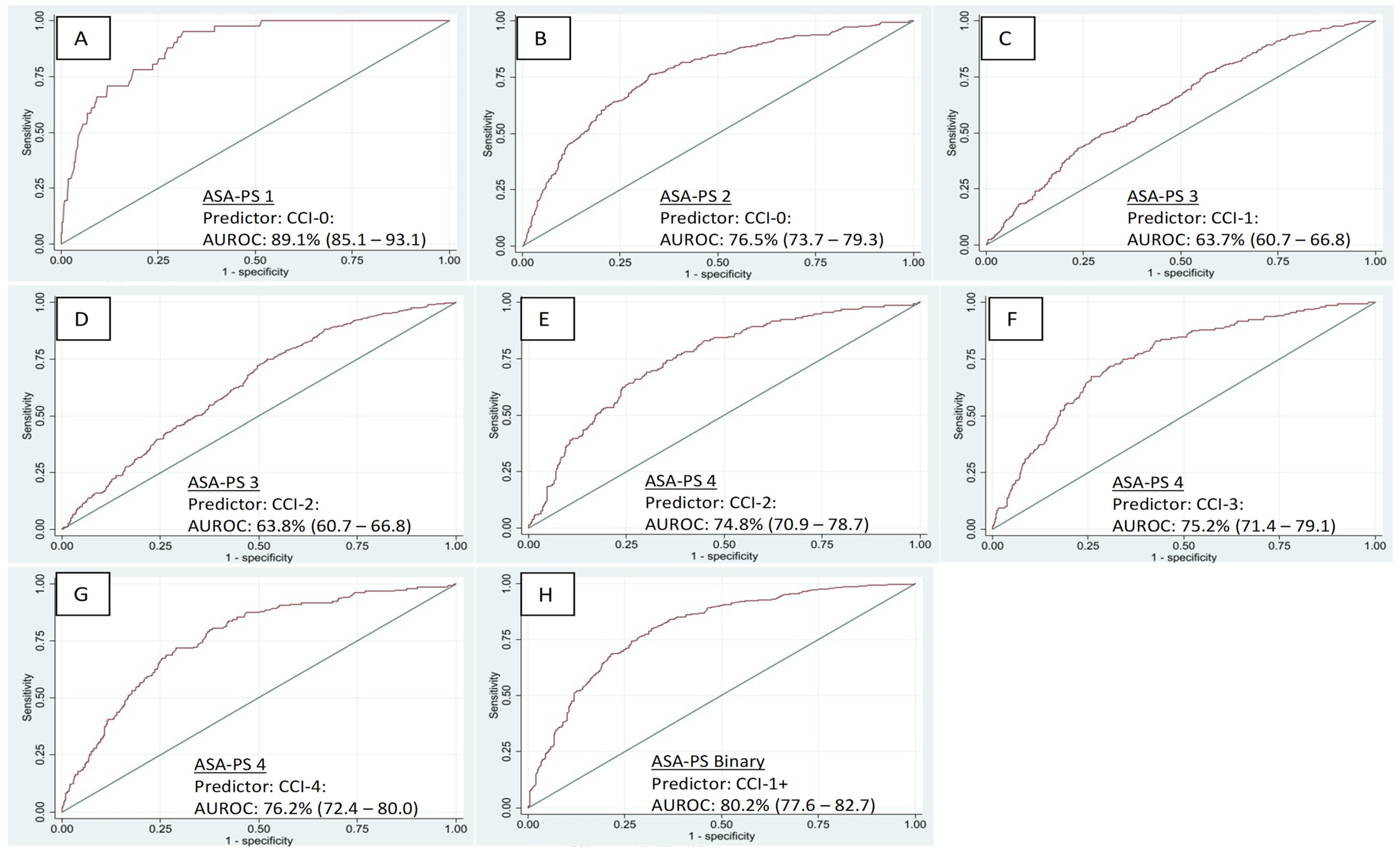
| Predicted ASA-PS Grade | Most Predictive CCI Category | Pseudo R2 (%) | Sensitivity | Specificity | Youden’s Index * | AUROC Training Dataset (%) ** | DeLong’s Test (p-Value) |
|---|---|---|---|---|---|---|---|
| ASA-PS 1 | CCI–0 | 20.50 | 88.8% | 37.7% | 61.9% | 85.2 (80.4–90.0) | N/A |
| ASA-PS 2 | CCI–0 | 15.80 | 68.6% | 58.2% | 43.0% | 76.6 (74.7–88.4) | N/A |
| ASA-PS 3 | CCI–1 | 4.36 | 51.1% | 61.7% | 22.1% | 64.7 (62.7–66.7) | 0.587 (CCI-2 vs. CCI-1) |
| ASA-PS 3 | CCI–2 | 3.96 | 49.6% | 62.6% | 21.9% | 64.4 (62.4–66.4) | |
| ASA-PS 4 | CCI–2 | 6.65 | 60.2% | 57.4% | 28.1% | 68.7 (66.0–71.3) | <0.001 (CCI-4 vs. CCI-2) |
| ASA-PS 4 | CCI–3 | 7.42 | 60.0% | 58.3% | 29.9% | 70.3 (67.7–72.9) | 0.047 (CCI-4 vs. CCI-3) |
| ASA-PS 4 | CCI–4+ | 9.71 | 60.7% | 60.4% | 34.9% | 72.6 (70.1–75.2) | |
| ASA-PS Binary | CCI 1–4+ vs. CCI–0 (ref) | 20.37 | 60.0% | 69.3% | 46.0% | 79.5 (77.7–81.2) | N/A |
| Parameter | Variable | Regression Coefficient | Standard Error | p-Value | 95% CI Lower | 95% CI Upper |
|---|---|---|---|---|---|---|
| Threshold | ASA-PS Grade 1 | −3.004 | 0.998 | 0.003 | −4.960 | −1.048 |
| ASA-PS Grade 2 | −7.385 | 0.341 | <0.001 | −6.010 | −4.761 | |
| ASA-PS Grade 3 | −13.265 | 0.456 | <0.001 | −12.784 | −9.747 | |
| Predictors | CCI Categories | |||||
| 0.662 | 0.176 | <0.001 | 0.318 | 1.006 | ||
| Age at Injury | ||||||
| Age | 0.095 | 0.015 | <0.001 | 0.066 | 0.124 | |
| Sex | ||||||
| Male | Ref | |||||
| Female | −0.908 | 0.304 | 0.003 | −1.504 | −0.312 | |
| Marital Status | ||||||
| Single | Ref | |||||
| Married | 0.072 | 0.274 | 0.793 | −0.465 | 0.609 | |
| Divorced | −0.376 | 0.398 | 0.345 | −1.157 | 0.405 | |
| Widowed | 0.306 | 0.530 | 0.563 | −0.732 | 1.345 | |
| BMI Categories | ||||||
| Normal Weight | Ref | |||||
| Underweight | −0.997 | 0.459 | 0.030 | −1.898 | −0.097 | |
| Overweight | 0.173 | 0.263 | 0.510 | −0.342 | 0.689 | |
| Obese | 1.841 | 0.618 | 0.003 | 0.631 | 3.051 | |
| Probability of ASA-PS 1 | ||||||
| Probability of ASA-PS 2 | ||||||
| Probability of ASA-PS 3 | ||||||
| Probability of ASA-PS 4 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyemi, O.J.; Meltzer-Bruhn, A.; Esper, G.; DiMaggio, C.; Grudzen, C.; Chodosh, J.; Konda, S. Crosswalk between Charlson Comorbidity Index and the American Society of Anesthesiologists Physical Status Score for Geriatric Trauma Assessment. Healthcare 2023, 11, 1137. https://doi.org/10.3390/healthcare11081137
Adeyemi OJ, Meltzer-Bruhn A, Esper G, DiMaggio C, Grudzen C, Chodosh J, Konda S. Crosswalk between Charlson Comorbidity Index and the American Society of Anesthesiologists Physical Status Score for Geriatric Trauma Assessment. Healthcare. 2023; 11(8):1137. https://doi.org/10.3390/healthcare11081137
Chicago/Turabian StyleAdeyemi, Oluwaseun John, Ariana Meltzer-Bruhn, Garrett Esper, Charles DiMaggio, Corita Grudzen, Joshua Chodosh, and Sanjit Konda. 2023. "Crosswalk between Charlson Comorbidity Index and the American Society of Anesthesiologists Physical Status Score for Geriatric Trauma Assessment" Healthcare 11, no. 8: 1137. https://doi.org/10.3390/healthcare11081137
APA StyleAdeyemi, O. J., Meltzer-Bruhn, A., Esper, G., DiMaggio, C., Grudzen, C., Chodosh, J., & Konda, S. (2023). Crosswalk between Charlson Comorbidity Index and the American Society of Anesthesiologists Physical Status Score for Geriatric Trauma Assessment. Healthcare, 11(8), 1137. https://doi.org/10.3390/healthcare11081137






