Efficiency of Primary Health Services in the Greek Public Sector: Evidence from Bootstrapped DEA/FDH Estimators
Abstract
:1. Introduction
1.1. Related Studies
1.2. Application Context
2. Materials and Methods
2.1. Methods
2.1.1. Data Envelopment Analysis (DEA)
- ▪
- Assumption of Free Disposability of Inputs and Outputs: If an activity belongs to P, then any activity with and will also belong to P.
- ▪
- Assumption of Convexity of Set P: Any weighted average of activities in P also belongs to P
- ▪
- Assumption of the Type of Returns to Scale: If an activity belongs to P then the activity also belongs to P, where
- i.
- under the assumption of non-increasing returns to scale (NIRS)
- ii.
- under the assumption of non-decreasing returns to scale (NDRS)
- iii.
- under the assumption of constant returns to scale (CRS)
2.1.2. Free Disposal Hull (FDH)
2.1.3. Peer Units
2.1.4. Super Efficiency
2.1.5. Weighted Average Efficiency Score
2.1.6. Outliers
2.1.7. Returns to Scale Assumption
2.1.8. Scale Efficiency: Most Productive Scale Size (MPSS)
2.1.9. Bootstrap
2.2. Software Tools
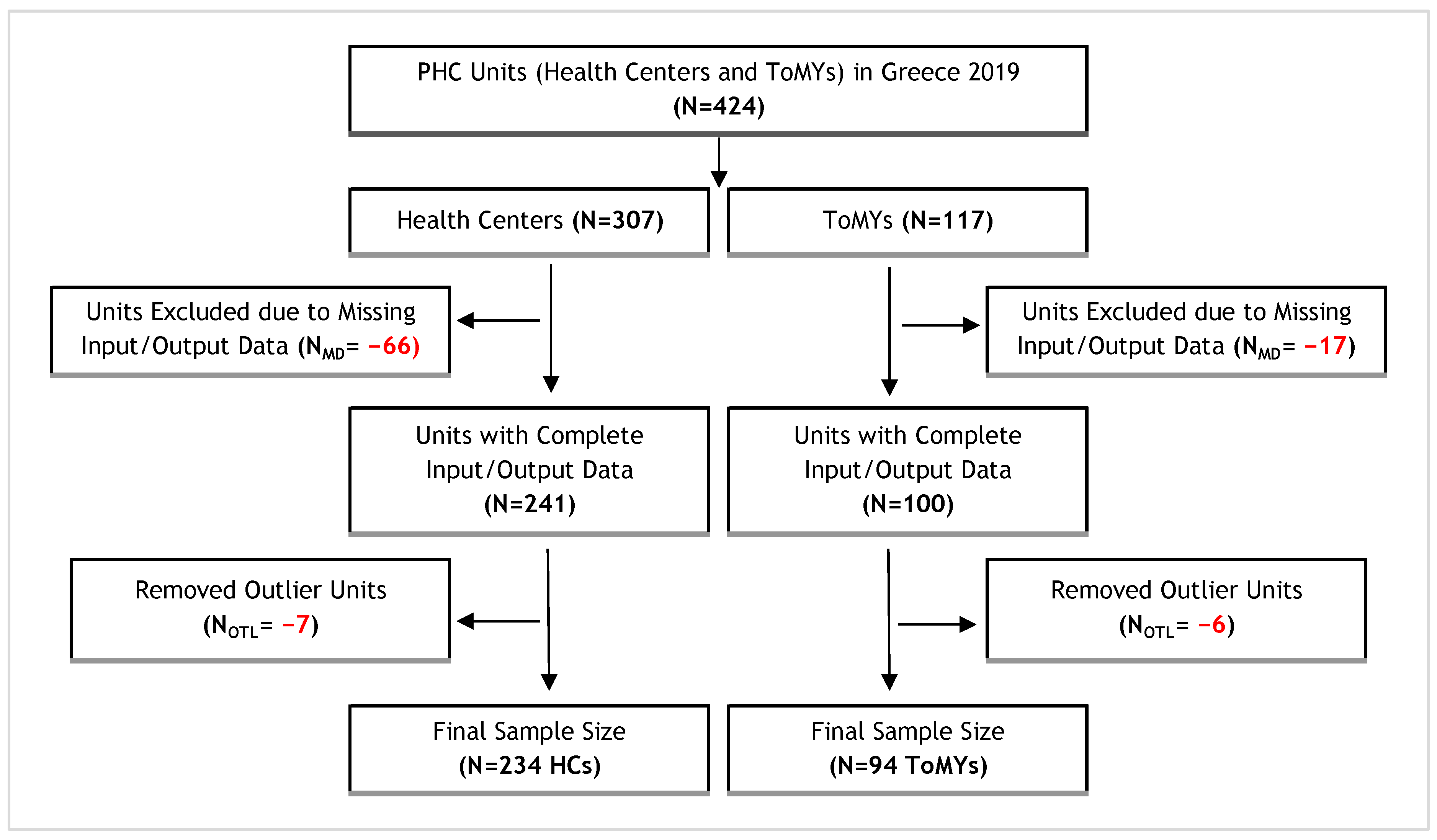
2.3. Data and Model Specification
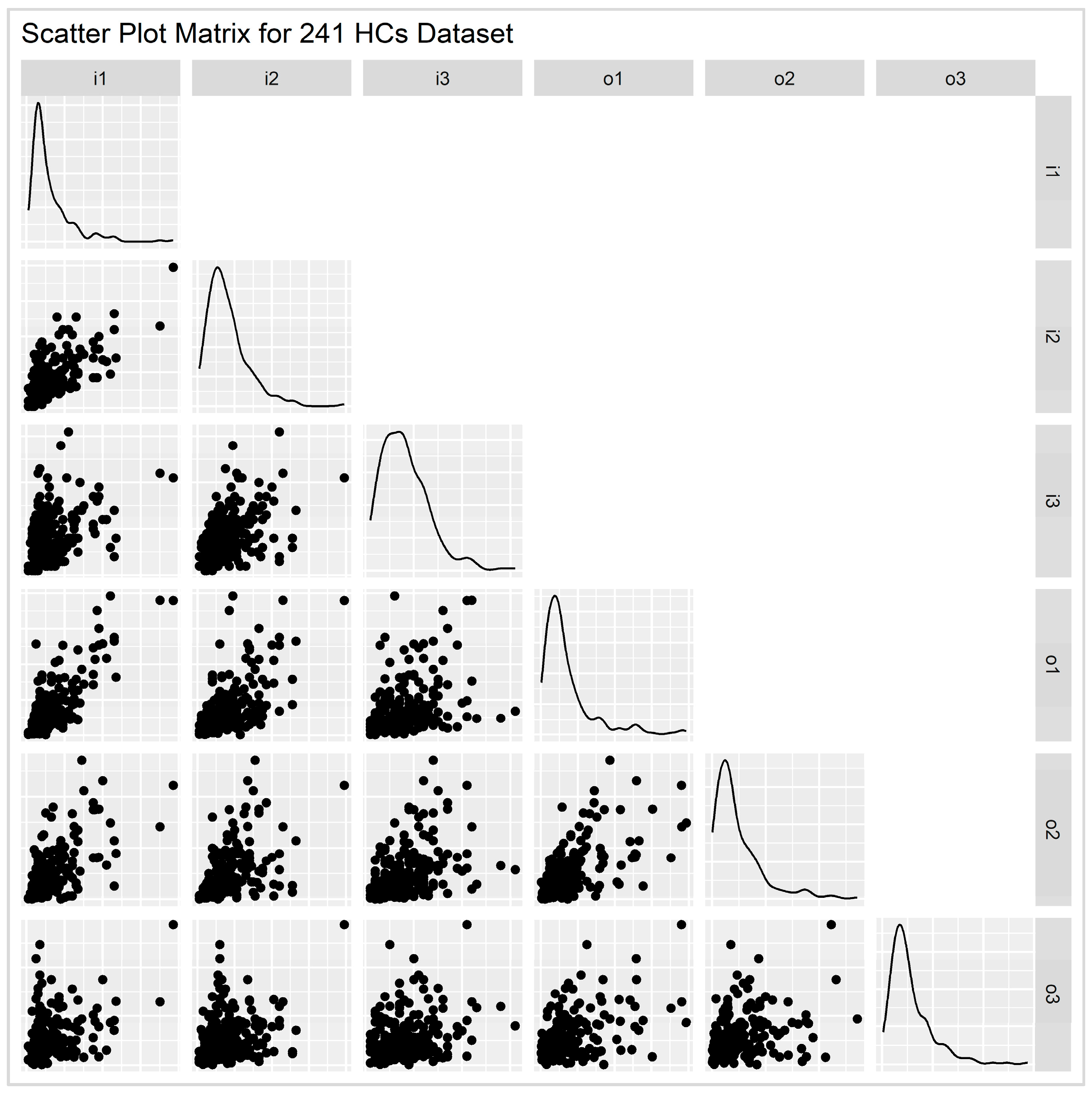
2.3.1. Sample
2.3.2. Inputs–Outputs
2.3.3. Discriminatory Power
2.3.4. Orientation
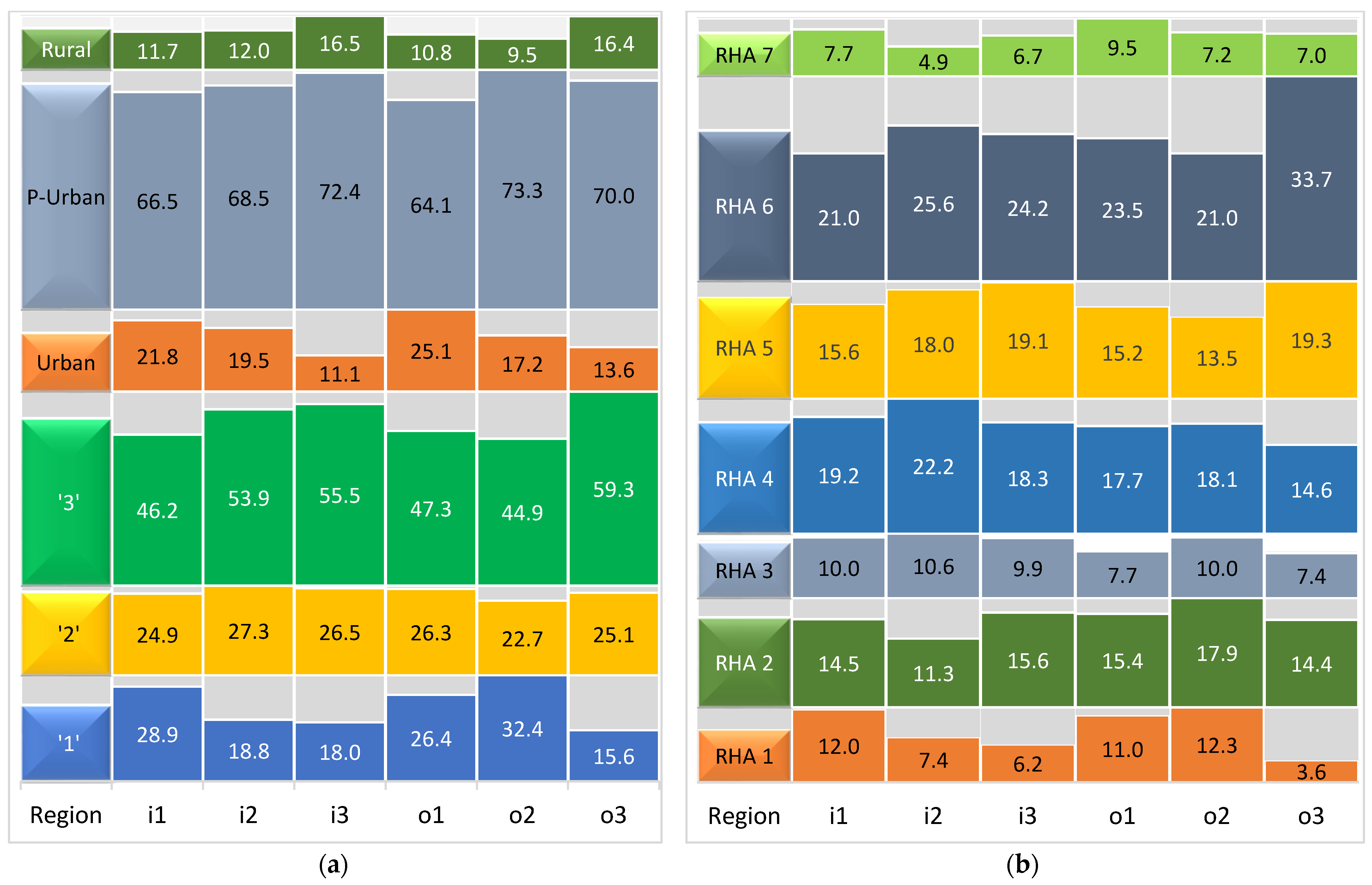
2.4. Classification by Urbanization Levels
3. Results
3.1. Input–Output Summary Statistics
3.2. Global Returns to Scale
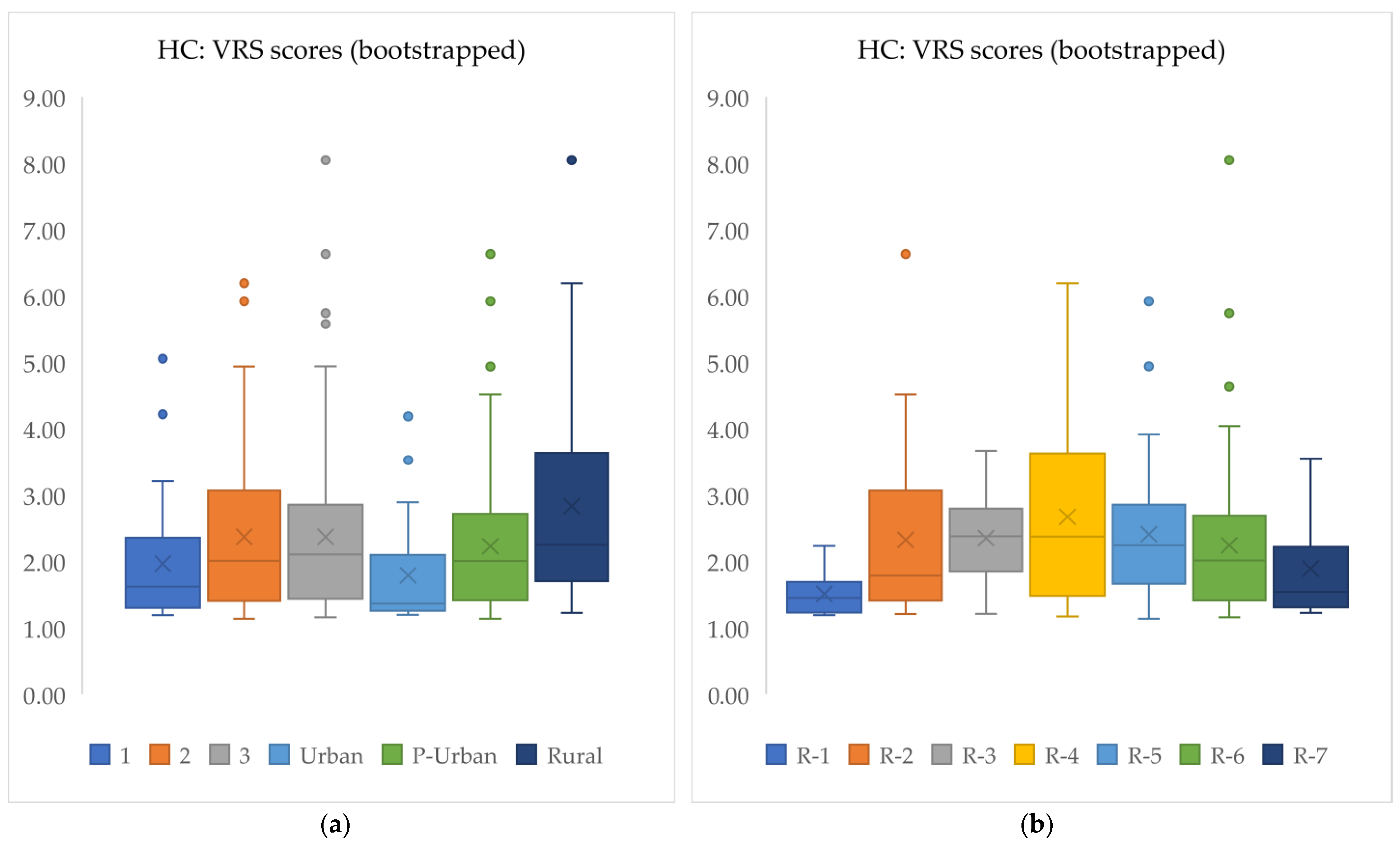
3.3. VRS Results
3.4. Super-Efficiency, Benchmarks, and Peer Counts
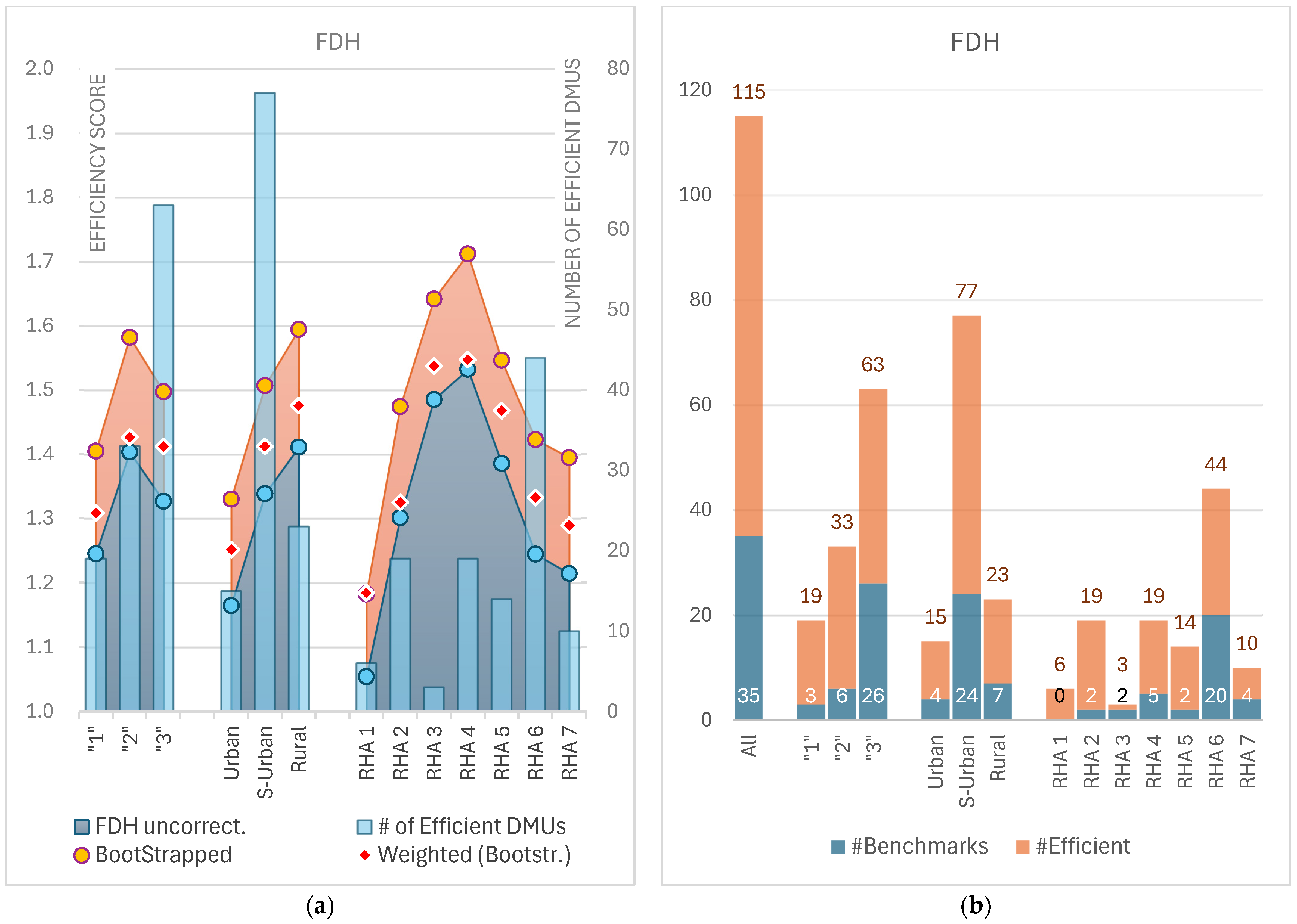
3.5. FDH Results
3.6. Kruskal–Wallis Test
3.7. Scale Efficiency
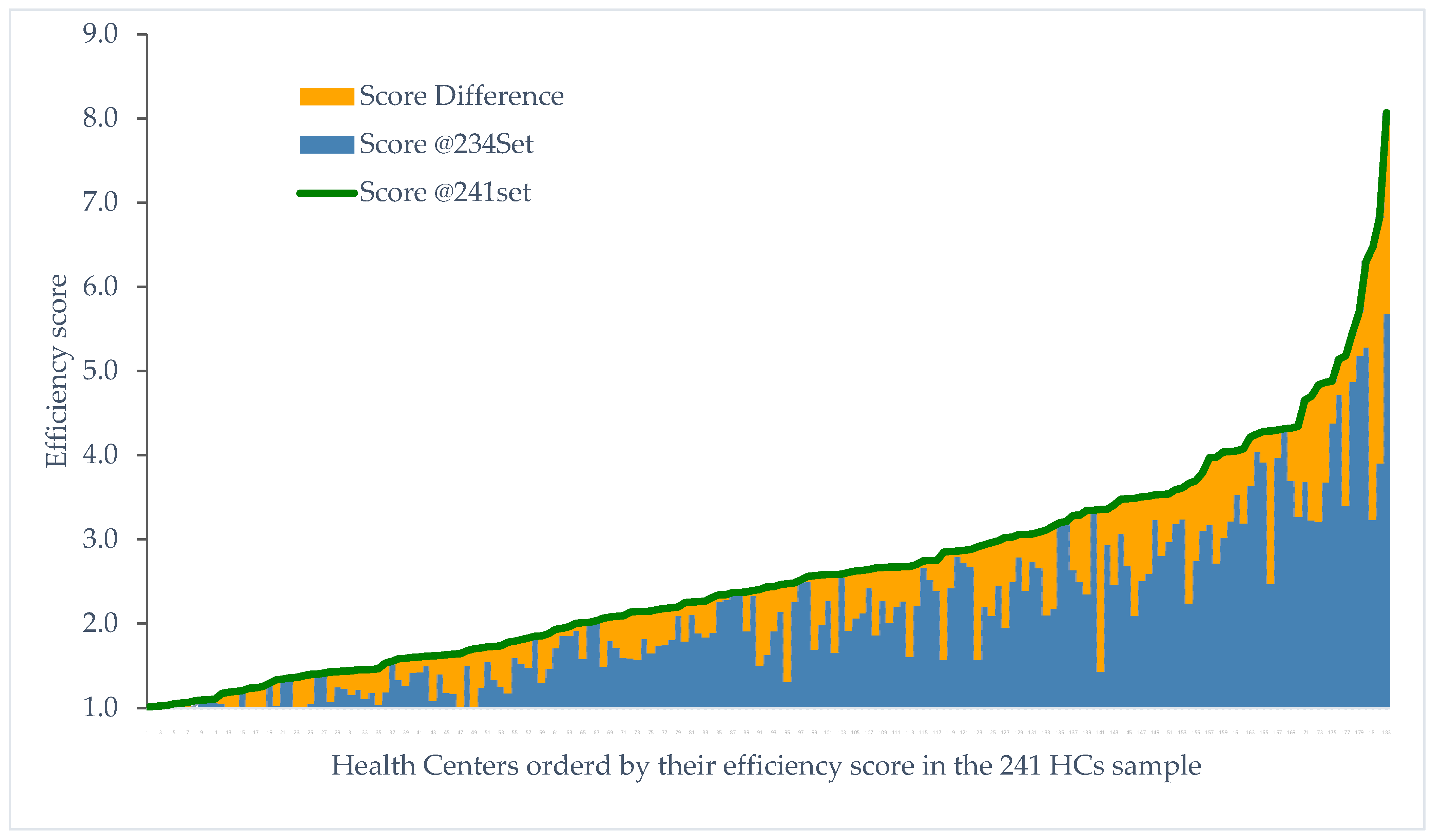
3.8. Outlier Influence: Bias
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Declaration of Astana. Available online: https://www.who.int/publications/i/item/WHO-HIS-SDS-2018.61 (accessed on 5 October 2024).
- Primary Health Care. Available online: https://www.who.int/news-room/fact-sheets/detail/primary-health-care (accessed on 4 October 2024).
- World Health Organization. Building the Economic Case for Primary Health Care: A Scoping Review. Available online: https://www.who.int/publications/i/item/WHO-HIS-SDS-2018.48 (accessed on 5 October 2024).
- Kontodimopoulos, N.; Moschovakis, G.; Aletras, V.H.; Niakas, D. The effect of environmental factors on technical and scale efficiency of primary health care providers in Greece. Cost Eff. Resour. Alloc. 2007, 5, 14. [Google Scholar] [CrossRef]
- Lionis, C.; Symvoulakis, E.K.; Markaki, A.; Vardavas, C.; Papadakaki, M.; Daniilidou, N.; Souliotis, K.; Kyriopoulos, I. Integrated primary health care in Greece, a missing issue in the current health policy agenda: A systematic review. Int. J. Integr. Care 2009, 9, e88. [Google Scholar] [CrossRef] [PubMed]
- Oikonomidou, E.; Anastasiou, F.; Dervas, D.; Patri, F.; Karaklidis, D.; Moustakas, P.; Andreadou, N.; Mantzanas, E.; Merkouris, B. Rural primary care in Greece: Working under limited resources. Int. J. Qual. Health Care J. Int. Soc. Qual. Health Care 2010, 22, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Economou, C. Greece: Health system review. Health Syst. Transit. 2010, 12, 1–177. [Google Scholar] [PubMed]
- Myloneros, T.; Sakellariou, D. The effectiveness of primary health care reforms in Greece towards achieving universal health coverage: A scoping review. BMC Health Serv. Res. 2021, 21, 628. [Google Scholar] [CrossRef]
- Lionis, C.; Symvoulakis, E.K.; Markaki, A.; Petelos, E.; Papadakis, S.; Sifaki-Pistolla, D.; Papadakakis, M.; Souliotis, K.; Tziraki, C. Integrated people-centred primary health care in Greece: Unravelling Ariadne’s thread. Prim. Health Care Res. Dev. 2019, 20, e113. [Google Scholar] [CrossRef]
- Kondilis, E.; Smyrnakis, E.; Gavana, M.; Giannakopoulos, S.; Zdoukos, T.; Iliffe, S.; Benos, A. Economic crisis and primary care reform in Greece: Driving the wrong way? Br. J. Gen. Pract. J. R. Coll. Gen. Pract. 2012, 62, 264–265. [Google Scholar] [CrossRef]
- Niakas, D. Greek economic crisis and health care reforms: Correcting the wrong prescription. Int. J. Health Serv. 2013, 43, 597–602. [Google Scholar] [CrossRef]
- Hellenic Republic. Law 3918: Structural Changes in the Health System and Other Provisions; Hellenic Republic: Athens, Greece, 2011.
- Hellenic Republic. Law 4238: Primary National Health Network (PEDY), Change of EOPYY’s Purpose and Other Provisions; Hellenic Republic: Athens, Greece, 2014; Volume 38, p. 28.
- OECD; European Observatory on Health Systems and Policies. State of Health in the EU. In Greece: Country Health Profile 2017; OECD: Paris, France, 2017. [Google Scholar] [CrossRef]
- Karaferis, D.C.; Niakas, D.A.; Balaska, D.; Flokou, A. Valuing Outpatients’ Perspective on Primary Health Care Services in Greece: A Cross-Sectional Survey on Satisfaction and Personal-Centered Care. Healthcare 2024, 12, 1427. [Google Scholar] [CrossRef]
- Hellenic Republic. Law 4486: Reform of Primary Health Care, Urgent Regulations of the Ministry of Health and Other Provisions; Hellenic Republic: Athens, Greece, 2017; Volume 115.
- Hellenic Statistical Authority. Census of Health Centers and Other Units Providing Primary Health Care Services: Year 2019. Available online: https://www.statistics.gr/documents/20181/a4d681a4-f8e2-df6f-95b9-3569321f0ce8 (accessed on 5 October 2024).
- Hellenic Statistical Authority. Hospitals and Local Health Centres (Beds, Staff, Equipment), 2010–2018. Available online: https://www.statistics.gr/en/statistics/-/publication/SHE06/2018 (accessed on 5 October 2024).
- Hellenic Statistical Authority. System of Health Accounts (SHA) of Year 2015. Available online: https://www.statistics.gr/en/statistics/-/publication/SHE35/2015 (accessed on 5 October 2024).
- Hellenic Statistical Authority. System of Health Accounts (SHA) of Year 2019. Available online: https://www.statistics.gr/en/statistics/-/publication/SHE35/2019 (accessed on 5 October 2024).
- Hardouvelis, G.A.; Karalas, G.; Karanastasis, D.; Samartzis, P. Economic Policy Uncertainty, Political Uncertainty and the Greek Economic Crisis. SSRN Electron. J. 2018, 100–104. [Google Scholar] [CrossRef]
- Economou, C.; Kaitelidou, D.; Kentikelenis, A.; Maresso, A.; Sissouras, A. The impact of the crisis on the health system and health in Greece. In Economic Crisis, Health Systems and Health in Europe: Country Experience [Internet]; European Observatory on Health Systems and Policies: Brussels, Belgium, 2015. Available online: https://www.ncbi.nlm.nih.gov/books/NBK447857/ (accessed on 5 October 2024).
- Hollingsworth, B. The measurement of efficiency and productivity of health care delivery. Health Econ. 2008, 17, 1107–1128. [Google Scholar] [CrossRef] [PubMed]
- Cantor, V.J.M.; Poh, K.L. Integrated Analysis of Healthcare Efficiency: A Systematic Review. J. Med. Syst. 2018, 42, 8. [Google Scholar] [CrossRef]
- Flokou, A.; Kontodimopoulos, N.; Niakas, D. Employing post-DEA Cross-evaluation and Cluster Analysis in a Sample of Greek NHS Hospitals. J. Med. Syst. 2011, 35, 1001–1014. [Google Scholar] [CrossRef]
- Aletras, V.; Kontodimopoulos, N.; Zagouldoudis, A.; Niakas, D. The short-term effect on technical and scale efficiency of establishing regional health systems and general management in Greek NHS hospitals. Health Policy Amst. Neth. 2007, 83, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Kohl, S.; Schoenfelder, J.; Fügener, A.; Brunner, J.O. The use of Data Envelopment Analysis (DEA) in healthcare with a focus on hospitals. Health Care Manag. Sci. 2019, 22, 245–286. [Google Scholar] [CrossRef]
- Flokou, A.; Aletras, V.; Niakas, D. Awindow-DEA based efficiency evaluation of the public hospital sector in Greece during the 5-year economic crisis. PLoS ONE 2017, 12, e0177946. [Google Scholar] [CrossRef] [PubMed]
- Flokou, A.; Aletras, V.; Niakas, D. Decomposition of potential efficiency gains from hospital mergers in Greece. Health Care Manag. Sci. 2017, 20, 467–484. [Google Scholar] [CrossRef]
- Pelone, F.; Kringos, D.S.; Romaniello, A.; Archibugi, M.; Salsiri, C.; Ricciardi, W. Primary care efficiency measurement using data envelopment analysis: A systematic review. J. Med. Syst. 2015, 39, 156. [Google Scholar] [CrossRef]
- Marathe, S.; Wan, T.T.H.; Zhang, J.; Sherin, K. Factors influencing community health centers’ efficiency: A latent growth curve modeling approach. J. Med. Syst. 2007, 31, 365–374. [Google Scholar] [CrossRef]
- Neri, M.; Cubi-Molla, P.; Cookson, G. Approaches to Measure Efficiency in Primary Care: A Systematic Literature Review. Appl. Health Econ. Health Policy 2022, 20, 19–33. [Google Scholar] [CrossRef]
- Zakowska, I.; Godycki-Cwirko, M. Data envelopment analysis applications in primary health care: A systematic review. Fam. Pract. 2020, 37, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Oikonomou, N.; Tountas, Y.; Mariolis, A.; Souliotis, K.; Athanasakis, K.; Kyriopoulos, J. Measuring the efficiency of the Greek rural primary health care using a restricted DEA model; the case of southern and western Greece. Health Care Manag. Sci. 2016, 19, 313–325. [Google Scholar] [CrossRef] [PubMed]
- Zavras, A.I.; Tsakos, G.; Economou, C.; Kyriopoulos, J. Using DEA to evaluate efficiency and formulate policy within a Greek national primary health care network. Data Envelopment Analysis. J. Med. Syst. 2002, 26, 285–292. [Google Scholar] [CrossRef]
- Mitropoulos, P.; Kounetas, K.; Mitropoulos, I. Factors affecting primary health care centers’ economic and production efficiency. Ann. Oper. Res. 2016, 247, 807–822. [Google Scholar] [CrossRef]
- Kontodimopoulos, N.; Nanos, P.; Niakas, D. Balancing efficiency of health services and equity of access in remote areas in Greece. Health Policy Amst. Neth. 2006, 76, 49–57. [Google Scholar] [CrossRef]
- European Commission, Statistical Office of the European Union, Eurostat. Urban Europe: Statistics on Cities, Towns and Suburbs: 2016 Edition; 2016. Available online: https://data.europa.eu/doi/10.2785/91120 (accessed on 5 October 2024).
- Eurostat. Rural Development. Methodology. Available online: https://ec.europa.eu/eurostat/web/rural-development/methodology (accessed on 5 October 2024).
- Food and Agriculture Organization of the United Nations. Guidelines on Defining Rural Areas and Compiling Indicators. Available online: https://openknowledge.fao.org/server/api/core/bitstreams/5fc6bb8d-32a7-4c5e-ac71-81c1f19d13e4/content (accessed on 5 October 2024).
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. Gen. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Bogetoft, P.; Otto, L. Production Models and Technology. In Benchmarking with DEA, SFA, and R; Bogetoft, P., Otto, L., Eds.; Springer: New York, NY, USA, 2011; pp. 57–80. [Google Scholar]
- Bogetoft, P.; Otto, L. Data Envelopment Analysis DEA. In Benchmarking with DEA, SFA, and R; Bogetoft, P., Otto, L., Eds.; Springer: New York, NY, USA, 2011; pp. 81–113. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. The CCR Model and Production Correspondence. In Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Cooper, W.W., Seiford, L.M., Tone, K., Eds.; Springer: New York, NY, USA, 2007; pp. 41–85. [Google Scholar]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Deprins, D.; Simar, L.; Tulkens, H. Measuring Labor-Efficiency in Post Offices. LIDAM Reprint CORE. 1984. Available online: https://ideas.repec.org//p/cor/louvrp/571.html (accessed on 10 October 2024).
- Tulkens, H. On FDH efficiency analysis: Some methodological issues and applications to retail banking, courts, and urban transit. J. Product. Anal. 1993, 4, 183–210. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Adler, N.; Friedman, L.; Sinuany-Stern, Z. Review of ranking methods in the data envelopment analysis context. Eur. J. Oper. Res. 2002, 140, 249–265. [Google Scholar] [CrossRef]
- The Measurement of Efficiency. In Advanced Robust and Nonparametric Methods in Efficiency Analysis: Methodology and Applications; Daraio, C.; Simar, L. (Eds.) Springer: Boston, MA, USA, 2007; pp. 13–42. [Google Scholar]
- Fare, R.; Zelenyuk, V. On aggregate Farrell efficiencies. Eur. J. Oper. Res. 2003, 146, 615–620. [Google Scholar] [CrossRef]
- Wilson, P.W. Detecting Outliers in Deterministic Nonparametric Frontier Models with Multiple Outputs. J. Bus. Econ. Stat. 1993, 11, 319–323. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Non-parametric tests of returns to scale. Eur. J. Oper. Res. 2002, 139, 115–132. [Google Scholar] [CrossRef]
- Banker, R.D. Estimating most productive scale size using data envelopment analysis. Eur. J. Oper. Res. 1984, 17, 35–44. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Sensitivity Analysis of Efficiency Scores: How to Bootstrap in Nonparametric Frontier Models. Manag. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Statistical Inference in Nonparametric Frontier Models: The State of the Art. J. Product. Anal. 2000, 13, 49–78. [Google Scholar] [CrossRef]
- Murillo-Zamorano, L.R.; Petraglia, C. Technical efficiency in primary health care: Does quality matter? Eur. J. Health Econ. HEPAC Health Econ. Prev. Care 2011, 12, 115–125. [Google Scholar] [CrossRef]
- da Encarnação Filipe Amado, C.A.; Santos, S.P.D. Challenges for performance assessment and improvement in primary health care: The case of the Portuguese health centres. Health Policy Amst. Neth. 2009, 91, 43–56. [Google Scholar] [CrossRef]
- González-de-Julián, S.; Barrachina-Martínez, I.; Vivas-Consuelo, D.; Bonet-Pla, Á.; Usó-Talamantes, R. Data Envelopment Analysis Applications on Primary Health Care Using Exogenous Variables and Health Outcomes. Sustainability 2021, 13, 1337. [Google Scholar] [CrossRef]
- Capeletti, N.M.; Amado, C.A.F.; Santos, S.P. Performance assessment of primary health care services using data envelopment analysis and the quality-adjusted malmquist index. J. Oper. Res. Soc. 2024, 75, 361–377. [Google Scholar] [CrossRef]
- Miclos, P.V.; Calvo, M.C.M.; Colussi, C.F. Evaluation of the performance of actions and outcomes in primary health care. Rev. Saude Publica 2017, 51, 86. [Google Scholar] [CrossRef]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Santamato, V.; Tricase, C.; Faccilongo, N.; Marengo, A.; Pange, J. Healthcare performance analytics based on the novel PDA methodology for assessment of efficiency and perceived quality outcomes: A machine learning approach. Expert Syst. Appl. 2024, 252, 124020. [Google Scholar] [CrossRef]
- Adler, N.; Golany, B. Evaluation of deregulated airline networks using data envelopment analysis combined with principal component analysis with an application to Western Europe. Eur. J. Oper. Res. 2001, 132, 260–273. [Google Scholar] [CrossRef]
- Pastor, J.T. Chapter 3 Translation invariance in data envelopment analysis: A generalization. Ann. Oper. Res. 1996, 66, 91–102. [Google Scholar] [CrossRef]
- Pereira, M.A.; Dinis, D.C.; Ferreira, D.C.; Figueira, J.R.; Marques, R.C. A network Data Envelopment Analysis to estimate nations’ efficiency in the fight against SARS-CoV-2. Expert Syst. Appl. 2022, 210, 118362. [Google Scholar] [CrossRef]
- Kirigia, J.M.; Sambo, L.G.; Renner, A.; Alemu, W.; Seasa, S.; Bah, Y. Technical efficiency of primary health units in Kailahun and Kenema districts of Sierra Leone. Int. Arch. Med. 2011, 4, 15. [Google Scholar] [CrossRef]
- Adang, E.M.M.; Gerritsma, A.; Nouwens, E.; van Lieshout, J.; Wensing, M. Efficiency of the implementation of cardiovascular risk management in primary care practices: An observational study. Implement. Sci. IS 2016, 11, 67. [Google Scholar] [CrossRef]
- González-de-Julián, S.; Vivas-Consuelo, D.; Barrachina-Martínez, I. Modelling efficiency in primary healthcare using the DEA methodology: An empirical analysis in a healthcare district. BMC Health Serv. Res. 2024, 24, 982. [Google Scholar] [CrossRef] [PubMed]
- Beiter, D.; Koy, S.; Flessa, S. Improving the technical efficiency of public health centers in Cambodia: A two-stage data envelopment analysis. BMC Health Serv. Res. 2023, 23, 912. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Valdivia, M.T.; Maturana, S.; Salvo-Garrido, S. A multiple stage approach for performance improvement of primary healthcare practice. J. Med. Syst. 2011, 35, 1015–1028. [Google Scholar] [CrossRef] [PubMed]
- Mariolis, A.; Mihas, C.; Alevizos, A.; Mariolis-Sapsakos, T.; Marayiannis, K.; Papathanasiou, M.; Gizlis, V.; Karanasios, D.; Merkouris, B. Comparison of primary health care services between urban and rural settings after the introduction of the first urban health centre in Vyronas, Greece. BMC Health Serv. Res. 2008, 8, 124. [Google Scholar] [CrossRef]
- Economou, C. Barriers and Facilitating Factors in Access to Health Services in Greece. Available online: https://www.who.int/publications/m/item/barriers-and-facilitating-factors-in-access-to-health-services-in-greece (accessed on 5 October 2024).
- Bogetoft, P.; Otto, L. Additional Topics in DEA. In Benchmarking with DEA, SFA, and R; Bogetoft, P., Otto, L., Eds.; Springer: New York, NY, USA, 2011; pp. 115–153. [Google Scholar]
- Simou, E.; Karamagioli, E.; Roumeliotou, A. Reinventing primary health care in the Greece of austerity: The role of health-care workers. Prim. Health Care Res. Dev. 2015, 16, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Dresios, C.; Rachiotis, G.; Symvoulakis, E.K.; Rousou, X.; Papagiannis, D.; Mouchtouri, V.; Hadjichristodoulou, C. Nationwide Epidemiological Study of Knowledge, Attitudes, and Practices Study of Greek General Practitioners Related to Screening. Int. J. Prev. Med. 2019, 10, 199. [Google Scholar] [CrossRef]
- World Health Organization. Monitoring and Documenting Systemic and Health Effects of Health Reforms in Greece: Assessment Report. Available online: https://iris.who.int/handle/10665/346262 (accessed on 5 October 2024).
- Peritogiannis, V.; Manthopoulou, T.; Gogou, A.; Mavreas, V. Mental Healthcare Delivery in Rural Greece: A 10-year Account of a Mobile Mental Health Unit. J. Neurosci. Rural Pract. 2017, 8, 556–561. [Google Scholar] [CrossRef]
- Kampouraki, M.; Paraskevopoulos, P.; Fachouri, E.; Terzoudis, S.; Karanasios, D. Building Strong Primary Healthcare Systems in Greece. Cureus 2023, 15, e41333. [Google Scholar] [CrossRef]
- Sbarouni, V.; Petelos, E.; Kamekis, A.; Tzagkarakis, S.I.; Symvoulakis, E.K.; Lionis, C. Discussing issues of health promotion and research in the context of primary care during the ongoing austerity period: An exploratory analysis from two regions in Greece. Med. Pharm. Rep. 2020, 93, 69–74. [Google Scholar] [CrossRef]
- Tountas, Y.; Karnaki, P.; Pavi, E.; Souliotis, K. The “unexpected” growth of the private health sector in Greece. Health Policy Amst. Neth. 2005, 74, 167–180. [Google Scholar] [CrossRef]
- Oikonomou, N.; Tountas, Y.; Kyriopoulos, J. The need for measurement of efficiency in Greek primary healthcare: The case for rural Southern and Western Greece. Appl. Health Econ. Health Policy 2012, 10, 143–144. [Google Scholar] [CrossRef]
- OECD; European Observatory on Health Systems and Policies. State of Health in the EU. In Greece: Country Health Profile 2021; OECD: Paris, France, 2021. [Google Scholar] [CrossRef]
- Kringos, D.; Boerma, W.; Bourgueil, Y.; Cartier, T.; Dedeu, T.; Hasvold, T.; Hutchinson, A.; Lember, M.; Oleszczyk, M.; Rotar Pavlic, D.; et al. The strength of primary care in Europe: An international comparative study. Br. J. Gen. Pract. J. R. Coll. Gen. Pract. 2013, 63, e742–e750. [Google Scholar] [CrossRef] [PubMed]
- Sifaki-Pistolla, D.; Chatzea, V.-E.; Markaki, A.; Kritikos, K.; Petelos, E.; Lionis, C. Operational integration in primary health care: Patient encounters and workflows. BMC Health Serv. Res. 2017, 17, 788. [Google Scholar] [CrossRef] [PubMed]
- Moran, V.; Suhrcke, M.; Nolte, E. Exploring the association between primary care efficiency and health system characteristics across European countries: A two-stage data envelopment analysis. BMC Health Serv. Res. 2023, 23, 1348. [Google Scholar] [CrossRef] [PubMed]
- Blöndal, B.; Ásgeirsdóttir, T.L. Costs and efficiency of gatekeeping under varying numbers of general practitioners. Int. J. Health Plann. Manag. 2019, 34, 140–156. [Google Scholar] [CrossRef] [PubMed]
- Tsimtsiou, Z.; Fragkoulis, E.; Koupidis, S.; Theodorakis, P. World Health Organization. Greece: Introducing Paperless, Remote ePRESCRIPTION—A Game-Changer for Primary Care Services (2021). Available online: https://www.who.int/europe/publications/m/item/greece-introducing-paperless-remote-eprescription-a-game-changer-for-primary-care-services-(2021) (accessed on 5 October 2024).
- Tsampouri, E.; Kapetaniou, K.; Missiou, A.; Bakola, M.; Willems, S.; Van Poel, E.; Tatsioni, A. Measures during the COVID-19 pandemic in public primary health care in Greece: Is there still a missing link to universal health coverage? BMC Prim. Care 2024, 24, 287. [Google Scholar] [CrossRef]
- Michalaki, F.; Triantafillopoulou, K.M.; Pagkozidis, I.; Tirodimos, I.; Dardavesis, T.; Tsimtsiou, Z. The impact of COVID-19 pandemic on Primary Health Care through “health providers” eyes’: A qualitative study of focus groups and individual interviews in Greece. Eur. J. Gen. Pract. 2024, 30, 2382218. [Google Scholar] [CrossRef]
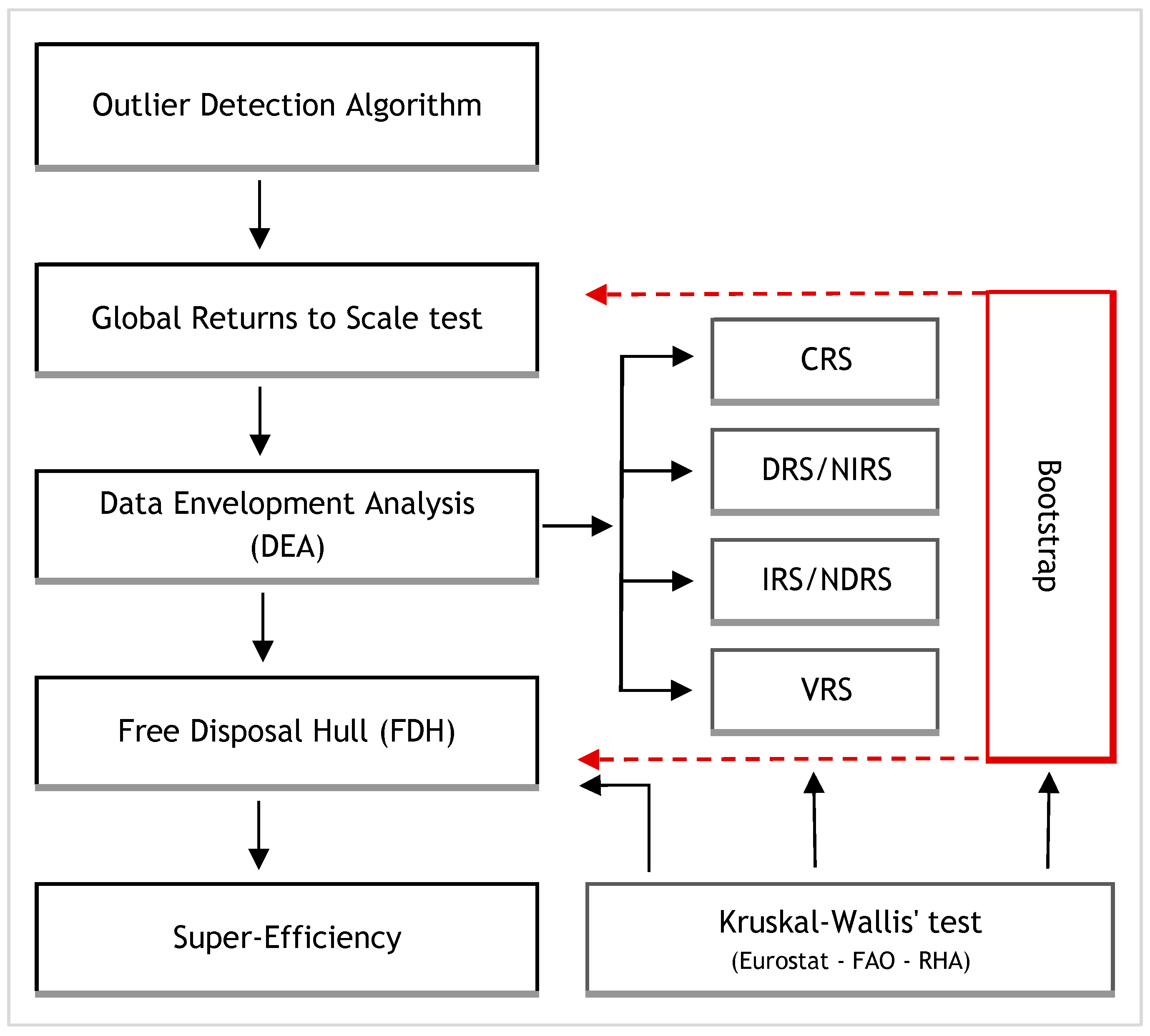


| Scaling | Free Disposability | Convexity | Returns to Scale |
|---|---|---|---|
| • | • | • (CRS) | |
| • | • | • (NIRS) | |
| • | • | • (NDRS) | |
| • | • | - | |
| • | - | - |
| Inputs | Outputs | Ref. | ||||
|---|---|---|---|---|---|---|
| i1 | i2 | i3 | o1 | o2 | o3 | |
| • | • | • | [59] | |||
| • | • | • | • | [61] | ||
| • | • | • | [60] | |||
| • | • | • | • | • | [4] | |
| • | • | [62] | ||||
| • | • | • | • | • | [36] | |
| • | • | • | • | • | [34] | |
| • | • | • | • | • | [33] * | |
| • | • | • | [35] | |||
| Data Sources | ||||||
| MoH | MoH | MoH | MoH | MoH | MoH | |
| Entity | Statistic | Inputs | Outputs | ||||
|---|---|---|---|---|---|---|---|
| i1 | i2 | i3 | o1 | o2 | o3 | ||
| HCs (N = 234) | |||||||
| Mean | 11.4 | 15.7 | 8.2 | 15,992.4 | 9255.6 | 10,409.4 | |
| St Dev | 8.7 | 10.0 | 4.9 | 13,975.1 | 8845.2 | 7185.5 | |
| Median | 8.0 | 13.5 | 7.5 | 11,917.0 | 6333.0 | 8529.5 | |
| Min | 1 | 1 | 1 | 341 | 75 | 364 | |
| Max | 47 | 53 | 31 | 75,381 | 54,156 | 36,929 | |
| Range | 46 | 52 | 30 | 75,040 | 54,081 | 36,565 | |
| Sum | 2665 | 3675 | 1908 | 3,742,211 | 2,165,821 | 2,435,798 | |
| ToMYs (N = 94) | |||||||
| Mean | 2.6 | 3.1 | 2.5 | 4944.7 | 1025.9 | 2860.5 | |
| St Dev | 1.2 | 0.9 | 0.7 | 3123.5 | 845.2 | 2019.9 | |
| Median | 3.0 | 3.0 | 3.0 | 4491.0 | 786.0 | 2419.0 | |
| Min | 1 | 1 | 1 | 465 | 12 | 109 | |
| Max | 5 | 5 | 5 | 14,161 | 3812 | 8737 | |
| Range | 4 | 4 | 4 | 13,696 | 3800 | 8628 | |
| Sum | 242 | 293 | 234 | 464,801 | 96,438 | 268,890 | |
| Test | Null vs. | Statistic | Significance Level | |
|---|---|---|---|---|
| Alternative | (ts1, ts2) | α = 0.01 | α = 0.05 | |
| test-1 | H0: CRS | 1.1526 | p < 0.001 | p < 0.001 |
| H1: VRS | ||||
| test-2 | H’0: NRS | 1.0256 | p = 0.005 | p = 0.0025 |
| H’1: VRS | ||||
| Region | Mean | Bootstrapped Scores (B = 2000 repls.) | Efficient DMUs | Weighted Mean Eff. | |||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | StDev | Median | Min | Max | No. | % Total | |||
| All | 1.97 | 2.31 | 1.13 | 2.02 | 1.13 | 8.04 | 38 | 100.00% | 1.92 |
| ‘1’ | 1.67 | 1.97 | 0.92 | 1.62 | 1.19 | 5.05 | 5 | 13.20% | 1.69 |
| ‘2’ | 2.02 | 2.37 | 1.21 | 2.01 | 1.13 | 6.19 | 11 | 28.90% | 1.99 |
| ‘3’ | 2.02 | 2.37 | 1.13 | 2.10 | 1.16 | 8.04 | 22 | 57.90% | 2.00 |
| Urban | 1.52 | 1.79 | 0.82 | 1.36 | 1.19 | 4.18 | 6 | 15.80% | 1.51 |
| P-Urban | 1.91 | 2.23 | 0.98 | 2.01 | 1.13 | 6.63 | 25 | 65.80% | 1.94 |
| Rural | 2.39 | 2.83 | 1.48 | 2.25 | 1.22 | 8.04 | 7 | 18.40% | 2.42 |
| RHA 1 | 1.30 | 1.51 | 0.32 | 1.45 | 1.19 | 2.23 | 1 | 2.60% | 1.51 |
| RHA 2 | 1.98 | 2.32 | 1.24 | 1.78 | 1.20 | 6.63 | 7 | 18.40% | 1.83 |
| RHA 3 | 2.04 | 2.35 | 0.72 | 2.38 | 1.21 | 3.67 | 2 | 5.30% | 2.12 |
| RHA 4 | 2.31 | 2.67 | 1.30 | 2.37 | 1.17 | 6.19 | 2 | 5.30% | 2.24 |
| RHA 5 | 2.06 | 2.41 | 1.07 | 2.24 | 1.13 | 5.92 | 6 | 15.80% | 2.05 |
| RHA 6 | 1.88 | 2.24 | 1.15 | 2.01 | 1.16 | 8.04 | 16 | 42.10% | 1.86 |
| RHA 7 | 1.59 | 1.89 | 0.77 | 1.54 | 1.22 | 3.55 | 4 | 10.50% | 1.64 |
| RHA | Mean | Bootstrapped Scores (B = 2000 repls.) | Efficient DMUs | Weighted Mean Eff. | |||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | StDev | Median | Min | Max | No. | % Total | |||
| All | 1.74 | 1.98 | 1.33 | 1.48 | 1.11 | 10.55 | 26 | 100.00% | 1.58 |
| RHA 1 | 1.41 | 1.60 | 0.59 | 1.32 | 1.13 | 3.03 | 3 | 11.50% | 1.46 |
| RHA 2 | 1.48 | 1.70 | 0.65 | 1.48 | 1.11 | 3.53 | 6 | 23.10% | 1.55 |
| RHA 3 | 1.64 | 1.87 | 1.87 | 1.87 | 1.87 | 0 | 0.00% | 1.87 | |
| RHA 4 | 1.65 | 1.88 | 0.95 | 1.52 | 1.13 | 3.94 | 3 | 11.50% | 1.55 |
| RHA 5 | 2.08 | 2.36 | 1.60 | 1.59 | 1.14 | 6.54 | 4 | 15.40% | 1.69 |
| RHA 6 | 1.91 | 2.19 | 1.83 | 1.51 | 1.15 | 10.55 | 7 | 26.90% | 1.63 |
| RHA 7 | 1.58 | 1.77 | 0.73 | 1.38 | 1.16 | 3.03 | 3 | 11.50% | 1.48 |
| DMU | Super-Eff CRS | Peer Count | Super-Eff VRS | Peer Count | Supper-Eff NDRS | Peer Count | Super-Eff NIRS | Peer Count | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | Rank | Score | Rank | Score | Rank | Score | Rank | |||||
| D-199 | 0.956 | 19 | 0 | - | 1 | 34 | - | 1 | 34 | 0.956 | 26 | 0 |
| D-212 | - | 1 | 11 | - | 1 | 11 | ||||||
| D-041 | 0.071 | 3 | 2 | 0.071 | 3 | 2 | ||||||
| D-184 | 0.211 | 4 | 2 | 0.211 | 4 | 2 | ||||||
| D-168 | 0.838 | 10 | 5 | 0.310 | 5 | 3 | 0.310 | 5 | 5 | 0.838 | 14 | 3 |
| D-043 | 0.314 | 6 | 0 | 0.314 | 6 | 0 | ||||||
| D-243 | 0.391 | 7 | 2 | 0.391 | 7 | 2 | ||||||
| D-153 | 0.393 | 8 | 16 | 0.393 | 8 | 16 | ||||||
| D-173 | 0.476 | 1 | 108 | 0.412 | 9 | 61 | 0.412 | 9 | 103 | 0.476 | 1 | 66 |
| D-048 | 0.745 | 7 | 33 | 0.428 | 10 | 14 | 0.428 | 10 | 35 | 0.745 | 8 | 12 |
| D-159 | 0.598 | 3 | 67 | 0.550 | 11 | 62 | 0.598 | 13 | 61 | 0.550 | 2 | 68 |
| D-172 | 0.611 | 4 | 94 | 0.555 | 12 | 66 | 0.555 | 11 | 94 | 0.611 | 5 | 66 |
| D-037 | 0.614 | 5 | 66 | 0.590 | 13 | 69 | 0.614 | 14 | 61 | 0.590 | 3 | 74 |
| D-252 | 0.596 | 2 | 70 | 0.594 | 14 | 70 | 0.594 | 12 | 67 | 0.596 | 4 | 73 |
| D-178 | 0.798 | 9 | 9 | 0.623 | 15 | 3 | 0.623 | 15 | 8 | 0.798 | 13 | 4 |
| D-256 | 0.695 | 6 | 97 | 0.682 | 16 | 70 | 0.695 | 17 | 94 | 0.682 | 6 | 73 |
| D-211 | 0.693 | 17 | 0 | 0.693 | 16 | 0 | ||||||
| D-035 | 0.739 | 18 | 31 | 0.739 | 7 | 31 | ||||||
| D-058 | 0.774 | 19 | 29 | 0.774 | 9 | 29 | ||||||
| D-093 | 0.795 | 8 | 22 | 0.775 | 20 | 16 | 0.775 | 18 | 22 | 0.795 | 12 | 16 |
| D-189 | 0.868 | 11 | 5 | 0.780 | 21 | 1 | 0.868 | 21 | 4 | 0.780 | 10 | 2 |
| D-166 | 0.871 | 13 | 59 | 0.781 | 22 | 81 | 0.871 | 22 | 56 | 0.781 | 11 | 84 |
| D-111 | 0.875 | 14 | 2 | 0.791 | 23 | 3 | 0.791 | 19 | 2 | 0.875 | 19 | 3 |
| D-044 | 0.842 | 24 | 8 | 0.842 | 15 | 8 | ||||||
| D-225 | 0.869 | 12 | 32 | 0.852 | 25 | 18 | 0.852 | 20 | 35 | 0.869 | 18 | 14 |
| D-057 | 0.879 | 16 | 43 | 0.853 | 26 | 33 | 0.879 | 25 | 38 | 0.853 | 16 | 38 |
| D-007 | 0.858 | 27 | 9 | 0.858 | 17 | 9 | ||||||
| D-260 | 0.876 | 15 | 48 | 0.875 | 28 | 23 | 0.876 | 24 | 47 | 0.875 | 20 | 24 |
| D-162 | 0.888 | 17 | 7 | 0.876 | 29 | 1 | 0.876 | 23 | 5 | 0.888 | 23 | 3 |
| D-028 | 0.885 | 30 | 21 | 0.885 | 21 | 21 | ||||||
| D-155 | 0.920 | 18 | 3 | 0.885 | 31 | 5 | 0.920 | 26 | 1 | 0.885 | 22 | 7 |
| D-203 | 0.910 | 32 | 25 | 0.910 | 24 | 25 | ||||||
| D-120 | 0.924 | 33 | 8 | 0.924 | 25 | 8 | ||||||
| D-262 | 0.959 | 34 | 1 | 0.959 | 27 | 1 | ||||||
| D-133 | 0.965 | 35 | 3 | 0.965 | 27 | 3 | ||||||
| D-238 | 0.982 | 36 | 3 | 0.982 | 28 | 3 | ||||||
| D-176 | 0.992 | 37 | 1 | 0.992 | 29 | 1 | ||||||
| D-152 | 0.999 | 38 | 2 | 0.999 | 30 | 2 | ||||||
| # DMUs | 19 | 38 | 27 | 30 | ||||||||
| Region | Mean | Bootstrapped Scores (B = 2000 repls.) | Efficient DMUs | Benchmarks | Weighted Mean Eff. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | StDev | Median | Min | Max | No. | % Total | No. | Peer Count | |||
| All | 1.34 | 1.51 | 0.56 | 1.22 | 1.09 | 4.28 | 115 | 100.0% | 35 | 119 | 1.39 |
| ‘1’ | 1.25 | 1.41 | 0.45 | 1.20 | 1.10 | 2.89 | 19 | 16.5% | 3 | 21 | 1.31 |
| ‘2’ | 1.40 | 1.58 | 0.67 | 1.22 | 1.09 | 4.28 | 33 | 28.7% | 6 | 12 | 1.43 |
| ‘3’ | 1.33 | 1.50 | 0.52 | 1.22 | 1.09 | 3.47 | 63 | 54.8% | 26 | 86 | 1.41 |
| Urban | 1.17 | 1.33 | 0.31 | 1.20 | 1.10 | 2.26 | 15 | 13.0% | 4 | 24 | 1.25 |
| P-Urban | 1.34 | 1.51 | 0.57 | 1.22 | 1.09 | 4.28 | 77 | 67.0% | 24 | 68 | 1.41 |
| Rural | 1.41 | 1.59 | 0.60 | 1.22 | 1.13 | 3.45 | 23 | 20.0% | 7 | 27 | 1.48 |
| RHA 1 | 1.05 | 1.18 | 0.10 | 1.15 | 1.11 | 1.44 | 6 | 5.2% | 0 | 0 | 1.18 |
| RHA 2 | 1.30 | 1.47 | 0.55 | 1.21 | 1.10 | 3.44 | 19 | 16.5% | 2 | 22 | 1.33 |
| RHA 3 | 1.49 | 1.64 | 0.47 | 1.68 | 1.13 | 3.07 | 3 | 2.6% | 2 | 2 | 1.54 |
| RHA 4 | 1.53 | 1.71 | 0.69 | 1.33 | 1.09 | 3.45 | 19 | 16.5% | 5 | 11 | 1.55 |
| RHA 5 | 1.39 | 1.55 | 0.67 | 1.25 | 1.09 | 4.28 | 14 | 12.2% | 2 | 4 | 1.47 |
| RHA 6 | 1.24 | 1.42 | 0.43 | 1.22 | 1.09 | 3.31 | 44 | 38.3% | 20 | 63 | 1.33 |
| RHA 7 | 1.21 | 1.39 | 0.47 | 1.21 | 1.12 | 2.69 | 10 | 8.7% | 4 | 17 | 1.29 |
| Count | Benchmark | Number of Benchmark Appearances as Peers | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | ‘1’ | ‘2’ | ‘3’ | Urban | P-Urban | Rural | Regional Health Authority | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||||||
| 1 | D-037 | 19 | 5 | 3 | 11 | · | 18 | 1 | 1 | 2 | 5 | 4 | 5 | 2 | |
| 2 | D-260 | 11 | 4 | 7 | 6 | 5 | 4 | 2 | 4 | 1 | |||||
| 3 | D-172 | 10 | 3 | 7 | 8 | 2 | 1 | 2 | 2 | 1 | 4 | ||||
| 4 | D-203 | 9 | 3 | 6 | 1 | 8 | 1 | 4 | 1 | 3 | |||||
| 5 | D-173 | 8 | 2 | 6 | 5 | 3 | 1 | 7 | |||||||
| 6 | D-166 | 6 | 3 | 3 | 6 | 1 | 1 | 1 | 2 | 1 | |||||
| 7 | D-225 | 5 | 2 | 3 | 2 | 2 | 1 | 3 | 1 | 1 | |||||
| 8 | D-178 | 4 | 1 | 3 | 1 | 3 | 1 | 1 | 2 | ||||||
| 9 | D-252 | 4 | 3 | · | 1 | 3 | 1 | 1 | 3 | · | |||||
| 10 | D-028 | 3 | 2 | 1 | 3 | · | 2 | 1 | |||||||
| 11 | D-091 | 3 | 3 | 3 | 2 | 1 | · | ||||||||
| 12 | D-092 | 3 | 1 | 2 | 3 | 1 | · | 1 | 1 | ||||||
| 13 | D-152 | 3 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | ||||||
| 14 | D-104 | 2 | 2 | 1 | 1 | · | 1 | 1 | |||||||
| 15 | D-118 | 2 | 1 | 1 | 1 | 1 | 1 | · | 1 | ||||||
| 16 | D-208 | 2 | 2 | · | 1 | 1 | 1 | 1 | |||||||
| 17 | D-210 | 2 | 2 | 1 | 1 | 2 | · | ||||||||
| 18 | D-222 | 2 | 1 | 1 | 2 | · | 1 | 1 | |||||||
| 19 | D-223 | 2 | 2 | · | 2 | 2 | |||||||||
| 20 | D-232 | 2 | · | 2 | 1 | 1 | 1 | · | 1 | ||||||
| 21 | D-236 | 2 | 1 | 1 | · | 2 | 1 | 1 | |||||||
| 22 | D-238 | 2 | 2 | · | 2 | 1 | 1 | · | |||||||
| 23 | D-057 | 1 | · | 1 | 1 | · | 1 | ||||||||
| 24 | D-058 | 1 | 1 | 1 | 1 | · | |||||||||
| 25 | D-088 | 1 | 1 | · | 1 | 1 | · | ||||||||
| 26 | D-159 | 1 | 1 | · | 1 | · | 1 | ||||||||
| 27 | D-162 | 1 | 1 | 1 | 1 | ||||||||||
| 28 | D-168 | 1 | 1 | 1 | 1 | · | |||||||||
| 29 | D-176 | 1 | 1 | 1 | 1 | · | |||||||||
| 30 | D-183 | 1 | 1 | 1 | 1 | · | |||||||||
| 31 | D-211 | 1 | · | 1 | · | 1 | 1 | · | |||||||
| 32 | D-216 | 1 | · | 1 | 1 | 1 | · | ||||||||
| 33 | D-233 | 1 | 1 | · | 1 | 1 | · | ||||||||
| 34 | D-250 | 1 | 1 | 1 | · | 1 | · | ||||||||
| 35 | D-253 | 1 | 1 | · | 1 | · | 1 | · | |||||||
| Total | Appearences | 119 | 13 | 31 | 75 | 9 | 82 | 28 | 4 | 14 | 13 | 25 | 25 | 33 | 5 |
| Benchmarks | 35 | 3 | 6 | 26 | 4 | 24 | 7 | 0 | 2 | 2 | 5 | 2 | 20 | 4 | |
| Region | Mean | Bootstrapped Scores (B = 2000 repls.) | Efficient DMUs | Benchmarks | Weighted Mean Eff. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | StDev | Median | Min | Max | No. | % Total | No. | Peer Count | |||
| All | 1.36 | 1.55 | 0.81 | 1.21 | 1.08 | 6.58 | 52 | 100.0% | 15 | 42 | 1.34 |
| RHA 1 | 1.25 | 1.42 | 0.39 | 1.22 | 1.14 | 2.25 | 6 | 11.5% | 2 | 6 | 1.34 |
| RHA 2 | 1.16 | 1.33 | 0.41 | 1.21 | 1.08 | 2.83 | 9 | 17.3% | 2 | 7 | 1.27 |
| RHA 3 | 1.64 | 1.82 | 1.82 | 1.82 | 1.82 | 0 | 0.0% | 0 | 0 | 1.82 | |
| RHA 4 | 1.30 | 1.47 | 0.66 | 1.20 | 1.09 | 3.47 | 7 | 13.5% | 1 | 1 | 1.31 |
| RHA 5 | 1.61 | 1.83 | 1.06 | 1.22 | 1.16 | 4.12 | 8 | 15.4% | 5 | 20 | 1.43 |
| RHA 6 | 1.45 | 1.63 | 1.05 | 1.20 | 1.10 | 6.58 | 18 | 34.6% | 4 | 6 | 1.34 |
| RHA 7 | 1.25 | 1.41 | 0.36 | 1.24 | 1.15 | 2.08 | 4 | 7.7% | 1 | 2 | 1.28 |
| Count | Benchmark | Number of Benchmark Appearances as Peers | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ALL | Regional Health Authority (RHA/YPE) | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1 | TM-047 | 10 | 1 | 1 | 3 | 2 | 3 | ||
| 2 | TM-021 | 6 | 2 | 2 | 1 | 1 | |||
| 3 | TM-010 | 4 | · | 2 | 2 | ||||
| 4 | TM-051 | 4 | 2 | 2 | |||||
| 5 | TM-054 | 4 | 1 | 1 | · | 2 | |||
| 6 | TM-073 | 3 | 2 | 1 | |||||
| 7 | TM-006 | 2 | 1 | 1 | |||||
| 8 | TM-091 | 2 | 1 | 1 | |||||
| 9 | TM-016 | 1 | · | 1 | |||||
| 10 | TM-042 | 1 | 1 | ||||||
| 11 | TM-045 | 1 | · | 1 | |||||
| 12 | TM-048 | 1 | 1 | · | |||||
| 13 | TM-064 | 1 | 1 | · | |||||
| 14 | TM-069 | 1 | · | 1 | |||||
| 15 | TM-084 | 1 | 1 | · | |||||
| Total | Appearances | 42 | 5 | 8 | 1 | 5 | 7 | 12 | 4 |
| Benchmarks | 15 | 2 | 2 | 0 | 1 | 5 | 4 | 1 | |
| (Sub)Categories | CRS | VRS | IRS | DRS | FDH | Bootstrapped | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tested | CRS | VRS | IRS | DRS | FDH | ||||||
| Kruskal–Wallis test | |||||||||||
| ‘1’, ‘2’,’3’ | χ2 (df = 2) | 1.97 | 3.89 | 0.93 | 5.92 | 1.56 | 2.31 | 4.80 | 1.52 | 5.76 | 4.85 |
| p-value | 0.37 | 0.14 | 0.63 | 0.05 | 0.46 | 0.32 | 0.09 | 0.47 | 0.06 | 0.09 | |
| Urban, P-Urban, Rural | χ2 (df = 2) | 6.05 | 12.40 | 3.17 | 18.28 | 3.28 | 6.15 | 16.34 | 4.33 | 19.10 | 5.03 |
| p-value | 0.05 | 0.00 | 0.21 | 0.00 | 0.19 | 0.05 | 0.00 | 0.12 | 0.00 | 0.08 | |
| RHA 1, 2, 3, 4, 5, 6, 7 | χ2 (df = 6) | 10.60 | 15.20 | 12.52 | 14.89 | 16.37 | 9.05 | 14.59 | 9.52 | 14.40 | 16.95 |
| p-value | 0.10 | 0.02 | 0.05 | 0.02 | 0.01 | 0.17 | 0.02 | 0.15 | 0.03 | 0.01 | |
| Median test | |||||||||||
| ‘1’, ‘2’, ‘3’ | χ2 (df = 2) | 1.65 | 5.98 | 1.65 | 5.54 | 1.65 | 1.39 | 5.98 | 1.39 | 5.54 | 4.23 |
| p-value | 0.44 | 0.05 | 0.44 | 0.06 | 0.44 | 0.50 | 0.05 | 0.50 | 0.06 | 0.12 | |
| Urban, P-Urban, Rural | χ2 (df = 2) | 0.71 | 5.76 | 0.35 | 10.47 | 2.00 | 1.28 | 9.32 | 1.28 | 10.47 | 3.63 |
| p-value | 0.70 | 0.06 | 0.84 | 0.01 | 0.37 | 0.53 | 0.01 | 0.53 | 0.01 | 0.16 | |
| RHA 1, 2, 3, 4, 5, 6, 7 | χ2 (df = 6) | 8.12 | 10.87 | 8.05 | 11.45 | 15.92 | 8.12 | 12.55 | 8.11 | 13.05 | 13.79 |
| p-value | 0.23 | 0.09 | 0.23 | 0.08 | 0.01 | 0.23 | 0.05 | 0.23 | 0.04 | 0.03 | |
| Statistic | All | ‘1’ | ‘2’ | ‘3’ | Urban | P-Urban | Rural | Regional Health Authority (RHA/YPE) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| Mean | 1.17 | 1.23 | 1.18 | 1.15 | 1.30 | 1.16 | 1.12 | 1.34 | 1.17 | 1.29 | 1.09 | 1.18 | 1.15 | 1.21 |
| StDev | 0.27 | 0.29 | 0.29 | 0.25 | 0.33 | 0.25 | 0.28 | 0.31 | 0.29 | 0.32 | 0.13 | 0.25 | 0.28 | 0.35 |
| Median | 1.05 | 1.09 | 1.06 | 1.05 | 1.24 | 1.05 | 1.04 | 1.24 | 1.05 | 1.15 | 1.05 | 1.09 | 1.04 | 1.04 |
| Min | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.03 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Max | 2.71 | 2.12 | 2.44 | 2.71 | 1.98 | 2.44 | 2.71 | 1.80 | 2.44 | 2.12 | 1.76 | 2.12 | 2.71 | 2.12 |
| Weighted mean | 1.19 | 1.24 | 1.21 | 1.15 | 1.35 | 1.17 | 1.08 | 1.36 | 1.15 | 1.25 | 1.11 | 1.19 | 1.16 | 1.30 |
| Statistic | All | Regional Health Authority (RHA/YPE) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Mean | 1.20 | 1.04 | 1.39 | 1.00 | 1.06 | 1.04 | 1.33 | 1.02 |
| StDev | 0.66 | 0.07 | 1.07 | 0.08 | 0.04 | 0.81 | 0.03 | |
| Median | 1.02 | 1.00 | 1.05 | 1.00 | 1.00 | 1.03 | 1.03 | 1.01 |
| Min | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Max | 5.43 | 1.22 | 5.43 | 1.00 | 1.25 | 1.16 | 4.02 | 1.07 |
| Weighted mean | 1.06 | 1.04 | 1.10 | 1.00 | 1.05 | 1.03 | 1.08 | 1.01 |
| Entity | 241 HCs Sample (Original) | 234 HCs Sample (Outliers Removed) |
|---|---|---|
| Number of decision-making units (DMUs) in sample | 241 | 234 |
| Number of outliers | 7 | - |
| Number of efficient DMUs | 31 | 38 |
| Number of efficient outliers | 4 | - |
| Number of inefficient outliers | 3 | - |
| Number of efficient DMUs common to both samples | 27 | 27 |
| Number of DMUs with at least one efficient outlier as a peer | 183 | - |
| Percentage of inefficient DMUs using at least one efficient outlier as a peer | 90.1% | - |
| Total occurrences of efficient outliers as peers | 261 | - |
| Total occurrences of all efficient DMUs as peers | 812 | - |
| Percentage of peer occurrences for efficient outliers (of total) | 32.1% | - |
| Mean efficiency score of all DMUs in sample | 2.33 | 1.97 |
| Number of inefficient DMUs common to both samples (using at least one efficient outlier as a peer in the 241 HCs sample) | 180 | 180 |
| Descriptive statistics of the subset (180 common DMUs) | 241 HCs Sample | 234 HCs Sample |
| Mean efficiency score | 2.65 | 2.14 |
| Standard deviation | 1.23 | 0.96 |
| Minimum efficiency score | 1.02 | 1.00 |
| Maximum efficiency score | 8.07 | 5.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flokou, A.; Aletras, V.H.; Miltiadis, C.; Karaferis, D.C.; Niakas, D.A. Efficiency of Primary Health Services in the Greek Public Sector: Evidence from Bootstrapped DEA/FDH Estimators. Healthcare 2024, 12, 2230. https://doi.org/10.3390/healthcare12222230
Flokou A, Aletras VH, Miltiadis C, Karaferis DC, Niakas DA. Efficiency of Primary Health Services in the Greek Public Sector: Evidence from Bootstrapped DEA/FDH Estimators. Healthcare. 2024; 12(22):2230. https://doi.org/10.3390/healthcare12222230
Chicago/Turabian StyleFlokou, Angeliki, Vassilis H. Aletras, Chrysovalantis Miltiadis, Dimitris Charalambos Karaferis, and Dimitris A. Niakas. 2024. "Efficiency of Primary Health Services in the Greek Public Sector: Evidence from Bootstrapped DEA/FDH Estimators" Healthcare 12, no. 22: 2230. https://doi.org/10.3390/healthcare12222230
APA StyleFlokou, A., Aletras, V. H., Miltiadis, C., Karaferis, D. C., & Niakas, D. A. (2024). Efficiency of Primary Health Services in the Greek Public Sector: Evidence from Bootstrapped DEA/FDH Estimators. Healthcare, 12(22), 2230. https://doi.org/10.3390/healthcare12222230






