Analytical Techniques for Supporting Hospital Case Mix Planning Encompassing Forced Adjustments, Comparisons, and Scoring
Abstract
1. Introduction
1.1. Background
1.2. Past Research and Current State of the Art
- Complexity and Customization: Healthcare systems are highly complex and vary widely across different hospitals, regions, and countries. Developing tools that are both sophisticated enough to address these complexities and flexible enough to be adapted to diverse settings is challenging. This often leads to slower adoption as hospitals must tailor solutions to their unique needs.
- High Costs: Developing and implementing advanced planning tools can be expensive. Hospitals, particularly those with limited budgets, may prioritize other areas of investment, such as staffing or medical equipment, over advanced software solutions.
- Resistance to Change: Healthcare organizations often have entrenched practices and workflows. There can be resistance from staff and management to adopt new technologies, particularly if these tools require significant changes to existing processes or a learning curve.
- Data Availability and Integration: Effective hospital planning tools require access to high-quality, comprehensive data, including patient outcomes, resource utilization, and financial metrics. In many cases, data is siloed or inconsistent, making it difficult to integrate and use effectively in planning tools.
- Regulatory and Privacy Concerns: Healthcare data is sensitive and subject to strict regulations (such as HIPAA in the U.S.). These regulations can create barriers to the development and deployment of tools that require large data sets or cross-organizational data sharing.
- Lack of Skilled Personnel: Developing and maintaining advanced planning tools requires specialized knowledge in both healthcare and data science. There may be a shortage of professionals with the expertise necessary to design, implement, and manage these systems within hospitals.
- Uncertainty of Return on Investment (ROI): Many healthcare administrators are cautious about investing in advanced planning tools without clear evidence of ROI. The potential benefits of such tools, such as improved efficiency or better resource allocation, may be difficult to quantify, leading to hesitation in adopting them.
1.3. Research Agenda
2. Methodology
2.1. Background Details and Notations
2.2. Impact of Case Mix Alterations
| Algorithm 1. Impact Assessment | |||
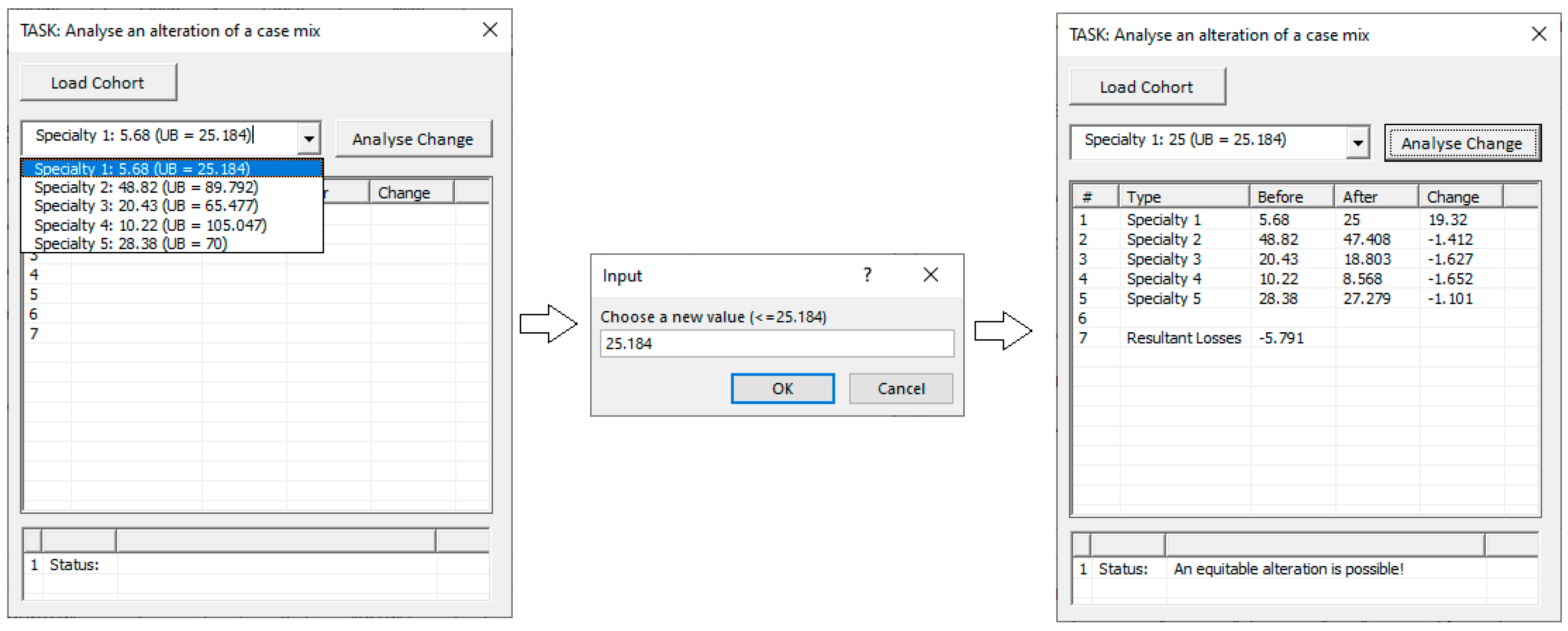
| Step 1. Select a case mix for analysis, hereby , and designate targets . | |||
| Step 2. Select a patient type , and force a change of units, where and | |||
| Step 3. If then differences in the case mix should be minimized, i.e., the 2-norm should be minimized, or else it should be maximized, where and or . | |||
| Step 4. Solve the optimization model below, and report the case mix and the differences . | |||
| Minimize where | (1) | ||
| Subject to: | |||
| [Anchored value] | (2) | ||
| [Scaled difference] | (3) | ||
| [Forced increase or decrease] | (4) | ||
| [Positive scaled difference] | (5) | ||
| Constraints (A2)–(A7) from Appendix A | |||
| Algorithm 2. Impact Assessment (SubTypes) | |
| Step 1. Select a case mix , and designate targets . | |
| Step 2. Select a change of units in one patient subtype , i.e., where and is the upper bound on the number of patients of subtype that are treatable. | |
| Step 3. Solve the model below to obtain a new case mix . | |
| Minimize | |
| where or or | (10) |
| Subject to: | |
| (11) | |
| and | (12) |
| (13) | |
| (CMQ-EQ only) | (14) |
| (15) | |
| (16) | |
| Constraints (A2)–(A6) from Appendix A | |
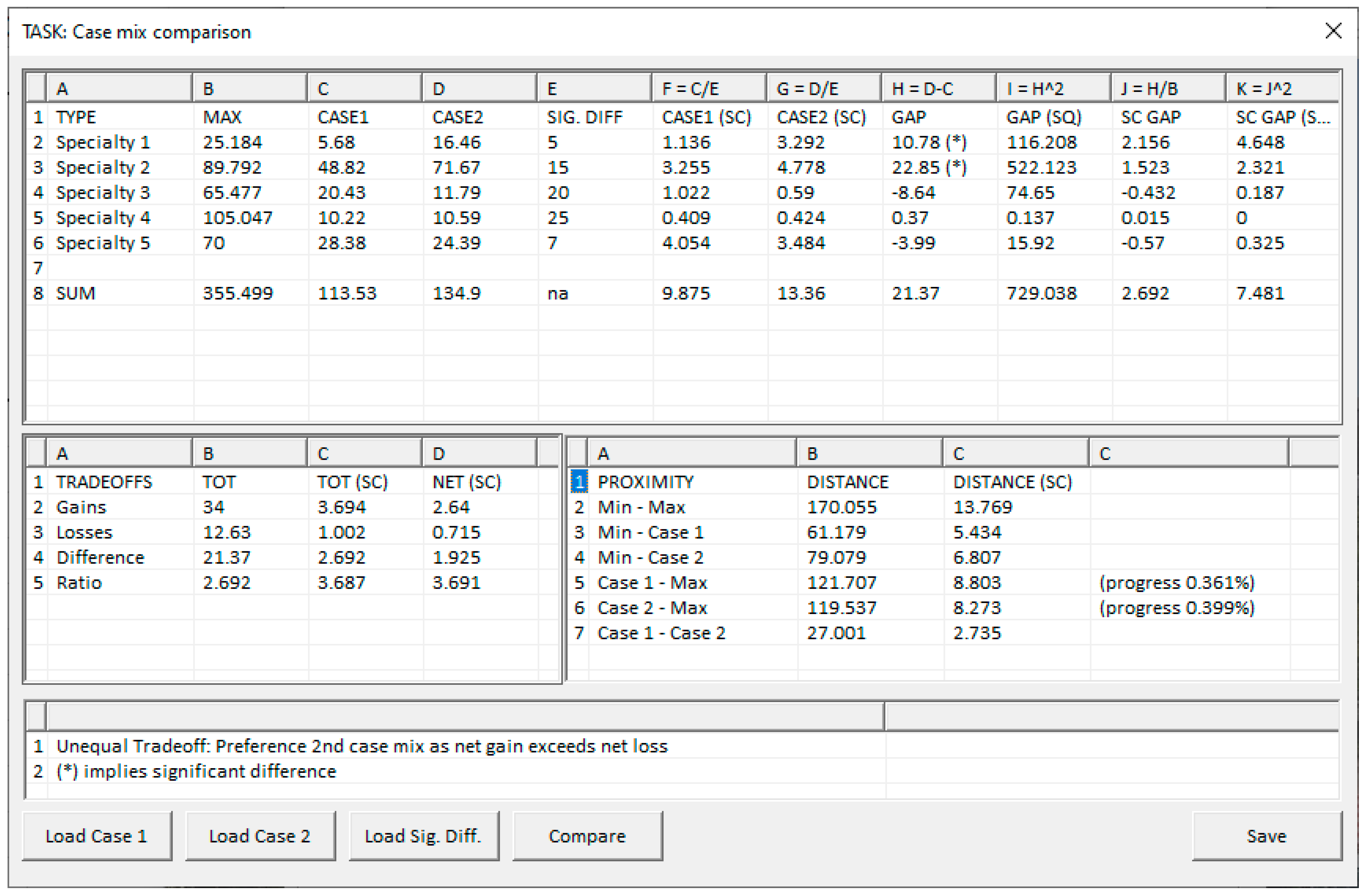
2.3. Case Mix Comparisons
2.3.1. Pareto Optimal Case Mix
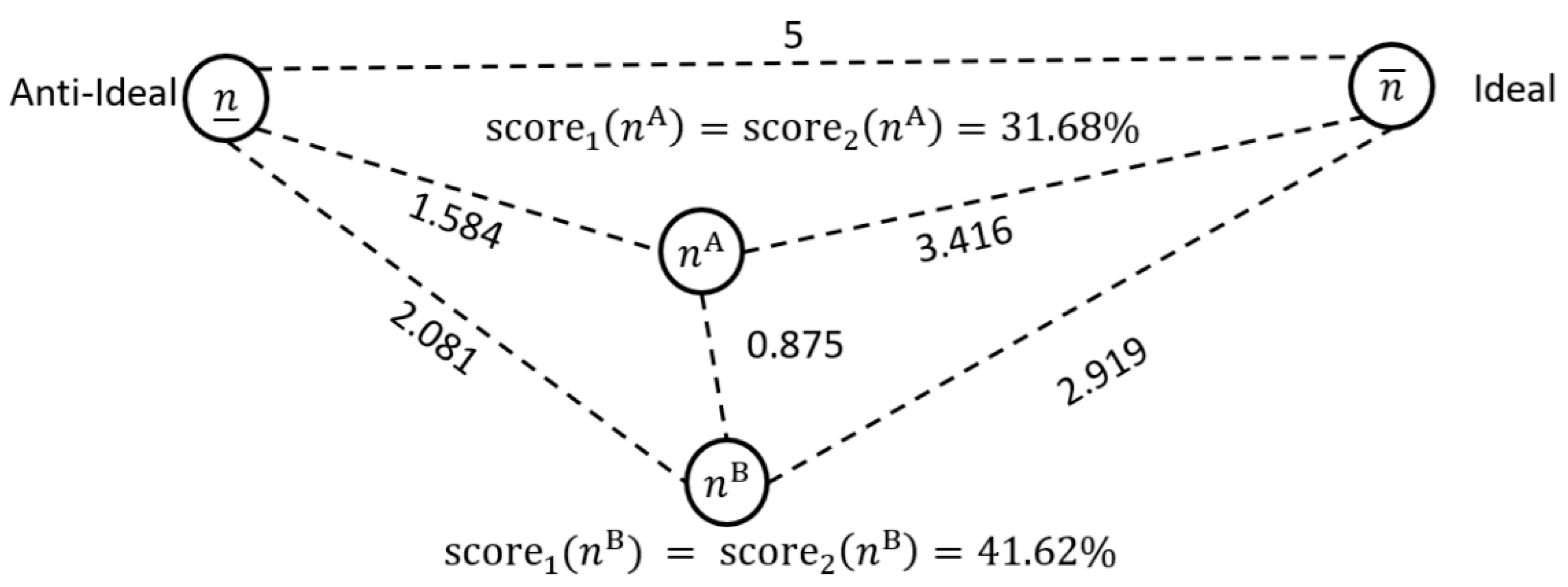
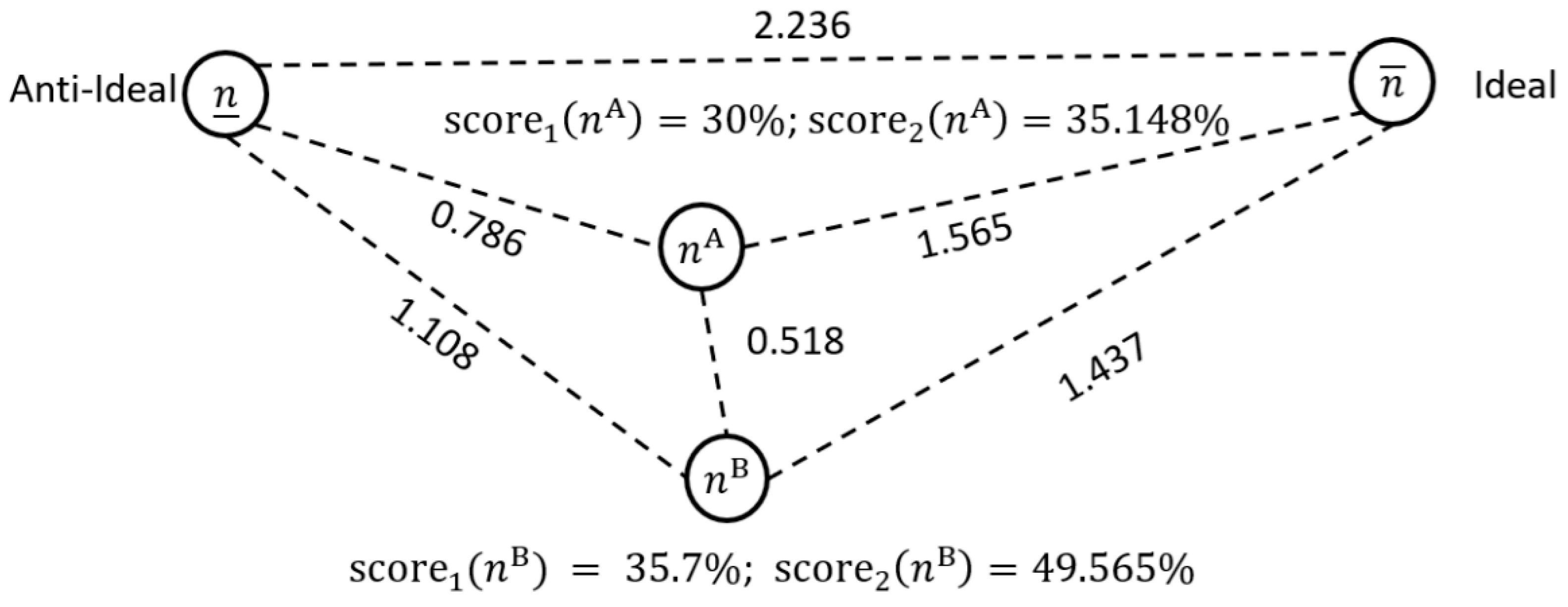
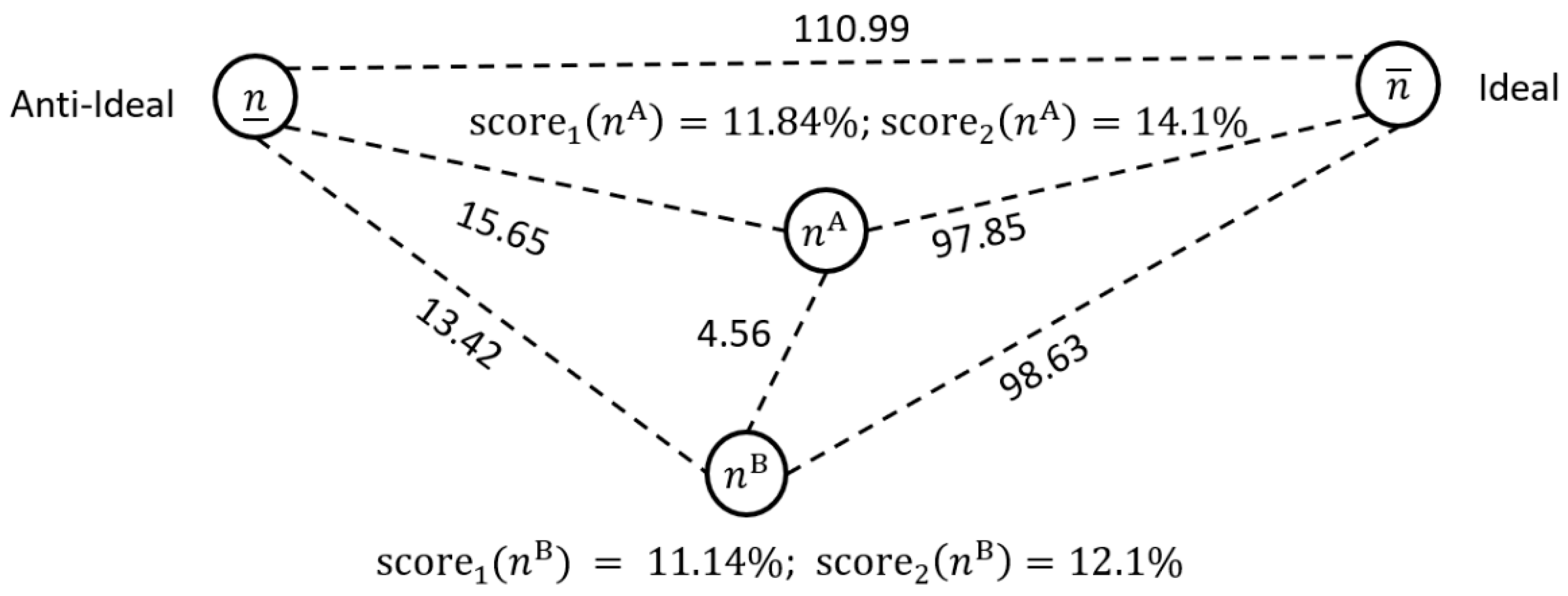
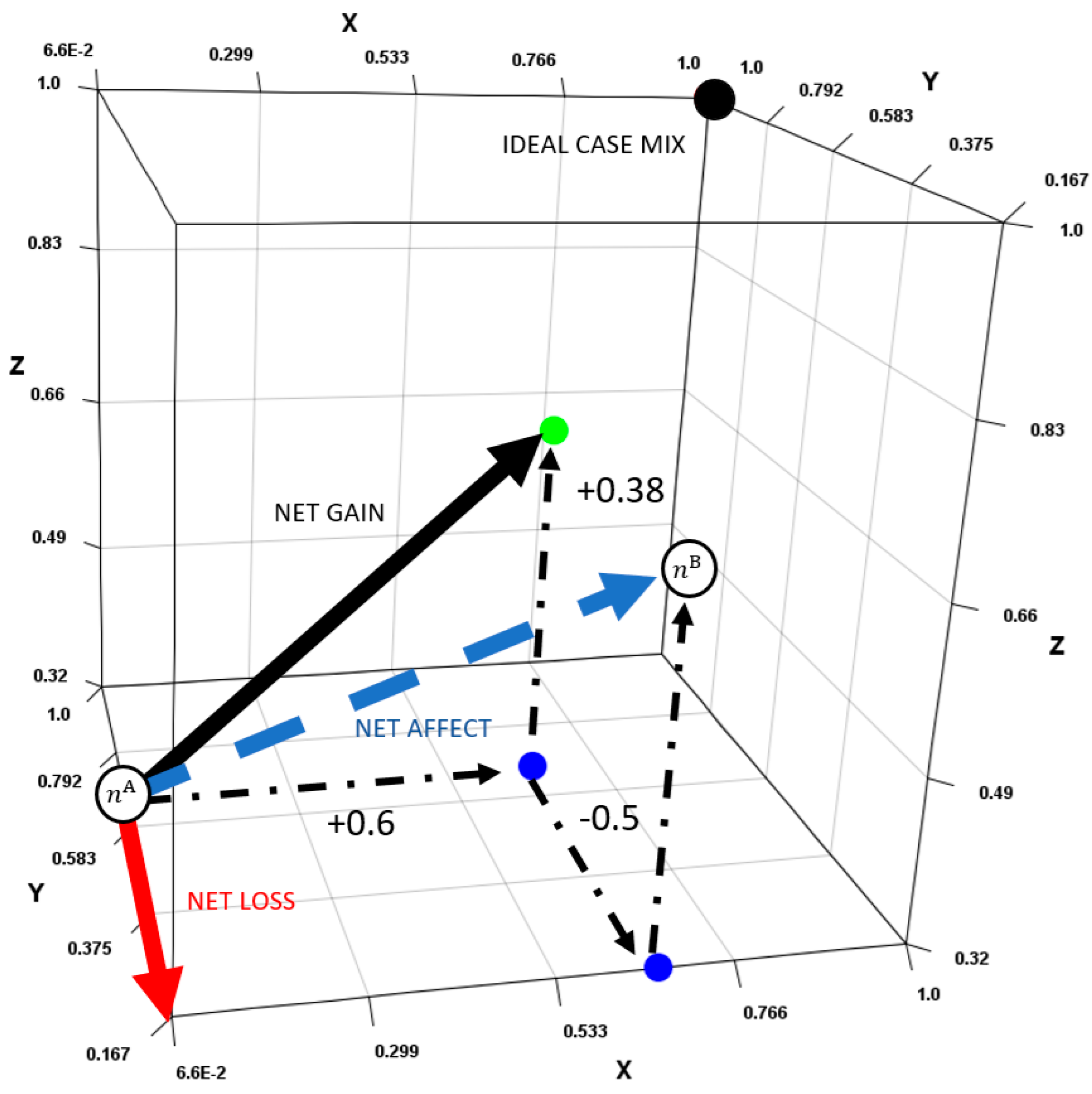
2.3.2. Scoring Case Mix
2.3.3. Quantifying Similarity and Dissimilarity
2.3.4. Comparing Case Mix
3. Putting Theory into Practice
3.1. Case Mix Alteration Assessments
3.2. Case Mix Comparisons
4. COVID-Inspired Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hof, S.; Fugener, A.; Schoenfelder, J.; Brunner, J.O. Case mix planning in hospitals: A review and future agenda. Health Care Manag. Sci. 2017, 20, 207–220. [Google Scholar] [CrossRef] [PubMed]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.; Cook, D.; Birgan, S. Multicriteria optimization techniques for understanding the case mix landscape of a hospital. Eur. J. Oper. Res. 2024, 319, 263–291. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Spratt, B.; Yarlagadda, P.; Cook, D. A stochastic programming approach to perform hospital capacity assessments. PLoS ONE 2023, 18, e0287980. [Google Scholar] [CrossRef] [PubMed]
- Andrews, R.; Goel, K.; Wynn, M.; Burdett, R.L.; Corry, P. Data analytics for hospital case mix planning. J. Biomed. Inform. 2022, 129, 104056. [Google Scholar] [CrossRef] [PubMed]
- Humphreys, P.; Spratt, B.; Tariverdi, M.; Burdett, R.L.; Cook, D.; Yarlagadda, P.; Corry, P. An overview of hospital capacity planning and optimisation. Healthcare 2022, 10, 826. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Guinet, A.; Ruiz, A. Modeling and simulation of a hospital evacuation before a forecasted flood. Oper. Res. Health Care 2015, 4, 36–43. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.; Ding, J.; Thomas, N. Patient flow scheduling and capacity planning in a smart hospital environment. IEEE Access 2015, 4, 135–148. [Google Scholar] [CrossRef]
- Spratt, B.; Kozan, E. Waiting list management through master surgical schedules: A case study. Oper. Res. Health Care 2016, 10, 49–64. [Google Scholar] [CrossRef]
- Liu, N.; Truong, V.A.; Wang, X.; Anderson, B.R. Integrated scheduling and capacity planning with considerations for patients length-of-stays. Prod. Oper. Manag. 2019, 28, 1735–1756. [Google Scholar] [CrossRef]
- Hawkinson, J.D.; Helm, J.E.; Huschka, T.; Kaufman, D.L.; Van Oyen, M.P. A capacity allocation planning model for integrated care and access management. Prod. Oper. Man. 2018, 27, 2270–2290. [Google Scholar] [CrossRef]
- Zhou, L.; Geng, N.; Jiang, Z.; Wang, X. Multi-objective capacity allocation of hospital wards combining revenue and equity. Omega 2017, 81, 220–233. [Google Scholar] [CrossRef]
- Resta, M.; Sonnessa, M.; Tanfani, E.; Testi, A. Unsupervised neural networks for clustering emergent patient flows. Oper. Res. Health Care 2018, 18, 41–51. [Google Scholar] [CrossRef]
- Krueger, R. Infusing Technology into Hospital Operational Decision Making. Jun 1, 08:15am. 2018. Available online: https://www.forbes.com/sites/forbestechcouncil/2018/06/01/infusing-technology-into-hospital-operational-decision-making/?sh=4b436ae367d4 (accessed on 25 December 2024).
- Burdett, R.L.; Corry, P.; Cook, D.; Yarlagadda, P. Developing a personal decision support tool for hospital capacity assessment, allocation and optimization. Expert. Syst. Appl. 2024, 248, 123367. [Google Scholar] [CrossRef]
- Pagel, C.; Banks, V.; Pope, C.; Whitmore, P.; Brown, K.; Goldman, A.; Utley, M. Development, implementation and evaluation of a tool for forecasting short term demand for beds in an intensive care unit. Oper. Res. Health Care 2017, 15, 19–31. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.; McPhail, S.; Cook, D.; Birgan, S. A mathematical framework for regional hospital case mix planning and capacity appraisal. OR Perspect. 2023, 10, 100261. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.; Cook, D.; Birgan, S. The efficacy of utility functions for multicriteria hospital case-mix planning. Int. Trans. Oper. Res. 2024, 31, 807–862. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P. Optimization approaches for organizing hospital infrastructure function. Int. J. Prod. Res. 2024, 62, 8678–8700. [Google Scholar] [CrossRef]
- Freeman, N.; Zhao, M.; Melouk, S. An iterative approach for case mix planning under uncertainty. Omega 2018, 76, 160–173. [Google Scholar] [CrossRef]
- McRae, S.; Brunner, J.O. Assessing the impact of uncertainty and the level of aggregation in case mix planning. Omega 2019, 97, 102086. [Google Scholar]
- McRae, S.; Brunner, J.O.; Bard, J.F. Analyzing economies of scale and scope in hospitals by use of case mix planning. Health Care Manag. Sci. 2018, 23, 80–101. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudzadeh, H.; Shalamzari, A.M.; Mehrizi, H.A. Robust multi-class multi-period patient scheduling with wait time targets. Oper. Res. Health Care 2020, 25, 100254. [Google Scholar] [CrossRef]
- Bruggemann, S.; Chan, T.; Wardi, G.; Mandel, J.; Fontanesi, J. Decision support tool for hospital resource allocation during the COVID-10 pandemic. Inform. Med. Unlocked 2021, 24, 100618. [Google Scholar] [CrossRef]
- Williams, E.; Gartner, D.; Harper, P. A survey of OR/MS models on care planning for frail and elderly patients. Oper. Res. Health Care 2021, 31, 100325. [Google Scholar] [CrossRef]
- Chalgham, M.; Khatrouch, I.; Masmoudi, M.; Walha, O.C.; Dammak, A. Inpatient admission management using multi criteria decision-making methods. Oper. Res. Health Care 2019, 23, 100173. [Google Scholar] [CrossRef]
- Malik, M.M.; Khan, M.; Abdallah, S. Aggregate capacity planning for elective surgeries: A bi-objective optimization approach to balance patients waiting with healthcare costs. Oper. Res. Health Care 2015, 7, 3–13. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K. Combining convergence and diversity in evolutionary multi-objective optimization. Evol. Comput. 2002, 10, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Hancock, B.J.; Nysetvold, T.B.; Mattson, C.A. L-dominance: An approximate-domination mechanism for adaptive resolution of Pareto frontiers. Struct. Multidisc Optim. 2015, 52, 269–279. [Google Scholar] [CrossRef]
- Gulsen, A. Simple classification of COVID-19 patients. J. Lung Pulm. Respir. Res. 2020, 7, 62–63. [Google Scholar] [CrossRef]
- Vekaria, B.; Overton, C.; Wiśniowski, A.; Ahmad, S.; Aparicio-Castro, A.; Curran-Sebastian, J.; Eddleston, J.; Hanley, N.A.; House, T.; Kim, J.; et al. Hospital length of stay for COVID-19 patients: Data-driven methods for forward planning. BMC Infect. Dis. 2021, 21, 700. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, G.P.; Harris, A.M.; Kadri, S.S.; Warner, S.; Bamrah Morris, S.; Giovanni, J.E.; Rogers-Brown, J.S.; Hinckley, A.F.; Kompaniyets, L.; Sircar, K.D.; et al. Trends in clinical severity of hospitalized patients with coronavirus disease in 2019–premier hospital dataset, April 2020–April 2021. Open Forum Infect. Dis. 2020, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
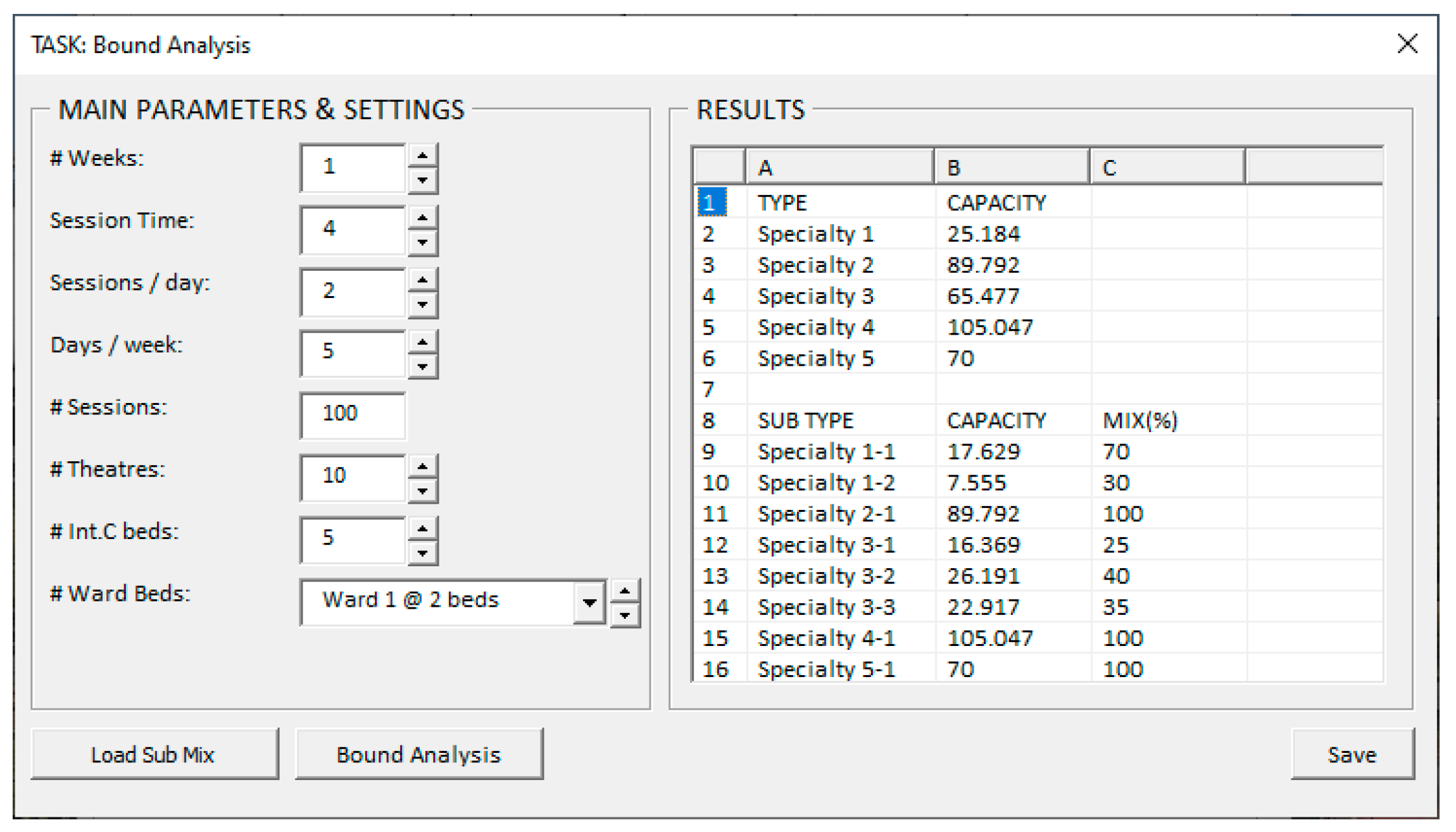

| Type | # Subtypes | Subtype | Subtype Mix (%) | (ic, sur, postop) Time (# h) | Wards Used | |
|---|---|---|---|---|---|---|
| T1 | 25.18 | 2 | T1–1 | 70 | (0, 1.2, 17.86) | W1 |
| T1–2 | 30 | (6, 1.25, 8.35) | W1, W2 | |||
| T2 | 89.79 | 1 | T2–1 | 100 | (0, 2.4, 16.31) | W1, W2, W5 |
| T3 | 65.48 | 3 | T3–1 | 25 | (0, 6.5, 12.94) | W3 |
| T3–2 | 40 | (0, 4.56, 12.39) | W3 | |||
| T3–3 | 35 | (0, 7.6, 5.54) | W3 | |||
| T4 | 105.05 | 1 | T4–1 | 100 | (0, 3.4, 18.99) | W4 |
| T5 | 70 | 1 | T5–1 | 100 | (12, 4.1, 22.81) | W4, W5 |
| Revision | Case Mix Alterations | New Case Mix | Impact | ||||
|---|---|---|---|---|---|---|---|
| T1 | 5.68 → 0 | −5.68 | (−5.68, 0.42, 0.48, 0.49, 0.33) | (0, 49.24, 20.91, 10.71, 28.71) | 109.57 | 1.71 | 0.0 |
| 5.68 → 2 | −3.68 | (−3.68, 0.27, 0.31, 0.32, 0.21) | (2, 49.09, 20.74, 10.54, 28.59) | 110.96 | 1.11 | 0.0 | |
| 5.68 → 25 | 19.32 | (19.32, −1.41, −1.63, −1.65, −1.10) | (25, 47.41, 18.8, 8.57, 27.28) | 127.06 | −5.79 | 0.02 | |
| 5.68 → 25.18 | 19.50 | (19.50, −1.43, −1.64, −1.67, −1.11) | (25.18, 47.39, 18.79, 8.55, 27.27) | 127.18 | −5.85 | 0.02 | |
| T2 | 48.82 → 0 | −48.82 | (2.26, −48.82, 9.28, 9.42, 6.28) | (7.94, 0, 29.71, 19.64, 34.66) | 91.95 | 27.23 | 0.09 |
| 48.82 → 30 | −18.82 | (0.87, −18.82, 3.58, 3.63, 2.42) | (6.55, 30, 24.01, 13.85, 30.8) | 105.21 | 10.5 | 0.04 | |
| 48.82 → 65 | 16.18 | (−0.75, 16.18, −3.07, −3.12, −2.08) | (4.93, 65, 17.36, 7.1, 26.3) | 120.69 | −9.02 | 0.03 | |
| 48.82 → 89.79 | 40.97 | (−1.89, 40.97, −7.78, −7.9, −5.27) | (3.78, 89.79, 12.65, 2.32, 23.11) | 131.65 | −22.84 | 0.08 | |
| T3 | 20.43 → 0 | −20.43 | (3.53, 12.59, −20.43, 14.73, 9.82) | (9.21, 61.41, 0, 24.95, 38.2) | 133.77 | 40.67 | 0.14 |
| 20.43 → 10 | −10.43 | (1.80, 6.43, −10.43, 7.52, 5.01) | (7.48, 55.25, 10, 17.74, 33.39) | 123.86 | 20.76 | 0.07 | |
| 20.43 → 30 | 9.57 | (−1.65, −5.9, 9.57, −6.9, −4.6) | (4.03, 42.93, 30, 3.32, 23.79) | 104.07 | −19.04 | 0.07 | |
| 20.43 → 65 | 44.57 | (−5.68, −47.61, 44.57, −10.22, −28.38) | (0, 1.215, 65, 0, 0) | 66.22 | −91.89 | 0.53 | |
| T4 | 10.22 → 0 | −10.22 | (0.75, 2.68, 3.09, −10.22, 2.09) | (6.43, 51.5, 23.52, 0, 30.47) | 111.92 | 8.61 | 0.03 |
| 10.22 → 3 | −7.22 | (0.53, 1.89, 2.18, −7.22, 1.48) | (6.21, 50.71, 22.61, 3, 29.86) | 112.39 | 6.08 | 0.02 | |
| 10.22 → 15 | 4.78 | (−0.35, −1.25, −1.44, 4.78, −0.98) | (5.33, 47.57, 18.99, 15, 27.41) | 114.3 | −4.02 | 0.01 | |
| 10.22 → 105.05 | 94.83 | (−5.68, −34.07, −20.43, 94.83, −26.56) | (0, 14.75, 0, 105.05, 1.82) | 121.62 | −86.74 | 0.38 | |
| T5 | 28.38 → 0 | −28.38 | (2.37, 8.46, 9.75, 9.9, −28.38) | (8.05, 57.28, 30.18, 20.12, 0) | 115.63 | 30.48 | 0.09 |
| 28.38 → 22 | −6.38 | (0.53, 1.90, 2.19, 2.26, −6.38) | (6.21, 50.72, 22.62, 12.48, 22) | 114.03 | 6.89 | 0.02 | |
| 28.38 → 32 | 3.62 | (-0.30, −1.08, −1.24, −1.26, 3.62) | (5.38, 47.74, 19.19, 8.96, 32) | 113.27 | −3.88 | 0.01 | |
| 28.38 → 57 | 28.62 | (-2.39, −8.53, −9.83, −9.98, 28.62) | (3.29, 40.29, 10.6, 0.24, 57) | 111.42 | −30.72 | 0.1 | |
| 28.38 → 57.9 | 29.52 | (-2.47, −8.82, −10.16, −10.22, 29.52) | (3.21, 40, 10.27, 0,57.9) | 111.38 | −31.69 | 0.1 | |
| 28.38 → 65 | 36.62 | (−3.31, −11.8, −13.59, −10.22, 36.62) | (2.37, 37.02, 6.84, 0, 65) | 111.23 | −75.54 | 0.13 | |
| 28.38 → 70 | 41.62 | (−5.68, −1.74, −20.43, −10.22, 41.62) | (0, 47.08, 0, 0, 70) | 117.08 | −38.07 | 0.23 |
| Revision | Alterations | New Case Mix | Impact | ||||
|---|---|---|---|---|---|---|---|
| T1 | 5.68 → 0 | −5.68 | (−5.68, 2.88, 0, 0, 0) | (0, 51.70, 20.43, 10.22, 28.38) | 110.73 | 2.88 | 0.03 |
| 5.68 → 2 | −3.68 | (−3.68, 1.88, 0, 0, 0) | (2, 50.69, 20.43, 10.22, 28.38) | 111.72 | 1.88 | 0.02 | |
| 5.68 → 25 | 19.32 | (19.32, 0, −3.84, 0, 0) | (25, 48.82, 16.59, 10.22, 28.38) | 129.01 | −3.84 | 0.04 | |
| 5.68 → 25.18 | 19.50 | (19.50, 0, −3.88, 0, 0) | (25.18, 48.82, 16.55, 10.22, 28.38) | 129.15 | −3.88 | 0.04 | |
| T2 | 48.82 → 0 | −48.82 | (19.50, −48.82, 0, 0, 22.8) | (25.18, 0, 20.43, 10.22, 51.18) | 107.01 | 42.30 | 1.10 |
| 48.82 → 30 | −18.82 | (19.50, −18.82, 0, 0, 5.24) | (25.18, 30, 20.43, 10.22, 33.62) | 119.45 | 24.74 | 0.85 | |
| 48.82 → 65 | 16.18 | (0, 16.18, −6.35, 0, 0) | (5.68, 65, 16.08, 10.22, 28.38) | 125.36 | −6.35 | 0.06 | |
| 48.82 → 89.79 | 40.97 | (0, 40.97, −16.09, 0, 0) | (5.68, 89.79, 4.34, 10.22, 28.28) | 138.31 | −16.09 | 0.16 | |
| T3 | 20.43 → 0 | −20.43 | (10.5, 31.01, −20.43, 0, 6.51) | (25.18, 79.83, 0, 10.22, 34.89) | 150.12 | 48.02 | 1.21 |
| 20.43 → 10 | −10.43 | (19.50, 16.68, −10.43, 0, 0) | (25.18, 65.5, 10, 10.22, 28.38) | 139.28 | 36.19 | 0.96 | |
| 20.43 → 30 | 9.57 | (0, 0, 9.57, −10.22, −5.78) | (5.68, 48.82, 30, 0, 22.6) | 107.1 | −16 | 0.18 | |
| 20.43 → 65 | 44.57 | (−3.28, −48.82, 44.57, −10.22, −28.38) | (2.4, 0, 65, 0, 0) | 67.4 | −90.7 | 1.18 | |
| T4 | 10.22 → 0 | −10.22 | (19.50, 4.61, 0, −10.22, 0) | (25.18, 53.43, 20.43, 0, 28.38) | 127.42 | 24.12 | 0.83 |
| 10.22 → 3 | −7.22 | (19.50, 0.36, 0, −7.22, 0) | (25.18, 49.18, 20.43, 3, 28.38) | 126.17 | 19.87 | 0.78 | |
| 10.22 → 15 | 4.78 | (0, 0, −2.66, 4.78, 0) | (5.68, 48.82, 17.77, 15, 28.38) | 115.65 | −2.66 | 0.03 | |
| 10.22 → 105.05 | 94.83 | (0, −33.85, −20.43, 94.83, −28.38) | (5.68, 14.96, 0, 105.05, 0) | 125.69 | −82.66 | 0.98 | |
| T5 | 28.38 → 0 | −28.38 | (19.50, 31.01, 0, 5.37, −28.38) | (25.18, 79.83, 20.43, 15.59, 0) | 141.03 | 55.88 | 1.17 |
| 28.38 → 22 | −6.38 | (19.50, 1.03, 0, 0, −6.38) | (25.18, 49.85, 20.43, 10.22, 22) | 127.68 | 20.54 | 0.79 | |
| 28.38 → 32 | 3.62 | (0, 0, −2.43, 0, 3.62) | (5.68, 48.82, 18, 10.22, 32) | 114.72 | −2.43 | 0.02 | |
| 28.38 → 57 | 28.62 | (0, 0, −19.21, 0, 28.62) | (5.68, 48.82, 1.23, 10.22, 57) | 122.95 | −19.21 | 0.19 | |
| 28.38 → 57.9 | 29.52 | (0, 0, −19.81, 0, 29.52) | (5.68, 48.82, 0.62, 10.22, 57.9) | 123.24 | −19.81 | 0.19 | |
| 28.38 → 65 | 36.62 | (0, 0, −20.43, −7.45, 36.62) | (5.48, 48.82, 0, 2.78, 65) | 122.08 | −27.88 | 0.27 | |
| 28.38 → 70 | 41.62 | (−5.68, −1.74, −20.43, −10.22, 41.62) | (0, 47.08, 0, 0, 70) | 117.08 | −38.07 | 0.54 |
| Revision | Alterations | New Case Mix | Impact | ||||
|---|---|---|---|---|---|---|---|
| T1 | 5.68 → 25 | 19.32 | (19.32, −0.69, −2.34, −1.34, −0.72) | (25, 48.13, 18.09, 8.89, 27. 66) | 100.11 | −5.09 | 0.0 |
| 5.68 → 25.18 | 19.50 | (19.50, −0.7, −2.36, −1.35, −0.73) | (25.18, 48.12, 18.07, 8.86, 27.66) | 127.89 | −5.14 | 0.0 | |
| T2 | 48.82 → 65 | 16.18 | (−0.05, 16.18, −4.16, −2.39, −1.28) | (5.63, 65, 16.27, 7.83, 27.10) | 121.83 | −7.88 | 0.0 |
| 48.82 → 89.79 | 40.97 | (−0.12, 40.97, −10.53, −6.04, −3.24) | (5.56, 89.79, 9.9, 4.18, 25.14) | 134.57 | −19.93 | 0.02 | |
| T3 | 20.43 → 30 | 9.57 | (−0.18, −4.4, 9.57, −8.52, −4.56) | (5.51, 44.43, 30, 1.7, 23.82) | 105.46 | −17.65 | 0.01 |
| 20.43 → 65 | 44.57 | (−3.28, −48.82, 44.57, −10.22, −28.38) | (2.4, 0, 65, 0, 0) | 67.4 | −90.7 | 0.49 | |
| T4 | 10.22 → 15 | 4.78 | (−0.02, −0.59, −2, 4.78, −0.62) | (5.66, 48.23, 18.42, 15, 27.76) | 115.07 | −3.234 | 0 |
| 10.22 → 105.05 | 94.83 | (−1.32, −33.18, −20.43, 94.83, −28.38) | (4.36, 15.64, 0, 105.05, 0) | 125.05 | −83.31 | 0.34 | |
| T5 | 28.38 → 32 | 3.62 | (−0.02, −0.5. −1.69, −0.97, 3.62) | (5.66, 48.32, 18.74, 9.25, 32) | 113.97 | −3.18 | 0 |
| 28.38 → 57 | 28.62 | (−0.16, −3.95, −13.36, −7.66, 28.62) | (5.23, 44.87, 7.07, 2.56, 57) | 116.73 | −25.13 | 0.02 | |
| 28.38 → 57.9 | 29.52 | (−0.16, −4.08, −13.78, −7.9, 29.52) | (5.52, 44.74, 6.65, 2.32, 57.9) | 117.13 | −25.92 | 0.03 | |
| 28.38 → 65 | 36.62 | (−0.2, −5.06, −17.09, −9.81, 36.62) | (5.48, 43.76, 3.34, 0.41, 65) | 117.99 | −32.16 | 0.04 | |
| 28.38 → 70 | 41.62 | (−5.68, −5.6, −18.91, −10.22, 41.62) | (0, 43.22, 1.52, 0, 70) | 114.74 | −40.41 | 0.1 |
| Revision | Alterations | New Case Mix | Impact | ||||
|---|---|---|---|---|---|---|---|
| T1 | 5.68 → 0 | −5.68 | (−5.68, 2.88, 0, 0, 0) | (0, 51.70, 20.43, 10.22, 28.38) | 110.73 | 2.88 | 0.0 |
| 5.68 → 2 | −3.68 | (−3.68, 1.87, 0, 0, 0) | (2, 50.69, 20.43, 10.22, 28.38) | 111.72 | 1.87 | 0 | |
| 5.68 → 25 | 19.324 | (19.32, −0.72, −2.39, −1.26, −0.7) | (25, 48.1, 18.04, 8.96, 27.68) | 127.78 | −5.07 | 0.0 | |
| 5.68 → 25.18 | 19.504 | (19.50, −0.72, −2.43, −1.26, −0.7) | (25.18, 48.1, 18, 8.96, 27.68) | 127.92 | −5.11 | 0.0 | |
| T2 | 48.82 → 0 | −48.82 | (19.50, −48.82, 0, 0, 22.80) | (25.18, 0, 20.43, 10.22, 51.18) | 107.01 | 42.3 | 0.71 |
| 48.82 → 30 | −18.82 | (19.50, −18.82, 0, 0, 5.24) | (25.18, 30, 20.43, 10.22, 33.62) | 119.45 | 24.74 | 0.61 | |
| 48.82 → 65 | 16.18 | (−0.05, 16.18, −4.13, −2.46, −1.26) | (5.63, 65, 16.3, 7.76, 27.12) | 121.81 | −7.9 | 0.0 | |
| 48.82 → 89.79 | 40.972 | (−0.151, 40.97, −10.52, −6.08, −3.21) | (5.53, 89.79, 9.91, 4.14, 25.17) | 134.54 | −19.96 | 0.02 | |
| T3 | 20.43 → 0 | −20.43 | (19.50, 31.01, −20.43, 0, 6.51) | (25.18, 79.83, 0, 10.22, 34.89) | 150.12 | 57.02 | 0.73 |
| 20.43 → 10 | −10.43 | (19.50, 16.68, −10.43, 0, 0) | (25.18, 65.5, 10, 10.22, 28.38) | 139.28 | 36.18 | 0.63 | |
| 20.43 → 30 | 9.57 | (−0.2, −4.48, 9.57, −8.4, −4.61) | (5.48, 44.34, 30, 1.83, 23.77) | 105.42 | −17.69 | 0.01 | |
| 20.43 → 65 | 44.57 | (−3.28, −48.82, 44.57, −10.22, −28.38) | (2.4, 0, 65, 0, 0) | 67.4 | −90.7 | 0.49 | |
| T4 | 10.22 → 0 | −10.22 | (19.50, 4.61, 0, −10.22, 0) | (25.184, 53.43, 20.43, 0, 28.38) | 127.424 | 24.11 | 0.6 |
| 10.22 → 3 | −7.22 | (19.50, 0, 0, −7.22, 0.21) | (25.184, 48.82, 20.43, 3, 28.59) | 126.024 | 19.71 | 0.6 | |
| 10.22 → 15 | 4.78 | (−0.05, −0.54, −2.06, 4.78, −0.56) | (5.63, 48.28, 18.37, 15, 27.82) | 115.1 | −3.21 | 0.0 | |
| 10.22 → 105.05 | 94.827 | (−1.31, −33.18, −20.43, 94.83, −28.38) | (4.37, 15.64, 0, 105, 0) | 125.01 | −83.3 | 0.33 | |
| T5 | 28.38 → 0 | −28.38 | (19.50, 31.01, 0, 5.37, −28.38) | (25.18, 79.83, 20.43, 15.59, 0) | 141.03 | 55.88 | 0.72 |
| 28.38 → 22 | −6.38 | (19.50, 1.03, 0, 0, −6.38) | (25.18, 49.85, 20.43, 10.22, 22) | 127.68 | 20.53 | 0.6 | |
| 28.38 → 32 | 3.62 | (−0.05, −0.54, −1.65, −0.99, 3.62) | (5.63, 48.28, 18.78, 9.23, 32) | 113.92 | −3.23 | 0 | |
| 28.38 → 57 | 28.62 | (−0.15, −3.94, −13.42, −7.55, 28.62) | (5.53, 44.88, 7.01, 2.67, 57) | 117.09 | −25.06 | 0.02 | |
| 28.38 → 57.9 | 29.52 | (−0.15, −4.12, −13.73, −7.97, 29.52) | (5.53, 44.7, 6.71, 2.25, 57.9) | 117.09 | −25.97 | 0.03 | |
| 28.38 → 65 | 36.62 | (−0.2, −5.02, −17.08, −9.86, 36.62) | (5.48, 43.8, 3.35, 0.37, 65) | 118 | −32.16 | 0.04 | |
| 28.38 → 70 | 41.62 | (−5.68, −5.56, −18.93, −10.22, 41.62) | (0, 43.26, 1.5, 0, 70) | 114.76 | −40.39 | 0.1 |
| 20% | 0.14 | 0.14 | 2.33 | 1.35 | |
| 20% | 3.32 | 3.32 | 7.12 | 4.56 | |
| 40% | 11.01 | 10.44 | 14.66 | 11.58 | |
| 60% | 5.18 | 3.67 | 8.79 | 5.21 | |
| 80% | 19.13 | 11.83 | 23.32 | 13.5 | |
| 100% | 461.3 | 268.28 | 466.3 | 270 |
| Sub Type | Mix (%) | Summary | Pathway | Length of Stay |
|---|---|---|---|---|
| T6–1 (mild) | 45 | Patients with mild upper respiratory tract infection | Ward | 0.25 days in a ward |
| T6–2 (moderate) | 35 | Patients requiring hospitalization, with pneumonia and with/without the need for oxygen | Ward | 5 days in a ward |
| T6–3 (severe) | 15 | Patients who need ICU treatment and require non-invasive or invasive mechanical ventilation, or with acute respiratory distress and/or non-pulmonary involvement | (Ward, ICU, Ward) | 2 days in ward prior to ICU, 5 days in ICU + 7 days in a ward |
| T6–4 (critical) | 5 | Patients who need immunomodulatory therapy or with multi-organ failure and/or cytokine storm | (ICU, Ward) | 14 days in ICU + 7 days in a ward |
| Ward | Repurposed for Covid | #Beds | Used For | Ward | Repurposed for COVID | #Beds | Used For |
|---|---|---|---|---|---|---|---|
| W1 | ✓ | 2 | T6 | W4 | ✕ | 14 | T4–1, T5–1, T1–1, T1–2, T2–1 |
| W2 | ✕ | 5 | T1–1, T1–2, T2–1 | W5 | ✓ | 3 | T6 |
| W3 | ✕ | 10 | T3–1, T3–2, T3–3 | W6 | ✓ | 6 | T6 |
| Type | # Subtypes | Subtype | Subtype Mix (%) | (ic, sur, postop) Time (# h) | Wards Used | ||
|---|---|---|---|---|---|---|---|
| (orig) | (new) | ||||||
| 1 | 201.47 | 1000 | 2 | 1–1 | 70 | (0, 1.2, 17.86) | W2, W4 |
| 1–2 | 30 | (6, 1.25,8.35) | W2, W4 | ||||
| 2 | 718.33 | 1000 | 1 | 2–1 | 100 | (0, 2.4, 16.31) | W2, W4 |
| 3 | 523.82 | 523.82 | 3 | 3–1 | 25 | (0, 6.5, 12.94) | W3 |
| 3–2 | 40 | (0, 4.56, 12.39) | W3 | ||||
| 3–3 | 35 | (0, 7.6, 5.54) | W3 | ||||
| 4 | 840.38 | 840.38 | 1 | 4–1 | 100 | (0, 3.4, 18.99) | W4 |
| 5 | 560 | 560 | 1 | 5–1 | 100 | (12, 4.1, 22.81) | W4 |
| 6 | na | 172.91 | 4 | 6–1 | 45 | (0, 0, 6) | W1, W5, W6 |
| 6–2 | 35 | (0, 0, 120) | W1, W5, W6 | ||||
| 6–3 | 15 | (120, 0, 216) | W1, W5, W6 | ||||
| 6–4 | 5 | (336, 0, 168) | W1, W5, W6 | ||||
| Alterations | ) ) | Ward Util (%) (ICU, OT, W1, W2, W3, W4, W5, W6) | |
|---|---|---|---|
| 50 | (−0.0025, −0.0026, −0.001, −0.002, −0.001, 100) | (45.41, 390.54, 163.48, 81.74, 227.06, 50) 958.22 (908.22) | (67.66, 100, 0, 9.02, 19.75, 81.73, 0, 53.01) |
| 100 | (−0.0025, −0.0026, −0.001, −0.002, −0.001, 100) | (45.41, 390.53, 163.48, 81.74, 227.06, 100) 1008.2 (908.22) | (93.55, 100, 100, 0, 19.75, 84.95, 100, 22.69) |
| 125 | (−45.41, −52.79, −27.65, −44.36, −29.56, 125) | (0, 337.75, 135.83, 37.38, 197.5, 125) 833.46 (708.46) | (100, 80.54, 100, 0, 16.41, 66.28, 100, 49.2) |
| 150 | (−45.41, −182.25, −95.47, −81.74, −102.06, 150) | (0, 208.29, 68.01, 0, 125, 150) 551.3 (401.3) | (100, 44.62, 100, 0, 8.22, 35.59, 100, 75.71) |
| 172 | (−45.41, −296.18, −155.14, −81.74, −165.86, 172) | (0, 94.36, 8.34, 0, 61.2, 172) 335.9 (163.9) | (100, 16.51, 100, 0, 1, 18.14, 100, 99.03) |
| Alterations | ) ) | Ward Util (%) (ICU, OT, W1, W2, W3, W4, W5, W6) | |
|---|---|---|---|
| 50 | (0, 0, −0.005, 0, 0, 50) | (45.41, 390.54, 163.48, 81.74, 227.06, 50) 958.22 (908.22) | (67.66, 100, 0, 9.02, 19.75, 81.73, 0, 53.01) |
| 100 | (0, 0, −0.005, 0, 0, 100) | (45.41, 390.53, 163.48, 81.74, 227.06, 100) 1008.2 (908.22) | (93.55, 100, 100, 0, 19.75, 84.95, 44.2, 50.6) |
| 125 | (0, 0, 0, 0, −36.37, 125) | (45.41, 390.54, 163.48, 81.74, 190.69, 125) 996.86 (871.86) | (100, 95.34, 100, 0, 19.75, 79.75, 89.58, 54.41) |
| 150 | (0, 0, 0, 0, −108.87, 150) | (45.41, 390.54, 163.48, 81.74, 118.19, 150) 949.36 (799.36) | (100, 86.05, 100, 0, 19.75, 69.38, 100, 75.71) |
| 172 | (0, 0, 0, 0, −172.67, 172) | (45.41, 390.54, 163.48, 81.74, 54.39, 172) 907.56 (735.56) | (100, 77.88, 100, 0, 19.75, 60.25, 100, 99.03) |
| Alterations | ) ) | Ward Util (%) (ICU, OT, W1, W2, W3, W4, W5, W6) | |
|---|---|---|---|
| 50 | (−0.01, −0.01, −0.01, −0.01, −0.01, 50) | (45.41, 390.54, 163.48, 81.74, 227.06, 50) 958.17 (908.17) | (67.66, 100, 0, 0, 19.75, 84.94, 0, 53.01) |
| 100 | (−0.01, −0.01, −0.01, −0.01, −0.01, 100) | (45.41, 390.53, 163.48, 81.74, 227.06, 100) 1008.2 (908.22) | (93.55, 100, 66.77, 0, 19.75, 84.95, 62.67, 52.43) |
| 125 | (−16.23, −0.012, −0.016, −0.014, −33.94, 125) | (29.18, 390.52, 163.46, 81.73, 193.12, 125) 983.01 (858.01) | (100, 95.03, 72.98, 0, 19.75, 78.69, 71.91, 72.25) |
| 150 | (−45.41, −0.012, −0.011, −0.011, −102.06, 150) | (0, 390.53, 163.47, 81.73, 125, 150) 910.73 (760.7) | (100, 85.2, 82.15, 0, 19.75, 66.44, 84.5, 89.41) |
| 172 | (−41.41, −0.014, −0.012, −0.013, −165.86, 172) | (0, 390.53, 163.47, 81.73, 61.12, 172) 868.92 (696.92) | (100, 77.02, 98.81, 0, 19.75, 57.31, 57.31, 99.29, 9.79) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burdett, R.L.; Corry, P.; Cook, D.; Yarlagadda, P. Analytical Techniques for Supporting Hospital Case Mix Planning Encompassing Forced Adjustments, Comparisons, and Scoring. Healthcare 2025, 13, 47. https://doi.org/10.3390/healthcare13010047
Burdett RL, Corry P, Cook D, Yarlagadda P. Analytical Techniques for Supporting Hospital Case Mix Planning Encompassing Forced Adjustments, Comparisons, and Scoring. Healthcare. 2025; 13(1):47. https://doi.org/10.3390/healthcare13010047
Chicago/Turabian StyleBurdett, Robert L., Paul Corry, David Cook, and Prasad Yarlagadda. 2025. "Analytical Techniques for Supporting Hospital Case Mix Planning Encompassing Forced Adjustments, Comparisons, and Scoring" Healthcare 13, no. 1: 47. https://doi.org/10.3390/healthcare13010047
APA StyleBurdett, R. L., Corry, P., Cook, D., & Yarlagadda, P. (2025). Analytical Techniques for Supporting Hospital Case Mix Planning Encompassing Forced Adjustments, Comparisons, and Scoring. Healthcare, 13(1), 47. https://doi.org/10.3390/healthcare13010047







