Artificial Intelligence for Forecasting the Prevalence of COVID-19 Pandemic: An Overview
Abstract
:1. Introduction
2. Artificial Intelligence Models
2.1. Nonlinear Autoregressive ANN
2.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.3. Hybrid Fractal-Fuzzy Approach
2.4. Long Short-Term Memory Network (LSTM)
2.5. Bayesian Neural Network (BNN)
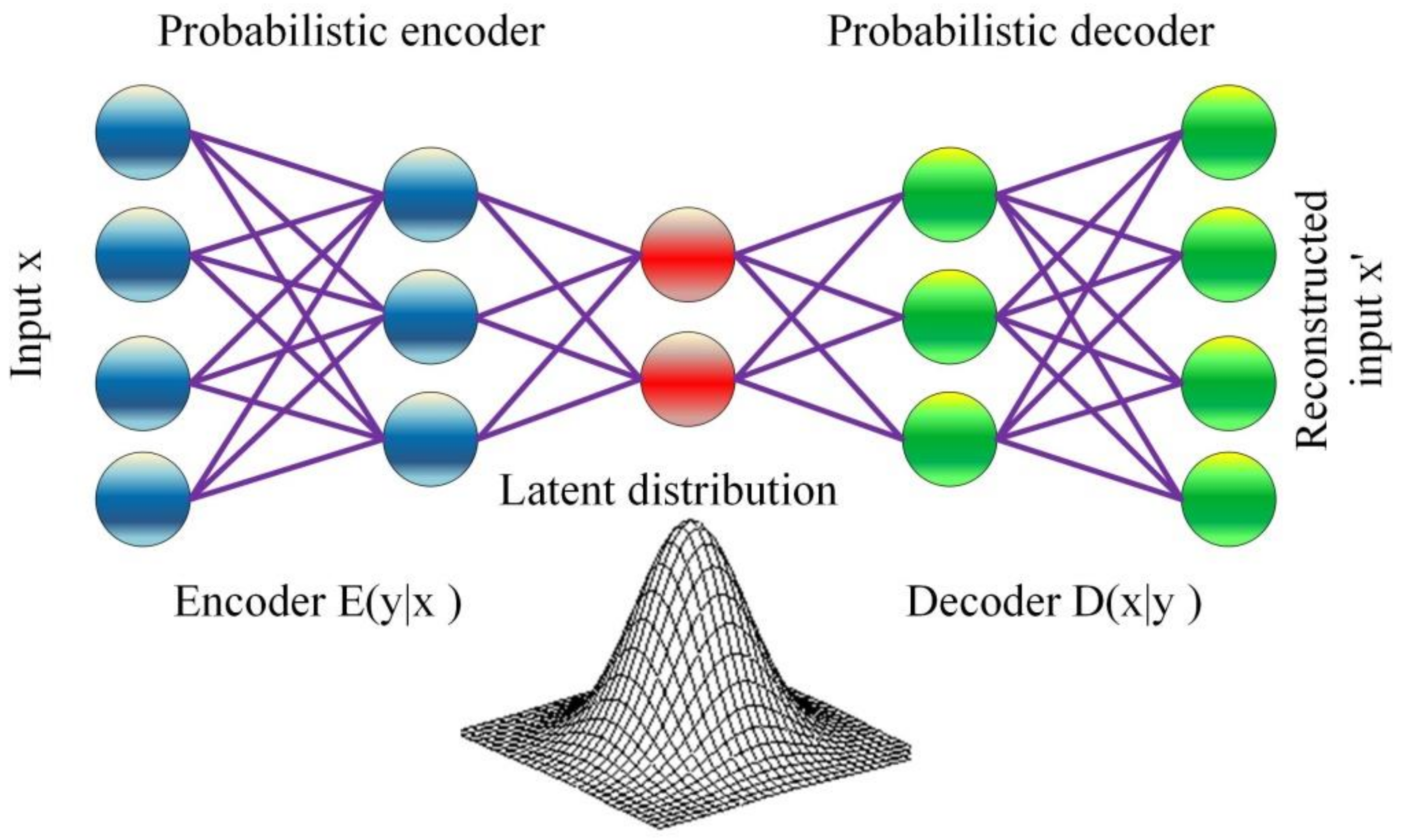
2.6. Variational AutoEncoder (VAE)
2.7. Singular Spectrum Analysis (SSA)
- The new time series is defined as follows:where the coefficients vector is computed as follows:
- The numbers represent the recurrent forecast with an step.
- Define a new time series vector as follows;where ,, , and represent a vector of last components.
- The time series is obtained by averaging the diagonal of constructed matrix .
- The numbers represent the vector forecast with an step.
3. Evaluation Criteria
4. Comparative Study and Discussion
4.1. Statistical Models
4.2. Artificial Intelligence Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, Y.; Li, M.; Zhong, Q.; Li, Q.; Yang, R.; Lin, J.; Zhang, X. The Chinese Government’s response to the pandemic: Measures, dynamic changes, and main patterns. Healthcare 2021, 9, 1020. [Google Scholar] [CrossRef]
- Xu, W.; Wu, J.; Cao, L. COVID-19 pandemic in China: Context, experience and lessons. Health Policy Technol. 2020, 9, 639–648. [Google Scholar] [CrossRef]
- Briz-Redón, Á. The impact of modelling choices on modelling outcomes: A spatio-temporal study of the association between COVID-19 spread and environmental conditions in Catalonia (Spain). Stoch. Environ. Res. Risk Assess. 2021, 35, 1701–1713. [Google Scholar] [CrossRef] [PubMed]
- Rakha, A.; Hettiarachchi, H.; Rady, D.; Gaber, M.M.; Rakha, E.; Abdelsamea, M.M. Predicting the economic impact of the COVID-19 pandemic in the United Kingdom using time-series mining. Economies 2021, 9, 137. [Google Scholar] [CrossRef]
- Alzahrani, S.I.; Aljamaan, I.A.; Al-Fakih, E.A. Forecasting the spread of the COVID-19 pandemic in Saudi Arabia using ARIMA prediction model under current public health interventions. J. Infect. Public Health 2020, 13, 914–919. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-P.; Wang, Y.; Khan, M.A.; Alshahrani, M.Y.; Muhammad, T. A dynamical study of SARS-COV-2: A study of third wave. Results Phys. 2021, 29, 104705. [Google Scholar] [CrossRef] [PubMed]
- Helwan, A.; Ma’Aitah, M.K.S.; Hamdan, H.; Ozsahin, D.U.; Tuncyurek, O. Radiologists versus deep convolutional neural networks: A comparative study for diagnosing COVID-19. Comput. Math. Methods Med. 2021, 2021, 5527271. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.I.; Shah, S.A.A.; Al-Khasawneh, M.A. A novel deep convolutional neural network model to monitor people following guidelines to avoid COVID-19. J. Sens. 2020, 2020, 8856801. [Google Scholar] [CrossRef]
- Kalantari, M. Forecasting COVID-19 pandemic using optimal singular spectrum analysis. Chaos Solitons Fractals 2021, 142, 110547. [Google Scholar] [CrossRef]
- Saba, A.I.; Elsheikh, A.H. Forecasting the prevalence of COVID-19 outbreak in Egypt using nonlinear autoregressive artificial neural networks. Process. Saf. Environ. Prot. 2020, 141, 1–8. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Saba, A.I.; Elaziz, M.A.; Lu, S.; Shanmugan, S.; Muthuramalingam, T.; Kumar, R.; Mosleh, A.O.; Essa, F.A.; Shehabeldeen, T.A. Deep learning-based forecasting model for COVID-19 outbreak in Saudi Arabia. Process. Saf. Environ. Prot. 2021, 149, 223–233. [Google Scholar] [CrossRef]
- Kırbaş, İ.; Sözen, A.; Tuncer, A.D.; Kazancıoğlu, F.Ş. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals 2020, 138, 110015. [Google Scholar] [CrossRef] [PubMed]
- Anam, S.; Maulana, M.H.A.A.; Hidayat, N.; Yanti, I.; Fitriah, Z.; Mahanani, D.M. Predicting the number of COVID-19 sufferers in Malang city using the backpropagation neural network with the Fletcher-Reeves method. Appl. Comput. Intell. Soft Comput. 2021, 2021, 6658552. [Google Scholar] [CrossRef]
- Potdar, K.; Kinnerkar, R. A non-linear autoregressive neural network model for forecasting Indian index of industrial production. In Proceedings of the 2017 IEEE Region 10 Symposium (TENSYMP), Cochin, India, 14–16 July 2017; pp. 1–5. [Google Scholar]
- Alsumaiei, A.A. A nonlinear autoregressive modeling approach for forecasting groundwater level fluctuation in urban aquifers. Water 2020, 12, 820. [Google Scholar] [CrossRef] [Green Version]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Mrabet Bellaaj, N. A nonlinear autoregressive exogenous (NARX) neural network model for the prediction of the daily direct solar radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef] [Green Version]
- Gautam, S.S. A novel moving average forecasting approach using fuzzy time series data set. J. Control Autom. Electr. Syst. 2019, 30, 532–544. [Google Scholar] [CrossRef]
- Bacanli, U.G.; Firat, M.; Dikbas, F. Adaptive neuro-fuzzy inference system for drought forecasting. Stoch. Environ. Res. Risk Assess. 2009, 23, 1143–1154. [Google Scholar] [CrossRef]
- Duong, T.H.; Nguyen, D.C.; Nguyen, S.D.; Hoang, M.H. An adaptive neuro-fuzzy inference system for seasonal forecasting of tropical cyclones making landfall along the Vietnam Coast. In Advanced Computational Methods for Knowledge Engineering; Springer: Heidelberg, Germany, 2013; pp. 225–236. [Google Scholar]
- Al-qaness, M.A.; Abd Elaziz, M.; Ewees, A.A.; Cui, X. A modified adaptive neuro-fuzzy inference system using multi-verse optimizer algorithm for oil consumption forecasting. Electronics 2019, 8, 1071. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Zhang, D.; Zhang, X.; Tian, A. Surface profile topography of ionic polymer metal composite based on fractal theory. Surf. Interfaces 2021, 22, 100834. [Google Scholar] [CrossRef]
- Karaca, Y.; Zhang, Y.-D.; Muhammad, K. Characterizing complexity and self-similarity based on fractal and entropy analyses for stock market forecast modelling. Expert Syst. Appl. 2020, 144, 113098. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Kumari, K.; Dey, P.; Kumar, C.; Pandit, D.; Mishra, S.S.; Kisku, V.; Chaulya, S.K.; Ray, S.K.; Prasad, G.M. UMAP and LSTM based fire status and explosibility prediction for sealed-off area in underground coal mine. Process. Saf. Environ. Prot. 2021, 146, 837–852. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm. Electr. Power Syst. Res. 2021, 192, 106995. [Google Scholar] [CrossRef]
- Zhang, N.; Shen, S.-L.; Zhou, A.; Jin, Y.-F. Application of LSTM approach for modelling stress–strain behaviour of soil. Appl. Soft Comput. 2021, 100, 106959. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Katekar, V.P.; Muskens, O.L.; Deshmukh, S.S.; Elaziz, M.A.; Dabour, S.M. Utilization of LSTM neural network for water production forecasting of a stepped solar still with a corrugated absorber plate. Process. Saf. Environ. Prot. 2021, 148, 273–282. [Google Scholar] [CrossRef]
- Chang, Y.-S.; Chiao, H.-T.; Abimannan, S.; Huang, Y.-P.; Tsai, Y.-T.; Lin, K.-M. An LSTM-based aggregated model for air pollution forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Zheng, S.; Zhong, Q.; Peng, L.; Chai, X. A simple method of residential electricity load forecasting by improved Bayesian neural networks. Math. Probl. Eng. 2018, 2018, 225–236. [Google Scholar] [CrossRef]
- Mbuvha, R.; Jonsson, M.; Ehn, N.; Herman, P. Bayesian neural networks for one-hour ahead wind power forecasting. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 591–596. [Google Scholar]
- Zhang, X.; Liang, F.; Yu, B.; Zong, Z. Explicitly integrating parameter, input, and structure uncertainties into Bayesian Neural Networks for probabilistic hydrologic forecasting. J. Hydrol. 2011, 409, 696–709. [Google Scholar] [CrossRef]
- Leles, M.C.R.; Sansão, J.P.H.; Mozelli, L.A.; Guimarães, H.N. A new algorithm in singular spectrum analysis framework: The Overlap-SSA (ov-SSA). SoftwareX 2018, 8, 26–32. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Ferreira, J.A.; Rocha, A.; Castanheira, J.M.; Melo-Gonçalves, P.; Vaz, N.; Dias, J.M. Singular spectrum analysis and forecasting of hydrological time series. Phys. Chem. Earth Parts A/B/C 2006, 31, 1172–1179. [Google Scholar] [CrossRef]
- Rodrigues, P.C.; Pimentel, J.; Messala, P.; Kazemi, M. The decomposition and forecasting of mutual investment funds using singular spectrum analysis. Entropy 2020, 22, 83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, S.R.; dos Santos Coelho, L. Wind speed forecasting approach based on singular spectrum analysis and adaptive neuro fuzzy inference system. Renew. Energy 2018, 126, 736–754. [Google Scholar] [CrossRef]
- Lima de Menezes, M.; Castro Souza, R.; Moreira Pessanha, J.F. Electricity consumption forecasting using singular spectrum analysis. Dyna 2015, 82, 138–146. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Abd Elaziz, M.; Kabeel, A.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Yousaf, M.; Zahir, S.; Riaz, M.; Hussain, S.M.; Shah, K. Statistical analysis of forecasting COVID-19 for upcoming month in Pakistan. Chaos Solitons Fractals 2020, 138, 109926. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Zhang, X. ARIMA modelling and forecasting of irregularly patterned COVID-19 outbreaks using Japanese and South Korean data. Data Brief 2020, 31, 105779. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Ghosh, I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals 2020, 135, 109850. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Parmar, K.S.; Kumar, J.; Makkhan, S.J.S. Development of new hybrid model of discrete wavelet decomposition and Autoregressive Integrated Moving Average (ARIMA) models in application to one month forecast the casualties cases of COVID-19. Chaos Solitons Fractals 2020, 135, 109866. [Google Scholar] [CrossRef] [PubMed]
- Ahmar, A.S.; del Val, E.B. SutteARIMA: Short-term forecasting method, a case: Covid-19 and stock market in Spain. Sci. Total. Environ. 2020, 729, 138883. [Google Scholar] [CrossRef]
- Aslam, M. Using the Kalman filter with ARIMA for the COVID-19 pandemic dataset of Pakistan. Data Brief 2020, 31, 105854. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Mariani, V.C.; Coelho, L.D.S. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar] [CrossRef] [PubMed]
- Barmparis, G.D.; Tsironis, G.P. Estimating the infection horizon of COVID-19 in eight countries with a data-driven approach. Chaos Solitons Fractals 2020, 135, 109842. [Google Scholar] [CrossRef] [PubMed]
- Arias Velásquez, R.M.; Mejía Lara, J.V. Forecast and evaluation of COVID-19 spreading in USA with reduced-space Gaussian process regression. Chaos Solitons Fractals 2020, 136, 109924. [Google Scholar] [CrossRef] [PubMed]
- Postnikov, E.B. Estimation of COVID-19 dynamics “on a back-of-envelope”: Does the simplest SIR model provide quantitative parameters and predictions? Chaos Solitons Fractals 2020, 135, 109841. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Zhao, L.; Zhang, A.; Song, L.; Liao, Y.; Lu, W.; Cui, C. Early forecasting of the potential risk zones of COVID-19 in China’s megacities. Sci. Total Environ. 2020, 729, 138995. [Google Scholar] [CrossRef]
- Şahin, U.; Şahin, T. Forecasting the cumulative number of confirmed cases of COVID-19 in Italy, UK and USA using fractional nonlinear grey Bernoulli model. Chaos Solitons Fractals 2020, 138, 109948. [Google Scholar] [CrossRef] [PubMed]
- Alberti, T.; Faranda, D. On the uncertainty of real-time predictions of epidemic growths: A COVID-19 case study for China and Italy. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105372. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Guo, S.; Xie, N.; Yao, L.; Cao, Y.; Day, S.W.; Howard, S.C.; Graff, J.C.; Gu, T.; et al. Real-time estimation and prediction of mortality caused by COVID-19 with patient information based algorithm. Sci. Total Environ. 2020, 727, 138394. [Google Scholar] [CrossRef] [PubMed]
- Perc, M.; Gorišek Miksić, N.; Slavinec, M.; Stožer, A. Forecasting COVID-19. Front. Phys. 2020, 8, 127. [Google Scholar] [CrossRef] [Green Version]
- Ayinde, K.; Lukman, A.F.; Rauf, R.I.; Alabi, O.O.; Okon, C.E.; Ayinde, O.E. Modeling Nigerian covid-19 cases: A comparative analysis of models and estimators. Chaos Solitons Fractals 2020, 138, 109911. [Google Scholar] [CrossRef] [PubMed]
- Singhal, A.; Singh, P.; Lall, B.; Joshi, S.D. Modeling and prediction of COVID-19 pandemic using Gaussian mixture model. Chaos Solitons Fractals 2020, 138, 110023. [Google Scholar] [CrossRef] [PubMed]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of the COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef] [PubMed]
- Ly, K.T. A COVID-19 forecasting system using adaptive neuro-fuzzy inference. Financ. Res. Lett. 2020, 41, 101844. [Google Scholar] [CrossRef] [PubMed]
- Alsayed, A.; Sadir, H.; Kamil, R.; Sari, H. Prediction of epidemic peak and infected cases for COVID-19 disease in Malaysia, 2020. Int. J. Environ. Res. Public Health 2020, 17, 4076. [Google Scholar] [CrossRef] [PubMed]
- Behnood, A.; Mohammadi Golafshani, E.; Hosseini, S.M. Determinants of the infection rate of the COVID-19 in the U.S. using ANFIS and Virus Optimization Algorithm (VOA). Chaos Solitons Fractals 2020, 139, 110051. [Google Scholar] [CrossRef]
- Al-qaness, M.A.A.; Saba, A.I.; Elsheikh, A.H.; Elaziz, M.A.; Ibrahim, R.A.; Lu, S.; Hemedan, A.A.; Shanmugan, S.; Ewees, A.A. Efficient artificial intelligence forecasting models for COVID-19 outbreak in Russia and Brazil. Process. Saf. Environ. Prot. 2021, 149, 399–409. [Google Scholar] [CrossRef] [PubMed]
- Castillo, O.; Melin, P. Forecasting of COVID-19 time series for countries in the world based on a hybrid approach combining the fractal dimension and fuzzy logic. Chaos Solitons Fractals 2020, 140, 110242. [Google Scholar] [CrossRef] [PubMed]
- Shaharudin, S.M.; Ismail, S.; Tan, M.L.; Mohamed, N.S.; AininaFilzaSulaiman, N. Predictive modelling of covid-19 cases in Malaysia based on recurrent forecasting-singular spectrum analysis approach. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9. [Google Scholar]
- Da Silva, R.G.; Ribeiro, M.H.D.M.; Mariani, V.C.; Coelho, L.D.S. Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables. Chaos Solitons Fractals 2020, 139, 110027. [Google Scholar] [CrossRef] [PubMed]
- Hazarika, B.B.; Gupta, D. Modelling and forecasting of COVID-19 spread using wavelet-coupled random vector functional link networks. Appl. Soft Comput. 2020, 96, 106626. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef] [PubMed]
- Shastri, S.; Singh, K.; Kumar, S.; Kour, P.; Mansotra, V. Deep-LSTM ensemble framework to forecast Covid-19: An insight to the global pandemic. Int. J. Inf. Technol. 2021, 13, 1291–1301. [Google Scholar] [CrossRef] [PubMed]
- Shastri, S.; Singh, K.; Kumar, S.; Kour, P.; Mansotra, V. Time series forecasting of Covid-19 using deep learning models: India-USA comparative case study. Chaos Solitons Fractals 2020, 140, 110227. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zheng, X.; Ai, G.; Liu, D.; Zhu, B. Time series prediction for the epidemic trends of COVID-19 using the improved LSTM deep learning method: Case studies in Russia, Peru and Iran. Chaos Solitons Fractals 2020, 140, 110214. [Google Scholar] [CrossRef] [PubMed]
- Gautam, Y. Transfer Learning for COVID-19 cases and deaths forecast using LSTM network. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Polyzos, S.; Samitas, A.; Spyridou, A.E. Tourism demand and the COVID-19 pandemic: An LSTM approach. Tour. Recreat. Res. 2020, 46, 175–187. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Prediction of COVID-19 confirmed cases combining deep learning methods and Bayesian optimization. Chaos Solitons Fractals 2020, 142, 110511. [Google Scholar] [CrossRef] [PubMed]
- Tomar, A.; Gupta, N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci. Total Environ. 2020, 728, 138762. [Google Scholar] [CrossRef]
- Torrealba-Rodriguez, O.; Conde-Gutiérrez, R.A.; Hernández-Javier, A.L. Modeling and prediction of COVID-19 in Mexico applying mathematical and computational models. Chaos Solitons Fractals 2020, 138, 109946. [Google Scholar] [CrossRef]
- Pathan, R.K.; Biswas, M.; Khandaker, M.U. Time series prediction of COVID-19 by mutation rate analysis using recurrent neural network-based LSTM model. Chaos Solitons Fractals 2020, 138, 110018. [Google Scholar] [CrossRef]
- Prasanth, S.; Singh, U.; Kumar, A.; Tikkiwal, V.A.; Chong, P.H.J. Forecasting spread of COVID-19 using google trends: A hybrid GWO-deep learning approach. Chaos Solitons Fractals 2020, 142, 110336. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef] [PubMed]
- Issa, M.; Helmi, A.M.; Elsheikh, A.H.; Abd Elaziz, M. A biological sub-sequences detection using integrated BA-PSO based on infection propagation mechanism: Case study COVID-19. Expert Syst. Appl. 2022, 189, 116063. [Google Scholar] [CrossRef]
- Salgotra, R.; Gandomi, M.; Gandomi, A.H. Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming. Chaos Solitons Fractals 2020, 138, 109945. [Google Scholar] [CrossRef] [PubMed]
- Al-Qaness, M.A.; Ewees, A.A.; Fan, H.; Abd El Aziz, M. Optimization method for forecasting confirmed cases of COVID-19 in China. J. Clin. Med. 2020, 9, 674. [Google Scholar] [CrossRef] [Green Version]
- Sitaula, C.; Hossain, M.B. Attention-based VGG-16 model for COVID-19 chest X-ray image classification. Appl. Intell. 2021, 51, 2850–2863. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Dahou, A.; Alsaleh, N.A.; Elsheikh, A.H.; Saba, A.I.; Ahmadein, M. Boosting COVID-19 Image Classification Using MobileNetV3 and Aquila Optimizer Algorithm. Entropy 2021, 23, 1383. [Google Scholar] [CrossRef]
- Wang, L.; Lin, Z.Q.; Wong, A. COVID-Net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest X-ray images. Sci. Rep. 2020, 10, 19549. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, W.; Qiu, X. Deep learning for COVID-19 detection based on CT images. Sci. Rep. 2021, 11, 14353. [Google Scholar] [CrossRef] [PubMed]
- Das, A.K.; Ghosh, S.; Thunder, S.; Dutta, R.; Agarwal, S.; Chakrabarti, A. Automatic COVID-19 detection from X-ray images using ensemble learning with convolutional neural network. Pattern Anal. Appl. 2021, 24, 1111–1124. [Google Scholar] [CrossRef]
- Rahimzadeh, M.; Attar, A. A modified deep convolutional neural network for detecting COVID-19 and pneumonia from chest X-ray images based on the concatenation of Xception and ResNet50V2. Inform. Med. Unlocked 2020, 19, 100360. [Google Scholar] [CrossRef]
- Aswathy, A.L.; Hareendran, A.; Vinod Chandra, S.S. COVID-19 diagnosis and severity detection from CT-images using transfer learning and back propagation neural network. J. Infect. Public Health 2021, 14, 1435–1445. [Google Scholar] [CrossRef]
- Li, X.; Zhai, M.; Sun, J. DDCNNC: Dilated and depthwise separable convolutional neural Network for diagnosis COVID-19 via chest X-ray images. Int. J. Cogn. Comput. Eng. 2021, 2, 71–82. [Google Scholar] [CrossRef]
- Marques, G.; Agarwal, D.; de la Torre Díez, I. Automated medical diagnosis of COVID-19 through EfficientNet convolutional neural network. Appl. Soft Comput. 2020, 96, 106691. [Google Scholar] [CrossRef]
- Khan, A.I.; Shah, J.L.; Bhat, M.M. CoroNet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020, 196, 105581. [Google Scholar] [CrossRef] [PubMed]
- Mishra, N.K.; Singh, P.; Joshi, S.D. Automated detection of COVID-19 from CT scan using convolutional neural network. Biomed. Signal. Process. Control 2021, 41, 572–588. [Google Scholar] [CrossRef] [PubMed]
- Fouladi, S.; Ebadi, M.J.; Safaei, A.A.; Bajuri, M.Y.; Ahmadian, A. Efficient deep neural networks for classification of COVID-19 based on CT images: Virtualization via software defined radio. Comput. Commun. 2021, 176, 234–248. [Google Scholar] [CrossRef] [PubMed]
- Sharifrazi, D.; Alizadehsani, R.; Roshanzamir, M.; Joloudari, J.H.; Shoeibi, A.; Jafari, M.; Hussain, S.; Sani, Z.A.; Hasanzadeh, F.; Khozeimeh, F.; et al. Fusion of convolution neural network, support vector machine and Sobel filter for accurate detection of COVID-19 patients using X-ray images. Biomed. Signal. Process. Control 2021, 68, 102622. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Sadi, M.S.; Islam, M.M. EMCNet: Automated COVID-19 diagnosis from X-ray images using convolutional neural network and ensemble of machine learning classifiers. Inform. Med. Unlocked 2021, 22, 100505. [Google Scholar] [CrossRef] [PubMed]
- Hassantabar, S.; Ahmadi, M.; Sharifi, A. Diagnosis and detection of infected tissue of COVID-19 patients based on lung x-ray image using convolutional neural network approaches. Chaos Solitons Fractals 2020, 140, 110170. [Google Scholar] [CrossRef]
- Shorfuzzaman, M.; Hossain, M.S. MetaCOVID: A Siamese neural network framework with contrastive loss for n-shot diagnosis of COVID-19 patients. Pattern Recognit. 2021, 113, 107700. [Google Scholar] [CrossRef] [PubMed]
- Oliva, D.; Elaziz, M.A.; Elsheikh, A.H.; Ewees, A.A. A review on meta-heuristics methods for estimating parameters of solar cells. J. Power Sources 2019, 435, 126683. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Elsheikh, A.H.; Oliva, D.; Abualigah, L.; Lu, S.; Ewees, A.A. Advanced Metaheuristic Techniques for Mechanical Design Problems: Review. Arch. Comput. Methods Eng. 2021. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Muthuramalingam, T.; Shanmugan, S.; Mahmoud Ibrahim, A.M.; Ramesh, B.; Khoshaim, A.B.; Moustafa, E.B.; Bedairi, B.; Panchal, H.; Sathyamurthy, R. Fine-tuned artificial intelligence model using pigeon optimizer for prediction of residual stresses during turning of Inconel 718. J. Mater. Res. Technol. 2021, 15, 3622–3634. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Abd Elaziz, M.; Vendan, A. Modeling ultrasonic welding of polymers using an optimized artificial intelligence model using a gradient-based optimizer. Weld. World 2021. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Abd Elaziz, M.; Ramesh, B.; Egiza, M.; Al-qaness, M.A.A. Modeling of drilling process of GFRP composite using a hybrid random vector functional link network/parasitism-predation algorithm. J. Mater. Res. Technol. 2021, 14, 298–311. [Google Scholar] [CrossRef]
- Essa, F.A.; Abd Elaziz, M.; Elsheikh, A.H. Prediction of power consumption and water productivity of seawater greenhouse system using random vector functional link network integrated with artificial ecosystem-based optimization. Process. Saf. Environ. Prot. 2020, 144, 322–329. [Google Scholar] [CrossRef]
- AbuShanab, W.S.; Abd Elaziz, M.; Ghandourah, E.I.; Moustafa, E.B.; Elsheikh, A.H. A new fine-tuned random vector functional link model using Hunger games search optimizer for modeling friction stir welding process of polymeric materials. J. Mater. Res. Technol. 2021, 14, 1482–1493. [Google Scholar] [CrossRef]
- Khoshaim, A.B.; Elsheikh, A.H.; Moustafa, E.B.; Basha, M.; Mosleh, A.O. Prediction of residual stresses in turning of pure iron using artificial intelligence-based methods. J. Mater. Res. Technol. 2021, 11, 2181–2194. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Elaziz, M.A.; Das, S.R.; Muthuramlddalingam, T.; Lu, S. A new optimized predictive model based on political optimizer for eco-friendly MQL-turning of AISI 4340 alloy with nano-lubricants. J. Manuf. Process. 2021, 67, 562–578. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsheikh, A.H.; Saba, A.I.; Panchal, H.; Shanmugan, S.; Alsaleh, N.A.; Ahmadein, M. Artificial Intelligence for Forecasting the Prevalence of COVID-19 Pandemic: An Overview. Healthcare 2021, 9, 1614. https://doi.org/10.3390/healthcare9121614
Elsheikh AH, Saba AI, Panchal H, Shanmugan S, Alsaleh NA, Ahmadein M. Artificial Intelligence for Forecasting the Prevalence of COVID-19 Pandemic: An Overview. Healthcare. 2021; 9(12):1614. https://doi.org/10.3390/healthcare9121614
Chicago/Turabian StyleElsheikh, Ammar H., Amal I. Saba, Hitesh Panchal, Sengottaiyan Shanmugan, Naser A. Alsaleh, and Mahmoud Ahmadein. 2021. "Artificial Intelligence for Forecasting the Prevalence of COVID-19 Pandemic: An Overview" Healthcare 9, no. 12: 1614. https://doi.org/10.3390/healthcare9121614
APA StyleElsheikh, A. H., Saba, A. I., Panchal, H., Shanmugan, S., Alsaleh, N. A., & Ahmadein, M. (2021). Artificial Intelligence for Forecasting the Prevalence of COVID-19 Pandemic: An Overview. Healthcare, 9(12), 1614. https://doi.org/10.3390/healthcare9121614







