Distal Symmetric Polyneuropathy Identification in Type 2 Diabetes Subjects: A Random Forest Approach
Abstract
:1. Introduction
- Clinical measures
- Morphological and biochemical analyses
- Electrodiagnostic assessment
- Quantitative sensory testing
- Autonomic nervous system testing
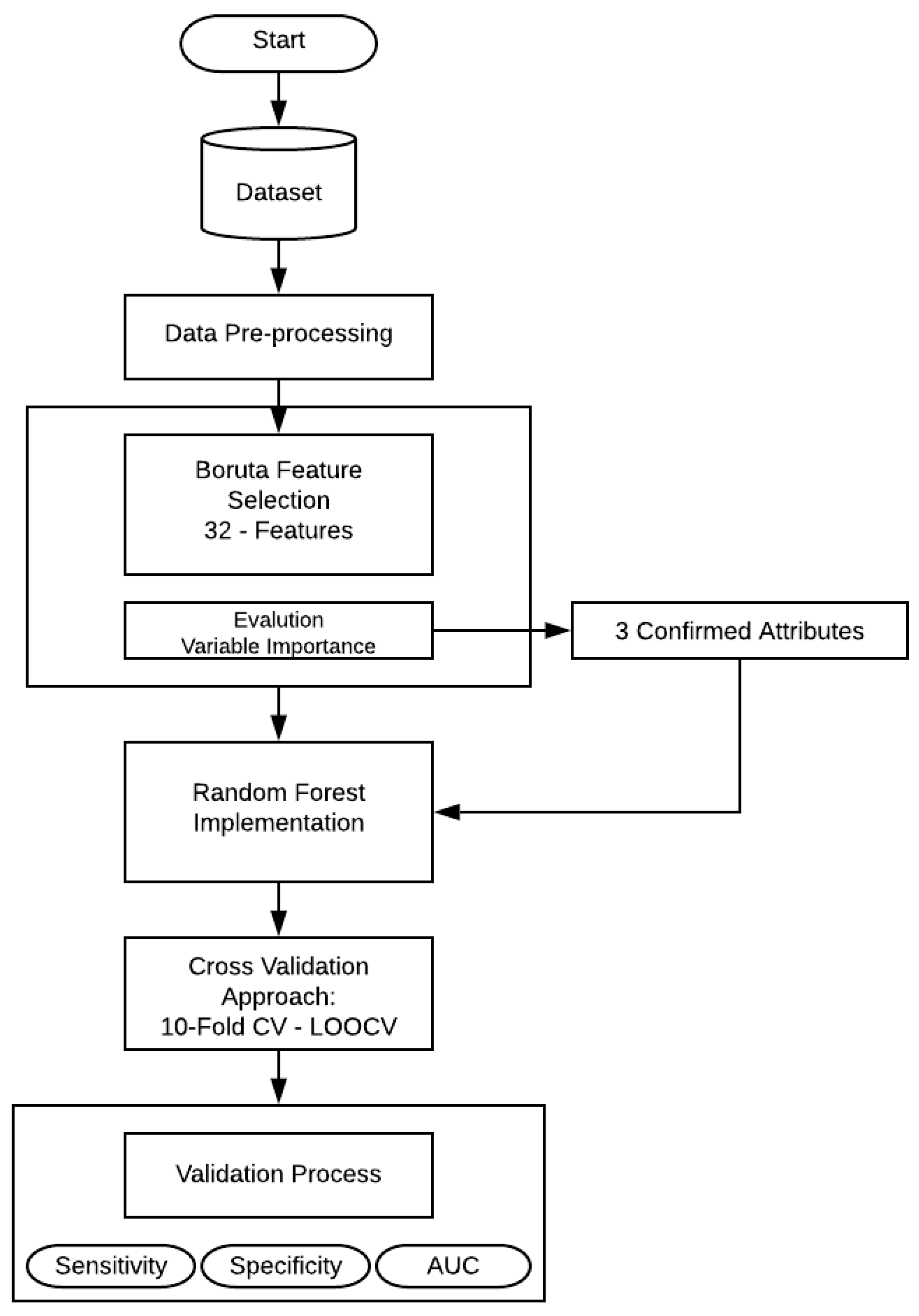
2. Materials and Methods
2.1. Data Description
2.2. Data Pre-Processing
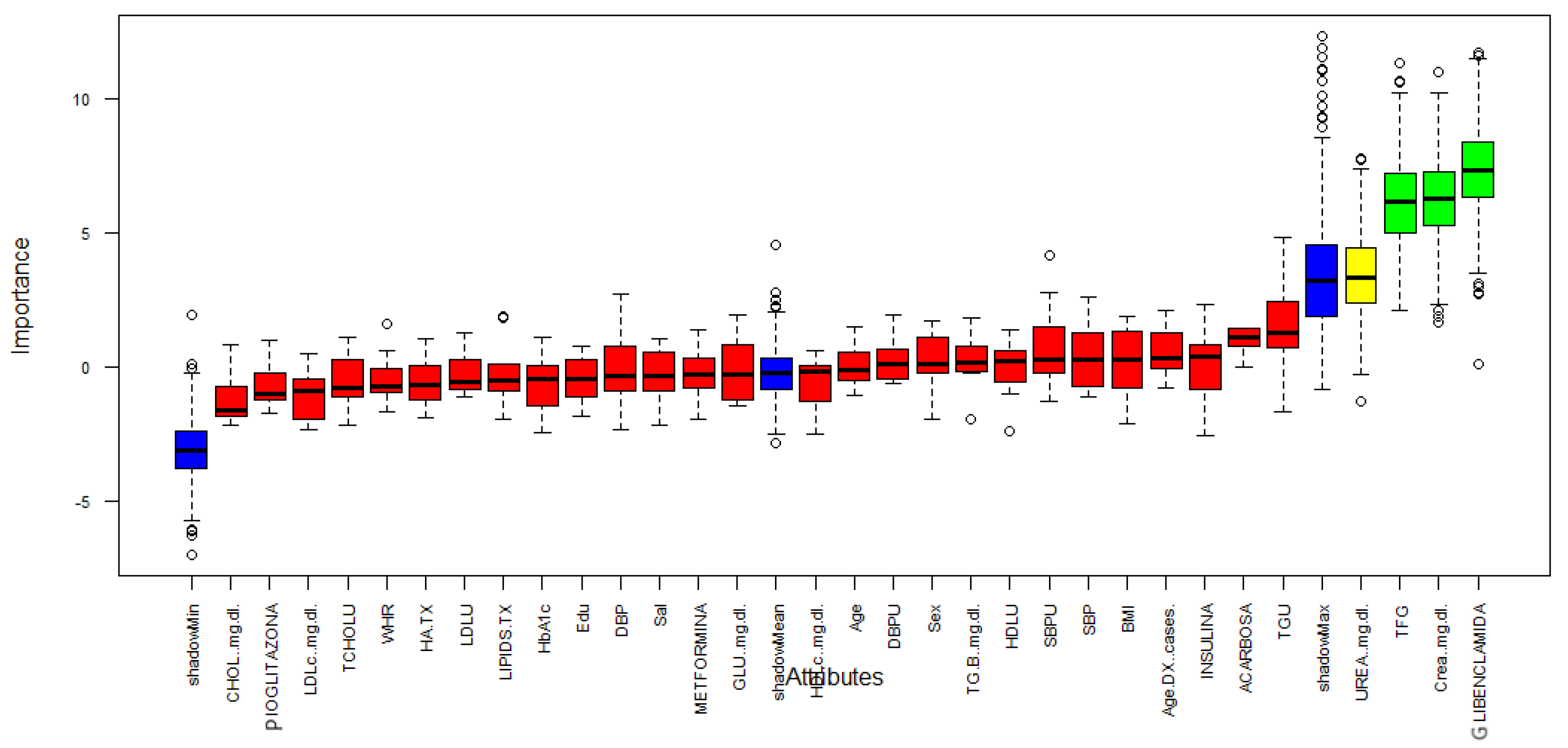
2.3. Boruta Feature Selection
- Generate copies of all variables.
- Shuffle the added variables (attributes) to eliminate their correlations with the response.
- A RF classifier is executed and gather the Z scores computed.
- Find the maximum Z score among shadow attributes (MZSA) and then assign a value to each attribute that scored better than MZSA.
- For each attribute of undetermined importance, a two-sided equality test should be performed with the MZSA.
- Consider the attributes which have importance significantly lower that MZSA as unimportant and permanently remove them from the system.
- Consider the attributes which have importance significantly higher than MZSA as important.
- Eliminate all shadow attributes.
2.4. Classification Method
Random Forest
- Fist, the dataset having m x n is given. Then, a new dataset is created from by sampling and eliminating a third part of the row data.
- The RF model is trained to generate a new dataset from the reduced samples, estimating the unbiased error.
- At each node point, the column is selected from the total n columns.
- Finally, several trees are growing and the final prediction is calculated based on individual decisions to obtain the best classification accuracy.
2.5. Validation
- : number of instances that are positive and are correctly identified.
- : negative cases that are negative and classified as negative.
- : defined by the negative instances that are incorrectly classified as positive cases.
- : number of positive cases that are misclassified as negative.
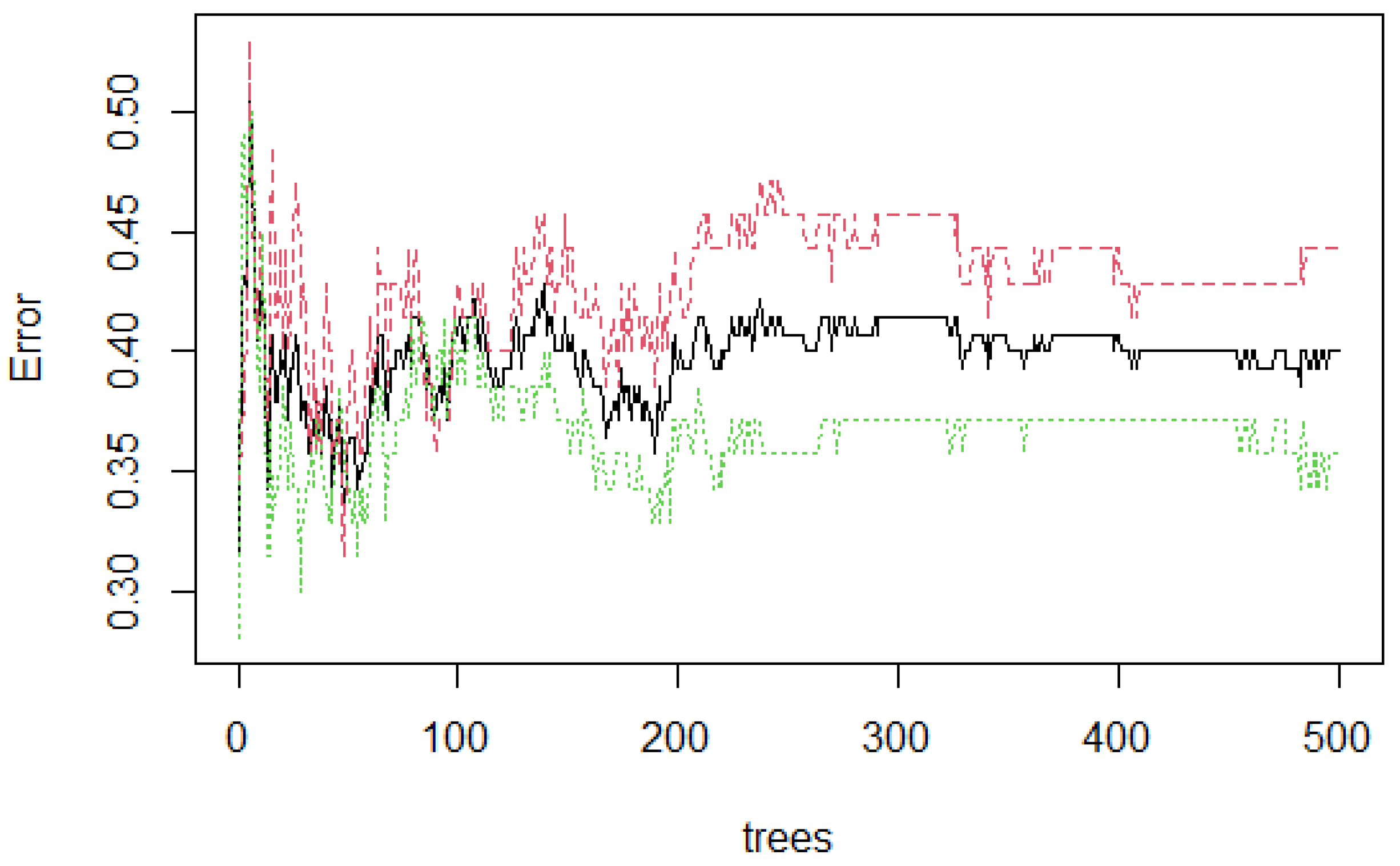
3. Experiments and Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Association, A.D. 2. Classification and diagnosis of diabetes: Standards of medical care in diabetes—2018. Diabetes Care 2018, 41, S13–S27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dagliati, A.; Sacchi, L.; Tibollo, V.; Cogni, G.; Teliti, M.; Martinez-Millana, A.; Traver, V.; Segagni, D.; Posada, J.; Ottaviano, M.; et al. A dashboard-based system for supporting diabetes care. J. Am. Med. Inform. Assoc. 2018, 25, 538–547. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Ley, S.H.; Hu, F.B. Global aetiology and epidemiology of type 2 diabetes mellitus and its complications. Nat. Rev. Endocrinol. 2018, 14, 88. [Google Scholar] [CrossRef] [PubMed]
- Bansal, V.; Kalita, J.; Misra, U. Diabetic neuropathy. Postgrad. Med. J. 2006, 82, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Román-Pintos, L.M.; Villegas-Rivera, G.; Rodríguez-Carrizalez, A.D.; Miranda-Díaz, A.G.; Cardona-Muñoz, E.G. Diabetic polyneuropathy in type 2 diabetes mellitus: Inflammation, oxidative stress, and mitochondrial function. J. Diabetes Res. 2016, 2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldstein, B.J.; Müller-Wieland, D. Type 2 Diabetes: Principles and Practice; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Callaghan, B.C.; Price, R.S.; Feldman, E.L. Distal symmetric polyneuropathy: A review. JAMA 2015, 314, 2172–2181. [Google Scholar] [CrossRef]
- Kasznicki, J. Advances in the diagnosis and management of diabetic distal symmetric polyneuropathy. Arch. Med Sci. AMS 2014, 10, 345. [Google Scholar] [CrossRef] [PubMed]
- Sabag-Ruiz, E.; Álvarez-Félix, A.; Celiz-Zepeda, S.; Gómez-Alcalá, A.V. Chronic complications of diabetes mellitus. What is the prevalence of diabetes in a family medical unit? Rev. Medica Inst. Mex. Seguro Soc. 2006, 44, 415–422. [Google Scholar]
- Dankwa-Mullan, I.; Rivo, M.; Sepulveda, M.; Park, Y.; Snowdon, J.; Rhee, K. Transforming diabetes care through artificial intelligence: The future is here. Popul. Health Manag. 2019, 22, 229–242. [Google Scholar] [CrossRef] [Green Version]
- Alcalá-Rmz, V.; Zanella-Calzada, L.A.; Galván-Tejada, C.E.; García-Hernández, A.; Cruz, M.; Valladares-Salgado, A.; Galván-Tejada, J.I.; Gamboa-Rosales, H. Identification of diabetic patients through clinical and para-clinical features in mexico: An approach using deep neural networks. Int. J. Environ. Res. Public Health 2019, 16, 381. [Google Scholar] [CrossRef] [Green Version]
- Alcalá-Rmz, V.; Maeda-Gutiérrez, V.; Zanella-Calzada, L.A.; Valladares-Salgado, A.; Celaya-Padilla, J.M.; Galván-Tejada, C.E. Convolutional Neural Network for Classification of Diabetic Retinopathy Grade. In Mexican International Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 104–118. [Google Scholar]
- Blobel, B. Identification of Diabetes Risk Factors in Chronic Cardiovascular Patients. In pHealth 2020: Proceedings of the 17th International Conference on Wearable Micro and Nano Technologies for Personalized Health; IOS Press: Amsterdam, The Netherlands, 2020; Volume 273, p. 136. [Google Scholar]
- Metsker, O.; Magoev, K.; Yakovlev, A.; Yanishevskiy, S.; Kopanitsa, G.; Kovalchuk, S.; Krzhizhanovskaya, V.V. Identification of risk factors for patients with diabetes: Diabetic polyneuropathy case study. BMC Med. Informat. Decis. Mak. 2020, 20, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Dagliati, A.; Marini, S.; Sacchi, L.; Cogni, G.; Teliti, M.; Tibollo, V.; De Cata, P.; Chiovato, L.; Bellazzi, R. Machine learning methods to predict diabetes complications. J. Diabetes Sci. Technol. 2018, 12, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, B.C.; Gao, L.; Li, Y.; Zhou, X.; Reynolds, E.; Banerjee, M.; Pop-Busui, R.; Feldman, E.L.; Ji, L. Diabetes and obesity are the main metabolic drivers of peripheral neuropathy. Ann. Clin. Transl. Neurol. 2018, 5, 397–405. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Pinto, L.N.; Venable, L.R.; Fahrenbach, J.; Churpek, M.M. Comparison of variable selection methods for clinical predictive modeling. Int. J. Med. Inform. 2018, 116, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.C.; Dewi, C.; Huang, S.W.; Caraka, R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data 2020, 7, 1–26. [Google Scholar] [CrossRef]
- Rghioui, A.; Lloret, J.; Sendra, S.; Oumnad, A. A Smart Architecture for Diabetic Patient Monitoring Using Machine Learning Algorithms; Healthcare, Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2020; Volume 8, p. 348. [Google Scholar]
- Chen, X.; Graham, J.; Dabbah, M.A.; Petropoulos, I.N.; Tavakoli, M.; Malik, R.A. An automatic tool for quantification of nerve fibers in corneal confocal microscopy images. IEEE Trans. Biomed. Eng. 2016, 64, 786–794. [Google Scholar] [CrossRef] [PubMed]
- Pourhamidi, K.; Dahlin, L.B.; Englund, E.; Rolandsson, O. Evaluation of clinical tools and their diagnostic use in distal symmetric polyneuropathy. Prim. Care Diabetes 2014, 8, 77–84. [Google Scholar] [CrossRef] [Green Version]
- Nowakowska, M.; Zghebi, S.S.; Ashcroft, D.M.; Buchan, I.; Chew-Graham, C.; Holt, T.; Mallen, C.; Van Marwijk, H.; Peek, N.; Perera-Salazar, R.; et al. The comorbidity burden of type 2 diabetes mellitus: Patterns, clusters and predictions from a large English primary care cohort. BMC Med. 2019, 17, 145. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Kleiman, M.J.; Barenholtz, E.; Galvin, J.E.; Initiative, A.D.N. Screening for Early-Stage Alzheimer’s Disease Using Optimized Feature Sets and Machine Learning. medRxiv 2020. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of Random Forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.; Wang, Y.; Nguyen, H.N. Random Forest Classifier Combined with Feature Selection for Breast Cancer Diagnosis and Prognostic; Scientific Research Publishing: Wuhan, China, 2013. [Google Scholar]
- Chen, X.; Ishwaran, H. Random Forests for genomic data analysis. Genomics 2012, 99, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Subudhi, A.; Dash, M.; Sabut, S. Automated segmentation and classification of brain stroke using expectation-maximization and Random Forest classifier. Biocybern. Biomed. Eng. 2020, 40, 277–289. [Google Scholar] [CrossRef]
- Japkowicz, N.; Shah, M. Evaluating Learning Algorithms: A Classification Perspective; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajian-Tilaki, K. Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation. Casp. J. Intern. Med. 2013, 4, 627. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0-86; Astrophysics Source Code Library: Cambridge, MA, USA, 2020. [Google Scholar]
- John, C.R. MLeval: Machine Learning Model Evaluation; Package Version 0.3; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Cui, M.; Gang, X.; Gao, F.; Wang, G.; Xiao, X.; Li, Z.; Li, X.; Ning, G.; Wang, G. Risk assessment of sarcopenia in patients with type 2 diabetes mellitus using data mining methods. Front. Endocrinol. 2020, 11. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. (Eds.) Leave-One-Out Cross-Validation. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 600–601. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection; Ijcai: Montreal, QC, Canada, 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Berrar, D. Cross-validation. Encycl. Bioinform. Comput. Biol. 2019, 1, 542–545. [Google Scholar]
- Bagherzadeh-Khiabani, F.; Ramezankhani, A.; Azizi, F.; Hadaegh, F.; Steyerberg, E.W.; Khalili, D. A tutorial on variable selection for clinical prediction models: Feature selection methods in data mining could improve the results. J. Clin. Epidemiol. 2016, 71, 76–85. [Google Scholar] [CrossRef]
- Tavakoli, M.; Gogas Yavuz, D.; Tahrani, A.A.; Selvarajah, D.; Bowling, F.L.; Fadavi, H. Diabetic neuropathy: Current status and future prospects. J. Diabetes Res. 2017, 2017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, Z.; Zhang, J.; Ding, H.; Zou, Q. RF-PseU: A Random Forest Predictor for RNA Pseudouridine Sites. Front. Bioeng. Biotechnol. 2020, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, P. Model selection via multifold cross validation. Annals Stat. 1993, 299–313. [Google Scholar] [CrossRef]
- Blum, A.; Kalai, A.; Langford, J. Beating the hold-out: Bounds for k-fold and progressive cross-validation. In Proceedings of the Twelfth Annual Conference on Computational Learning Theory, Santa Cru, CA, USA, 6–9 July 1999; pp. 203–208. [Google Scholar]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- López-Úbeda, P.; Díaz-Galiano, M.C.; Martín-Noguerol, T.; Luna, A.; Ureña-López, L.A.; Martín-Valdivia, M.T. COVID-19 detection in radiological text reports integrating entity recognition. Comput. Biol. Med. 2020, 127, 104066. [Google Scholar] [CrossRef]
- Bolboacă, S.D. Medical diagnostic tests: A review of test anatomy, phases, and statistical treatment of data. Comput. Math. Methods Med. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Caminha, T.C.; Ferreira, H.S.; Costa, N.S.; Nakano, R.P.; Carvalho, R.E.S.; Xavier, A.F., Jr.; Assunção, M.L. Waist-to-height ratio is the best anthropometric predictor of hypertension: A population-based study with women from a state of northeast of Brazil. Medicine 2017, 96, e5874. [Google Scholar] [CrossRef]
- Zou, K.H.; Liu, A.; Bandos, A.I.; Ohno-Machado, L.; Rockette, H.E. Statistical Evaluation of Diagnostic Performance: Topics in ROC Analysis; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Lasko, T.A.; Bhagwat, J.G.; Zou, K.H.; Ohno-Machado, L. The use of receiver operating characteristic curves in biomedical informatics. J. Biomed. Inform. 2005, 38, 404–415. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Ang, J.C.; Mirzal, A.; Haron, H.; Hamed, H.N.A. Supervised, unsupervised, and semi-supervised feature selection: A review on gene selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 13, 971–989. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.; Zhang, D. Feature selection and analysis on correlated gas sensor data with recursive feature elimination. Sens. A Actuator B Chem. 2015, 212, 353–363. [Google Scholar] [CrossRef]
- Awada, W.; Khoshgoftaar, T.M.; Dittman, D.; Wald, R.; Napolitano, A. A review of the stability of feature selection techniques for bioinformatics data. In Proceedings of the 2012 IEEE 13th International Conference on Information Reuse and Integration (IRI), Las Vegas, NV, USA, 8–10 August 2012; pp. 356–363. [Google Scholar]
- Mandrekar, J.N. Receiver operating characteristic curve in diagnostic test assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vinik, A.I. Diabetic sensory and motor neuropathy. N. Engl. J. Med. 2016, 374, 1455–1464. [Google Scholar] [CrossRef] [PubMed]
- Akinci, B.; Yesil, S.; Bayraktar, F.; Kucukyavas, Y.; Yener, S.; Comlekci, A.; Eraslan, S. The effect of creatinine clearance on the short-term outcome of neuropathic diabetic foot ulcers. Prim. Care Diabetes 2010, 4, 181–185. [Google Scholar] [CrossRef] [PubMed]
- Flyvbjerg, A. The role of the complement system in diabetic nephropathy. Nat. Rev. Nephrol. 2017, 13, 311–318. [Google Scholar] [CrossRef]
- Dyck, P.J.; Davies, J.L.; Wilson, D.M.; Melton, L.J.; O’Brien, P.C. Risk factors for severity of diabetic polyneuropathy: Intensive longitudinal assessment of the Rochester Diabetic Neuropathy Study cohort. Diabetes Care 1999, 22, 1479–1486. [Google Scholar] [CrossRef]
- Kärvestedt, L.; Mårtensson, E.; Grill, V.; Elofsson, S.; Von Wendt, G.; Hamsten, A.; Brismar, K. Peripheral sensory neuropathy associates with micro-or macroangiopathy: Results from a population-based study of type 2 diabetic patients in Sweden. Diabetes Care 2009, 32, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Arno, A.G.; Cases, M.M. El Empleo racional de la terapia combinada en la diabetes mellitus tipo 2. Criterios y pautas. Documento de consenso del proyecto COMBO. Med. Integr. Med. Prev. Asist. Aten. Primaria Salud 2001, 38, 270–289. [Google Scholar]
- Hovind, P.; Rossing, P.; Tarnow, L.; Smidt, U.M.; Parving, H.H. Progression of diabetic nephropathy. Kidney Int. 2001, 59, 702–709. [Google Scholar] [CrossRef] [Green Version]

| Feature | Description | Possible Values |
|---|---|---|
| Education | Studies concluded by the patient | 1 - Elementary School 2 - Secondary School 3 - Technical level 4 - High School 5 - Professional 6 - Postgraduate |
| Salary | Monthly income | 1 - Less than $2000.00 2 - Between $2000.00 and $5000.00 3 - More than $5000.00 |
| Sex | Patients sex | 0 - Male 1 - Female |
| Age | Age in years | Numeric Integer |
| Age DX | Diagnosis age of diabetes | Numeric Integer |
| WHR | Waist Hip Ratio | Numeric |
| BMI | Body Mass Index | Numeric |
| Glucose | Blood glucose levels | Numeric |
| Urea | Waste product resulting from the breakdown of protein in the patient body. The test can provide important information about the kidney function | Numeric Integer |
| Creatinine | Waste product produced by muscles as part of regular daily activity. The test is used to see if the kidneys are working normally | Numeric |
| Cholesterol | Fat-like substance that is found in all cells of the patient body | Numeric |
| HDL | Stands for High Density Lipoprotein (corrected for medication) | Numeric |
| LDL | Stands of Low Density Lipoprotein (corrected for medication) | Numeric |
| Triglycerides | Type of fat found in the patient body | Numeric |
| TCHOLU | Total Cholesterol (uncorrected) | Numeric Integer |
| HDLU | High Density Lipoprotein (uncorrected) | Numeric Integer |
| LDLU | Low Density Lipoprotein (uncorrected) | Numeric Integer |
| TGU | Triglycerides (uncorrected) | Numeric Integer |
| SBP | Systolic Blood Pressure (corrected for medication) | Numeric Integer |
| DBP | Diastolic Blood Pressure (corrected for medication) | Numeric Integer |
| SBPU | Systolic Blood Pressure (uncorrected) | Numeric Integer |
| DBPU | Diastolic Blood Pressure (uncorrected) | Numeric Integer |
| HA-TX | Hypertension Treatment | 0 - No 1 - Yes |
| Lipids TX | Lipids Treatment | 0 - No 1 - Yes |
| HbA1c | Glycated Hemoglobin | Numeric |
| GFR | Glomerular Filtration Rate (blood test that checks how well the kidneys are working) | Numeric Integer |
| Glibenclamide | Drug Treatment | 0 - No 1 - Yes |
| Metformin | Drug Treatment | 0 - No 1 - Yes |
| Pioglitazone | Drug Treatment | 0 - No 1 - Yes |
| Rosiglitazone | Drug Treatment | 0 - No 1 - Yes |
| Acarbose | Drug Treatment | 0 - No 1 - Yes |
| Insuline | Drug Treatment | 0 - No 1 - Yes |
| Output | Neuropathy State | 0 - No 1 - Yes |
| Parameters | |
|---|---|
| Type of Random Forest (y): | Classification |
| Number of trees (ntree): | 500 |
| No. of variables tried at each split (mtry): | 2, 3, 17 and 32 |
| mtry | Sensitivity | Specificity | AUC |
|---|---|---|---|
| 2 | 63.80% | 55.71% | 61.42% |
| 17 | 64.91% | 62.85% | 62.85% |
| 32 | 64.27% | 62.85% | 65.71% |
| Reference | ||||
|---|---|---|---|---|
| 0 | 1 | Class. Error | ||
| Prediction | 0 | 43 | 27 | 0.3857 |
| 1 | 26 | 44 | 0.3714 | |
| Features | |
|---|---|
| 1 | GFR |
| 2 | Creatinine |
| 3 | Glibenclamide |
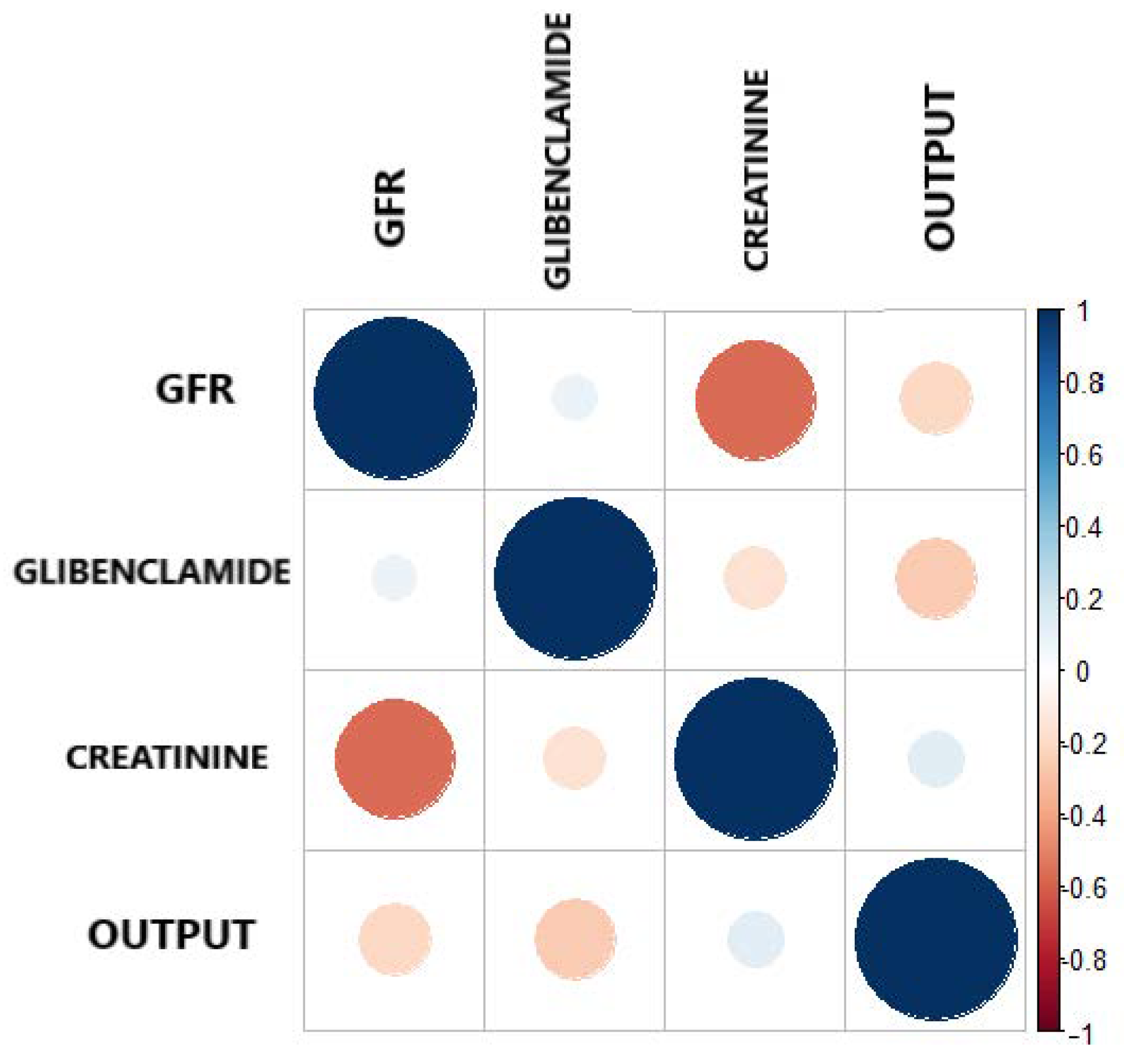
| GFR | Glibenclamide | Creatinine | Output | |
|---|---|---|---|---|
| GFR | 1.0 | 0.0840 | ||
| Gliblenclamide | 0.0840 | 1.0 | −0.1585 | |
| Creatinine | 1.0 | 0.1219 | ||
| Output | 0.1219 | 1.0 |
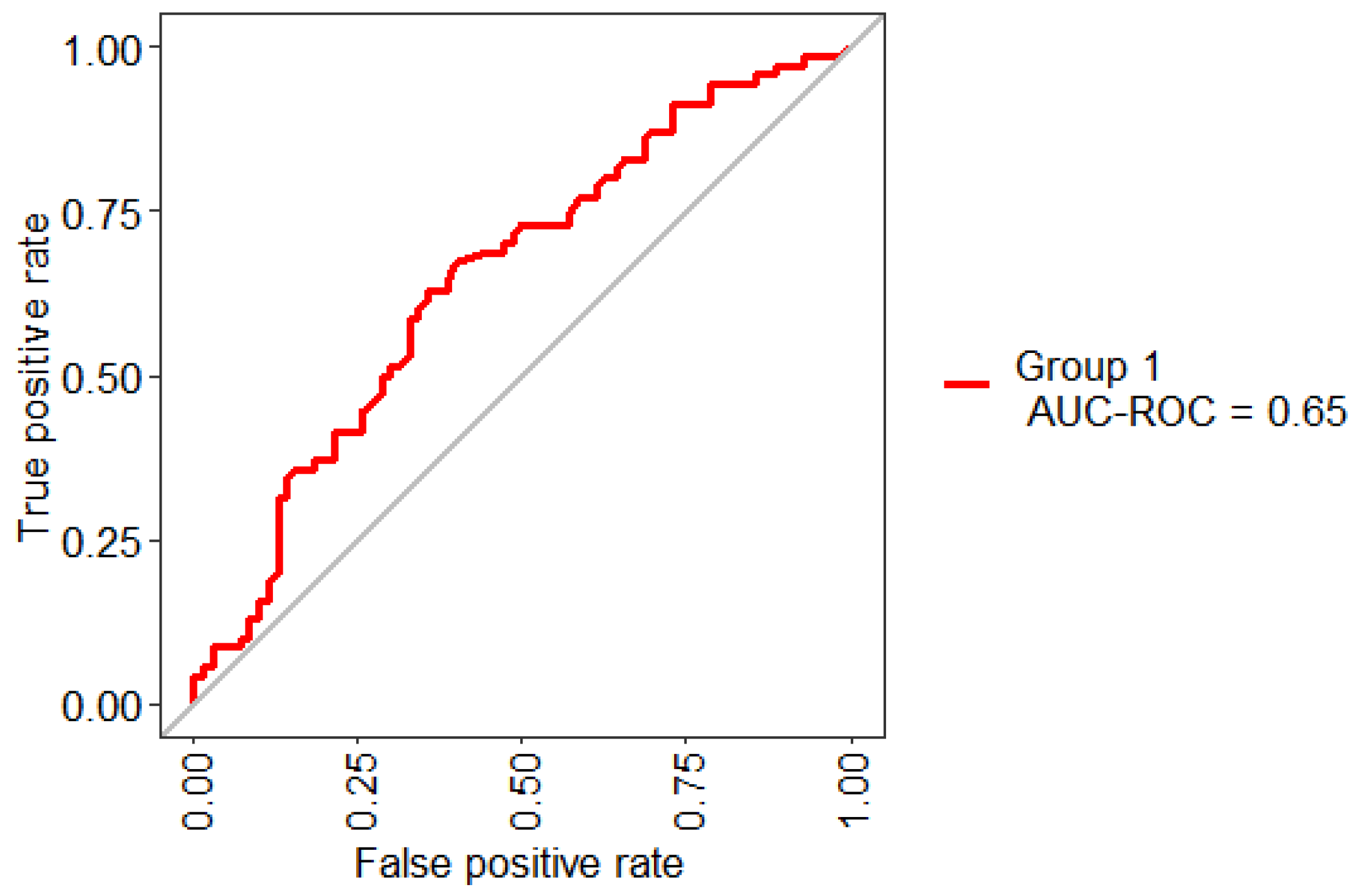
| mtry | Sensitivity | Specificity | AUC |
|---|---|---|---|
| 2 | 55.71% | 65.71% | 67.01% |
| 3 | 55.71% | 65.71% | 66.05% |
| Reference | ||||
|---|---|---|---|---|
| 0 | 1 | Class. Error | ||
| Prediction | 0 | 39 | 31 | 0.4428 |
| 1 | 25 | 45 | 0.3571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maeda-Gutiérrez, V.; Galván-Tejada, C.E.; Cruz, M.; Valladares-Salgado, A.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; García-Hernández, A.; Luna-García, H.; Gonzalez-Curiel, I.; Martínez-Acuña, M. Distal Symmetric Polyneuropathy Identification in Type 2 Diabetes Subjects: A Random Forest Approach. Healthcare 2021, 9, 138. https://doi.org/10.3390/healthcare9020138
Maeda-Gutiérrez V, Galván-Tejada CE, Cruz M, Valladares-Salgado A, Galván-Tejada JI, Gamboa-Rosales H, García-Hernández A, Luna-García H, Gonzalez-Curiel I, Martínez-Acuña M. Distal Symmetric Polyneuropathy Identification in Type 2 Diabetes Subjects: A Random Forest Approach. Healthcare. 2021; 9(2):138. https://doi.org/10.3390/healthcare9020138
Chicago/Turabian StyleMaeda-Gutiérrez, Valeria, Carlos E. Galván-Tejada, Miguel Cruz, Adan Valladares-Salgado, Jorge I. Galván-Tejada, Hamurabi Gamboa-Rosales, Alejandra García-Hernández, Huizilopoztli Luna-García, Irma Gonzalez-Curiel, and Mónica Martínez-Acuña. 2021. "Distal Symmetric Polyneuropathy Identification in Type 2 Diabetes Subjects: A Random Forest Approach" Healthcare 9, no. 2: 138. https://doi.org/10.3390/healthcare9020138
APA StyleMaeda-Gutiérrez, V., Galván-Tejada, C. E., Cruz, M., Valladares-Salgado, A., Galván-Tejada, J. I., Gamboa-Rosales, H., García-Hernández, A., Luna-García, H., Gonzalez-Curiel, I., & Martínez-Acuña, M. (2021). Distal Symmetric Polyneuropathy Identification in Type 2 Diabetes Subjects: A Random Forest Approach. Healthcare, 9(2), 138. https://doi.org/10.3390/healthcare9020138








