Applying Two-Dimensional Correlation Spectroscopy and Principal Component Analysis to Understand How Temperature Affects the Neptunium(V) Absorption Spectrum

Abstract

The visible-near infrared (Vis-NIR) electronic absorption spectrum of neptunium(V) (NpO₂⁺) comprises numerous f-f electronic transitions with mostly undocumented temperature dependencies. The effect of temperature on the absorption spectrum of the pentavalent neptunyl dioxocation (NpO₂⁺) is an important factor to consider with spectrophotometric applications but has often been overlooked. Optical Vis-NIR absorption spectra (400–1700 nm) of Np(V) (0.017–0.89 M) in 1 M nitric acid were evaluated with varying temperatures (T = 10–80 °C). The intensity, position, and overall shape of the bands were sensitive to interactions with the solvent and coordination environment. Numerous temperature-induced isosbestic points were identified resulting from dynamic, overlapping peak shifts. Spectral variations were characterized using principal component analysis (PCA) and 2D correlation spectroscopy (COS). 2D-COS revealed that the absorption band near 1095 nm likely consists of two bands centered near 1087 and 1096 nm, which cannot be explained by current computational methods. 2D-COS analysis also provided an unambiguous assignment of unresolved peaks in the visible region for comparison with computational predictions. PCA was used to identify nonlinearity in the spectral response at elevated Np(V) concentrations ≥ 0.5 M. This unique experimental data and interpretation will foster a deeper understanding of the absorption spectra for complex actinyl ions.

1. Introduction

Neptunium (Np) is the first transuranium element in the periodic table and, although it has chemical properties like uranium (U) and plutonium (Pu), many of its fundamental properties are not fully understood [1]. Neptunium-237 (t_½ = 2.14 × 10⁶ years) is the isotope most suitable for laboratory handling, and a large inventory has been accumulated worldwide as a by-product of the neutron irradiation of uranium fuel. Neptunium-237 is an important precursor to the production of ²³⁸Pu, a heat source material used by the National Aeronautics and Space Administration to power deep space missions [2,3]. The chemistry of Np is complex with respect to redox properties and coordination chemistry. Neptunium exists in the +4 to +6 oxidation states in aqueous solutions relevant to spent fuel reprocessing conditions in nitric acid [1,4]. Although Np adopting the +3 oxidation state is possible, it is only generated under highly reducing conditions in the absence of oxygen. The mono-charged pentavalent neptunyl dioxocation (Np(V) = NpO₂⁺) is the most prevalent species in aqueous conditions, in the absence of redox active species and at acid concentrations of <5 M nitric acid (HNO₃) [5]. At ≥5 M HNO₃, Np(V) is unstable and will disproportionate to Np(IV) and Np^VIO₂²⁺, primarily because of the presence of nitrous acid (HNO₂), which exists at higher concentrations of HNO₃. A thorough understanding of aqueous neptunium chemistry is needed for reprocessing, waste storage, and environmental applications. In particular, understanding the absorption spectrum of Np(V) is needed to advance spectrophotometric applications to measure Np concentration in dynamic conditions [2,6,7,8].

Characteristically sharp absorption bands in the actinides generally arise from forbidden transitions in the f shell (5f^x). Np(V) has an electronic configuration of [Rn]5f² and exists as the linear Np^VO₂⁺ aquo ion, coordinated by five water molecules [9,10,11,12,13,14] The two f electrons in each electronic state for NpO₂⁺ have gerade parity, and the transitions are therefore forbidden by Laporte’s rule. In this f² system, each state up to energies near 23,079 cm⁻¹ or 433 nm is considered an f-f transition [14]. Near and above this energy level charge transfer transitions take place. The absorption bands > 433 nm in the visible-near infrared (Vis-NIR) region originate from f-f transitions closely related to the symmetry of the Np(V) complexes. If the linear Np(V) ion was truly centrosymmetric, it would have an inversion center, and the absorption bands would be silent [9]. The arrangement of ligands, or water molecules, in the primary hydration sphere destroys the center of inversion and plays a significant role in absorption by inducing electric dipole transitions.

The Vis-NIR absorption spectrum of the free NpO₂⁺ ion is dominated by an electronic transition in the 5f shell (5f-5f transition) near 980 nm, which is also the case for the isoelectronic plutonyl ion (PuO₂²⁺) at a shorter wavelength near 830 nm [12]. The intense 980 nm (Є = 395 M⁻¹·cm⁻¹) band and a less intense band at 616 nm (Є = 22 M⁻¹·cm⁻¹) have been used analytically to determine the concentration of NpO₂⁺ in solution [11]. The 980 nm absorption band is widely used in the literature to study Np(V) complexation with various ligands in the equatorial plan since the band intensity and position are sensitive to the coordination environment of NpO₂⁺ and most studies are at relatively low Np concentrations (~1 mM) [15,16,17,18]. At elevated concentrations > ~0.2 M Np, cation-cation complexes from between Np(V) and hexavalent actinides (e.g., U(IV), Np(VI), Pu(VI)) and dimeric Np(V)-Np(V) complexes can also form [19,20,21]. Although the absorption spectrum of Np(V) is sensitive to solution conditions, it is much less sensitive to factors such as ligand concentration (e.g., nitrate) compared with tetravalent Np(IV) ions that form various nitrato complexes at high levels of nitric acid concentration (e.g., Np(IV)(NO₃⁻)₆²⁻ [22,23,24].

The temperature dependence of the Np(V) absorption peak at 980 nm was recently reported for the first time [17]. The temperature-induced effects on other peaks in the spectrum have not been documented in the literature. Accounting for dynamic temperature conditions is highly relevant to operations taking place in glove box and hot cell environments where temperatures can vary by more than 20 °C compared with benchtop operations [2,3] Characterizing the entire spectrum will bolster the spectrophotometric approach for the quantification of Np(V) in processing solutions to support various fuel cycle applications and Np processing operations for the ²³⁸Pu Supply Program [3].

Numerous methods can describe the structured variation of multiple components in convoluted spectral data sets [25,26]. Two complementary and widely used techniques are 2D correlation spectroscopy (2D-COS) and principal component analysis (PCA). 2D-COS is a strong visualization tool based on the correlation analysis of perturbation-induced variations of spectral intensity [27,28,29,30,31,32]. Such spectra enhance the resolution of a measurement and emphasize features not easily observed in conventional 1D spectra. PCA is valuable for exploratory data analysis and reveals hidden structure in data using a bilinear model, which estimates changes along sample and variable vectors [33]. We combined the information acquired from each approach to characterize temperature- and concentration-dependent features in the Np(V) spectrum and test the limits of 2D-COS in a practical real-world setting.

Herein, characteristic 2D-COS patterns and temperature-induced (T = 10–80 °C) spectral variations were used to identify Vis-NIR Np(V) (0.017–0.89 M) absorption bands without the ambiguity of peak fitting. Several areas of scientific advancement are discussed in this work including (1) characterization of temperature-dependent shifts for numerous peaks in the Np(V) absorption spectrum, (2) the unambiguous assignment of peak energies to numerous Vis-NIR absorption bands previously undescribed experimentally, (3) PCA quantification of nonlinear spectral response at elevated Np concentration > 0.5 M, and (4) identifying the position of isosbestic points by analyzing synchronous 2D-COS spectra with PCA and multivariate curve resolution (MCR) [34]. This work also articulates the challenges that arise when applying 2D-COS analysis to convoluted spectral features and best practices pertinent to many applications.

2. Methods

2.1. Materials

All chemicals were commercially obtained (ACS grade) and used as received unless otherwise stated. Concentrated HNO₃ (70%) was purchased from Sigma Aldrich. All solutions were prepared using deionized water with a resistivity of 18.2 MΩ cm at 25 °C.

2.2. Methodology

NpO₂ was prepared in house at Oak Ridge National Laboratory (ORNL) and was dissolved in 8 M HNO₃ and adjusted to achieve a solution of 210 ± 7 g Np/L (0.886 M Np) in one molar nitric acid. Inductively coupled plasma mass spectrometry (ICP-MS) was used to determine the concentration of Np in this sample using an iCAP Q ICP-MS by Thermo Fisher Scientific. The stock solution was used to prepare numerous samples ranging from 0.017–0.89 M total Np. Concentrations levels included 0.017, 0.034, 0.069, 0.17, 0.34, 0.51, 0.69 and 0.89 M Np, Aliquots from the stock solution were taken and sequentially diluted in 1.0 M HNO₃ using a 1 mL volumetric flask (1.00 ± 0.01 mL) to achieve the desired Np concentration. Increasing the solution temperature increased the sample volume, which could account in part for decreasing spectral intensity. The density of solutions changed slightly (~3%) with increasing temperature over the entire range 10–80 °C [35]. In general, samples closer to the highest Np concentration (0.89 M Np, <3% Np(VI)) had more Np(VI) than samples near the lower concentrations (≤0.068 M Np, ~0% Np(VI)). No attempts were made to adjust the natural Np valence of the solutions. Np(V) will convert to Np(VI) with increasing temperature at higher acid concentrations [36]. An increase or decrease in Np(VI) concentration due to temperature fluctuations was not observed in any sample studied here.

2.3. Absorbance Spectroscopy

QEPro and NIRQuest spectrometers were used for ultraviolet (UV)-Vis and NIR absorption measurements, respectively. UV-Vis spectra included absorbance measurements every 0.79 nm from 199–985 nm, and NIR spectra included absorbance measurements recorded every 1.65 nm from 897–1717 nm. Triplicate spectra were recorded for each sample, and each spectrum was an average of five scans. Spectra were processed using OceanView 2.0 software (Ocean insight). The spectrometers were referenced to pure water at 20 °C before each measurement unless otherwise stated. A stabilized incoherent light source (Vis-NIR range from 360–2600 nm) made by Thorlabs (SLS201L) was used for each measurement.

Light was transmitted in and out of a negative pressure glove box with several meters of multimode SMA fiber-optic cables made by ThorLabs with a core diameter of 550 µm. A syringe was used to push samples through a Hellma quartz micro flow cell with an optical pathlength of 1 mm and a Z height of 8.5 mm. The same cuvette was used for all measurements to ensure a consistent optical quality. A separate cuvette with an optical path length of 0.2 mm was used to determine molar absorptivity values for the concentrated Np solutions. A Quantum Northwest’s qpod 2e temperature-controlled sample compartment holder, purchased from Avantes (CUV UV–Vis TC), was used to adjust the temperature of the samples with an accuracy of 0.05 °C from 10–80 °C. The incident and transmitted light sources were passed through two quantum cascade laser–UV collimating lenses placed on either side of the cuvette compartment. Samples were equilibrated in the sample compartment for 2 min before collecting the spectra. Given the small volume of sample in the cell, this was sufficient to adjust the temperature such that no spectral variations were observed after this time.

2.4. Multivariate Analysis

PCA and MCR were performed using the Unscrambler X (version 10.4) software package from Camo Analytics AS (Camo Analytics AS, Oslo, Norway). PCA and MCR are well-established techniques used to reduce the dimensionality of large data sets and extract pure components from a mixture, respectively. A detailed description is provided elsewhere [2,33,34]. Spectra were mean-normalized (divided each column by their mean values) before PCA analysis to assign a comparable absorption coefficient to each species and equalize the influence of each wavelength. A full cross validation, leaving one sample out at a time, was used to calculate validation scores. MCR was applied with a nonnegative concentration constraint and without a nonnegative spectral constraint.

2.5. 2D COS

ORIGINPro graphing software was used to calculate 2D correlation spectra. The average spectrum (reference) and pareto scaling (0.5) were typically used for each analysis. A zero-reference spectrum was also used to minimize the contribution of noise from the detector [30,32]. Synchronous and asynchronous correlation spectra (VV = variable-variable) are calculated by Equations (1) and (2).

$$V{V}_{synchronous }=\frac{1}{v-1} X^{T}X, \mathrm{and}$$

(1)

$$V{V}_{asynchronous}=\frac{1}{v-1} X^{T}HX$$

(2)

where v is the number of samples, X is the spectral matrix, H denotes Noda’s modification of the Hilbert transform matrix that is an orthogonalization operator, and X^T is the transform of the spectral matrix. 2D-COS spectra were evaluated in large and small increments across the spectrum because of the complexity of the multitude of peaks in the spectrum. The colors red, yellow, green, and blue represent positive, slightly positive, near zero and negative intensity in each 2D COS spectrum.

2.6. Pretreatment

Spectral data is often pretreated before 2D-COS analysis because spectral noise can result in artifacts in the data, especially in the asynchronous spectrum, making interpretation difficult or even impossible [32]. Noise can originate from baseline fluctuations and random noise (e.g., detector). Common pretreatment methods including scaling, baseline offset, derivatives, fitting, smoothing, and interpolation were tested using OriginPro. A Savitzky-Golay algorithm was tested to smooth the data using a variety of polynomial orders and smoothing points. Smoothing can distort spectral features, so great caution should be exercised when applying this pretreatment. In the data set evaluated here, minor baseline fluctuations and random noise from the detector had to be accounted for in the NIR regions. A series of Gaussian-Lorentzian cross-product functions were fit under each spectrum. Gaussian and Voigt functions were also tested. Fitting functions helped smooth the spectra by interpolating the data near the maxima of the peaks, leading to a more accurate fit of the data with minimal distortion to peak shape often associated with smoothing.

3. Results and Discussion

3.1. Np(V) Absorption Spectrum and Temperature-Induced Changes

The Np(V) absorption spectrum is well documented both experimentally and computationally in the literature [1,14,15]. The energy levels for each transition in the absorption spectrum of Np(V) are complex and related to the whole system, not the ion itself, because NpO₂⁺ ions are not fixed in solution, but the environment adapts itself to the ion [13]. Solvent molecules interact with the solute in its ground state or excited state through intermolecular bonding. Numerous peak energies predicted by computations have not been assigned to experimental data because many bands are unresolved [14]. Assigning each absorption band is challenging because most are broad, asymmetric, and overlapping, due in part to the availability of numerous vibrational and rotational energy levels and unresolved vibrational fine structure [13]. Here, we apply a temperature perturbation and advanced spectral analysis to uncover convoluted peaks in the Np(V) absorption spectrum.

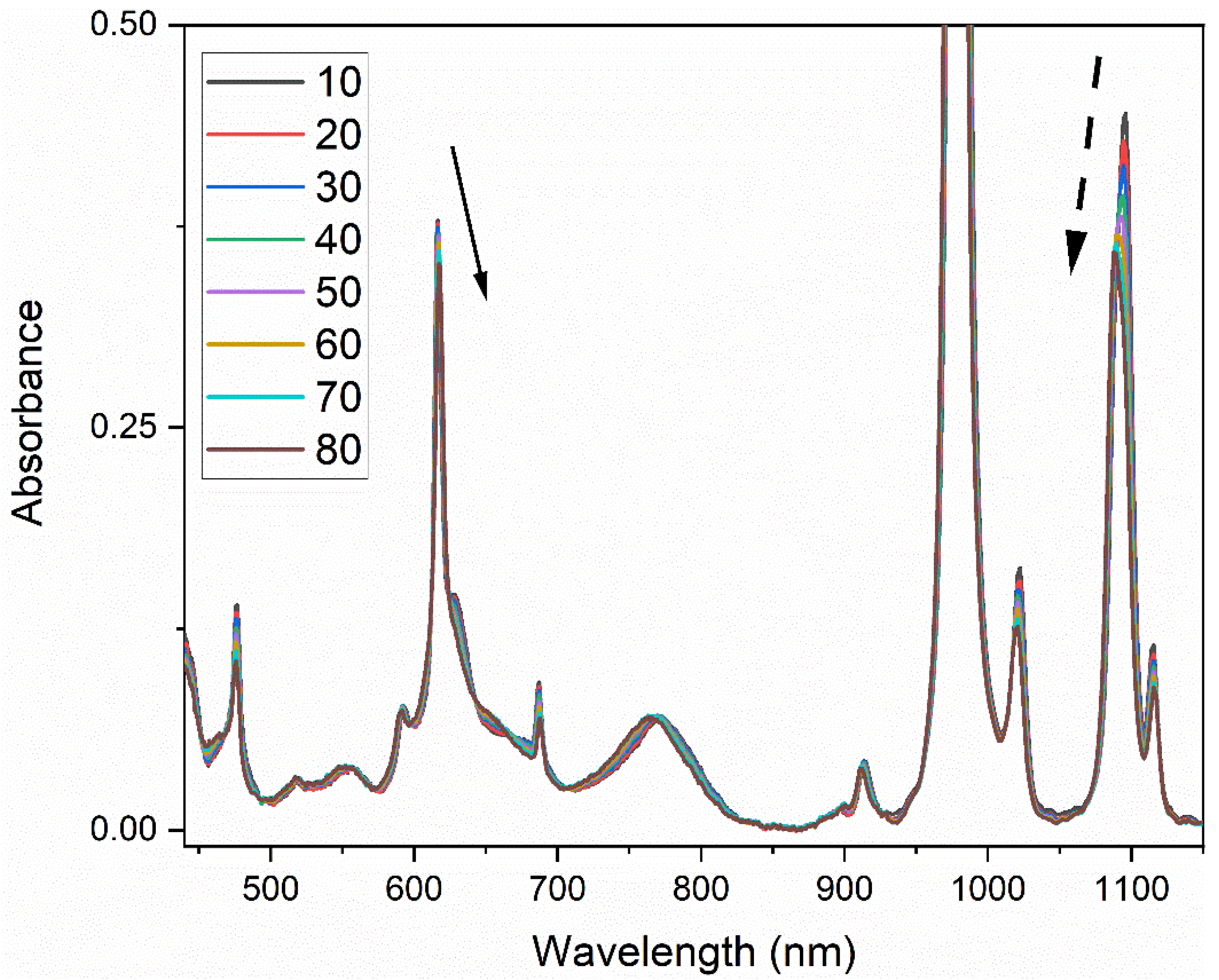
Absorption spectra of Np(V) in 1 M HNO₃ (T = 10–80 °C) are shown in Figure 1. The Np(V) spectrum is very similar to the spectrum in perchloric acid because of comparably weak interactions between nitrate/perchlorate ions and the neptunyl(V) cation [14,15,23]. The hydrated NpO₂⁺ cation has intense and relatively sharp absorption bands near 980 and 616 nm, often used for quantitative analysis [11]. Additional bands occur from 400–1700 nm with large differences in molar absorptivity values, but most have not been studied in detail. The dominant peak at 979.5 nm is outside the dynamic range of the spectrophotometer at the Np concentration reported in Figure 1. Several distinct absorption bands were also observed at 433, 476.5, 616.4, 687.0, 769.5, 914, 1023, 1095, 1116, and 1616 nm with molar absorptivity values ranging from 2.5–27 M⁻¹∙cm⁻¹ [3]. Several peaks, like the sharp 616 nm band and low-intensity peaks from 500–600 nm, are complex and confounded by overlapping peaks that are difficult to resolve.

The spectrophotometer was blanked in water, so the resulting NIR spectrum was composed of a spectral response from both Np(V), nitric acid, and temperature (Figure S1). Prominent water bands occur near 970, 1190, 1450, and 1940 nm in the NIR spectrum [37]. The band centered near 1450 nm is related to the first overtone of water. It is sensitive to perturbations altering the local tetrahedral structure of water (ionic strength, temperature, etc.). A positive peak at 1407 nm and a negative peak at 1490 nm in the NIR region grew with increasing temperature (Figure S2). At elevated temperature, intermolecular H-bonds are generally weakened (1490 nm peak), and covalent O-H bonds are strengthened and vibrate at higher frequencies (1407 nm peak). This interpretation comes from a two-state mixture model [21]. In addition to temperature effects, nitrate (NO₃⁻) ions and hydrogen ions (H⁺) are order destroying and order producing, respectively, and also impact the NIR spectrum [37]. NpO₂⁺ ions have unique characteristics and can be described as having structure-maker qualities because the absorption in the range from 1450–1650 nm increases with increasing Np(V) concentration at Np(V) concentrations > ~0.2 M. A small contribution from Np(VI) was noted in several spectra near 1222 nm. This is the most intense peak in the Np(VI) spectrum and is completely resolved from Np(V) peaks [2,36]. Thus, the impact of Np(VI) on the Np(V) spectrum was negligible.

The baseline from 400–950 fluctuates minimally with changing temperature because there are no significant water bands in this region. This region is characterized by a nearly linear baseline offset and a slight decrease of ~0.006 absorbance units over the entire temperature range, an effect simply accounted for by a baseline offset correction. Absorption peaks from 450–950 nm are therefore independent of temperature-induced fluctuations from the solvent.

3.2. Peak Shifts

The electric dipole–allowed absorption band near 979.5 nm was hypsochromically shifted (i.e., blue shifted) by 1.9 nm from T = 10–80 °C, which is consistent with previous work [17,18]. The band wavelength position blue shifted linearly by 0.0279 nm per degree Celsius, and the peak intensity decreased linearly by an average of 0.00087 absorbance units per degree Celsius. If the band at 914 nm is associated with the symmetric stretching vibrational mode of the NpO₂⁺ [12] then a blue shift indicates shortening of the neptunyl(V) bond with increasing temperature, which is consistent with Raman studies of the uranyl(VI) cation [38]. Bathochromic (i.e., red) shifts were identified for multiple peaks in the spectrum at 616.4, 686.9, 1115, and 1616 nm. Two of these transitions at 1616 and 686.9 nm were assigned as magnetic dipole–allowed transitions [14]. The peak position for the rest of the bands either blue shifted or changed very slightly.

In general, the wavelength position changed linearly with temperature; however, the intensity changes were not as straightforward. For example, the intensity of the 1616 nm peak did not begin decreasing until >50 °C, while the band 979.5 nm peak intensity decreased linearly. The band centered near 1095 nm changed the most with temperature and is discussed in a later section. The results, summarized in

Table 1. Experimental wavelengths for the primary peaks in the Np(V) absorption spectrum. The rate of peak position shift and rate of absorbance (Abs) intensity change due to temperature are tabulated for each peak < 0.2 M Np.

Experimental Wavelength @ 20 °C (nm)	Rate of Peak Position Shift (nm °C−1)	Rate of Intensity Change (Abs °C−1)
476.1	−0.0065 ± 0.0006	−5.5 × 10−4 ± 1 × 10−5
616.4	0.0176 ± 0.0008	−6.3 × 10−4 ± 7 × 10−5
686.9	0.0090 ± 0.0003	−3.8 × 10−4 ± 1 × 10−5
914	−0.029 ± 0.001	−1.8 × 10−4 ± 1 × 10−5
979.5	−0.0279 ± 0.0001	−8.7 × 10−4 ± 4 × 10−5
1022	−0.024 ± 0.001	−5.87 × 10−4 ± 9 × 10−6
1115	0.0121 ± 0.0002	−5.05 × 10−4 ± 9 × 10−6
1616	0.067 ± 0.002	−4.3 × 10−5 ± 7 × 10−6

Note: Errors are reported at the 95% confidence level.

, indicate that temperature must be accounted for to obtain quantitative Np(V) concentration measurements by spectrophotometry.

Peaks in the Np(V) absorption spectrum arise from the numerous electronic and magnetic dipole–allowed transitions and are related to changes in the vibrational motion of the environment (e.g., hydration sphere). The solvent affects the absorption spectrum because of solvent-solute interaction(s) and various short-range water complexation and/or hydrogen bonding effects [38,39]. The neptunyl ion (NpO₂⁺) is complex and capable of internal vibrations and rotations, which can be excited in an electronic transition [11]. Temperature alters the hydration sphere and vibrational/rotational states of the Np(V) ion, which changes the transition energy and line width of the absorption bands. Pairing spectrophotometry with Raman spectroscopy, in conjunction with computational modeling, would be interesting to pursue as future work and could provide insight into the exact mechanism(s) behind the shifts [14,20,37]. However, this is outside the scope of work presented here.

3.3. 2D-COS and Derivative Analysis of the NIR Region

The amplitude and peak widths for each absorption band can be estimated by peak fitting with Gaussian or Lorentzian functions. If the peaks are relatively narrow, then the peak centroid corresponds to the sum of the ionic energy. Fitting overlapping absorption peaks lacks any theoretical justification and should be taken lightly. Therefore, 2D-COS analysis was applied for unambiguous interpretations.

2D-COS is useful for the elucidation of convoluted peaks and for describing how peaks are related by interpreting characteristic patterns of correlation peaks in both the synchronous and asynchronous plots [26,27,28,29,30,31,32]. 2D-COS was applied to this system to identify convoluted peak positions. Derivatives can be used, in conjunction with 2D-COS, to help identify the presence of peaks with very similar positions and 2D-COS patterns [31,32]. When combined, both 2D-COS and second derivative spectra can unambiguously explain complicated peak characteristics [32].

A 2D correlation spectrum of the 979.5 nm peak, without subtracting a reference spectrum, is shown in Figure S3. Calculating 2D-COS spectra without subtracting a reference reduces the effect of the intensity changes due to band shift but can also make the spectrum more complex [30]. The observed pattern consists of a nearly symmetrical synchronous peak and two asynchronous peaks at 976 and 980 nm (Figure S3). A shift for a single band always generates two asynchronous peaks (Figure S4b) [32]. There is one peak in the second derivative spectrum for the 980 nm band (Figure S4). For comparison, the average reference synchronous correlation spectrum consists of two auto peaks at 975 and 980 nm, negative cross peaks, and a characteristic angel pattern with cross peak wings (Figure S5). In the asynchronous spectrum, the off-diagonal cross peaks were elongated, the characteristic “butterfly” pattern (distorted) was observed, and secondary cross peaks of opposite sign were identified. In either case, the 2D-COS spectra and second derivative spectra indicate that the peak is shifting to the left (i.e., blue shift) and that the origin of the peak is a single band shifting in intensity and position [32].

One of the most interesting peaks in the Np(V) spectrum occurs near 1095 nm. When this peak was initially described, in 1966, it was noted that the band had a “curious top” and could possibly be two peaks [12]. In more recent years, computational models have assumed the peak near 1095 nm is a single peak corresponding to one electronic transition [14]. 2D-COS spectra revealed characteristic patterns indicating two extensively overlapped peaks, at 1087 and 1096 nm, that blue shift in the same direction but change intensity at different rates [32]. The reference spectrum was set equal to zero to reduce the baseline fluctuation and spectral noise, which eliminated streaking and removed unexpected cross peaks, as shown in Figure 2 [30]. An asymmetric autopeak at 1095 nm and another autopeak at 1115 nm were identified in the synchronous spectrum (Figure 2a). The two satellite peaks in Figure 2b correspond to the correlation between the 1087 (1086, 1115) and 1096 nm (1097, 1117) peaks with the 1115 nm peak. The presence of three peaks at 1087, 1096, and 1115 nm, in the region from 1050–1150 mm, were also identified (Figure S6) using an average reference spectrum. Streaking was also observed as weak cross peaks at 1070 and 1130 nm, but these were caused by slight baseline fluctuations. These spectra support the conclusion that the 1095 nm band is composed of two peaks centered near 1087 and 1096 nm. The second derivative spectrum corroborates this finding (Figure S4) [32].

The complicated band near 1095 nm was fit using Gaussian-Lorentzian functions to show the position and intensity changes for each component at 1087 and 1096 nm (Figure S7). The rate of peak position shift for the 1087 and 1096 nm bands was −0.0173 ± 0.0004 and −0.021 ± 0.001 nm °C⁻¹, respectively. The 1096 nm peak decreased significantly (−2.2 × 10⁻³ ± 1 × 10⁻⁴ Abs °C⁻¹) with temperature, while the intensity of the component near 1087 nm increased (−6.5 × 10⁻⁴ ± 3 × 10⁻⁵ Abs °C⁻¹). A mechanistic understanding for these peak characteristics should be explored in future work.

3.4. 2D-COS Analysis of the VIS Region

The visible region of the Np(V) spectrum is particularly complicated and includes numerous overlapping peaks with disparate intensities, spectral bandwidths, and broad asymmetries, which make it difficult to assign energies to peak positions for many electronic levels. It is possible to fit this region using a series of Gaussian-Lorentzian functions, but this is a relatively ambiguous exercise. Instead, a synchronous spectrum was calculated using an average reference and pareto scaling to obtain the power spectrum. A complicated synchronous spectrum of the entire region is shown in Figure S8. Correlation peaks in the asynchronous spectrum appeared due to the combination of weak artifacts and strong bands. Because of the complexity of this 2D-COS spectrum (~440–940 nm), the power spectrum and smaller portions of the spectrum were individually evaluated by 2D-COS to help simplify interpretations.

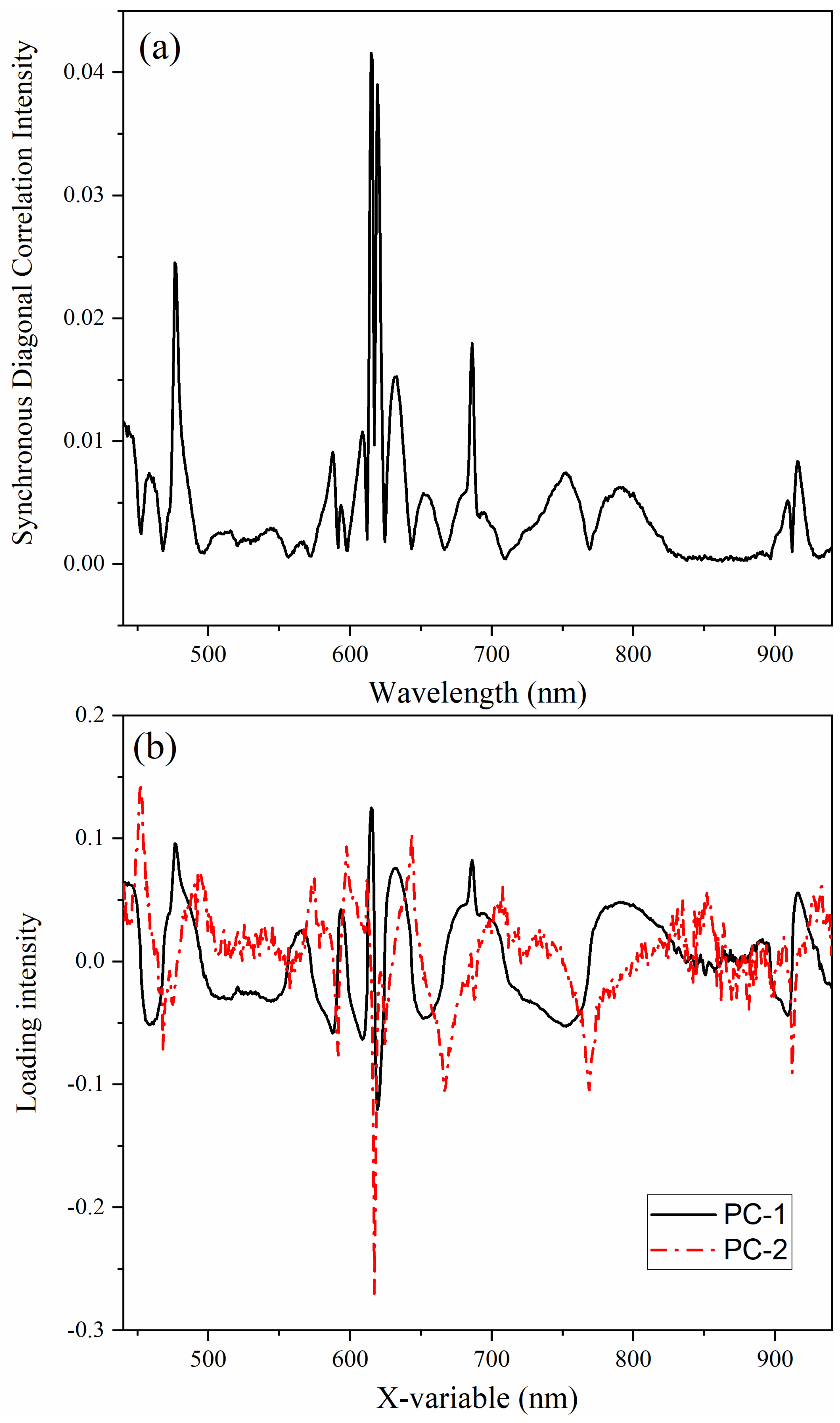
The power spectrum is the diagonal of the synchronous correlation spectrum and corresponds to the wavelength positions most susceptible to change by the perturbation (i.e., temperature). The peaks in the power spectrum correspond to autopeaks, which often coincide with the peaks in the absorption spectrum experiencing the largest change (Figure 3a) [31]. However, the presence of complicated characteristics such as the four-leaf clover, butterfly, or angel patterns can obfuscate interpretation. To support the interpretation of the autopower spectrum, the asynchronous correlation spectrum was examined at the wavelengths corresponding to autopeaks and cross peaks in the synchronous spectrum. The autopower spectrum was also compared with PCA and MCR analysis of the synchronous spectrum.

PCA was used to characterize horizontal cross sections from the synchronous spectrum (Figure 3b). PC-1 explained 99.86% of the variance, while PC-2 described 0.13% of the variance. The scores and loadings were identical in terms of shape and intensity. PC-1 looked like the autopower spectrum; where the loading intensity was negative, the scores were also negative. The PC-2 loadings were particularly interesting. The sharp peaks in PC-2, aligning with inflection points in PC-1, were indicative of isosbestic points in the spectrum. This approach helped identify a total of 17 isosbestic points in the spectrum from 450–930 nm with changing temperature. The most prominent isosbestic points occurred near 468.1, 591.5, 617.2, 624.7, 667.5, 768.8, and 912.1 nm based on MCR analysis of the horizontal spectra (Figure S9). The regions of the spectrum with the smallest variation, or “tightest” tolerance, resulted in the greatest residual error. The most defined points (i.e., sharpest peaks) in the residual spectrum occurred at 591.5, 617.2, 627.7, and 912.1 nm. Additional isosbestic points in the NIR region occurred near 1014, 1071, and 1137 nm.

The isosbestic points near the 616 nm peak at 625 and 643 nm have the largest epsilon values of 8.7 and 4.6 M⁻¹∙cm⁻¹, respectively. These can be useful for quantification by univariate approaches like Beer’s law. The three isosbestic points in the NIR region (1014, 1071, and 1137 nm) are more sensitive to baseline fluctuations resulting from the influence of temperature on water absorption bands. These could be used for quantification if the sample cuvette were blanked in air; but in practice, it is difficult to ensure that only air is in the cuvette while referencing. Each isosbestic point arose because of peak intensity and position fluctuations. These points are not indicative of a transition from one Np(V) species to another (i.e., chemical equilibrium) but more likely correspond to a physical change of the local [NpO₂(H₂O)₅]⁺ cluster environment induced by temperature.

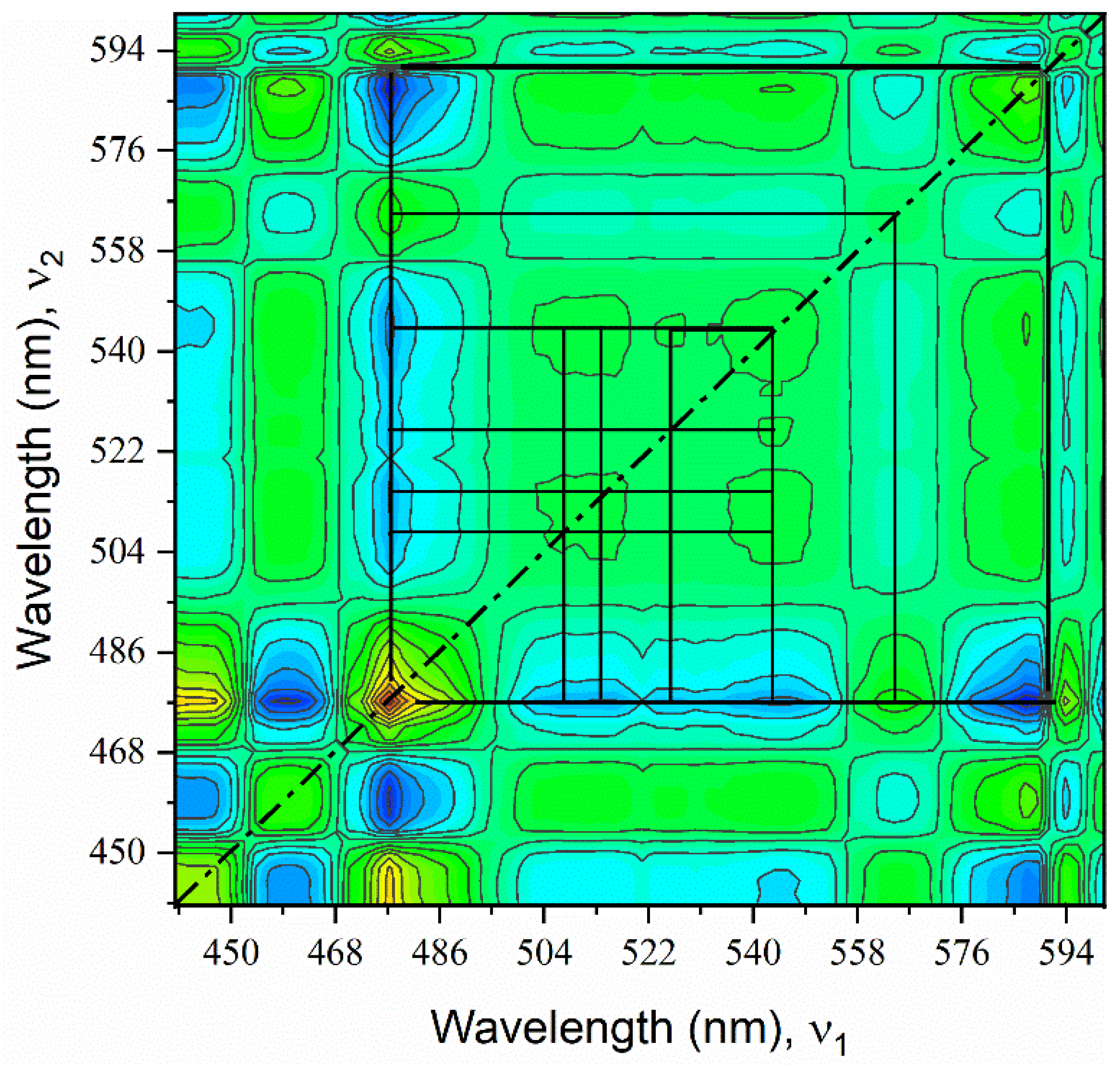
Numerous peaks were predicted by Edelstein in the region from ~450–600 nm in the Np(V) spectrum but were not assigned to experimental data [14]. These peaks were difficult to identify because they are highly convoluted, and this region has a low signal-to-noise ratio. A 2D-COS synchronous spectrum indicated numerous peaks from ~440–600 nm, and these agreed with computations (Figure 4). Cross peaks are normally identified between significant spectral features in the synchronous spectrum if the peaks truly correspond to bands in the absorption spectrum [31]. Cross peaks, located at off-diagonal positions, represent simultaneous changes of spectral intensities at two distinct spectral locations (i.e., peaks). Correlation squares joining pairs of cross peaks show coherent variation of spectral intensities at vertex locations [26]. The location of cross peaks, identified by the correlation squares, suggests that distinct peaks occur near 460, 477.5, 508, 513, 525, 543, 563, and 591.5 nm. The peaks in the synchronous spectrum were compared with the asynchronous correlation spectrum to confirm the presence of peak locations.

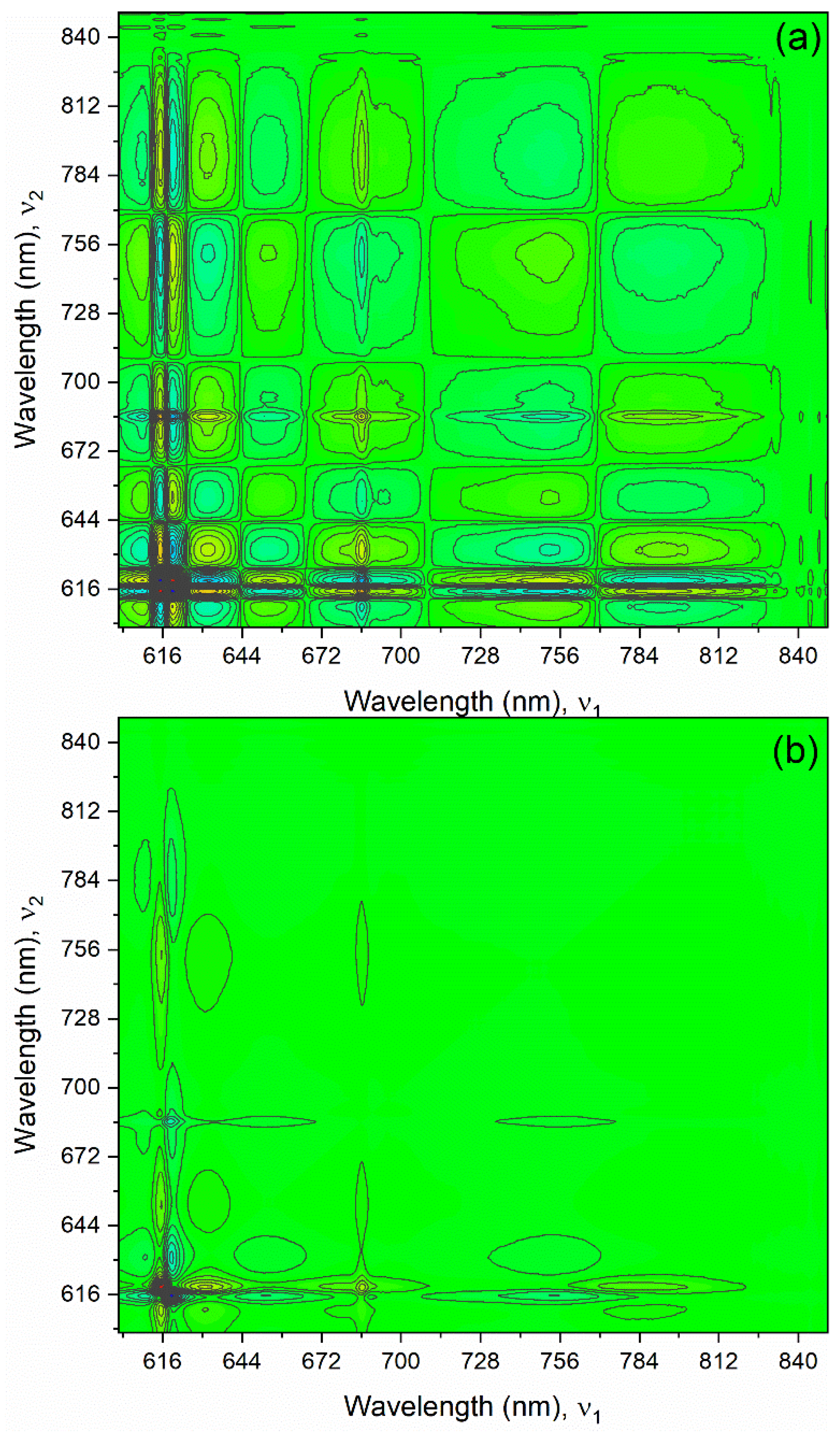
The most apparent peaks in the Np(V) absorption spectrum from 600–850 nm are located near 616, 687, and 770 nm. Gaussian-Lorentzian peak fitting suggests that additional peaks are present from this region (Figure S10). The bands surrounding the 616 nm peak are highly overlapped and result in complicated 2D-COS patterns. The complexity is due to combinations of highly overlapped variations with band position shifts in the opposite direction and band width broadening [28,32]. The synchronous and asynchronous 2D correlation spectra for this region suggest that additional peaks occurred near 627, 655, and 695 nm (Figure 5). Evidence for the peak near 695 nm comes from the distortion of the auto and cross peaks centered near the sharp peak at 687 nm. This peak, void of any underlying offset, would have a distinct star-like pattern [30]. However, the broad, off-centered, and asymmetric pattern to the left and the peak to the right of 687 nm suggest that there is another underlying peak near 695 nm. This peak is likely much broader than the sharp 687 nm band and falls nearly directly under it. Thus, it is difficult to identify the exact position of the band, even using 2D correlation spectra. The region from 870–925 nm was also analyzed by 2D-COS to reveal two peaks in this region near 897 and 913 nm (Figure S11).

The identified peaks were compared with the ones calculated by Edelstein [14]. In the most recent computational description of the Np(V) spectrum, peaks assigned by Edelstein to experimental data included 11 peaks at 1620, 1117, 1093, 1023, 979.6, 911.6, 765.6, 686.0, 621.1, 616.5, and 591.5 nm. Each peak was confirmed in this work (

Table 2. Calculated wavelengths for each transition based on computations compared with previous experimental work by Edelstein¹⁴ and this work.

Transition	Calculated nm	Previous Work [14]	This Work
E4g	82644.6	-	-
A1g	4599.8	-	-
E1g	2725.5	-	-
E5g	1637.7	1620.0	1617
A2g	1111.1	1116.9	1116
E1g	1107.7	1093.4	1096
Added peak	-	-	1087
A1g	1039.5	1022.5	1022
E2g	979.6	979.6	979.5
E6g	911.7	911.6	914
Added peak	-	-	896.8
E4g	765.6	765.6	769
A1g	703.3	-	~695
E3g	689.7	686.0	687.0
Added peak	-	-	656
E1g	621.5	621.1	627.7
E2g	615.9	616.5	616.4
A1g	589.1	591.5	591
E2g	545.8	-	563
E5g	543.9	-	543
E4g	526.4	-	525
E1g	517.3	-	513
E1g	509.3	-	508
E3g	491.6	-	477.5
E6g	466.5	-	460

). Several peaks were not calculated by Edelstein but were identified in this work near 653, 897, and 1086 nm. The 897 nm peak was characterized by Eisenstein and Pryce in an earlier work [12]. This should be taken lightly, as the calculations by Eisenstein and Pryce were performed assuming a D_6h symmetry. More recent work suggests D_5h should be used (i.e., NpO₂⁺ coordinated by five water molecules) [14]. Differences between the experimental data and computation could be due to assumptions necessary for modeling. For example, if the symmetry of the Np(V) ion in aqueous solution changes slightly, the assumptions required to predict transition energies would be inaccurate.

3.5. Principal Component Analysis

PCA is useful for reducing spectral dimensionality to recognize groups, trends, and outliers in the data. It is used in many classification applications as an unsupervised method because it requires only X (i.e., spectra) as the input. Principal components (PCs) contain a portion of the total information needed to explain the variance in a spectrum, and each PC contains less information than the previous one. The total explained variance measures how much of the variation in the data is described by PCs in the PCA model. The primary results from a PCA analysis include scores and loadings, and both must be considered for correct interpretation. Loadings with nonzero positive or negative values contribute information, while loadings near zero do not (i.e., noise). In general, variables with small loadings are not used for interpretation. Scores describe how the variables are related to one another (i.e., trends). PCA analysis revealed interesting relationships in the data set.

Figure 6 a and b show scores and loadings for the first two PCs in a PCA model used to describe the spectra from 450–950 nm of Np(V) from 0.034–0.89 M with varying temperature (10–80 °C). The system is described using the first and second PCs, PC-1, and PC-2, which account for 99.12% and 0.59% of the explained validation X-variance (99.71%). The calibration (99.71%) and validation (99.67%) explained X-variances agreed, which suggests that the data is representative of the system and the model can describe new data well. Additional PCs have noisy score vectors with little structure. PC-3 explains another 0.28% of the explained variation, but the relationship to PC-1 and PC-2 is somewhat sporadic.

PC-1 accounts for most (99.1%) of the structured variation in the data set with a loading X-variable (nm) vector that appears to be nearly identical to an average Np(V) absorption spectrum (Figure 6b). The score vector for PC-1 increases sequentially with increasing Np concentration until > 0.5 M, which is consistent with observations that molar absorptivity values decrease at elevated Np(V) concentrations [3]. Each step corresponds to different Np concentrations, and each plateau corresponds to a nearly constant contribution from PC-1 with varying temperature. The vector for PC-2 represents the X-loading structure that describes temperature-induced spectral variations. The score vector for PC-2 shows the linear temperature variation for each concentration level, but the slope of each line differs. Thus, the rate of spectral change is proportional to Np concentration and increases sequentially between samples until ~0.5 M Np. The magnitude of temperature-induced fluctuations is nearly constant when normalized to total Np concentration until >0.5 M Np, when it decreases. PCA can be used to describe these concentration-dependent temperature-induced spectral fluctuations when a linear function would not be able to account for the variation. A 2D scatter plot (i.e., bi-plot) of scores 1 and 2 supported this interpretation of sample properties and variable relationships simultaneously (Figure S12).

In concentrated solutions, solute molecules influence one another because of their proximity, which changes their properties and molar absorptivity values. The absorptivity changes at high concentrations when an absorbing molecule participates in a concentration-dependent chemical equilibrium. At Np concentrations near >0.2 M Np, the self-association of NpO₂⁺ ions form dimers and even higher polymers in concentrated solutions. These have been characterized by Raman spectroscopy, which describes complex spectra [20,21]. However, the electronic spectra presented here appear to be less sensitive to these species until higher Np concentrations. The sharp absorption bands at 616 and 980 nm did not shift in wavelength position, even at 0.89 M Np. However, the 616 nm peak deviated from linearity ≥0.5 M Np, and the overall shape of the convoluted peaks in the Vis region changed slightly (Figure S13) [3]. This suggests that spectrophotometric measurements might be particularly amiable to analytical applications Np(V) concentrations >0.2 M.

PCA results for the peaks centered near 1095 nm and the water band region (1300–1650 nm) are shown in the supporting information. These regions were separately analyzed because the water band has unique characteristics relative to the Np(V) absorption bands, although these can be modeled simultaneously. PCA analysis describes the more than 99.7% of the total explained X-variance for the peaks in the spectral range from 1050–1140 nm. PC-1 accounts for most (97.4%) of the structured variation in the data set, and the loading vector appears to be nearly identical to an average Np(V) absorption spectrum (Figure S14). PC-2 accounts for an additional 2.3%. Contrary to the PCA analysis results describing the peaks in the 460–950 nm range (Figure S12), PC-1 does not increase sequentially with increasing Np concentration but decreases with increasing temperature at each Np concentration level, as shown in a bi-plot for PC-1/PC-2 (Figure S14). The rate of change in scores for PC-1 versus temperature became sequentially more linear at each lower Np concentration and it was relatively constant until it decreased below 0.17 M Np. Normalizing to total Np concentration revealed that PC-1 scores rate of change relative to temperature decreased slightly with increasing Np concentration.

This result is contrary to data presented in Figure 6 describing the Vis region. This suggests that PC-1 also contained some information related to temperature and that temperature affects this region (1050–1140 nm) greater than the Vis region. The difference between the PCA analysis and interpretation for raw data and background subtracted data in this region was inconsequential. The rate of change in scores for PC-2 versus temperature increased nearly linearly until it began to plateau at ~0.5 M Np. Normalizing to total Np concentration revealed that PC-2 scores rate of change relative to temperature decreased slightly with increasing Np concentration like PC-1. The magnitude of change related to PC-2 scores was overall greater than PC-1, meaning it contributes the most to the structured variation relative to temperature fluctuations. The intense peak at 979.5 nm and the small peak near 1015 nm were not included in the analysis because the 980 nm peak saturates the detector in most samples and is somewhat convoluted with the 1015 nm peak.

PCA analysis described 99.99% of the total explained variance for the NIR overtone water band peak in the spectral range from 1280–1650 nm in a control containing 1 M HNO₃. PC-1 accounted for most (99.64%) of the structured variation in the data set, while PC-2 accounted for 0.35%. The bi-plot has a parabolic shape, consistent with other reports of scores and loadings in this region of the spectrum (Figure S15). The largest positive peak in the PC-1 loadings spectrum occurred at 1497 nm, and a negative peak appeared at 1404 nm. The overall shape of the loading was comparable with a study describing pure water [29]. The second loading was composed of a peak near 1417 nm that appeared to be unique relative to water (Figure S15). These results suggest that acid might impact the temperature response in the NIR region.

Another PCA model of the same NIR region in the presence of Np (0.034–0.89 M) changes the scores and loadings significantly (Figure S16). PC-1 accounted for most (83.3%) of the structured variation in the data set, while PC-2 accounted for 16.1%. The loadings were comparable with pure nitric acid; however, the 1616 nm Np(V) absorption band contributed significantly. The increased percentage of the explained variance for PC-2 was likely due to the impact Np(V) had on the NIR water band, an effect that became more pronounced at concentrations ≥0.5 M Np. The PC-1 scores decreased with increasing temperature and decreasing concentration, while the PC-2 scores increased with increasing concentration and decreased with decreasing Np concentration. A 2D scores plot describes the relationship between PC-1 and PC-2 (Figure S16).

Np(V) absorption peaks in the 1050–1140 nm region are more dynamic than any other peak in the spectrum with temperature. These peaks could be used to quantify the temperature of process solutions. Modeling this region could be challenging because it is convoluted with water absorption bands. The contribution from the water band is minimized using a small path length (≤1 mm). Quantitative regression modeling of spectra collected with water blanked at various temperatures could be pursued in future work. On the other hand, applying a first derivative to spectra from 400–950 nm accounts for baseline offset in this region and could result in a measurement that is independent of the temperature of the reference solution.

4. Conclusions

The Np(V) absorption spectrum is composed of numerous peaks with unique temperature dependencies. The position of numerous absorption peak intensities and positions as a function of temperature were reported for the first time. Temperature caused unique spectral changes for each peak in the absorption spectrum; however, the wavelength position of each band changed linearly with temperature. Numerous peaks in the visible region were identified experimentally by evaluating the 2D correlation synchronous power spectrum. 2D-COS also revealed a new set of peaks at 1087 and 1096 nm, as opposed to the previously interpreted position of a single peak at 1095 nm, which are the most dynamic with temperature variations. PCA was used to model the complicated, nonlinear concentration and temperature-related spectral variations where standard univariate approaches would fail. A nonlinear concentration and temperature dependence was noted at ≥0.5 M Np concentrations where the molar absorptivity of each peak in the spectrum decreased. This may be related to the self-association of NpO₂⁺ ions. Future work might include developing hierarchical regression models that can account for the nonlinear response in this system and expand the solution conditions to include varying nitric acid concentration and Np oxidation states.