Abstract
Potentiometric multisensor systems were shown to be very promising tools for the quantification of numerous analytes in complex radioactive samples deriving from spent nuclear fuel reprocessing. Traditional multivariate calibration for these multisensor systems is performed with partial least squares regression—an intrinsically linear regression method that can provide suboptimal results when handling potentiometric signals from very complex multi-component samples. In this work, a thorough investigation was performed on the performance of a multisensor system in combination with non-linear multivariate regression models for the quantification of analytes in the PUREX (Plutonium–URanium EXtraction) process. The multisensor system was composed of 17 cross-sensitive potentiometric sensors with plasticized polymeric membranes containing different lipophilic ligands capable of heavy metals, lanthanides, and actinides binding. Regression algorithms such as support vector machines (SVM), random forest (RF), and kernel-regularized least squares (KRLS) were tested and compared to the traditional partial least squares (PLS) method in the simultaneous quantification of the following elements in aqueous phase samples of the PUREX process: U, La, Ce, Sm, Zr, Mo, Zn, Ru, Fe, Ca, Am, and Cm. It was shown that non-linear methods outperformed PLS for most of the analytes.
1. Introduction
Chemical monitoring of spent nuclear fuel reprocessing poses a challenging analytical task for a variety of reasons. To this day, the PUREX (Plutonium–URanium EXtraction) process remains the most common industrial method of SNF (spent nuclear fuel) reprocessing [1,2]. The main goal of this process is to separate uranium and plutonium from other compounds, i.e., fission products and minor actinides, through several extraction/re-extraction cycles. The final products of interest are uranyl nitrate, uranium, and plutonium oxide, and these can be reused as nuclear fuel [3].
Current analytical control of PUREX technological media is based on spectroscopic methods such as ICP-MS and ICP-AES (inductively coupled plasma mass spectrometry and atomic emission spectrometry) [4,5,6]. These methods have the necessary qualities for performing this type of analysis, where low detection limits, high accuracy, and good reproducibility are the most important. However, the realization of these methods is demanding work that requires special working conditions and difficult sampling, which affects the safety of the analysis in general [7]. The far bigger disadvantage is the fact that none of these methods can provide us with immediate, real-time results because they require sampling, and there is no possible way that they can be set up for on-line analysis. It can take up to several hours from the moment of taking samples to obtaining the results. Finding a method that would allow on-line process monitoring would not only improve the process in terms of automation but would also improve its safety and reliability. This would be a common-sense tendency and requirement in terms of further development of SNF reprocessing technologies. North-East Atlantic Environment Strategy and IAEA (International Atomic Energy Agency) are strongly focused on the development of automated analytical techniques that are capable of reliable detecting discharges of radioactive substances [8,9].
It was shown that optical spectroscopic methods, such as UV-Vis spectrometry, IR-spectrometry, Raman spectrometry, and their various combinations, can accurately quantify concentrations of analytes in the processing of nuclear materials in on-line and near-real-time regimes [10,11]. Although such methods have good and reliable results, there are several drawbacks associated with them. Turbidity and gas formation in the analyzed media affect light scattering and deteriorate the results, and high detection limits are another concern for optical methods [12].
Potentiometric multisensor systems show promise in the analytical determination of compounds in nuclear fuel reprocessing. Earlier works that are based on combining chemometrics with potentiometric multisensor systems show that lanthanides and some of the tetra- and hexa-valent actinides (thorium, uranium, plutonium) in multi-component mixtures can be determined with appropriate accuracy [13,14,15]. The processing of the data in these works was performed using traditional partial least squares (PLS) regression method in order to relate the response of the multisensor arrays to the concentration of target elements. While being a powerful chemometric tool, PLS is an intrinsically linear method. At the same time, for complex chemical mixtures, such as the technological media of the PUREX process, it would be much more suitable to apply a nonlinear regression model for determining the concentrations of analytes. The nonlinearity of the potentiometric sensor response in complex multi-component solutions derives from the logic of Nikolsky’s equation describing the response function in potentiometry:
The sum of the products of selectivity coefficients and contributing ion activities is under a logarithm in order to linearize the response in E − ln(aI) coordinates. Thus, PLS modeling works well when the modeled concentration is expressed in logarithmic scale; however, this is neither convenient for narrow nor for rather broad concentration ranges as the modeling errors, in this case, are also expressed in logarithmic scale.
The purpose of this study was to explore the potential of nonlinear regression methods in the construction of predictive models for the quantification of various analytes in SNF reprocessing media. The traditional PLS regression algorithm was considered as a benchmark for comparison.
2. Materials and Methods
2.1. Sensor Array
The potentiometric multisensor data were obtained using an array of 17 electrodes with PVC-plasticized sensor membranes and a standard pH glass electrode ESL 63-07 (ZIP, Gomel, Belorussia). The polymeric sensor membranes were produced using the ligands with pronounced binding ability towards actinides and lanthanides, described in our previous studies [13,14,15]. The concentration of each ligand in the sensor membrane was 50 mmol/kg. The employed ligands are presented in Table S1 (Supplementary Materials). The membrane matrix of all the electrodes was made of poly(vinylchloride) (PVC) (33 wt%) and 2-nitrophenyloctyl ether (NPOE) as a plasticizer (64–65 wt%). Potassium tetrakis[3,5-bis(trifluorometyl)phenyl]borate (KTFPB) and the acidic (H+) form of chlorinated cobalt dicarbollide (CCD) in a concentration of 10 mmol/kg were employed as cation exchangers. PVC, NPOE, and KTFPB were obtained from Sigma-Aldrich (Darmstadt, Germany). CCD was kindly provided by Catchem (Prague, Czech Republic). Polymeric sensor membranes were prepared through a standard protocol: the required amounts of membrane components were dissolved in freshly distilled tetrahydrofuran and then poured in Teflon beakers with a flat bottom. The resulting membrane mixtures were left for 48 h for solvent evaporation. After that, sensor membranes 8 mm in diameter were cut from the parent membranes and glued upon the tops of PVC sensor bodies with PVC–cyclohexanone mixture. The visual appearance of the potentiometric multisensor system is provided in Figure S1 (Supplementary Materials).
2.2. Samples
The samples for analysis were acquired from the pilot extraction stand equipped with SCEK-342 extractors (Khlopin Radium Institute, St. Petersburg, Russia) during the trial experiments on the combined scheme of SNF reprocessing, which includes the first extraction cycle with separated re-extraction of U, Np, Pu, and Tc, intermediate evaporation of highly active raffinate, and its fractioning with single extracting agent based on 45% tributyl phosphate (TBP) in Isopar-M (isoparaffin C13-C14). Thus, the samples represent complex mixtures of multiple elements in highly acidic solutions (pH around 2). In total, 23 samples of aqueous phase were acquired from three different extraction blocks. The volume of each sample was 20 mL. The potentiometric multisensor measurements were performed directly without any sample pretreatment. The measurement time in each sample was 3 min; the sensors were washed with several portions of distilled water between the samples.
2.3. Reference Analysis
The concentrations of the following elements Na, Mg, K, Ca, Cr, Mn, Fe, Ni, Zn, Y, Zr, Mo, Ru, La, Ce, Pr, Nd, Sm, Eu, and U in the samples of aqueous phases from the extraction stand were determined with an inductively coupled plasma–atomic emission spectrometry (ICP-AES) (Technologies, Inc., Santa Clara, CA, USA) instrument Varian 725 (Agilent Technologies, Inc., Santa Clara, CA, USA). The concentrations of radioactive isotopes of americium and curium were determined using alpha- and gamma-spectrometry. The content of the nitric acid varied over the samples in the pH range 1.5–2. The specific activities of gamma-emitting isotopes 241Am, 243Am, and 243Cm were quantified with a Canberra gamma-spectrometer (Canberra, Australia) equipped with a GC1018 detector (Canberra, Australia), DSA-1000 analyzer (Canberra, Australia), and Genie-2000 ver.3.1 software package. The specific activities of alpha-emitting isotopes 241Am, 243Am, 242Cm, and 244Cm were evaluated with alpha-spectrometer Canberra 7401 (Canberra, Australia). The obtained specific activities were recalculated into the concentrations of elements. The content of the elements in the analyzed samples is provided in Table S2 (Supplementary Materials).
2.4. Data Processing
2.4.1. Partial Least Squares (PLS)
Partial least squares is a well-known multivariate regression tool and its description can be found elsewhere [16].
2.4.2. Support Vector Machines (SVM)
Support vector machines are used for solving both classification and regression problems with linear and non-linear models. The method is based on projecting an original input space to a high-dimensional feature space. After that, a linear regression function is constructed in a high-dimensional space for obtaining non-linear models in an original space by using kernel functions in accordance with Mercer’s theorem. SVM, in comparison with traditional regression methods such as PLS, does not rely on minimizing the observed training error alone. Instead, it minimizes the generalization error bound to achieve a higher generalization performance. Moreover, because of the model complexity control, SVM can avoid overfitting [17,18].
For this research, we used nonlinear regression with Gaussian radial basis function kernel:
where is squared Euclidean distance between two vectors from samples xi and xj, and σ is a free parameter/constant value.
2.4.3. Random Forest (RF)
Random forest represents an ensemble of fully grown decision trees in combination with a bootstrap sampling technique. In regression problems, every tree depends on the values of a random vector in a way that the tree predictor has its numerical values. Each of the built trees offers a specific prediction value, and on the output, we have the mean prediction value of these individual trees [19].
This method has two major advantages. First, it has very few tuning parameters, which makes it simpler to manipulate, and it is computationally fast. Second, it handles non-linear correlations well within the model. Moreover, it allows judging on variable importance [20].
2.4.4. Kernel Regularized Least Squares (KRLS)
Kernel regularized least squares (KRLS) was first introduced by Hazlett and Hainmueller [21]. KRLS is a machine learning method for solving regression and classification problems without assumptions on linearity or additivity of the features. We did not find the applications of this method in chemometrics.
KRLS creates hypothesis space by using kernels as radial basis functions to find a best-fitting surface in created space for a certain model. This is achieved through the minimization of a complexity-penalized least squares problem.
Function should be thought of as a measure of similarity between and . This is the so-called ”similarity-based view“. Considering this, we can write a formulation for space of functions:
where is the weight for each input pattern and , once again, represents the similarity between point of interest and , one of the input patterns. The weights are calculated using kernel function (Gaussian in our case) and their values depend on the distance between the data points.
Finally, we can consider regularization to obtain the following:
where H is the reproducing Hilbert space of functions and λ is the always positive scalar parameter governing the trade-off between model fit and complexity.
KRLS is somewhat similar to k-nearest neighbors regression, but the averaging of the response of the predicting neighbors is carried out with the weights dependent on kernel function.
Prior to regression modeling, the data were explored using principal component analysis (PCA)—a common dimensionality reduction tool that decomposes the initial data matrix into the product of scores and loadings matrices, where scores matrices describe the relationship between the samples, their similarity and dissimilarity, and loadings matrices describe the relationship between the variables and their influence on sample grouping [22].
All calculations were performed in R programming language and R version 4.0.5. software with packages mdatools [23], e1071 [24], randomForest [25], KRLS [26], and caret [27]. For the analysis of multivariate data obtained from the multisensor system, four methods were applied and compared to each other.
The initial dataset from the multi-sensor system was a matrix consisting of 23 rows, which represent samples from three different extraction blocks, and 17 columns, which represent sensor data. In the analysis of some elements, the dataset was modified because of the large variations in concentration ranges between the three extraction blocks. This adjustment usually involves the exclusion of samples from the first block, which left us with 17 samples we could operate with.
Root mean square error of cross-validation/prediction was used to evaluate the performance of the models:
where and are the reference and predicted concentrations of an analyte in the ith sample, n is a total number of samples in a test set. Two distinct approaches were used in the evaluation of the models: leave one out cross-validation over the whole set of samples, and Monte Carlo cross-validation.
- Leave one out cross-validation (LOOCV) is a well-known method that estimates the performance of a model by leaving one point out of the full dataset, with the rest being used to train the model. After training, the left-out data point is used to test the model. The process is repeated throughout the whole initial dataset on all the samples. The main disadvantage of this method is that it provides too optimistic/unrealistic results.
- Monte Carlo cross-validation (MCCV) has a somewhat different algorithm. The data are randomly split to make training sets and test sets. In our case, we had 25–75% split in favor of the training set in each iteration. After that, the model is tested by calculating the average error after 100 iterations. This method offers a better insight into the performance of the model and provides somewhat more realistic results than LOOCV.
- Finally, the performance of the regression tools was tested on the most interesting analytes through calculating the RMSEP on the test set that was made by randomly picking the samples from the full dataset. The training set from the remaining samples was used to build the models of corresponding methods.
3. Results and Discussion
In order to explore the reference data on the element content in the samples (Table S2), we applied principal component analysis (PCA). Figure 1 shows the loadings plot for the first two principal components. The close grouping of certain variables in the loadings plot implies a strong correlation between them. In this way, the content of Am, U, and Cm is correlated in the samples; the same holds for Pr, Nd, Sm, and Eu and for Mg, Ni, Cr, Fe, Ru, and Ca.
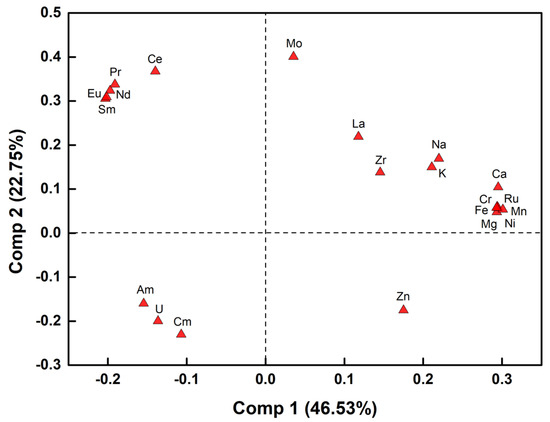
Figure 1.
The loadings plot for PCA model constructed for reference data on the content of the elements.
These correlated variables may pose a certain problem for regression modeling as the selectivity of such models among correlated target elements will be not clear. After considering this plot, the following elements, which were most important from a technological point of view, were chosen as targets for regression models: U, La, Ce, Sm, Zr, Mo, Zn, Ru, Fe, Ca, Am, and Cm.
Using various regression methods, we constructed and optimized the calibration models relating the responses of potentiometric multisensor systems in the samples to the content of the elements. Figure 2 shows typical ”measured vs predicted” plots obtained with different algorithms for the quantification of uranium. SVM models were optimized with respect to epsilon, cost, and gamma parameters. KRLS models were optimized with respect to lambda and sigma parameters. The optimal number of PLS components was chosen based on the minimum on RMSECV–number of LVs plot.
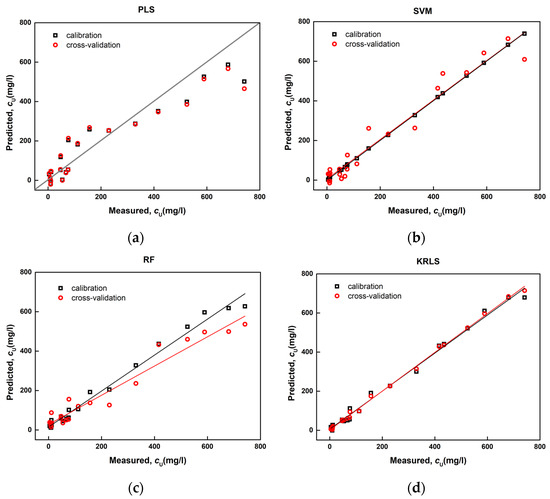
Figure 2.
The “measured vs predicted“ plots for PLS (a), SVM (b), RF (c), and KRLS (d) models obtained with full cross-validation.
The visual appearance of the plots indicates that, in the case of uranium, KRLS outperforms the rest of the regression methods. Table 1 summarizes the RMSECV values obtained for all studied elements in Monte Carlo cross-validation. Table S2 (Supplementary materials) shows the RMSECV values obtained in full cross-validation. Noteworthily, the discrepancy between these two cross-validation approaches is not very large, with the Mont Carlo procedure offering slightly higher values for most of the cases. The bold typing is used to indicate the best performance.

Table 1.
RMSECV values for regression models obtained in Monte Carlo cross-validation.
Based on these results, it can be concluded that, in general, KRLS provides higher modeling precision. KRLS has the best performance for six elements out of twelve modeled and it provides the worst RMSECV for none of the elements. Although for most of the cases the differences between the RMSECV obtained with four methods are not dramatic, in the case of uranium, KRLS offers more than two times the improvement in modeling error compared to PLS. RF was the best for three elements; however, it was inferior in four cases. This type of performance can probably be explained by the fact that RF is intrinsically not very suitable for processing small datasets such as ours. PLS was the worst for six elements. These results confirm our initial guess on the better suitability of non-linear models for describing potentiometric sensor responses in complex multicomponent media.
An important feature of PLS is that it allows the assessment of the contribution of variables in model performance through the analysis of regression coefficients. This feature is very valuable in the context of multisensor arrays as it provides a way for the optimization of sensor arrays by the elimination of poorly contributing sensors and offers the idea for further sensor development. KRLS also has this opportunity. As an example, Figure 3 shows the relative importance of the employed sensors in the quantification of four different elements. It can be seen that the most contributing sensors vary depending on the element and these plots can also be employed for sensor array optimization.
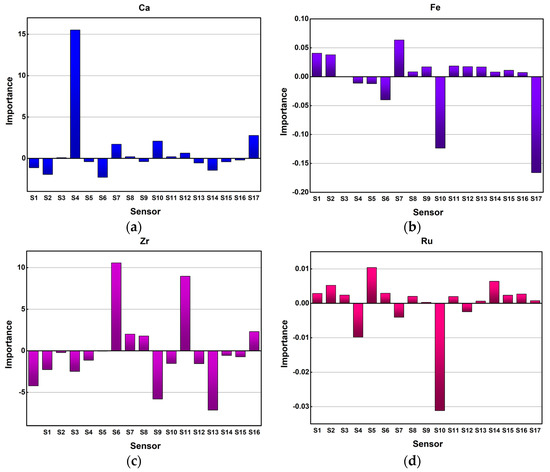
Figure 3.
The importance of sensors in determining the concentrations of Ca (a), Fe (b), Zr (c), and Ru (d).
As a final step of the study, we assessed the performance of the models in the independent test sets for several key elements of the PUREX process. Table 2 shows the resulting RMSEP values.

Table 2.
RMSEP values for quantification of U, Sm, Am, and Cm in PUREX solutions.
As can be seen from Table 2, the precision in the quantification of Sm, U, Am, and Cu is sufficient for expressing technological monitoring needs. Taking into account the ultimate simplicity of direct potentiometric measurements and their suitability for on-line implementation, these results have a good potential for the development of a novel on-line industrial chemical monitoring protocol. Considering the radiation stability of the potentiometric sensors [28], this protocol appears to be suitable for the nuclear industry as the sensors can withstand the absorbed radiation doses of 50–100 kGy depending on the membrane composition. Further radiation dose accumulation may lead to gradual decay in sensor sensitivity. This stability is sufficient for continuous sensor application in SNF process streams for at least one month, which is a reasonable duration when taking into account the overall challenging character of the analytical problem.
4. Conclusions
The response of cross-sensitive potentiometric sensors in multi-component samples can have a very complex character, and thus non-linear regression algorithms can be better suited for making quantitative predictive models. This hypothesis was confirmed for analysis of spent nuclear fuel reprocessing media with a potentiometric multisensor system. The system is capable of simultaneous quantification of Ca, Fe, Zn, Y, Zr, Mo, Ru, La, Ce, Sm, U, Am, and Cm. The possibility of potentiometric quantification of Am and Cm is demonstrated for the first time, to the best of our knowledge. The comparison of the intrinsically linear PLS algorithm with three non-linear regression methods (SVM, RF, and KRLS) has revealed that the latter, on average, demonstrates higher precision. KRLS outperformed the rest of the methods in most cases. These results imply the relevance of a broad study and application of non-linear regression algorithms for processing the data from multisensor arrays.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemosensors10030090/s1, Table S1: Sensor membrane composition; Figure S1: Visual appearance of the multisensor system; Table S2: Elemental composition of the samples taken from the pilot extraction unit.
Author Contributions
Formal Analysis, Investigation, Data Curation, N.K., J.S. and M.A.-M.; Writing—Original Draft, Visualization, N.K., D.K. and V.B.; Methodology, D.K. and V.B.; Writing—Review and Editing, Project Administration, D.K. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by Russian Science Foundation, grant #18-19-00151.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sood, D.D.; Patil, S.K. Chemistry of nuclear fuel reprocessing: Current status. J. Radioanal. Nucl. Chem. 1996, 203, 547–573. [Google Scholar] [CrossRef]
- Herbst, R.S.; Baron, P.; Nilsson, M. Standard and advanced separation: PUREX processes for nuclear fuel reprocessing. In Advanced Separation Techniques for Nuclear Fuel Reprocessing and Radioactive Waste Treatment; Woodhead Publishing: Oxford, UK, 2011; pp. 141–175. [Google Scholar]
- Miguirditchian, M.; Grandjean, S.; Sorel, C.; Vanel, V.; Delahaye, T.; Pillon, S.; Ramond, L.; Ladirat, C.; Giboire, I.; Poinssot, C.; et al. Advanced concepts for uranium and plutonium multi-recycling. In Proceedings of the GLOBAL 2017 International Nuclear Fuel Cycle conference, Seoul, Korea, 24–29 September 2017; p. ffhal-02418116. [Google Scholar]
- Günther-Leopold, I.; Kivel, N.; Waldis, J.K.; Wernli, B. Characterization of nuclear fuels by ICP mass-spectrometric techniques. Anal. Bioanal. Chem. 2008, 390, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Croudace, I.W.; Russell, B.C.; Warwick, P.W. Plasma source mass spectrometry for radioactive waste characterisation in support of nuclear decommissioning: A review. J. Anal. Atom. Spectrom. 2017, 32, 494–526. [Google Scholar] [CrossRef] [Green Version]
- Naumova, Y.A.; Sapozhnikova, N.V.; Egorova, O.N.; Lumpov, A.A. Determination of concentrations of fission products by ICP–AES in solutions from spent nuclear fuel reprocessing. Radiochemistry 2017, 59, 618–623. [Google Scholar] [CrossRef]
- Ache, H.J. Analytical chemistry in nuclear technology. Fresen. J. Anal. Chem. 1992, 343, 852–862. [Google Scholar] [CrossRef]
- The North-East Atlantic Environment Strategy, OSPAR Agreement 2010–2013. 2010. Available online: https://www.cbd.int/doc/nbsap/rbsap/ospar-rbsap.pdf (accessed on 30 December 2021).
- International Atomic Energy Agency Safety Standards, Safety of Nuclear Fuel Reprocessing Facilities, SSG-42. 2017. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/P1744_web.pdf (accessed on 30 December 2021).
- Kirsanov, D.; Rudnitskaya, A.; Legin, A.; Babain, V. UV–Vis spectroscopy with chemometric data treatment: An option for on-line control in nuclear industry. J. Radioanal. Nucl. Chem. 2017, 312, 461–470. [Google Scholar] [CrossRef]
- Tse, P.; Bryan, S.A.; Bessen, N.P.; Lines, A.M.; Shafer, J.C. Review of on-line and near real-time spectroscopic monitoring of processes relevant to nuclear material management. Anal. Chim. Acta 2020, 1107, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Debus, B.; Kirsanov, D.; Ruckebusch, C.; Agafonova-Moroz, M.; Babain, V.; Lumpov, A.; Legin, A. Restoring important process information from complex optical spectra with MCR-ALS: Case study of actinide reduction in spent nuclear fuel reprocessing. Chemom. Intell. Lab. Syst. 2015, 146, 241–249. [Google Scholar] [CrossRef]
- Agafonova-Moroz, M.; Savosina, J.; Voroshilov, Y.; Lukin, S.; Lumpov, A.; Babain, V.; Legin, A.; Kirsanov, D. Quantification of thorium and uranium in real process streams of Mayak radiochemical plant using potentiometric multisensor array. J. Radioanal. Nucl. Chem. 2020, 323, 605–612. [Google Scholar] [CrossRef]
- Savosina, J.; Agafonova-Moroz, M.; Yaroshenko, I.; Ashina, J.; Babain, V.; Lumpov, A.; Legin, A.; Kirsanov, D. Plutonium (IV) quantification in technologically relevant media using potentiometric sensor array. Sensors 2020, 20, 1604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oleneva, E.; Savosina, J.; Agafonova-Moroz, M.; Lumpov, A.; Babain, V.; Jahatspanian, I.; Legin, A.; Kirsanov, D. Potentiometric multisensor system for tetra-and hexavalent actinide quantification in complex rare earth metal mixtures related to spent nuclear fuel reprocessing. Sens. Actuat. B Chem. 2019, 288, 155–162. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Yang, T.; Sundling, M.C.; Freed, A.S.; Breneman, C.M.; Cramer, S.M. Prediction of pH-dependent chromatographic behavior in ion-exchange systems. Anal. Chem. 2007, 79, 8927–8939. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, L.; Niu, D.; Tan, Z. An annual load forecasting model based on support vector regression with differential evolution algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Rajappan, R.; Shingade, P.D.; Natarajan, R.; Jayaraman, V.K. Quantitative Structure—Property Relationship (QSPR) Prediction of Liquid Viscosities of Pure Organic Compounds Employing Random Forest Regression. Ind. Eng. Chem. Res. 2009, 8, 9708–9712. [Google Scholar] [CrossRef]
- Hainmueller, J.; Hazlett, C. Kernel regularized least squares: Reducing misspecification bias with a flexible and interpretable machine learning approach. Polit. Anal. 2014, 22, 143–168. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef] [Green Version]
- Kucheryavskiy, S. Mdatools–R package for chemometrics. Chemom. Intell. Lab. Syst. 2020, 198, 103937. [Google Scholar] [CrossRef]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.-C.; Lin, C.-C. 2021, Package ‘e1071’, ver. 1.7–9. Available online: https://cran.r-project.org/web/packages/e1071/index.html (accessed on 30 December 2021).
- Breiman, L.; Cutler, A.; Liaw, A.; Wiener, M. 2018, Package ‘randomForest’, ver. 4.6–14. Available online: https://cran.r-project.org/web/packages/randomForest/ (accessed on 30 December 2021).
- Hainmueller, J.; Hazlett, C. 2017, Package ‘KRLS’, ver. 1.0–0. Available online: https://cran.r-project.org/web/packages/KRLS/index.html (accessed on 30 December 2021).
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B. 2021, Package ‘caret’, ver. 6.0–90. Available online: https://cran.r-project.org/web/packages/caret/ (accessed on 30 December 2021).
- Savosina, J.; Agafonova-Moroz, M.; Khaydukova, M.; Legin, A.; Babain, V.; Tolstoy, P.; Kirsanov, D. On the Radiolytic Stability of Potentiometric Sensors with Plasticized Polymeric Membranes. Chemosensors 2021, 9, 214. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).