Hierarchical Modeling to Enhance Spectrophotometry Measurements—Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methodology
2.3. Spectrophotometry
2.4. Multivariate Data Analysis
2.5. Statistics
3. Results and Discussion
3.1. Np Vis-NIR Spectra
3.2. Principal Component Analysis
3.3. Hierarchical Modeling
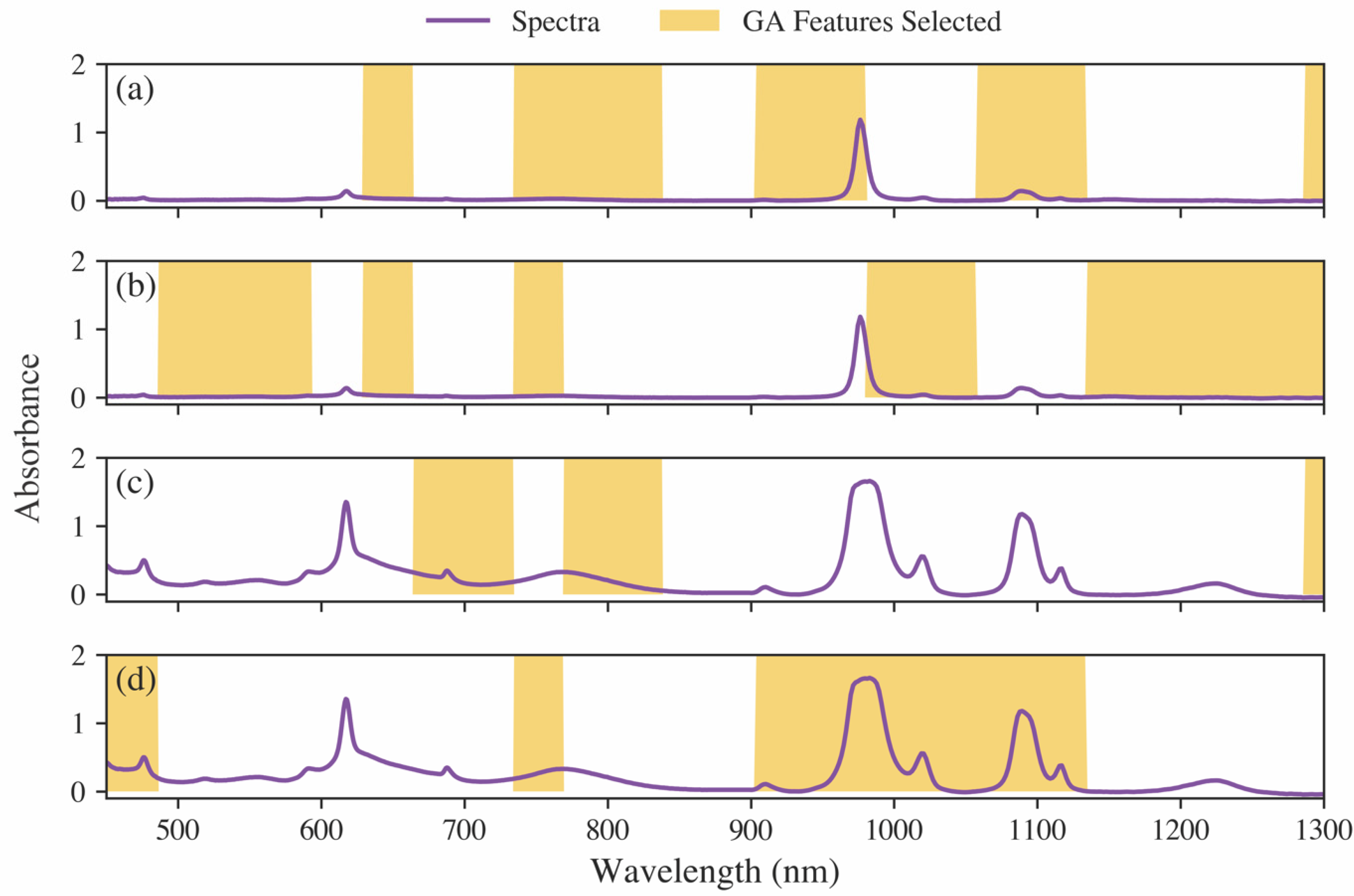
3.4. Feature Selection for Model Optimization
3.5. Final PLSR Model Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, D.C. Chapter 18: Fundamentals of Spectrophotometry. In Quantitative Chemical Analysis, 7th ed.; W. H. Freeman and Company: New York, NY, USA, 2007. [Google Scholar]
- Sadergaski, L.R.; Myhre, K.G.; Delmar, L.H. Multivariate chemometric methods and Vis-NIR spectrophotometry for monitoring plutonium-238 anion exchange column effluent in a radiochemical hot cell. Talanta Open 2022, 5, 1000120. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; DePaoli, D.W.; Myhre, K.G. Monitoring the caustic dissolution of aluminum in a hot cell by Raman spectroscopy. Appl. Spectrosc. 2020, 74, 1252–1262. [Google Scholar] [CrossRef] [PubMed]
- Kirsanov, D.; Rudnitskaya, A.; Legin, A.; Babain, V. UV-Vis spectroscopy with chemometric data treatment: An option for on-line control in nuclear industry. J. Radioanal. Nucl. Chem. 2017, 312, 461–470. [Google Scholar] [CrossRef]
- Lascola, R.; O’Rourke, P.E.; Kyser, E.A. A Piecewise Local Partial Least Squares (PLS) Method for the Quantitative Analysis of Plutonium Nitrate Solutions. Appl. Spectrosc. 2017, 71, 2579–2594. [Google Scholar] [CrossRef]
- Ikedo-Ohno, A.; Hennig, C.; Rossberg, A.; Funke, H.; Scheinost, A.C.; Bernhard, G.; Yaita, T. Electrochemical and Complexation Behavior of Neptunium in Aqueous Perchlorate and Nitrate Solutions. Inorg. Chem. 2008, 47, 8294–8305. [Google Scholar] [CrossRef] [PubMed]
- Matsika, S.; Pitzer, R.M.; Reed, D.T. Intensities in the Spectra of Actinyl Ions. J. Phys. Chem. A 2000, 104, 11983–11992. [Google Scholar] [CrossRef]
- Matsika, S.; Pitzer, R.M. Electronic Spectrum of the NpO22+ and NpO2+ Ions. J. Phys. Chem. A 2000, 104, 4064–4068. [Google Scholar] [CrossRef]
- Eisenstein, J.C.; Pryce, M.H.L. Interpretation of the Solution Absorption Spectra of the (PuO2)++ and (NpO2)+ Ions. J. Res. Natl. Bur. Stand. A 1966, 70, 165–173. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Morgan, K. Applying Two-Dimensional Correlation Spectroscopy and Principal Component Analysis to Understand How Temperatures Affects the Neptunium(V) Absorption Spectrum. Chemosensors 2022, 10, 475. [Google Scholar] [CrossRef]
- Maiwald, M.M.; Skerencak-Frech, A.; Panak, P.J. The complexation and thermodynamics of neptunium(V) with acetate in aqueous solution. New J. Chem. 2018, 42, 7796–7802. [Google Scholar] [CrossRef]
- Maiwald, M.M.; Sittel, T.; Fellhauer, D.; Skerencak-Frech, A.; Panak, P.J. Thermodynamics of neptunium(V) complexation with sulfate in aqueous solution. J. Chem. Thermodyn. 2018, 116, 309–315. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bryan, S.A.; Casella, A.J.; Peterson, J.M.; Levitskaia, T.G. Mechanisms of neptunium redox reactions in nitric acid solutions. Inorg. Chem. Front. 2017, 4, 581–594. [Google Scholar] [CrossRef]
- Edelstein, N.M. Reanalysis of the Aqueous Spectrum of the Neptunyl(V) [NpO2+] Ion. J. Phys. Chem. A 2015, 119, 11146–11153. [Google Scholar] [CrossRef] [PubMed]
- Dupont, F.M.; Elbourne, A.; Cozzolino, D.; Chapman, J.; Truong, V.K.; Crawford, R.J.; Latham, K. Chemometrics for environmental monitoring: A review. Anal. Methods 2020, 12, 4597–4620. [Google Scholar] [CrossRef]
- Sadergaski, L.R.; Andrews, H.B. Simultaneous quantification of uranium(VI), samarium, nitric acid, and temperature with combined ensemble learning, laser fluorescence, and Raman scattering for real-time monitoring. Analyst 2022, 147, 4014–4025. [Google Scholar] [CrossRef]
- Ban, Y.; Hakamatsuka, Y.; Tsutsui, N.; Urabe, S.; Hagiya, H.; Matsumura, T. Spectroscopic study of Np(V) oxidation to Np(VI) in 3 mol/dm3 nitric acid at elevated temperatures. Radiochim. Acta 2014, 102, 775–780. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.K. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- Andrews, H.B.; Myhre, K.G. Quantification of lanthanides in a molten salt reactor surrogate off-gas stream using laser-induced breakdown spectroscopy. Appl. Spectrosc. 2022, 76, 877–886. [Google Scholar] [CrossRef]
- Andrews, H.B.; Sadergaski, L.R.; Cary, S.K. Pursuit of the Ultimate Regression Model for Samarium(III), Europium(III), and LiCl using Laser-Induced Fluorescence, Design of Experiments, and a Genetic Algorithm for Feature Selection. ACS Omega 2023, 8, 2281–2290. [Google Scholar] [CrossRef]
- Leardi, R.; Boggia, R.; Terrile, M. Genetic algorithms as a strategy for feature selection. J. Chemom. 1992, 6, 267–281. [Google Scholar] [CrossRef]
- Leardi, R.; Gonzalez, A.L. Extraction of representative subsets by potential functions method and genetic algorithms . J. Chemom. Intell. Lab. Syst. 1998, 40, 33–52. [Google Scholar]
- Andrews, H.B.; Sadergaski, L.R. Leveraging visible and near-infrared spectroelectrochemistry to calibrate a robust model for Vanadium (IV/V) in varying nitric acid and temperature levels. Talanta 2023, 259, 124554. [Google Scholar] [CrossRef]
- McNaught, A.D.; Wilkinson, A. (Eds.) IUPAC Compendium of Chemical Terminology (the “Gold Book”), 2nd ed.; Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Ortiz, M.C.; Sarabia, L.A.; Herrero, A.; Sánchez, M.S.; Sanz, M.B.; Giménez, D.; Meléndez, M.E. Capability of detection of an analytical method evaluating false positive and false negative (ISO 11843) with partial least squares. Chemom. Intell. Lab. Syst. 2003, 69, 21–33. [Google Scholar] [CrossRef]
- Toney, G.K.; Delmau, L.H.; Myhre, K.G. Chemometrics and Experimental Design for the Quantification of Nitrate Salts in Nitric Acid: Near-Infrared Spectroscopy Absorption Analysis. Appl. Spectrosc. 2021, 75, 1155–1167. [Google Scholar]
- Segtnan, V.H.; Sasic, S.; Isaksson, T.; Ozaki, Y. Studies on the Structure of Water Using Two-Dimensional Near-Infrared Correlation Spectroscopy and Principal Component Analysis. Anal. Chem. 2001, 73, 3153–3161. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.; Shinzawa, H.; Chung, H. Concentration determination of inorganic acids that do not absorb near-infrared (NIR) radiation through recognizing perturbed NIR water bands by them and investigation of accuracy dependency on their acidities. Microchem. J. 2018, 139, 443–449. [Google Scholar] [CrossRef]





| Sample Set | Sample Tag | Np Concentration (M) | Tested Temperatures (°C) |
|---|---|---|---|
| Calibration | C1 | 0.00 | 10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0 |
| C2 | 0.00075 | ||
| C3 | 0.0069 | ||
| C4 | 0.034 | ||
| C5 | 0.069 | ||
| C6 | 0.34 | ||
| C7 | 0.52 | ||
| C8 | 0.89 | ||
| Validation | V1 | 0.00 | 15.0, 16.5, 24.0, 25.0, 35.0, 45.0, 48.8, 55.0, 56.7, 65.0, 71.6, 75.0 |
| V2 | 0.00075 | ||
| V3 | 0.0044 | ||
| V4 | 0.0088 | ||
| V5 | 0.017 | ||
| V6 | 0.069 | ||
| V7 | 0.17 | ||
| V8 | 0.34 | ||
| V9 | 0.64 | ||
| V10 | 0.89 |
| RMSE | |||||||
|---|---|---|---|---|---|---|---|
| Submodel | C | C% | CV | CV% | P | P% | |
| Low Np concentration | Conc. | 0.0004 | 0.78% | 0.0034 | 6.89% | 0.0004 | 0.85% |
| T | 0.1471 | 0.42% | 0.3838 | 1.10% | 0.9892 | 2.83% | |
| High Np concentration | Conc. | 0.0032 | 0.80% | 0.0088 | 2.20% | 0.0220 | 5.49% |
| T | 0.1157 | 0.33% | 0.3964 | 1.13% | 1.7967 | 5.13% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrews, H.B.; Sadergaski, L.R. Hierarchical Modeling to Enhance Spectrophotometry Measurements—Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium. Chemosensors 2023, 11, 274. https://doi.org/10.3390/chemosensors11050274
Andrews HB, Sadergaski LR. Hierarchical Modeling to Enhance Spectrophotometry Measurements—Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium. Chemosensors. 2023; 11(5):274. https://doi.org/10.3390/chemosensors11050274
Chicago/Turabian StyleAndrews, Hunter B., and Luke R. Sadergaski. 2023. "Hierarchical Modeling to Enhance Spectrophotometry Measurements—Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium" Chemosensors 11, no. 5: 274. https://doi.org/10.3390/chemosensors11050274
APA StyleAndrews, H. B., & Sadergaski, L. R. (2023). Hierarchical Modeling to Enhance Spectrophotometry Measurements—Overcoming Dynamic Range Limitations for Remote Monitoring of Neptunium. Chemosensors, 11(5), 274. https://doi.org/10.3390/chemosensors11050274







