Next Article in Journal
The Potential of Antibody Technology and Silver Nanoparticles for Enhancing Photodynamic Therapy for Melanoma
Previous Article in Journal
Detection of Preclinical Orthostatic Disorders in Young African and European Adults Using the Head-Up Tilt Test with a Standardized Hydrostatic Column Height: A Pilot Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomedicines
Volume 10
Issue 9
10.3390/biomedicines10092157
biomedicines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Interplay between Artificial Intelligence and Biomechanics Modeling in the Cardiovascular Disease Prediction

by
Xiaoyin Li
1,
Xiao Liu
1,*,
Xiaoyan Deng
1 and
Yubo Fan
1,2,*
1
Beijing Advanced Innovation Centre for Biomedical Engineering, Key Laboratory for Biomechanics and Mechanobiology of Chinese Education Ministry, School of Biological Science and Medical Engineering, Beihang University, Beijing 100083, China
2
School of Engineering Medicine, Beihang University, Beijing 100083, China
*
Authors to whom correspondence should be addressed.
Biomedicines 2022, 10(9), 2157; https://doi.org/10.3390/biomedicines10092157
Submission received: 13 July 2022 / Revised: 26 August 2022 / Accepted: 28 August 2022 / Published: 1 September 2022
(This article belongs to the Topic Blood Physiology: Molecular Mechanisms of Vascular Wall Functioning)
Browse Figures
Review Reports Versions Notes

Abstract

:
Cardiovascular disease (CVD) is the most common cause of morbidity and mortality worldwide, and early accurate diagnosis is the key point for improving and optimizing the prognosis of CVD. Recent progress in artificial intelligence (AI), especially machine learning (ML) technology, makes it possible to predict CVD. In this review, we first briefly introduced the overview development of artificial intelligence. Then we summarized some ML applications in cardiovascular diseases, including ML−based models to directly predict CVD based on risk factors or medical imaging findings and the ML−based hemodynamics with vascular geometries, equations, and methods for indirect assessment of CVD. We also discussed case studies where ML could be used as the surrogate for computational fluid dynamics in data−driven models and physics−driven models. ML models could be a surrogate for computational fluid dynamics, accelerate the process of disease prediction, and reduce manual intervention. Lastly, we briefly summarized the research difficulties and prospected the future development of AI technology in cardiovascular diseases.

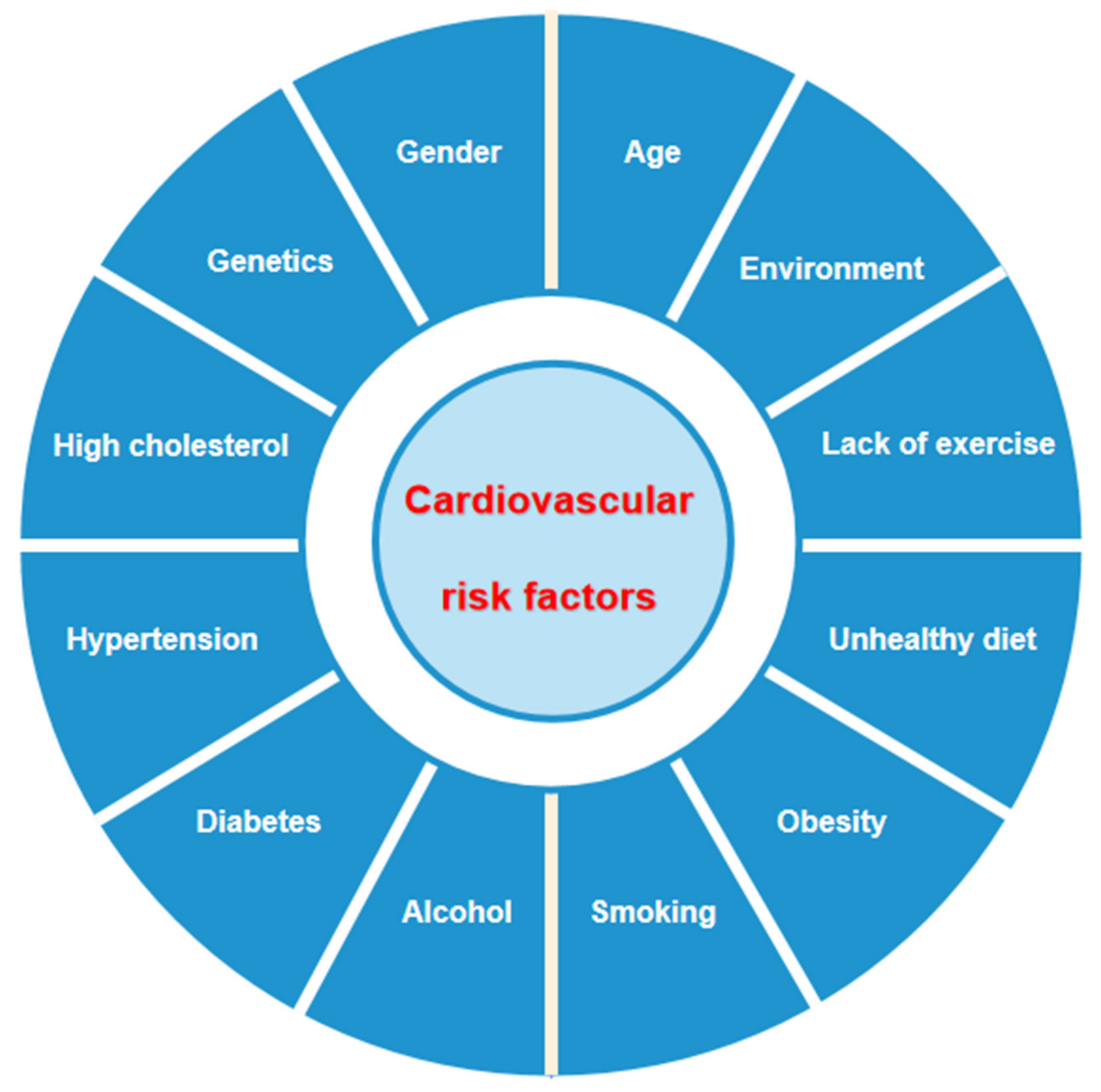
1. Introduction

Cardiovascular disease (CVD) is an important cause that threatens human health and represents a heavy economic burden on society and families [1,2]. Etiological investigations have found that the occurrence of cardiovascular disease involves a variety of risk factors [3,4,5], including high cholesterol, hypertension, diabetes, age, gender, genetics, unhealthy diet, obesity, smoking, alcohol, lack of exercise and environmental factors, as shown in Figure 1. Although managing these risk factors contributes to the control of cardiovascular disease, it remains the most common cause of morbidity and mortality worldwide [6,7]. Therefore, early, accurate diagnosis and prognosis assessments are the key point for improving and optimizing the prognosis of CVD [8].
Artificial intelligence (AI) is an exciting new field in cardiovascular disease, revolutionizing medical practice [9]. AI can effectively assist physicians in diagnosing cardiovascular diseases and conducting continuous monitoring so as to achieve early detection and treatment, thus reducing the occurrence of acute cardiovascular events and improving the prognosis [10]. AI has quite a few successful applications, such as imaging and pathological diagnosis [11], drug design and discovery [12], health management [13], disease prediction [14], medical rehabilitation [15], and laboratory medicine [16]. Advanced imaging and testing techniques have accumulated vast amounts of raw data, which are the basis of AI exploration. Fully use of artificial intelligence can revolutionize the current diagnosis and treatment model due to the complex and changeable structure of the cardiovascular system and play an important role in the prevention of cardiovascular diseases.
In this review, we systematically summarized the recent research progress of artificial intelligence applications for cardiovascular diseases, including the prediction of morbidity or mortality of the cardiovascular disease and the prediction of cardiovascular biomechanics modeling. We focused on machine learning−based models to predict CVD and ML−based vascular hemodynamic geometries, equations, and methods. Finally, we briefly summarized several common difficulties of AI technology and prospected the future development of AI technology in cardiovascular disease.

2. Overview of Artificial Intelligence

Artificial intelligence can be referred to as the science of realizing human intelligence on machines (Computers). In the past 70 years, artificial intelligence has been widely applied to many subjects and achieved fruitful results [17]. Machine learning (ML) is a subset of artificial intelligence, which refers to algorithms and statistical models that machines can learn independently, learn hidden patterns in data, and make accurate predictions to improve the performance of specific tasks [18]. According to how the data is learned, machine learning is mainly divided into reinforcement learning, supervised learning, semi−supervised learning, and unsupervised learning [19].
Since the 2010′s, ML algorithms have continuously improved, becoming more sophisticated and containing hierarchies, which gave rise to the popular Deep Learning (DL). Deep learning, a sub−field of machine learning, has been extensively studied and imitates the working model of the human brain and uses a multi−layer neural network to train data and develop an automatic prediction model (Figure 2) [20,21,22]. The DL−based model could automatically extract meaningful features from data on multiple levels. At the same time, the algorithm requires a certain degree of judgment by analysts in ML approaches to defining relevant features, such as feature selection, and it is popular in complex physical modeling, especially in nonlinear and high−dimensional functions [23,24]. Today, DL models have reached some important milestones, and various frameworks are emerging, such as the artificial neural network (ANN) [25], the deep neural network (DNN) [26], the convolutional neural network (CNN) [27] and the physics−informed neural network (PINN) [28], and so on.
Machine learning and deep learning algorithms have been used to accelerate the diagnosis and prediction of cardiovascular diseases [27,29,30,31]. For more detailed examples of the performance of ML and DL approaches for cardiovascular applications, we refer to Section 3.

3. Application of Artificial Intelligence in the Prediction of Cardiovascular Disease

We mainly discuss two types of ML−based approaches to predict cardiovascular diseases. The first approach is to build a machine learning model that directly outputs the incidence, mortality, or prognosis of CVDs by inputting clinical follow−up data and risk factors of subjects without CVDs, or clinical data and medical imaging of patients with CVDs. However, it requires massive patient data for training, and conventional prediction models are inadequate for assessing disease progression in complex lesions owing to the patient−specific anatomical, physiological, and functional difficulties. Another approach is to predict the complex patient−specific pathological process of CVDs by learning cardiovascular biomechanics based on numerical simulation. Computational models based on physical principles of cardiovascular systems, combined with medical imaging and patient characteristics, enable the derivation of hemodynamic information (e.g., velocity, pressure, and stress) inaccessible by medical images alone. Machine learning could be applied to the basic model and governing equations of the cardiovascular system and new numerical methods to accelerate the simulation process and realize personalized flow simulation. Both approaches are of great significance in evaluating the occurrence of cardiovascular diseases (Figure 3).

3.1. Prediction of Cardiovascular Morbidity or Mortality

Cardiovascular disease has long incubation periods and complicated pathogenic factors, which leads to the failure of timely identification and treatment [8]. A risk assessment system for CVDs could be established by mining the quantitative relationship between various related risk factors and their influence on the results. The most widely used model for cardiovascular diseases is the Framingham risk score (FRS) [32]. It predicted the occurrence probability of cardiovascular and cerebrovascular diseases in the next ten years according to the cholesterol level and non−cholesterol level factors and evaluated the risk by scoring the corresponding indicators. In addition to the FRS, the commonly adopted conventional risk prediction models are the systematic coronary risk evaluation score (SCORE) [33] and the atherosclerosis cardiovascular disease (ASCVD) [34]. Different predictive indicators were constructed through their research methods to study the risk factors of CVDs.
To improve the accuracy and speed of disease diagnosis of the above prediction models, AI−based approaches were applied to CVDs, which would help doctors to identify patients with different risk layers in advance and further reduce the incidence of mortality and adverse events. Several studies compared the ML−based model with the traditional risk prediction model (Table 1). For example, 13−year follow−up data from 6459 participants without cardiovascular disease were used to construct a machine learning model to calculate CVDs risk, which believed that the machine learning risk calculator could significantly improve risk stratification and reduce adverse events, resulting in the sensitivity of 0.86, specificity of 0.95, and the area under the curve (AUC) of 0.92 [35]. Data from the prospective study of 2020 adults trained in three ML models obtained similar results, in which random forest gave the best results [36]. Additionally, Alaa et al. [37] developed a DL−based prediction model with 473 reference variables in each case from 423,604 residents without cardiovascular disease, and their AutoPrognosis model improved risk prediction (AUC: 0.774) compared to the FRS (AUC: 0.724) and COX PH mode (AUC: 0.758), which proved that the automatic prediction model has better performance.
Artificial intelligence is also utilized in prognosticating cardiovascular outcomes based on imaging data combined with clinically available risk predictors, effectively reducing complications and sudden death events. Motwani et al. [38] used a regression model based on an iterative LogitBoost algorithm for mortality prognostication of 10,030 patients with suspected coronary artery diseases (CADs) who underwent coronary computed tomography angiography (CCTA) imaging and 5−year followup, and their performance (AUC: 0.79) was better compared to the FRS or CCTA severity scores alone. Another study [39] obtained similar results by using the ML−based model to predict the prognosis of 8844 patients with complete CCTA risk score information and at least 3−year follow−up for myocardial infarction and death, resulting in an AUC of 0.771. Coronary artery calcification (CAC) is one of the independent predictors of cardiovascular events, and machine learning has been combined with coronary artery calcification measurement to realize automatic identification [40]. Wolterink et al. [48] used a CNN to automatically identify and quantify CAC in CCTA images of 50 patients, which eliminated the need for coronary artery extraction and was expected to reduce unnecessary radiation doses in the future. Determining the degree of coronary artery stenosis is particularly important for patients with CADs, which determines the next treatment plan for patients. Detection and quantification of coronary artery stenosis is probably the most important clinical application of CCTA. Kelm et al. [49] used the ML algorithm to automatically identify and classify coronary artery stenosis caused by calcified and non−calcified plaques. Similarly, Zreik et al. [41] used multi−scale CNN to automatically identify functionally significant coronary artery stenosis in CCTA images of 166 patients. The results suggested that functional coronary artery stenosis could be determined by automatic analysis of myocardium in resting CCTA images without observation of the patient’s coronary artery anatomy, which might reduce unnecessary invasive fractional flow reserve (FFR) examination in the future. Besides CCTA, other imaging techniques combined with artificial intelligence methods have also been applied to predict CADs. Myocardial perfusion imaging showed [27] that the DL algorithm could predict the occurrence of adverse events more accurately and with higher accuracy than traditional prediction models. In addition, a CNN−based plaque detection system was employed to learn plaque classification directly from intravascular optical coherence tomography (IVOCT), resulting in an accuracy of 0.917, sensitivity of 0.909, and specificity of 0.924. Their results demonstrated that it was feasible to establish a plaque detection system based on deep learning [42].
Artificial intelligence also has many applications for other cardiovascular diseases besides CADs. Based on echocardiographic data, ML algorithms were used to establish the discrimination models between hypertrophic cardiomyopathy from physiological hypertrophy seen in athletes [43] and between hypertrophic cardiomyopathy and constrictive pericarditis [44]. Their ML−based models had higher diagnostic sensitivity and specificity. Diller et al. used a Deep learning algorithm to categorize diagnosis, disease complexity, and NYHA class in adult congenital heart disease or pulmonary hypertension through an 8−year follow−up of 10,019 adult patients, with an accuracy of 0.911, 0.97, and 0.906, respectively [31]. Additionally, the heart sound−based detection methods for heart failure were proposed through machine learning and end−to−end deep learning [45]. Based on the records of 947 subjects, 15 repeatable machine learning models were identified to distinguish the different stages of chronic heart failure with an accuracy of 0.929. This approach made it easier to identify patients with heart failure, which has the potential of a home chronic heart failure monitor. Artificial neural networks (ANNs) could also identify stroke and stroke−like diseases intelligently by analyzing a large amount of data [25]. The application of ML in predicting postoperative mortality and rehospitalization after surgery would also be of great significance. Data from 11,709 patients undergoing percutaneous coronary intervention verified that machine learning was more predictive in identifying postoperative mortality 180d after surgery and rehospitalization for chronic heart failure 30 d after surgery [46]. Another study [47] also showed that the ML model (AUC: 0.795) was more accurate in predicting mortality after elective cardiac surgery than EuroSCORE II (AUC: 0.737) or the logistic regression model (AUC: 0.742). Compared with the traditional prediction score and prediction model, the ML−based model would be faster and more accurate, which could alter the prediction method of cardiovascular disease and improve the prediction accuracy.

3.2. Prediction of Cardiovascular Biomechanics Modeling

Cardiovascular biomechanics could also be applied to predict the occurrence of cardiovascular diseases [50,51] as the critical roles of blood flow and arterial wall mechanics and their interactions in the function of the human cardiovascular system [52,53,54,55]. Therefore, from the perspective of cardiovascular biomechanics, it is feasible to diagnose or prevent cardiovascular diseases indirectly through hemodynamic parameters, such as velocity [56,57], pressure [56,58], and wall shear stress (WSS) [59,60,61,62]. It is well documented that the flow in blood vessels is very complicated, and it is difficult to predict directly [63]. The development of vascular fluid dynamics has depended on basic geometries, equations, and computational methods [64,65,66]. Based on artificial intelligence technology, the basic model and governing equations of the fluid system and new numerical methods could be developed to accelerate the process and reduce manual intervention.

3.2.1. Traditional Computational Modeling and Simulation

Computational modeling and simulation methods were frequently applied to solve flow problems in blood vessels. Numerical analysis methods of cardiovascular biomechanics mainly rely on a grid−based approach, including finite difference analysis (FDA) [67], finite volume analysis (FVA) [68], or finite element analysis (FEA) [69,70]. Combined with medical images, it is very effective for cardiovascular function analysis in solving the basic physical equations of the flow field with high precision in discrete form and studying the fluid motion and its interaction with other media [71,72,73,74,75,76]. The current workflow for patient−specific computational modeling and simulation applications mainly consists of three steps [77]: (1) the vascular anatomic geometry of the patient is obtained from clinical image data, mainly through manual labeling; (2) the specifying constitutive relation of material properties, boundaries, and hemodynamic loading conditions are set up in the computational model; (3) the computational model is submitted to an appropriate numerical solver to obtain the simulation results. The computational modeling needs a lengthy model setup and long computing time to complete the analysis of one single patient [78,79]. Therefore, the computational fluid dynamics (CFD) method cannot be applied for large queues of patients or time−sensitive clinical applications requiring rapid feedback to clinicians, such as percutaneous coronary intervention [46]. Although the present model reduction methods, such as dynamic modal decomposition (DMD) [80] and proper orthogonal decomposition (POD) [81], greatly reduce the solution of complex systems and improve the efficiency of modeling and solving, the traditional model reduction methods are still difficult to be applied to multi−scale, transient and discontinuous processes [82,83].
Machine learning could break down computing tasks and make all kinds of machine assistance possible in cardiovascular biomechanics modeling. In particular, the ML approach could be applied to the extraction of geometric features, the study of governing equations, and the surrogate for CFD [84,85,86]. In addition, replacing certain finite element components with machine learning models can achieve faster computation time, especially for multi−scale problems that require nested finite element simulations [87,88,89].

3.2.2. ML−Based Hemodynamics with Vascular Geometries, Equations and Methods

Geometric Modeling

The traditional method of computational fluid dynamics needs to extract structures and features of blood vessels manually [77,78,79], which is labor and time−consuming. In recent years, artificial intelligence technology was proposed to automatically and quickly extract geometric features as input in the computational model. For example, the nearest distance was used between each grid point in the rectangular grid and the boundary as input to predict the resistance coefficient, which achieved good results in simple two−dimensional geometric shapes such as circles [90]. In addition, there were related studies using features extracted by deep learning technology [91,92], and the compressed expression of geometric shapes of autoencoders was put into neural networks. Other studies represented the geometry by image pixels [93], which are discretized into a 2D/3D image.
ML models have been used to automatically segment medical images for creating 3D computer models in recent years. Especially in patient−specific biomechanical modeling, each cardiovascular disease leads to multi−feature 3D morphologies, such as atherosclerosis [94], aneurysm [95], and occlusive diseases [96,97]. For instance, Berhane et al. [98] used deep learning to generate an automatic 3D segmentation model of the aorta based on 4D−flow magnetic resonance imaging (MRI). The feasibility of using ML techniques and deformable methods for automatic geometry reconstruction and modeling of human organs from 3D medical images has been proved [99,100,101]. Liang et al. [85,102] used ML algorithms for automatic geometry modeling of aortic aneurysms from 3D medical images. Luo et al. [103] developed ML classifiers to infer the strength of ascending thoracic aneurysm from elastic properties. Zheng et al. [104] reduced the complexity of computerized tomography (CT) data for carotid artery bifurcation detection. Moeskops et al. [105] trained a single CNN model to segment the coronary arteries in cardiac computed tomography angiography. The complex shapes of atherosclerosis are mainly derived from vascular imaging [106], including intravascular ultrasound (IVUS) [107,108], angioplasty [109], MRI [98], and IVOCT [110]. ML−based approaches have been used for the analysis of imaging data to characterize plaque morphology. Iyer et al. [111] designed a CNN model for vessel segmentation in X−ray angiography images. To visualize the severity of coronary artery stenosis, Lee et al. [112] constructed a CNN−based fully−automated semantic segmentation model of coronary plaque in IVOCT images, resulting in high sensitivity and specificity classification of lipid and calcified plaque (the sensitivity/specificity were 87.4%/89.5% and 85.1%/94.2%, respectively). In addition, Tang et al. [113] proposed a deep neural network based on multi−scale features for automatic lumen segmentation for IVOCT images. Athanasiou et al. [114] used the ML−based OCT image segmentation to identify areas of atherosclerotic plaque. Abdolmanafifi et al. [115] compared the image segmentation accuracy of three models, and they demonstrated that the convolutional neural network (CNN) was very effective when applied as a feature extractor. In addition, ML was also widely used in cardiac image segmentation, including congenital heart disease [116] and whole−heart [117]. A fully automated approach has been developed for segmenting the mitral leaflets from 3D transesophageal echocardiography image data to facilitate visual and quantitative image analysis [118] and aortic valve modeling [119,120]. Oktay et al. [121] confirmed that CNN could accurately segment the left ventricle and depict anatomical morphological changes related to cardiac pathology. Other studies obtained similar results [122,123]. At present, the ML segmentation models cannot fully reach an agreement with anatomical structures or experts [124]. It is difficult to build ML−based models that can appropriately represent all morphologies due to the complexity of patient−specific shapes, and feature extraction with wide generalization remains a challenge (Table 2).

Governing Equation (ML−Based Partial Differential Equation)

The governing equation of the flow in blood vessels is generally regarded as Navier−Stokes (N−S) equation, which is a highly nonlinear partial differential equation (PDE) system [130], and the solution of the equation is always a difficult problem because of its complicated process. Nowadays, the machine learning approach is explored to assist solutions from the perspective of partial differential equations.
The sparse regression technology was used to learn the coefficients and derivative forms of each order in the Taylor series. This method implemented interpretable machine learning techniques but requires the construction of function libraries to ensure that the function involved is included [131,132]. Raissi et al. [87] learned coefficients and function terms in the Taylor series by constructing two neural networks of different depths. Since the function items were represented by neural networks, this approach could only learn the abstract expression of the original function but did not affect its application for practical problems, such as the solution of the N−S equation. Additionally, the data−driven method with the data assimilation method was combined to identify PDEs, which broadened the application scope of PDEs identification. For the known structure of PDEs, machine learning methods based on the Gaussian process were introduced into linear differential equation systems [133] and nonlinear partial differential equation systems [134] to identify scalar coefficients in the equations. In addition, the multi−fidelity Gaussian process was also introduced to predict random fields [135]. However, these methods were only applicable to models with fewer data.
A more recent ML paradigm, a physics−informed neural network, has been proposed to identify scalar parameters in partial differential equations [28,136,137]. It took partial differential equations as regularization terms in the process of neural network fitting data, which avoided the inapplicability of traditional numerical differentiation to noisy data. Alternatively, some methods were mainly introduced into the network training process in the form of the loss function, which focused on data fitting rather than solving mathematical equations itself [126,138]. In terms of future work, quantifying the uncertainty associated with neural network predictions is the focus of research. For data−driven differential equations, how to combine the basic law of conservation of physics to ensure the conservation law is worthy of being studied further.

A ML−Based Surrogate for Computational Fluid Dynamics

The artificial intelligence−based solution method for computational fluid dynamics is driven by data or physical models. The data−driven model is based on existing model equations, which constantly update or optimize the original empirical coefficients [129]. The physics−driven model completely abandons the existing model equations and builds a specific input−output relationship through machine learning based on certain physical knowledge (Table 2) [86].
The neural networks based on data firstly obtain high fidelity data according to the existing flow field simulation or experimental methods and then construct the neural network mapping relationship to replace the original partial differential equation after learning the data based on machine learning technology, which could obtain the numerical solution to the flow field quickly and efficiently [86,103]. Moreover, various data assimilation methods have been developed to combine experimental data with computational hemodynamic data to improve data fidelity [139,140,141]. Artificial intelligence algorithms usually take biomechanics simulation results as training data to predict interested hemodynamic parameters. For instance, Jordanski et al. constructed three ML approaches (Gaussian conditional random fields, multilayer perceptron neural network, and multivariate linear regression) to predict the WSS distribution of abdominal aortic aneurysm and carotid bifurcation models, and the strong determination coefficient of CFD simulation was verified [125]. Another study used the decision tree to estimate FFR from 34 pre−defined coronary arteries [142]. Similarly, other ML models were proposed to measure FFR from coronary computed tomography angioplasty, in which ML models were trained on a synthetic FFR dataset obtained from CFD simulation [143,144].
The successful development of ML models has been verified in massive applications. Recent work in machine learning combined with finite element calculations has also shown promise for collagen tissues [145].
The deep learning approach has gradually emerged in cardiovascular biomechanics modeling with the rapid development of artificial intelligence. For example, DL models were developed to directly evaluate the stress distribution of thoracic aortic aneurysms bypassing the finite element calculation process [102]. Liang et al. [77] demonstrated that DL models could quickly and accurately substitute for stress analysis, which is shown in Figure 4. Recent studies using ML models to predict blood flow velocity vector fields have obtained similar results [58], which is shown in Figure 5. Subsequently, the study demonstrated the feasibility of using a deep neural network as a fast and accurate surrogate for computational fluid dynamics to estimate the hemodynamics of the human arteries [57]. In addition, the convolutional neural networks have been wildly constructed as finite element alternatives to fluid dynamics analysis, which could compress the simulated state size and learn dynamics [91,146]. For instance, CNN could be used to reconstruct the high−resolution turbulent field without solving the governing equation. The input of the network was the low−resolution flow field pooled from high−resolution flow field images obtained from the direct numerical simulation method (DNS), and the method was validated in laminar cylindrical flow and isotropic turbulence [147]. Similarly, CNN also could be used to perform the parameter estimation in cardiovascular hemodynamics [128]. Five different neural networks were used to predict arterial wall stress in atherosclerotic patients, which also proved the superiority of convolution networks [127].
As a general−purpose function approximation [148], the AI−based model only approximates the complex nonlinear relationship between the input and output variables of the system. Given input parameters such as initial/boundary/operating conditions, parameters of interest such as velocity, pressure, and shear stress are obtained without traditional CFD simulations. For example, a physics−informed neural network has been proposed recently [149,150], in which the governing physical equation, such as Navier−Stokes equations, could be integrated into the neural network frameworks where the physical variables of interest could be expressed as functions of space and time. Raissi et al. [126,151] developed a physics−informed deep−learning framework to solve partial differential equations, and the neural networks were trained in several observed values of a specific flow field. With the governing equation as the constraint, the flow field prediction in a specific region could be realized without introducing boundary conditions, which is shown in Figure 6. Similarly, the conservative PINN method could be used to solve the flow field in multiple different sub−regions, which improved the applicability of the original method for solving complex boundary flow field problems [152]. The physics−informed neural network, which uses sparse measurement data to solve uncertain problems and simultaneously identify unknown parameters, has gained much attention in cardiovascular modeling [129,153]. In addition, PINN could be applied to improve the WSS quantification in blood flow problems where the inlet and outlet boundary conditions were not known but instead by assimilating a few measurement points [154].
The data−driven neural network requires quantities of high−fidelity data, but it is difficult to apply it when the sample data is small or cannot be obtained [155]. In the context of surrogate modeling, if boundary conditions are properly applied, the physical−driven deep learning model without labeled data could be developed to directly integrate physical equations and boundary conditions into the loss function of the neural networks. For instance, a physics−constrained, deep learning model could be developed to solve the high−dimensional stochastic elliptic partial differential equations based on the sample−free data method [156]. Similarly, CNN models also could be used in solving the partial differential equation with numerical methods. The image data of the flow field was put into networks as the initial solution instead of training sample data, and their result was better than data−driven networks [157,158]. Recent studies demonstrated that DL models also had great promise in solving high−dimensional nonlinear uncertainty quantification (UQ) problems [159]. PINN could find flow velocity, stress or pressure fields satisfying N−S equations at any specified point in the domain without any training data, which can be used as a substitute for traditional CFD. For example, Sun et al. [86] used a physics−constrained neural network−based alternative model to solve the parameterized N−S equations and simulated the ideal vascular flow without using any labeled training data (Figure 6). The flexibility provided by PINN makes it possible to solve complex cardiovascular biomechanical problems. In addition, PINN could also be used in varieties of complex flow fields [160,161,162].
Both data−driven models and physical−driven models have promoted the development of computational fluid dynamics and explored a new way for cardiovascular disease prediction. However, the success has only been demonstrated on several canonical issues [86,126,127], and further research is needed on the broader impact of complex cardiovascular disease. Therefore, the prediction and modeling techniques of cardiovascular fluid mechanics should be problem−oriented, and a broadly applicable ML model may require more effort in the future.

4. Challenges and Future Prospects

The increasing maturity of artificial intelligence and the continuous expansion of its application in the medical field brought revolutionary changes to medical practice. ML−based models could predict the morbidity or mortality of CVDs more accurately and faster than the traditional prediction model, which could alter the prediction method of CVDs. ML models could also provide new theories, methods, and research paradigms for biomechanics modelling. However, there are still several challenges that need ironing out. (1) Database: The early prediction of CVDs is inseparable from massive datasets and data quality. The high−precision mechanical calculation needs huge computing resources, and it is difficult to obtain data on some rare diseases [163]. In addition, the applications of medical data also involve patient privacy and ethical issues [164]. Therefore, it is necessary to obtain more accurate, authentic, and appropriate datasets and train and improve the algorithm on small samples [165]. High−quality data and appropriate storage methods are critical to the development of AI technology. (2) Validity and stability: Studies demonstrated that AI−based models usually have better prediction performance compared with traditional prediction models [38]. To make the models have clinical practical value, further testing with massive pathological datasets is significant to verify the effectiveness and stability of the proposed method [166], and the results from single−center also need to be verified by the multi−center and massive cases. (3) Generalization: Numerous ML models have been successfully used to predict CVDs in recent years [57,58,102,127]. However, it remains a challenge to better generalize the AI−based prediction models to future data for specific patients. For example, in patient−specific biomechanics applications, it is hard to develop ML−based models that can appropriately represent all complex 3D morphologies of each cardiovascular disease. Thus, a broadly applicable ML−based prediction model might require learning vast physiologically possible datasets. (4) Explainability: Artificial intelligence technology has high predictive performance in the medical field, but it is still hard to explain the decision−making process clearly. Machine learning has always been used as a “black box” in the research process, which leads to the inexplicability and uncertainty of the model [167,168]. Moreover, various subjective factors and the complexity of models affect the design and evaluation of AI models. The explainable AI model has received sustained attention in recent years [169], but the results were not perfect, and a universal system and unified evaluation index are lacking. In addition, models are valued more for accuracy than explainability. A research method with reproducibility and standard must be found in the future to compare and evaluate the explainability of the AI-based prediction model.
Given the above, artificial intelligence has made remarkable achievements in the past decades, but the data quality, as well as the validity, stability, generalization, and explainability of the model need to be further improved. AI will be a development direction and trend of medical treatment in the future, and it will alleviate the pressure of medical treatment in some aspects, improve the speed and quality of medical services, and promote the continuous development and progress of human medicine.

5. Conclusions

We summarized the recent advances of the machine learning−based model to directly predict CVDs based on risk factors or medical imaging findings, as well as the machine learning−based hemodynamics with vascular geometries, equations, and methods for indirect assessment of cardiovascular diseases. Machine learning models could be a surrogate for computational fluid dynamics, accelerate the process of disease prediction and reduce manual intervention.

Funding

This work was funded by the National Natural Science Research Foundation of China Grants-in-Aid (No. 11827803, 31971244, 31570947, 32071311, and U20A20390).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Virani, S.S.; Alonso, A.; Benjamin, E.J.; Bittencourt, M.S.; Tsao, C.W. Heart Disease and Stroke Statistics—2020 Update: A Report From the American Heart Association. Circulation 2020, 141, e139–e596. [Google Scholar] [CrossRef] [PubMed]
  2. Joseph, P.; Leong, D.; Mckee, M.; Anand, S.S.; Schwalm, J.D.; Teo, K.; Mente, A.; Yusuf, S. Reducing the Global Burden of Cardiovascular Disease, Part 1: The Epidemiology and Risk Factors. Circ. Res. 2017, 121, 677. [Google Scholar] [CrossRef] [PubMed]
  3. Yichong, L.; Limin, W.; Yong, J.; Mei, Z. GW24-e1907Association between changes in status of multiple cardiovascular risk factors and carotid atherosclerosis progression: A population-based cohort study. Heart 2013, 99, E126–E127. [Google Scholar]
  4. Heb, A.; Prt, B.; Ee, B.; Edm, C.; Raf, C.; Alb, D.; Hmk, E.; Kcf, F.; Mre, G.; Hw, H. Ten things to know about ten cardiovascular disease risk factors—ScienceDirect. Am. J. Prev. Cardiol. 2021, 5, 100149. [Google Scholar]
  5. Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Group G-N-JGBoCDW. Global Burden of Cardiovascular Diseases and Risk Factors, 1990–2019 Update From the GBD 2019 Study. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef]
  6. Timmis, A.; Vardas, P.; Townsend, N.; Torbica, A.; Katus, H.; De Smedt, D.; Gale, C.P.; Maggioni, A.P.; Petersen, S.E.; Huculeci, R. European Society of Cardiology: Cardiovascular disease statistics 2021. Eur. Heart J. 2022, 43, 716–799. [Google Scholar] [CrossRef]
  7. Andersson, C.; Johnson, A.D.; Benjamin, E.J.; Levy, D.; Vasan, R.S. 70-year legacy of the Framingham Heart Study. Nat. Rev. Cardiol. 2019, 16, 1–12. [Google Scholar] [CrossRef]
  8. Pitchai, B.; Khin, M.-U.; Gowraganahalli, J. Prevalence and prevention of cardiovascular disease and diabetes mellitus. Pharmacol. Res. Off. J. Ital. Pharmacol. Soc. 2016, 113, 600–609. [Google Scholar]
  9. Briganti, G.; Le Moine, O. Artificial intelligence in medicine: Today and tomorrow. Front. Med. 2020, 7, 27. [Google Scholar] [CrossRef]
  10. Lüscher, T.F.; Lyon, A.; Amstein, R.; Maisel, A. Artificial Intelligence: The Pathway to the Future of Cardiovascular Medicine; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
  11. Dey, D.; Slomka, P.J.; Leeson, P.; Comaniciu, D.; Shrestha, S.; Sengupta, P.P.; Marwick, T.H. Artificial intelligence in cardiovascular imaging: JACC state-of-the-art review. J. Am. Coll. Cardiol. 2019, 73, 1317–1335. [Google Scholar] [CrossRef]
  12. Zhang, L.; Tan, J.; Han, D.; Zhu, H. From machine learning to deep learning: Progress in machine intelligence for rational drug discovery. Drug Discov. Today 2017, 22, 1680–1685. [Google Scholar] [CrossRef]
  13. Hamet, P.; Tremblay, J. Artificial intelligence in medicine. Metabolism 2017, 69, S36–S40. [Google Scholar] [CrossRef]
  14. Kohli, P.S.; Arora, S. Application of machine learning in disease prediction. In Proceedings of the 2018 4th International conference on computing communication and automation (ICCCA), Greater Noida, India, 14–15 December 2018; pp. 1–4. [Google Scholar]
  15. Kaelin, V.C.; Valizadeh, M.; Salgado, Z.; Parde, N.; Khetani, M.A. Artificial intelligence in rehabilitation targeting the participation of children and youth with disabilities: Scoping review. J. Med. Internet Res. 2021, 23, e25745. [Google Scholar] [CrossRef]
  16. Ialongo, C.; Pieri, M.; Bernardini, S. Artificial neural network for total laboratory automation to improve the management of sample dilution: Smart automation for clinical laboratory timeliness. Slas Technol. Transl. Life Sci. Innov. 2017, 22, 44–49. [Google Scholar] [CrossRef]
  17. Mehta, M.C.; Katz, I.T.; Jha, A.K. Transforming global health with AI. N. Engl. J. Med. 2020, 382, 791–793. [Google Scholar] [CrossRef]
  18. Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
  19. Ayodele, T.O. Types of machine learning algorithms. New Adv. Mach. Learn. 2010, 3, 19–48. [Google Scholar]
  20. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  21. Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
  22. Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
  23. Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
  24. Aggarwal, C.C. Neural networks and deep learning. Springer 2018, 10, 978-3. [Google Scholar]
  25. Abedi, V.; Goyal, N.; Tsivgoulis, G.; Hosseinichimeh, N.; Hontecillas, R.; Bassaganya-Riera, J.; Elijovich, L.; Metter, J.E.; Alexandrov, A.W.; Liebeskind, D.S. Novel screening tool for stroke using artificial neural network. Stroke 2017, 48, 1678–1681. [Google Scholar] [CrossRef] [PubMed]
  26. Liu, M.; Liang, L.; Sun, W. Estimation of in vivo constitutive parameters of the aortic wall using a machine learning approach. Comput. Methods Appl. Mech. Eng. 2019, 347, 201–217. [Google Scholar] [CrossRef]
  27. Betancur, J.; Commandeur, F.; Motlagh, M.; Sharir, T.; Einstein, A.J.; Bokhari, S.; Fish, M.B.; Ruddy, T.D.; Kaufmann, P.; Sinusas, A.J. Deep learning for prediction of obstructive disease from fast myocardial perfusion SPECT: A multicenter study. JACC Cardiovasc. Imaging 2018, 11, 1654–1663. [Google Scholar] [CrossRef]
  28. Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2018, 378, 686–707. [Google Scholar] [CrossRef]
  29. Shameer, K.; Johnson, K.W.; Glicksberg, B.S.; Dudley, J.T.; Sengupta, P.P. Machine learning in cardiovascular medicine: Are we there yet? Heart 2018, 104, 1156–1164. [Google Scholar] [CrossRef]
  30. Arzani, A.; Wang, J.-X.; Sacks, M.S.; Shadden, S.C. Machine Learning for Cardiovascular Biomechanics Modeling: Challenges and Beyond. Ann. Biomed. Eng. 2022, 50, 615–627. [Google Scholar] [CrossRef]
  31. Diller, G.-P.; Kempny, A.; Babu-Narayan, S.V.; Henrichs, M.; Brida, M.; Uebing, A.; Lammers, A.E.; Baumgartner, H.; Li, W.; Wort, S.J. Machine learning algorithms estimating prognosis and guiding therapy in adult congenital heart disease: Data from a single tertiary centre including 10 019 patients. Eur. Heart J. 2019, 40, 1069–1077. [Google Scholar] [CrossRef]
  32. D’Agostino Sr, R.B.; Vasan, R.S.; Pencina, M.J.; Wolf, P.A.; Cobain, M.; Massaro, J.M.; Kannel, W.B. General cardiovascular risk profile for use in primary care: The Framingham Heart Study. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef]
  33. Conroy, R.M.; Pyörälä, K.; Fitzgerald, A.E.; Sans, S.; Menotti, A.; De Backer, G.; De Bacquer, D.; Ducimetiere, P.; Jousilahti, P.; Keil, U. Estimation of ten-year risk of fatal cardiovascular disease in Europe: The SCORE project. Eur. Heart J. 2003, 24, 987–1003. [Google Scholar] [CrossRef]
  34. Goff, D.C.; Lloyd-Jones, D.M.; Bennett, G.; Coady, S.; D’agostino, R.B.; Gibbons, R.; Greenland, P.; Lackland, D.T.; Levy, D.; O’donnell, C.J. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J. Am. Coll. Cardiol. 2014, 63, 2935–2959. [Google Scholar] [CrossRef] [PubMed]
  35. Kakadiaris, I.A.; Vrigkas, M.; Yen, A.A.; Kuznetsova, T.; Budoff, M.; Naghavi, M. Machine learning outperforms ACC/AHA CVD risk calculator in MESA. J. Am. Heart Assoc. 2018, 7, e009476. [Google Scholar] [CrossRef]
  36. Dimopoulos, A.C.; Nikolaidou, M.; Caballero, F.F.; Engchuan, W.; Sanchez-Niubo, A.; Arndt, H.; Ayuso-Mateos, J.L.; Haro, J.M.; Chatterji, S.; Georgousopoulou, E.N. Machine learning methodologies versus cardiovascular risk scores, in predicting disease risk. BMC Med. Res. Methodol. 2018, 18, 1–11. [Google Scholar] [CrossRef] [PubMed]
  37. Alaa, A.M.; Bolton, T.; Di Angelantonio, E.; Rudd, J.H.; Van der Schaar, M. Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLoS ONE 2019, 14, e0213653. [Google Scholar] [CrossRef]
  38. Motwani, M.; Dey, D.; Berman, D.S.; Germano, G.; Achenbach, S.; Al-Mallah, M.H.; Andreini, D.; Budoff, M.J.; Cademartiri, F.; Callister, T.Q. Machine learning for prediction of all-cause mortality in patients with suspected coronary artery disease: A 5-year multicentre prospective registry analysis. Eur. Heart J. 2017, 38, 500–507. [Google Scholar] [CrossRef] [Green Version]
  39. van Rosendael, A.R.; Maliakal, G.; Kolli, K.K.; Beecy, A.; Al’Aref, S.J.; Dwivedi, A.; Singh, G.; Panday, M.; Kumar, A.; Ma, X. Maximization of the usage of coronary CTA derived plaque information using a machine learning based algorithm to improve risk stratification; insights from the CONFIRM registry. J. Cardiovasc. Comput. Tomogr. 2018, 12, 204–209. [Google Scholar] [CrossRef]
  40. Tourassi, G.D.; Armato, S.G.; Lessmann, N.; Isgum, I.; Setio, A.; Vos, B.D.; Ciompi, F.; Jong, P.D.; Oudkerk, M.; Mali, W. Deep convolutional neural networks for automatic coronary calcium scoring in a screening study with low-dose chest CT. Med. Imaging Comput. Aided Diagnosis. SPIE 2016, 9785, 978511. [Google Scholar]
  41. Zreik, M.; Lessmann, N.; van Hamersvelt, R.W.; Wolterink, J.M.; Voskuil, M.; Viergever, M.A.; Leiner, T.; Išgum, I. Deep learning analysis of the myocardium in coronary CT angiography for identification of patients with functionally significant coronary artery stenosis. Med. Image Anal. 2018, 44, 72–85. [Google Scholar] [CrossRef]
  42. Gessert, N.; Lutz, M.; Heyder, M.; Latus, S.; Leistner, D.M.; Abdelwahed, Y.S.; Schlaefer, A. Automatic plaque detection in IVOCT pullbacks using convolutional neural networks. IEEE Trans. Med. Imaging 2018, 38, 426–434. [Google Scholar] [CrossRef]
  43. Narula, S.; Shameer, K.; Omar, A.S.; Dudley, J.T.; Sengupta, P.P. Machine-Learning Algorithms to Automate Morphological and Functional Assessments in 2D Echocardiography. J. Am. Coll. Cardiol. 2016, 68, 2287–2295. [Google Scholar] [CrossRef]
  44. Sengupta, P.P.; Huang, Y.M.; Bansal, M.; Ashrafi, A.; Dudley, J.T. Cognitive Machine-Learning Algorithm for Cardiac Imaging: A Pilot Study for Differentiating Constrictive Pericarditis From Restrictive Cardiomyopathy. Circ. Cardiovasc. Imaging 2016, 9, e004330. [Google Scholar] [CrossRef]
  45. Gjoreski, M.; Gradišek, A.; Budna, B.; Gams, M.; Poglajen, G. Machine learning and end-to-end deep learning for the detection of chronic heart failure from heart sounds. IEEE Access 2020, 8, 20313–20324. [Google Scholar] [CrossRef]
  46. Zack, C.J.; Senecal, C.; Kinar, Y.; Metzger, Y.; Bar-Sinai, Y.; Widmer, R.J.; Lennon, R.; Singh, M.; Bell, M.R.; Lerman, A. Leveraging machine learning techniques to forecast patient prognosis after percutaneous coronary intervention. Cardiovasc. Interv. 2019, 12, 1304–1311. [Google Scholar] [CrossRef]
  47. JérMe, A.; Nicolas, A.; Pascal, A.; Ivan, P.; Olivier, M.; Myriem, B.; Sophie, P.; Philippe, M.; Cyril, F.; Alessandro, P. A Comparison of a Machine Learning Model with EuroSCORE II in Predicting Mortality after Elective Cardiac Surgery: A Decision Curve Analysis. PLoS ONE 2017, 12, e0169772. [Google Scholar]
  48. Wolterink, J.M.; Leiner, T.; de Vos, B.D.; van Hamersvelt, R.W.; Viergever, M.A.; Išgum, I. Automatic coronary artery calcium scoring in cardiac CT angiography using paired convolutional neural networks. Med. Image Anal. 2016, 34, 123–136. [Google Scholar] [CrossRef] [PubMed]
  49. Kelm, M.B.; Mittal, S.; Zheng, Y.; Tsymbal, A.; Comaniciu, D. Detection, Grading and Classification of Coronary Stenoses in Computed Tomography Angiography; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
  50. Hu, H.; Liu, Z.; Chen, G.; Yuan, D.; Zheng, T. Analysis of aortic wall stress and morphology in patients with type B aortic dissection. Med. Nov. Technol. Dev. 2021, 11, 100081. [Google Scholar] [CrossRef]
  51. Gong, X.; Liang, Z.; Wang, Y.; Zhang, C.; Xie, S.; Fan, Y. Comparative study on hemodynamic environments around patient-specific carotid atherosclerotic plaques with different symmetrical features. Med. Nov. Technol. Dev. 2021, 11, 100079. [Google Scholar] [CrossRef]
  52. Arzani, A. Coronary artery plaque growth: A two-way coupled shear stress-driven model. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3293. [Google Scholar] [CrossRef]
  53. Hoogendoorn, A.; Kok, A.M.; Hartman, E.M.J.; Nisco, G.D.; Wentzel, J.J. Multidirectional wall shear stress promotes advanced coronary plaque development—Comparing five shear stress metrics. Cardiovasc. Res. 2019, 116, 1136–1146. [Google Scholar] [CrossRef]
  54. Domanin, M.; Gallo, D.; Vergara, C.; Biondetti, P.; Forzenigo, L.V.; Morbiducci, U. Prediction of long term restenosis risk after surgery in the carotid bifurcation by hemodynamic and geometric analysis. Ann. Biomed. Eng. 2019, 47, 1129–1140. [Google Scholar] [CrossRef]
  55. Gallo, D.; Steinman, D.A.; Morbiducci, U. An insight into the mechanistic role of the common carotid artery on the hemodynamics at the carotid bifurcation. Ann. Biomed. Eng. 2015, 43, 68–81. [Google Scholar] [CrossRef]
  56. Pouch, A.M.; Wang, H.; Takabe, M.; Jackson, B.M.; Gorman, J.H.; Gorman, R.C.; Yushkevich, P.A.; Sehgal, C.M. Fully automatic segmentation of the mitral leaflets in 3D transesophageal echocardiographic images using multi-atlas joint label fusion and deformable medial modeling. Med. Image Anal. 2014, 18, 118–129. [Google Scholar] [CrossRef]
  57. Li, G.; Wang, H.; Zhang, M.; Tupin, S.; Qiao, A.; Liu, Y.; Ohta, M.; Anzai, H. Prediction of 3D Cardiovascular hemodynamics before and after coronary artery bypass surgery via deep learning. Commun. Biol. 2021, 4, 99. [Google Scholar] [CrossRef]
  58. Feiger, B.; Gounley, J.; Adler, D.; Leopold, J.A.; Randles, A. Accelerating massively parallel hemodynamic models of coarctation of the aorta using neural networks. Sci. Rep. 2020, 10, 9508. [Google Scholar]
  59. Zarins, C.K.; Giddens, D.P.; Bharadvaj, B.K.; Sottiurai, V.S.; Mabon, R.F.; Glagov, S. Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ. Res. 1983, 53, 502–514. [Google Scholar] [CrossRef]
  60. Stone, P.H.; Coskun, A.U.; Kinlay, S.; Clark, M.E.; Sonka, M.; Wahle, A.; Ilegbusi, O.J.; Yeghiazarians, Y.; Popma, J.J.; Orav, J.E.; et al. Effect of Endothelial Shear Stress on the Progression of Coronary Artery Disease, Vascular Remodeling, and In-Stent Restenosis in Humans: In Vivo 6-Month Follow-Up Study. Circ. J. Am. Heart Assoc. 2003, 108, 438–444. [Google Scholar] [CrossRef]
  61. Toba, T.; Otake, H.; Choi, G.; Kim, H.J.; Onishi, H.; Sugizaki, Y.; Takeshige, R.; Nagasawa, A.; Nagano, Y.; Tsukiyama, Y.; et al. Wall Shear Stress and Plaque Vulnerability: Computational Fluid Dynamics Analysis Derived from cCTA and OCT. JACC Cardiovasc. Imaging 2020, 14, 315–317. [Google Scholar] [CrossRef]
  62. Mahmoudi, M.; Farghadan, A.; McConnell, D.; Barker, A.J.; Wentzel, J.J.; Budoff, M.J.; Arzani, A. The Story of Wall Shear Stress in Coronary Artery Atherosclerosis: Biochemical Transport and Mechanotransduction. J. Biomech. Eng. 2020, 143, 4049026. [Google Scholar] [CrossRef]
  63. Lee, S.W.; Antiga, L.; Steinman, D.A. Correlations Among Indicators of Disturbed Flow at the Normal Carotid Bifurcation. J. Biomech. Eng. 2009, 131, 061013. [Google Scholar] [CrossRef]
  64. Liu, X.; Pu, F.; Fan, Y.; Deng, X.; Li, D.; Li, S. A numerical study on the flow of blood and the transport of LDL in the human aorta: The physiological significance of the helical flow in the aortic arch. Am. J. Physiol. 2009, 297, 163–170. [Google Scholar] [CrossRef]
  65. Li, X.; Liu, X.; Liang, Y.; Deng, X.; Fan, Y. Spatiotemporal changes of local hemodynamics and plaque components during atherosclerotic progression in rabbit. Comput. Methods Programs Biomed. 2022, 220, 106814. [Google Scholar] [CrossRef] [PubMed]
  66. Suo, J.P.; Ferrara, D.E.; Sorescu, D.C.; Guldberg, R.E.; Taylor, W.R.R.; Giddens, D.P. Hemodynamic Shear Stresses in Mouse Aortas: Implications for Atherogenesis. Arterioscler. Thromb. Vasc. Biol. 2007, 27, 346–351. [Google Scholar] [CrossRef] [PubMed]
  67. Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.-M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. -Heart Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef] [PubMed]
  68. Gibson, C.M.; Díaz, L.; Kandarpa, K.; Sacks, F.M.; Pasternak, R.C.; Sandor, T.; Feldman, C.; Stone, P.H. Relation of vessel wall shear stress to atherosclerosis progression in human coronary arteries. Arterioscler. Thromb. J. Vasc. Biol. 1993, 13, 310–315. [Google Scholar] [CrossRef]
  69. Martin, C.; Sun, W.; Elefteriades, J. Patient-specific finite element analysis of ascending aorta aneurysms. Am. J. Physiol. Heart Circ. Physiol. 2015, 308, H1306–H1316. [Google Scholar] [CrossRef]
  70. Lopes, D.; Agujetas, R.; Puga, H.; Teixeira, J.; Lima, R.; Alejo, J.; Ferrera, C. Analysis of finite element and finite volume methods for fluid-structure interaction simulation of blood flow in a real stenosed artery. Int. J. Mech. Sci. 2021, 207, 106650. [Google Scholar] [CrossRef]
  71. Taylor, C.A.; Hughes, T.J.R.; Zarins, C.K. Finite element modeling of blood flow in arteries. Comput. Methods Appl. Mech. Eng. 1998, 158, 155–196. [Google Scholar] [CrossRef]
  72. Samady, H.; Eshtehardi, P.; McDaniel, M.C.; Suo, J.P.; Dhawan, S.S.; Maynard, C.; Timmins, L.H.; Quyyumi, A.A.; Giddens, D.P. Coronary Artery Wall Shear Stress Is Associated With Progression and Transformation of Atherosclerotic Plaque and Arterial Remodeling in Patients With Coronary Artery Disease. Circulation 2011, 124, 779–788. [Google Scholar] [CrossRef] [Green Version]
  73. Li, X.; Liu, X.; Zhang, P.; Feng, C.; Sun, A.; Kang, H.; Deng, X.; Fan, Y. Numerical simulation of haemodynamics and low-density lipoprotein transport in the rabbit aorta and their correlation with atherosclerotic plaque thickness. J. R. Soc. Interface 2017, 14, 20170140. [Google Scholar] [CrossRef]
  74. Stone, P.H.; Saito, S.; Takahashi, S.; Makita, Y.; Nakamura, S.; Kawasaki, T.; Takahashi, A.; Katsuki, T.-A.; Nakamura, S.; Namiki, A.; et al. Prediction of Progression of Coronary Artery Disease and Clinical Outcomes Using Vascular Profiling of Endothelial Shear Stress and Arterial Plaque Characteristics: The PREDICTION Study. Circulation 2012, 126, 172–181. [Google Scholar] [CrossRef]
  75. Peiffer, V.; Sherwin, S.J.; Weinberg, P.D. Computation in the rabbit aorta of a new metric—The transverse wall shear stress—To quantify the multidirectional character of disturbed blood flow. J. Biomech. 2013, 46, 2651–2658. [Google Scholar] [CrossRef]
  76. Amirhossein, A.; Shadden, C.S. Wall shear stress fixed points in cardiovascular fluid mechanics. J. Biomech. 2018, 73, 145–152. [Google Scholar]
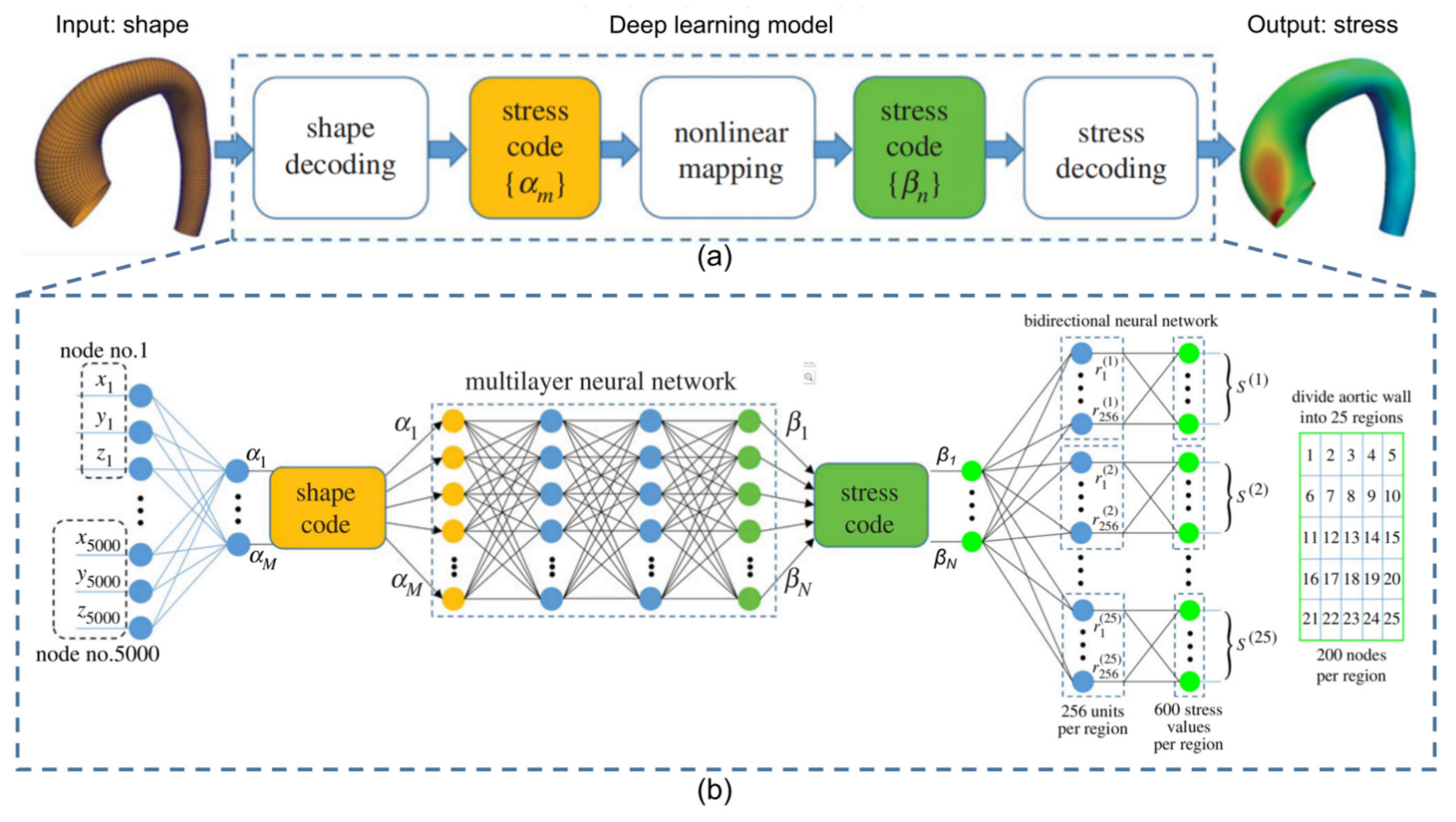
  77. Liang, L.; Minliang, L.; Caitlin, M.; Wei, S. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
  78. Mao, W.; Caballero, A.; Mckay, R.; Primiano, C.; Sun, W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729. [Google Scholar] [CrossRef]
  79. Wittek, A.; Derwich, W.; Karatolios, K.; Fritzen, C.P.; Blase, C. A finite element updating approach for identification of the anisotropic hyperelastic properties of normal and diseased aortic walls from 4D ultrasound strain imaging. J. Mech. Behav. Biomed. Mater. 2016, 58, 122–138. [Google Scholar] [CrossRef]
  80. Schmid, P.J.; Sesterhenn, J. Dynamic Mode Decomposition of Numerical and Experimental Data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
  81. Dowell, E.H.; Hall, K.C.; Romanowski, M.C. Eigenmode Analysis in Unsteady Aerodynamics: Reduced Order Models. Appl. Mech. Rev. 1997, 50, 371. [Google Scholar] [CrossRef]
  82. Weinberg, E.J.; Mofrad, M. Transient, Three-dimensional, Multiscale Simulations of the Human Aortic Valve. Cardiovasc. Eng. 2007, 7, 140–155. [Google Scholar] [CrossRef]
  83. Liang, L.; Liu, M.; Martin, C.; Elefteriades, J.A.; Sun, W. A machine learning approach to investigate the relationship between shape features and numerically predicted risk of ascending aortic aneurysm. Biomech. Modeling Mechanobiol. 2017, 16, 1519–1533. [Google Scholar] [CrossRef]
  84. Raissi, M. Deep Hidden Physics Models: Deep Learning of Nonlinear Partial Differential Equations. J. Mach. Learn. Res. 2018. [Google Scholar]
  85. Chi, Z.; Beile, L.; Deyu, L.; Yubo, F. Application of multiscale coupling models in the numerical study of circulation system. Med. Nov. Technol. Devices 2022, 14, 100117. [Google Scholar] [CrossRef]
  86. Sun, L.; Gao, H.; Pan, S.; Wang, J.X. Surrogate Modeling for Fluid Flows Based on Physics-Constrained Deep Learning Without Simulation Data. Comput. Methods Appl. Mech. Eng. 2019, 361, 112732. [Google Scholar] [CrossRef]
  87. Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2018, 861, 119–137. [Google Scholar] [CrossRef]
  88. Huang, J.; Liu, H.; Cai, W. Online in situ prediction of 3-D flame evolution from its history 2-D projections via deep learning. J. Fluid Mech. 2019, 875, R2. [Google Scholar] [CrossRef]
  89. Peng, G.; Alber, M.; Tepole, A.B.; Cannon, W.R.; Kuhl, E. Multiscale Modeling Meets Machine Learning: What Can We Learn? Arch. Comput. Methods Eng. 2020, 28, 1017–1037. [Google Scholar] [CrossRef]
  90. Miyanawala, T.P.; Jaiman, R.K. An Efficient Deep Learning Technique for the Navier-Stokes Equations: Application to Unsteady Wake Flow Dynamics. arXiv 2017, arXiv:1710.09099. [Google Scholar]
  91. Guo, X.; Wei, L.; Iorio, F. Convolutional Neural Networks for Steady Flow Approximation. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, San Francisco, CA, USA, 13–17 August, 2016; pp. 481–490. [Google Scholar]
  92. Ribeiro, M.D.; Rehman, A.; Ahmed, S.; Dengel, A. DeepCFD: Efficient Steady-State Laminar Flow Approximation with Deep Convolutional Neural Networks. arXiv 2020, arXiv:2004.08826. [Google Scholar]
  93. Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating Eulerian Fluid Simulation With Convolutional Networks. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August, 2017; pp. 3424–3433. [Google Scholar]
  94. Umberto, M.; Kok, A.M.; Kwak, B.R.; Stone, P.H.; Steinman, D.A.; Wentzel, J.J. Atherosclerosis at arterial bifurcations: Evidence for the role of haemodynamics and geometry. Thromb. Haemost. 2016, 115, 484–492. [Google Scholar]
  95. Arzani, A.; Shadden, S.C. Characterization of the transport topology in patient-specific abdominal aortic aneurysm models. Phys. Fluids 2012, 24, 81901. [Google Scholar] [CrossRef]
  96. Shavelle, D.M. Mathematical Modeling of Blood Flow to Evaluate the Hemodynamic Significance of Peripheral Vascular Lesions. Angiol. Vasc. Surg. 2021, 6, 76. [Google Scholar] [CrossRef]
  97. Vardhan, M.; Gounley, J.; Chen, S.J.; Chi, E.C.; Randles, A. Non-invasive characterization of complex coronary lesions. Sci. Rep. 2021, 11, 1–15. [Google Scholar]
  98. Berhane, H.; Scott, M.B.; Elbaz, M.S.M.; Jarvis, K.; McCarthy, P.M.; Carr, J.C.; Malaisrie, C.; Avery, R.J.; Barker, A.J.; Robinson, J.D.; et al. Fully automated 3D aortic segmentation of 4D flow MRI for hemodynamic analysis using deep learning. Magn. Reson. Med. 2020, 84, 2204–2218. [Google Scholar] [CrossRef]
  99. Yu, Y.; Zhang, S.; Huang, J.; Metaxas, D.; Axel, L. Sparse Deformable Models with Application to Cardiac Motion Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
  100. Zhang, S.; Zhan, Y.; Metaxas, D.N. Deformable segmentation via sparse representation and dictionary learning. Med. Image Anal. 2012, 16, 1385–1396. [Google Scholar] [CrossRef]
  101. Litjens, G.J.S.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Laak, J.v.d.; Ginneken, B.v.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
  102. Liang, L.; Mao, W.; Sun, W. A feasibility study of deep learning for predicting hemodynamics of human thoracic aorta. J. Biomech. 2019, 99, 109544. [Google Scholar] [CrossRef]
  103. Luo, Y.; Fan, Z.; Baek, S.; Lu, J. Machine learning–aided exploration of relationship between strength and elastic properties in ascending thoracic aneurysm. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2977.2971–e2977.2912. [Google Scholar] [CrossRef]
  104. Zheng, Y.; Liu, D.; Georgescu, B.; Nguyen, H.V.; Comaniciu, D. 3D Deep Learning for Efficient and Robust Landmark Detection in Volumetric Data. In Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; Volume 9349, pp. 565–572. [Google Scholar]
  105. Moeskops, P.; Wolterink, J.M.; Velden, B.H.M.v.d.; Gilhuijs, K.G.A.; Leiner, T.; Viergever, M.A.; Išgum, I. Deep Learning for Multi-Task Medical Image Segmentation in Multiple Modalities. arXiv 2016, arXiv:1704.03379. [Google Scholar]
  106. Groenendyk, J.W.; Mehta, N.N. Applying the ordinal model of atherosclerosis to imaging science: A brief review. Open Heart 2018, 5, e000861. [Google Scholar] [CrossRef]
  107. Hitchner, E.; Zayed, M.A.; Lee, G.K.; Morrison, D.E.; Lane, B.; Zhou, W. Intravascular ultrasound as a clinical adjunct for carotid plaque characterization. J. Vasc. Surg. 2014, 59 3, 774–780. [Google Scholar] [CrossRef]
  108. Zacharatos, H.; Hassan, A.E.; Qureshi, A.I. Intravascular Ultrasound: Principles and Cerebrovascular Applications. Am. J. Neuroradiol. 2010, 31, 586–597. [Google Scholar] [CrossRef] [PubMed]
  109. Randoux, B.; Marro, B.; Koskas, F.; Duyme, M.; Sahel, M.; Zouaoui, A.; Marsault, C. Carotid artery stenosis: Prospective comparison of CT, three-dimensional gadolinium-enhanced MR, and conventional angiography. Radiology 2001, 220 1, 179–185. [Google Scholar] [CrossRef]
  110. Loizou, P.C.; Pattichis, C.S.; Pantziaris, M.; Nicolaides, A.N. An integrated system for the segmentation of atherosclerotic carotid plaque ultrasound video. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014, 61, 86–101. [Google Scholar] [CrossRef] [PubMed]
  111. Iyer, K.; Najarian, C.; Fattah, A.A.; Arthurs, C.J.; Soroushmehr, S.M.R.; Subban, V.; Sankardas, M.A.; Nadakuditi, R.R.; Nallamothu, B.K.; Figueroa, C.A. AngioNet: A convolutional neural network for vessel segmentation in X-ray angiography. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
  112. Lee, J.; Prabhu, D.; Kolluru, C.; Gharaibeh, Y.; Wilson, D.L. Automated plaque characterization using deep learning on coronary intravascular optical coherence tomographic images. Biomed. Opt. Express 2019, 10, 6497. [Google Scholar] [CrossRef] [PubMed]
  113. Tang, J.; Lan, Y.; Chen, S.; Zhong, Y.; Che, W. Lumen contour segmentation in IVOCT based on N-type CNN. IEEE Access 2019, 7, 135573–135581. [Google Scholar] [CrossRef]
  114. Athanasiou, L.S.; Bourantas, C.V.; Rigas, G.; Sakellarios, A.I.; Exarchos, T.P.; Siogkas, P.K.; Ricciardi, A.; Naka, K.K.; Papafaklis, M.I.; Michalis, L.K.; et al. Methodology for fully automated segmentation and plaque characterization in intracoronary optical coherence tomography images. J. Biomed. Opt. 2014, 19, 026009. [Google Scholar] [CrossRef]
  115. Abdolmanafi, A.; Duong, L.; Dahdah, N.; Cheriet, F. Deep feature learning for automatic tissue classification of coronary artery using optical coherence tomography. Biomed. Opt. Express 2017, 8 (Pt 2), 1203–1220. [Google Scholar] [CrossRef]
  116. Karimi-Bidhendi, S.; Arafati, A.; Cheng, A.L.; Wu, Y.; Kheradvar, A.; Jafarkhani, H. Fully-automated deep-learning segmentation of pediatric cardiovascular magnetic resonance of patients with complex congenital heart diseases. J. Cardiovasc. Magn. Reson. 2020, 22, 1–24. [Google Scholar] [CrossRef]
  117. Kong, F.; Wilson, N.; Shadden, S. A deep-learning approach for direct whole-heart mesh reconstruction. Med. Image Anal. 2021, 74, 102222. [Google Scholar] [CrossRef]
  118. Weng, W.; Zhu, X. INet: Convolutional Networks for Biomedical Image Segmentation. IEEE Access 2021, 9, 16591–16603. [Google Scholar] [CrossRef]
  119. Liang, L.; Kong, F.; Martin, C.K.; Pham, T.; Wang, Q.; Duncan, J.S.; Sun, W. Machine learning-based 3-D geometry reconstruction and modeling of aortic valve deformation using 3-D computed tomography images. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2827. [Google Scholar] [CrossRef]
  120. Zheng, Y.; John, M.; Liao, R.; Nöttling, A.; Boese, J.M.; Kempfert, J.; Walther, T.; Brockmann, G.; Comaniciu, D. Automatic Aorta Segmentation and Valve Landmark Detection in C-Arm CT for Transcatheter Aortic Valve Implantation. IEEE Trans. Med. Imaging 2012, 31, 2307–2321. [Google Scholar] [CrossRef]
  121. Oktay, O.; Ferrante, E.; Kamnitsas, K.; Heinrich, M.P.; Bai, W.; Caballero, J.; Cook, S.A.; de Marvao, A.; Dawes, T.J.W.; O’Regan, D.P.; et al. Anatomically Constrained Neural Networks (ACNNs): Application to Cardiac Image Enhancement and Segmentation. IEEE Trans. Med. Imaging 2018, 37, 384–395. [Google Scholar] [CrossRef]
  122. Kong, F.; Shadden, S.C. Automating Model Generation for Imagebased Cardiac Flow Simulation. J. Biomech. Eng. 2020, 142, 111011. [Google Scholar] [CrossRef] [PubMed]
  123. Poudel, R.P.K.; Lamata, P.; Montana, G. Recurrent Fully Convolutional Neural Networks for Multi-slice MRI Cardiac Segmentation. arXiv 2016, arXiv:1608.03974. [Google Scholar]
  124. Bernard, O.; Lalande, A.; Zotti, C.; Cervenansky, F.; Yang, X.; Heng, P.-A.; Cetin, I.; Lekadir, K.; Camara, O.; González Ballester, M.A.; et al. Deep Learning Techniques for Automatic MRI Cardiac Multi-Structures Segmentation and Diagnosis: Is the Problem Solved? IEEE Trans. Med. Imaging 2018, 37, 2514–2525. [Google Scholar] [CrossRef]
  125. Jordanski, M.; Radovic, M.D.; Milosevic, Z.; Filipovic, N.D.; Obradovic, Z. Machine Learning Approach for Predicting Wall Shear Distribution for Abdominal Aortic Aneurysm and Carotid Bifurcation Models. IEEE J. Biomed. Health Inform. 2018, 22, 537–544. [Google Scholar] [CrossRef]
  126. Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
  127. Madani, A.; Bakhaty, A.; Kim, J.; Mubarak, Y.; Mofrad, M. Bridging Finite Element and Machine Learning Modeling: Stress Prediction of Arterial Walls in Atherosclerosis. J. Biomech. Eng. 2019, 141, 084502. [Google Scholar] [CrossRef]
  128. Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
  129. Arzani, A.; Wang, J.-X.; D’Souza, R.M. Uncovering near-wall blood flow from sparse data with physics-informed neural networks. Phys. Fluids 2021, 33, 071905. [Google Scholar] [CrossRef]
  130. Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
  131. Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
  132. Hayden, S. Learning partial differential equations via data discovery and sparse optimization. Proc. R. Society. Math. Phys. Eng. Sci. 2017, 473, 20160446. [Google Scholar]
  133. Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 2017, 348, 683–693. [Google Scholar] [CrossRef]
  134. Raissi, M.; Karniadakis, G.E. Hidden Physics Models: Machine Learning of Nonlinear Partial\n Differential Equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
  135. Parussini, L.; Venturi, D.; Perdikaris, P.; Karniadakis, G.E. Multi-fidelity Gaussian process regression for prediction of random fields. J. Comput. Phys. 2017, 336, 36–50. [Google Scholar] [CrossRef] [Green Version]
  136. Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
  137. Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
  138. Lee, S.; You, D. Data-driven prediction of unsteady flow over a circular cylinder using deep learning. J. Fluid Mech. 2019, 879, 217–254. [Google Scholar] [CrossRef]
  139. Gaidzik, F.; Stucht, D.; Roloff, C.; Speck, O.; Janiga, G. Transient flow prediction in an idealized aneurysm geometry using data assimilation. Comput. Biol. Med. 2019, 115, 103507. [Google Scholar] [CrossRef]
  140. Funke, S.W.; Nordaas, M.; Evju, Y.; Alnaes, M.S.; Mardal, K.A. Variational data assimilation for transient blood flow simulations—Cerebral aneurysms as an illustrative example. Int. J. Numer. Methods Biomed. Eng. 2018, 35, e3152. [Google Scholar] [CrossRef]
  141. Habibi, M.; D’Souza, R.M.; Dawson, S.; Arzani, A. Integrating multi-fidelity blood flow data with reduced-order data assimilation. Comput. Biol. Med. 2021, 135, 104566. [Google Scholar] [CrossRef]
  142. Adriaan, C.; Young-Hak, K.; Mariusz, K.; Christian, T.; Jakob, D.G.; Akira, K.; Lubbers, M.L.; Joost, D.; Lucian, I.; Saikiran, R. Diagnostic Accuracy of a Machine-Learning Approach to Coronary Computed Tomographic Angiography–Based Fractional Flow Reserve. Circ. Cardiovasc. Imaging 2018, 11, e007217. [Google Scholar]
  143. Itu, L.; Rapaka, S.; Passerini, T.; Georgescu, B.; Schwemmer, C.; Schoebinger, M.; Flohr, T.; Sharma, P.; Comaniciu, D. A machine-learning approach for computation of fractional flow reserve from coronary computed tomography. J. Appl. Physiol. 2016, 121, 42–52. [Google Scholar] [CrossRef]
  144. Hu, X.; Yang, M.; Han, L.; Du, Y. Diagnostic performance of machine-learning-based computed fractional flow reserve (FFR) derived from coronary computed tomography angiography for the assessment of myocardial ischemia verified by invasive FFR. Int. J. Cardiovasc. Imaging 2018, 34, 1987–1996. [Google Scholar] [CrossRef]
  145. Liang, L.; Liu, M.; Sun, W. A Deep Learning Approach to Estimate Chemically-Treated Collagenous Tissue Nonlinear Anisotropic Stress-Strain Responses from Microscopy Images. Acta Biomater. 2017, 63, 227–235. [Google Scholar] [CrossRef]
  146. Hennigh, O. Lat-Net: Compressing Lattice Boltzmann Flow Simulations using Deep Neural Networks. arXiv 2017, arXiv:1705.09036. [Google Scholar]
  147. Zhou, Y.; He, Y.; Wu, J.; Cui, C.; Chen, M.; Sun, B. A method of parameter estimation for cardiovascular hemodynamics based on deep learning and its application to personalize a reduced-order model. Int. J. Numer. Methods Biomed. Eng. 2021, 38, e3533. [Google Scholar] [CrossRef]
  148. Sonoda, S.; Murata, N. Neural Network with Unbounded Activation Functions is Universal Approximator. Appl. Comput. Harmon. Anal. 2017, 43, 233–268. [Google Scholar] [CrossRef] [Green Version]
  149. Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. arXiv 2022, arXiv:2105.09506. [Google Scholar] [CrossRef]
  150. Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
  151. Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden Fluid Mechanics: A Navier-Stokes Informed Deep Learning Framework for Assimilating Flow Visualization Data. arXiv 2018, arXiv:1808.04327. [Google Scholar]
  152. Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
  153. Buoso, S.; Joyce, T.; Kozerke, S. Personalising left-ventricular biophysical models of the heart using parametric physics-informed neural networks. Med. Image Anal. 2021, 71, 102066. [Google Scholar] [CrossRef]
  154. Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2019, 358, 112623. [Google Scholar] [CrossRef]
  155. Clauset, A.; Larremore, D.B.; Sinatra, R. Data-driven predictions in the science of science. Science 2017, 355, 477. [Google Scholar] [CrossRef]
  156. Karumuri, S.; Tripathy, R.; Bilionis, I.; Panchal, J. Simulator-free Solution of High-Dimensional Stochastic Elliptic Partial Differential Equations using Deep Neural Networks. J. Comput. Phys. 2019, 404, 109120. [Google Scholar] [CrossRef]
  157. Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-Constrained Deep Learning for High-dimensional Surrogate Modeling and Uncertainty Quantification without Labeled Data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
  158. Geneva, N.; Zabaras, N. Modeling the Dynamics of PDE Systems with Physics-Constrained Deep Auto-Regressive Networks. J. Comput. Phys. 2019, 403, 109056. [Google Scholar] [CrossRef]
  159. Gao, H.; Sun, L.; Wang, J.X. Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels. Phys. Fluids 2021, 33, 073603. [Google Scholar] [CrossRef]
  160. Wessels, H.; Weißenfels, C.; Wriggers, P. The Neural Particle Method—An Updated Lagrangian Physics Informed Neural Network for Computational Fluid Dynamics. arXiv 2020, arXiv:2003.10208. [Google Scholar] [CrossRef]
  161. Lucor, D.; Agrawal, A.; Sergent, A. Physics-Aware Deep Neural Networks for Surrogate Modeling of Turbulent Natural Convection. arXiv 2021, arXiv:2103.03565. [Google Scholar]
  162. Gasmi, C.F.; Tchelepi, H. Physics Informed Deep Learning for Flow and Transport in Porous Media. arXiv 2021, arXiv:2104.02629. [Google Scholar]
  163. Holzinger, A. Interactive machine learning for health informatics: When do we need the human-in-the-loop? Brain Inform. 2016, 3, 119–131. [Google Scholar] [CrossRef]
  164. Siau, K.L.; Wang, W. Artificial Intelligence (AI) Ethics: Ethics of AI and Ethical AI. J. Database Manag. 2020, 31, 74–87. [Google Scholar] [CrossRef]
  165. Seetharam, K.; Shrestha, S.; Sengupta, P.P. Artificial Intelligence in Cardiovascular Medicine. Curr. Treat. Options Cardiovasc. Med. 2019, 21, 1–14. [Google Scholar] [CrossRef]
  166. Kagiyama, N.; Shrestha, S.; Farjo, P.D.; Sengupta, P.P. Artificial Intelligence: Practical Primer for Clinical Research in Cardiovascular Disease. J. Am. Heart Assoc. Cardiovasc. Cerebrovasc. Dis. 2019, 8, e012788. [Google Scholar] [CrossRef]
  167. Arrieta, A.B.; Rodríguez, N.D.; Ser, J.D.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
  168. Guidotti, R.; Monreale, A.; Turini, F.; Pedreschi, D.; Giannotti, F. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. (CSUR) 2019, 51, 1–42. [Google Scholar] [CrossRef]
  169. Reyes, M.; Meier, R.; Pereira, S.; Silva, C.A.; Dahlweid, F.-M.; von Tengg-Kobligk, H.; Summers, R.M.; Wiest, R. On the Interpretability of Artificial Intelligence in Radiology: Challenges and Opportunities. Radiol. Artif. Intell. 2020, 2, e190043. [Google Scholar] [CrossRef] [PubMed]
Biomedicines 10 02157 g001 550
Figure 1. Risk factors associated with cardiovascular disease.
Figure 1. Risk factors associated with cardiovascular disease.
Biomedicines 10 02157 g001
Biomedicines 10 02157 g002 550
Figure 2. The overview development of artificial intelligence and the relationship between artificial intelligence, machine learning, and deep learning.
Figure 2. The overview development of artificial intelligence and the relationship between artificial intelligence, machine learning, and deep learning.
Biomedicines 10 02157 g002
Biomedicines 10 02157 g003 550
Figure 3. Two types of machine learning−based approaches were applied to evaluate cardiovascular disease risk.
Figure 3. Two types of machine learning−based approaches were applied to evaluate cardiovascular disease risk.
Biomedicines 10 02157 g003
Biomedicines 10 02157 g004 550
Figure 4. Case study using the deep learning (DL) technique as a surrogate of finite−element analysis for stress analysis. (a) The overall structure of the DL model, in which the input is an aorta shape and the output is the stress distribution of the artery wall. (b) The neural network for the shape encoding, mapping the shape code to the stress code, and the stress decoding and encoding. Panel (a,b) are adapted with permission from Reference [77], Journal of the Royal Society Interface.
Figure 4. Case study using the deep learning (DL) technique as a surrogate of finite−element analysis for stress analysis. (a) The overall structure of the DL model, in which the input is an aorta shape and the output is the stress distribution of the artery wall. (b) The neural network for the shape encoding, mapping the shape code to the stress code, and the stress decoding and encoding. Panel (a,b) are adapted with permission from Reference [77], Journal of the Royal Society Interface.
Biomedicines 10 02157 g004
Biomedicines 10 02157 g005 550
Figure 5. Case study for machine learning framework for surrogate modeling of pressure gradient and WSS for patients with coarctation of the aorta [58] (a) Design of experiments workflow. (b) ML results comparing predicted and simulated pressure. (c) ML results comparing predicted and simulated TAWSS.
Figure 5. Case study for machine learning framework for surrogate modeling of pressure gradient and WSS for patients with coarctation of the aorta [58] (a) Design of experiments workflow. (b) ML results comparing predicted and simulated pressure. (c) ML results comparing predicted and simulated TAWSS.
Biomedicines 10 02157 g005
Biomedicines 10 02157 g006 550
Figure 6. Case study for the physics−constrained, data−driven framework and data−free framework for surrogate modeling of fluid flows in aneurysms. (a) The data−driven structure of the Navier−Stokes−informed neural networks. The input data c is generated by using a direct numerical simulation, and the output is the quantitative hemodynamic parameters. (b) Contours of reference and regressed concentration, velocity, and pressure fields within the 3D intracranial aneurysm sac. (c) The data−free neural network is developed by coding boundary conditions with construction and trained by minimizing the loss function based on equations instead of CFD simulation data. (d) Contours of physics−constrained deep neural network predictions and CFD solutions of three different aneurysm geometries. Panel (a,b) are adapted with permission from Reference [126]. Science. Panel (c,d) are adapted with permission from Reference [86]. Elsevier.
Figure 6. Case study for the physics−constrained, data−driven framework and data−free framework for surrogate modeling of fluid flows in aneurysms. (a) The data−driven structure of the Navier−Stokes−informed neural networks. The input data c is generated by using a direct numerical simulation, and the output is the quantitative hemodynamic parameters. (b) Contours of reference and regressed concentration, velocity, and pressure fields within the 3D intracranial aneurysm sac. (c) The data−free neural network is developed by coding boundary conditions with construction and trained by minimizing the loss function based on equations instead of CFD simulation data. (d) Contours of physics−constrained deep neural network predictions and CFD solutions of three different aneurysm geometries. Panel (a,b) are adapted with permission from Reference [126]. Science. Panel (c,d) are adapted with permission from Reference [86]. Elsevier.
Biomedicines 10 02157 g006
Table
Table 1. Machine learning−based prediction models of cardiovascular diseases.
Table 1. Machine learning−based prediction models of cardiovascular diseases.
FocusAlgorithmData SizeInput VariablesPerformance (AUC)Significant Discovery
CVD risk prediction [35]ML (SVM)6459clinical data0.92ML algorithms significantly improved risk stratification while reducing adverse events.
CVD risk prediction [36]ML (KNN, RF
and DT)		2020clinical dataAccu.: 0.83
Sens.: 0.89
Spec.: 0.46		The RF gave the best results, while the
k−NN gave the poorest results.
CVD risk prediction [37]AutoPrognosis
(SVM, RF, kNN, AdaBoost and GBM)		423,604clinical data0.774ML model had better efficiency than
traditional risk calculators.
CAD mortality
prediction [38]		ML (LogitBoost)10,030clinical and
CCTA data		0.79The accuracy of the ML model was better compared to the traditional or CCTA severity scores alone.
CAD risk prediction [39]ML (XGBoost)8844clinical and
CCTA data		0.771The risk score based on ML had greater prognostic accuracy than current CCTA integrated risk scores.
CAC identification [40] CNN + RF50CCTA data/CAC could be automatically identified and classified in CCTA using CNN and RF algorithms.
Coronary artery stenosis identification [41] CNN + CAE
+ SVM		166FFR and
CCTA data		0.74The CNN could be used to automatically identify functionally significant coronary artery stenosis.
Obstructive disease prediction [27]DL1638MPI data0.80/0.76The DL algorithm could automatically
interpret MPI more accurately.
CHD Plaque detection [42]CNN49IVOCT dataAccu.: 0.917
Sens.: 0.909
Spec.: 0.924		It’s feasible to construct a DL−based clinical decision support system for plaque detection.
HCM discrimination [43]ML (SVMs + RF)
+ ANN		139STE data0.795The ML−based models had higher diagnostic sensitivity and specificity.
CP/ RCM discrimination [44]ML (AMC, RF,
SVM and kNN)		94Clinical and
STE data		0.962The AMC gave the best results.
Prognosis prediction [31]DL10,019Clinical and
ECG data		Accu.: 0.906It was feasible to build a DL−based model to estimate the prognosis in ACHD.
CHF identification [45]ML (RF) + DL947Clinical and
heart sounds data		0.893The heart sound−based detection methods for different CHF phases were proposed through ML and DL.
ACI identification [25]ANN260clinical dataSpec.: 0.862
Sens.: 0.8		ANN could be used for the recognition of ACI and differentiation of ACI from stroke intelligently.
Perioperative mortality prediction + Readmission [46]ML (RF)11,709Perioperative
clinical data		0.9/0.88ML was more predictive in identifying postoperative mortality 180d after PCI and rehospitalization for CHF 30d after surgery.
Perioperative
Mortality prediction [47]		ML (GBM, RF,
Naïve Bayes, SVM)		6520Perioperative
clinical data		0.795ML model was more accurate in predicting mortality after elective cardiac surgery
than the traditional prediction model.
(AUC: Area under the curve; CVD: Cardiovascular disease; ML: Machine learning; SVM: Support vector machine; KNN: K−Nearest neighbor; RF: Random forests; DT: Decision tree; Accu.: Accuracy; Sens.: Sensitivity; Spec.: Specificity; GBM: Gradient boosting machines; CAD: Coronary artery disease; CCTA: Coronary computed tomography angiography; CAC: Coronary artery calcification; CNN: Convolutional neural network; CAE: Convolutional autoencoder; FFR: Fractional flow reserve; DL: Deep learning; MPI: Myocardial perfusion imaging; CHD: Coronary heart disease; IVOCT: Intravascular optical coherence tomography; HCM: Hypertrophic cardiomyopathy; ANN: Artificial neural network; STE: Speckle−tracking echocardiographic; CP: Constrictive pericarditis; RCM: Restrictive cardiomyopathy; AMC: Associative memory classifier; ECG: Electrocardiograph; ACHD: Adult congenital heart disease; CHF: Chronic heart failure; ACI: Acute cerebral ischemia; PCI: Percutaneous coronary intervention; GBM: Gradient boosting machines).
Table
Table 2. Artificial intelligence−based surrogate for computational fluid dynamics.
Table 2. Artificial intelligence−based surrogate for computational fluid dynamics.
AlgorithmsName of AuthorsObjectivesTraining SetSignificant Discovery
MLJordanski et al. [125]WSSFEA resultsThree ML models (MLR, MLP, GCRF) were developed for the
calculation of WSS distribution, and the GCRF achieved the highest
coefficient of determination (0.930–0.948) for the AAA model
and (0.946–0.954) for carotid bifurcation model.
MLFeiger et al. [58]Pressure,
WSS		LBM resultsThe 3D simulation−based ML model was developed to accurately
predict pressure gradient across the stenosis and WSS for patients
with coarctation of the aorta.
DLLi et al. [57]Velocity,
Pressure gradient		FEA resultsThe hemodynamic prediction results of deep learning was in
agreement with the conventional CFD method, but the calculation
time was reduced 600−fold.
DLRaissi et al. [126]Velocity,
Pressure		DNS resultsA physics−informed deep−learning framework was capable of encoding the Navier−Stokes equations into the neural networks while being agnostic to the geometry or the initial and boundary conditions.
DNNMadani et al. [127]Stress FEA resultsThe DNNs outperformed alternative prediction models and
performance scales with the amount of training data.
DNNliang et al. [102]Pressure,
Velocity		FEA resultsThe trained DNNs were capable of predicting the steady−state
distributions of pressure and flow velocity inside the thoracic
aorta with an average error of 1.9608% and 1.4269%.
CNNKai et al. [128]Velocity DNS resultsThe CNN model was found to reconstruct turbulent flows from
extremely coarse flow field images with remarkable accuracy.
PINNArzani et al. [129]WSS N−S equationsPINN was used to obtain near−wall hemodynamics and WSS data from sparse velocity measurements and without knowledge of the inlet/outlet boundary conditions.
FC−NNSun et al. [86]Velocity,
Pressure		N−S equationsA physics−constrained deep neural network−based approach was
developed for surrogate modeling of fluid flows without relying
on any simulation data.
(ML: Machine learning; WSS: Wall shear stress; FEA: Finite element analysis; MLR: Multivariate linear regression; MLP: Multilayer perceptron neural network; GCRF: Gaussian conditional random fields; AAA: Abdominal aortic aneurysm; LBM: Lattice Boltzmann method; DL: Deep learning; CFD: Computational fluid dynamics; DNS: Direct numerical simulation; DNN: Deep neural network; CNN: Convolutional neural network; PINN: Physics−informed neural network; N−S equations: Navier−Stokes equations; FC−NN: Fully−connected neural network).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Li, X.; Liu, X.; Deng, X.; Fan, Y. Interplay between Artificial Intelligence and Biomechanics Modeling in the Cardiovascular Disease Prediction. Biomedicines 2022, 10, 2157. https://doi.org/10.3390/biomedicines10092157

AMA Style

Li X, Liu X, Deng X, Fan Y. Interplay between Artificial Intelligence and Biomechanics Modeling in the Cardiovascular Disease Prediction. Biomedicines. 2022; 10(9):2157. https://doi.org/10.3390/biomedicines10092157

Chicago/Turabian Style

Li, Xiaoyin, Xiao Liu, Xiaoyan Deng, and Yubo Fan. 2022. "Interplay between Artificial Intelligence and Biomechanics Modeling in the Cardiovascular Disease Prediction" Biomedicines 10, no. 9: 2157. https://doi.org/10.3390/biomedicines10092157

APA Style

Li, X., Liu, X., Deng, X., & Fan, Y. (2022). Interplay between Artificial Intelligence and Biomechanics Modeling in the Cardiovascular Disease Prediction. Biomedicines, 10(9), 2157. https://doi.org/10.3390/biomedicines10092157

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop