Improved Survival Analyses Based on Characterized Time-Dependent Covariates to Predict Individual Chronic Kidney Disease Progression
Abstract
:1. Introduction
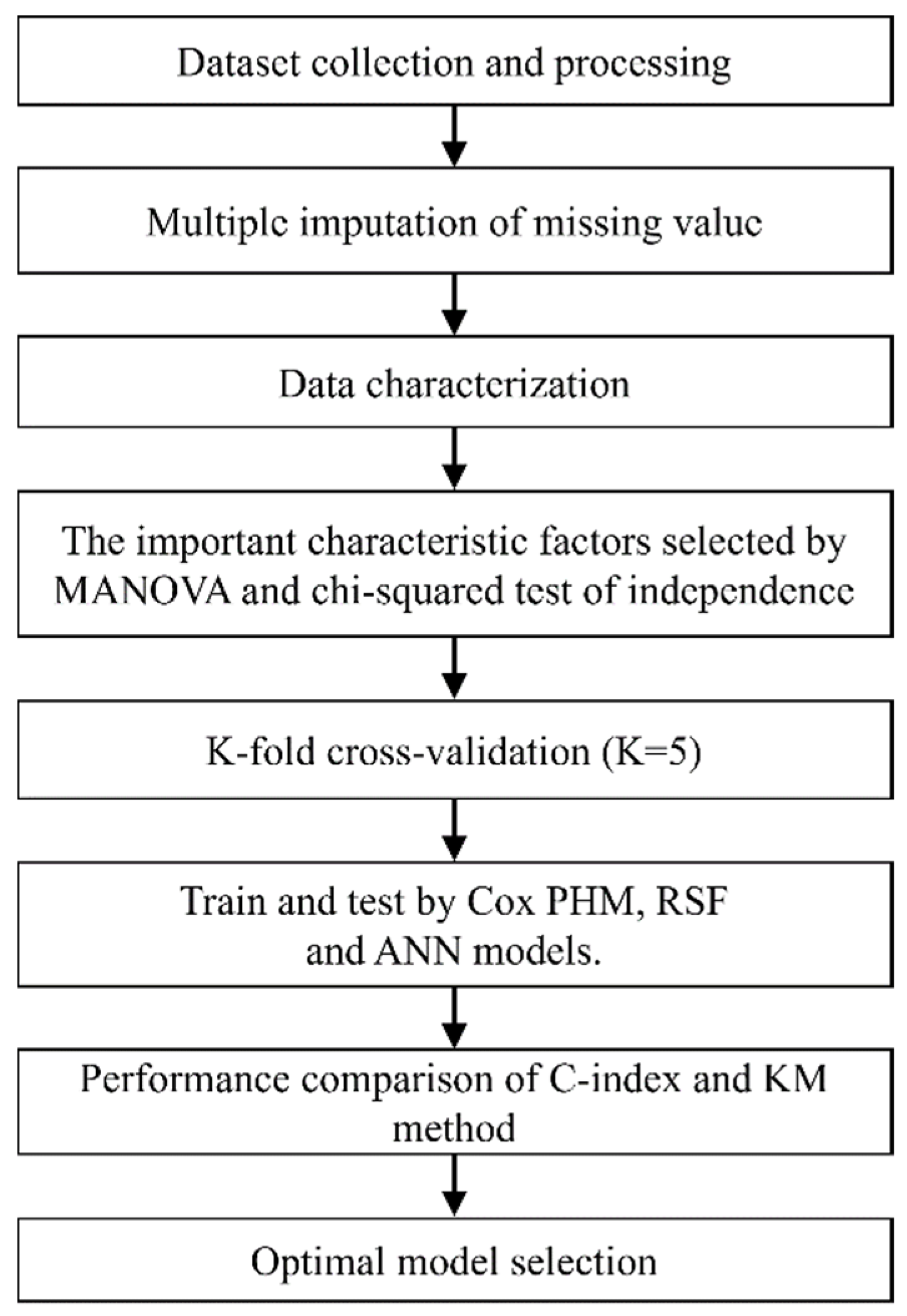
2. Materials and Methods
2.1. Patient Population and Study Design
2.2. Mathematical Modeling
2.3. Variables
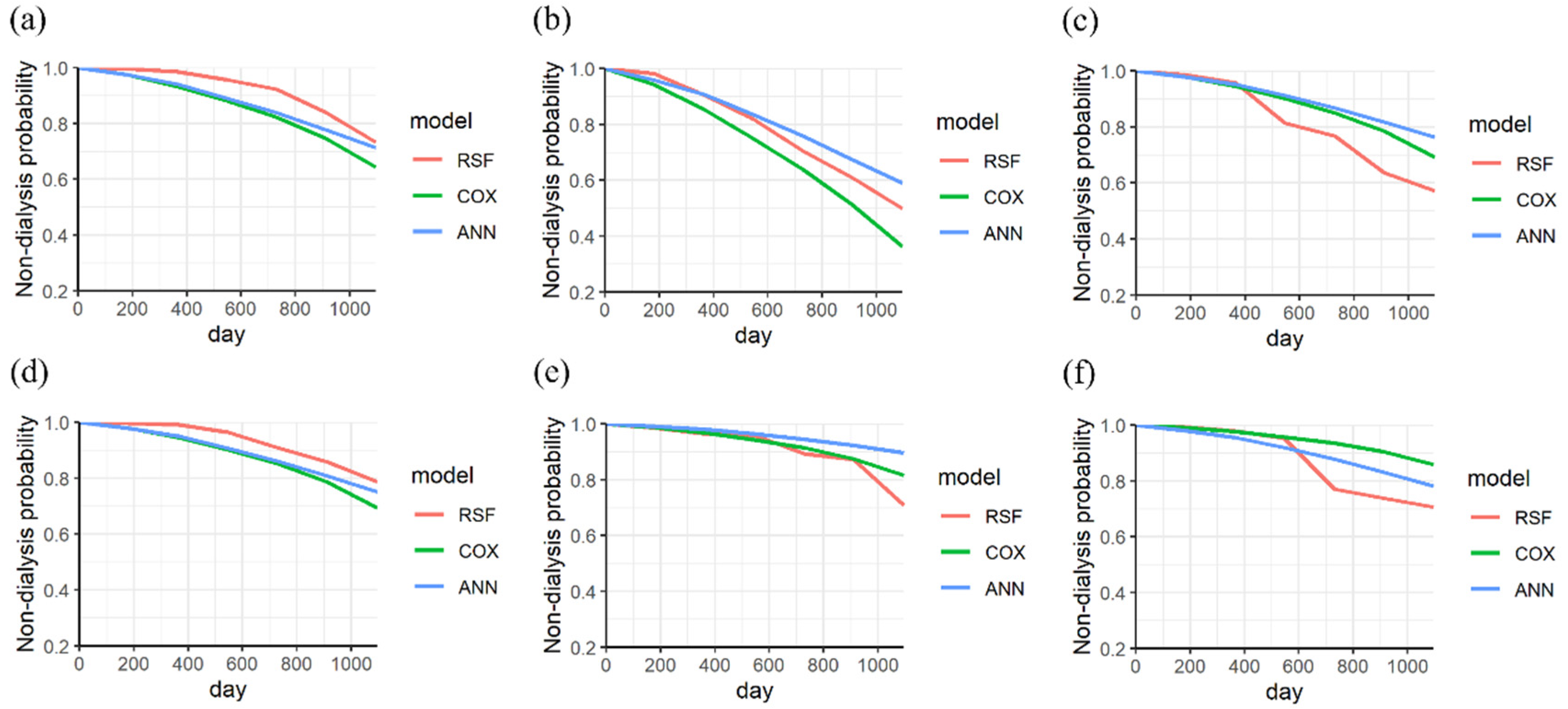
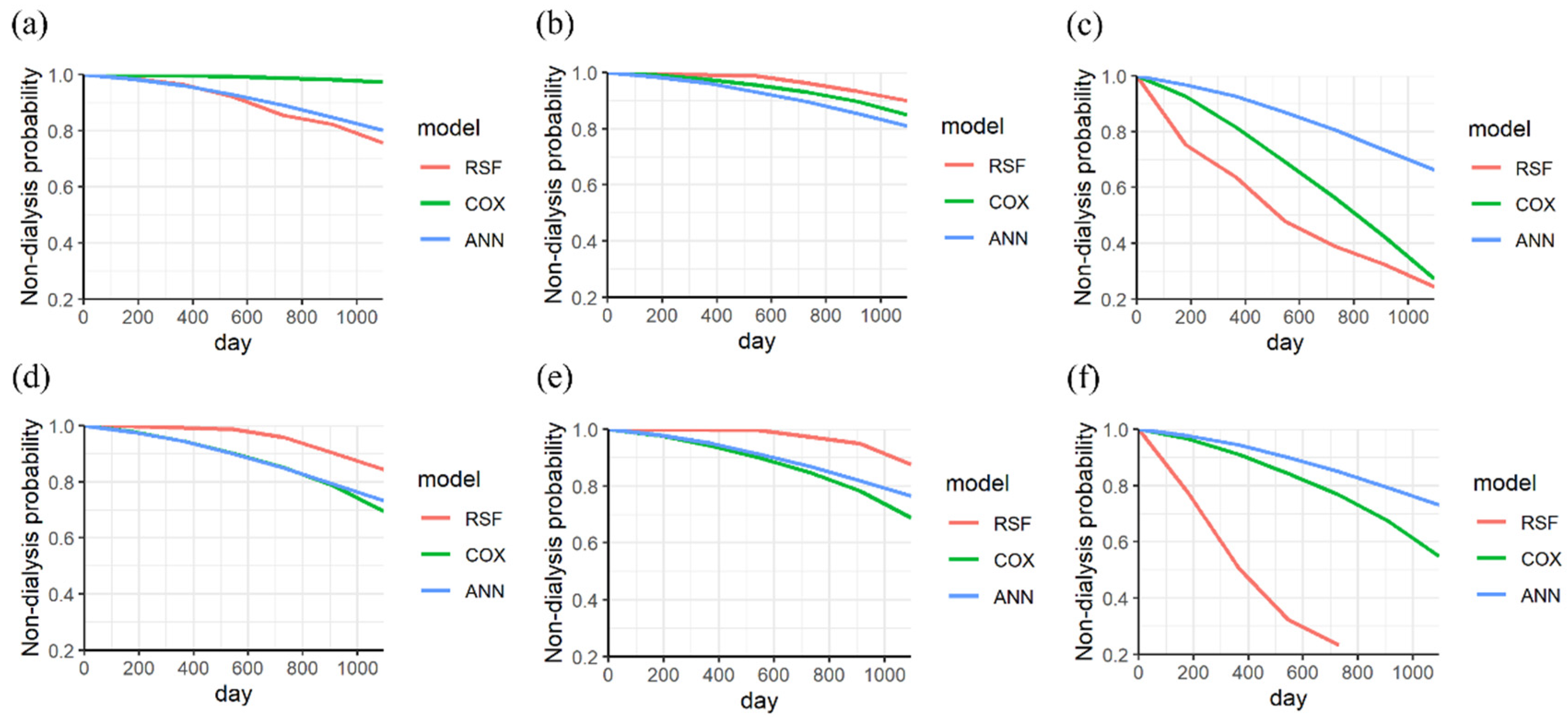
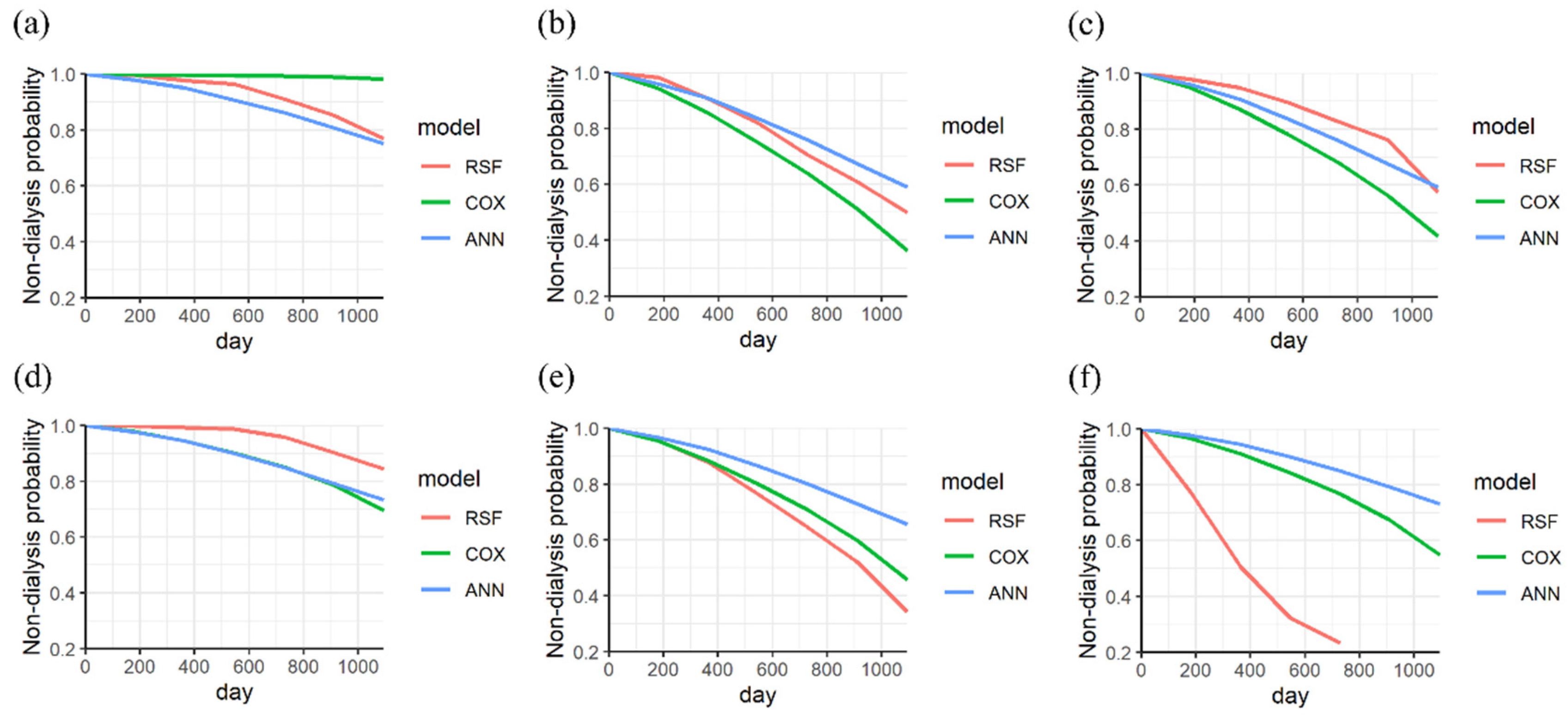
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kovesdy, C.P. Epidemiology of chronic kidney disease: An update 2022. Kidney Int. Suppl. 2002, 12, 7–11. [Google Scholar] [CrossRef] [PubMed]
- Chapin, E.; Zhan, M.; Hsu, V.D.; Seliger, S.L.; Walker, L.D.; Fink, J.C. Adverse safety events in chronic kidney disease: The frequency of “multiple hits”. Clin. J. Am. Soc. Nephrol. 2010, 5, 95–101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Go, A.S.; Chertow, G.M.; Fan, D.; McCulloch, C.E.; Hsu, C.Y. Chronic kidney disease and the risks of death, cardiovascular events, and hospitalization. N. Engl. J. Med. 2004, 351, 1296–1305. [Google Scholar] [CrossRef] [PubMed]
- Kuo, H.W.; Tsai, S.S.; Tiao, M.M.; Yang, C.Y. Epidemiological features of CKD in Taiwan. Am. J. Kidney Dis. 2007, 49, 46–55. [Google Scholar] [CrossRef] [PubMed]
- Klag, M.J.; Whelton, P.K.; Randall, B.L.; Neaton, J.D.; Brancati, F.L.; Ford, C.E.; Shulman, N.B.; Stamler, J. Blood pressure and end stage renal disease in men. N. Engl. J. Med. 1996, 334, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Di Lullo, L.; House, A.; Gorini, A.; Santoboni, A.; Russo, D.; Ronco, C. Chronic kidney disease and cardiovascular complications. Heart Fail. Rev. 2015, 20, 259–272. [Google Scholar] [CrossRef]
- Zhang, L.; Long, J.; Jiang, W.; Shi, Y.; He, X.; Zhou, Z.; Li, Y.; Yeung, R.O.; Wang, J.; Matsushita, K.; et al. Trends in chronic kidney disease in China. N. Engl. J. Med. 2016, 375, 905–906. [Google Scholar] [CrossRef] [PubMed]
- Levey, A.S.; Coresh, J.; Bolton, K.; Culleton, B.; Harvey, K.S.; Ikizler, T.A.; Johnson, C.A.; Kausz, A.; Kimmel, P.L.; Kusek, J.; et al. K/DOQI clinical practice guidelines for chronic kidney disease: Evaluation, classification, and stratification. Am. J. Kidney Dis. 2002, 39, S1–S266. [Google Scholar]
- Tangri, N.; Inker, L.A.; Hiebert, B.; Wong, J.; Naimark, D.; Kent, D.; Levey, A.S. A dynamic predictive model for progression of CKD. Am. J. Kidney Dis. 2017, 69, 514–520. [Google Scholar] [CrossRef] [PubMed]
- Taal, M.W.; Brenner, B.M. Renal risk scores: Progress and prospects. Kidney Int. 2008, 73, 1216–1219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoy, W.E.; Wang, Z.; vanBuynder, P.; Baker, P.R.A.; Mathews, J.D. The natural history of renal disease in Australian Aborigines. Part 1. Changes in albuminuria and glomerular filtration rate over time. Kidney Int. 2001, 60, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Hoy, W.E.; Wang, Z.; vanBuynder, P.; Baker, P.R.A.; Mcdonald, A.M.; Mathews, J.D. The natural history of renal disease in Australian Aborigines. Part 2. Albuminuria predicts natural death and renal failure. Kidney Int. 2001, 60, 249–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keane, W.F.; Zhang, Z.; Lyle, P.A.; Cooper, M.E.; de Zeeuw, D.; Grunfeld, J.P.; Lash, J.P.; McGill, J.B.; Mitch, W.E.; Remuzzi, G.; et al. Risk scores for predicting outcomes in patients with type 2 diabetes and nephropathy: The RENAAL study. Clin. J. Am. Soc. Nephrol. 2006, 1, 761–767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, C.T.; Chang, Y.P.; Ku, Y.T.; Lin, C.M. Machine learning models for the prediction of renal failure in chronic kidney disease: A retrospective cohort study. Diagnostics 2022, 12, 2454. [Google Scholar] [CrossRef] [PubMed]
- Ou, S.M.; Tsai, M.T.; Lee, K.H.; Tseng, W.C.; Yang, C.Y.; Chen, T.H.; Bin, P.J.; Chen, T.J.; Lin, Y.P.; Sheu, W.H.H.; et al. Prediction of the risk of developing end-stage renal diseases in newly diagnosed type 2 diabetes mellitus using artificial intelligence algorithms. BioData Min. 2023, 16, 8. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; An, S.; Gao, Y.; Xie, E.; Zhao, X.; Guo, Z.; Li, Y.; Shen, N.; Ren, J.; Zheng, J. The prediction of in-hospital mortality in chronic kidney disease patients with coronary artery disease using machine learning models. Eur. J. Med. Res. 2023, 28, 33. [Google Scholar] [CrossRef]
- Sawhney, R.; Malik, A.; Sharma, S.; Narayan, V.A. comparative assessment of artificial intelligence models used for early prediction and evaluation of chronic kidney disease. Decis. Anal. J. 2023, 6, 100169. [Google Scholar] [CrossRef]
- Tangaro, S.; Fanizzi, A.; Amoroso, N.; Corciulo, R.; Garuccio, E.; Gesualdo, L.; Loizzo, G.; Procaccini, D.A.; Vernò, L.; Bellotti, R. Computer aided detection system for prediction of the malaise during hemodialysis. Comput. Math Methods Med. 2016, 2016, 10. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.Y.; Liao, C.M.; Wang, L.H.; Hu, H.H.; Lin, C.M. Static and dynamic prediction of chronic renal disease progression using longitudinal clinical data from Taiwan’s National Prevention Programs. J. Clin. Med. 2021, 10, 3085. [Google Scholar] [CrossRef]
- Echouffo-Tcheugui, J.B.; Kengne, A.P. Risk models to predict chronic kidney disease and its progression: A systematic review. PLoS. Med. 2012, 9, e1001344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tangri, N.; Kitsios, G.D.; Inker, L.A.; Griffith, J.; Naimark, D.M.; Walker, S.; Rigatto, C.; Uhlig, K.; Kent, D.M.; Levey, A.S. Risk prediction models for patients with chronic kidney disease: A systematic review. Ann. Intern. Med. 2013, 158, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Asari, V.K.; Rajasekaran, R. A deep neural network for early detection and prediction of chronic kidney disease. Diagnostics 2022, 12, 116. [Google Scholar] [CrossRef]
- de Bruijne, M.H.J.; Sijpkens, Y.W.J.; Paul, L.C.; Westendorp, R.G.J.; van Houwelingen, H.C.; Zwinderman, A.H. Predicting kidney graft failure using time-dependent renal function covariates. J. Clin. Epidemiol. 2003, 56, 448–455. [Google Scholar] [CrossRef] [PubMed]
- Hamidi, O.; Poorolajal, J.; Farhadian, M.; Tapak, L. Identifying important risk factors for survival in kidney graft failure patients using random survival forests. Iran. J. Public Health 2016, 45, 27–33. [Google Scholar] [PubMed]
- Mondol, C.; Shamrat, F.M.J.M.; Hasan, M.R.; Alam, S.; Ghosh, P.; Tasnim, Z.; Ahmed, K.; Bui, F.M.; Ibrahim, S.M. Early prediction of chronic kidney disease: A comprehensive performance analysis of deep learning models. Algorithms 2022, 15, 308. [Google Scholar] [CrossRef]
- Radespiel-Tröger, M.; Rabenstein, T.; Schneider, H.T.; Lausen, B. Comparison of tree-based methods for prognostic stratification of survival data. Artif. Intell. Med. 2003, 28, 323–341. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Mogensen, U.B.; Ishwaran, H.; Gerds, T.A. Evaluating random forests for survival analysis using prediction error curves. J. Stat. Softw. 2012, 50, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Van Allen, E.M.; Omberg, L.; Wagle, N.; Amin-Mansour, A.; Sokolov, A.; Byers, L.A.; Xu, Y.; Hess, K.R.; Diao, L.; et al. Assessing the clinical utility of cancer genomic and proteomic data across tumor types. Nat. Biotechnol. 2014, 32, 644–652. [Google Scholar] [CrossRef] [PubMed]
- Sloan, R.A.; Haaland, B.A.; Sawada, S.S.; Lee, I.M.; Sui, X.; Lee, D.C.; Ridouane, Y.; Müller-Riemenschneider, F.; Blair, S.N. A fit-fat index for predicting incident diabetes in apparently healthy men: A prospective cohort study. PLoS ONE 2016, 11, e0157703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; Feng, D. Deep neural networks for survival analysis using pseudo values. IEEE J. Biomed. Health Inform. 2020, 24, 3308–3314. [Google Scholar] [CrossRef] [PubMed]
- Rubin, D.B.; Schenker, N. Multiple imputation for interval estimation from simple random samples with ignorable nonresponse. J. Am. Stat. Assoc. 1986, 81, 366–374. [Google Scholar] [CrossRef]
- Fisher, L.D.; Lin, D.Y. Time-dependent covariates in the Cox proportional-hazards regression model. Annu. Rev. Public Health 1999, 20, 145–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Reinikainen, J.; Adeleke, K.A.; Pieterse, M.E.; Groothuis-Oudshoorn, C.G.M. Time-varying covariates and coefficients in Cox regression models. Ann. Transl. Med. 2018, 6, 121. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, M.; Mboya, I.B.; Mwambi, H.; Murtada, K.; Elbashir, M.K.; Omolo, B. Predictors of colorectal cancer survival using cox regression and random survival forests models based on gene expression data. PLoS ONE 2021, 16, e0261625. [Google Scholar] [CrossRef] [PubMed]
- Pollock, K.H.; Winterstein, S.R.; Bunck, C.M.; Curtis, P.D. Survival analysis in telemetry studies: The staggered entry design. J. Wildl. Manag. 1989, 53, 7–15. [Google Scholar] [CrossRef]
- Feng, D.; Zhao, L. BDNNSurv: Bayesian deep neural networks for survival analysis using pseudo values. arXiv 2021, arXiv:2101.03170. [Google Scholar] [CrossRef]
- Mayr, A.; Schmid, M. Boosting the concordance index for survival data–a unified framework to derive and evaluate biomarker combinations. PLoS ONE 2014, 9, e84483. [Google Scholar] [CrossRef] [Green Version]
- Guyot, P.; Ades, A.E.; Ouwens, M.J.; Welton, N.J. Enhanced secondary analysis of survival data: Reconstructing the data from published Kaplan-Meier survival curves. BMC. Med. Res. Methodol. 2012, 12, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levey, A.S.; Bosch, J.P.; Lewis, J.B.; Greene, T.; Rogers, N.; Roth, D. A more accurate method to estimate glomerular filtration rate from serum creatinine: A new prediction equation. Ann. Intern. Med. 1999, 130, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Seyedzadeh, A.; Tohidi, M.R.; Golmohamadi, S.; Omrani, H.R.; Seyedzadeh, M.S.; Amiri, S.; Hookari, S. Prevalence of renal osteodystrophy and its related factors among end-stage renal disease patients undergoing hemodialysis: Report from Imam Reza referral hospital of medical university of Kermanshah, Iran. Oman. Med. J. 2022, 37, e335. [Google Scholar] [CrossRef]
- Beladi Mousavi, S.S.; Hayati, F.; Mousavi, M. What is the difference between causes of ESRD in Iran and developing countries? Shiraz. Med. J. 2012, 13, 63–71. [Google Scholar]
- Al Wakeel, J.S.; Mitwalli, A.H.; Al Mohaya, S.; Abu-Aisha, H.; Tarif, N.; Malik, G.H.; Hammad, D. Morbidity and mortality in ESRD patients on dialysis. Saudi. J. Kidney Dis. Transpl. 2002, 13, 473–477. [Google Scholar]
- Christensen, E.; Schlichting, P.; Andersen, P.K.; Fauerholdt, L.; Schou, G.; Vestergaard Pedersen, B.; Juhl, E.; Poulsen, H.; Tygstrup, N.; Copenhagen Study Group for Liver Diseases. Updating prognosis and therapeutic effect evaluation in cirrhosis with Cox’s multiple regression model for time-dependent variables. Scand. J. Gastroenterol. 1986, 21, 163–174. [Google Scholar] [CrossRef]
- Salinas-Escudero, G.; Carrillo-Vega, M.F.; Granados-Garcia, V.; Martínez-Valverde, S.; Toledano-Toledano, F.; Garduño-Espinosa, J. A survival analysis of COVID-19 in the Mexican population. BMC Public Health 2020, 20, 1616. [Google Scholar]
- Zhang, L.; Wang, Z.; Chen, Z.; Wang, X.; Tian, Y.; Shao, L.; Zhu, M. Central aortic systolic blood pressure exhibits advantages over brachial blood pressure measurements in chronic kidney disease risk prediction in women. Kidney Blood Press. Res. 2018, 43, 1375–1387. [Google Scholar] [CrossRef]
- Ramani, R.; Vimala Devi, K.; Ruba Soundar, K. MapReduce-based big data framework using modified artificial neural network classifier for diabetic chronic disease prediction. Soft. Comput. 2020, 24, 16335–16345. [Google Scholar] [CrossRef]
- Dutta, A.; Batabyal, T.; Basu, M.; Acton, S.T. An efficient convolutional neural network for coronary heart disease prediction. Expert. Syst. Appl. 2020, 159, 113408. [Google Scholar] [CrossRef]
- Sandhu, R.; Sood, S.K.; Kaur, G. An intelligent system for predicting and preventing MERS-CoV infection outbreak. J. Supercomput 2016, 72, 3033–3056. [Google Scholar] [CrossRef] [PubMed]

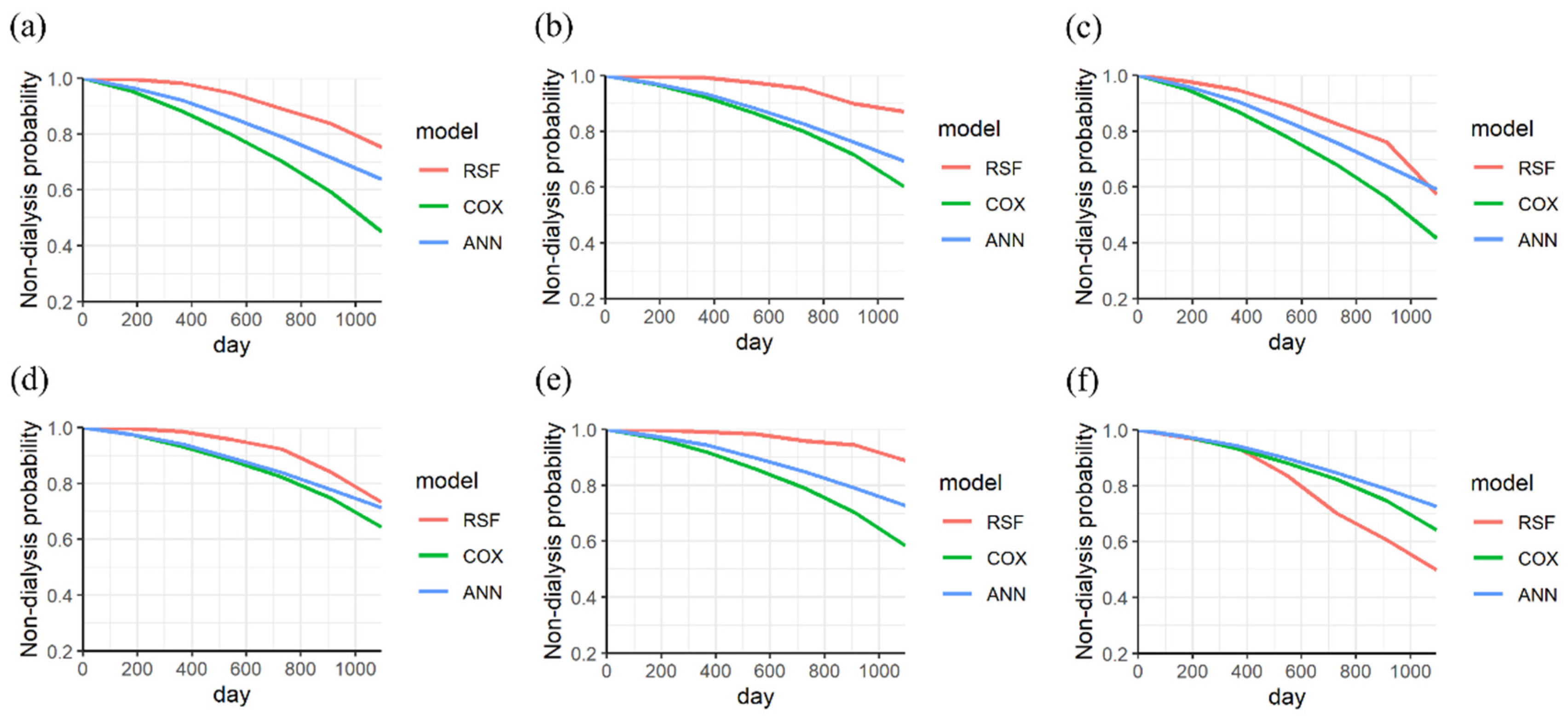
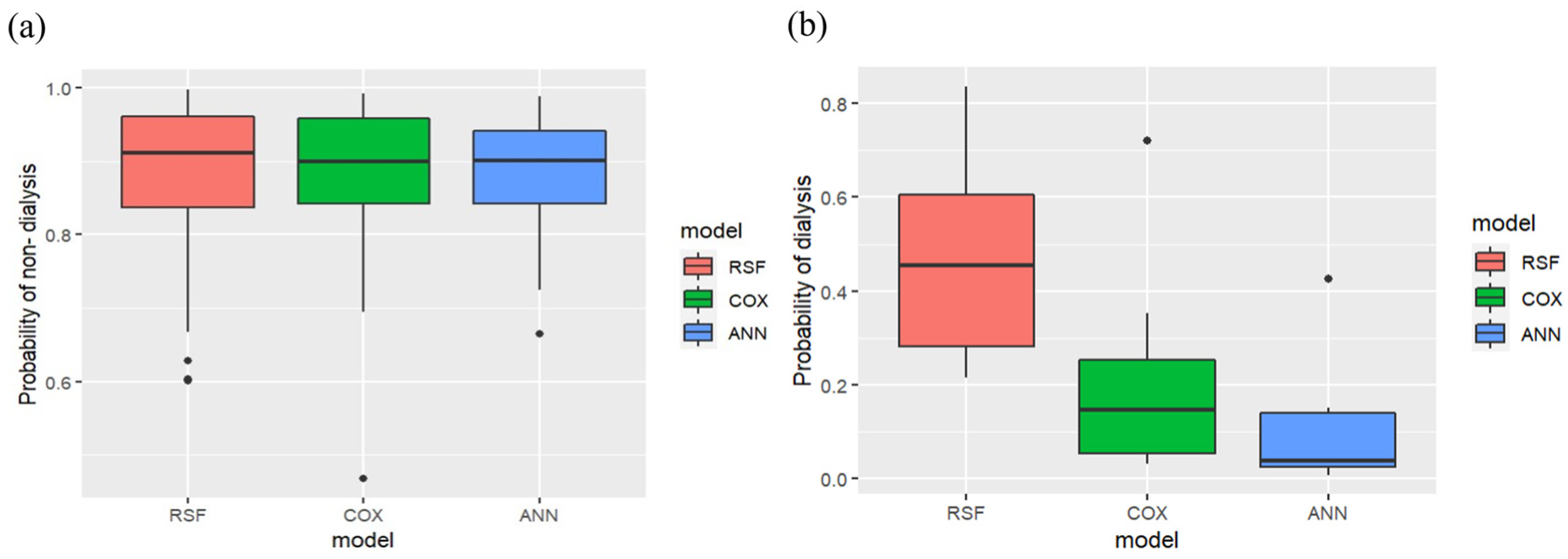
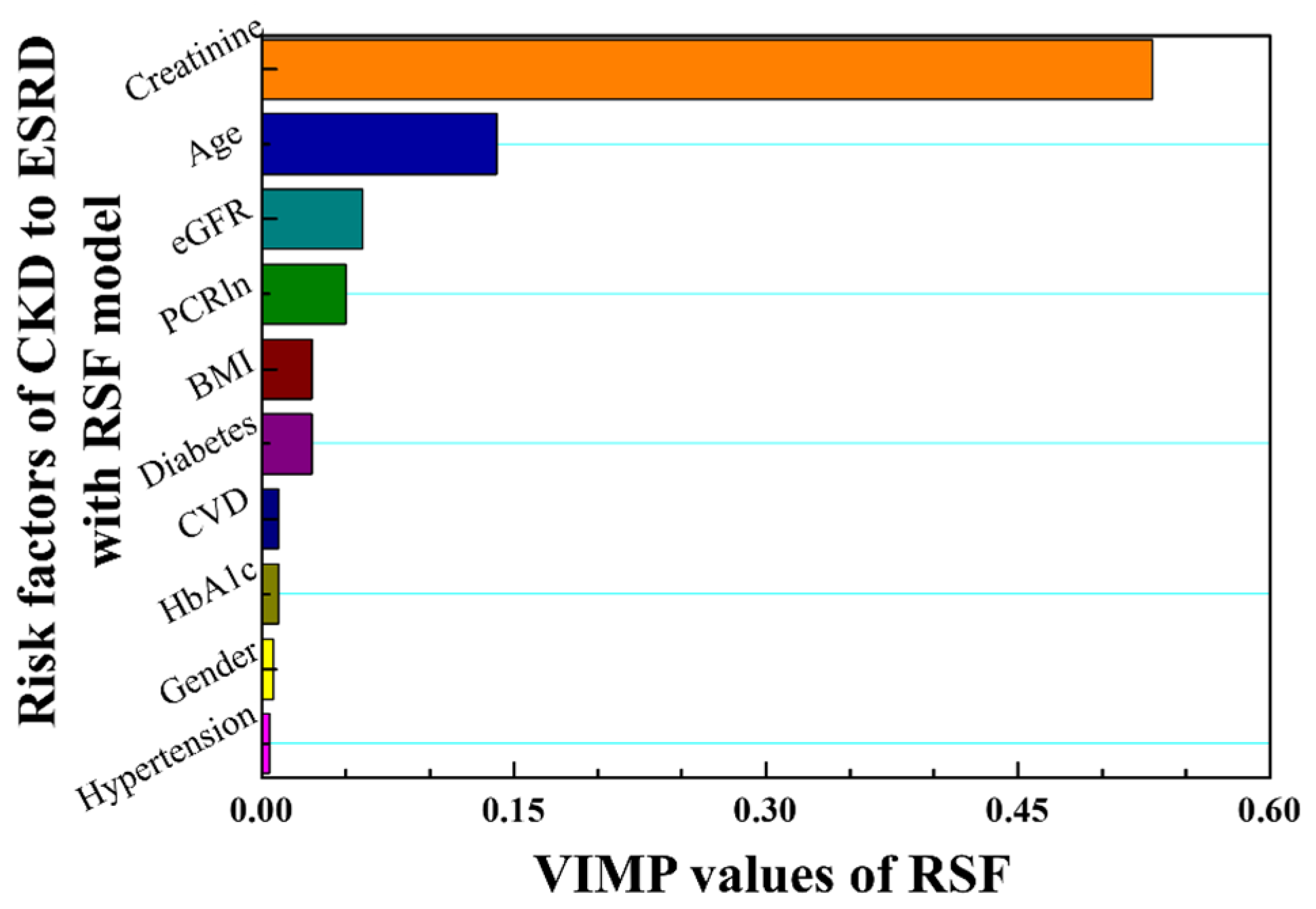
| Variances | Stage 3 (Sub Dataset = 935) | Stage 4 (Sub Dataset = 416) | Stage 5 (Sub Dataset = 213) | Stages 3–5 (Dataset = 1564) | |||
|---|---|---|---|---|---|---|---|
| With Dialysis (Sub Dataset = 247) | Without Dialysis (Sub Dataset = 1317) | χ2 | p Value | ||||
| Male | 568 (61%) | 324 (78%) | 126 (59%) | 167 (68%) | 851 (65%) | 0.6944 | 0.4047 |
| Hypertension | 611 (65%) | 326 (78%) | 175 (81%) | 194 (79%) | 918 (70%) | 14.554 | 0.00013 |
| Diabetes | 552 (59%) | 205 (49%) | 105 (49%) | 164 (66%) | 698 (53%) | 7.4833 | 0.0062 |
| CVD | 148 (16%) | 40 (10%) | 3 (1%) | 7 (3%) | 184 (14%) | 23.036 | 1.58 × 10−6 |
| Variances | Stage 3 (Sub Dataset = 935) | Stage 4 (Sub Dataset = 416) | Stage 5 (Sub Dataset = 213) | Stages 3–5 (Dataset = 1564) | ||
|---|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | Mean (SD) | With Dialysis (Sub Dataset = 247) | Without Dialysis (Sub Dataset = 1317) | F Value | |
| Mean (SD) | Mean (SD) | |||||
| Age | 80.57 (11.14) | 87.00 (13.11) | 76.14 (13.48) | 75.85 (13.15) | 81.35 (11.77) | 43.649 *** |
| SBP | 136.20 (17.92) | 136.40 (19.22) | 139.60 (19.25) | 138.72 (18.65) | 136.37 (18.43) | 3.391 |
| DBP | 73.44 (26.47) | 70.34 (12.77) | 73.06 (13.21) | 73.32 (13.24) | 72.42 (23.36) | 0.345 |
| Creatinine | 1.49 (0.30) | 2.56 (0.66) | 6.27 (3.55) | 4.7 (3.23) | 1.99 (1.46) | 440.43 *** |
| HbA1c | 6.79 (2.33) | 6.47 (1.30) | 6.27 (1.17) | 6.69 (1.47) | 6.61 (2.06) | 0.347 |
| PCRln | 5.63 (1.49) | 6.02 (2.10) | 6.78 (2.04) | 6.81 (1.93) | 5.71 (1.7) | 82.182 *** |
| BMI | 26.43 (7.00) | 26.66 (15.30) | 27.22 (18.16) | 26.99 (6.05) | 26.52 (12.44) | 0.33 |
| eGFR | 44.73 (8.18) | 22.59 (4.16) | 10.15 (3.77) | 20.3 (14.19) | 36.72 (13.78) | 292.58 *** |
| C-Index | Average | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Cox PHM | 0.73 | 0.61 | 0.73 | 0.77 | 0.72 | 0.71 |
| RSF | 0.95 | 0.91 | 0.91 | 0.88 | 0.81 | 0.89 |
| ANN | 0.75 | 0.62 | 0.74 | 0.73 | 0.73 | 0.72 |
| Model | Cut off Point | Sensitivity | Specificity | Accuracy | Precision | F1 Score |
|---|---|---|---|---|---|---|
| RSF | 0.65 | 0.708 | 0.897 | 0.867 | 0.567 | 0.630 |
| 0.70 | 0.791 | 0.880 | 0.897 | 0.792 | 0.791 | |
| 0.75 | 0.917 | 0.794 | 0.813 | 0.458 | 0.610 | |
| Cox PHM | 0.65 | 0.083 | 0.929 | 0.793 | 0.181 | 0.114 |
| 0.70 | 0.125 | 0.920 | 0.793 | 0.231 | 0.162 | |
| 0.75 | 0.125 | 0.897 | 0.920 | 0.187 | 0.150 | |
| ANN | 0.65 | 0.000 | 0.984 | 0.827 | 0.000 | 0.000 |
| 0.70 | 0.000 | 0.952 | 0.800 | 0.000 | 0.000 | |
| 0.75 | 0.041 | 0.913 | 0.773 | 0.083 | 0.055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, C.-M.; Su, C.-T.; Huang, H.-C.; Lin, C.-M. Improved Survival Analyses Based on Characterized Time-Dependent Covariates to Predict Individual Chronic Kidney Disease Progression. Biomedicines 2023, 11, 1664. https://doi.org/10.3390/biomedicines11061664
Liao C-M, Su C-T, Huang H-C, Lin C-M. Improved Survival Analyses Based on Characterized Time-Dependent Covariates to Predict Individual Chronic Kidney Disease Progression. Biomedicines. 2023; 11(6):1664. https://doi.org/10.3390/biomedicines11061664
Chicago/Turabian StyleLiao, Chen-Mao, Chuan-Tsung Su, Hao-Che Huang, and Chih-Ming Lin. 2023. "Improved Survival Analyses Based on Characterized Time-Dependent Covariates to Predict Individual Chronic Kidney Disease Progression" Biomedicines 11, no. 6: 1664. https://doi.org/10.3390/biomedicines11061664
APA StyleLiao, C. -M., Su, C. -T., Huang, H. -C., & Lin, C. -M. (2023). Improved Survival Analyses Based on Characterized Time-Dependent Covariates to Predict Individual Chronic Kidney Disease Progression. Biomedicines, 11(6), 1664. https://doi.org/10.3390/biomedicines11061664







