Application of I-Optimal Design for Modeling and Optimizing the Operational Parameters of Ibuprofen Granules in Continuous Twin-Screw Wet Granulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
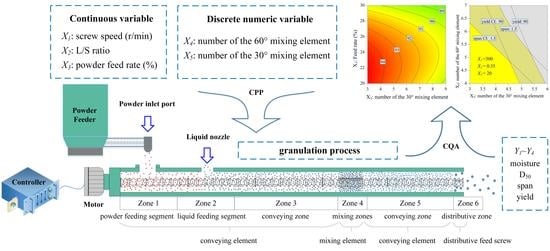
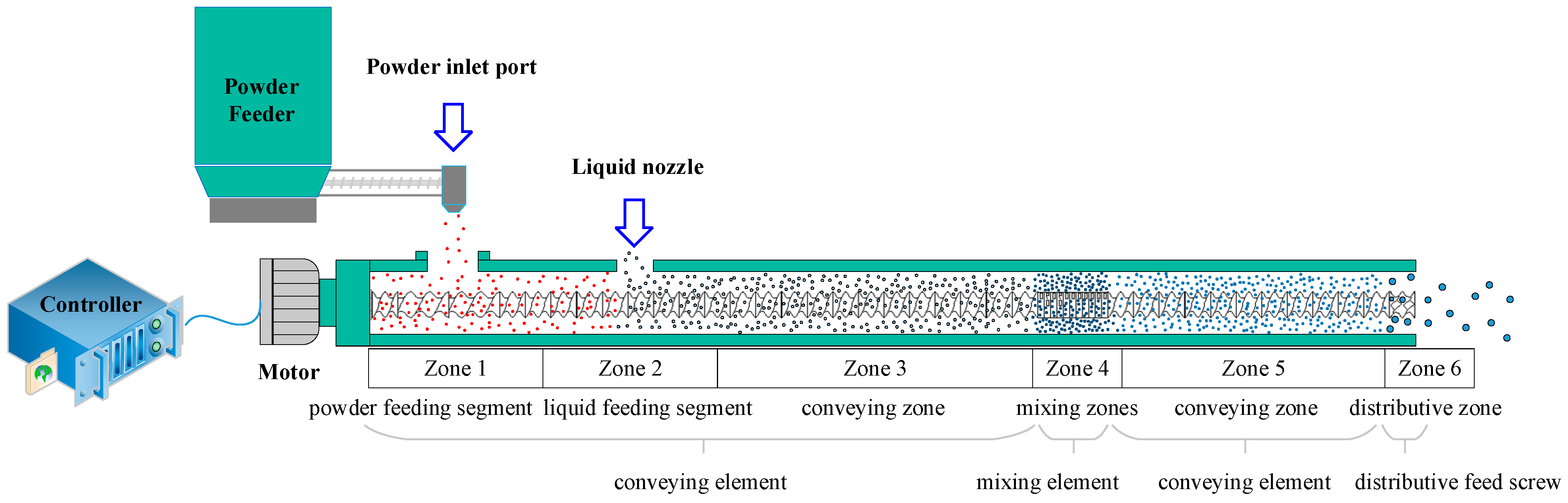
2.2. Continuous Twin-Screw Wet Granulation
2.3. Experimental Design
2.4. Characterization of Particle Properties
2.5. Method Validation
2.6. Data Analysis and Modeling
3. Results and Discussion
3.1. Fitting Data to the Model
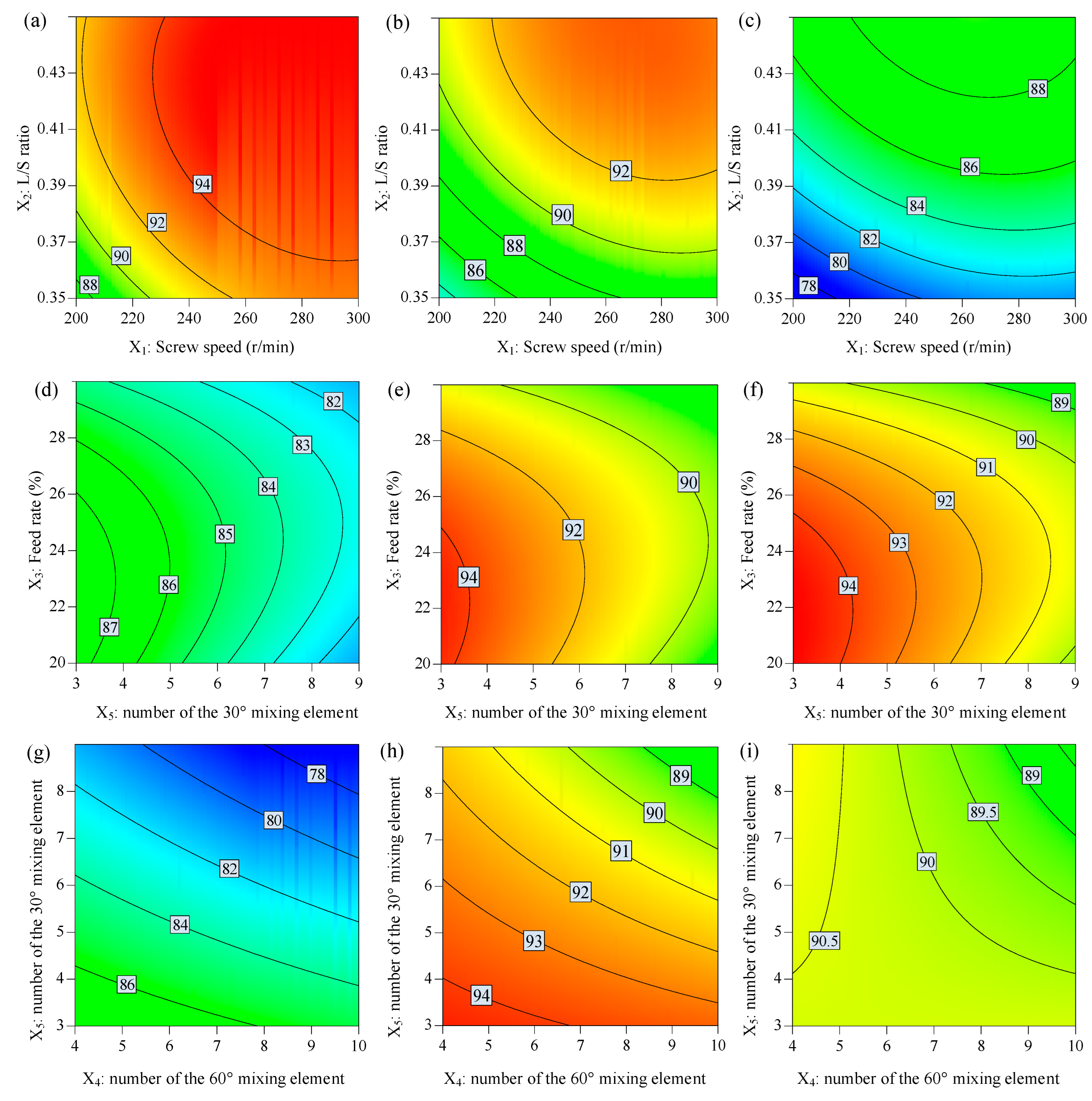
3.2. The Effect of Factors on the Moisture Content
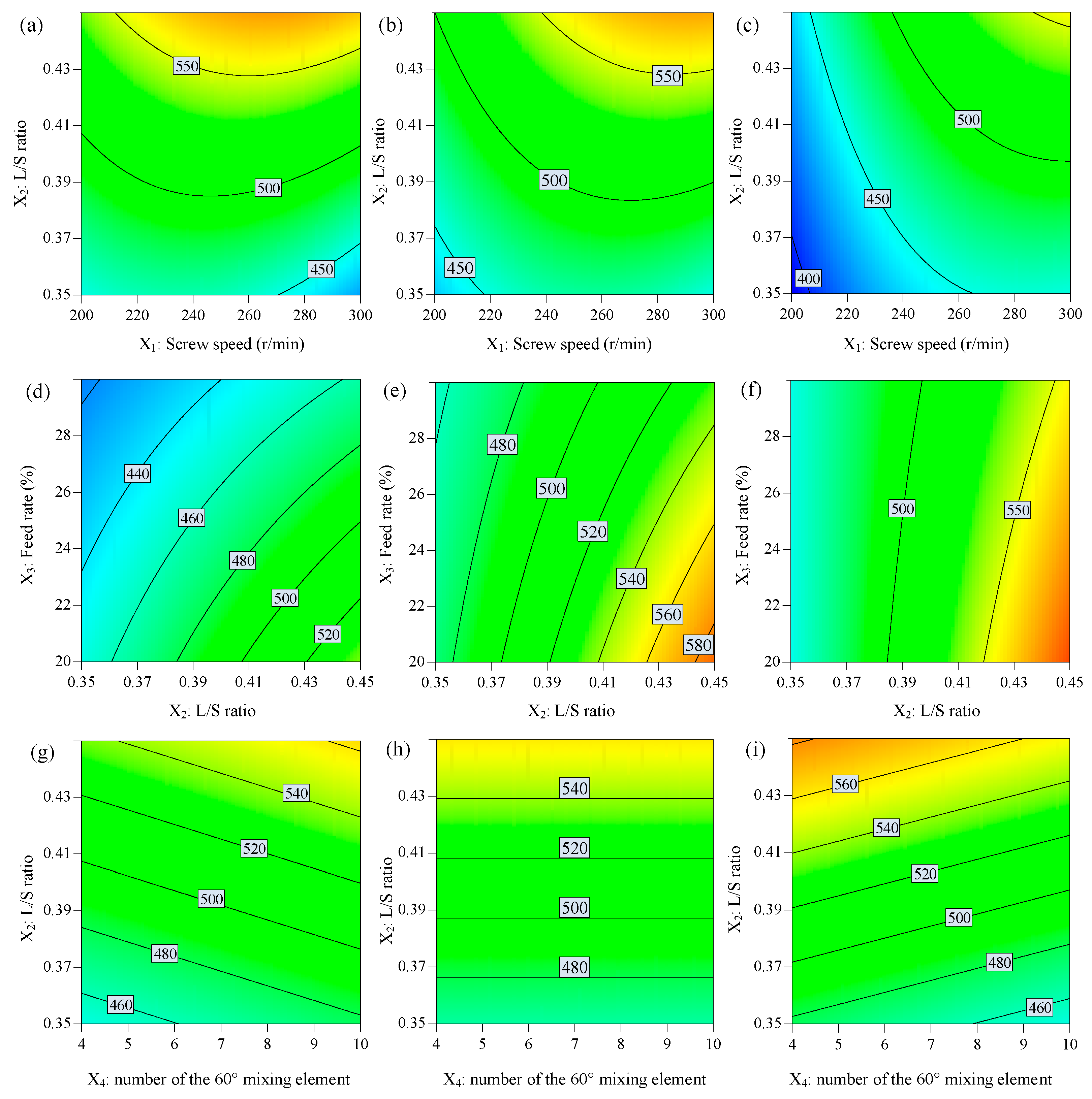
3.3. The Effect of Factors on the Mean Particle Size
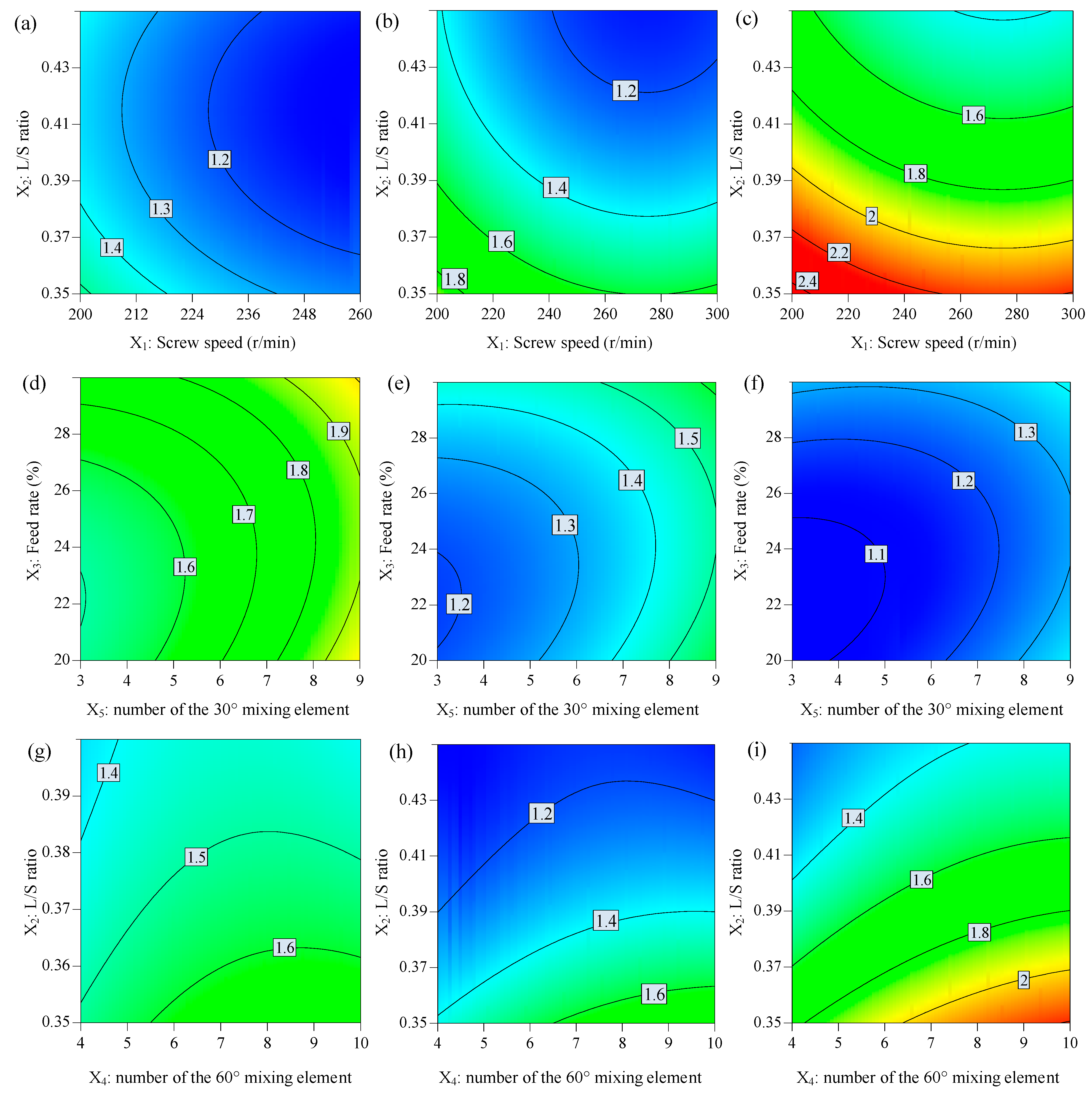
3.4. The Effect of Factors on the Span
3.5. The Effect of Factors on the Production Yield
3.6. Defining a Design Space and Validation of the TWSG Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muddu, S.V.; Kotamarthy, L.; Ramachandran, R. A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation. Pharmaceutics 2021, 13, 393. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.L.; O’Connor, T.F.; Yang, X.; Cruz, C.N.; Chatterjee, S.; Madurawe, R.D.; Moore, C.M.V.; Yu, L.X.; Woodcock, J. Modernizing Pharmaceutical Manufacturing: From Batch to Continuous Production. J. Pharm. Innov. 2015, 10, 191–199. [Google Scholar] [CrossRef]
- Gorringe, L.J.; Kee, G.S.; Saleh, M.F.; Fa, N.H.; Elkes, R.G. Use of the channel fill level in defining a design space for twin screw wet granulation. Int. J. Pharm. 2017, 519, 165–177. [Google Scholar] [CrossRef]
- Vercruysse, J.; Peeters, E.; Fonteyne, M.; Cappuyns, P.; Delaet, U.; Van Assche, I.; De Beer, T.; Remon, J.P.; Vervaet, C. Use of a continuous twin screw granulation and drying system during formulation development and process optimization. Eur. J. Pharm. Biopharm. 2015, 89, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Portier, C.; Vervaet, C. Continuous Twin Screw Granulation: A Review of Recent Progress and Opportunities in Formulation and Equipment Design. Pharmaceutics 2021, 13, 668. [Google Scholar] [CrossRef]
- Morrissey, J.P.; Hanley, K.J.; Ooi, J.Y. Conceptualisation of an Efficient Particle-Based Simulation of a Twin-Screw Granulator. Pharmaceutics 2021, 13, 2136. [Google Scholar] [CrossRef]
- Liu, H.; Ricart, B.; Stanton, C.; Smith-Goettler, B.; Verdi, L.; O’Connor, T.; Lee, S.; Yoon, S. Design space determination and process optimization in at-scale continuous twin screw wet granulation. Comput. Chem. Eng. 2019, 125, 271–286. [Google Scholar] [CrossRef]
- Fülp, G.; Domokos, A.; Galata, D.; Szabó, E.; Nagy, Z.K. Integrated Twin-Screw Wet Granulation, Continuous Vibrational Fluid Drying and Milling: A fully continuous powder to granule line. J. Int. J. Pharm. 2020, 594, 120126. [Google Scholar] [CrossRef]
- Fonteyne, M.; Vercruysse, J.; Díaz, D.C.; Gildemyn, D.; Vervaet, C.; Remon, J.P.; Beer, T.D. Real-time assessment of critical quality attributes of a continuous granulation process. Pharm. Dev. Technol. 2013, 18, 85–97. [Google Scholar] [CrossRef]
- Seem, T.C.; Rowson, N.A.; Ingram, A.; Huang, Z.; Yu, S.; Matas, M.D.; Gabbott, I.; Reynolds, G.K. Twin Screw Granulation—A Literature Review. Powder Technol. 2015, 276, 89–102. [Google Scholar] [CrossRef]
- Kumar, A.; Alakarjula, M.; Vanhoorne, V.; Toiviainen, M.; De Leersnyder, F.; Vercruysse, J.; Juuti, M.; Ketolainen, J.; Vervaet, C.; Remon, J.P.; et al. Linking granulation performance with residence time and granulation liquid distributions in twin-screw granulation: An experimental investigation. Eur. J. Pharm. Sci. 2016, 90, 25–37. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Kotamarthy, L.; Panikar, S.; Sen, M.; Pradhan, S.; Marc, M.; Litster, J.D.; Muzzio, F.J.; Ramachandran, R. Statistical analysis and comparison of a continuous high shear granulator with a twin screw granulator: Effect of process parameters on critical granule attributes and granulation mechanisms. Int. J. Pharm. 2016, 513, 357–375. [Google Scholar] [CrossRef]
- Ozdemir, A. An I -optimal experimental design-embedded nonlinear lexicographic goal programming model for optimization of controllable design factors. Eng. Optim. 2020, 53, 392–407. [Google Scholar] [CrossRef]
- Jones, B.; Goos, P. I-Optimal Versus D-Optimal Split-Plot Response Surface Designs. J. Qual. Technol. 2012, 44, 85–101. [Google Scholar] [CrossRef]
- Willecke, N.; Szepes, A.; Wunderlich, M.; Remon, J.P.; Vervaet, C.; De Beer, T. A novel approach to support formulation design on twin screw wet granulation technology: Understanding the impact of overarching excipient properties on drug product quality attributes. Int. J. Pharm. 2018, 545, 128–143. [Google Scholar] [CrossRef]
- Stauffer, F.; Vanhoorne, V.; Pilcer, G.; Chavez, P.-F.; Vervaet, C.; De Beer, T. Managing API raw material variability during continuous twin-screw wet granulation. Int. J. Pharm. 2019, 561, 265–273. [Google Scholar] [CrossRef]
- Meng, W.; Rao, K.S.; Snee, R.D.; Ramachandran, R.; Muzzio, F.J. A comprehensive analysis and optimization of continuous twin-screw granulation processes via sequential experimentation strategy. Int. J. Pharm. 2019, 556, 349–362. [Google Scholar] [CrossRef]
- Zhao, J.; Li, W.; Qu, H.; Tian, G.; Wei, Y. Application of definitive screening design to quantify the effects of process parameters on key granule characteristics and optimize operating parameters in pulsed-spray fluid-bed granulation. Particuology 2019, 43, 56–65. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Cartwright, J.J.; Hounslow, M.J.; Salman, A.D. Twin screw granulation: Steps in granule growth. Int. J. Pharm. 2012, 438, 20–32. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Fyles, R.S.; Cartwright, J.J.; Doughty, D.G.; Hounslow, M.J.; Salman, A.D. Twin screw wet granulation: Granule properties. Chem. Eng. J. 2010, 164, 322–329. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Washino, K.; Cartwright, J.J.; Hounslow, M.J.; Salman, A.D. Twin screw granulation using conveying screws: Effects of viscosity of granulation liquids and flow of powders. Powder Technol. 2013, 238, 77–90. [Google Scholar] [CrossRef]
- Djuric, D.; Kleinebudde, P. Technology, Continuous granulation with a twin-screw extruder: Impact of material throughput. Pharm. Dev. 2010, 15, 518–525. [Google Scholar] [CrossRef]
- El Hagrasy, A.; Litster, J. Granulation rate processes in the kneading elements of a twin screw granulator. AIChE J. 2013, 59, 4100–4115. [Google Scholar] [CrossRef]
- Yu, S.; Reynolds, G.K.; Huang, Z.; de Matas, M.; Salman, A.D. Granulation of increasingly hydrophobic formulations using a twin screw granulator. Int. J. Pharm. 2014, 475, 82–96. [Google Scholar] [CrossRef] [PubMed]
- El Hagrasy, A.; Hennenkamp, J.; Burke, M.; Cartwright, J.; Litster, J. Twin screw wet granulation: Influence of formulation parameters on granule properties and growth behavior. Powder Technol. 2013, 238, 108–115. [Google Scholar] [CrossRef]
- Guideline, I. Pharmaceutical development Q8. Curr. Step 2005, 4, 11. [Google Scholar]
- Shekunov, B.Y.; Chattopadhyay, P.; Tong, H.; Chow, A. Particle Size Analysis in Pharmaceutics: Principles, Methods and Applications. J. Pharm. Res. 2007, 24, 203–227. [Google Scholar]


| Independent Variables | Levels | |||
|---|---|---|---|---|
| Minimum (−1) | Intermediate (0) | Maximum (+1) | ||
| Continuous | X1: screw speed (r/min) | 200 | 250 | 300 |
| X2: L/S ratio | 0.35 | 0.4 | 0.45 | |
| X3: powder feed rate (%) | 20 | 25 | 30 | |
| Discrete numeric | X4: number of the 60° mixing elements (pcs) | 4 | 7 | 10 |
| X5: number of the 30° mixing elements (pcs) | 3 | 6 | 9 | |
| Run Order | Pattern | Independent Variables | ||||
|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | ||
| 1 | 0--++ | 250 | 0.35 | 20 | 10 | 9 |
| 2 | 0---- | 250 | 0.35 | 20 | 4 | 3 |
| 3 | +-0-+ | 300 | 0.35 | 25 | 4 | 9 |
| 4 | 0+-+0 | 250 | 0.45 | 20 | 10 | 6 |
| 5 | -++00 | 200 | 0.45 | 30 | 7 | 6 |
| 6 | 0-00- | 250 | 0.35 | 25 | 7 | 3 |
| 7 | +++-0 | 300 | 0.45 | 30 | 4 | 6 |
| 8 | --0+- | 200 | 0.35 | 25 | 10 | 3 |
| 9 | -0-0- | 200 | 0.4 | 20 | 7 | 3 |
| 10 | -00++ | 200 | 0.4 | 25 | 10 | 9 |
| 11 | +0--+ | 300 | 0.4 | 20 | 4 | 9 |
| 12 | +-+0- | 300 | 0.35 | 30 | 7 | 3 |
| 13 | 00+-+ | 250 | 0.4 | 30 | 4 | 9 |
| 14 | --+0+ | 200 | 0.35 | 30 | 7 | 9 |
| 15 | -+--+ | 200 | 0.45 | 20 | 4 | 9 |
| 16 | 00000 | 250 | 0.4 | 25 | 7 | 6 |
| 17 | +-++0 | 300 | 0.35 | 30 | 10 | 6 |
| 18 | 00000 | 250 | 0.4 | 25 | 7 | 6 |
| 19 | +0-+- | 300 | 0.4 | 20 | 10 | 3 |
| 20 | 00000 | 250 | 0.4 | 25 | 7 | 6 |
| 21 | ++0++ | 300 | 0.45 | 25 | 10 | 9 |
| 22 | 0+++- | 250 | 0.45 | 30 | 10 | 3 |
| 23 | -0+-- | 200 | 0.4 | 30 | 4 | 3 |
| 24 | 0--00 | 250 | 0.35 | 20 | 7 | 6 |
| 25 | --0-0 | 200 | 0.35 | 25 | 4 | 6 |
| 26 | +---0 | 300 | 0.35 | 20 | 4 | 6 |
| 27 | 0+0-- | 250 | 0.45 | 25 | 4 | 3 |
| NO. | Y1: Moisture Content | Y2: D50 | Y3: Span | Y4: Yield |
|---|---|---|---|---|
| % | μm | % | ||
| 1 | 30.49 | 498.5 | 2.16 | 81.19 |
| 2 | 31.74 | 463.1 | 1.24 | 92.12 |
| 3 | 28.14 | 450.9 | 1.58 | 88.18 |
| 4 | 35.86 | 609.1 | 1.14 | 92.20 |
| 5 | 33.57 | 441.9 | 1.60 | 88.64 |
| 6 | 29.50 | 498.6 | 1.37 | 91.31 |
| 7 | 32.53 | 592.0 | 1.24 | 91.58 |
| 8 | 29.65 | 438.3 | 1.74 | 84.82 |
| 9 | 32.20 | 481.8 | 1.48 | 90.12 |
| 10 | 30.78 | 464.4 | 1.88 | 85.00 |
| 11 | 31.22 | 476.8 | 1.42 | 90.87 |
| 12 | 27.90 | 446.9 | 1.71 | 86.61 |
| 13 | 29.63 | 485.6 | 1.47 | 89.45 |
| 14 | 28.39 | 389.6 | 2.25 | 78.37 |
| 15 | 33.47 | 555.4 | 1.38 | 89.27 |
| 16 | 32.19 | 508.4 | 1.30 | 92.73 |
| 17 | 29.12 | 454.9 | 1.87 | 83.81 |
| 18 | 31.99 | 521.9 | 1.22 | 90.81 |
| 19 | 32.02 | 515.4 | 1.11 | 95.05 |
| 20 | 32.28 | 528.5 | 1.34 | 91.86 |
| 21 | 33.57 | 586.5 | 1.32 | 90.08 |
| 22 | 32.80 | 517.2 | 1.36 | 91.13 |
| 23 | 30.67 | 461.8 | 1.54 | 88.40 |
| 24 | 30.52 | 438.9 | 1.73 | 86.66 |
| 25 | 29.50 | 438.0 | 1.68 | 85.38 |
| 26 | 29.01 | 440.0 | 1.53 | 89.37 |
| 27 | 32.80 | 536.2 | 1.24 | 93.65 |
| Response Variable | Regression Equation | R 2 | Adj R2 * | Pre R2 * | p (Lack-of-Fit Test) | PRESS * | |
|---|---|---|---|---|---|---|---|
| Y1 | =32.15 − 0.25X1 + 2.07X2 − 0.86X3 + 0.33X4 − 0.23X5 − 0.46X12 − 0.67X52 | (3) | 0.9402 | 0.9182 | 0.8740 | 0.0615 | 12.47 |
| Y2 | =512.16 + 22.95X1 + 47.68X2 − 18.24X3 + 14.75X1X2 + 21.91X1X3 − 9.96X2X3 − 13.30X3X4 − 22.42X12 | (4) | 0.9072 | 0.8659 | 0.7844 | 0.2183 | 16088.62 |
| Y3 | =1.31 − 0.12X1 − 0.23X2 + 0.068X3 + 0.088X4 + 0.14X5 − 0.062X2X4 − 0.11X2X5 − 0.054X3X5 + 0.069X4X5 + 0.12X12 + 0.093X22 + 0.11X32 − 0.058X42 + 0.051X52 | (5) | 0.9706 | 0.9364 | 0.7750 | 0.4604 | 0.4937 |
| Y4 | =91.90 + 1.85X1 + 2.99X2 − 1.09X3 − 1.17X4 − 2.06X5 − 0.62X1X2 − 0.38X1X3+ 0.51X2X4 + 0.92X2X5 + 0.77X3X5 − 0.66X4X5 − 1.54X12 − 1.54X22 − 1.55X32 | (6) | 0.9791 | 0.9548 | 0.8633 | 0.7291 | 52.71 |
| Model Terms | Y1: Moisture Content | Y2: D50 | Y3: Span | Y4: Yield | ||||
|---|---|---|---|---|---|---|---|---|
| Coef. | p-Values | Coef. | p-Values | Coef. | p-Values | Coef. | p-Values | |
| Intercept | 32.15 | 512.16 | 1.31 | 91.90 | ||||
| X1 | −0.25 | 0.0968 | 22.95 | 0.0003 | −0.12 | <0.0001 | 1.85 | < 0.0001 |
| X2 | 2.07 | <0.0001 | 47.68 | <0.0001 | −0.23 | <0.0001 | 2.99 | <0.0001 |
| X3 | −0.86 | <0.0001 | −18.24 | 0.0017 | 0.07 | 0.0043 | −1.09 | 0.0003 |
| X4 | 0.33 | 0.0215 | 0.09 | 0.0003 | −1.17 | <0.0001 | ||
| X5 | −0.23 | 0.1070 | 0.14 | <0.0001 | −2.06 | <0.0001 | ||
| X1X2 | 14.75 | 0.0364 | −0.62 | 0.0477 | ||||
| X1X3 | 21.91 | 0.0026 | −0.38 | 0.2213 | ||||
| X1X4 | ||||||||
| X1X5 | ||||||||
| X2X3 | −9.96 | 0.1270 | ||||||
| X2X4 | −0.06 | 0.0131 | 0.51 | 0.069 | ||||
| X2X5 | −0.11 | 0.0008 | 0.92 | 0.0066 | ||||
| X3X4 | −13.30 | 0.0463 | ||||||
| X3X5 | −0.05 | 0.0413 | 0.77 | 0.015 | ||||
| X4X5 | 0.07 | 0.0070 | −0.66 | 0.0171 | ||||
| X12 | −0.46 | 0.0569 | −22.42 | 0.0133 | 0.12 | 0.0033 | −1.54 | 0.001 |
| X22 | 0.09 | 0.0140 | −1.54 | 0.0012 | ||||
| X32 | 0.11 | 0.0044 | −1.55 | 0.001 | ||||
| X42 | −0.06 | 0.1333 | ||||||
| X52 | −0.67 | 0.0085 | 0.05 | 0.1302 | ||||
| Dependent Responses | Constraints | Optimum |
|---|---|---|
| X1: L/S ratio | 0.35 ≤ X1 ≤ 0.45 | minimum |
| Y2: Mean particle size D50 | 400 μm ≤ Y2 ≤ 600 μm | - |
| Y3: Span of granule | Y3 ≤ 1.5 | minimum |
| Y4: Yield | 90 ≤ Y4 ≤ 100 | maximize |
| CPP (X1; X2; X3; X4; X5) | CQA | Experimental Value (y) | ARD (%) | |
|---|---|---|---|---|
| (240; 0.45; 30; 4; 7) | Y1 | 33.1 | 30.5 | 7.7 |
| Y2 | 532.1 | 494.2 | 7.1 | |
| Y3 | 1.3 | 1.3 | 5.2 | |
| Y4 | 91.2 | 97.4 | 6.8 | |
| (200; 0.4; 25; 7; 7) | Y1 | 33.2 | 31.8 | 4.3 |
| Y2 | 466.8 | 499.1 | 6.9 | |
| Y3 | 1.6 | 1.5 | 4.9 | |
| Y4 | 87.8 | 94.8 | 7.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Tian, G.; Qu, H. Application of I-Optimal Design for Modeling and Optimizing the Operational Parameters of Ibuprofen Granules in Continuous Twin-Screw Wet Granulation. Biomedicines 2023, 11, 2030. https://doi.org/10.3390/biomedicines11072030
Zhao J, Tian G, Qu H. Application of I-Optimal Design for Modeling and Optimizing the Operational Parameters of Ibuprofen Granules in Continuous Twin-Screw Wet Granulation. Biomedicines. 2023; 11(7):2030. https://doi.org/10.3390/biomedicines11072030
Chicago/Turabian StyleZhao, Jie, Geng Tian, and Haibin Qu. 2023. "Application of I-Optimal Design for Modeling and Optimizing the Operational Parameters of Ibuprofen Granules in Continuous Twin-Screw Wet Granulation" Biomedicines 11, no. 7: 2030. https://doi.org/10.3390/biomedicines11072030
APA StyleZhao, J., Tian, G., & Qu, H. (2023). Application of I-Optimal Design for Modeling and Optimizing the Operational Parameters of Ibuprofen Granules in Continuous Twin-Screw Wet Granulation. Biomedicines, 11(7), 2030. https://doi.org/10.3390/biomedicines11072030