Evolutionary Mechanism Based Conserved Gene Expression Biclustering Module Analysis for Breast Cancer Genomics
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition of Breast Cancer Samples
2.2. Overview of Biclustering
2.3. Conserved Biclustering Algorithm
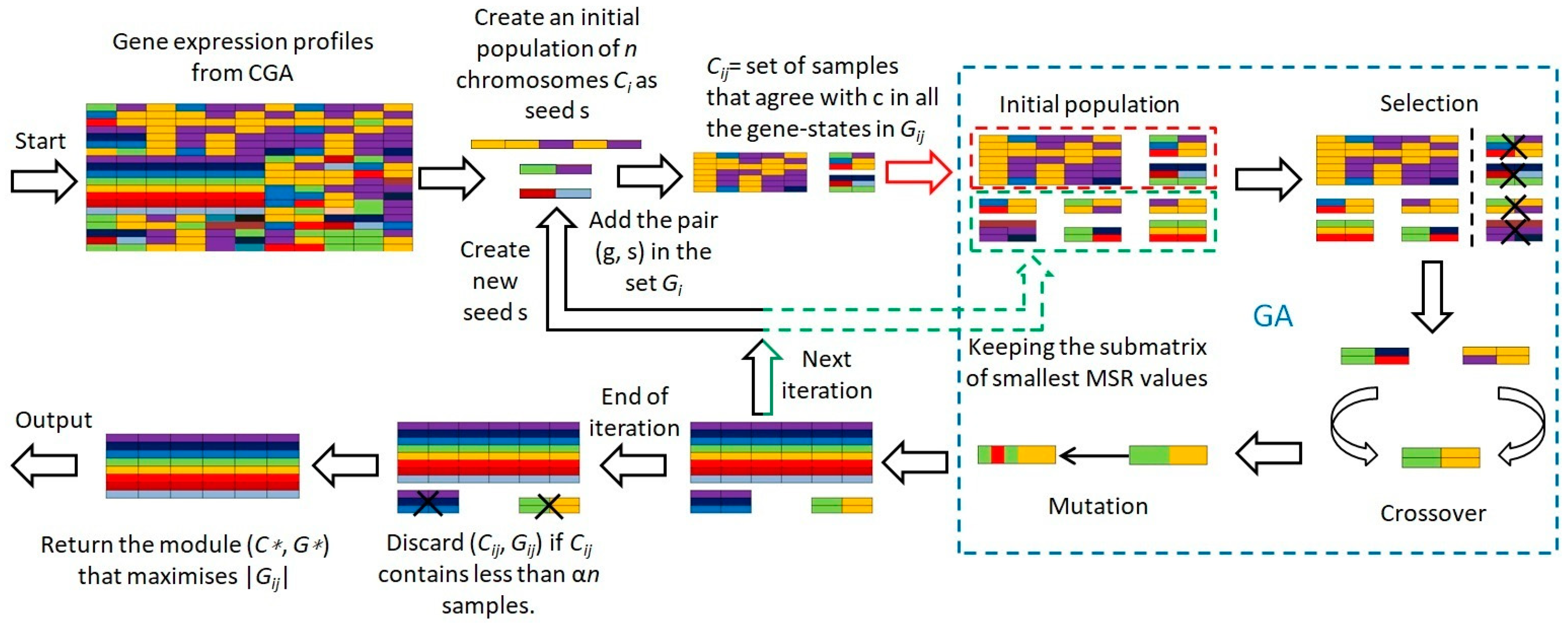
2.4. Evolutionary Mechanism-Based Conserved Gene Expression Biclustering Module
- 1.
- Initiate with a population of chromosomes () as potential seeds .
- 2.
- For each chromosome , identify a subset of samples of size .
- 3.
- Include gene-sample pairs () in set if gene exists in state across all samples in , and also incorporate samples matching across all gene states in .
- 4.
- Compute the MSR fitness value for each chromosome.
- 5.
- Apply GA’s selection, mutation, and crossover operations to optimize based on the MSR fitness value, thereby deriving the optimal solution.
- 6.
- Exclude any representing less than a fraction of the samples.
- 7.
- Select the module with the lowest MSR from all as the final choice.
2.5. Evaluation Metrics
3. Results
3.1. Experiment Setup
3.2. Ablation Study
3.2.1. Evolutionary Effect
3.2.2. Stability Analysis
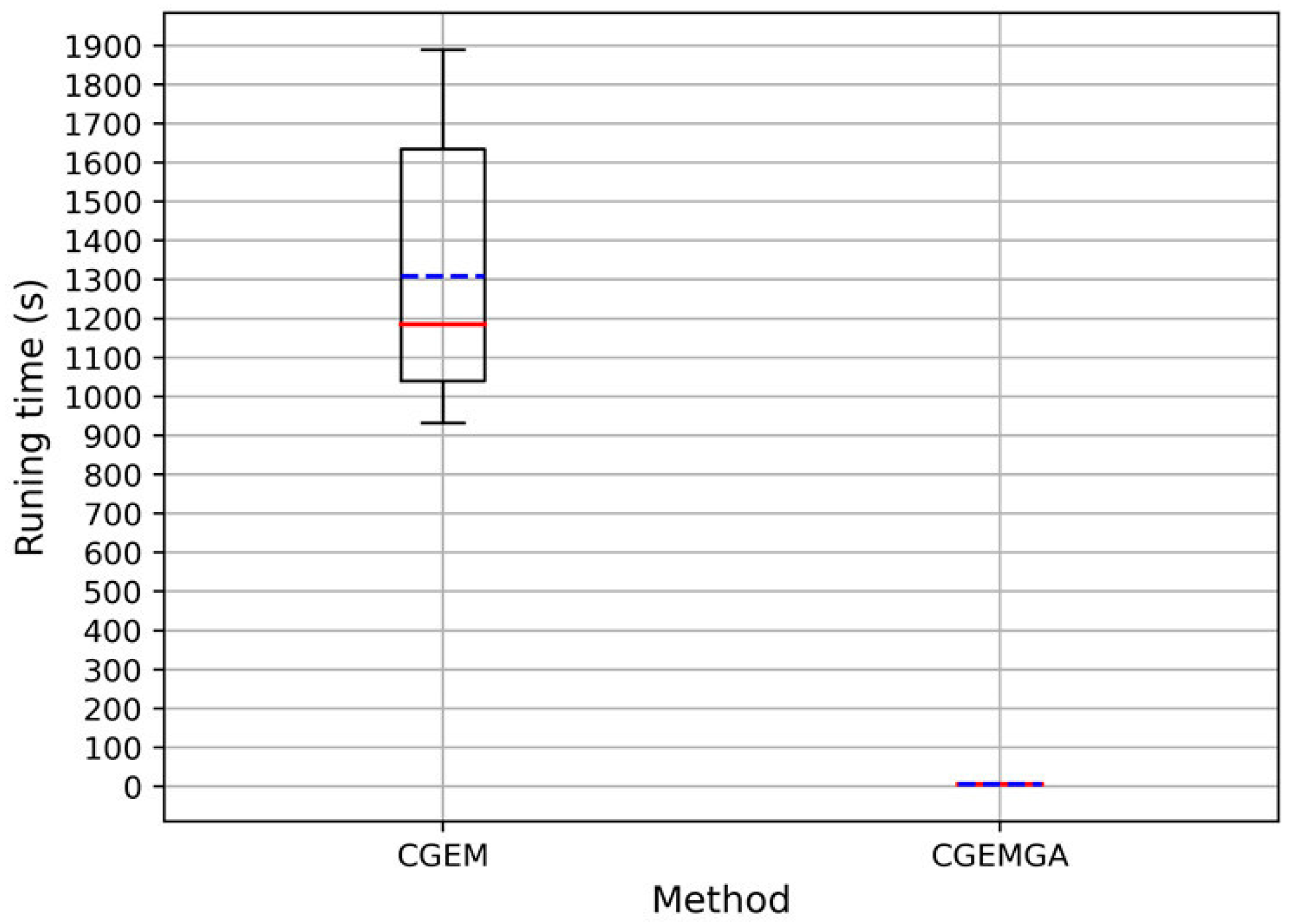
3.2.3. Computational Cost
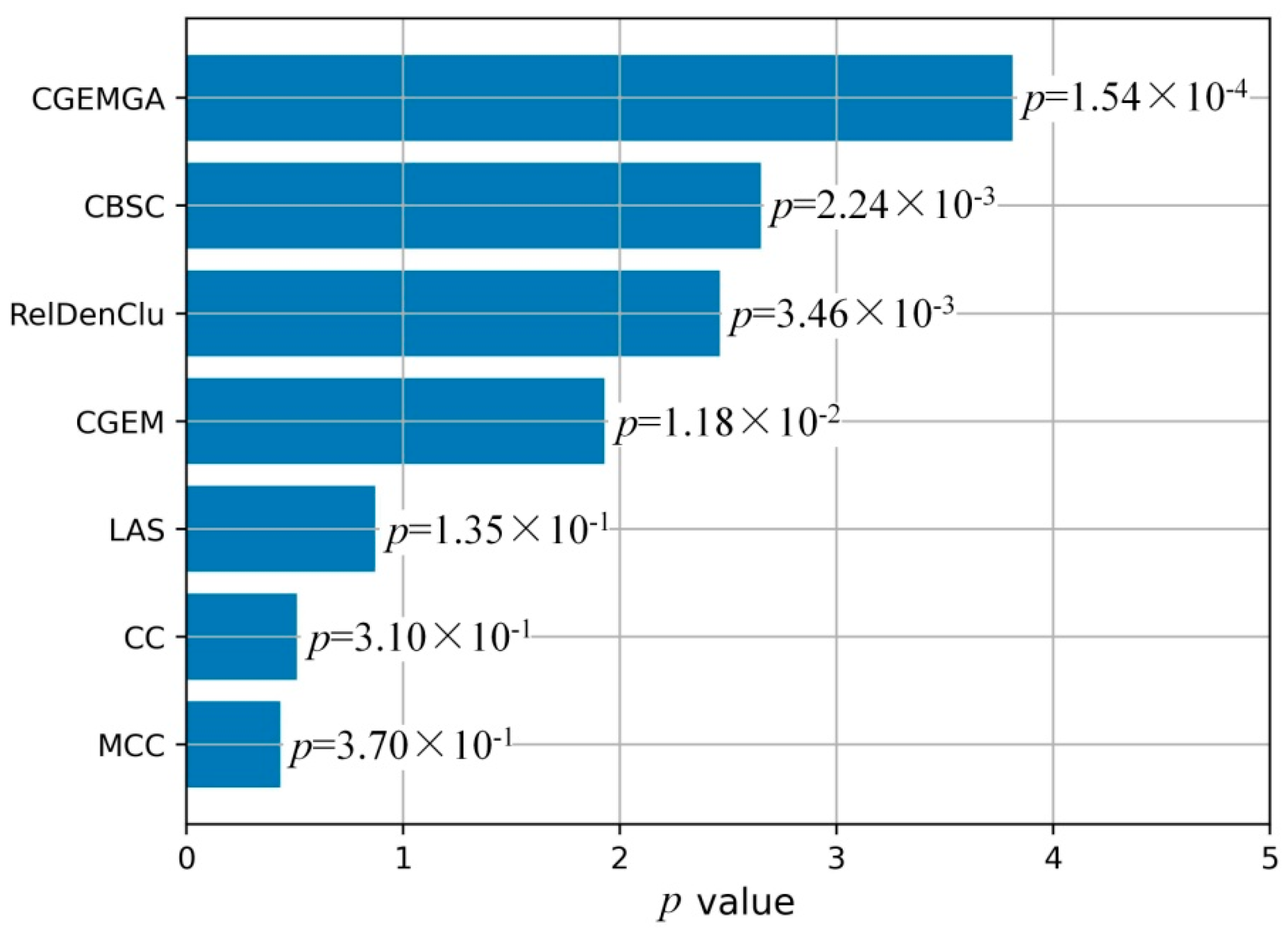
3.3. Comparison Study
3.4. Functional Enrichment Analysis
4. Discussion and Conclusion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Jing, Y.; Chen, B.; Zhang, H.; Liu, T.; Dong, S.; Zhang, L.; Yan, X.; Yang, S.; Chen, L.; et al. The application of targeted RNA sequencing for the analysis of fusion genes, gene mutations, IKZF1 intragenic deletion, and CRLF2 overexpression in acute lymphoblastic leukemia. Int. J. Lab. Hematol. 2024, 46, 670–677. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Luan, Y.; Cai, X.; Liu, Q.; Ren, P.; Xin, P.; Yu, Y.; Song, B.; Wang, Y.; Chang, H.; et al. Predicting mechanism of immune response in microsatellite instability colorectal cancer. Heliyon 2024, 10, e28120. [Google Scholar] [CrossRef] [PubMed]
- Ye, G.; Zhang, C.; Zhuang, Y.; Liu, H.; Song, E.; Li, K.; Liao, Y. An advanced nomogram model using deep learning radiomics and clinical data for predicting occult lymph node metastasis in lung adenocarcinoma. Transl. Oncol. 2024, 44, 101922. [Google Scholar] [CrossRef]
- Wang, L.; Hong, C.; Song, J.; Yao, J. CTEC: A cross-tabulation ensemble clustering approach for single-cell RNA sequencing data analysis. Bioinformatics 2024, 40, btae130. [Google Scholar] [CrossRef] [PubMed]
- Watts, J.; Allen, E.; Mitoubsi, A.; Khojandi, A.; Eales, J.; Jalali-Najafabadi, F.; Papamarkou, T. Adapting Random Forests to Predict Obesity-Associated Gene Expression. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022; pp. 4407–4410. [Google Scholar]
- Resmini, R.; Silva, L.; Araujo, A.S.; Medeiros, P.; Muchaluat-Saade, D.; Conci, A. Combining Genetic Algorithms and SVM for Breast Cancer Diagnosis Using Infrared Thermography. Sensors 2021, 21, 4802. [Google Scholar] [CrossRef]
- Seifert, S.; Gundlach, S.; Junge, O.; Szymczak, S. Integrating biological knowledge and gene expression data using pathway-guided random forests: A benchmarking study. Bioinformatics 2020, 36, 4301–4308. [Google Scholar] [CrossRef]
- Kim, W.-J.; Choi, B.R.; Noh, J.J.; Lee, Y.-Y.; Kim, T.-J.; Lee, J.-W.; Kim, B.-G.; Choi, C.H. Comparison of RNA-Seq and microarray in the prediction of protein expression and survival prediction. Front. Genet. 2024, 15, 1342021. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Y.; Capstick, A.; Palermo, F.; Haddadi, H.; Barnaghi, P. Analyzing entropy features in time-series data for pattern recognition in neurological conditions. Artif. Intell. Med. 2024, 150, 102821. [Google Scholar] [CrossRef]
- Ha, C.T.; Tageldein, M.M.; Harding, S.M. The entanglement of DNA damage and pattern recognition receptor signaling. DNA Repair 2024, 133, 103595. [Google Scholar] [CrossRef]
- Hauschild, A.-C.; Lemanczyk, M.; Matschinske, J.; Frisch, T.; Zolotareva, O.; Holzinger, A.; Baumbach, J.; Heider, D. Federated Random Forests can improve local performance of predictive models for various healthcare applications. Bioinformatics 2022, 38, 2278–2286. [Google Scholar] [CrossRef]
- Chu, H.-M.; Liu, J.-X.; Zhang, K.; Zheng, C.-H.; Wang, J.; Kong, X.-Z. A binary biclustering algorithm based on the adjacency difference matrix for gene expression data analysis. BMC Bioinform. 2022, 23, 381. [Google Scholar] [CrossRef]
- Cheng, Y.; Church, G.M. Biclustering of expression data. In Proceedings of the 8th International Conference on Intelligent Systems for Molecular Biology (ISMB 2000), San Diego, CA, USA, 19–23 August 2000; Volume 8, pp. 93–103. [Google Scholar]
- Hanczar, B.; Nadif, M. Ensemble methods for biclustering tasks. Pattern Recognit. 2012, 45, 3938–3949. [Google Scholar] [CrossRef]
- Andrey, A.S.; Weigman, V.J.; Perou, C.M.; Nobel, A.B. Finding large average submatrices in high dimensional data. Ann. Appl. Stat. 2009, 3, 985–1012. [Google Scholar]
- Jain, N.; Ghosh, S.; Murthy, C.A. RelDenClu: A Relative Density based Biclustering Method for identifying non-linear feature relations. arXiv 2021, arXiv:1811.04661. [Google Scholar]
- Jain, N.; Murthy, C.A. Connectedness-based subspace clustering. Knowl. Inf. Syst. 2019, 58, 9–34. [Google Scholar] [CrossRef]
- Xi, J.; Wang, M.; Li, A. DGPathinter: A novel model for identifying driver genes via knowledge-driven matrix factorization with prior knowledge from interactome and pathways. PeerJ Comput. Sci. 2017, 3, e133. [Google Scholar] [CrossRef]
- Xi, J.; Li, A.; Wang, M. HetRCNA: A Novel Method to Identify Recurrent Copy Number Alternations from Heterogeneous Tumor Samples Based on Matrix Decomposition Framework. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 422–434. [Google Scholar] [CrossRef]
- Murali, T.M.; Kasif, S. Extracting conserved gene expression motifs from gene expression data. In Proceedings of the Pacific Symposium on Biocomputing (PSB), Kauai, HI, USA, 3–7 January 2003; pp. 77–88. [Google Scholar]
- Williams, A.; Halappanavar, S. Application of bi-clustering of gene expression data and gene set enrichment analysis methods to identify potentially disease causing nanomaterials. Data Brief 2017, 15, 933–940. [Google Scholar] [CrossRef]
- Madeira, S.C.; Oliveira, A.L. Biclustering algorithms for biological data analysis: A survey. IEEE/ACM Trans. Comput. Biol. Bioinform. 2004, 1, 24–45. [Google Scholar] [CrossRef]
- Tang, C.Y.; Hung, C.L.; Zheng, H.; Lin, C.Y.; Jiang, H. Novel Computational Technologies for Next-Generation Sequencing Data Analysis and Their Applications. Int. J. Genom. 2015, 2015, 254685. [Google Scholar] [CrossRef]
- Xi, J.; Yuan, X.; Wang, M.; Li, A.; Li, X.; Huang, Q. Inferring subgroup-specific driver genes from heterogeneous cancer samples via subspace learning with subgroup indication. Bioinformatics 2020, 36, 1855–1863. [Google Scholar] [CrossRef] [PubMed]
- Craven, K.E.; Gökmen-Polar, Y.; Badve, S.S. CIBERSORT analysis of TCGA and METABRIC identifies subgroups with better outcomes in triple negative breast cancer. Sci. Rep. 2021, 11, 4691. [Google Scholar] [CrossRef]
- Thennavan, A.; Beca, F.; Xia, Y.; Garcia-Recio, S.; Allison, K.; Collins, L.C.; Tse, G.M.; Chen, Y.-Y.; Schnitt, S.J.; Hoadley, K.A.; et al. Molecular analysis of TCGA breast cancer histologic types. Cell Genom. 2021, 1, 100067. [Google Scholar] [CrossRef] [PubMed]
- Linehan, W.M.; Ricketts, C.J. The Cancer Genome Atlas of renal cell carcinoma: Findings and clinical implications. Nat. Rev. Urol. 2019, 16, 539–552. [Google Scholar] [CrossRef] [PubMed]
- Rau, A.; Flister, M.; Rui, H.; Auer, P.L. Exploring drivers of gene expression in the Cancer Genome Atlas. Bioinformatics 2019, 35, 62–68. [Google Scholar] [CrossRef]
- Malhotra, S.; Alsulami, A.F.; Heiyun, Y.; Ochoa, B.M.; Jubb, H.; Forbes, S.; Blundell, T.L. Understanding the impacts of missense mutations on structures and functions of human cancer-related genes: A preliminary computational analysis of the COSMIC Cancer Gene Census. PLoS ONE 2019, 14, e0219935. [Google Scholar] [CrossRef]
- Alsulami, A.F.; Torres, P.H.; Moghul, I.; Arif, S.M.; Chaplin, A.; Vedithi, S.; Blundell, T. COSMIC Cancer Gene Census 3D database: Understanding the impacts of mutations on cancer targets. Brief. Bioinform. 2021, 22, bbab220. [Google Scholar] [CrossRef]
- De Jong, K. Learning with genetic algorithms: An overview. Mach. Learn. 1988, 3, 121–138. [Google Scholar] [CrossRef]
- Liu, X.; Yu, T.; Zhao, X.; Long, C.; Han, R.; Su, Z.; Li, G. ARBic: An all-round biclustering algorithm for analyzing gene expression data. NAR Genom. Bioinform. 2023, 5, lqad009. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Eisen, M.B.; Alizadeh, A.; Levy, R.; Staudt, L.; Chan, W.C.; Botstein, D.; Brown, P. ‘Gene shaving’ as a method for identifying distinct sets of genes with similar expression patterns. Genome Biol. 2000, 1, research0003.1. [Google Scholar] [CrossRef]
- Li, J.; Wong, L. Identifying good diagnostic gene groups from gene expression profiles using the concept of emerging patterns. Bioinformatics 2002, 18, 725–734. [Google Scholar] [CrossRef]
- Castanho, E.N.; Aidos, H.; Madeira, S.C. Biclustering fMRI time series: A comparative study. BMC Bioinform. 2022, 23, 192. [Google Scholar] [CrossRef] [PubMed]
- Colin, P.J.; Eleveld, D.J.; Thomson, A.H. Genetic Algorithms as a Tool for Dosing Guideline Optimization: Application to Intermittent Infusion Dosing for Vancomycin in Adults. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 294–302. [Google Scholar] [CrossRef] [PubMed]
- Connelly, L.M. Fisher’s Exact Test. Medsurg. Nurs. 2016, 25, 58–61. [Google Scholar]
- Lopez-Gimenez, M.R.; Garcia Gomez, J.J. The Fisher’s test. Med. Clin. 1993, 101, 156–157. [Google Scholar]
- Blevins, L.; McDonald, C.J. Fisher’s Exact Test: An easy-to-use statistical test for comparing outcomes. MD Comput. 1985, 2, 15–19, 68. [Google Scholar]
- Wang, S.; Cui, H. Generalized F test for high dimensional linear regression coefficients. J. Multivar. Anal. 2013, 117, 134–149. [Google Scholar] [CrossRef]
- Sammons, S.; Elliott, A.; Barroso-Sousa, R.; Chumsri, S.; Tan, A.R.; Sledge, G.W., Jr.; Tolaney, S.M.; Torres, E.T.R. Concurrent predictors of an immune responsive tumor microenvironment within tumor mutational burden-high breast cancer. Front. Oncol. 2023, 13, 1235902. [Google Scholar] [CrossRef] [PubMed]
- Perez-Duran, J.; Luna, A.; Portilla, A.; Martínez, P.; Ceballos, G.; Ortíz-Flores, M.Á.; Solis-Paredes, J.M.; Nájera, N. (-)-Epicatechin Inhibits Metastatic-Associated Proliferation, Migration, and Invasion of Murine Breast Cancer Cells In Vitro. Molecules 2023, 28, 6229. [Google Scholar] [CrossRef]
- Xu, L.; Shen, J.M.; Qu, J.L.; Song, N.; Che, X.F.; Hou, K.Z.; Shi, J.; Zhao, L.; Shi, S.; Liu, Y.P.; et al. FEN1 is a prognostic biomarker for ER+ breast cancer and associated with tamoxifen resistance through the ERα/cyclin D1/Rb axis. Ann. Transl. Med. 2021, 9, 258. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, K.; Jun, H.; Kim, K.; Bae, J.M.; Song, M.G.; Yi, H.; Park, S.; Woo, G.U.; Lee, D.W.; et al. Mutations of TP53 and genes related to homologous recombination repair in breast cancer with germline BRCA1/2 mutations. Hum. Genom. 2023, 17, 2. [Google Scholar] [CrossRef]
- Grote, I.; Poppe, A.; Lehmann, U.; Christgen, M.; Kreipe, H.; Bartels, S. Frequency of genetic alterations differs in advanced breast cancer between metastatic sites. Genes Chromosomes Cancer 2023, 63, e23199. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S. A novel coherence measure for discovering scaling biclusters from gene expression data. J. Bioinform. Comput. Biol. 2009, 7, 853–868. [Google Scholar] [CrossRef]
- Teng, L.; Chan, L. Discovering Biclusters by Iteratively Sorting with Weighted Correlation Coefficient in Gene Expression Data. J. Signal Process. Syst. 2008, 50, 267–280. [Google Scholar] [CrossRef]
- Carlsson, G.E.; Gabrielsson, R.B. Topological Approaches to Deep Learning. arXiv 2018, arXiv:1811.01122. [Google Scholar]
- Zhang, T.; Tan, T.; Han, L.; Appelman, L.; Veltman, J.; Wessels, R.; Duvivier, K.M.; Loo, C.; Gao, Y.; Wang, X.; et al. Predicting breast cancer types on and beyond molecular level in a multi-modal fashion. npj Breast Cancer 2023, 9, 16. [Google Scholar] [CrossRef]
- Gamble, P.; Jaroensri, R.; Wang, H.; Tan, F.; Moran, M.; Brown, T.; Flament-Auvigne, I.; Rakha, E.A.; Toss, M.; Dabbs, D.J.; et al. Determining breast cancer biomarker status and associated morphological features using deep learning. Commun. Med. 2021, 1, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Molecular Classification of Breast Cancer: Relevance and Challenges. Arch. Pathol. Lab. Med. 2022, 147, 46–51. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, T.P.; Miskiewicz, J.; Szostak, N.; Szachniuk, M.; Grodecka-Gazdecka, S.; Jagodziński, P.P. In Vitro and in Silico Analysis of miR-125a with rs12976445 Polymorphism in Breast Cancer Patients. Appl. Sci. 2020, 10, 7275. [Google Scholar] [CrossRef]
- Cura, Y.; Ramírez, C.P.; Martín, A.S.; Martínez, F.M.; Hernández, M.C.; Tortosa, M.d.C.R.; Morales, A.J. Genetic polymorphisms on the effectiveness or safety of breast cancer treatment: Clinical relevance and future perspectives. Mutat. Res./Rev. Mutat. Res. 2021, 788, 108391. [Google Scholar] [CrossRef]


| Characteristics | Algorithms | |||||
|---|---|---|---|---|---|---|
| CC | MCC | LAS | CGEM | RelDenClu | CBSC | |
| Core Idea | Iterative spectral method for finding co-expressed gene and condition submatrices | Ensemble learning method combining multiple base biclustering algorithms for improved stability | Statistical method for finding large average submatrices in high-dimensional data, focusing on numerical features | Graph-based method for extracting conserved gene expression motifs | Find sets of observations with high local density | Find subspaces with high connectivity |
| Algorithm Type | Spectral clustering | Ensemble learning | Statistical method | Graph-based method | Density clustering | Connectivity clustering |
| Time Complexity | High | Moderate to high (depending on the number and type of base algorithms) | High | Moderate | High | High |
| Space Complexity | Moderate | High (requires storage of results from multiple base algorithms) | High (requires storage of extensive submatrix information) | Moderate | High | High |
| Applicable Data Type | Expression data | General (applicable to various types of data) | General (applicable to various types of data) | Expression data | Microarray data | High-dimensional data |
| Robustness | Moderate (sensitive to noise) | High (ensemble methods reduce the impact of noise) | High (statistical methods have some resistance to noise) | Moderate (depends on the stability of the graph structure) | High | High |
| Scalability | Moderate (suitable for medium to small-scale data) | Good (can be scaled to large-scale data) | Good (suitable for large-scale data) | Moderate (suitable for medium to small-scale data) | Moderate (suitable for medium to small-scale data) | Medium |
| Pattern Type Discovered | Co-expression patterns | Diverse patterns (depending on the base algorithms) | Numerically significant submatrices | Conserved expression motifs | Nonlinear relationships between features | Subspace structures based on connectivity |
| Real-world Applications | Gene expression analysis in bioinformatics | Widely applied in bioinformatics and machine learning | Bioinformatics, image processing, and other fields | Gene network analysis in bioinformatics | Gene functional grouping in microarray data | Gene functional grouping in bioinformatics |
| Algorithm 1 FINDMODULE(): algorithm for computing the largest module. |
| 1. for i = 1 to ns do 2. GA begin 3. Create an initial population of n chromosomes Ci (i = 1, 2, …, n) as seeds 4. Set iteration counter t = 0 5. Choose a subset Di of the samples with size sd 6. For every gene g in Di, include the pair (g, s) in the set Gij if g is in the state s in c and all Di samples 7. Cij = set of samples that agree with c in all the gene-states in Gij 8. Calculate the MSR fitness value for each chromosome 9. while (t < MAX) 10. Select a pair of chromosomes form initial population based on MSR fitness 11. Apply crossover operation on selected pair with crossover probability 12. Apply mutation on the offspring with mutation probability 13. Replace old population with newly generated population 14. Increment the current iteration t by 1. 15. end while 16. Discard (Cij, Gij) if Cij contains less than αn samples. 17. returen the best solution, Ci with min MSR 18. GA end 19. return the module (C*, G*) that maximises |Gij|, 1 ≤ i ≤ ns |
| No. | Method | |||
|---|---|---|---|---|
| CGEM | CGEMGA | |||
| p Value | MSR Value | p Value | MSR Value | |
| 1 | 9.62 × 10−6 | 4.71 × 10−2 | 1.13 × 10−4 | 9.37 × 10−2 |
| 2 | 2.47 × 10−5 | 1.27 × 10−1 | 1.19 × 10−4 | 9.37 × 10−2 |
| 3 | 1.73 × 10−4 | 1.29 × 100 | 1.25 × 10−4 | 9.37 × 10−2 |
| 4 | 1.84 × 10−4 | 1.44 × 100 | 1.28 × 10−4 | 9.37 × 10−2 |
| 5 | 6.54 × 10−4 | 5.44 × 100 | 1.55 × 10−4 | 9.37 × 10−2 |
| 6 | 1.20 × 10−3 | 6.89 × 100 | 1.63 × 10−4 | 9.37 × 10−2 |
| 7 | 1.90 × 10−3 | 1.15 × 10 | 1.75 × 10−4 | 9.37 × 10−2 |
| 8 | 6.00 × 10−3 | 2.95 × 10 | 1.81 × 10−4 | 9.37 × 10−2 |
| 9 | 1.08 × 10−2 | 5.78 × 10 | 1.91 × 10−4 | 9.37 × 10−2 |
| 10 | 9.71 × 10−2 | 7.12 × 102 | 1.91 × 10−4 | 9.37 × 10−2 |
| Mean ± SD | 1.18 × 10−2 ± 3.01 × 10−2 | 8.26 × 10 ± 2.21 × 102 | 1.54 × 10−4 ± 3.06 × 10−5 | 9.37 × 10−2 ± 0 |
| Method | Times (n = 10) | Mean ± SD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| CGEM | 1.89 × 103 | 1.79 × 103 | 1.77 × 103 | 1.23 × 103 | 1.21 × 103 | 1.16 × 103 | 1.13 × 103 | 1.01 × 103 | 9.59 × 102 | 9.32 × 102 | 1.31 × 103 ± 3.66 × 102 |
| CGEMGA | 4.94 × 100 | 5.02 × 100 | 5.11 × 100 | 5.13 × 100 | 5.25 × 100 | 5.29 × 100 | 5.30 × 100 | 5.33 × 100 | 5.39 × 100 | 5.45 × 100 | 5.22 × 100 ± 1.65 × 10−1 |
| Method | Fisher’ Test p Values (n = 10) | Mean ± SD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| MCC | 1.50 × 10−3 | 7.30 × 10−3 | 9.20 × 10−3 | 1.03 × 10−1 | 1.75 × 10−1 | 4.31 × 10−1 | 5.09 × 10−1 | 6.67 × 10−1 | 8.98 × 10−1 | 9.03 × 10−1 | 3.70 × 10−1 ± 3.62 × 10−1 |
| CC | 1.50 × 10−3 | 7.30 × 10−3 | 4.99 × 10−2 | 1.74 × 10−1 | 1.78 × 10−1 | 1.95 × 10−1 | 4.12 × 10−1 | 5.59 × 10−1 | 6.73 × 10−1 | 8.54 × 10−1 | 3.10 × 10−1 ± 3.00 × 10−1 |
| LAS | 6.68 × 10−5 | 6.44 × 10−4 | 6.44 × 10−4 | 1.70 × 10−3 | 6.70 × 10−3 | 3.04 × 10−2 | 6.65 × 10−2 | 7.56 × 10−2 | 5.44 × 10−1 | 6.26 × 10−1 | 1.35 × 10−1 ± 2.40 × 10−1 |
| CGEM | 9.62 × 10−6 | 2.47 × 10−5 | 1.73 × 10−4 | 1.84 × 10−4 | 6.54 × 10−4 | 1.20 × 10−3 | 1.90 × 10−3 | 6.00 × 10−3 | 1.08 × 10−2 | 9.71 × 10−2 | 1.18 × 10−2 ± 3.01 × 10−2 |
| RelDenClu | 1.40 × 10−68 | 1.43 × 10−67 | 1.34 × 10−34 | 1.35 × 10−34 | 6.33 × 10−34 | 3.05 × 10−13 | 7.49 × 10−13 | 1.44 × 10−8 | 1.45 × 10−2 | 2.01 × 10−2 | 3.46 × 10−3 ± 6.98 × 10−3 |
| CBSC | 1.54 × 10−13 | 1.57 × 10−13 | 1.48 × 10−12 | 3.35 × 10−11 | 1.48 × 10−10 | 6.97 × 10−10 | 8.23 × 10−6 | 1.58 × 10−4 | 1.60 × 10−4 | 2.21 × 10−2 | 2.24 × 10−3 ± 7.41 × 10−3 |
| CGEMGA | 1.13 × 10−4 | 1.19 × 10−4 | 1.25 × 10−4 | 1.28 × 10−4 | 1.55 × 10−4 | 1.63 × 10−4 | 1.75 × 10−4 | 1.81 × 10−4 | 1.91 × 10−4 | 1.91 × 10−4 | 1.54 × 10−4 ± 3.06 × 10−5 |
| No. | Gene Symbol | Name | Cytogenetic Band | No. | Gene Symbol | Name | Cytogenetic Band |
|---|---|---|---|---|---|---|---|
| 1 | MTOR | mechanistic target of rapamycin | 1p36.22 | 24 | SDHAF2 | succinate dehydrogenase complex assembly factor 2 | 11q12.2 |
| 2 | SF3B1 | splicing factor 3b, subunit 1, 155 kDa | 2q33.1 | 25 | KDM5A | lysine (K)-specific demethylase 5A, JARID1A | 12p13.33 |
| 3 | POLQ | DNA polymerase theta | 3q13.33 | 26 | PRPF40B | pre-mRNA processing factor 40 homolog B | 12q13.12 |
| 4 | MECOM | MDS1 and EVI1 complex locus | 3q26.2 | 27 | NCOR2 | nuclear receptor corepressor 2 | 12q24.31 |
| 5 | TET2 | tet oncogene family member 2 | 4q24 | 28 | RAD51B | RAD51 paralog B | 14q24.1 |
| 6 | FAT1 | FAT atypical cadherin 1 | 4q35.2 | 29 | TCL1A | T-cell leukemia/lymphoma 1A | 14q32.13 |
| 7 | TLX3 | T-cell leukemia, homeobox 3 (HOX11L2) | 5q35.1 | 30 | DROSHA | drosha ribonuclease III | 15p13.3 |
| 8 | SRSF3 | serine/arginine-rich splicing factor 3 | 6p21.31 | 31 | CHD2 | chromodomain helicase DNA binding protein 2 | 15q26.1 |
| 9 | DEK | DEK oncogene (DNA binding) | 6p22.3 | 32 | PRKCB | protein kinase C beta | 16p12.2 |
| 10 | SGK1 | serum/glucocorticoid regulated kinase 1 | 6q23.2 | 33 | RMI2 | RecQ mediated genome instability 2 | 16p13.13 |
| 11 | EZR | ezrin | 6q25.3 | 34 | CDH1 | cadherin 1, type 1, E-cadherin (epithelial) (ECAD) | 16q22.1 |
| 12 | MACC1 | MET transcriptional regulator MACC1 | 7p21.1 | 35 | TP53 | tumor protein p53 | 17p13.1 |
| 13 | SBDS | Shwachman-Bodian-Diamond syndrome protein | 7q11.21 | 36 | KAT7 | lysine acetyltransferase 7 | 17q21.33 |
| 14 | CUX1 | cut-like homeobox 1 | 7q22.1 | 37 | SRSF2 | serine/arginine-rich splicing factor 2 | 17q25.2 |
| 15 | KAT6A | K(lysine) acetyltransferase 6A | 8p11.21 | 38 | KDSR | 3-ketodihydrosphingosine reductase | 18q21.33 |
| 16 | GNAQ | guanine nucleotide binding protein (Gprotein), q polypeptide | 9q21.2 | 39 | CEP89 | centrosomal protein 89 kDa | 19q13.11 |
| 17 | CNTRL | centriolin | 9q33.2 | 40 | ARHGAP35 | Rho GTPase activating protein 35 | 19q13.32 |
| 18 | LARP4B | La ribonucleoprotein domain family member 4B | 10p15.3 | 41 | TOP1 | topoisomerase (DNA) I | 20q12 |
| 19 | A1CF | APOBEC1 complementation factor | 10q11.23 | 42 | KDM5C | lysine (K)-specific demethylase 5C (JARID1C) | Xp11.22 |
| 20 | KAT6B | K(lysine) acetyltransferase 6B | 10q22.2 | 43 | KDM6A | lysine (K)-specific demethylase 6A, UTX | Xp11.3 |
| 21 | NUP98 | nucleoporin 98kDa | 11p15.4 | 44 | TMSB4X | Thymosin Beta 4 X-Linked | Xp22.2 |
| 22 | CLP1 | cleavage and polyadenylation factor I subunit 1 | 11q12.1 | 45 | CRLF2 | cytokine receptor-like factor 2 | Xp22.33 |
| 23 | FEN1 | flap structure-specific endonuclease 1 | 11q12.2 |
| Term | Percentage | p-Value | FDR |
|---|---|---|---|
| hsa05205:Proteoglycans in cancer | 11.1 | 3.8 × 10−3 | 5.98 × 10−1 |
| hsa05214:Glioma | 6.7 | 2.4 × 10−2 | 7.75 × 10−1 |
| hsa04971:Gastric acid secretion | 6.7 | 2.4 × 10−2 | 7.75 × 10−1 |
| hsa05200:Pathways in cancer | 13.3 | 2.4 × 10−2 | 7.75 × 10−1 |
| h_pkcPathway:Activation of PKC through G protein coupled receptor | 4.4 | 3.0 × 10−2 | 7.53 × 10−1 |
| hsa03040:Spliceosome | 8.9 | 3.1 × 10−2 | 7.75 × 10−1 |
| hsa05163:Human cytomegalovirus infection | 8.9 | 3.4 × 10−2 | 7.75 × 10−1 |
| hsa04670:Leukocyte transendothelial migration | 6.7 | 5.1 × 10−2 | 7.75 × 10−1 |
| hsa04935:Growth hormone synthesis, secretion and action | 6.7 | 5.6 × 10−2 | 7.75 × 10−1 |
| hsa04071:Sphingolipid signaling pathway | 6.7 | 5.6 × 10−2 | 7.75 × 10−1 |
| hsa04919:Thyroid hormone signaling pathway | 6.7 | 5.6 × 10−2 | 7.75 × 10−1 |
| h_myosinPathway:PKC-catalyzed phosphorylation of inhibitory phosphoprotein of myosin phosphatase | 4.4 | 5.9 × 10−2 | 7.53 × 10−1 |
| h_ccr5Pathway:Pertussis toxin-insensitive CCR5 Signaling in Macrophage | 4.4 | 7.1 × 10−2 | 7.53 × 10−1 |
| hsa04371:Apelin signaling pathway | 6.7 | 7.2 × 10−2 | 7.75 × 10−1 |
| hsa05206:MicroRNAs in cancer | 8.9 | 7.4 × 10−2 | 7.75 × 10−1 |
| hsa05017:Spinocerebellar ataxia | 6.7 | 7.6 × 10−2 | 7.75 × 10−1 |
| h_calcineurinPathway:Effects of calcineurin in Keratinocyte Differentiation | 4.4 | 7.9 × 10−2 | 7.53 × 10−1 |
| hsa05226:Gastric cancer | 6.7 | 8.1 × 10−2 | 7.75 × 10−1 |
| hsa04150:mTOR signaling pathway | 6.7 | 8.8 × 10−2 | 7.75 × 10−1 |
| h_par1pathway:Thrombin signaling and protease-activated receptors | 4.4 | 9.1 × 10−2 | 7.53 × 10−1 |
| h_chemicalPathway:Apoptotic Signaling in Response to DNA Damage | 4.4 | 9.1 × 10−2 | 7.53 × 10−1 |
| h_ccr3Pathway:CCR3 signaling in Eosinophils | 4.4 | 9.5 × 10−2 | 7.53 × 10−1 |
| h_eif4Pathway:Regulation of eIF4e and p70 S6 Kinase | 4.4 | 9.9 × 10−2 | 7.53 × 10−1 |
| h_cxcr4Pathway:CXCR4 Signaling Pathway | 4.4 | 9.9 × 10−2 | 7.53 × 10−1 |
| hsa05225:Hepatocellular carcinoma | 6.7 | 1.0 × 10−1 | 7.75 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W.; Li, Y.; Han, Z.; Chen, Y.; Xie, J.; Chen, J.; Bi, Z.; Xi, J. Evolutionary Mechanism Based Conserved Gene Expression Biclustering Module Analysis for Breast Cancer Genomics. Biomedicines 2024, 12, 2086. https://doi.org/10.3390/biomedicines12092086
Yuan W, Li Y, Han Z, Chen Y, Xie J, Chen J, Bi Z, Xi J. Evolutionary Mechanism Based Conserved Gene Expression Biclustering Module Analysis for Breast Cancer Genomics. Biomedicines. 2024; 12(9):2086. https://doi.org/10.3390/biomedicines12092086
Chicago/Turabian StyleYuan, Wei, Yaming Li, Zhengpan Han, Yu Chen, Jinnan Xie, Jianguo Chen, Zhisheng Bi, and Jianing Xi. 2024. "Evolutionary Mechanism Based Conserved Gene Expression Biclustering Module Analysis for Breast Cancer Genomics" Biomedicines 12, no. 9: 2086. https://doi.org/10.3390/biomedicines12092086
APA StyleYuan, W., Li, Y., Han, Z., Chen, Y., Xie, J., Chen, J., Bi, Z., & Xi, J. (2024). Evolutionary Mechanism Based Conserved Gene Expression Biclustering Module Analysis for Breast Cancer Genomics. Biomedicines, 12(9), 2086. https://doi.org/10.3390/biomedicines12092086






