1. Introduction
The global financial crisis 2007–2009, which severely affected the world economies, showed the great importance of the appropriate calculation of credit risk in pricing financial contracts. The most important determinants of credit risk are default probability (PD) and recovery rate (RR) or Loss Given Default (LGD), i.e., 1 − RR. There are a couple of important reasons why those parameters should be taken into consideration. Firstly, they could be used to estimate the expected financial loss. Secondly, the estimations of PD and RR could help to determine an individual risk policy, e.g., if the values of the parameters are exceptionally high, more effort could be committed in order to mitigate the loss. Moreover, the financial risk of a portfolio, which is calculated using default probabilities and recovery rates, is essential for fulfilling the capital requirements of Basel accords.
The appearance of contingent claims on recoveries e.g., CDS (Credit Default Swap) as well as the variability and severity of the defaults during the financial crisis have shown the necessity to predict the recovery rates more precisely. We intuitively expect the recovery rate to be dependent on various factors: endogenous (characteristics of the lender and the conditions of the contract, e.g., rating, transaction amount, collateral) and exogenous (macroeconomic conditions, e.g., GDP (gross domestic product), unemployment or inflation rate). The modelling of recovery rates taking into consideration endogenous variables essentially started with
Asarnow and Edwards (
1995) and
Altman and Kishore (
1996). The first authors analyze US C&I (Commercial and Industrial) corporate loans and US structured loans and observe that structured loans have much higher RR than C&I loans. The latter examines the impact of collateralization, seniority and industry affiliation on individual recovery rates.
Eales and Bosworth (
1998) report that the size of the loan positively influences recovery rates for loan data in Australia.
Carrizosa and Ryan (
2013) and
Donovan et al. (
2015) find that creditors of firms with more conservative accounting prior to default have significantly higher recovery rates and
Amiram and Owens (
2021) show that accounting measures available to lenders at the contracting date are informative about future loss given default.
The influence of exogenous variables is examined e.g., by
Altman et al. (
2001), who find secondary effects of macroeconomic variables on annual recovery rates.
Hu and Perraudin (
2002) determine a negative correlation between the quarterly default rates and recovery rates.
Jankowitsch et al. (
2014) reach a more clear conclusion, which is also consistent with the result of
Hu and Perraudin (
2002). By examining US corporate bonds, they find that high default rates imply lower recoveries. Further,
Bellotti and Crook (
2012) shows that higher interest rates (measured by selected UK retail banks’ base interest rates) and higher unemployment at the time of default lead to lower recovery rates, but a higher earnings growth leads to increased RR. Surprisingly,
Ingermann et al. (
2016) claims that unemployment and inflation lead to an increase in recovery rates.
Krüger and Rösch (
2017) consider a quantile regression with endogenous as well as exogenous variables and show that this regression model outperforms the classical regression as well as its modification with a transformed response, beta regression, mixture regression with two components, and regression trees.
Most researchers agree that during economic downturns recovery rates are lower.
Frye (
2000) shows that during crisis times, RR might decline 20–25% with respect to prosperity times.
Brumma et al. (
2014) states that the economic situation at the date of the cash-flow weighted median of recovery payments has the highest impact on the recovery rate.
Wang et al. (
2020) also report that loan characteristics influence different recovery rates during good and bad times.
Min et al. (
2020) combine endogenous and exogenous variables together with crisis prediction during the average resolution time of 18 months to model individual recovery rates. They compare regression models as well as their combination with decision trees, neural networks, and mixture models. They found that the mixture regression model with regressed means of the components as well as with regressed probabilities provides the best fit among all considered models. This shows that the potential of regression models including crisis prediction as a regressor is not exhausted yet and that those models could serve as attractive competitors to modern machine learning methods. We refer to
Qi and Zhao (
2011) and
Bellotti et al. (
2021) for a comparison of machine learning techniques with regression methods.
Felsovalyi and Hurt (
1998) consider 1149 defaults from 27 countries in Latin America over a time horizon of 27 years from 1970 to 1996. According to their empirical study, the recovery rates are higher for larger loans which are in contrast to
Bastos (
2010). Surprisingly, the authors claim that neither the economic fluctuations (measured by annual GDP growth of Latin America) nor the sovereign events affect RR. In contrast,
Covitz and Han (
2004) report a positive correlation between GDP and annually aggregated RR.
Khieu et al. (
2012) examine the determinants of bank loans recoveries using the “Ultimate Recovery Database”, a broad database supplied by Moody’s covering various debt instruments from the US defaulted companies. These authors report a positive impact of annual GDP growth on RR. From the more recent studies,
Calabrese (
2014) examines the impact of default rate, unemployment, and GGDP (annual growth of GDP from previous years) using data from the Bank of Italy’s Survey. Only the default rate turns out to be statistically significant, but the value of its coefficient is close to zero.
Gambetti et al. (
2019) consider a general class of beta regression models for bond recovery rates and investigate the impact of regressors on the shape of an underlying beta distribution. They also consider GDP for the US and linearly interpolate it for monthly observations. Depending on a considered model, they observe either a negative nonsignificant influence of GDP or a positive statistically significant one at a
level.
Recently, several works propose interesting frameworks for modeling recovery rates.
Sopitpongstorn et al. (
2021) use nonparametric logit regressions with regression parameters depending on covariate values. A remarkable feature of this approach is its robustness with respect to distributional assumptions on the response variable, bimodality, and asymmetry.
Candian and Dmitriev (
2020) consider a dynamic stochastic general equilibrium (DSGE) model to explain fluctuation of recovery rates.
Ye and Bellotti (
2019) employ a beta mixture model combined with a logistic regression model. This is a two-stage model, which first fits a logistic regression to predict full recovery and then fits a beta mixture regression for recovery rates in an open unit interval.
Fermanian (
2020) models the joint distribution of default times and recovery rates using a Gaussian copula. In this way, he is able to quantify the influence of default probabilities on recovery rates in different scenarios of structural models.
In this article, we explain the behavior of monthly aggregated recovery rates (ARR) from the Global Credit Data (GCD) database using monthly and quarterly macroeconomic variables in a regression framework. The individual recovery rate of a specific loan is an important input variable for internal rating models but very hard to predict. In contrast, the ARR can be forecasted more significantly and may serve as a good proxy for an individual recovery rate. The database of GCD includes the default cases from 5 continents and over 120 countries. GCD was formed in December 2004 as a credit risk data-pooling initiative primarily designed to assist member-banks in enhancing their internal credit risk models, completing the Basel II preparations in pursuit of the International Ratings Based Advanced Status, and improving their risk assessment for risk and credit portfolio management purposes. Since then, GCD has enjoyed remarkable success, both in terms of growing its membership and establishing its international reputation through the creation of the largest existing loss and recovery dataset for commercial loans worldwide.
Previous studies are restricted to quarterly or annual GDP growth. We first model monthly ARR using monthly signals extracted from quarterly GDP derived from other monthly macroeconomic variables. For this, we consider a dynamic factor model for mixed-frequency panel data and estimate them as described in
Banbura and Modugno (
2014).
Keijsers et al. (
2018) also consider a similar factor model to couple individual recovery rates, three macroeconomic variables including GDP, and individual characteristics of loan and borrower. They are able to explain the cyclicality in recovery rates and default rates driven by latent factors for all observed variables. In contrast, we consider the ARR and do not mix it with macroeconomic variables. Further, we consider 19 (34) macroeconomic variables for Europe (US) to estimate monthly GDP growth rates from quarterly GDP growth rates. Using the estimated factors, we are especially able to quantify an undisturbed influence of GDP on monthly ARR. In order to improve the regression fit, shifts of covariates in time are considered. A Markov switching model with two states is applied to show that the distribution of the ARR and their dependence on explanatory variables may vary between different states.
The structure of the article is as follows. In
Section 2, the derivation of monthly estimates of GDP growth using a dynamic factor model for mixed-frequency data is presented. A description of the general idea of dynamic factor models and panel data is given in
Appendix A. In
Section 3, the explanatory variables for the regression models are introduced.
Section 4 presents several regression models for the ARR. Here, we apply time shifts to explanatory variables and combine a linear regression with a Markov switching model.
Section 5 summarizes and concludes the paper.
2. Estimating Monthly GGDP
We model monthly aggregated recovery rates using monthly and quarterly observed data. In particular, the GDP in Europe and in the US is released only on a quarterly basis. A rather naive approach to derive monthly estimates out of quarterly data is a linear interpolation. In this paper, we will apply a dynamic factor model to estimate the monthly growth of the GDP (GGDP). The monthly GGDP is observed at a particular month if this month is the last month of a quarter. It is then computed as a log-return of the GDP assigned to the quarter of the considered month and the GDP of the previous quarter. For the first and second months of a quarter, the GGDP is missing. A detailed description of the model can be found e.g., in
Banbura and Modugno (
2014).
As input data in our factor model, we use a data set containing quarterly GDP as well as many other monthly and quarterly observed economic variables describing the macroeconomic environment, interest-rate movements, and stock-markets behavior. The list of variables can be found in
Appendix A. The GCD data, which was available to us, covers the period from January 2000 until January 2014. For quarterly variables like GDP, only every third observation is available and other values are missing. Out of this mixed frequency data, we derive the factors which will be used for modeling the ARR.
Similar to
Banbura and Modugno (
2014), we use transformations of the variables instead of the original data. We take the difference of consecutive observations or the difference of the logarithms of consecutive observations to make the observed time series stationary. In the case of the European GDP and the US GDP, we transform the variables by taking the difference of logarithms, which results in quarterly log returns. Our goal is to reconstruct monthly time series from the quarterly growth of GDP for Europe and the US using dynamic factor models. The considered mixed frequency panel data sets are similar to those in
Schumacher and Breitung (
2008), who were estimating the GDP of Germany.
In the case of Europe, the quarterly GDP data and most of the other observable variables used for the estimation are average values of 19 European countries. The derived GGDP will also be the estimation of the average GGDP of those countries. For the European GGDP estimation, 29 variables are used and the data is almost entirely taken from the website of the European central bank (
http://sdw.ecb.europa.eu/, accessed on 31 March 2017). Only the VSTOXX volatility index observations are taken from a different source. Those are available at
https://www.investing.com/indices (accessed on 5 April 2017). The data used for estimating the US GGDP consists of 34 variables and is available on the webpage of the Research Division of the Federal Reserve Bank of St. Louis (
https://fred.stlouisfed.org/ accessed on 27 March 2017).
2.1. Estimation with Dynamic Factor Models
The main idea of a factor model is to derive a few unobserved (latent) factors, which describe the behavior of high-dimensional data. The model consists of two equations. The first is the observation equation, which explains the relation between observation vector
and the latent factors
for
. It has the following form:
where
,
is a normally distributed error term with
, and
is a diagonal matrix.
The second equation is called state or transition equation. It describes the dynamics of the unknown factors
over time. We assume that
follows a vector autoregressive model of order
p:
where
,
is a parameter matrix,
is a normally distributed and independent white noise error term with
for
,
. The whole available data is centralized, i.e., the mean of the time series was subtracted. We define
and
.
For the European and the US GGDP, we obtain monthly estimates by treating quarterly growths as monthly data with missing values. In the observation vector
, the missing values are denoted by NA. To deal with the incomplete data,
Banbura and Modugno (
2014) suggested introducing a diagonal matrix
with 0 on the diagonal if the corresponding observation is missing and 1 if the observation is available. Using the matrix
, we can split the observation vector
into two parts, one corresponding to observed values and one corresponding to missing values:
where
denotes the identity matrix of dimension
n. Hence, the vector
does not contain any missing values denoted by NA any more. Due to the diagonal structure of
D, the log-likelihood function of the dynamic factor model (
1)–(
2) can be integrated with respect to
and
and depends on the matrix
. For details, we refer to
Banbura and Modugno (
2014).
The parameters
are unknown and need to be estimated. As in
Defend et al. (
2021), we choose
for an initial estimate of
and for an initial estimate of
Q we choose
. The initial values
and
are calculated according to a probabilistic principal component analysis (see
Tipping and Bishop (
1999)). Having the initial estimates, we proceed with the estimation using the expectation-maximization algorithm (see
Dempster et al. (
1977)). The main idea of the algorithm is to write the log-likelihood as if the data
was complete and to iterate between the expectation and maximization steps. In the expectation step, we take the expectation of the log-likelihood function
, which is dependent on the unknown model parameters
given the data
, under the current
j estimate
of the parameters given
, the observations available up to time
T. As in our situation, some observations are missing,
does not contain every value from
Y. In the maximization step, we compute the maximum of the just calculated expected log-likelihood function to derive the maximum likelihood estimates of
under the current estimates of
. The steps of the algorithm are as follows:
Expectation step (E-step):
Maximization step (M-step):
As derived in
Banbura and Modugno (
2014), the parameter estimates after the
th iteration have the following form:
In Equation (
3), ⊗ denotes the tensor product. The above estimators depend on the conditional moments
,
,
and
. To estimate them, we use the Kalman filter and Kalman smoother (see, e.g.,
Nakata and Tonetti (
2010). The estimators of the latent factors
are then given by
where
is an estimator of
using the Kalman smoother based on the whole available information
. The termination criterion
is defined after
Doz et al. (
2011) and stops the iteration procedure if
Since factor dimension
q and autoregressive order
p are not known, we estimate the model (
1) and (
2) for different combinations of
q and
p. We considered the five following combinations of parameters (
,
), (
,
), (
,
), (
,
), (
,
) and decided to choose the model, whose estimates provide the best fit in a linear regression for aggregated recovery rates (see
Section 4). According to this criterion, in case of the European GGDP the dynamic factor model with parameters (
,
) is the best and for the US GGDP the one with (
,
).
Estimators of Missing Data
In the dynamic factor model, we derive the latent factors using the observed data. In order to derive the monthly estimators of missing data, we perform the opposite operation. Thus, we calculate the estimator
of data
Y using
and an estimator
of
W by
The above equation is the observation equation with the neglected error term. The fitted data has no missing values and we get the estimator of the GGDP from the appropriate column of matrix
. In
Figure 1 and
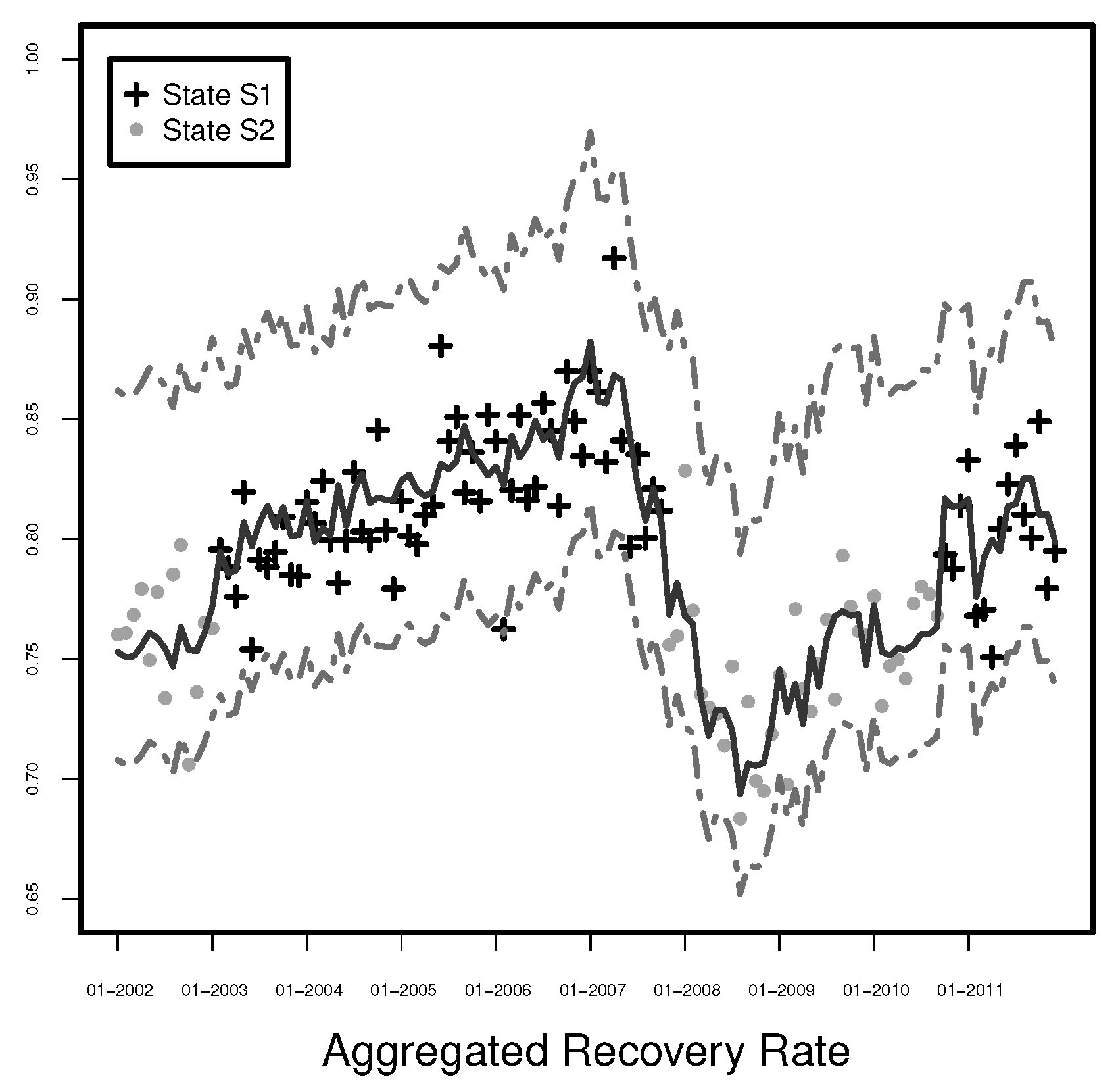
Figure 2, we present the original quarterly data and the estimated monthly values of the GGDP for Europe and the US, respectively.
From
Figure 1 and
Figure 2, we clearly see that the estimators of the GGDP are different compared to the estimators obtained by linear interpolation. In contrast to the linear interpolation, where only the GDP values observed every quarter matter and other monthly fluctuations in the economy within those 3-months periods are completely neglected, our estimates reflect the information about changes in the economy contained in the broad data set used for estimation of the dynamic factor model. In the linear interpolation, we need to know the first and last observation of the considered period to estimate the values in between and thus this is a forward-looking estimation. In contrast to the linear interpolations, we do not use the observed, quarterly values, but the corresponding fitted monthly values. Especially, we expect that the estimated GGDP will let us predict the behavior of the aggregated recovery rates better. This statement is examined in the next section.
In the literature, a special case of factor models, called static factor models, is also used. In a static framework latent factors are assumed to be independent, State Equation (
2) is omitted and the model is given by Equation (
1) only. We have also estimated the European GGDP and US GGDP using the static factor model (for
). However, the corresponding estimators of the GGDP have less explanatory power for aggregated recovery rates than the ones resulting from the dynamic model, which are presented in
Figure 1 and
Figure 2.
3. Data for Regression Models
The recovery rates are taken from the Loss Given Default (LGD) database of GCD (formerly known as Pan-European Credit Data Consortium or PECDC). Global Data Consortium was founded by 13 European banks to provide a collection of historical loss data, analysis, and research resources to contribute to a better understanding of credit risk. The database contains over 110,000 individual facility default records from over 50,000 obligors over a period from 1990 to date. The data is collected on the basis of 11 distinct asset classes (all except retail), which mirror those defined in the Capital Requirements Directive. The more than 50 member-banks are from Europe, Africa, Asia, Australia, and North America. This is also reflected in the geographical coverage of the database which, originally limited to Europe, has been extended to include global exposures and the records from over 120 countries.
The database available to us includes the loss data from the period 1990–2014. The defaults from the years 2012–2014 are partially unresolved and the banking regulations before 2002 were significantly different. Therefore, we analyze the data from 2002 till the end of 2011 in our study. This period covers more than one full economic cycle as postulated in §472 of the
Basel Committee on Banking Supervision (
2004).
The other variables used in the regression models, 1-month Euro Interbank Offered Rate (EURIBOR: 1M), 3-months Euro Interbank Offered Rate (EURIBOR: 3M), industrial production of European countries (Production), 5-year Euro area Government Benchmark Bond yield (GY), average inflation of European countries (Inflation) and average unemployment of European countries (Unemployment) are taken from the website of the European central bank (
http://sdw.ecb.europa.eu/, accessed on 31 March 2017). The VSTOXX volatility index, Dow Jones Euro STOXX 50 (STOXX 50), and S&P500 are available at
https://www.investing.com/indices, accessed on 5 April 2017. In the case of Production, Inflation, and Unemployment the data concerns 19 European countries.
3.1. Recovery Rates
The recovery rate is usually defined as the fraction of the exposure at default (EAD) that is recovered from a defaulted entity. The recovery rate could be also defined as 1 −
Loss Given Default (
LGD). More information on the definition of default and estimation of LGD can be found in the guidelines
EBA/GL/2016/07 (
2016) and
EBA/GL/2017/16 (
2017) of the European Banking Authority. According to the
EBA/GL/2017/16 (
2017), the workout LGD, i.e., losses computed using discounted cash-flows during a workout process, based on the institution’s experience in terms of recovery processes and losses is considered to be the main, superior methodology that should be used by institutions. Therefore, in this paper, we use the workout method to calculate the LGD as provided by the GCD.
Since we are only interested in real losses, all facilities for which the default amount is 0 were excluded from our database. Furthermore, in order to exclude all cases with unreasonable cash flows and the cases which are not fully resolved, we exclude all entities for which the total sum of reported cash flows (including chargeoffs and waivers which are not present in the calculation of economic recovery rates) divided by the outstanding amount at default is smaller than 90% or greater than 105% of the outstanding amount at default. In order to exclude exceptionally low or high recoveries, we remove observations with recovery rates outside the interval
. Those situations are possible because of costs and fees associated with recovery rates. Note that this sample selection is in line with
Krüger and Rösch (
2017) and
Keijsers et al. (
2018).
Table 1 presents some basic statistics of the recovery rates. In the column “Weighted”, the statistics are computed by using the default amount as weight. “Simple” statistics are, in contrast, equally weighted. The figures in both cases are similar.
Therefore, we decided to use equally-weighted recovery rates.
Figure 3 shows the distribution of the resulting recovery rates. Thus, we can conclude that the distribution is bimodal.
3.2. Explanatory Variables
To model the monthly aggregated recovery rates, we use the European GGDP (GGDP Europe), the GGDP of United States (GGDP USA), average inflation of European countries (Inflation), average unemployment of European countries (Unemployment), industrial production of European countries (Production), 1-month Euro Interbank Offered Rate (EURIBOR: 1M), 3-months Euro Interbank Offered Rate (EURIBOR: 3M), 5-year Euro area Government Benchmark Bond yield (GY), S&P500, Dow Jones Euro STOXX 50 (STOXX 50) and VSTOXX volatility index (VSTOXX). The first five variables describe the macroeconomic environment, the following three refer to interest-rate movements and the last two are proxies for stock market behavior. The 1-month and 3-months European interbank offered rates (EURIBOR) serve as proxies for the short-term interest rates in the Eurozone, GY is calculated as the weighted mean of bond yields with maturities between 4.5 and 5.5 years, with default amount as weight, the Dow Jones STOXX 50 and S&P500 are proxies for equity markets and eventually, VSTOXX is a volatility index calculated from the implied volatilities of STOXX 50.
The impact of all those variables on the recovery rates is rather small when we consider every default individually.
Figure 4 shows the average recovery rate computed for every percentile of the considered explanatory variables. None of the variables shows any significant correlation with recovery rates. Our observations are consistent with
Grunert and Weber (
2005);
Dermine and Neto De Carvalho (
2006) or
Calabrese (
2014) who did not find any dependencies between exogenous variables and RR on the unaggregated level. The exogenous explanatory variables become much more important when we consider monthly aggregated recovery rates, i.e., equally-weighted monthly averages of recovery rates based on the default date. We will examine the monthly aggregated recovery rates in the next section.
5. Summary and Conclusions
In this paper, we examine the relation between monthly aggregated recovery rates and different exogenous factors describing the macroeconomic environment, interest-rate movements, and stock markets. For this, we consider the Global Credit Data, which is the biggest loan loss and recovery data set worldwide containing over 110,000 individual facility default records from all over the world. Furthermore, we use the quarterly released GDP of the US and Europe and derive monthly estimates of their growth using a dynamic factor model for mixed frequency data. To our best knowledge, stochastic monthly estimated GGDP is introduced to models for the ARR for the first time and this assures better fitting than a naive linear interpolation.
It is also shown that models for the ARR with time-shifted explanatory variables outperform the ones with unshifted explanatory variables. Thus, our finding suggests that modeling with forecasted explanatory variables can improve the prediction power of statistical models for recovery rates. In particular, we apply optimal time shifts separately for every single variable. As the restructuring effort and the liquidation of collaterals do not realize immediately, the behavior of explanatory variables after a default significantly influences the monthly ARR. Since relevant values of explanatory variables are not available at the time of default, we empirically sample their monthly changes from the corresponding last 120 ones to construct prediction intervals.
We have also considered beta, logit, probit, and log transformation of the ARR in the framework of linear regression as well as beta regression for the ARR. The linear regression model with a logarithmized response variable fits the ARR best and is extended in two directions. The first extension is built by adding interactions to the linear regression model. The second extension is a combination of the linear regression and a Markov switching model with two states, which can be interpreted as crisis and prosperity times. The reduced Markov switching model explains over of the variability of the aggregated recovery rates and outperforms the model with interactions. In prosperity times, the variables EURIBOR:3M, Unemployment, STOXX 50, and GGDP Europe are significant (at 5% or 1% level) drivers of the aggregated recovery rate at least while PRODUCTION (at level 10%) and GGDP (at 5% level) are significant indicators in crises times. Our out-of-sample comparison of the considered models shows the superiority of the Markov switching model in general and a good potential of the linear model with intersections.
Overall, the final model we propose uses a dynamic factor model with mixed frequency data to forecast the monthly GGDP, an optimal time shift in the variables, and a Markov switching model. The forecasted ARR could be used as an explanatory variable to model individual recovery rates. We expect that the modeling framework of
Min et al. (
2020);
Sopitpongstorn et al. (
2021) as well as
Ye and Bellotti (
2019) could gain more prediction power by considering the predicted ARR as an additional explanatory variable. The limitation of the proposed methodology is that the state of the Markov switching model is not known. For applications, this state should be predicted similarly to
Hauptmann et al. (
2014). Much empirical research on individual recovery rates using GDP or its interpolation, see, e.g.,
Calabrese (
2014) and
Gambetti et al. (
2019), could be reconsidered by employing monthly extracted signals from GDP. Finally, the approach of
Fermanian (
2020) shows a great potential of copulas for describing the dependence structure of recovery rates and macroeconomic variables. This all is a topic of future research.