Gaussian Process Regression for Swaption Cube Construction under No-Arbitrage Constraints

Abstract

In this paper, we introduce a 3D finite dimensional Gaussian process (GP) regression approach for learning arbitrage-free swaption cubes. Based on the possibly noisy observations of swaption prices, the proposed ‘constrained’ GP regression approach is proven to be arbitrage-free along the strike direction (butterfly and call-spread arbitrages are precluded on the entire 3D input domain). The cube is free from static arbitrage along the tenor and maturity directions if swaption prices satisfy an infinite set of in-plane triangular inequalities. We empirically demonstrate that considering a finite-dimensional weaker form of this condition is enough for the GP to generate swaption cubes with a negligible proportion of violation points, even for a small training set. In addition, we compare the performance of the GP approach with the SABR model, which is applied to a data set of payer and receiver out-of-the-money (OTM) swaptions. The constrained GP approach provides better prediction results compared to the SABR approach. In addition, we show that SABR calibration is better when using the GP cube output as new observations (in terms of predictive error and absence of arbitrage). Finally, the GP approach is able to quantify in- and out-of-sample uncertainty through Hamiltonian Monte Carlo simulations, allowing for the computation of model risk Additional Valuation Adjustment (AVA).

1. Introduction

The swaption cube is an important financial object as it is used as an input of many interest-rate derivative pricing engines. It consists in a swaption implied volatility surface, which is indexed by maturity, strike and tenor. The swaption market is one of the biggest in the interest rate derivatives market. Swaptions are usually used to hedge, and while at-the-money (ATM) swaptions are observed to be very liquid, out-of-the-money swaption prices are often missing or not reliable. The major issue with the swaption cube is that along its three axes, missing quotes must be interpolated in an arbitrage-free way in order to be used as the input of some pricing or hedging models.

For equity options, the volatility surface, indexed by the maturity and the strike of the derivative, is a topic that has been thoroughly studied. A number of machine learning methods for learning pricing functions have emerged (see, e.g., Ruf and Wang (2019) for an in-depth literature review). For these volatility surfaces, absence of arbitrage is guaranteed if there is no call spread, butterfly spread and calendar spread arbitrage opportunities. A Gaussian process regression methodology, constrained on the no-arbitrage conditions for equity options, has been introduced in Chataigner et al. (2021). Using this approach, they achieved to produce arbitrage-free interpolated prices, and local volatility surfaces, with their uncertainties. In the literature, several ways of interpolating the missing prices or volatilities of the swaption cube have been introduced. A distinction needs to be made between functional interpolation, which is for example polynomial interpolation, and stochastic interpolation, where stochastic models such as SABR and CEV models are used. The most common method for interpolating in an arbitrage-free way between quoted strikes, as well as extrapolating beyond, is to use the SABR model. However, this construction method requires several observed quotes at different strikes for each considered pair of tenors and maturities. When there is only one quoted strike observation, for a given tenor and maturity, three methods are usually employed in the industry to interpolate the swaption smile. Two of them are based on the cap market. The first approach consists of using caplet SABR parameters as a basis for the calibration of the swaption SABR parameters (see, e.g., Hagan and Konikov (2004)). The second, discussed in Skantzos and Garston (2019), consists of mapping underlying caplet volatilities to the swaption volatility by making an assumption in relating the moneyness of the swaption to the moneyness of the underlying caplets. The validity of both approaches decreases when the tenor of the considered swaptions increases. When cap market data are not available, parameters of the SABR model are taken as the closest SABR parameters that are calibrated with quotes. In order to interpolate with respect to maturity and tenor, it is possible to use functional interpolation directly on swaptions prices, or in a more elaborate manner, to use functional interpolation on the parameters of stochastic models. As explained in Johnson and Nonas (2009), in addition to the no call spread and butterfly spread arbitrage, the interpolated swaption prices must also respect an additional arbitrage condition, named “in-plane triangular”.

Inspired by the local volatility construction proposed by Chataigner et al. (2021), the main goal of this paper is to present and study a 3D-constrained GP construction method for interpolating arbitrage-free swaption price cubes at a given quotation date. Compared to the equity local volatility construction method proposed in Chataigner et al. (2021), several improvements have been added:

• The constrained GP regression approach has been extended to an input space of dimension 3. Numerical implementation of the 3D ‘constrained’ kriging problem is much more involved than in the 2D case considered in Chataigner et al. (2021). We show that considering an anisotropic stationary kernel allows us to benefit from the tensorization of the GP covariance matrix, and it significantly reduces numerical complexity.
• Compared to the equity price surface, the no-arbitrage constraints on swaption prices are no more directional. Indeed, the in-plane triangular inequality involves prices of swaptions with different maturities and tenors. This constraint is by far more complex to handle than the no calendar spreads arbitrage constraint in the equity option case. It can be viewed as a weaker form of the no calendar spreads arbitrage condition, and it requires an infinite number of checks in order to be imposed everywhere on the domain. In our methodology, we consider a weaker version of the in-plane inequality constraint, and we empirically check in Section 4 that the weaker form is enough to ensure no arbitrage almost everywhere.
• Computation of the GP prior hyperparameters by Maximum Likelihood Estimation (MLE) is much longer in the swaption case than in the equity case (see Section 3.3). Search for the maximal likelihood has been considerably improved by explicitly computing the Jacobian of the log-likelihood function.

The paper is organized as follows. In Section 2, we present the conditions on European swaption prices that preclude from any static arbitrage opportunity at a particular quotation date. These arbitrage-free conditions on the swaption cube translate into a convexity and a monotonicity constraints in strike, and into an “in-plane triangular” constraint in maturity and tenor. In Section 3, we detail the constrained GP regression methodology used to construct swaption price cubes that do not lead to arbitrage opportunities. Finally, in Section 4, we apply the presented GP methodology to a data set of payer and receiver OTM swaptions, and we compare the result to a SABR construction approach, which is the standard market practice to parameterize rate volatilities.

2. Absence of Static Arbitrages for the Swaption Cube

Before establishing the arbitrage-free constraints for the swaption cube, we set some notation.

Let $S_w(T_s, T_e, K)$ be the price, at a given quotation date, of a European payer (receiver) swaption, with a payer (receiver) swap $S(T_s, T_e, K)$ as underlying asset, where $T_s$ and $T_e$ are, respectively, the first and last payment date of the swap with fixed interest rate K. For equity options, in order to construct an arbitrage-free price or volatility surface, we must verify that the price of call spreads, butterfly spreads and calendar spreads are positive. In the strike direction, the butterfly and call-spread arbitrage conditions also apply to the swaption cube. However, the calendar spread condition does not hold here, as explained in Johnson and Nonas (2009). A non-trivial no-arbitrage constraint between European swaptions with the same strike and different option expiries was introduced in this article. Since this condition translates into an inequality between the price of three swaptions with the same strikes, it is called an “in-plane triangular condition”.

Proposition 1.

The European payer (receiver) swaption price cube $(T,t,K)\to S_w(T,T+t,K)$ is free of static arbitrage if and only if the three following conditions hold:

(i) 

For all $T,t,K\ge 0$, $S_w(T,T+t,K)\ge 0$;

(ii) 

$K\to S_w(T,T+t,K)$ is a convex, decreasing (increasing) function;

(iii) 

The in-plane triangular condition holds:

For all $T,t,h,K\ge 0$, $S_w(T,T+t,K)+S_w(T+t,T+t+h,K)\ge S_w(T,T+t+h,K)$.

Item $\left(ii\right)$ comes from the need for call spreads and butterfly spreads to be positive.

A proof of $\left(iii\right)$ is given in Johnson and Nonas (2009).

3. GP Regression to Construct an Arbitrage Free Swaption Cube

In this section, we present a GP-based methodology to build an arbitrage-free European payer (receiver) swaption cube.

For an input domain $\mathcal{D}$ of maturities, tenors and strikes, we build at quotation date $t_0$, a payer (receiver) swaption price cube

$$\begin{array}{l}{S}_w:\mathcal{D}\to {\mathbb{R}}^{+}\\ (T,t,K)\mapsto S_w(T,T+t,K),\end{array}$$

satisfying the no arbitrage conditions given in Proposition 1, from n noisy observations $\mathit{y}={[y_1,\dots ,y_n]}^{\top }$ of the function $S_w$ at input points $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n]$ where ${\mathbf{x}}_i=(T_i,t_i,K_i)$, $i=1,\dots ,n$. We assume that the price function $S_w$ is represented as a Gaussian process. The market fit condition is then written as

$$\mathit{y}=S_w\left(\mathbf{X}\right)+\mathit{\epsilon },$$

(1)

where $S_w\left(\mathbf{X}\right):={[S_w\left({\mathbf{x}}_1\right),\dots ,S_w\left({\mathbf{x}}_n\right)]}^{\top }$ is the vector of the values of the GP at the input points $\mathbf{X}$. The additive noise term $\mathit{\epsilon }={[{\epsilon }_1,\dots ,{\epsilon }_n]}^T$ is assumed to be a zero-mean Gaussian vector, independent from $S_w$, and with a homoscedastic covariance matrix given as ${\varsigma }^2{I}_n$, where $I_n$ is the identity matrix of size n.

3.1. Classical 3-Dimensional Gaussian Regression

We consider a zero-mean Gaussian process prior on the mapping $S_w=S_w{\left(\mathbf{x}\right)}_{\mathbf{x}\in D}$ with covariance function c.

Then, the output vector $S_w\left(\mathbf{X}\right)$ has a normal distribution with zero mean and covariance matrix $\mathbf{C}$ with components $\mathrm{cov}(S_w(T_i,T_i+t_i,K_i),S_w(T_j,T_j+t_j,K_j))=c((T_i,t_i,K_i),(T_j,t_j,K_j))=c({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})$. We consider a 3-dimensional anisotropic, stationary covariance kernel given as, for $\mathbf{x}$ and ${\mathbf{x}}^{\prime }\in \mathcal{D}$,

$$c(\mathbf{x},{\mathbf{x}}^{\prime })={\sigma }^2{R}_T(T-T^{\prime },{\theta }_T)R_t(t-t^{\prime },{\theta }_t)R_K(K-K^{\prime },{\theta }_K),$$

where ${\theta }_T$, ${\theta }_t$, ${\theta }_K$ are the length scale parameters associated with directions $T,t,K$, and ${\sigma }^2$ is the marginal variance of the GP prior. The functions $R_T,R_t$ and $R_K$ are kernel correlation functions. As explained in Rasmussen and Williams (2005), $S_w|\mathit{y}=S_w\left(\mathbf{X}\right)+\mathit{\epsilon }$ is again a GP with mean function $\eta$ and covariance function $c^{\star }$ given respectively by

$$\eta \left(\mathbf{x}\right)=\mathbf{c}{\left(\mathbf{x}\right)}^{\top }{(\mathbf{C}+{\varsigma }^2{I}_n)}^{-1}\mathit{y},\mathbf{x}\in \mathcal{D}$$

(2)

and

$$c^{\star }(\mathbf{x},{\mathbf{x}}^{\prime })=c(\mathbf{x},{\mathbf{x}}^{\prime })-\mathbf{c}{\left(\mathbf{x}\right)}^{\top }{(\mathbf{C}+{\varsigma }^2{I}_n)}^{-1}\mathbf{c}\left({\mathbf{x}}^{\prime }\right),\mathbf{x},{\mathbf{x}}^{\prime }\in \mathcal{D},$$

(3)

where $\mathbf{c}\left(\mathbf{x}\right)={[c(\mathbf{x},{\mathbf{x}}_1),\dots ,c(\mathbf{x},{\mathbf{x}}_n)]}^{\top }$.

Prediction and uncertainty quantification are made using the conditional distribution $S_w|\mathit{y}=S_w\left(\mathbf{X}\right)+\mathit{\epsilon }$. The best linear unbiased estimator of $S_w$ is given as the conditional mean function (2). The conditional covariance function $c^{*}$ can be used to obtain confidence bounds around the predicted price surface. The hyperparameters of the kernel function c, as well as the variance of the noise, can be estimated using a maximum likelihood approach or a cross-validation approach (see Rasmussen and Williams (2005)). The model described in this subsection corresponds to unconstrained Gaussian process regression, which therefore does not take into account the arbitrage-free conditions as described in Proposition 1.

3.2. Imposing No Arbitrage Constraints to GP Regression

Conditional on the inequality constraints given in Proposition 1, the process $S_w$ is no longer Gaussian, and this leads to two difficulties. The first is that we depart from the classical framework of GP regression, where the posterior distribution remains Gaussian. The second is that testing the inequality constraints on the entire input domain would require an infinite number of checks. We will use the solution proposed by Cousin et al. (2016) which consists of constructing a finite-dimensional approximation $S_w^N$ of the Gaussian prior $S_w$, which is designed in such a way that the constraints can be imposed for the entire domain $\mathcal{D}$ with a finite number of checks. We then recover the constrained posterior distribution by sampling a truncated Gaussian vector. Let us describe the methodology with more details.

We first rescale the input domain $\mathcal{D}$ to ${[0,1]}^3$. Without loss of generality, we then consider a discretized version of this rescaled domain as a 3-dimensional regular grid with nodes $(T_i,t_j,K_k)$, $i=1,\dots ,N_T$, $j=1,\dots ,N_t$, $k=1,\dots ,N_K$, where $N_T,N_t,N_K$ are, respectively, the number of maturities, tenors and strikes we chose for our grid, and $({\delta }_T,{\delta }_t,{\delta }_K)$ the corresponding constant steps1. Then, $N=N_T\times N_t\times N_K$ is the total number of nodes of the 3-dimensional grid. Now, each node of the grid is associated with a hat basis function defined as:

$${\varphi }_{i,j,k}(T,t,K):=\max (1-\frac{|T-T_i|}{{\delta }_T},0)\max (1-\frac{|t-t_j|}{{\delta }_t},0)\max (1-\frac{|K-K_k|}{{\delta }_K},0).$$

Then, the GP prior $S_w$ is approximated on $\mathcal{D}$ by the following finite-dimensional process:

$$S_w^N(T,T+t,K)=\sum _{i=1}^{N_T}\sum _{j=1}^{N_t}\sum _{k=1}^{N_K}{S}_w(T_i,T_i+t_j,K_k){\varphi }_{i,j,k}(T,t,K),\mathrm{for}\mathrm{all}(T,t,K)\in \mathcal{D}.$$

(4)

Note that the process $S_w^N$ corresponds to a piecewise linear interpolation of $S_w$ at nodes $(T_i,t_j,K_k)$, for $i=1,\cdots ,N_T$, $j=1,\cdots ,N_t$, and $k=1,\cdots ,N_K$.

If we denote $S_w(T_i,T_i+t_j,K_k)$ as ${\xi }_{i,j,k}$, then the vector $\mathit{\xi }={[{\xi }_{1,1,1},\cdots ,{\xi }_{i,j,k}\cdots ,{\xi }_{N_T,N_t,N_K}]}^{\top }$ is a zero-mean Gaussian vector with $N\times N$ covariance matrix ${\mathrm{\Gamma }}^N$ with components ${\mathrm{\Gamma }}_{\mathbf{x},{\mathbf{x}}^{\prime }}^N=c(\mathbf{x},{\mathbf{x}}^{\prime })$ for $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$ two nodes of the grid. Let us define $\mathit{\varphi }(T,t,K)$ as the N dimensional vector given as:

$$\mathit{\varphi }(T,t,K)=[{\varphi }_{1,1,1}(T,t,K),\dots ,{\varphi }_{i,j,k}(T,t,K),\dots ,{\varphi }_{N_T,N_t,N_K}(T,t,K)].$$

Then, the finite-dimensional GP prior defined in (4) can be restated in matrix form: Equality (4) can then be written as:

$$S_w^N(T,T+t,K)=\mathit{\varphi }(T,t,K)·\mathit{\xi }.$$

Then, if we define $\mathbf{\Phi }\left(\mathbf{X}\right)$ as the $n\times N$ matrix of basis functions such that each row i corresponds to the vector $\mathit{\varphi }\left({\mathbf{x}}_i\right)$, we have that $S_w^N\left(\mathbf{X}\right)=\mathbf{\Phi }\left(\mathbf{X}\right)·\mathit{\xi }$, with $S_w^N\left(\mathbf{X}\right):={[S_w^N\left({\mathbf{x}}_1\right),\dots ,S_w^N\left({\mathbf{x}}_n\right)]}^{\top }$.

From now on, we will refer to $\mathbf{\Phi }\left(\mathbf{X}\right)$ as $\mathbf{\Phi }$.

Proposition 2.

The following statements hold for European payer swaptions.

(i) 

The finite-dimensional process $S_w^N$ uniformly converges to $S_w$ on $\mathcal{D}$ as $N_T\to \infty$, $N_t\to \infty$ and $N_K\to \infty$, almost surely;

(ii) 

$S_w^N$ is a decreasing function of K on $\mathcal{D}$ if and only if ${\xi }_{i,j,k}\ge {\xi }_{i,j,k+1}$;

(iii) 

$S_w^N$ is a convex function of K on $\mathcal{D}$ if and only if ${\xi }_{i,j,k+2}-{\xi }_{i,j,k+1}\ge {\xi }_{i,j,k+1}-{\xi }_{i,j,k}$.

These properties can be proved using the same methodology as in Maatouk and Bay (2017) for proving monotonicity and convexity. Note that these inequality constraints are linear in the components of $\mathit{\xi }$.

Remark 1.

For a European receiver swaption, the above properties are the same for $\left(i\right)$ and $\left(iii\right)$. However, $\left(ii\right)$ has to be replaced by: $S_w^N$ is an increasing function of K if and only if ${\xi }_{i,j,k}\le {\xi }_{i,j,k+1}$.

However, it is not possible to impose the in-plane triangular condition everywhere on the domain $\mathcal{D}$ with a finite number of checks. In empirical Section 4, we consider a weaker version of this constraint by only imposing its validity for time steps of size 1 year.

This constraint is set using a “fictitious grid” of maturities $T^{*}=[T_1^{*},T_2^{*},\cdots ,T_{N_T^{*}}^{*}]$, where $T_1^{*}=T_1$, $T_{N_T^{*}}=T_{N_T}$ and the step ${\delta }_T^{*}=\frac{1}{T_1-T_{N_T}}$. Therefore, it is a rescaled 1 year step.

Formally, we consider the following weaker version of the in-plane triangular condition:

$$S_w^N(T_l^{*},T_{l+1}^{*},K)+S_w^N(T_{l+1}^{*},T_{l+2}^{*},K)-S_w^N(T_l^{*},T_{l+2}^{*},K)\ge 0,l=1,\cdots ,N_T^{*}.$$

(5)

This is equivalent to:

$$\mathit{\varphi }(T_l^{*},T_{l+1}^{*},K)·\mathit{\xi }+\mathit{\varphi }(T_{l+1}^{*},T_{l+2}^{*},K)·\mathit{\xi }-\mathit{\varphi }(T_l^{*},T_{l+2}^{*},K)·\mathit{\xi }\ge 0.$$

(6)

Then, (6) is linear in $\mathit{\xi }$ and can be added to the constraints defined in Proposition 2.

Given property $\left(i\right)$ of Proposition 2, if we define $\mathcal{M}$ as the set of 3-dimensional continuous functions which are increasing and monotonic with respect to K, and respecting the in-plane triangular inequality (for steps of size 1 year, defined as (5)), then our construction problem consists in finding the conditional distribution of $S_w^N$ such that

$$\begin{array}{c}\left\{\begin{array}{l}\mathit{y}=S_w^N\left(\mathbf{X}\right)+\mathit{\epsilon }\\ S_w^N\in \mathcal{M}.\end{array}\right.\end{array}$$

Given properties $\left(ii\right)$ and $\left(iii\right)$ of Proposition 2, our process $S_w^N$ satisfies the no-arbitrage conditions in the strike direction on the entire domain $\mathcal{D}$ when these constraints are satisfied at the nodes. The problem above can then be restated as follows

$$\begin{array}{l}\left\{\begin{array}{l}\mathit{y}=\mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }\\ \mathit{\xi }\in {\mathcal{C}}_{ineq}.\end{array}\right.\end{array}$$

Indeed, $S_w^N\in \mathcal{M}\iff \mathit{\xi }\in {\mathcal{C}}_{ineq}$, where ${\mathcal{C}}_{ineq}$ is a set of linear inequality constraints as defined in $\left(ii\right)$, $\left(iii\right)$ of Proposition 2 and the relaxed in-plane triangular inequality constraint (6).

3.3. Maximum Likelihood Estimation

The parameters of the kernel function c and the noise parameter $\varsigma$ can be given as an input or estimated. Let $\mathrm{\Theta }={[{\theta }_T,{\theta }_t,{\theta }_K,\sigma ,{\varsigma }^2]}^{\top }$. In our approach, we estimate $\mathrm{\Theta }$ as the hyperparameter vector that maximizes the marginal log likelihood $\mathcal{L}\left(\mathrm{\Theta }\right)$ for the process $S_w^N$.

The unconstrained Gaussian Likelihood is written as $\mathbb{P}(\mathit{y}=\mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }|\mathrm{\Theta })$. Under the finite dimensional approximation, the marginal log likelihood can be expressed as:

$$\mathcal{L}\left(\mathrm{\Theta }\right)=-\frac{1}{2}{\mathit{y}}^{\top }{(\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }+{\varsigma }^2{I}_n)}^{-1}\mathit{y}-\frac{1}{2}\log (det(\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }+{\varsigma }^2{I}_n))-\frac{n}{2}\log \left(2\pi \right).$$

(7)

This marginal log likelihood also has a closed form derivative with respect to each parameter ${\mathrm{\Theta }}_i$ (see Rasmussen and Williams (2005)), which is given as:

$$\frac{\partial \mathcal{L}\left(\mathrm{\Theta }\right)}{\partial {\mathrm{\Theta }}_i}=\frac{1}{2}{\mathit{y}}^{\top }{A}^{-1}\frac{\partial A}{\partial {\mathrm{\Theta }}_i}\mathit{y}-\frac{1}{2}tr\left(A^{-1}\frac{\partial A}{\partial {\mathrm{\Theta }}_i}\right).$$

(8)

Here, $A=(\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }+{\varsigma }^2{I}_n)$ and $\frac{\partial A}{\partial {\mathrm{\Theta }}_i}$ is the element-wise derivative of A with respect to ${\mathrm{\Theta }}_i$.

This closed form can be used in order to shorten the computation time of the MLE in practice. This is useful because the computation of the MLE is longer for the swaption cube than for the equity surface, since the product $\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }$ depends on the dimension of the problem.

Remark 2.

The reason for the choice of maximizing the unconstrained likelihood instead of maximizing the constrained likelihood $\mathbb{P}(\mathit{y}=\mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }|\mathit{\xi }\in {\mathcal{C}}_{ineq},\mathrm{\Theta })$ is discussed in Bachoc et al. (2019). In this paper, it is explained that constraining the GP increases the computational burden of the maximization, with a negligible impact on the resulting MLE.

3.4. The Most Probable Response Cube and Measurement Noises

In the constrained GP regression case, we consider the mode of the truncated Gaussian process as an estimator for the cube instead of the mean. For the unconstrained GP regression case, mean and mode coincide because of the Gaussian profile of the conditional distribution, but the mode is easier to compute.

The maximum a posteriori (MAP) of $S_w^N$ given the constraints satisfies the constraints on the entire domain. In the sense of Bayesian statistics, it coincides with the mode of the truncated Gaussian process. Its expression is given in Cousin et al. (2016),

$${\mathbf{M}}_{S_w^N}(T,t,K):=\sum _{i=1}^{N_T}\sum _{j=1}^{N_t}\sum _{k=1}^{N_K}{\widehat{\mathit{\xi }}}^{i,j,k}{\varphi }_{i,j,k}(T,t,K),$$

(9)

where $\widehat{\mathit{\xi }}={\left({\widehat{\mathit{\xi }}}^{(1,1,1)},\cdots {\widehat{\mathit{\xi }}}^{(i,j,k)},\cdots ,{\widehat{\mathit{\xi }}}^{(N_T,N_t,N_K)}\right)}^{\top }$ is the MAP of the Gaussian coefficients $\mathit{\xi }$, which satisfies the inequality constraints. In order to locate the largest noise terms, we proceed as in Chataigner et al. (2021). We compute the joint MAP($\widehat{\mathit{\xi }},\widehat{\mathit{\epsilon }}$) of the truncated Gaussian vector $(\mathit{\xi },\mathit{\epsilon })$. This joint MAP ($\widehat{\mathit{\xi }},\widehat{\mathit{\epsilon }}$) is solution of:

$$\underset{\mathit{\vartheta },\mathit{e}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\mathbb{P}\left(\mathit{\xi }\in [\mathit{\vartheta },\mathit{\vartheta }+d\mathit{\vartheta }],\mathit{\epsilon }\in [\mathit{e},\mathit{e}+d\mathit{e}]\mid \mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }=\mathit{y},\mathit{\xi }\in {\mathcal{C}}_{ineq}\right).$$

The fact that $(\mathit{\xi },\mathit{\epsilon })$ is Gaussian with a mean 0 with the covariance matrix and the block-diagonal matrix

$$\left(\begin{array}{cc}{\mathrm{\Gamma }}^N& 0\\ 0& {\varsigma }^2{I}_n\end{array}\right),$$

implies that ($\widehat{\mathit{\xi }},\widehat{\mathit{\epsilon }}$) is a solution to the quadratic problem:

$$\underset{\mathbf{\Phi }·\mathit{\vartheta }+\mathit{e}=\mathit{y},\mathit{\vartheta }\in {\mathcal{C}}_{ineq}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathit{\vartheta }}^{\top }{\left({\mathrm{\Gamma }}^N\right)}^{-1}\mathit{\vartheta }+{\mathit{e}}^{\top }{\left({\varsigma }^2{I}_n\right)}^{-1}\mathit{e}\right).$$

(10)

The most probable response cube is then $M_{S_w^N}\left(\mathbf{x}\right)=\mathbf{\Phi }\left(\mathbf{x}\right)·\widehat{\mathit{\xi }}$, for $\mathbf{x}\in \mathcal{D}$, and the most probable measurement noise is $\widehat{\mathit{\epsilon }}$.

3.5. Sampling

Contrary to constrained spline interpolation approaches, the GP regression is a truly probabilistic approach. Sampling of the posterior distribution can be used for uncertainty quantification. The sampling paths of the swaption price cube consist of sampling $\mathit{\xi }$ truncated on ${\mathcal{C}}_{ineq}$, such that $\mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }=\mathit{y}$. The conditional distribution of $\mathit{\xi }|\mathit{y}=\mathbf{\Phi }·\mathit{\xi }+\mathit{\epsilon }$ is multivariate normal with mean vector ${\mu }_{\mathrm{cond}}$ and covariance matrix ${\mathrm{\Sigma }}_{\mathrm{cond}}$ defined as follows:

$$\begin{array}{c}\hfill {\mu }_{\mathrm{cond}}={\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }{(\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }+{\varsigma }^2{I}_n)}^{-1}\mathit{y},\end{array}$$

(11)

and

$$\begin{array}{c}\hfill {\mathrm{\Sigma }}_{\mathrm{cond}}={\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }{(\mathbf{\Phi }{\mathrm{\Gamma }}^N{\mathbf{\Phi }}^{\top }+{\varsigma }^2{I}_n)}^{-1}\mathbf{\Phi }{\mathrm{\Gamma }}^N.\end{array}$$

(12)

In practice, we will sample this truncated distribution by using Hamiltonian Monte Carlo, as presented in Pakman and Paninski (2012). The starting vector we must choose has to satisfy the constraints. Thus, $\widehat{\mathit{\xi }}$, the MAP of $\mathit{\xi }$ defined in Section 3.4, is an ideal candidate.

4. Empirical Results

This section compares the performance of the “constrained” GP regression with a calibrated SABR approach.

4.1. Data

For our empirical study, our data set consists of, at a quotation date $t_0$, 112 OTM payer swaptions, 28 ATM swaptions and 112 OTM receiver swaptions with maturities $T=[5,10,15,20]$ and tenors $t=[1,2,5,10,15,20,30]$. There is then $N=252$ input prices. For OTM payer swaptions, quotes are provided for the relative strikes $K_{re{l}_{Payer}}=[0.0025,0.005,0.01,0.02]$. For the OTM receiver swaptions, we have $K_{re{l}_{Receiver}}=[-0.02,-0.01,-0.005,-0.0025]$. At the money, the prices of payer and receiver swaptions coincide. Each option of our data set is listed with market price, market implied normal volatility, forward swap rate, absolute strike and annuity. The annuities are computed from a yield curve, and they are built from the observed swap rates.

Absence of Arbitrages in the Data Set

The first step of our analysis is to check if the data set itself is exempted from arbitrages, as defined in Proposition 1. The in-plane triangular condition compares swaptions with the same absolute strike and different options expiries. Since the options in our data set are quoted for relatives strikes, we do not have multiple observations for the same absolute strike; then, we lack the data to test the in-plane triangular constraint. We can, however, test the monotonicity and convexity constraint in the strike direction for both payer and receiver swaptions and for each pair (Maturity, Tenor) := $(T,t)$. In this data set, there are 28 pairs of maturities and tenors.

As stated in

Table 1. Percent of pairs (T, t) respecting the absence of arbitrage in strike constraints defined in Proposition 1.

Pairs (T, t) Respecting the AOA Constraints Input Data	Monotonicity Constraint in K	Convexity Constraint in K
Payer	100%	67.86%
Receiver	100%	100%

, there are no violations of the monotonicity constraint; therefore, the data set is exempted from call spreads arbitrage. The data set is not exempted from butterfly spreads arbitrage because, for the payer swaptions, only $67.86\%$ of the pairs $(T,t)$ respect the convexity constraint. Nevertheless, arbitrable observations are not removed from the data set, since the magnitude of constraint violation is relatively low2, and we consider that these data bring valuable information to the swaption cube construction problem. In our GP methodology, we assume that violations of the no-arbitrage constraints are due to measurement noises. The idea is that even if observations may slightly violate the convexity constraints, due to, e.g., a lack of market liquidity, the predicted GP surface is guaranteed to respect this constraint everywhere on the input domain.

4.2. SABR Model Benchmark

In all our study, we will use the SABR model as a benchmark regarding the prediction performance for our Gaussian process model. The SABR model has become a market standard for interpolation of swaption volatilities in the strike direction.

In this section, we briefly explain the calibration of the SABR model and how we estimate the parameters of the model.

4.2.1. SABR Model

SABR is a dynamic model in which the forward process F and the volatility process $\widehat{\sigma }$ satisfy the following system of SDE:

$$\begin{array}{c}\left\{\begin{array}{l}d\widehat{F}\left(t\right)=\widehat{\sigma }\left(t\right)\widehat{F}{\left(t\right)}^{\beta }dW\left(t\right),\widehat{F}\left(0\right)=f\\ d\widehat{\sigma }\left(t\right)=\alpha \widehat{\sigma }\left(t\right)dZ\left(t\right),\widehat{\sigma }\left(0\right)=\sigma \\ dW\left(t\right)dZ\left(t\right)=\rho dt\end{array}\right.\end{array}$$

where W, Z are Wiener processes with correlation $\rho \in [-1,1]$, $\alpha \ge 0$, $0\le \beta \le 1$ and $\sigma >0$. In our study, we fix $\beta =1$. In order to construct the swaption price cube via the SABR model, we consider as many SABR models as underlying swap, i.e., pair $(T,t)$.

For a pair $(T,t)$, the calibration procedure is explained in Section 4.3.4. To accommodate with negative rates, we use the so-called Shifted SABR model defined as follows:

$$\begin{array}{c}\left\{\begin{array}{l}d\widehat{F}\left(t\right)=\widehat{\sigma }\left(t\right){(\widehat{F}\left(t\right)+s)}^{\beta }dW\left(t\right),\widehat{F}\left(0\right)=f\\ d\widehat{\sigma }\left(t\right)=\alpha \widehat{\sigma }\left(t\right)dZ\left(t\right),\widehat{\sigma }\left(0\right)=\sigma \\ dW\left(t\right)dZ\left(t\right)=\rho dt\end{array}\right.\end{array}$$

where s is the shift parameter.

4.2.2. Model Calibration and Pricing

As explained in Hagan et al. (2002), an approximated analytical solution for the implied volatility exists. The volatility of a swaption with maturity $T_{ex}$ is given as the following asymptotic approximation, where we consider $\beta$ = 1:

$${\sigma }_N\left(K\right)=\sigma \frac{f-K}{\log \frac{f}{K}}·\left(\frac{z}{x\left(z\right)}\right)·\left[1+(-\frac{1}{24}{\sigma }^2+\frac{1}{4}\rho \sigma \alpha +\frac{1}{24}(2-3{\rho }^2){\alpha }^2)T_{ex}\right],$$

where

$$z=\frac{\alpha }{\sigma }\log \frac{f}{K},x\left(z\right)=\log \left(\frac{\sqrt{1-2\rho z+z^2}-\rho +z}{1-\rho }\right).$$

This model is free of arbitrage except for very low strikes and large maturities $T_{ex}$, for which the smile ${\sigma }_N\left(K\right)$ leads to negative probabilities and therefore arbitrages. This behavior of the smile for such strikes and maturities has been empirically shown in Hagan et al. (2014). The normal volatilities of the shifted SABR model are obtained by replacing in the formula above f by $f+s$ and K by $K+s$, where s is the shift parameter, which is chosen according to the data set. In our study, we consider $s=0.025$.

In this approach, a set of parameters $(\beta ,\sigma ,\alpha ,\rho )$ is mapped to each distinct pair $(T,t)$ observed. Once we fixed $\beta =1$, the other parameters $(\sigma ,\alpha ,\rho )$ are calibrated by minimizing the following across the m strikes observed for the observed pair $(T,t)$:

$$\begin{array}{c}\hfill {\displaystyle \sum _{k=1}^m}{[{\sigma }_N(K_k;\sigma ,\alpha ,\rho )-{\sigma }^{MARKET}\left(K_k\right)]}^2,m>0.\end{array}$$

(13)

Then, once the parameters are calibrated for each observed pair $(T,t)$, the price of European payer and receiver swaptions $S_w(T,t,K)$ is obtained using the normal SABR volatility ${\sigma }_N\left(K\right)$ as input in Bachelier’s pricing formula.

4.2.3. Unobserved Parameter Estimation

The previous section explained how to calibrate the parameters of the shifted SABR model for each pair $(T,t)$, where we have at least one observation of swaptions prices. In order to reconstruct the cube, a set of parameters $(\beta ,\sigma ,\alpha ,\rho )$ needs to be mapped to each unobserved couple $(T,t)$. As previously, $\beta$ is set to 1. Then, for each unobserved pairs $(T,t)$, each parameter of the set $(\sigma ,\alpha ,\rho )$ is chosen as the weighted average of the corresponding parameter of the four nearest calibrated pairs $(T,t)$. The weight is the inverse of the distance between the unobserved pair and the four nearest calibrated pairs. This method of interpolation and extrapolation has been chosen because it offered better results than a cubic spline approach, especially when extrapolating in-sample. From now on, this method will be referred to as the “barycentric mean” approach. One problem of such a method of interpolation and extrapolation is that the SABR model parameters $(\beta ,\sigma ,\alpha ,\rho )$, for each unobserved pair $(T,t)$, are estimated independently in contrary to the classical calibration. For an unobserved pair $(T,t)$, there is then no guarantee that the resulting smile will be free of arbitrage. The absence of arbitrage of the swaption cube obtained using this method is investigated in Section 4.3.3.

4.3. Absence of Arbitrage, Calibration and Prediction Performance

In this section, we compare the violation of AOA, calibration and prediction performance for the cubes constructed from the constrained GP approach and the SABR benchmark approach introduced in Section 4.2.

4.3.1. Implementation of the GP Regression Approach

Since OTM payer and receiver swaptions are different contracts, with different domains of strike (absolute and relative), they need to be considered separately. For the OTM payer swaptions, the limits of the 3-dimensional grid are defined by ${\mathcal{D}}_{Payer}$ where T : $[5,20]$, t : $[1,30]$ and K : $K_{Payer}$, and the limits of the 3-dimensional grid for OTM receiver swaptions are defined by ${\mathcal{D}}_{Receiver}$ where T : $[5,20]$, t : $[1,30]$ and K : $K_{Receiver}$. For both payer and receiver swaptions, we consider a GP method with matern $5/2$ kernels3 over a ${[0,1]}^3$ rescaled domain. The parameters of the kernels $[{\theta }_T,{\theta }_t,{\theta }_K,\sigma ]$ and the homoscedastic noise variance are fitted through MLE as described in Section 3.3. Each different set of observed data will lead to a different metamodel. The MLE is maximized with the function ’minimize’, with the method ’L-BFGS-B’, from the Python library ’Scipy.optimize’. With the purpose of not ending up with a local minimum, the algorithm is restarted 20 timed with random starting points. In order to speed up the computation time, the Jacobian of the log likelihood is given as the input of the optimizer routine.

The grid of basis functions for constructing the finite-dimensional process $S_w^N$ consists of $six$ nodes in the absolute strike direction, $seven$ nodes in the tenor direction and $six$ nodes in the maturity direction.

In order to solve the quadratic problem (10), and thereby find the MAP, the Python library ’quadprog’ is used. Sampling of the posterior swaption cubes distribution is conducted by Hamiltonian Monte Carlo (see Section 3.5). Its implementation is inspired by the algorithm described in Pakman and Paninski (2012).

4.3.2. Calibration and Testing Methodology

Let us now explain the methodology used for calibration and testing in practice for our GP regression model and for the SABR model.

GP regression models and the SABR model are fitted on the same randomly generated subsets of the whole data set. Each random subset is divided in two equally sized subsets: one with prices of OTM payer swaptions and ATM swaptions and the other with prices of OTM receiver swaptions and ATM swaptions. For the prediction performance, the whole dataset is chosen as the testing dataset.

For the SABR model to calibrate correctly, each pair $(T,t)$ needs at least one ATM swaption observation, one OTM payer swaption observation, and one OTM receiver swaption observation. When a small random training set is chosen, it is possible that some pairs $(T,t)$ end up with one or two observations; then, the calibration could lead to absurd results. To address this issue, we decided that each random training set will always contain one observation of the ATM price and at least one observation of a payer and receiver OTM price for the pairs $(5,5)$, $(5,10)$, $(10,5)$ and $(10,10)$. Those points are very liquid in the market, and quotes are then expected in practice. The details of the SABR calibration procedure are explained in Appendix A.

For the sake of comparability, the observed data for the $(T,t)$ pairs $(5,5)$, $(5,10)$, $(10,5)$ and $(10,10)$ are also included in the training data for the GP.

All results below are produced from the following experimental procedure. We first choose a percentage p. Then, the training set is constituted of two random subsets $S_1$ and $S_2$. $S_1$ includes a random $p\%$ of the ATM swaptions and OTM payer swaptions, and $S_2$ includes a random $p\%$ of the ATM swaptions and OTM receiver swaptions. The SABR model is fitted on the union of $S_1$ and $S_2$ (there is one set of parameters $(\beta ,\sigma ,\alpha ,\rho )$ for each pair $(T,t)$, which is obtained through calibration or interpolation and extrapolation). The GP regression model is fitted two times, once on $S_1$ and once on $S_2$, and then, the results for the payer and receiver swaptions are gathered together. For each ATM value, the value kept is the average of the values obtained for the swaptions payer and receiver ATM if there is zero or two observations of this value. If there is only one observation, then the predicted value is taken from the output of the GP which was fitted on this observation. For each percentage of training data p we consider, random sampling, fitting, and testing is repeated 200 times. Then, the performance results are averaged and presented in the tables of Section 4.3.3, Section 4.3.4 and Section 4.3.5.

4.3.3. Absence of Arbitrage in the Predicted Swaption Cube

In this subsection, we compare the performances of the constrained GP regression model and the SABR model with respect to the arbitrage-free constraints defined in Proposition 1. The grid we use for testing is a grid of maturities, tenors such that, $T=[5,6,\cdots ,19,20]$, $t=[1,2,\cdots ,29,30]$ and of $nine$ strikes K evenly spaced between the minimum and the maximum of $K_{Payer}$ when testing the payer swaption cube, and between the minimum and maximum of $K_{Receiver}$ when testing the receiver swaption cube. More precisely, for the monotonicity and convexity in strike constraints, we check how many pairs $(T,t)$ among the 480 pairs of the testing grid respect the constraints. For the in-plane triangular constraint, we check the constraints on 5000 randomly selected $T_1$, $T_2$, $T_3$, K values in the the testing grid.

Table 2. Respect of the no-arbitrage constraints for the predicted OTM payer swaptions priced by constrained and unconstrained GP regression, for increasing sizes of training set.

Respect of the AOA Constraints GP Payer	Decrease in Strike (Constrained)	Convexity in Strike (Constrained)	In-Plane Triangular Inequality (Constrained)	Decrease in Strike (Unconstrained)	Convexity in Strike (Unconstrained)	In-Plane Triangular Inequality (Unconstrained)
p = 15%	100%	100%	100%	87.84%	8.18%	99.58%
p = 30%	100%	100%	100%	93.79%	13.22%	99.97%
p = 50%	100%	100%	100%	94.37%	10.24%	99.98%
p = 70%	100%	100%	100%	99.55%	5.98%	99.97%
p = 90%	100%	100%	100%	92.17%	1.51%	99.92%

and

Table 3. Respect of the no-arbitrage constraints for the predicted OTM payer swaptions priced by the chosen SABR model with barycentric mean parameter interpolation, for increasing sizes of training set.

Respect of the AOA Constraints SABR Payer	Decrease in Strike	Convexity in Strike	In-Plane Triangular Inequality
p = 15%	99.00%	99.70%	98.09%
p = 30%	99.49%	99.82%	97.96%
p = 50%	99.82%	99.91%	99.186%
p = 70%	99.96%	99.99%	99.90%
p = 90%	100%	100%	100%

(respectively,

Table 4. Respect of the no-arbitrage constraints for the predicted OTM receiver swaptions priced by constrained and unconstrained GP regression, for increasing sizes of training set.

Respect of the AOA Constraints GP Payer	Increase in Strike (Constrained)	Convexity in Strike (Constrained)	In-Plane Triangular Inequality (Constrained)	Increase in Strike (Unconstrained)	Convexity in Strike (Unconstrained)	In-Plane Triangular Inequality (Unconstrained)
p = 15%	100%	100%	99.51%	31.46%	82.67%	97.10%
p = 30%	100%	100%	99.08%	49.29%	82.08%	97.37%
p = 50%	100%	100%	99.53%	56.49%	86.41%	98.00%
p = 70%	100%	100%	99.78%	60.03%	93.69%	97.95%
p = 90%	100%	100%	99.94%	56.36%	91.74%	97.87%

and

Table 5. Respect of the no-arbitrage constraints for the predicted OTM receiver swaptions priced by the SABR model with barycentric mean parameter interpolation, for increasing sizes of training set.

Respect of the AOA Constraints SABR Receiver	Increase in Strike	Convexity in Strike	In-Plane Triangular Inequality
p = 15%	99.77%	98.73%	97.67%
p = 30%	99.82%	99.22%	97.62%
p = 50%	99.94%	99.67%	99.05%
p = 70%	100%	99.94%	99.88%
p = 90%	100%	100%	100%

) show the results for payer (respectively, receiver) swaptions.

We can observe that the prices produced by the SABR model, for a training set of size p = $50\%$ of the total input data size or lower, do not respect the monotonicity and convexity constraints. Still, the number of pairs $(T,t)$ violating the constraints compared to the total number of pairs is very low. When we check for which pairs $(T,t)$ the constraints are not respected, we see that our method for avoiding absurd parameters values during the calibration of the SABR model does not prevent arbitrage for the observed pairs. For instance, pairs $(T,t)$ with less than three observations or no observations of one side of the smile can produce parameters leading to arbitrage. Arbitrage is also violated for unobserved pairs, for which the parameters are interpolated or extrapolated by barycentric mean. For training sets of size higher than $50\%$ of the total input size, we can consider that the SABR model produces free of arbitrages prices.

For payer and receiver swaptions, the monotonicity and convexity constraints in strike are always ensured for prices estimated through constrained Gaussian process regression (CGPR), unlike prices predicted through unconstrained Gaussian process regression (UGPR). We can remark that receiver swaptions prices estimated through UGPR achieve $91.74\%$ on the convexity in strike test, while payer swaptions achieve only $1.51\%$ even when the $90\%$ of the data set is given as training data. This difference in performance could be explained by the fact that the payer swaption database is not convex everywhere in strike.

In Section 3.2, we explain that we implement the in-plane triangular inequality constraints only for time steps of length 1 year. For payer swaptions, we see that the in-plane triangular constraint is always respected by the CGPR, and we can consider that it is also respected by the UGPR. The receiver swaptions table (Table 4) shows the impact of the 1-year step constraint. While the UGPR does not respect the in-plane triangular constraint everywhere, the CGPR produces a negligible error. Although this error is negligible, it is proof that this 1-year step constraint for the GPR is not enough to ensure that the in-plane triangular inequality is respected everywhere in the estimated price cube. In Johnson and Nonas (2009), it is mentioned that practitioners only consider the monotonicity and convexity of Proposition 1. Our empirical results support their decision. Even though our 1-year step constraint does not totally prevent in-plane triangular arbitrage, it could still be helpful for extrapolation.

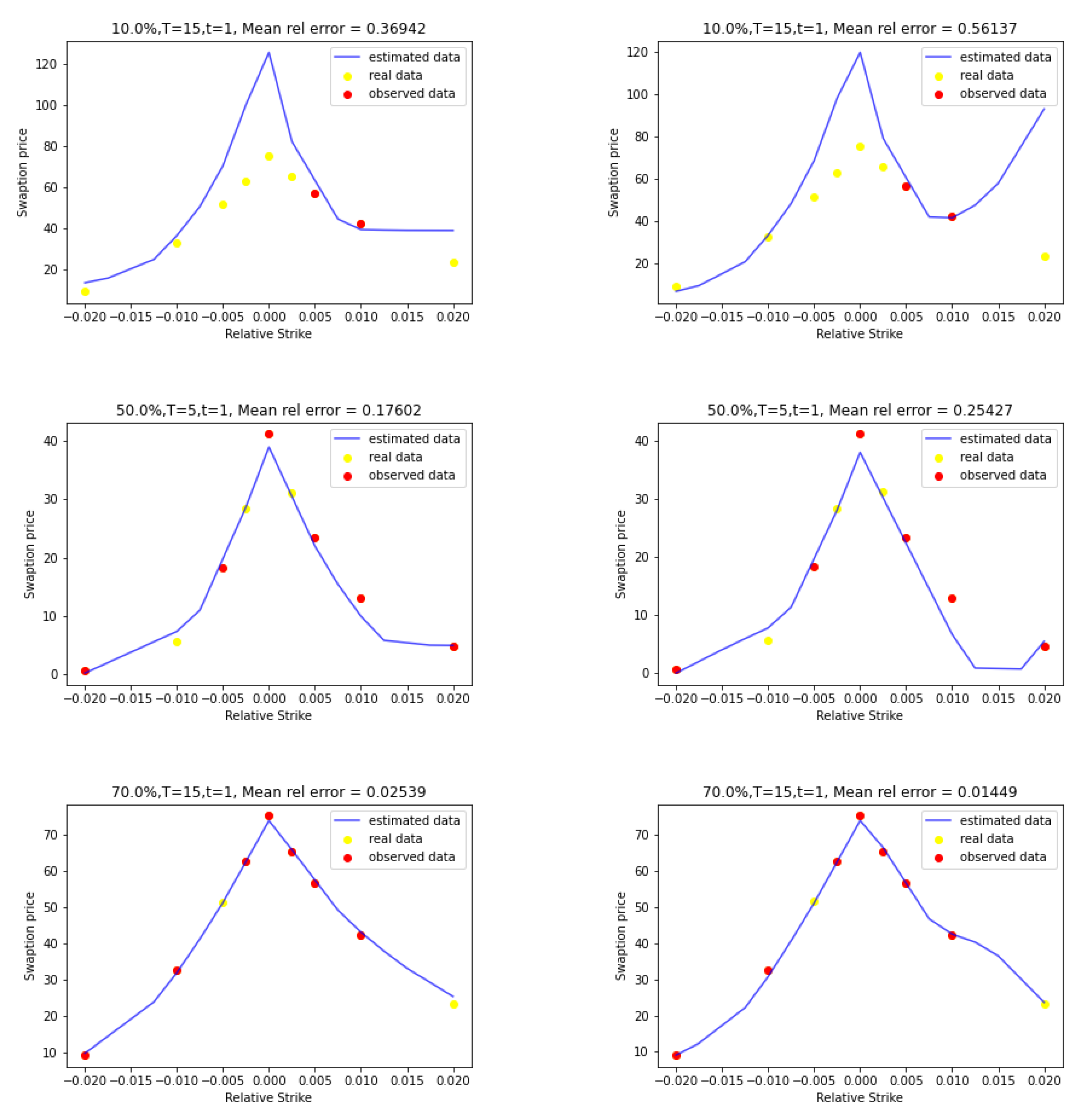
Figure 1 below presents a few graphical examples of price curves for fixed tenors and maturities produced by constrained Gaussian process regression (left side) and unconstrained Gaussian process regression (right side). We can easily observe the impact of the monotonicity and convexity along the strike direction constraint. In the bottom row of Figure 1, we can notice that the mean relative error of the unconstrained GP regression is lower than the one of the constrained GP regression. If we observe those two graphs, we can see that the unconstrained GP price crosses the option data price with the higher relative strike while the constrained GP price does not. The constrained GP regression forces the path of the mode of the GP to be convex and increasing/decreasing in strike. Since the payer data set is not convex everywhere, it is not surprising that the convexity constraint increases the testing error.

4.3.4. Calibration Performance

Table 6. Mean relative calibration error and calibration RMSE of the constrained GP regression and SABR model with barycentric mean parameter interpolation, for increasing sizes of training set.

Average Calibration Error	Constrained GP Mean Relative Error	SABR Mean Relative Error	Constrained GP RMSE	SABR RMSE
p = 15%	1.77%	1.61%	2.68	12.65
p = 30%	2.29%	1.47%	2.78	10.56
p = 50%	2.67%	2.21%	3.43	11.67
p = 70%	3.02%	2.87%	3.88	13.85
p = 90%	3.25%	3.22%	4.11	14.59

shows the calibration performance of our models.

Based on the mean relative error metric, the SABR model calibrates better than the constrained GP model. That was to be expected, because the constrained GP regression assumes that the observations are noisy in order to avoid over-fitting and to respect the constraints of no arbitrage. Since the SABR model is not constrained, it gives better mean relative error. We can observe that the mean relative error increases with the size of the training set, and that the error of the GP regression model converges to the error of the SABR model. However, the constrained GP model average RMSE is lower than the average RMSE of the SABR model on all percentages p tested. This means that the estimated standard deviation of the distribution of the absolute errors of the SABR model is on average higher than the one of the constrained GP model.

4.3.5. Prediction Performance

Table 7. RMSE of the constrained GP regression and SABR model with barycentric mean parameter interpolation, for increasing sizes of training set.

Average Prediction Error	Constrained GP RMSE	SABR RMSE
p = 15%	29.01	172.42
p = 30%	27.83	58.55
p = 50%	9.98	33.25
p = 70%	6.30	20.57
p = 90%	4.71	16.54

shows the prediction performance of our models.

Based on the mean RMSE metric, the constrained GP regression performs better than the SABR model for all percentages. For larger and larger training sets, the two models perform better and better in prediction with respect to the RMSE.

The complexity of the GP regression is dominated by the inversion of the matrix of size $(N_{obs},N_{obs})$, where $N_{obs}$ is the number of observations in $S_1$ when we fit the payer swaption cube or the the number of observations in $S_2$ otherwise. The total complexity when producing the cube is then a $O((N_{ob{s}_{payer}}^3+N_{ob{s}_{receiver}}^3)\times L_1)$, where $L_1$ is the computation cost of the function ’minimize’ with 20 restarts and with the input of the Jacobian matrix of the MLE, defined in (8), as it significantly speeds up the minimization. The complexity of the calibration of the SABR model is $O((N_{ob{s}_{payer}}+N_{ob{s}_{receiver}})\times L_2)$ where $N_{obs}$ is the total number of observed data and $L_2$ is the computation cost of the function ’minimize’ with 20 restarts and without inputing a Jacobian4. Thus, one of the main drawbacks of GP-based interpolation is the computer time that can be quite substantial for a large dataset.

4.3.6. SABR Model Calibrated on the GP Predicted Cube

Instead of calibrating the SABR model directly on the observations, it is possible to use the GP-predicted cube as input.

Table 8. Average gain in RMSE when calibrating the SABR model with the output of the GP regression model.

Percentage of Data Used as Input	p = 15%	p = 30%	p = 50%	p = 70%	p = 90%
RMSE relative gain	63%	68%	59%	35%	19%

shows a significant improvement with respect to the RMSE between the two methods, especially for low percentage of input data. Indeed, for these ones, the SABR model cannot be calibrated properly because the smile is not well enough described. In fact, we need for each tenor and maturity at least one receiver OTM and one payer OTM to define the skew rho and the convexity alpha, plus a point near the ATM to define the model volatility sigma. As the percentage decreases, this condition is less satisfied. Thus, by using the GP cube, we provide an idea of the whole smile and get around the issue. We can see that the gain for $p=15\%$ is lower than for $p=30\%$. This can be explained by the fact that the performance of the GP model deteriorates when there are too few observations.

Table 9. Respect of the no-arbitrage constraints for the predicted OTM payer swaptions priced by the SABR model calibrated on observations or on the output of the GP model, for increasing sizes of training set.

Respect of the AOA Constraints Payer	Decrease in Strike (SABR)	Convexity in Strike (SABR)	In-Plane Triangular Inequality (SABR)	Decrease in Strike (GP-SABR)	Convexity in Strike (GP-SABR)	In-Plane Triangular Inequality (GP-SABR)
p = 15%	99.45%	99.80%	98.51%	99.90%	99.98%	100%
p = 30%	99.68%	99.98%	96.63%	100%	100%	100%
p = 50%	99.75%	99.90%	99.37%	100%	100%	100%
p = 70%	100%	100%	100%	100%	100%	100%
p = 90%	100%	100%	100%	100%	100%	100%

and

Table 10. Respect of the no-arbitrage constraints for the predicted OTM receiver swaptions priced by the SABR model calibrated on observations or on the output of the GP model, for increasing sizes of training set.

Respect of the AOA Constraints Receiver	Increase in Strike (SABR)	Convexity in Strike (SABR)	In-Plane Triangular Inequality (SABR)	Increase in Strike (GP-SABR)	Convexity in Strike (GP-SABR)	In-Plane Triangular Inequality (GP-SABR)
p = 15%	99.87%	99.20%	98.22%	99.99%	99.53%	99.52%
p = 30%	99.88%	99.40%	96.43%	100%	99.76%	99.97%
p = 50%	99.88%	99.70%	99.10%	100%	99.80%	100%
p = 70%	100%	100%	100%	100%	99.80%	100%
p = 90%	100%	100%	100%	100%	99.80%	100%

provide a comparison of the performance of the SABR model and GP-SABR model with respect to the no arbitrage constraints.

4.4. Uncertainty Quantification

By sampling the truncated Gaussian distribution described in Section 3.5, it is possible to obtain uncertainties for all the prices estimated through GP regression. The sampling is performed by Hamiltonian Monte Carlo, using the mode $\widehat{\xi }$ as the starting vector. In practice, we sample the distribution 5000 times. Therefore, we obtain 5000 GP paths of the swaption price cube, all respecting the constraints. These samplings could be used to generate quantiles and calculate model error due to uncertainty. Uncertainties due to interpolation/extrapolation could also be propagated into rate models to see the impact on exotic products pricing. For example, we could calibrate an HJM model with “a percentile 90” cube swaption and “a percentile 10” cube swaption; then, we price a basket of bermuda options with these two models and study the differences (AVA model).

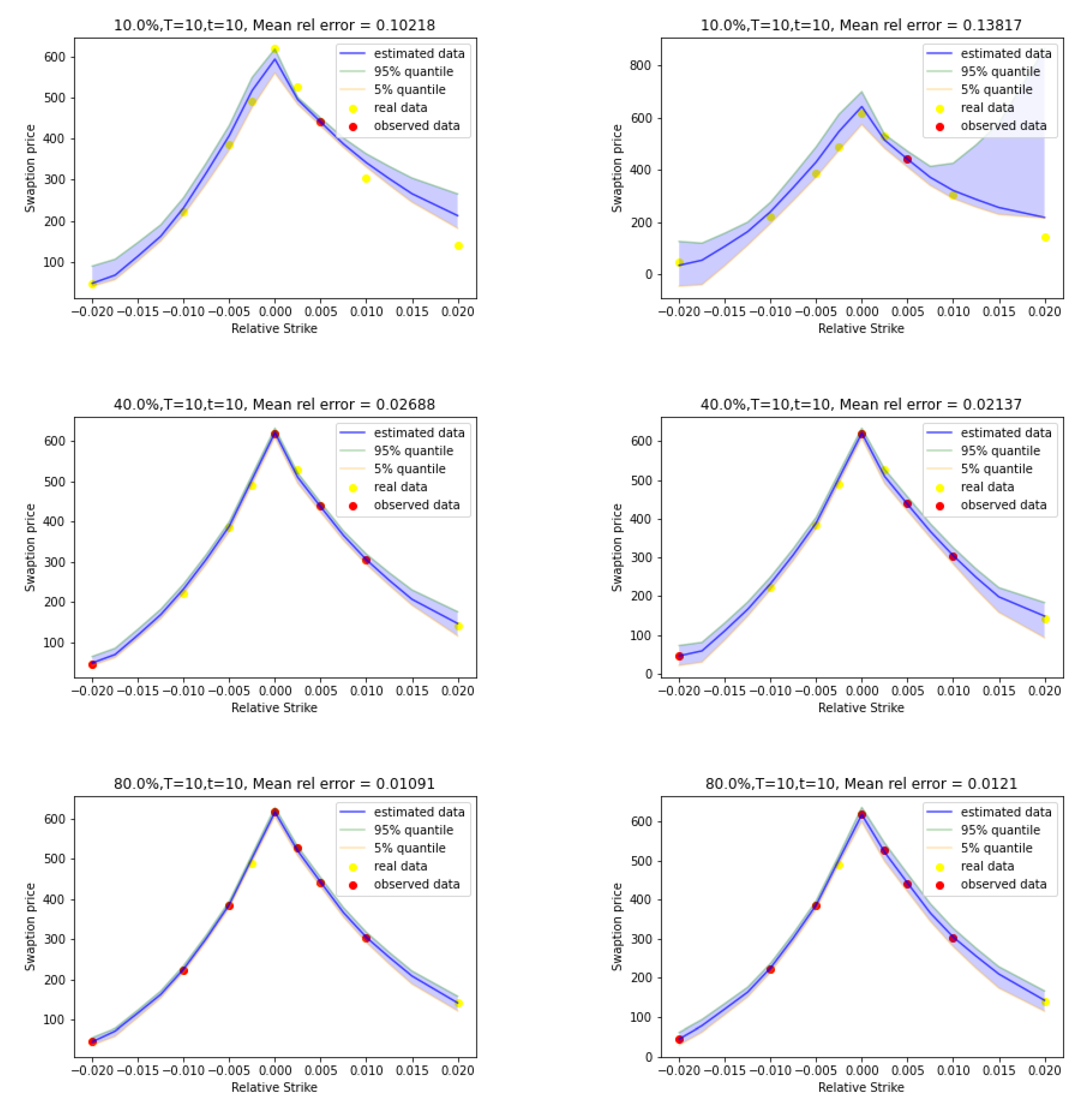
Figure 2 shows examples of price curves produced by constrained and unconstrained GP regression alongside their empirical pointwise quantiles. We can observe that adding observations reduces the size of the pointwise confidence intervals. We can also observe that unconstrained GP regression leads to wider pointwise confidence intervals. In Figure 2 (right-top), the $5\%$ empirical quantile of the posterior of the unconstrained GP is even negative, which is not allowed for prices.

5. Conclusions

In this paper, we introduce a methodology to construct a free of arbitrage swaption price cube based on GP regression. We apply this methodology on a data set of ATM, OTM payer and OTM receiver swaptions. We show that the constrained GP regression leads to arbitrage-free swaption cubes along the strike direction for any size of the training data. Even though the practitioners were usually satisfied by the fact that there are no call spreads and butterfly spreads, we go further by considering the in-plane triangular inequality introduced by Johnson and Nonas (2009). We empirically demonstrate that imposing a finite-dimensional weaker form of this condition is enough for the GP to generate swaption cubes with a negligible proportion of violation points, even for a small training set. We then compare the constrained GP model to a state-of-the-art SABR model fitted on the same data set. We show that the constrained GP performs better in prediction than the SABR model. The predictive performance of SABR seems to improves significantly when the model is calibrated on the GP-predicted cube. Finally, the GP approach is able to quantify in- and out-of-sample uncertainty through Hamiltonian Monte Carlo simulations, allowing for computation of model risk Additional Valuation Adjustment.

6. Further Research

A topic left to be addressed is the update of GP hyperparameters when a new quote streams in. A straightforward solution could be to use the last estimation of the maximum log-likelihood as the new starting point of the optimizer routine. However, since the computation cost of the GP regression increases when the number of observation increases, this solution could be intractable in practice. For this problem, Bayesian Optimization could be considered. As explained in Shahriari et al. (2016), Bayesian Optimization consists of selecting the $n+1$-th set of hyperparameters, based on an acquisition function computed with the current posterior distribution of the likelihood function. Yin et al. (2019) present another way of selecting the $n+1$-th point, based on a mean square error criteria.