Equivalent Risk Indicators: VaR, TCE, and Beyond
Abstract
:1. Introduction
2. VaR and TCE
2.1. Definitions
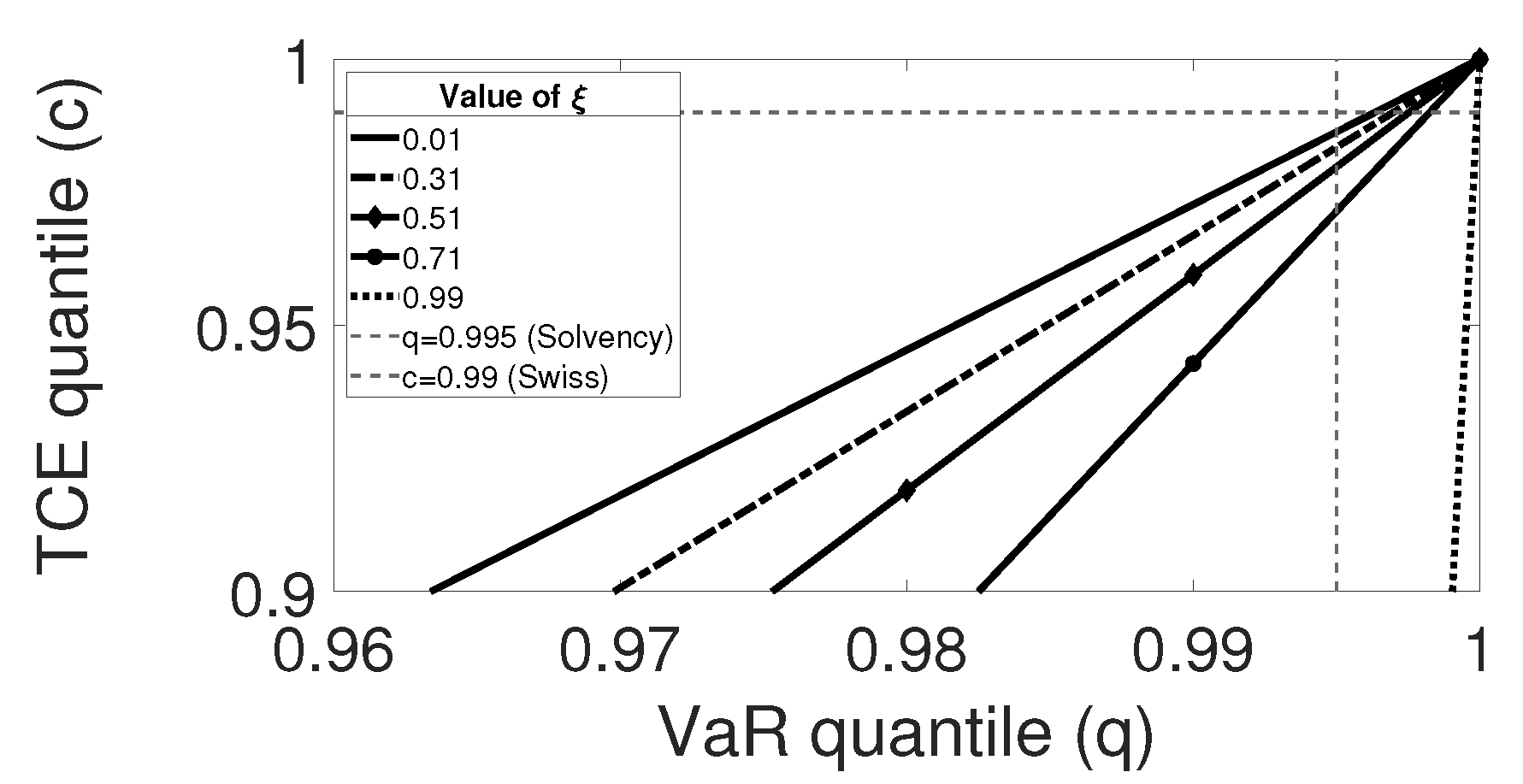
2.2. Relation between VaR and TCE Quantiles
2.3. Illustration
3. A New High-Order TCE Indicator
3.1. Definition
3.2. Pareto Distributed Losses
3.3. GPD Losses
- , to avoid the appearance of complex numbers in Equation (15).
- , which is a necessary property of the fourth parameter of the hypergeometric function.
4. Equivalence between High-Order Indicators
4.1. Pareto Distributed Losses
4.2. GPD Losses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Theorem 3
Appendix A.4. Proof of Theorem 4
References
- Acerbi, Carlo, and Dirk Tasche. 2002. On the coherence of expected shortfall. Journal of Banking & Finance 26: 1487–503. [Google Scholar]
- Acerbi, Carlo, Claudio Nordio, and Carlo Sirtori. 2001. Expected shortfall as a tool for financial risk management. arXiv arXiv:cond-mat/0102304. [Google Scholar]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Barbosa, Antonio, and Miguel Ferreira. 2004. Beyond Coherence and Extreme Losses: Root Lower Partial Moment as a Risk Measure. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=609221 (accessed on 15 May 2022).
- Barczy, Matyas, Fanni K. Nedényi, and László Sütő. 2022. Probability equivalent level of value at risk and higher-order expected shortfalls. arXiv arXiv:2202.09770. [Google Scholar]
- Basel Committee on Banking Supervision. 2019. The Market Risk Framework: In Brief. Available online: https://www.bis.org/bcbs/publ/d457_inbrief.pdf (accessed on 15 May 2022).
- Basel Committee on Banking Supervision. 2022. Basel iii: International Regulatory Framework for Banks. Available online: https://www.bis.org/bcbs/basel3.htm (accessed on 15 May 2022).
- Canada Office of Supervision of Financial Institutions. 2022. Regulatory Capital and Internal Capital Targets. Available online: https://www.osfi-bsif.gc.ca/Eng/fi-if/rg-ro/gdn-ort/gl-ld/Pages/a4_gd18.aspx (accessed on 15 May 2022).
- CEA. 2007. Solvency ii Glossary. Available online: https://piu.org.pl/public/upload/ibrowser/sol2_glossary_final_160307.pdf (accessed on 15 May 2022).
- Comité Européen des Assurances, and Mercer Oliver Wyman Limited. 2005. Solvency Assessment Models Compared: Essential Groundwork for the Solvency ii Project. Available online: https://www.naic.org/documents/committees_smi_int_solvency_eu_II-cea.pdf (accessed on 15 May 2022).
- Denuit, Michel, Jan Dhaene, Marc Goovaerts, and Rob Kaas. 2006. Actuarial Theory for Dependent Risks: Measures, Orders and Models. Hoboken: John Wiley & Sons. [Google Scholar]
- Fadina, Tolulope, Peng Liu, and Ruodu Wang. 2021. One Axiom to Rule Them All: An Axiomatization of Quantiles. Available online: https://ssrn.com/abstract=3944312 (accessed on 15 May 2022).
- Fiori, Anna Maria, and Emanuela Rosazza Gianin. 2021. Generalized Pelve and Applications to Risk Measures. Available online: https://ssrn.com/abstract=3949592 (accessed on 15 May 2022).
- Fuchs, Sebastian, Ruben Schlotter, and Klaus D. Schmidt. 2017. A review and some complements on quantile risk measures and their domain. Risks 5: 59. [Google Scholar] [CrossRef] [Green Version]
- Gatzert, Nadine, and Hans Wesker. 2011. A comparative assessment of basel ii/iii and solvency ii. Geneva Papers on Risk and Insurance: Issues and Practice 37: 539–70. [Google Scholar] [CrossRef] [Green Version]
- Hill, Bruce. 1975. A simple general approach to inference about the tail of a distribution. Annals of Statistics 3: 1163–74. [Google Scholar] [CrossRef]
- Hosking, John, and Jeremy Wallis. 1987. Parameter and quantile estimation for the generalized pareto distribution. Technometrics 29: 339–49. [Google Scholar] [CrossRef]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models: From Data to Decisions. Hoboken: John Wiley & Sons, vol. 715. [Google Scholar]
- Krokhmal, Pavlo. 2007. Higher moment coherent risk measures. Quantitative Finance 7: 373–87. [Google Scholar] [CrossRef]
- Lebedev, Nicolai. 1972. Special Functions and Their Applications. Mineola: Dover Publications. [Google Scholar]
- Le Courtois, Olivier. 2018. Some further results on the tempered multistable approach. Asia-Pacific Financial Markets 25: 87–109. [Google Scholar] [CrossRef]
- Le Courtois, Olivier, and Christian Walter. 2014. The computation of risk budgets under the lévy process assumption. Revue Finance 35: 203–28. [Google Scholar] [CrossRef]
- Le Courtois, Olivier, Jacques Lévy-Véhel, and Christian Walter. 2020. Regulation risk. North American Actuarial Journal 24: 463–74. [Google Scholar] [CrossRef]
- Li, Hanson, and Ruodu Wang. 2022. Pelve: Probability equivalent level of var and es (November 25, 2019). Journal of Econometrics. [Google Scholar] [CrossRef]
- Linsmeier, Thomas J., and Neil D. Pearson. 2000. Value at risk. Financial Analysts Journal 56: 47–67. [Google Scholar] [CrossRef]
- National Association of Insurance Commissioners. 2007. Own Risk and Solvency Assessment (ORSA) Guidance Manual. Kansas City: NAIC. [Google Scholar]
- Rostek, Marzena. 2010. Quantile maximization in decision theory. The Review of Economic Studies 77: 339–71. [Google Scholar] [CrossRef]
- Society of Actuaries. 2000. Getting to Know cte. Risk Management Newsletter. Available online: https://www.soa.org/globalassets/assets/library/newsletters/risk-management-newsletter/2004/july/rm-2004-iss02-ingram-b.pdf (accessed on 15 May 2022).
- Wang, Ruodu, and Ričardas Zitikis. 2021. An axiomatic foundation for the expected Shortfall. Management Science 67: 1413–29. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faroni, S.; Le Courtois, O.; Ostaszewski, K. Equivalent Risk Indicators: VaR, TCE, and Beyond. Risks 2022, 10, 142. https://doi.org/10.3390/risks10080142
Faroni S, Le Courtois O, Ostaszewski K. Equivalent Risk Indicators: VaR, TCE, and Beyond. Risks. 2022; 10(8):142. https://doi.org/10.3390/risks10080142
Chicago/Turabian StyleFaroni, Silvia, Olivier Le Courtois, and Krzysztof Ostaszewski. 2022. "Equivalent Risk Indicators: VaR, TCE, and Beyond" Risks 10, no. 8: 142. https://doi.org/10.3390/risks10080142
APA StyleFaroni, S., Le Courtois, O., & Ostaszewski, K. (2022). Equivalent Risk Indicators: VaR, TCE, and Beyond. Risks, 10(8), 142. https://doi.org/10.3390/risks10080142






