Claims Modelling with Three-Component Composite Models
Abstract
:1. Introduction
1.1. Current Literature
1.2. Proposed Composite Models
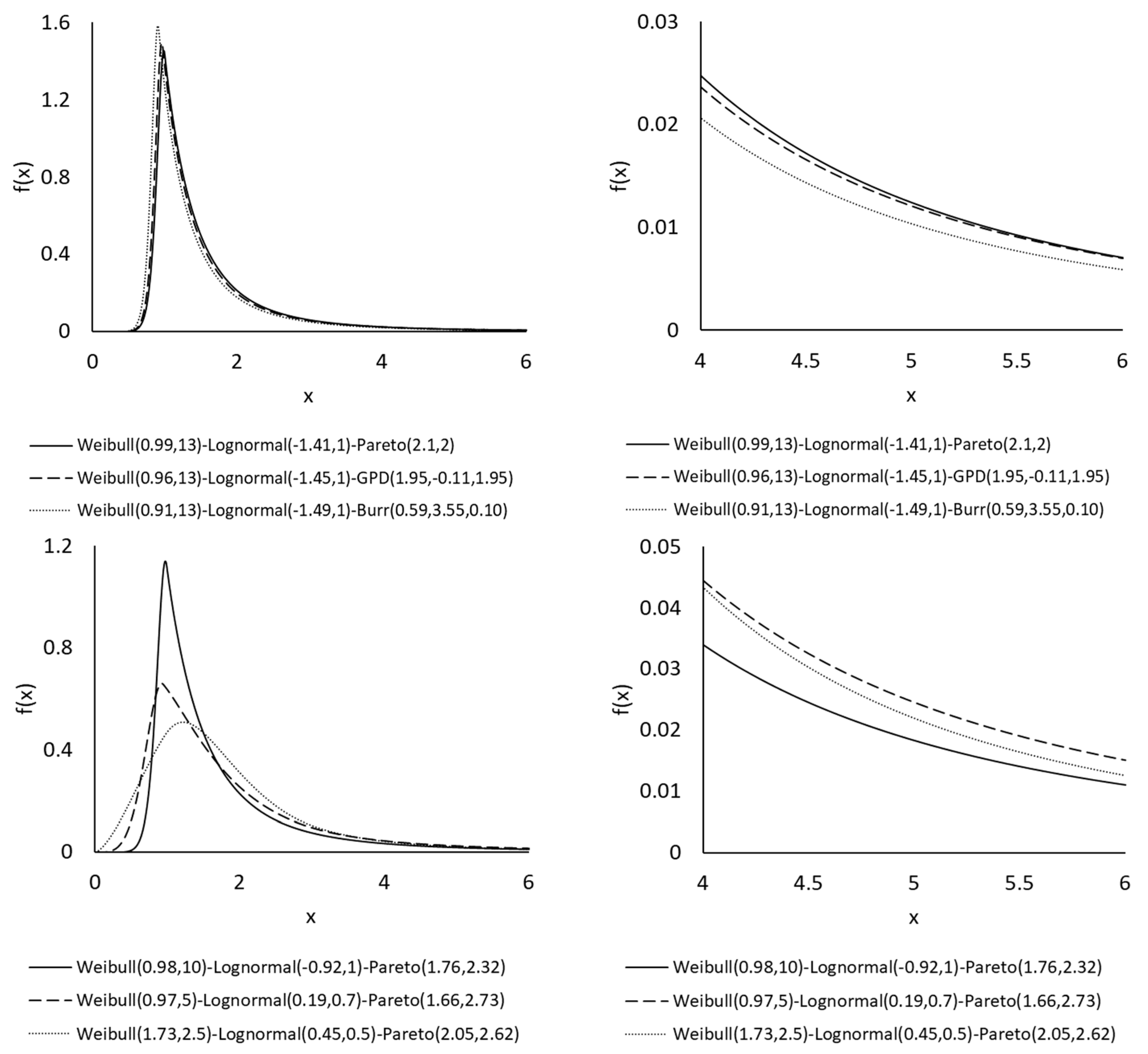
2. Weibull-Lognormal-Pareto Model
3. Weibull-Lognormal-GPD Model
4. Weibull-Lognormal-Burr Model
5. Application to Two Data Sets
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
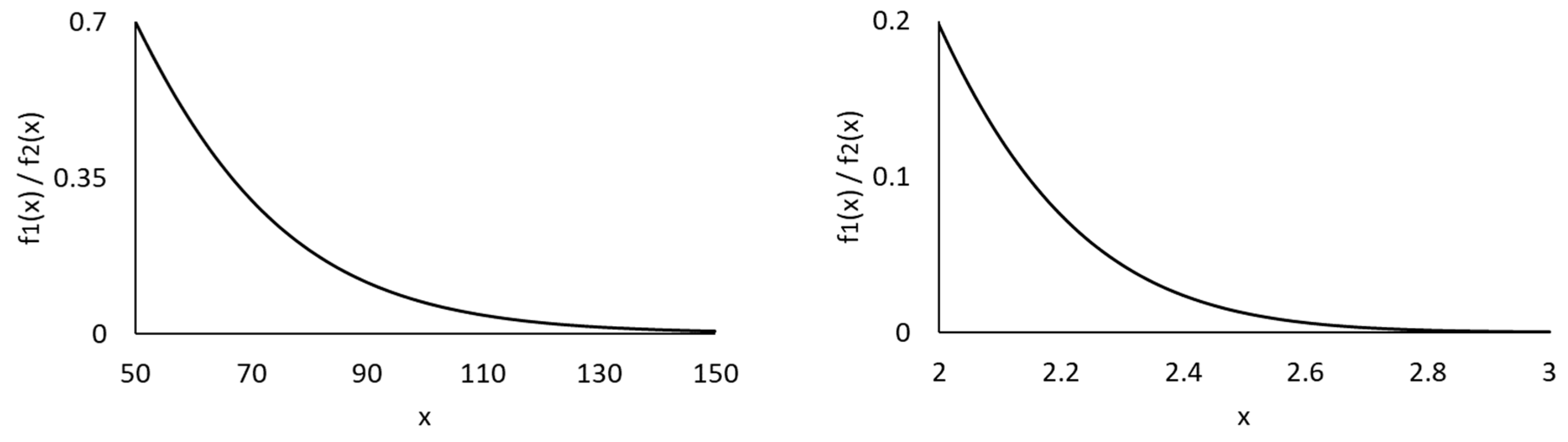
| 1 | The AIC is defined as , and the BIC as , where is the computed maximum log-likelihood value, is the effective number of parameters estimated, and is the number of observations. The KS test statistic is calculated as , that is, the maximum distance between the empirical and fitted distribution functions. The DIC is computed as the posterior mean of the deviance plus the effective number of parameters under the Bayesian framework (Spiegelhalter et al. 2003). |
| 2 | The link functions are , , and , where ’s are the regression coefficients and , , , are the four covariates. We have checked the covariates in the data, and there is no multicollinearity issue. |
References
- Bakar, S. A. Abu, Nor A. Hamzah, Mastoureh Maghsoudi, and Saralees Nadarajah. 2015. Modeling loss data using composite models. Insurance: Mathematics and Economics 61: 146–54. [Google Scholar]
- Blostein, Martin, and Tatjana Miljkovic. 2019. On modeling left-truncated loss data using mixtures of distributions. Insurance: Mathematics and Economics 85: 35–46. [Google Scholar] [CrossRef]
- Calderín-Ojeda, Enrique, and Chun Fung Kwok. 2016. Modeling claims data with composite Stoppa models. Scandinavian Actuarial Journal 2016: 817–36. [Google Scholar] [CrossRef]
- Cebrián, Ana C., Michel Denuit, and Philippe Lambert. 2003. Generalized Pareto fit to the Society of Actuaries’ large claims database. North American Actuarial Journal 7: 18–36. [Google Scholar] [CrossRef]
- Cooray, Kahadawala, and Malwane M. A. Ananda. 2005. Modeling actuarial data with a composite lognormal-Pareto model. Scandinavian Actuarial Journal 2005: 321–34. [Google Scholar] [CrossRef]
- Dickson, David C. M. 2016. Insurance Risk and Ruin, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Dong, Alice X. D., and Jennifer S. K. Chan. 2013. Bayesian analysis of loss reserving using dynamic models with generalized beta distribution. Insurance: Mathematics and Economics 53: 355–65. [Google Scholar] [CrossRef]
- Frees, Edward W., Gee Lee, and Lu Yang. 2016. Multivariate frequency-severity regression models in insurance. Risks 4: 4. [Google Scholar] [CrossRef]
- Grün, Bettina, and Tatjana Miljkovic. 2019. Extending composite loss models using a general framework of advanced computational tools. Scandinavian Actuarial Journal 2019: 642–60. [Google Scholar] [CrossRef]
- Laudagé, Christian, Sascha Desmettre, and Jörg Wenzel. 2019. Severity modeling of extreme insurance claims for tariffication. Insurance: Mathematics and Economics 88: 77–92. [Google Scholar] [CrossRef]
- Li, Jackie. 2014. A quantitative comparison of simulation strategies for mortality projection. Annals of Actuarial Science 8: 281–97. [Google Scholar] [CrossRef]
- McNeil, Alexander J. 1997. Estimating the tails of loss severity distributions using extreme value theory. ASTIN Bulletin 27: 117–37. [Google Scholar] [CrossRef]
- Millennium, Ratih Kusuma, and Rosita Kusumawati. 2022. The simulation of claim severity and claim frequency for estimation of loss of life insurance company. In AIP Conference Proceedings. College Park: AIP Publishing, vol. 2575. [Google Scholar]
- Nadarajah, Saralees, and SA Abu Bakar. 2014. New composite models for the Danish fire insurance data. Scandinavian Actuarial Journal 2014: 180–87. [Google Scholar] [CrossRef]
- Pigeon, Mathieu, and Michel Denuit. 2011. Composite lognormal-Pareto model with random threshold. Scandinavian Actuarial Journal 2011: 177–92. [Google Scholar]
- Plummer, Martyn. 2017. JAGS Version 4.3.0 User Manual. Available online: https://sourceforge.net/projects/mcmc-jags/files/Manuals/ (accessed on 1 November 2023).
- Poufinas, Thomas, Periklis Gogas, Theophilos Papadimitriou, and Emmanouil Zaganidis. 2023. Machine learning in forecasting motor insurance claims. Risks 11: 164. [Google Scholar] [CrossRef]
- Reynkens, Tom, Roel Verbelen, Jan Beirlant, and Katrien Antonio. 2017. Modelling censored losses using splicing: A global fit strategy with mixed Erlang and extreme value distributions. Insurance: Mathematics and Economics 77: 65–77. [Google Scholar] [CrossRef]
- Scollnik, David P. M. 2007. On composite lognormal-Pareto models. Scandinavian Actuarial Journal 2007: 20–33. [Google Scholar] [CrossRef]
- Scollnik, David PM, and Chenchen Sun. 2012. Modeling with Weibull-Pareto models. North American Actuarial Journal 16: 260–72. [Google Scholar] [CrossRef]
- Spiegelhalter, David, Andrew Thomas, Nicky Best, and Dave Lunn. 2003. WinBUGS User Manual. Available online: https://www.mrc-bsu.cam.ac.uk/software/bugs/ (accessed on 1 September 2023).
- Venter, Gary C. 1983. Transformed beta and gamma distributions and aggregate losses. Proceedings of the Casualty Actuarial Society 70: 156–93. [Google Scholar]
- Wang, Yinzhi, Ingrid Hobæk Haff, and Arne Huseby. 2020. Modelling extreme claims via composite models and threshold selection methods. Insurance: Mathematics and Economics 91: 257–68. [Google Scholar] [CrossRef]



| Model | NLL | AIC | BIC | KS | DIC |
|---|---|---|---|---|---|
| Weibull | 5270.47 (14) | 10,544.94 (14) | 10,556.58 (14) | 0.2555 (13) | 33,495 (14) |
| Lognormal | 4433.89 (12) | 8871.78 (12) | 8883.42 (12) | 0.1271 (12) | 31,822 (12) |
| Pareto | 5051.91 (13) | 10107.81 (13) | 10119.45 (13) | 0.2901 (14) | 33,058 (13) |
| Burr | 3835.12 (7) | 7676.24 (6) | 7693.70 (6) | 0.0383 (9) | 30,625 (6) |
| GB2 | 3834.77 (6) | 7677.53 (7) | 7700.82 (7) | 0.0602 (11) | 30,626 (7) |
| Lognormal-Pareto | 3865.86 (11) | 7737.73 (11) | 7755.19 (11) | 0.0323 (8) | 30,687 (11) |
| Lognormal-GPD | 3860.47 (10) | 7728.94 (10) | 7752.23 (9) | 0.0196 (6) | 30,677 (10) |
| Lognormal-Burr | 3857.83 (9) | 7725.65 (9) | 7754.76 (10) | 0.0193 (5) | 30,673 (9) |
| Weibull-Pareto | 3840.38 (8) | 7686.75 (8) | 7704.21 (8) | 0.0516 (10) | 30,636 (8) |
| Weibull-GPD | 3823.70 (5) | 7655.40 (5) | 7678.68 (3) | 0.0255 (7) | 30,604 (5) |
| Weibull-Burr | 3817.57 (4) | 7645.14 (3) | 7674.24 (2) | 0.0147 (4) | 30,593 (4) |
| Weibull-Lognormal-Pareto | 3815.89 (2) | 7641.77 (1) | 7670.88 (1) | 0.0114 (2) | 30,589 (1) |
| Weibull-Lognormal-GPD | 3815.88 (1) | 7643.76 (2) | 7678.69 (4) | 0.0113 (1) | 30,590 (3) |
| Weibull-Lognormal-Burr | 3815.89 (3) | 7645.77 (4) | 7686.52 (5) | 0.0114 (3) | 30,590 (2) |
| Quantile | Empirical | Weibull-Lognormal-Pareto | Weibull-Lognormal-GPD | Weibull-Lognormal-Burr |
|---|---|---|---|---|
| 1% | 0.845 | 0.811 | 0.811 | 0.811 |
| 5% | 0.905 | 0.905 | 0.905 | 0.905 |
| 10% | 0.964 | 0.967 | 0.967 | 0.967 |
| 25% | 1.157 | 1.164 | 1.164 | 1.164 |
| 50% | 1.634 | 1.620 | 1.619 | 1.620 |
| 75% | 2.645 | 2.654 | 2.651 | 2.654 |
| 90% | 5.080 | 5.081 | 5.080 | 5.081 |
| 95% | 8.406 | 8.303 | 8.317 | 8.303 |
| 99% | 24.614 | 25.971 | 26.172 | 25.971 |
| Model | Maximum Likelihood | Bayesian MCMC (Posterior Distribution) | |||
|---|---|---|---|---|---|
| Estimate | Standard Error | Mean | Median | Standard Deviation | |
| Weibull-Lognormal-Pareto | τ = 16.253 | 1.290 | 16.127 | 16.073 | 1.351 |
| σ = 0.649 | 0.089 | 0.716 | 0.705 | 0.110 | |
| α = 1.411 | 0.040 | 1.416 | 1.415 | 0.042 | |
| θ1 = 0.947 | 0.011 | 0.952 | 0.951 | 0.013 | |
| θ2 = 1.976 | 0.189 | 2.113 | 2.078 | 0.254 | |
| Weibull-Lognormal-GPD | τ = 16.252 | 1.289 | 16.165 | 16.101 | 1.373 |
| σ = 0.648 | 0.088 | 0.728 | 0.719 | 0.113 | |
| α = 1.402 | 0.097 | 1.440 | 1.432 | 0.096 | |
| λ = −0.018 | 0.174 | 0.041 | 0.034 | 0.178 | |
| θ1 = 0.947 | 0.011 | 0.952 | 0.951 | 0.013 | |
| θ2 = 1.988 | 0.218 | 2.106 | 2.070 | 0.291 | |
| Weibull-Lognormal-Burr | τ = 16.253 | 1.290 | 16.14 | 16.106 | 1.376 |
| σ = 0.649 | 0.089 | 0.725 | 0.718 | 0.113 | |
| α = 0.449 | 1.575 | 0.526 | 0.477 | 0.193 | |
| γ = 3.143 | 1.015 | 3.069 | 2.994 | 1.010 | |
| β = 0.001 | 0.039 | 0.391 | 0.358 | 0.260 | |
| θ1 = 0.947 | 0.011 | 0.952 | 0.951 | 0.013 | |
| θ2 = 1.976 | 0.189 | 2.045 | 2.015 | 0.273 | |
| Model | NLL | AIC | BIC | KS | DIC |
|---|---|---|---|---|---|
| Weibull | 7132.74 (14) | 14,269.47 (14) | 14,282.02 (14) | 0.1414 (13) | 50,289 (14) |
| Lognormal | 6567.94 (12) | 13,139.87 (12) | 13,152.42 (12) | 0.0816 (5) | 49,160 (12) |
| Pareto | 6906.02 (13) | 13,816.03 (13) | 13,828.57 (13) | 0.1471 (14) | 49,836 (13) |
| Burr | 6292.07 (10) | 12,590.15 (10) | 12,608.96 (10) | 0.0911 (10) | 48,609 (10) |
| GB2 | 6300.41 (11) | 12,608.82 (11) | 12,633.90 (11) | 0.0783 (4) | 48,627 (11) |
| Lognormal-Pareto | 6281.18 (9) | 12,568.36 (9) | 12,587.17 (9) | 0.0934 (12) | 48,587 (9) |
| Lognormal-GPD | 6153.72 (7) | 12,315.43 (7) | 12,340.52 (7) | 0.0853 (8) | 48,333 (7) |
| Lognormal-Burr | 6076.13 (4) | 12,162.27 (4) | 12,193.62 (4) | 0.0766 (3) | 48,178 (4) |
| Weibull-Pareto | 6249.84 (8) | 12,505.67 (8) | 12,524.49 (8) | 0.0933 (11) | 48,524 (8) |
| Weibull-GPD | 6144.36 (6) | 12,296.72 (6) | 12,321.81 (6) | 0.0891 (9) | 48,314 (6) |
| Weibull-Burr | 6062.21 (3) | 12,134.43 (3) | 12,165.78 (3) | 0.0827 (7) | 48,150 (3) |
| Weibull-Lognormal-Pareto | 6088.95 (5) | 12,187.91 (5) | 12,219.27 (5) | 0.0822 (6) | 48,204 (5) |
| Weibull-Lognormal-GPD | 5971.78 (1) | 11,955.56 (1) | 11,993.19 (1) | 0.0764 (2) | 48,090 (2) |
| Weibull-Lognormal-Burr | 6025.74 (2) | 12,065.48 (2) | 12,109.38 (2) | 0.0743 (1) | 46,355 (1) |
| Quantile | Empirical | Weibull-Lognormal-Pareto | Weibull-Lognormal-GPD | Weibull-Lognormal-Burr |
|---|---|---|---|---|
| 1% | 0.234 | 0.250 | 0.250 | 0.252 |
| 5% | 0.338 | 0.318 | 0.314 | 0.317 |
| 10% | 0.354 | 0.361 | 0.353 | 0.358 |
| 25% | 0.440 | 0.510 | 0.493 | 0.496 |
| 50% | 1.045 | 0.964 | 0.961 | 0.968 |
| 75% | 2.560 | 2.257 | 2.346 | 2.473 |
| 90% | 5.813 | 5.464 | 5.762 | 5.711 |
| 95% | 8.993 | 9.600 | 8.852 | 8.887 |
| 99% | 18.845 | 28.889 | 18.167 | 18.842 |
| Model | Maximum Likelihood | Bayesian MCMC (Posterior Distribution) | |||
|---|---|---|---|---|---|
| Estimate | Standard Error | Mean | Median | Standard Deviation | |
| Weibull-Lognormal-Pareto | τ = 7.373 | 0.331 | 7.383 | 7.376 | 0.326 |
| σ = 1.789 | 0.047 | 1.797 | 1.795 | 0.063 | |
| α = 2.632 | 0.267 | 2.492 | 2.521 | 0.254 | |
| θ1 = 0.365 | 0.004 | 0.365 | 0.365 | 0.004 | |
| θ2 = 1312 | 1077 | 1054 | 1057 | 544 | |
| Weibull-Lognormal-GPD | τ = 7.707 | 0.304 | 7.856 | 7.851 | 0.244 |
| σ = 16.917 | 0.053 | 17.454 | 17.451 | 0.386 | |
| α = 4.483 | 0.016 | 4.428 | 4.428 | 0.039 | |
| λ = 12.717 | 0.054 | 12.444 | 12.443 | 0.122 | |
| θ1 = 0.366 | 0.003 | 0.357 | 0.357 | 0.003 | |
| θ2 = 4.626 | 0.033 | 4.699 | 4.699 | 0.093 | |
| Weibull-Lognormal-Burr | τ = 7.647 | 0.341 | 7.784 | 7.943 | 0.258 |
| σ = 12.401 | 0.210 | 12.392 | 12.288 | 0.231 | |
| α = 9.034 | 0.110 | 9.164 | 9.232 | 0.218 | |
| γ = 0.724 | 0.020 | 0.667 | 0.607 | 0.067 | |
| β = 35.198 | 0.371 | 35.297 | 35.595 | 0.514 | |
| θ1 = 0.367 | 0.004 | 0.366 | 0.366 | 0.003 | |
| θ2 = 3.538 | 0.092 | 3.683 | 3.848 | 0.255 | |
| Model Component | Covariate | Estimate | Standard Error | t-Ratio | p-Value |
|---|---|---|---|---|---|
| Weibull Component (small claims) | Intercept | 0.850 | 0.644 | 1.32 | 0.19 |
| Exposure | −0.085 | 0.055 | −1.54 | 0.12 | |
| Vehicle Age | 0.233 | 0.253 | 0.92 | 0.36 | |
| Driver Age | 1.921 | 0.013 | 143.55 | 0.00 | |
| Gender | −0.012 | 0.009 | −1.29 | 0.20 | |
| Lognormal Component (medium claims) | Intercept | −57.411 | 26.128 | −2.20 | 0.03 |
| Exposure | 8.179 | 26.821 | 0.30 | 0.76 | |
| Vehicle Age | 7.670 | 5.425 | 1.41 | 0.16 | |
| Driver Age | −5.023 | 4.670 | −1.08 | 0.28 | |
| Gender | −1.221 | 11.118 | −0.11 | 0.91 | |
| GPD Component (large claims) | Intercept | 2.269 | 0.192 | 11.80 | 0.00 |
| Exposure | −1.028 | 0.186 | −5.52 | 0.00 | |
| Vehicle Age | −0.116 | 0.043 | −2.71 | 0.01 | |
| Driver Age | −0.049 | 0.023 | −2.08 | 0.04 | |
| Gender | 0.275 | 0.074 | 3.72 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, J. Claims Modelling with Three-Component Composite Models. Risks 2023, 11, 196. https://doi.org/10.3390/risks11110196
Li J, Liu J. Claims Modelling with Three-Component Composite Models. Risks. 2023; 11(11):196. https://doi.org/10.3390/risks11110196
Chicago/Turabian StyleLi, Jackie, and Jia Liu. 2023. "Claims Modelling with Three-Component Composite Models" Risks 11, no. 11: 196. https://doi.org/10.3390/risks11110196
APA StyleLi, J., & Liu, J. (2023). Claims Modelling with Three-Component Composite Models. Risks, 11(11), 196. https://doi.org/10.3390/risks11110196





