Abstract
In the insurance industry, life insurers are required by regulators to meet capital requirements to avoid insolvency caused by, for example, sudden mortality changes due to the COVID-19 pandemic. To prevent any large movements in this required capital, insurance companies are motivated to establish hedging strategies to mitigate the inherent risk exposures they face. Nonetheless, devising and implementing risk mitigation solutions to risk managing capital requirement is frequently impeded by the computational complexities stemming from the extensive simulations required. In this paper, we delve into a simulation quandary concerning the management of solvency capital risk associated with mortality and longevity. More specifically, we introduce a thin-plate regression spline method as a surrogate alternative to the standard nested simulation approach. Using this efficient simulation method, we further investigate hedging strategies that utilize mortality-linked securities coupled with stochastic mortality dynamics. Our simulation results provide a numerical justification to the market-making of mortality-linked securities in the context of mortality and longevity capital risk management.
1. Introduction
Regulatory frameworks play a crucial role in maintaining the stability and reliability of the insurance industry. In both the United States (US) and the European Union (EU), these regulatory frameworks ensure that life insurance companies maintain sufficient reserves to fulfill their obligations during exceptional events, such as the COVID-19 pandemic. Two prominent examples of such regulatory structures are those established by the National Association of Insurance Commissioners (NAIC) in the US and Solvency II in the EU.
In the EU, Solvency II utilizes a risk-based framework that emphasizes a proactive and dynamic approach to prevent financial insolvency. At the core of this framework lies the concept of the Solvency Capital Requirement (SCR), which mandates life insurance companies to compute and maintain adequate capital reserves, enabling them to absorb losses and avert insolvency. This regulation translates into the stipulation of maintaining capital at a level that provides a 99.5% confidence level of solvency over a one-year timeframe. In the US, the NAIC emphasizes the importance of capital adequacy for life insurances companies, but with a slightly different approach than Solvency II. The NAIC has established a factor-based framework that requires the calculation of various types of risk to which insurance companies are exposed, including asset risk, insurance risk, interest rate risk and business risk.
The capital requirements set by Solvency II is the 99.5% Value-at-Risk (VaR) of the difference between asset and liability (i.e., capital) distribution in one year. In addition to VaR, insurers also pay close attention to other risk measures, such as the Expected Shortfall (ES) and Conditional Tail Expectation (CTE). An important component in the Solvency II calculation is the mortality/longevity SCR. The importance of longevity and mortality risks cannot be overstated in the domain of life insurance. The uncertainty surrounding these risk exposures underscores the critical need for maintaining capital adequacy for life insurers. By accurately quantifying and securing sufficient capital to cover these two risks, life insurers can secure their financial solvency, ensuring their ability to meet insurance obligations even under adverse scenarios.
As insurance regulations grow increasingly complex, the industry is leaning towards the so-called ‘internal model’ approach for calculating capital requirements, instead of the traditional approach, which is mostly based on certain stressed scenarios. The key feature of the internal model approach is it uses the Monte-Carlo simulation over a large number of stochastic scenarios to calculate the quantity of interest. This method relies on using random sampling to predict future outcomes in terms of the solvency situation for an insurance policy. Comparing to the traditional shocked-based approach, the internal model approach can better capture the risk profile underlying the insurance portfolio. Cappiello (2020) provided a detailed discussion on the main characteristics of the internal model approach and also compared it with traditional methods such as the standardized formula approach.
In the context of the internal model approach within Solvency II, the time-0 mortality and longevity SCR (denoted as ) as:
where r is the risk-free interest rate from time 0 to 11, and and are the best estimate liability at time 0 and 1, respectively. More information regarding the SCR calculation of different types of risks can be found in, for example, Eling et al. (2007), Coppola and D’Amato (2012) and Doff (2016). For the sake of simplicity in notation, let be the liability random variable of the underlying insurance product, such as a life insurance or annuity policy, valued at time t. Then, Equation (1) can be re-written as
where and are the expectation of the liability random variable evaluated at time and , respectively.
Numerous research papers have delved into the realm of risk mitigation strategies concerning through mortality-dependent products. Notably, Plat (2011) explored the one-year VaR for longevity and mortality risks, offering valuable sights for capital risk management for life insurers. Zhou et al. (2014) studied the calculation of SCR under multi-population mortality models, while Hainaut et al. (2018) further explored the calculation of SCR for participating life insurances. Additionally, Börger et al. (2021a) presented an integrated analysis of hedge effectiveness and capital efficiency in longevity hedging, revealing the implications of capital risk management for longevity and mortality risks. Other studies on this topic include Börger et al. (2014), Jarner and Møller (2015), Blackburn et al. (2017), Rödel et al. (2021) and Clemente et al. (2022).
In addition, numerous studies have paid particular attention to the construction of an optimal hedging strategy using mortality-linked derivatives. To illustrate, suppose that the hedging objective is to minimize by adding u units of a mortality-linked derivative to the portfolio of liabilities. There is a wide range of possible mortality-linked derivatives that can be utilized for this hedging objective. For instance, to manage extreme mortality risk, the hedger can consider a catastrophe put option (see, e.g., Chang et al. 2011; Chen et al. 2022; Wang 2016). Another possible choice is indexed-based mortality derivatives (see, e.g., Chan et al. 2014, 2016; Li et al. 2021; Tan et al. 2014). Assume that the mortality-linked derivative added has price at time 0 and payoff random variable at time t. Following the general idea of Liu and Li (2021), the goal is to solve for an optimal hedging unit such that
Other related research work on this topic includes Li and Luo (2012), Meyricke and Sherris (2014), Asimit et al. (2015), Cairns and El Boukfaoui (2021) and Börger et al. (2021a, 2021b).
The aforementioned research works have provided valuable insights into managing the time-0 SCR value. However, in instances where actual mortality trends significantly diverge from expectations, such as witnessed during the global COVID-19 pandemic, the SCR value at future time points can experience abrupt fluctuations from one period to another. This volatility in SCR values (e.g., from the time-0 SCR value to the time-1 SCR value) can lead to an unstable capital position and uncertain earnings for insurance companies. We thus suspect that concentrating solely on managing the time-0 SCR value is inadequate in addressing predictive risks, and we emphasize that the risk management of SCR should not be limited to the immediate value but also the predicted values.
The prospective viewpoint on both the immediate and predicted SCR values is crucial in maintaining the financial stability and the long-term viability of an insurer. Observed in industry practices, insurance companies generally focus on their capital position and distributable earnings over time, particularly when faced with an increasingly volatile and unpredictable market. Thus, many insurance companies have shifted their focus toward developing strategies that not only control the time-0 SCR value, but also manage its variability over time. However, a practical challenge in this pursuit lies in calculating the predicted SCR under the internal model approach, given its substantial computational cost. This practical challenge has emerged as a significant barrier, deterring companies from implementing such strategies.
The computational burden associated with calculating the predicted SCR originates from the stochastic nature of mortality dynamics under the internal model approach. The traditional nested simulation approach can quickly become unwieldy, particularly when a substantial number of mortality scenarios is involved (see, e.g., Lin and Yang 2020a, 2020b). To overcome the computational challenge, we introduce the thin-plate regression spline method as a highly efficient surrogate alternative to nested simulations. Our numerical analysis suggests that the surrogate method is able to closely approximate predicted SCR values, achieving an error margin of less than 5% for both life insurance and annuity providers. This finding underscores the effectiveness of the proposed approach in alleviating the computational burden associated with SCR calculations under stochastic mortality scenarios.
Using the efficient surrogate simulation approach, this paper further undertakes an investigation into a problem where the primary concern of a life insurer goes beyond managing the SCR value at time 0 and also the distribution of the SCR values at time 1. In particular, we consider the utilization of mortality-linked securities as a hedging instrument for managing the time-0 and time-1 SCR values. The hedging strategy devised is based on two different criteria for finding the optimal hedging unit and is evaluated by two types of risk measure in our numerical illustration. Our numerical findings provide a justification for the market-making of the mortality-linked securities in the context of mortality and longevity capital risk management.
The rest of this paper is organized in terms of the following sections. Section 2 introduces the predictive hedging framework in detail. As discussed in Section 2.1, calculating the predicted SCR distribution is often extremely time consuming due to the need for a triple-nested simulation algorithm. To address this run-time issue, in Section 2.2, we propose an efficient surrogate method based on the thin-plate spline regression to approximate the predicted SCR distribution. The simulation study is then conducted in Section 3. The stochastic mortality model used in this paper is described in Section 3.1, while the hedging strategy along with the mortality-linked security considered is given in Section 3.2. Our numerical results are presented and analyzed in Section 3.3. Finally, Section 4 concludes the paper with limitations and potential future work.
2. Managing SCR for Mortality and Longevity Risks
2.1. Calculation via Triple-Nested Simulation
Following the above notations, the mortality/longevity SCR at a future time point, , can be calculated as:
where for simplicity we assume the discount rate is a constant. It is worth noticing that by switching the subscript of SCR from 0 to 1, the nature of this calculation is changed. Given the information at time 0, the result of the above calculation is a predicted distribution of the SCR value across different stochastic mortality scenarios from time 0 to 1. Therefore, to calculate this distribution, the first step is to simulate paths from time 0 to 1. The second step is calculating the value of for each member of the paths. This would require simulating another number of stochastic mortality scenarios from time 1 to the end of the projection date. The third step is calculating the value of , which is more complicated than the calculation of . In order to calculate , one needs to simulate paths from time 2 to the end of the projection period for each member of the paths. This implies that the simulation now has a triple-nested structure, and the total simulation time would be proportional to the product of .
2.2. A Thin-Plate Regression Spline-Based Approximation Algorithm
As mentioned before, the nested simulation can be extremely computationally intensive when the number of scenarios and time steps become large. Several shortcut methods to the nested simulation method have been studied by various papers. A review of the current literature on this topic is provided below.
Gordy and Juneja (2010) delved into the ideal distribution of computational resources between the inner and outer layers. Bauer et al. (2012) made strides in numerical advancements for nested simulations for calculating the SCR under Solvency II. Li and Feng (2021) introduced a partial differential equation (PDE) numerical approximation to replace the inner layer of the nested simulations. Alfonsi et al. (2021) pioneered the use of Multilevel MC methods to refine the computation of SCR, offering innovative strategies for stress testing. Lastly, Feng and Li (2022) proposed a recycled sampling approach that involves running the inner layer on a small set of outer simulations and recycling those known inner simulations to estimate other scenarios.
Among the numerous enhancements to the nested simulation method, a common strategy involves using surrogate models. A surrogate model (or meta-model) is a technique to reduce the simulation time by approximating the functional relationship between the simulation inputs and the outputs. It has been widely adopted in many areas such as engineering, finance and insurance. One example of the surrogate modeling approach is the least-squares Monte Carlo (LSMC) simulation method. This method employs least-squares regression to optimize the information obtained from outer simulations and reduce the total number of inner simulations needed.
Costabile and Viviano (2020) notably demonstrated a significant reduction in computational cost in LSMC simulations compared to nested simulations in calculating SCR for life insurance policies. The use of neural network methods has emerged as a potential solution to the computational issue of nested methods in calculating the SCR. Hejazi and Jackson (2017) have proposed a neural network approach to reduce the number of nested simulations to streamline the complexity of SCR calculations.
Similarly, Nilsson and Sandberg (2018) demonstrated the efficiency of neural network methods in estimating SCR for various insurance products. However, despite the clear computational benefits, the neural network approach is not without their limitations. For instance, Krah et al. (2020) noted that the neural network approach does not significantly outperform the LSMC method. Additionally, potential obstacles such as computational complexity, difficulty in interpreting outcomes, and overfitting issues must also be addressed when considering neural network methods for SCR calculations.
Another efficient simulation method, known as Green simulation, has been developed on the basis of likelihood ratio (Feng et al. 2022). This simulation method has demonstrated its capability in the rapid valuation of variable annuities under different settings (e.g., Dang et al. 2020; Feng et al. 2020). Additionally, Dang et al. (2023) have leveraged Green simulation to manage tail risks associated with variable annuities. On longevity risk management, Feng et al. (2022) have extended the application of Green simulation for the evaluation of life insurance products and mortality-linked securities.
Recently, Lin and Yang (2020b) applied the thin-plate regression spline model to speed up the nested simulation for variable annuity portfolio hedging. Moreover, the authors proposed a clustering-based method in selecting the training set to fit the surrogate model, and proved that this selection method is asymptotically optimal in one dimension case. In a parallel study, Lin and Yang (2020a) further explored the use of surrogate methods for variable annuity portfolios with multiple underlying assets.
In this paper, we follow the method proposed by Lin and Yang (2020b) to approximate the SCR values. In the following, we briefly introduce the thin-plate regression spline model.
2.2.1. Thin-Plate Regression Spline
As an extension of the one-dimensional regression spline model, the thin-plate regression spline is commonly used to approximate unknown smooth functional relationships in the multi-dimensional case. Following the notation used in Section 5.5 of Wood et al. (2017), let be the observed data where and each is a -dimensional vector . We assume the predictor variable and the response variable satisfy the following mathematical relation:
where the error term are assumed to be independently distributed with zero mean. Denote the thin-plate spline estimator of by , and it is obtained by minimizing the following objective function:
where the penalty term controls the smoothness of the fitted function, and it is given by the following expression:
The thin-plate spline estimator admits a close form solution:
where are defined as
and , , are linear independent polynomials of degree less than m, which span the space of functions whose values equal zero. Lastly, the estimated parameter satisfies the constraint with the th entry of matrix being , .
Despite the flexibility of the thin-plate splines, the number of unknown parameters is usually very large (the same order as the number of the data points). In addition, as pointed out in Wood et al. (2017), the computing time for fitting the splines is of the cubical order of the number of unknown parameters. Therefore, fitting a set of thin-plate splines can be extremely time-consuming. This motivates the development of the so-called thin-plate regression spline estimator, which is the surrogate model used in this project.
The first term in Formula (3) is usually referred to as the ‘wiggly component’, and the second term is usually called the ‘zero wiggliness component’. The idea behind the thin-plate regression spline estimator is to truncate the space of the ‘wiggly component’ such that the number of unknown parameters to fit is significantly reduced. As a result, the spline model can be fitted in a reasonable time frame without losing too much accuracy. With some algebra, it can be shown that the objective function similar to (2) for fitting the thin-plate regression spline can be expressed in matrix form. To avoid a lengthy review, we refer the interested readers to Wood et al. (2017) for more references.
Although the mathematical framework of the thin-plate regression spline seems complicated, the model can be easily fitted using the R package ‘mgcv’. Having introduced the basics of the thin-plate regression spline, we now show how this model is used as the surrogate model to estimate the predicted solvency capital requirement (SCR) at different predicted stochastic mortality scenarios.
2.2.2. Approximating the Predicted SCR
We start with notations. We denote as the vector of predicted parameters associated with the stochastic mortality model at a future time t and scenario s. For example, in the Cairns–Blake–Dowd (CBD) model Cairns et al. (2006), and could be the vector containing both risk factors at a predicted time point t and scenario s. Let u be the hedging units invested in the mortality/longevity-linked derivative at time 0.2 Furthermore, we denote the predicted mortality/longevity SCR at a future time t, scenario s, and with u units invested in the hedging derivatives. The calculation of this SCR is product-specific, and we will elaborate the detail of this calculation in the context of simple life annuity and insurance products in Section 3.2.
We assume this SCR amount can be closely approximated by a smooth function , which is the surrogate model or the simulation meta-model used to approximate the relationship between the predicted stochastic mortality parameters and the SCR amount. Next, we will fit this function using the thin-plate regression spline by assuming the following model for the function :
where are assumed to be independently distributed with zero mean.
In order to fit this model, one should have a training set where the predictor variables are a set of vectors with different values of and u, and a set of response variables which are the predicted SCRs, obtained from the triple-nested simulation at each predicted stochastic mortality scenario. However, due to the aforementioned computational challenge, generating a large training set is in-feasible and also diminishes the purpose of establishing the surrogate model. Here, we adopt the approach proposed by Lin and Yang (2020b) where the model is trained only on a small set of training data whose locations are selected via a clustering algorithm. To be more specific, in the context of this paper, the following are the main steps for training this model:
- Generate N vectors of predicted parameters at a future time t: , where .
- For each predicted vector, associate it with M hedging units and create a new data set where each data point is now where and .
- Partition the N data points into n clusters where . This could be carried out through a k-means clustering algorithm where .
- For each resulting cluster, pick the point that is closest3 to the cluster center. The resulting n points give a representative set of the predictors.
- Run the triple-nested simulation4 at the representative predictors to obtain a set of representative SCRs.
- The resulting n pairs of the representative predictors and SCRs will give a set of representative points to fit the thin-plate regression spline surrogate model.
Lin and Yang (2020b) showed that the above procedure is asymptotically optimal in the one-dimensional case. This result is difficult to be generalized into higher dimensions due to the difficulties in finding the asymptotic behavior of the thin-plate regression spline estimator and its derivatives. Yet, it can produce a sufficiently accurate surrogate model for estimating the SCR value, as will be demonstrated in later sections.
Let be the fitted thin-plate regression spline. The approximated predicted SCR, denoted by at an arbitrary predicted stochastic mortality scenario and hedging unit is therefore
2.3. A Hedging Framework
After the predicted SCR can be efficiently and effectively approximated, one can see how different hedging units impact the predicted SCR distribution across a large number of scenarios. Furthermore, one can define the hedging criteria based on their specific risk preference.
In this paper, we consider a case where the optimal hedging unit is calculated based on two criteria:
- A time-0 criterion: this criterion defines a hedging objective in terms of the current SCR value.
- A time-t criterion: this criterion defines a hedging objective function in terms of the predicted SCR distribution.
The following is an example of the hedging objective for finding an optimal hedging unit :
- The time-0 SCR value is reduced:
- The expected value of the predicted time-t SCR is minimized:
Note that since the predicted SCR distribution does not admit close-form expression. Solving the optimal hedging units is usually through a numerical procedure. A common approach is to first set up a range for possible hedging units, then calculate all the values of for each unit in this range. This possible hedging range is normally related to insurer’s hedging budget or regulatory requirement.
From the first step, a range of feasible hedging units can be obtained in which the first criterion listed above is satisfied. Next, the surrogate model can be fitted only for the feasible units, and an optimal unit can be found according to the second hedging criterion. We will give a more detailed walk-through of this process in the following simulation study section.
3. Simulation Studies
This section contains several parts. In the first part, we provide a brief review of the Cairns–Blake–Dowd (CBD) model for stochastic mortality modeling (Cairns et al. 2006). This is the model that all hedging calculations, including the hedging derivatives and the predicted SCR distribution in this paper, are based on. Next, we introduce the hedging derivative: the K-put option. This is a mortality-linked derivative that has been studied by Li et al. (2021). Following the hedging derivative, we introduced the two simple illustrative contracts used for simulation studies: an annuity contract and an insurance contract. The purpose of choosing these two contracts is to demonstrate how hedging results are different for different providers that are facing opposite risks. Lastly, we present the results from the simulation studies.
3.1. The Mortality Model
In this part, we briefly introduced the CBD stochastic mortality model. Let be the probability that an individual, who has survived to age x at the beginning of year t, dies in year t (between time and time t). The Cairns–Blake–Dowd (CBD) model is built on as
- and respectively represent the period effect of the level and slope of the mortality curve in year t, and
- is the mean age of the data.
Following the work of Cairns et al. (2006), is modeled by a bi-variate random walk with drift:
where is the constant drift term, and follows a bi-variate normal distribution with mean zero and a variance–covariance matrix.
3.2. Sample Contracts and the Calculation of SCR
To illustrate the risk management for both longevity and mortality risks, we consider two insurance contracts: a life annuity contract and a life insurance contract. The followings are the detailed contract parameters:
- Annuity: The age of the policyholder is 60, the deferral period of the annuity is 5 years, the term of the annuity is 20 years, and the annual payment is $100.
- Insurance: The age of the policyholder is 60, the deferral period of the life insurance is 5 years, the term of the life insurance is 20 years, and the annual payment is $1000.
In the following subsections, we elaborate on how the SCR is obtained for these two contracts with and without an implemented hedging strategy.
3.2.1. The Hedging Instrument
Consider a K-put option on the i-th CBD period effect . Suppose that this K-put is issued at time , matures at time T, and has a strike value of K. The discounted payoff of this K-put at maturity is
per $1 notional. For , the price of this K-put at time t is
where the filtration that contains the evolution of up time and including time t. The full derivation of the K-put pricing formula is available in Li et al. (2021). The price of a K-put at time t obtained from Equation (6) can be influenced by a number of risk factors, including basis risk, calibration risk, credit risk and model risk. Numerous studies in the actuarial literature have been conducted on the pricing of mortality-linked securities (see, e.g., Freimann 2021; Lin et al. 2013; Yang and Wang 2013).
3.2.2. The SCR Calculation
Consider a single premium -year deferred life annuity, sold to an individual who has survived to age x at time 0. After the deferral period, an annuity payment of $1 is payable to the annuitant at the end of each year until death. The time-t value of the annuity liabilities during the deferral period is
where is the probability that an individual who has survived to age x at time t would have survived to time , and r is the constant interest rate. We can further express as
where is directly given by the CBD model. Note that the survival probability depends on the value of the period effects at time . The expression for a -year deferred life annuity can be easily modified for expressing a -year deferred life insurance product.
Assume that a K-put option written on with a discounted payoff of is added to the annuity liability. The number of units purchased for is denoted by u, and the cost of each unit is at time 0. To obtain the SCR at time t, we calculate
3.3. Results
This subsection presents the numerical results of the approximation algorithm and the hedging framework introduced in Section 2.2 and Section 2.3.
For illustration purposes, we use mortality data from the England & Wales female population, obtained from the Human Mortality Database.5 The age range is from age 40 to age 90, while the sample period is from year 1967 to year 2016. We fit the CBD mortality model to this data set using the method of maximum likelihood estimation.
3.3.1. The Thin-Plate Regression Spline Approximation
In order to illustrate the efficiency of this surrogate model approximation, we compare the approximated SCR to the ‘true’ SCR, which is calculated from the brute force simulation. To conduct this numerical study, we simulate from the CBD model 1000 stochastic mortality scenarios in one year. Hence, we have 1000 vectors of where . For the hedging units, we initially chose a range from −8.0 to 8.0 with 0.5 units increment. Hence, we have 33 initial hedging units to start with. We remark that the range considered in this paper is arbitrary, and as mentioned before, this range is usually a subjective choice of the modeler.
As a result, we have 1000 × 33 = 33,000 vectors of predicted variables in one year (). One could imagine the extremely long computing time if the predicted SCR is to be calculated for all those predicted vectors with the full triple-nested simulation. When the portfolio size becomes large and as the product becomes more complicated, it may be even impossible to calculate the predicted SCR in legacy systems where the computing power is not strong enough.
Followed the steps introduced in Section 2.2.2, we run a k-means clustering algorithm with the 33,000 vectors where . We created a set of 500 representative predictor vectors and simulated the SCR values at those vectors for both the annuity contract and the insurance contract. Then, we fit two thin-plate regression models using the 500 training points for the annuity and the insurance contract, respectively. Loosely speaking, this approximation can reduce the total run time by approximately 60 times (33,000/500).
To evaluate the performance of the fitted regression models, we also run the full triple-nested simulation to obtain the predicted SCR values, and we treat these SCR values as the benchmark when assessing the approximation method. The numerical results are shown in Figure 1 via QQ-plots, comparing the SCR values obtained from the triple-nested simulation method and the proposed approximation method.
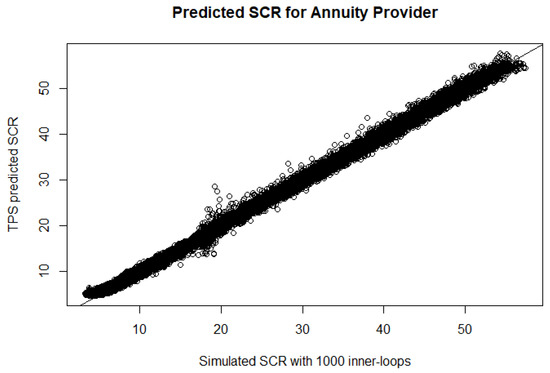
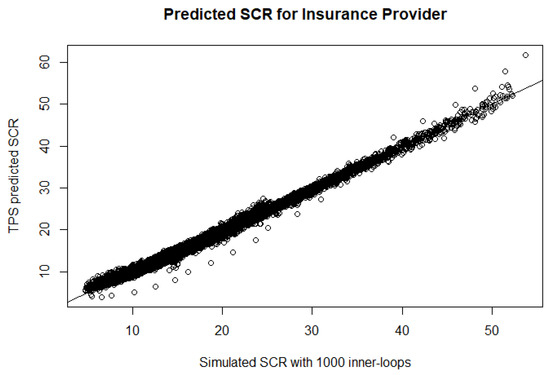
Figure 1.
The predicted SCR at time 1 for the annuity provider (top panel) and insurance provider (bottom panel).
From the QQ-plots, the trained thin-plate spline models are able to closely approximate the predicted SCR for both insurance and annuity providers with less than 5% error.6 It is expected that the approximation error will become smaller if more input points are selected. In practice, the number of training points is mainly determined by two factors: estimation accuracy and run time. A bonus feature of using the surrogate model is that not only can it be used to approximate the values at the non-selected predictor vectors, but it can also predict the SCR values at any arbitrary ‘out-of-sample’ predictor vector7.
3.3.2. Optimal SCR Hedging Strategy for the Insurance and the Annuity Providers
There are two steps in finding the optimal units. The first one is filtering out the unfeasible strategy from the initial strategies, based on the hedging objective(s) at time 0. The second step is to identify an optimal strategy among the feasible strategies, obtained from the first step. In the following, we present the numerical results of two sets of SCR hedging strategies. As defined in Section 2.3, the feasible strategies in this paper are determined based on whether the current is reduced.
For illustration purposes, we consider hedging units u ranging from −8.0 to 8.0 with increments of 0.1. A total of 161 values of is calculated from the simulation results. We can observe from Figure 2 that the pattern of for the insurance provider is almost a mirror image of that for the annuity provider. This is expected as the two parties are facing opposite risks. Implied by these findings, we conclude that the feasible strategies for the two parties are:
- Insurance provider: hedging units between −8.0 to 0, with optimal unit around −5.0.
- Annuity provider: hedging units between 0 to 8.0, with optimal unit around 4.8.
Note that the unhedged position, where the hedging unit u is 0, is included in the above ranges of u.
We now shift our focus to the predicted . For illustration purposes, we consider two time-1 hedging objectives:
- Minimizing the mean of the predicted distribution.
- Minimizing the Value-at-Risk at 95% confidence (VaR95) of the predicted distribution.
The first objective concerns the average value or average movement in the SCR at time 1. The second one concerns more of the tail risk of the predicted distribution. This is an example where the insurer wants to control the capital and earning volatility.
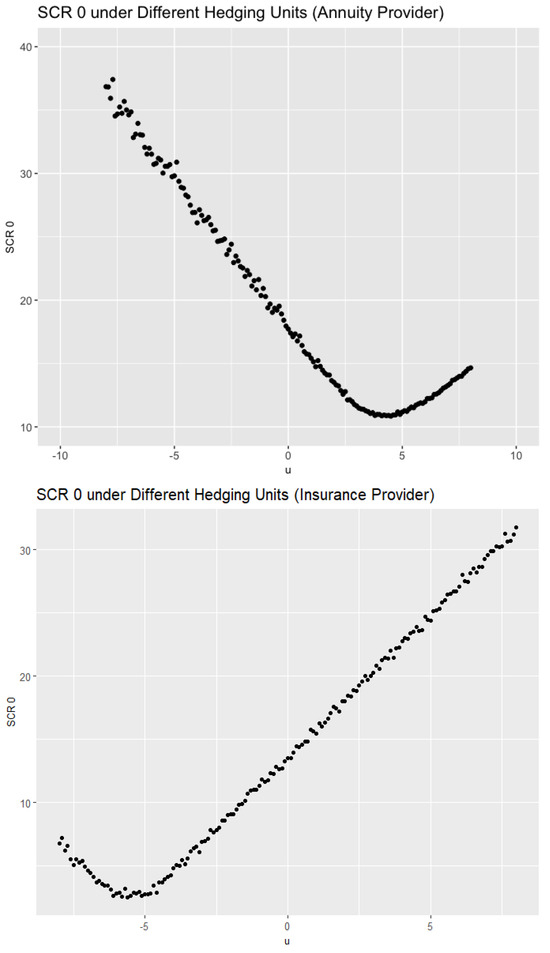
Figure 2.
The obtained SCR at time 0 under different hedging units for the annuity provider (top panel) and insurance provider (bottom panel).
The results are shown in Figure 3 for the insurance provider and in Figure 4 for the annuity provider. The optimal units are summarized in Table 1. From the above numerical results, we can see that under all the hedging objectives considered here, the optimal hedging units for annuity and insurance providers are of opposite signs. On one hand, this finding is intuitive as the two providers are on the opposite side of mortality/longevity risks. On the other hand, from a economics prospective, the fact that the signs for the hedging units are different creates a market for the longevity derivative.
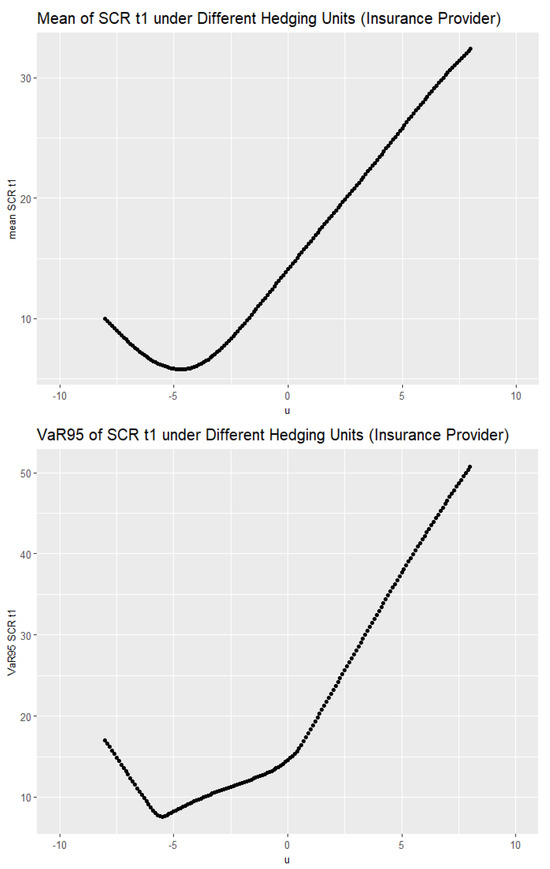
Figure 3.
The mean (top panel) and VaR95 (bottom panel) of the SCR at time 1 under different hedging units for the insurance provider.
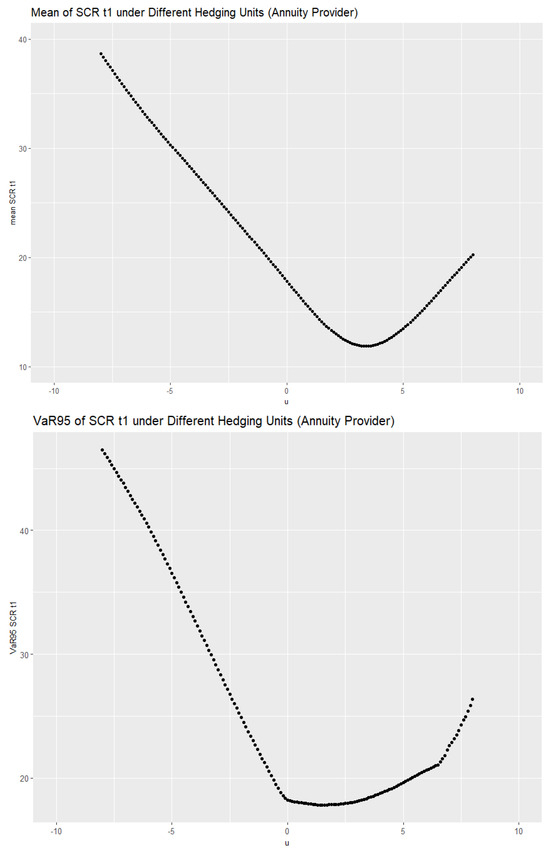
Figure 4.
The mean (top panel) and VaR95 (bottom panel) of the SCR at time 1 under different hedging units for the annuity provider.

Table 1.
Optimal hedging units for different objective functions.
4. Conclusions
In this paper, we studied the problem of capital risk management for mortality and longevity risks. The Solvency Capital Requirement (SCR), required by Solvency II, serves as a regulatory backbone, ensuring that insurers maintain the necessary capital reserves to avoid insolvency. Our research goal targets an important aspect of this regulatory framework, and emphasizes that the risk management of SCR should not be limited to the immediate SCR at time 0. Instead, an insurer should additionally anticipate and prepare for the predicted SCR in future periods, such as the end of the next year. We remark that the prospective viewpoint on both the immediate and predicted SCR values is crucial in maintaining the financial stability and the long-term viability of an insurance company.
Addressing the practical concerns faced by life insurers, we explored the use of mortality-linked securities as a capital risk management tool. To avoid sudden changes in SCR, caused possibly by extreme mortality chocks, life insurers are incentivized to employ mortality-linked securities to mitigate their underlying risk exposures. Through our hedging analysis with different objectives, we examined the optimal unit of a put option written on a mortality index that both life insurance and annuity providers should procure. Moreover, we illustrated that these optimal units are opposed in sign for insurance and annuity providers, underscoring the potential for a robust market of mortality-linked securities for mortality and longevity capital risk management.
Under a stochastic mortality setting, the computational requirement of calculating SCR at future time points cannot be understated. The traditional nested simulation method can become unwieldy when confronted with a large number of mortality scenarios that each requires separate SCR calculations for all future time points. To overcome the computational burden, we introduced the thin-plate regression spline method as an efficient surrogate alternative to nested simulation. Our numerical results validate the surrogate method’s ability to closely approximate the predicted SCR, achieving an error margin that is below 5% for both insurance and annuity providers.
We remark that the risk management of SCR resulting from extreme mortality shocks, such as the COVID-19 pandemic, can be strengthened by leveraging existing risk mitigation tools originally developed for natural catastrophes. The observed resemblance between pandemic mortality risk and natural catastrophe risk suggests a parallel in their nature, indicating that risk management tools designed for catastrophe risk, such as catastrophe equity put options, can be suitably borrowed and adapted for mitigating extreme mortality risk in the insurance context. We refer the interested reader to Zhao et al. (2021) for a detailed review of catastrophe risk management.
Our study has certain limitations that will require further investigations in future research. First, although we have emphasized that the risk management of SCR should be targeted towards future time points, our numerical analysis mainly focused on a single-period approach from time 0 to time 1. While we acknowledge the critical importance of adopting a multi-period approach from time 0 to time T, it is noteworthy that the existing body of literature is relatively sparse in terms of studies focusing on multiple periods. The few that have considered more than one period include Rödel (2017), Zhou and Li (2019) and Börger et al. (2021a). Utilizing these past studies, an extension of this paper can span multiple periods with a dynamic recalibration of the optimal hedging strategy.
Second, our selection of the CBD model for simulating stochastic mortality is merely illustrative. It is essential to note that the mortality modeling literature encompasses a diverse range of stochastic models, presenting ample opportunities for integration with our paper. Further exploration of these models could significantly contribute to the examination of capital risk management concerning mortality and longevity risks. Moreover, beyond the K-put option considered in this paper, other state-of-the-art mortality-linked securities can be further investigated to compare their degree of hedge effectiveness in the risk management of capital requirements.
Lastly, although the thin-plate regression spline employed in this paper stands as a valuable surrogate method, it is important to recognize that the field offers a multitude of alternative methods. Our study has demonstrated the efficacy of using surrogate methods in managing capital requirements for mortality and longevity risks. However, we acknowledge the limitation of not explicitly comparing the thin-plate regression spline with other existing methods. Subsequent studies could delve into these alternatives to refine simulation accuracy and enhance efficiency.
Author Contributions
Conceptualization, S.Y. and K.Q.Z.; methodology, S.Y. and K.Q.Z.; software, S.Y. and K.Q.Z.; formal analysis, S.Y. and K.Q.Z.; investigation, S.Y. and K.Q.Z.; data curation, K.Q.Z.; writing—original draft preparation, S.Y. and K.Q.Z.; writing—review and editing, S.Y. and K.Q.Z.; visualization, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this paper were obtained from the Human Mortality Database, Max Planck Institute for Demographic Research (Germany), University of California, Berkeley (USA), and French Institute for Demographic Studies (France), and is available at www.mortality.org accessed on 29 May 2020.
Acknowledgments
The authors acknowledge valuable comments and feedback provided by conference attendees at the 2022 Canadian Operational Research Society/Institute for Operations Research and the Management Sciences International Conference and the 2023 Institute for Operations Research and the Management Sciences Annual Meeting.
Conflicts of Interest
Author Shuai Yang works for Aon PathWise Solutions Group LLC and may have potential commercial conflicts of interest. Author Shuai Yang contributed to this article in his own capacity. The views and opinions presented in this paper are his own and do not reflect the views or official stance of Aon PathWise Solutions Group LLC.
Notes
| 1 | It is assumed, without loss of generality, that a constant interest rate is used in this paper. |
| 2 | In this paper, we consider only a single hedging instrument. However, our approximation method could be easily modified to a vector when multiple hedging instruments are considered. |
| 3 | Usually, this step is performed after the data points are standardized so that all dimensions have roughly the same weights. The closeness is commonly measured by some distance metric such as Euclidean distance. |
| 4 | Since a fitting procedure will be performed afterwards, the numbers of outer/middle/inner-loop of this triple-nested simulation do not have to be too large. |
| 5 | Human Mortality Database. Max Planck Institute for Demographic Research (Germany), University of California, Berkeley (USA), and French Institute for Demographic Studies (France). Available at www.mortality.org (data downloaded on 29 May 2020). |
| 6 | The error between the triple-nested simulation method and the approximation method is measured by
|
| 7 | We remark that to ensure the predicted SCR is of high confidence, the ‘out-of-sample’ predictor vector should fall in the range of the training set. |
References
- Alfonsi, Aurélien, Adel Cherchali, and Jose Arturo Infante Acevedo. 2021. Multilevel monte-carlo for computing the scr with the standard formula and other stress tests. Insurance: Mathematics and Economics 100: 234–60. [Google Scholar] [CrossRef]
- Asimit, Alexandru V., Alexandru M. Badescu, Tak Kuen Siu, and Yuriy Zinchenko. 2015. Capital requirements and optimal investment with solvency probability constraints. IMA Journal of Management Mathematics 26: 345–75. [Google Scholar] [CrossRef]
- Bauer, Daniel, Andreas Reuss, and Daniela Singer. 2012. On the calculation of the solvency capital requirement based on nested simulations. ASTIN Bulletin: The Journal of the IAA 42: 453–99. [Google Scholar]
- Blackburn, Craig, Katja Hanewald, Annamaria Olivieri, and Michael Sherris. 2017. Longevity risk management and shareholder value for a life annuity business. ASTIN Bulletin: The Journal of the IAA 47: 43–77. [Google Scholar] [CrossRef]
- Börger, Matthias, Arne Freimann, and Jochen Ruß. 2021a. A combined analysis of hedge effectiveness and capital efficiency in longevity hedging. Insurance: Mathematics and Economics 99: 309–26. [Google Scholar] [CrossRef]
- Börger, Matthias, Daniel Fleischer, and Nikita Kuksin. 2014. Modeling the mortality trend under modern solvency regimes. ASTIN Bulletin: The Journal of the IAA 44: 1–38. [Google Scholar] [CrossRef]
- Börger, Matthias, Jochen Russ, and Johannes Schupp. 2021b. It takes two: Why mortality trend modeling is more than modeling one mortality trend. Insurance: Mathematics and Economics 99: 222–32. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., and Ghali El Boukfaoui. 2021. Basis risk in index-based longevity hedges: A guide for longevity hedgers. North American Actuarial Journal 25: S97–S118. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cappiello, Antonella. 2020. The European Insurance Industry: Regulation, Risk Management, and Internal Control. Berlin: Springer Nature. [Google Scholar]
- Chan, Wai-Sum, Johnny Siu-Hang Li, and Jackie Li. 2014. The cbd mortality indexes: Modeling and applications. North American Actuarial Journal 18: 38–58. [Google Scholar] [CrossRef]
- Chan, Wai-Sum, Johnny Siu-Hang Li, Kenneth Q. Zhou, and Rui Zhou. 2016. Towards a large and liquid longevity market: A graphical population basis risk metric. The Geneva Papers on Risk and Insurance-Issues and Practice 41: 118–27. [Google Scholar] [CrossRef]
- Chang, Chia-Chien, Shih-Kuei Lin, and Min-Teh Yu. 2011. Valuation of catastrophe equity puts with markov-modulated poisson processes. Journal of Risk and Insurance 78: 447–73. [Google Scholar] [CrossRef]
- Chen, Jun-Home, Yu-Min Lian, and Szu-Lang Liao. 2022. Pricing catastrophe equity puts with counterparty risks under markov-modulated, default-intensity processes. The North American Journal of Economics and Finance 61: 101699. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Francesco Della Corte, and Nino Savelli. 2022. A stochastic model for capital requirement assessment for mortality and longevity risk, focusing on idiosyncratic and trend components. Annals of Actuarial Science 16: 527–46. [Google Scholar] [CrossRef]
- Coppola, Mariarosaria, and Valeria D’Amato. 2012. Backtesting the solvency capital requirement for longevity risk. The Journal of Risk Finance 13: 309–19. [Google Scholar] [CrossRef]
- Costabile, Massimo, and Fabio Viviano. 2020. Testing the least-squares monte carlo method for the evaluation of capital requirements in life insurance. Risks 8: 48. [Google Scholar] [CrossRef]
- Dang, Ou, Mingbin Feng, and Mary R. Hardy. 2020. Efficient nested simulation for conditional tail expectation of variable annuities. North American Actuarial Journal 24: 187–210. [Google Scholar] [CrossRef]
- Dang, Ou, Mingbin Feng, and Mary R. Hardy. 2023. Two-stage nested simulation of tail risk measurement: A likelihood ratio approach. Insurance: Mathematics and Economics 108: 1–24. [Google Scholar] [CrossRef]
- Doff, René. 2016. The final solvency ii framework: Will it be effective? The Geneva Papers on Risk and Insurance-Issues and Practice 41: 587–607. [Google Scholar] [CrossRef]
- Eling, Martin, Hato Schmeiser, and Joan T. Schmit. 2007. The solvency ii process: Overview and critical analysis. Risk Management and Insurance Review 10: 69–85. [Google Scholar] [CrossRef]
- Feng, Ben Mingbin, Johnny Siu-Hang Li, and Kenneth Q. Zhou. 2022. Green nested simulation via likelihood ratio: Applications to longevity risk management. Insurance: Mathematics and Economics 106: 285–301. [Google Scholar] [CrossRef]
- Feng, Ben Mingbin, Zhenni Tan, and Jiayi Zheng. 2020. Efficient simulation designs for valuation of large variable annuity portfolios. North American Actuarial Journal 24: 275–89. [Google Scholar] [CrossRef]
- Feng, Runhuan, and Peng Li. 2022. Sample recycling method—A new approach to efficient nested monte carlo simulations. Insurance: Mathematics and Economics 105: 336–59. [Google Scholar] [CrossRef]
- Freimann, Arne. 2021. Pricing longevity-linked securities in the presence of mortality trend changes. ASTIN Bulletin: The Journal of the IAA 51: 411–47. [Google Scholar] [CrossRef]
- Gordy, Michael B., and Sandeep Juneja. 2010. Nested simulation in portfolio risk measurement. Management Science 56: 1833–48. [Google Scholar] [CrossRef]
- Hainaut, Donatien, Pierre Devolder, and Antoon Pelsser. 2018. Robust evaluation of scr for participating life insurances under solvency ii. Insurance: Mathematics and Economics 79: 107–23. [Google Scholar] [CrossRef]
- Hejazi, Seyed Amir, and Kenneth R. Jackson. 2017. Efficient valuation of scr via a neural network approach. Journal of Computational and Applied Mathematics 313: 427–39. [Google Scholar] [CrossRef]
- Jarner, Søren Fiig, and Thomas Møller. 2015. A partial internal model for longevity risk. Scandinavian Actuarial Journal 2015: 352–82. [Google Scholar] [CrossRef]
- Krah, Anne-Sophie, Zoran Nikolić, and Ralf Korn. 2020. Least-squares monte carlo for proxy modeling in life insurance: Neural networks. Risks 8: 116. [Google Scholar] [CrossRef]
- Li, Johnny Siu-Hang, and Ancheng Luo. 2012. Key q-duration: A framework for hedging longevity risk. Astin Bulletin: The Journal of the IAA 42: 413–52. [Google Scholar]
- Li, Johnny Siu-Hang, Jackie Li, Uditha Balasooriya, and Kenneth Q. Zhou. 2021. Constructing out-of-the-money longevity hedges using parametric mortality indexes. North American Actuarial Journal 25: S341–S372. [Google Scholar] [CrossRef]
- Li, Peng, and Runhuan Feng. 2021. Nested monte carlo simulation in financial reporting: A review and a new hybrid approach. Scandinavian Actuarial Journal 2021: 744–78. [Google Scholar] [CrossRef]
- Lin, X. Sheldon, and Shuai Yang. 2020a. Efficient dynamic hedging for large variable annuity portfolios with multiple underlying assets. ASTIN Bulletin: The Journal of the IAA 50: 913–57. [Google Scholar] [CrossRef]
- Lin, X. Sheldon, and Shuai Yang. 2020b. Fast and efficient nested simulation for large variable annuity portfolios: A surrogate modeling approach. Insurance: Mathematics and Economics 91: 85–103. [Google Scholar] [CrossRef]
- Lin, Yijia, Sheen Liu, and Jifeng Yu. 2013. Pricing mortality securities with correlated mortality indexes. Journal of Risk and Insurance 80: 921–48. [Google Scholar] [CrossRef]
- Liu, Yanxin, and Johnny Siu-Hang Li. 2021. An efficient method for mitigating longevity value-at-risk. North American Actuarial Journal 25: S309–S340. [Google Scholar] [CrossRef]
- Meyricke, Ramona, and Michael Sherris. 2014. Longevity risk, cost of capital and hedging for life insurers under solvency ii. Insurance: Mathematics and Economics 55: 147–55. [Google Scholar] [CrossRef]
- Nilsson, Mattias, and Erik Sandberg. 2018. Application and Evaluation of Artificial Neural Networks in Solvency Capital Requirement Estimations for Insurance Products. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1194280&dswid=8213 (accessed on 30 March 2023).
- Plat, Richard. 2011. One-year value-at-risk for longevity and mortality. Insurance: Mathematics and Economics 49: 462–70. [Google Scholar] [CrossRef]
- Rödel, Karen Tanja. 2017. Analysis of Solvency Capital on a Multi-Year Basis. Ph.D. thesis, University of Ulm, Ulm, Germany. [Google Scholar]
- Rödel, Karen Tanja, Stefan Graf, Alexander Kling, and Andreas Reuß. 2021. Measuring profitability of life insurance products under solvency ii. European Actuarial Journal 11: 349–76. [Google Scholar] [CrossRef]
- Tan, Chong It, Jackie Li, Johnny Siu-Hang Li, and Uditha Balasooriya. 2014. Parametric mortality indexes: From index construction to hedging strategies. Insurance: Mathematics and Economics 59: 285–99. [Google Scholar] [CrossRef]
- Wang, Xingchun. 2016. Catastrophe equity put options with target variance. Insurance: Mathematics and Economics 71: 79–86. [Google Scholar] [CrossRef]
- Wood, Simon N., Zheyuan Li, Gavin Shaddick, and Nicole H. Augustin. 2017. Generalized additive models for gigadata: Modeling the uk black smoke network daily data. Journal of the American Statistical Association 112: 1199–210. [Google Scholar] [CrossRef]
- Yang, Sharon S., and Chou-Wen Wang. 2013. Pricing and securitization of multi-country longevity risk with mortality dependence. Insurance: Mathematics and Economics 52: 157–69. [Google Scholar] [CrossRef]
- Zhao, Yang, Jin-Ping Lee, and Min-Teh Yu. 2021. Catastrophe risk, reinsurance and securitized risk-transfer solutions: A review. China Finance Review International 11: 449–73. [Google Scholar] [CrossRef]
- Zhou, Kenneth Q., and Johnny Siu-Hang Li. 2019. Delta-hedging longevity risk under the m7–m5 model: The impact of cohort effect uncertainty and population basis risk. Insurance: Mathematics and Economics 84: 1–21. [Google Scholar] [CrossRef]
- Zhou, Rui, Yujiao Wang, Kai Kaufhold, Johnny Siu-Hang Li, and Ken Seng Tan. 2014. Modeling period effects in multi-population mortality models: Applications to solvency II. North American Actuarial Journal 18: 150–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).