Performance of the Realized-GARCH Model against Other GARCH Types in Predicting Cryptocurrency Volatility

Abstract

Cryptocurrencies have increasingly attracted the attention of several players interested in crypto assets. Their rapid growth and dynamic nature require robust methods for modeling their volatility. The Generalized Auto Regressive Conditional Heteroskedasticity (GARCH) model is a well-known mathematical tool for predicting volatility. Nonetheless, the Realized-GARCH model has been particularly under-explored in the literature involving cryptocurrency volatility. This study emphasizes an investigation on the performance of the Realized-GARCH against a range of GARCH-based models to predict the volatility of five prominent cryptocurrency assets. Our analyses have been performed in both in-sample and out-of-sample cases. The results indicate that while distinct GARCH models can produce satisfactory in-sample fits, the Realized-GARCH model outperforms its counterparts in out of-sample forecasting. This paper contributes to the existing literature, since it better reveals the predictability performance of Realized-GARCH model when compared to other GARCH-types analyzed when an out-of-sample case is considered.

1. Introduction

Volatility modeling serves as a cornerstone in the landscape of financial markets research, boasting an ever-evolving repertoire of methodological choices. While the vast array of models available in the literature offers versatility, it also poses challenges for researchers and practitioners in selecting an optimally performing yet parsimonious model. As with all modeling, a key tenet is that gains with in-sample fit can come at the expense of a lack of generalization (overfitting).

The demand for investment in assets such as cryptocurrencies has grown substantially in recent years. Baur et al. (2018) document a change in behavior in the market, identifying more buy-and-hold investors on the blockchain from 2016. Around the same time, Urquhart (2016) documents a change in the price behavior of Bitcoin (BTC), reflecting an increase in market efficiency, and Conlon and McGee (2020) document a reduction in the link between on chain gambling and the Bitcoin price around the same time frame. As well as some new investors ventured into this market, large financial institutions also started to include these assets in their portfolios, with their involvement steadily increasing (see, e.g., Huang et al. (2022)). The emergence of this new asset class provides a new test bed to compare the generalizability of volatility modeling techniques developed in traditional asset classes.

Firstly, Hansen and Lunde (2005) argued that a simple Generalized Auto Regressive Conditional Heteroskedasticity (GARCH(1,1)) model is hard to beat in volatility studies in traditional financial markets and, for this reason, the selection of a GARCH(1,1) model, may make a good Bayesian prior for financial economists. In later years, Hansen et al. (2012) proposed the Realized-GARCH model, and applied this model to Dow Jones Industrial Average (DJIA) stocks and an exchange traded index fund, SPY, and found substantial improvements in the loglikelihood function (both in-sample and out-of-sample) when benchmarked to a standard GARCH model.

Thereafter, Hansen and Huang (2016) suggested the existence of more advantages of this model. Such advantages of the new structure were documented in the form of better empirical fit in the time series they analyzed. The authors also argue that realized measures have proven to be very valuable in GARCH modeling and, when estimating a standard GARCH, the lagged squared returns are typically estimated to have a coefficient around 5%, which causes GARCH models to be slow at adjusting the level of volatility. Nonetheless, there exist few studies that provide Realized-GARCH analysis for cryptocurrency returns and volatility.

Hung et al. (2020) investigated the role of volatility proxy in a Realized-GARCH analysis particularly for BTC data, and find that the jump-robust realized measure is a more relevant and efficient way to forecast BTC volatility. These authors recommended to academic researchers to adopt Realized-GARCH to model other cryptocurrencies.

Chen et al. (2023) investigated the role of the probability distribution in forecasting the volatility and value-at-risk (VaR) of BTC and ETH returns using some GARCH-type models. The authors state that the Realized-GARCH model outperforms its benchmark models for both volatility and VaR forecasting. However, this better performance of the Realized-GARCH to model and describe volatility to other cryptocurrencies remained unclear, motivating our present study.

We also highlight that the remarkable volatility of cryptocurrency markets, far surpassing, in general, that of traditional financial assets poses significant challenges for existing volatility models. We are convinced to the critical need for analysis in this area by investigating the applicability and the performance of different models in a deeper way when consider the peculiar cryptocurrency market, including GARCH-type approaches and, notedly, the Realized-GARCH model.

In this context, this paper aims to extend this line of inquiry into the burgeoning domain of cryptocurrency markets such as BTC, Ethereum (ETH), Ripple (XRP), Binance Coin (BNB), and Cardano (ADA).

The paper is structured as follows: In Section 2, a detailed review of the literature is presented. In Section 3, the selected data are described, and the necessary mathematical and computational methods are introduced. In Section 4, the results obtained by means of numerical simulations, alternating the conditional variance models, are presented and discussed. Finally, in Section 5, our concluding remarks are outlined.

2. Literature Review

The seminal paper that motivates our analysis was written by Hansen and Lunde (2005), who argue that the basic GARCH(1,1) model often outperforms more complex models in various asset markets. However, they note that some GARCH models incorporating a leverage effect can outperform in specific equities.

In this section, we summarize existing work, including some of the alternative volatility modeling techniques that have been applied to cryptocurrencies, and we also include a brief analysis of why some of these may not have universal appeal, in particular for practitioners that are highly sensitive to model risks and relatively unsophisticated investors.

In relevant work on traditional GARCH models and their extensions, Tiwari et al. (2019) compared stochastic volatility models and GARCH models in BTC and LTC markets, and found that class t-models, such as GARCH-t, provided good results for both currencies. Furthermore, they found that the leverage effect was not relevant, contrary to findings in equity markets. Katsiampa (2017) proposed that the AR-CGARCH model is most effective for modeling BTC prices. Meanwhile, Ngunyi et al. (2019) focused on selecting the best GARCH-type models for cryptocurrencies such as BTC, ETH, LTC, and XRP for one-day-ahead risk prediction. Fakhfekh and Jeribi (2020) evaluated various types of GARCH models for their fit with cryptocurrency time series (TS), using the Akaike (AIC) and Bayesian information criteria (BIC) for model selection. Caporale and Zekokh (2019) look at modeling from the perspective of value at risk and expected shortfall, and find that it is necessary to incorporate regime switching to obtain good estimates when using GARCH-style models for these measures. Bouri et al. (2022) explored the pronounced volatility within cryptocurrencies. They demonstrated that idiosyncratic volatility is notably priced in, especially for less liquid cryptocurrencies, highlighting the influence of microstructure noise on their dynamics. In turn, Ji et al. (2021) explored realized volatility connectedness among Bitcoin exchange markets, shedding light on market efficiency and information transfer between different trading platforms. The aforementioned studies contribute to a nuanced understanding of cryptocurrency volatility beyond what traditional models might capture.

In other contexts, Kristoufek (2023), in his research, seeks to provide insights into the long-term stability prospects of BTC, a topic under debate and concern among both academics and practitioners. David et al. (2021) adopted fractal and fractional methods applied to price series of cryptocurrencies, to assess behaviors such as theirs persistence, randomness, predictability and chaoticity. The findings suggest that, except for BTC, the other cryptocurrencies exhibit characteristics of mean-revert, and the results for BTC indicate long-memory effect. Pichl and Kaizoji (2017) delved into the volatility patterns for BTC, providing another layer of understanding to its pricing dynamics. Sapuric and Kokkinaki (2014), in their study conducted in the early years of the cryptocurrency, explore the extreme volatility that has characterized BTC since its inception. They underscore how the asset’s price unpredictability has been both an attraction and a deterrent for investors, and their work serves as a foundational study for understanding Bitcoin’s essential nature and its challenges in becoming a mainstream financial asset.

Also, Hamayel and Owda (2021) proposed the use of recurrent neural network (RNN) algorithms in order to predict the price of BTC, LTC, and ETH, and obtained good results through the use of gated recurrent unit (GRU), compared to other algorithms related to long short term memory (LSTM) and bidirectional LSTM (bi-LSTM) models. Christensen et al. (2022) find that Machine Learning (ML) techniques such as trees and recurrent neural nets outperform time series models in forecasting volatility. However, such ML methods are not universally palatable, especially in view of model risk where practitioners may have concerns around using black box techniques.

Corsi (2009) Heterogeneous Autoregressive model of Realized Volatility (HAR-RV) offers an innovative approach by considering volatility components over different time horizons, which aligns with our analysis of cryptocurrency markets. Kambouroudis et al. (2021) extends the HAR model to include various factors such as implied volatility and leverage effect, providing insights into more complex market dynamics. Patton (2011) contributes to this discourse by highlighting the challenges associated with using standard volatility proxies, proposing robust loss functions that are resistant to noise in volatility measurements.

Advancements have also been made in high-frequency volatility modeling, such as the work published by Liu et al. (2015), who suggested that models based on high-frequency intraday price changes, such as the Realized-GARCH model, are difficult to beat in traditional markets. Wang et al. (2020) introduces Realized-GARCH-Kernel-type models that avoid specific distribution assumptions, aligning with the unpredictable nature of cryptocurrency markets. Lastly, the exploration by Hansen et al. (2021) of the Realized GARCH model and its application to the Volatility Index and volatility risk premium offers valuable perspectives for understanding risk and return dynamics in our study’s context.

This study focuses on methodologies that are both robust and accessible. While we employ high-frequency data to perform a granular comparison between different GARCH models, our analysis is primarily geared toward making these complex models more accessible and understandable for a broad audience of investors and practitioners. The models and techniques we discuss, primarily GARCH time series models and their extensions, are chosen for their robustness and ability to be easily interpreted, thereby minimizing model risk.

3. Materials and Methods

We analyze the historical returns of five major cryptocurrencies: BTC, ETH, XRP, BNB, and ADA. They were selected based on their market capitalization as listed on the Binance website, accessed on 31 August 2023. Together, the aforesaid cryptocurrencies account for a cumulative market cap of nearly USD 800 billion.

In our analysis, we utilized two different data frequencies to construct a comprehensive dataset. Hourly data were specifically employed to construct the realized volatility measures, given their relevance in capturing intra-day market dynamics. On the other hand, daily data were used for evaluating the overall model performance, including fitting and forecasting, as they provide a broader view of market trends over time. These datasets were sourced from Cryptocompare API and integrated into a unique dataframe for each cryptocurrency. The period under consideration spans from 1 January 2018 to 31 August 2023.

In assessing the performance of our chosen models, both in-sample and out-of-sample evaluations were conducted. Our approach utilizes a one-day-ahead forecasting methodology with an expanding window strategy. This means that each out-of-sample forecast is based on all available historical data up to that point, thus reflecting both historical and recent market dynamics in the model’s predictive capabilities. The fixed in-sample period for our analysis begins on 1 January 2018, and extends up to 5 September 2022. Correspondingly, the out-of-sample data set comprises the most recent 360 observations, spanning from 6 September 2022 to 31 August 2023.

For model accuracy assessment, we employ the Mean Absolute Error (MAE) as our primary evaluation metric. We adopted R as programming language for data processing, descriptive statistics, stationarity, and volatility analysis. We also applied the rugarch package Ghalanos (2023) to different GARCH-type models described in this work.

Table 1. Descriptive statistics of cryptocurrencies’ daily returns.

Crypto	Mean	Min.	Max.	Std. Dev.	ADF	L-Jung
BTC	0.0002	−0.4647	0.1718	0.0375	−12.136	8.912
ETH	0.0003	−0.5507	0.2306	0.0484	−11.853	17.145
XRP	−0.0007	−0.5505	0.5485	0.0582	−12.802	39.555
BNB	0.0015	−0.5430	0.5292	0.0541	−11.671	142.92
ADA	−0.0005	−0.5036	0.3217	0.0565	−11.507	26.749

presents a summary of the daily return metrics for the cryptocurrencies analyzed. The stationarity of the TSs are evaluated by means of the Augmented Dickey–Fuller (ADF) test proposed by Dickey and Fuller (1979). One can note that all series are stationary, with an average close to zero. Moreover, volatility clusters are verified through the p-value of L-jung Box test suggested by Ljung and Box (1978). One can also observe that they are dependent on squared returns, and we emphasize that our objective is to model the ARCH effects of the previously mentioned series of returns.

3.1. GARCH

The GARCH model Bollerslev (1986) is an evolution of the ARCH method, elaborated by Engle (1982). It can be used to describe volatility using fewer parameters compared to the ARCH, and its conditional variance is indicated by ${\sigma }_t^2$ as an indicator of volatility. The GARCH model is defined by

$${\sigma }_t^2=\omega +\sum _{i=1}^q{\alpha }_i{ϵ}_{t-i}^2+\sum _{i=1}^p{\beta }_i{\sigma }_{t-i}^2$$

(1)

where ${\alpha }_i\ge 0$ and ${\beta }_i\ge 0$.

Equation (1) takes into account the intercept $\omega >0$, the innovations ${ϵ}_{t-i}^2$, and is also dependent on past volatility values ${\sigma }_{t-i}^2$. The order of the model is represented by (q,p), where q is the ARCH order and p the GARCH one.

3.2. GJR-GARCH

The model proposed by Glosten et al. (1993) is a variation of the GARCH model that considers the asymmetry of returns. It is denoted by GJR-GARCH and defined by

$${\sigma }_t^2=\omega +\sum _{i=1}^q{\alpha }_i{ϵ}_{t-i}^2+\sum _{i=1}^q{\gamma }_i{ϵ}_{t-i}^2{I}_{[{ϵ}_{t-i}<0]}+\sum _{i=1}^p{\beta }_i{\sigma }_{t-i}^2$$

(2)

The indicator I assumes 1 for cases where the error term is zero or negative and 0 for positive cases. In turn, ${\gamma }_i$ represents the ‘leverage’ term.

3.3. Realized-GARCH

The Realized-GARCH model introduced by Hansen et al. (2012) fuses both daily returns and realized measures of volatility into a unified framework. In this approach, the conditional variance ${\sigma }_t^2$ is not directly observed, but an auxiliary measure called realized volatility, $x_t$, is used to improve its estimation. The idea is that the conditional variance from high-frequency data informs the low-frequency returns data.

$$log{\sigma }_t^2=\omega +\sum _{i=1}^q{\alpha }_{i}log{x}_{t-i}+\sum _{i=1}^p{\beta }_{i}log{\sigma }_{t-i}^2$$

(3)

$$log{x}_t=c+\varphi log{\sigma }_t^2+{\nu }_t$$

(4)

This is a volatility modeling technique that takes advantage of realized measures of volatility in order to enhance volatility forecasts. However, its reliance on high-frequency data to inform the low-frequency returns data can be a disadvantage. This dependency can be a constraint in scenarios where high-frequency data are not readily available, potentially limiting the model’s applicability in certain market conditions. Furthermore, the assumption of a specific form of the relationship between realized measures and conditional variance may not always capture the complex dynamics of financial markets accurately.

3.4. E-GARCH

This model was introduced by Nelson (1991) in order to allow the asymmetric effects of negative and positive shocks, already empirically observed, to be considered through weighting. The coefficient ${\alpha }_i$ captures the sign effect, ${\gamma }_i$ carry the size effect and $z_{t-i}$ indicates a generalized error distribution.

The E-GARCH model is defined by

$${log}_e\left({\sigma }_t^2\right)=\omega +\sum _{i=1}^q\left({\alpha }_i{z}_{t-i}+{\gamma }_i\left(\left|z_{t-i}\right|-E\left|z_{t-i}\right|\right)\right)+\sum _{i=1}^p{\beta }_i{log}_e\left({\sigma }_{t-i}^2\right)$$

(5)

3.5. FI-GARCH

Baillie et al. (1996) proposed the development of the integrated fractional GARCH model in order to capture the effects of long memory on TS processes. In this case, the modeled shocks decay smoothly at a hyperbolic rate.

Considering the L lag operator such that the traditional GARCH equation, one can write Equation (1) as follows

$${\sigma }_t^2=\omega +\alpha \left(L\right){ϵ}_t^2+\beta \left(L\right){\sigma }_t^2$$

(6)

and,

$${\sigma }_t^2=\omega +\left\{1-\beta \left(L\right)-\left(1-\alpha \left(L\right)\right){\left(1-L\right)}^d\right\}{ϵ}_t^2+\beta \left(L\right){\sigma }_t^2$$

(7)

where d is a positive exponent between 0 and 1.

3.6. CS-GARCH

Lee and Engle (1993) studied short-term and long-term volatility movements by decomposing the conditional variance into a transient and a permanent component.

The CS-GARCH is defined and denoted by

$${\sigma }_t^2=q_t+\sum _{i=1}^q{\alpha }_i\left({\epsilon }_{t-i}^2-q_{t-i}\right)+\sum _{i=1}^p{\beta }_i\left({\sigma }_{t-i}^2-q_{t-i}\right)$$

(8)

$$q_t=\omega +\rho q_{t-1}+\varphi \left({\epsilon }_{t-1}^2-{\sigma }_{t-1}^2\right)$$

(9)

The latter is represented by $q_t$ while the transient component is given by the difference.

We adopt multiple variants of the GARCH approach to evaluate the predictive performance of Realized-GARCH model against other GARCH types analyzed in this study. Each variant of the GARCH models has distinct characteristics: The traditional GARCH model focuses on capturing volatility clustering with a relatively simple structure. The GJR-GARCH model extends this by accounting for the asymmetric impact of negative shocks, often observed in financial markets. The Realized-GARCH model further innovates by incorporating high-frequency data to refine volatility estimates, though it faces limitations in data availability and complexity. E-GARCH offers an approach to model the asymmetric effects of shocks without the constraint of non-negative coefficients, while FI-GARCH captures long memory effects in volatility. Lastly, the CS-GARCH model distinguishes itself by decomposing volatility into transient and permanent components, offering insights into different volatility dynamics. These variations in model structure and assumptions are critical in understanding their performance in predicting cryptocurrency volatility, as explored in the subsequent results section.

In this study, we utilize the sum of squared hourly returns within each day as our realized measure of volatility. This approach, while deviating from traditional methods that may account for overnight returns as a special case (as noted by Koopman et al. (2005)), is particularly suited for the cryptocurrency market. Cryptocurrencies operate in an environment markedly different from typical stock markets; they trade on a 24-h basis without the traditional overnight closure. Consequently, the concept of ’overnight returns’ is not applicable in the same way. By employing the sum of squared hourly returns, we capture a continuous and comprehensive measure of volatility, reflective of the unique trading nature of cryptocurrencies.

4. Results

4.1. GARCH Models Comparison

In order to model the volatility effects, we performed 768 simulations for each cryptocurrency explored, alternating the conditional variance models between GARCH, GJR-GARCH, Realized-GARCH, E-GARCH, FI-GARCH and CS-GARCH. In addition, we considered the p and q orders of the GARCH models from 1 to 4 and concomitantly with the types of distribution of returns: Normal, Student t, Skew Student t, Generalized Error, Skew Generalized Error, Johnson’s reparametrized SU, Generalized Hyperbolic and Normal Inverse Gaussian distributions.

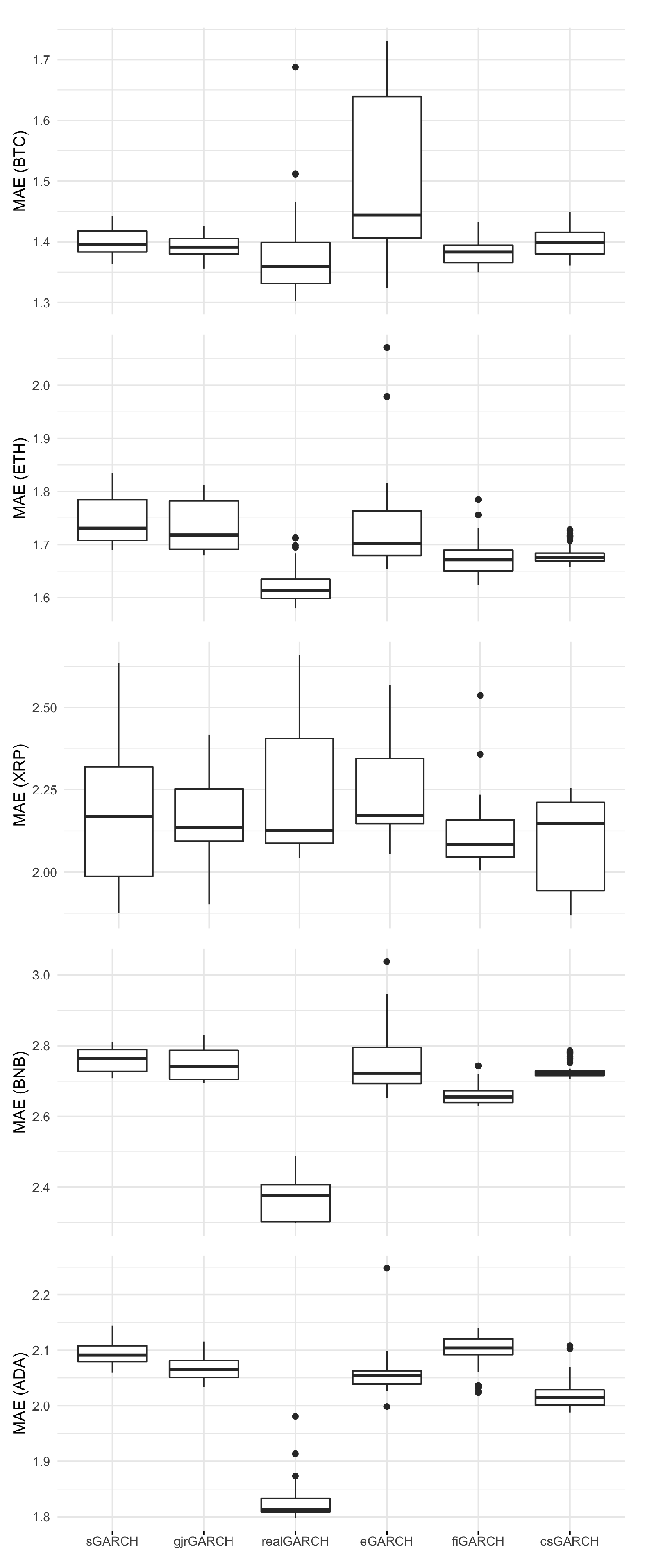
In the in-sample data, the MAE values (MAE (IS)) show similar ranges across different types of GARCH models for most cryptocurrencies. However, in the out-of-sample data, the difference in MAE values (MAE (OOS)) is more pronounced, particularly for Realized GARCH models. While they demonstrate solid performance in the training phase, its efficacy is more pronounced when applied to new, unseen data, delivering consistently lower MAE values compared to its counterparts. As a result, only Realized GARCH models are listed in

Table 2. Best models according to the smallest MAE on out-of-sample (OOS) data.

Crypto	Best Model	q	p	Distribution	MAE		MSPE
					IS	OOS	IS	OOS
BTC	RealGARCH	2	4	Johnson’s	1.337	0.812	3.408	1.587
ETH	RealGARCH	2	4	Student	1.632	0.888	4.823	2.038
XRP	RealGARCH	3	3	Student	2.149	1.260	10.37	6.190
BNB	RealGARCH	4	3	Normal	2.365	1.094	35.56	14.54
ADA	RealGARCH	1	2	Student	1.804	1.027	7.891	2.686

, underscoring their superior predictive accuracy. The corresponding MAE (IS) and MAE (OOS) values can be observed in Figure 1 and in Figure 2, respectively.

Alongside MAE, we also present the Mean Squared Prediction Error (MSPE) both in-sample and out-of-sample in the tables. While MSPE offers a metric that emphasizes larger errors by squaring them, we prioritized MAE in our main discussion as it provides a more direct and interpretable measure of forecast accuracy. It is worth noting that the optimal combination of model parameters for each cryptocurrency, across all GARCH types, is detailed in the table located in Appendix A.

Delving deeper into the statistical analysis, these figures are instrumental in illustrating the comparative performance of the GARCH models. In Figure 1, while the in-sample MAE values exhibit a degree of similarity across the models, indicating a consistent level of accuracy in fitting historical data, Figure 2 reveals a more nuanced story in the out-of-sample context. Here, the Realized-GARCH models stand out, demonstrating a marked improvement in forecasting accuracy. This is particularly evident in the lower MAE (OOS) values, suggesting that these models are not only adept at learning from past data but also excel in adapting to new, unseen market conditions. The MSPE values, presented alongside MAE in our tables, further corroborate these findings. Although MSPE accentuates larger errors, its trends align with the MAE results, reinforcing the superior performance of the Realized GARCH models in out-of-sample forecasting. This comprehensive analysis of both MAE and MSPE across in-sample and out-of-sample data provides a holistic view of the model performances, underpinning the selection of the Realized-GARCH model as the most effective tool for predicting cryptocurrency volatility in our study.

After training the models with the best parameters, we perform the analysis of the standardized residuals. Thereby, it is possible to check whether (or not) the model adheres to the process created by the returns. We verified for the best fitted models that there was no serial correlation on standard residuals or on the squared of the standard residuals, and that one may observe the absence of ARCH effects in the model residuals through the Lagrange multiplier test on fitted models.

Figure 3 depicts the realized intraday volatility, delineated in blue, and the predicted volatility from the best specification model, showcased in red. Upon closer inspection, one can discern that the forecasted values tend to follow the trajectory of the actual values. Nevertheless, a key observation is that the model’s forecasted volatility spikes, while present, are not as pronounced as the actual fluctuations. This suggests that while the model can anticipate the direction and general magnitude of volatility shifts, it may be more conservative in its predictions.

In synthesis, the modeling of cryptocurrencies’ returns can be performed satisfactorily through generalized models of conditional auto-regressive heteroskedasticity. Nonetheless, the Realized-GARCH model exhibits better performance than the other GARCH models for all cryptocurrencies analyzed.

4.2. Critical Analysis and Comments

It is important to acknowledge the potential influence of macroeconomic events on the cryptocurrency market. These broader economic forces are not only reflected in price changes, but also manifest in the volatility dynamics captured by GARCH models explored in this work. For instance, the onset of the COVID-19 pandemic in 2020 introduced significant market uncertainty, leading to spikes in estimated variance. Similarly, policy changes, such as the mid-2021 crackdown on Bitcoin mining, also had a notable impact, resulting in a downturn in cryptocurrency prices. This impact of the COVID-19 pandemic is particularly evident in our empirical results. In Figure 4, which illustrates the cryptocurrency return series, one can distinctly observe pronounced spikes around March 2020, coinciding with the global escalation of the pandemic. These spikes in volatility are reflective of the heightened market uncertainty during this period, and one may observe that the GARCH model follows its movement.

These events manifest in our graphical representations, effectively showcasing the responsiveness of our optimally fitted models to unexpected market developments. As can be seen in Figure 4, cryptocurrency returns are plotted in blue, alongside a red line indicating two standard deviations as a measure of risk. What stands out in this visualization is the remarkable adaptability of the two-standard-deviation bounds to the well-documented phenomenon of volatility clustering in financial time series.

The importance of a well-fitted model becomes especially evident in times of crisis or significant events. Accurate volatility estimates are crucial for risk management, option pricing, and various other financial applications. A model that effectively captures sudden increases or changes in volatility can be an invaluable tool for investors navigating through the uncertainty that significant geopolitical events often bring. In our analysis, the selected GARCH models have proven adept at this, affirming their utility in an increasingly interconnected and event-driven global financial landscape.

5. Conclusions

The cryptocurrency market, with its rapid growth and dynamic nature, necessitates robust methods for volatility modeling. This study has highlighted the effectiveness of Realized-GARCH model in capturing the intricacies of volatility in this emerging asset class. The results indicate that while various GARCH models can produce satisfactory in-sample fits, the Realized-GARCH model outperforms its counterparts in out-of-sample forecasting. This underscores the model’s strength not just in fitting past data, but also in making robust future predictions, thereby reducing the risk of overfitting.

This study examines the volatility dynamics of cryptocurrencies using GARCH-type models and observes conservatism in capturing extreme spikes, indicating areas for potential improvement. Considering the noted influence of macroeconomic and geopolitical events on cryptocurrency volatility, future research may benefit from incorporating external regressors to more accurately capture such extreme events. Moving forward, an intriguing prospect for further research is the examination of the HAR model, as proposed by Corsi (2009). Future investigations could involve a comparative study between the HAR model and Realized GARCH models in cryptocurrency contexts.

In summary, this paper contributes to the literature by establishing the efficacy of Realized-GARCH model in the context of cryptocurrency volatility. The findings not only validate the versatility of GARCH models, but we also hope that it can contribute to encouraging and motivating future studies into the financial modeling of digital assets. Given the growing significance of cryptocurrencies in the global financial landscape, we believe that aforesaid future studies are indispensable for both academic scholars and industry professionals.