A Note on a Modified Parisian Ruin Concept
Abstract
1. Introduction
- (i)
- A model where the event of ruin is only checked periodically (Albrecher et al. 2013) by a Poissonian observer with nice identities known from Albrecher and Ivanovs (2013, 2017) and Albrecher et al. (2016) and exotic ruin quantities from Landriault et al. (2019, Section 3.2) and Li and Zhou (2022);
- (ii)
- A model where the insurer declares bankruptcy at a constant rate (that is the reciprocal of the mean of the exponential grace period) as in Albrecher et al. (2011b), Gerber et al. (2012) and Albrecher and Lautscham (2013).
2. Problem Formulation and Preliminaries
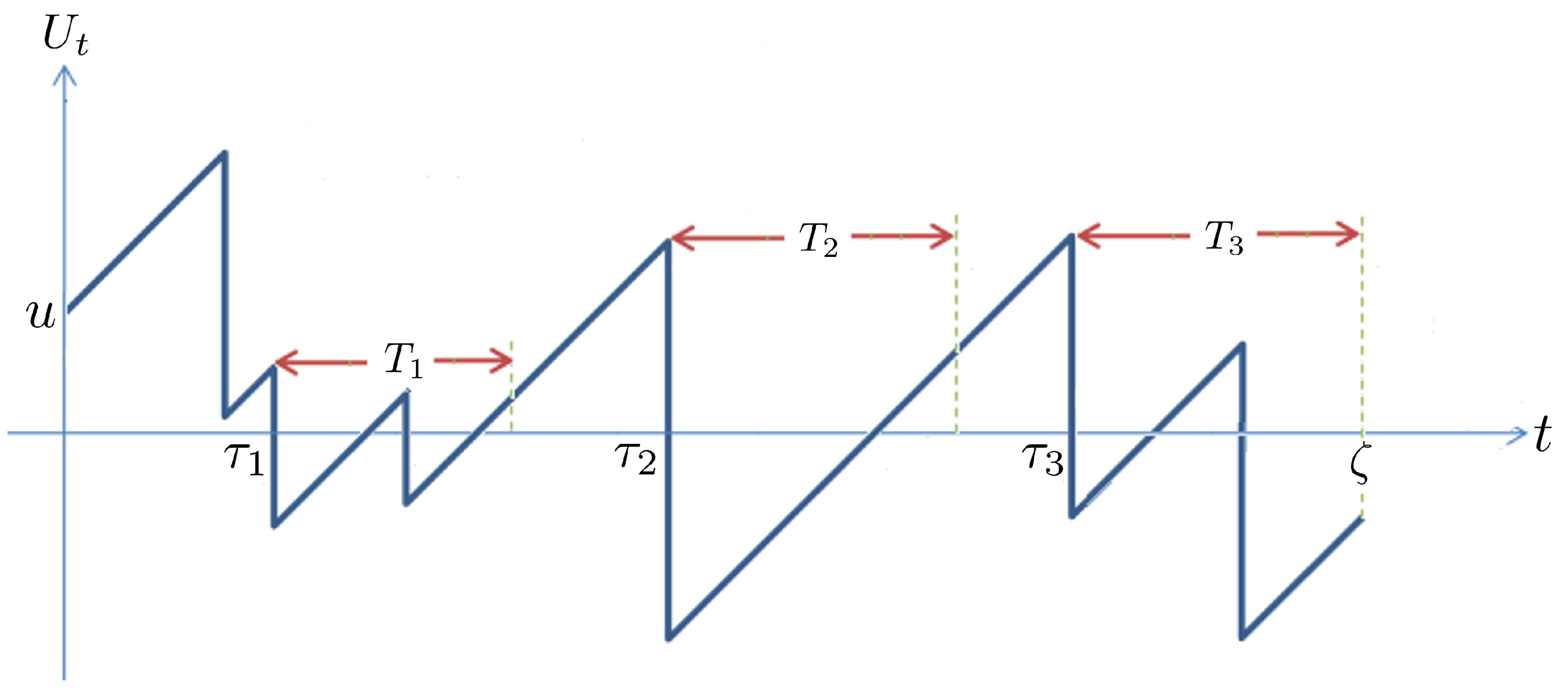
2.1. Modified Parisian Ruin Time and Gerber–Shiu Function
2.2. Discounted Density of the Increment in a Grace Period
3. Main Results
3.1. General Expressions for Gerber–Shiu Function and Discounted Density of Deficit
- if there is a positive net loss of (with discounted density ), then ruin happens with a deficit of ;
- if there is a positive net gain of (with discounted density ), then the gain is insufficient for the process to recover to a non-negative surplus and ruin happens with a deficit of ; and
- if there is a positive net gain of , then the process recovers and restarts at the newly achieved non-negative surplus level .
3.2. Laplace Transform of Ruin Time When Claims Follow a Combination of Exponentials
4. Numerical Illustrations
- When , the two Parisian ruin probabilities are identical for each fixed pair of ). This is a direct consequence of the memoryless property of exponential grace periods.
- The modified Parisian ruin probability is smaller than the classical ruin probability . This must be the case because modified Parisian ruin can only occur if the surplus process ever falls below zero. On the other hand, for fixed triplet , the modified Parisian ruin probability is no less than the standard Parisian ruin probability. Recall that, according to the definition of standard Parisian ruin, the business is deemed to have recovered as long as the surplus attains a non-negative level at any time point within the grace period. However, under the modified Parisian ruin, this is not sufficient to avoid ruin: the surplus has to be non-negative at the end of the grace period in order to survive the regulatory check. As a result, our proposed definition of ruin is more stringent than standard Parisian ruin from a regulatory point of view, and the modified Parisian ruin probability could potentially be a risk quantity to consider if one wishes to be conservative.
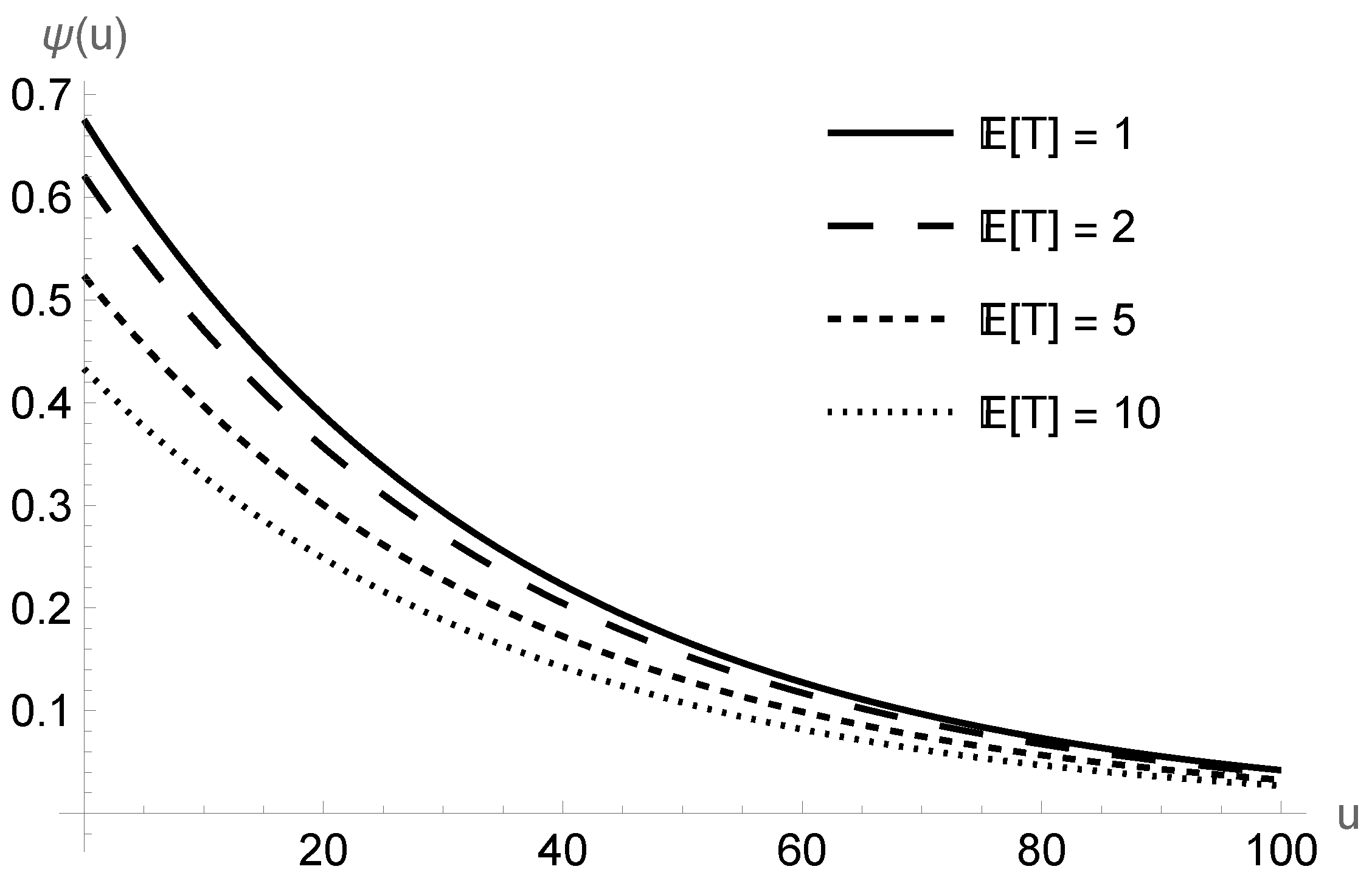
- For fixed , the modified Parisian ruin probability decreases when the expected grace period increases. For reference, in Figure 2, we have further plotted as a function of u for in the case where to observe that the curves are ordered. Recall that the insurer’s surplus process has a positive trend under the positive loading condition. Therefore, the business is more likely to survive the regulatory check if it is given a longer grace period so that profits can be accumulated, thereby lowering the modified Parisian ruin probability.
- For fixed , the difference between the two Parisian ruin probabilities increases in . Intuitively, when is small, there is insufficient time for the insurer to collect a premium for recovery. Consequently, it is more likely for the surplus process to remain negative for the entire grace period, leading to ruin under both definitions and hence a small difference in the ruin probabilities.
- As n increases down each column, the modified Parisian ruin probability converges because one approaches the case of deterministic grace periods thanks to the Erlangization procedure. The use of moderate values of n (around ) often leads to excellent results.
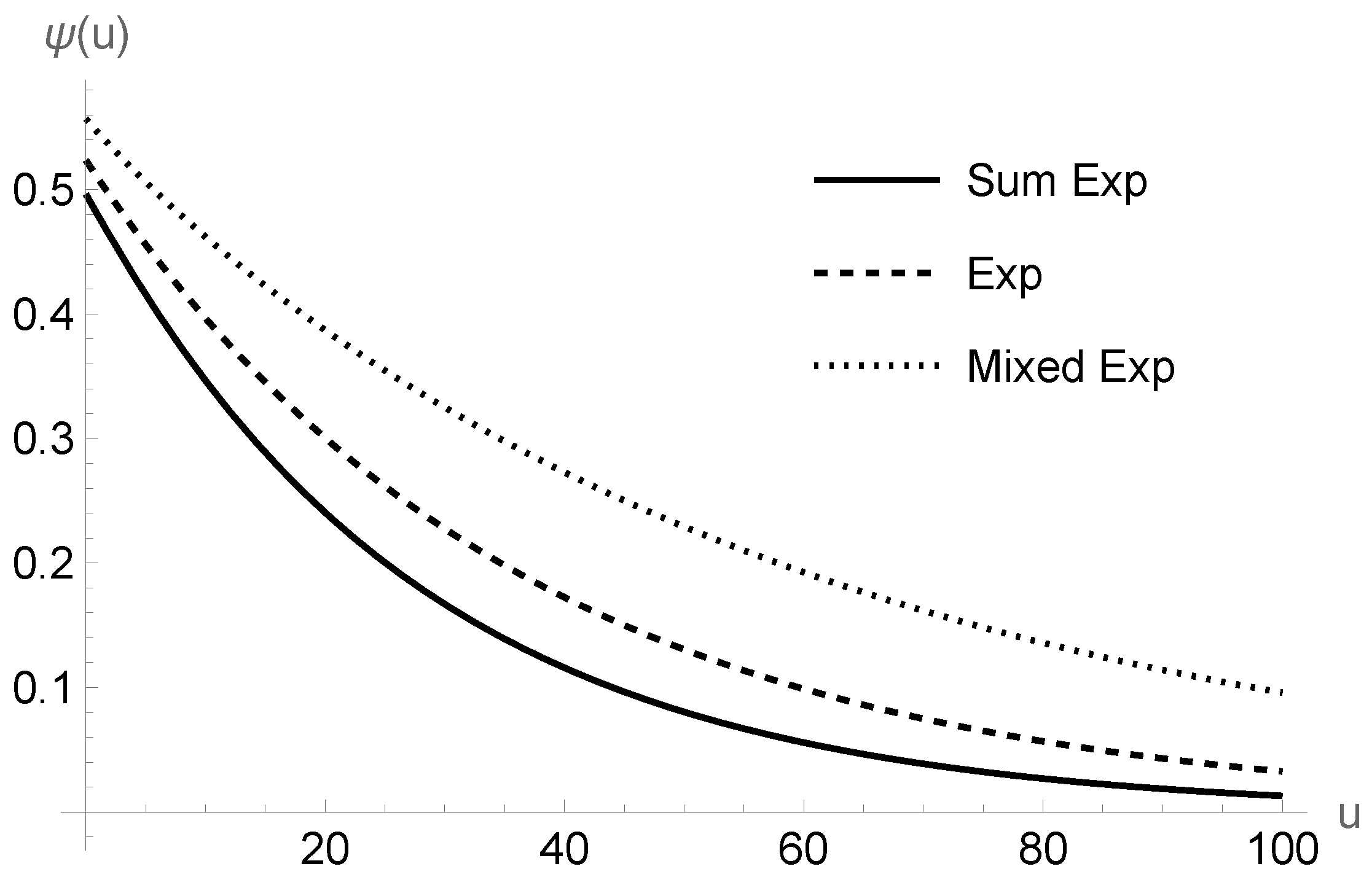
- A sum of two independent exponential variables (possessing respective means 3 and 6) with density ;
- A mixture of two exponentials with density .
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albrecher, Hansjoerg, and Jevgenijs Ivanovs. 2013. A risk model with an observer in a Markov environment. Risks 1: 148–61. [Google Scholar] [CrossRef]
- Albrecher, Hansjoerg, and Jevgenijs Ivanovs. 2017. Strikingly simple identities relating exit problems for Lévy processes under continuous and Poisson observations. Stochastic Processes and Their Applications 127: 643–56. [Google Scholar] [CrossRef]
- Albrecher, Hansjoerg, and Volkmar Lautscham. 2013. From ruin to bankruptcy for compound Poisson surplus processes. ASTIN Bulletin 43: 213–43. [Google Scholar] [CrossRef]
- Albrecher, Hansjoerg, Eric C. K. Cheung, and Stefan Thonhauser. 2011a. Randomized observation periods for the compound Poisson risk model: Dividends. ASTIN Bulletin 41: 645–72. [Google Scholar]
- Albrecher, Hansjoerg, Eric C. K. Cheung, and Stefan Thonhauser. 2013. Randomized observation periods for the compound Poisson risk model: The discounted penalty function. Scandinavian Actuarial Journal 2013: 424–52. [Google Scholar] [CrossRef]
- Albrecher, Hansjoerg, Hans U. Gerber, and Elias S. W. Shiu. 2011b. The optimal dividend barrier in the Gamma-Omega model. European Actuarial Journal 1: 43–55. [Google Scholar] [CrossRef]
- Albrecher, Hansjoerg, Jevgenijs Ivanovs, and Xiaowen Zhou. 2016. Exit identities for Lévy processes observed at Poisson arrival times. Bernoulli 22: 1364–82. [Google Scholar] [CrossRef]
- Antill, Samuel, and Steven R. Grenadier. 2019. Optimal capital structure and bankruptcy choice: Dynamic bargaining versus liquidation. Journal of Financial Economics 133: 198–224. [Google Scholar] [CrossRef]
- Asmussen, Soren, Florin Avram, and Miguel Usabel. 2002. Erlangian approximations for finite-horizon ruin probabilities. ASTIN Bulletin 32: 267–81. [Google Scholar] [CrossRef]
- Baurdoux, E. J., J. C. Pardo, J. L. Pérez, and J. F. Renaud. 2016. Gerber-Shiu distribution at Parisian ruin for Lévy insurance risk processes. Journal of Applied Probability 53: 572–84. [Google Scholar] [CrossRef]
- Bladt, Mogens, Bo Friis Nielsen, and Oscar Peralta. 2019. Parisian types of ruin probabilities for a class of dependent risk-reserve processes. Scandinavian Actuarial Journal 2019: 32–61. [Google Scholar] [CrossRef]
- Broadie, Mark, Mikhail Chernov, and Suresh Sundaresan. 2007. Optimal debt and equity values in the presence of Chapter 7 and Chapter 11. Journal of Finance 62: 1341–77. [Google Scholar] [CrossRef]
- Carr, Peter. 1998. Randomization and the American put. Review of Financial Studies 11: 597–626. [Google Scholar] [CrossRef]
- Chesney, Marc, Monique Jeanblanc-Picqué, and Marc Yor. 1997. Brownian excursions and Parisian barrier options. Advances in Applied Probability 29: 165–84. [Google Scholar] [CrossRef]
- Cheung, Eric C. K., and Jeff T. Y. Wong. 2017. On the dual risk model with Parisian implementation delays in dividend payments. European Journal of Operational Research 257: 159–73. [Google Scholar] [CrossRef]
- Czarna, Irmina. 2016. Parisian ruin probability with a lower ultimate bankrupt barrier. Scandinavian Actuarial Journal 2016: 319–37. [Google Scholar] [CrossRef]
- Czarna, Irmina, and Zbigniew Palmowski. 2011. Ruin probability with Parisian delay for a spectrally negative Lévy risk process. Journal of Applied Probability 48: 984–1002. [Google Scholar] [CrossRef][Green Version]
- Czarna, Irmina, Yanhong Li, Zbigniew Palmowski, and Chunming Zhao. 2017. The joint distribution of the Parisian ruin time and the number of claims until Parisian ruin in the classical risk model. Journal of Computational and Applied Mathematics 313: 499–514. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Shanle Wu. 2008a. Parisian Ruin with Exponential Claims. Available online: http://stats.lse.ac.uk/angelos/docs/exponentialjump.pdf (accessed on 15 January 2023).
- Dassios, Angelos, and Shanle Wu. 2008b. Ruin Probabilities of the Parisian Type for Small Claims. Available online: http://stats.lse.ac.uk/angelos/docs/paper5a.pdf (accessed on 15 January 2023).
- Dufresne, Daniel. 2007. Fitting combinations of exponentials to probability distributions. Applied Stochastic Models in Business and Industry 23: 23–48. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Elisa S. W. Shiu. 1998. On the time value of ruin. North American Actuarial Journal 2: 48–72. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Elisa S. W. Shiu. 2005. The time value of ruin in a Sparre Andersen model. North American Actuarial Journal 9: 49–69. [Google Scholar] [CrossRef]
- Gerber, Hans U., Elisa S. W. Shiu, and Hailiang Yang. 2012. The Omega model: From bankruptcy to occupation times in the red. European Actuarial Journal 2: 259–72. [Google Scholar] [CrossRef]
- Kyprianou, Andreas. E., and M. R. Pistorius. 2003. Perpetual options and Canadization through fluctuation theory. Annals of Applied Probability 13: 1077–98. [Google Scholar] [CrossRef]
- Landriault, David, Bin Li, Tianxiang Shi, and Di Xu. 2019. On the distribution of classic and some exotic ruin times. Insurance: Mathematics and Economics 89: 38–45. [Google Scholar] [CrossRef]
- Landriault, David, Jean-François Renaud, and Xiaowen Zhou. 2014. An insurance risk model with Parisian implementation delays. Methodology and Computing in Applied Probability 16: 583–607. [Google Scholar] [CrossRef]
- Li, Bin, Qihe Tang, Lihe Wang, and Xiaowen Zhou. 2014. Liquidation risk in the presence of Chapters 7 and 11 of the US bankruptcy code. Journal of Financial Engineering 1: 1450023. [Google Scholar] [CrossRef]
- Li, Shu, and Xiaowen Zhou. 2022. The Parisian and ultimate drawdowns of Lévy insurance models. Insurance: Mathematics and Economics 107: 140–60. [Google Scholar] [CrossRef]
- Li, Xin, Haibo Liu, Qihe Tang, and Jinxia Zhu. 2020. Liquidation risk in insurance under contemporary regulatory frameworks. Insurance: Mathematics and Economics 93: 36–49. [Google Scholar] [CrossRef]
- Lkabous, Mohamed Amine, Irmina Czarna, and Jean-François Renaud. 2017. Parisian ruin for a refracted Lévy process. Insurance: Mathematics and Economics 74: 153–63. [Google Scholar] [CrossRef]
- Loeffen, Ronnie, Irmina Czarna, and Zbigniew Palmowski. 2013. Parisian ruin probability for spectrally negative Lévy processes. Bernoulli 19: 599–609. [Google Scholar] [CrossRef]
- Loeffen, Ronnie, Zbigniew Palmowski, and Budhi A. Surya. 2018. Discounted penalty function at Parisian ruin for Lévy insurance risk process. Insurance: Mathematics and Economics 83: 190–97. [Google Scholar] [CrossRef]
- Ramaswami, V., Douglas G. Woolford, and David A. Stanford. 2008. The Erlangization method for Markovian fluid flows. Annals of Operations Research 160: 215–25. [Google Scholar] [CrossRef]
- Schröder, Michael. 2003. Brownian excursions and Parisian barrier options: A note. Journal of Applied Probability 40: 855–64. [Google Scholar]
- Stanford, David A., Florin Avram, A. L. Badescu, L. Breuer, A. Da Silva Soares, and G. Latouche. 2005. Phase-type approximations to finite-time ruin probabilities in the Sparre-Anderson and stationary renewal risk models. ASTIN Bulletin 35: 131–44. [Google Scholar] [CrossRef]
- Wong, Jeff T. Y., and Eric C. K. Cheung. 2015. On the time value of Parisian ruin in (dual) renewal risk processes with exponential jumps. Insurance: Mathematics and Economics 65: 280–90. [Google Scholar] [CrossRef]
- Zhang, Zhimin, and Eric C. K. Cheung. 2016. The Markov additive risk process under an Erlangized dividend barrier strategy. Methodology and Computing in Applied Probability 18: 275–306. [Google Scholar] [CrossRef][Green Version]
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Standard | Modified | Standard | Modified | Standard | Modified | Standard | Modified | |
| 1 | 0.6886 | 0.6886 | 0.6478 | 0.6478 | 0.5676 | 0.5676 | 0.4867 | 0.4867 |
| 5 | 0.6767 | 0.6786 | 0.6195 | 0.6275 | 0.5020 | 0.5322 | 0.3879 | 0.4423 |
| 10 | 0.6748 | 0.6770 | 0.6144 | 0.6241 | 0.4910 | 0.5273 | 0.3737 | 0.4370 |
| 15 | 0.6741 | 0.6764 | 0.6126 | 0.6229 | 0.4873 | 0.5257 | 0.3690 | 0.4353 |
| 20 | 0.6737 | 0.6761 | 0.6117 | 0.6223 | 0.4854 | 0.5250 | 0.3667 | 0.4344 |
| 25 | 0.6735 | 0.6759 | 0.6112 | 0.6219 | 0.4842 | 0.5245 | 0.3653 | 0.4339 |
| 30 | 0.6733 | 0.6758 | 0.6108 | 0.6217 | 0.4835 | 0.5242 | 0.3644 | 0.4336 |
| 35 | 0.6732 | 0.6757 | 0.6105 | 0.6215 | 0.4829 | 0.5240 | 0.3637 | 0.4333 |
| 40 | 0.6732 | 0.6756 | 0.6103 | 0.6214 | 0.4825 | 0.5238 | 0.3633 | 0.4331 |
| 45 | 0.6731 | 0.6755 | 0.6102 | 0.6213 | 0.4822 | 0.5237 | 0.3629 | 0.4330 |
| 50 | 0.6731 | 0.6755 | 0.6100 | 0.6212 | 0.4820 | 0.5236 | 0.3626 | 0.4329 |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Standard | Modified | Standard | Modified | Standard | Modified | Standard | Modified | |
| 1 | 0.1717 | 0.1717 | 0.1615 | 0.1615 | 0.1415 | 0.1415 | 0.1213 | 0.1213 |
| 5 | 0.1687 | 0.1692 | 0.1545 | 0.1565 | 0.1252 | 0.1327 | 0.0967 | 0.1103 |
| 10 | 0.1683 | 0.1688 | 0.1532 | 0.1556 | 0.1224 | 0.1315 | 0.0932 | 0.1090 |
| 15 | 0.1681 | 0.1687 | 0.1528 | 0.1553 | 0.1215 | 0.1311 | 0.0920 | 0.1085 |
| 20 | 0.1680 | 0.1686 | 0.1525 | 0.1552 | 0.1210 | 0.1309 | 0.0914 | 0.1083 |
| 25 | 0.1679 | 0.1685 | 0.1524 | 0.1551 | 0.1207 | 0.1308 | 0.0911 | 0.1082 |
| 30 | 0.1679 | 0.1685 | 0.1523 | 0.1550 | 0.1206 | 0.1307 | 0.0909 | 0.1081 |
| 35 | 0.1679 | 0.1685 | 0.1522 | 0.1550 | 0.1204 | 0.1306 | 0.0907 | 0.1081 |
| 40 | 0.1679 | 0.1685 | 0.1522 | 0.1549 | 0.1203 | 0.1306 | 0.0906 | 0.1080 |
| 45 | 0.1679 | 0.1684 | 0.1521 | 0.1549 | 0.1202 | 0.1306 | 0.0905 | 0.1080 |
| 50 | 0.1678 | 0.1684 | 0.1521 | 0.1549 | 0.1202 | 0.1305 | 0.0904 | 0.1079 |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.6813 | 0.1110 | 0.6347 | 0.1031 | 0.5451 | 0.0883 | 0.4573 | 0.0740 |
| 5 | 0.6693 | 0.1086 | 0.6100 | 0.0988 | 0.5053 | 0.0818 | 0.4093 | 0.0663 |
| 10 | 0.6671 | 0.1082 | 0.6058 | 0.0980 | 0.5002 | 0.0810 | 0.4038 | 0.0654 |
| 15 | 0.6664 | 0.1081 | 0.6043 | 0.0978 | 0.4986 | 0.0807 | 0.4019 | 0.0651 |
| 20 | 0.6660 | 0.1080 | 0.6036 | 0.0977 | 0.4978 | 0.0806 | 0.4010 | 0.0649 |
| 25 | 0.6657 | 0.1080 | 0.6031 | 0.0976 | 0.4973 | 0.0805 | 0.4005 | 0.0649 |
| 30 | 0.6656 | 0.1079 | 0.6028 | 0.0975 | 0.4970 | 0.0805 | 0.4001 | 0.0648 |
| 35 | 0.6655 | 0.1079 | 0.6026 | 0.0975 | 0.4968 | 0.0804 | 0.3999 | 0.0648 |
| 40 | 0.6654 | 0.1079 | 0.6024 | 0.0975 | 0.4966 | 0.0804 | 0.3997 | 0.0647 |
| 45 | 0.6653 | 0.1079 | 0.6023 | 0.0975 | 0.4965 | 0.0804 | 0.3995 | 0.0647 |
| 50 | 0.6652 | 0.1079 | 0.6022 | 0.0974 | 0.4964 | 0.0804 | 0.3994 | 0.0647 |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.6943 | 0.2775 | 0.6600 | 0.2660 | 0.5930 | 0.2416 | 0.5237 | 0.2147 |
| 5 | 0.6853 | 0.2754 | 0.6433 | 0.2616 | 0.5641 | 0.2319 | 0.4857 | 0.2002 |
| 10 | 0.6838 | 0.2751 | 0.6406 | 0.2609 | 0.5600 | 0.2304 | 0.4809 | 0.1982 |
| 15 | 0.6833 | 0.2750 | 0.6397 | 0.2606 | 0.5587 | 0.2299 | 0.4793 | 0.1975 |
| 20 | 0.6830 | 0.2749 | 0.6393 | 0.2605 | 0.5580 | 0.2297 | 0.4785 | 0.1972 |
| 25 | 0.6829 | 0.2749 | 0.6390 | 0.2604 | 0.5576 | 0.2295 | 0.4780 | 0.1970 |
| 30 | 0.6827 | 0.2748 | 0.6388 | 0.2604 | 0.5573 | 0.2294 | 0.4777 | 0.1968 |
| 35 | 0.6827 | 0.2748 | 0.6387 | 0.2603 | 0.5571 | 0.2294 | 0.4775 | 0.1968 |
| 40 | 0.6826 | 0.2748 | 0.6386 | 0.2603 | 0.5570 | 0.2293 | 0.4773 | 0.1967 |
| 45 | 0.6826 | 0.2748 | 0.6385 | 0.2603 | 0.5569 | 0.2293 | 0.4772 | 0.1966 |
| 50 | 0.6825 | 0.2748 | 0.6384 | 0.2603 | 0.5568 | 0.2292 | 0.4771 | 0.1966 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheung, E.C.K.; Wong, J.T.Y. A Note on a Modified Parisian Ruin Concept. Risks 2023, 11, 56. https://doi.org/10.3390/risks11030056
Cheung ECK, Wong JTY. A Note on a Modified Parisian Ruin Concept. Risks. 2023; 11(3):56. https://doi.org/10.3390/risks11030056
Chicago/Turabian StyleCheung, Eric C. K., and Jeff T. Y. Wong. 2023. "A Note on a Modified Parisian Ruin Concept" Risks 11, no. 3: 56. https://doi.org/10.3390/risks11030056
APA StyleCheung, E. C. K., & Wong, J. T. Y. (2023). A Note on a Modified Parisian Ruin Concept. Risks, 11(3), 56. https://doi.org/10.3390/risks11030056







