Bankruptcy Prediction for Micro and Small Enterprises Using Financial, Non-Financial, Business Sector and Macroeconomic Variables: The Case of the Lithuanian Construction Sector

Abstract

Credit-risk models that are designed for general application across sectors may not be suitable for the construction industry, which has unique characteristics and financial risks that require specialised modelling approaches. Moreover, advanced bankruptcy-prediction models are often used to achieve the highest accuracy in large modern datasets. Therefore, the aim of this research is the creation of enterprise-bankruptcy prediction (EBP) models for Lithuanian micro and small enterprises (MiSEs) in the construction sector. This issue is analysed based on classification models and the specific types of variable used. Firstly, four types of variable are proposed. In EBP models, financial variables substantially explain an enterprise’s financial statements and performance from different perspectives. Including enterprises’ non-financial, construction-sector and macroeconomic variables improves the characteristics of EBP models. The inclusion of macroeconomic variables in the model has a particularly significant impact. These findings can be of great significance to investors, creditors, policymakers and practitioners in assessing financial risks and making informed decisions. The second question is related to the classification models used. To develop the EBP models, logistic regression (LR), artificial neural networks (ANNs) and multivariate adaptive regression splines (MARS) were used. In addition, this study developed two-stage hybrid models, i.e., the LR is combined with ANNs. The findings show that two-stage hybrid models do not improve bankruptcy prediction. It cannot be argued that ANN models are more accurate in predicting bankruptcy. The MARS model demonstrates the best bankruptcy prediction, i.e., this model could be a valuable tool for stakeholders to evaluate enterprises’ financial risk.

1. Introduction

Maintaining a stable business is crucial in a constantly changing business environment. Veganzones and Severin (2021) point out that, since the beginning of the 21st century, “an increasing number of firms suffering from financial difficulties and/or having to cease their activities altogether.” It should be noted that enterprise bankruptcy is not a rare phenomenon in market conditions, i.e., companies that engage in all types of economic activity go bankrupt. The literature highlights that enterprise bankruptcies have serious financial (“for financial creditors, managers, shareholders, investors, employees, and even a country’s economy” (Korol 2019)) and social consequences (Cao et al. 2020). Therefore, evaluating the probability of bankruptcy is an essential instrument for financial management.

To identify as early as possible the reasons for the deterioration of the financial position of enterprises and the factors that lead to their decline, enterprise managers should regularly carry out bankruptcy predictions. In addition, other business entities (shareholders, investors, suppliers, regulators, etc.) also assess the enterprise’s financial position, going concerns and business prospects, as well as using bankruptcy-prediction models. As Korol (2019) points out, accurate bankruptcy prediction provides a wide range of benefits (e.g., “cost reduction in credit analysis, better monitoring and an increased debt-collection rate”). Therefore, bankruptcy prediction is highly relevant currently (Korol 2019; Bateni and Asghari 2020; Veganzones and Severin 2021).

The topic of bankruptcy prediction is not new. The first bankruptcy-prediction models were developed in the 1960s. Since then, many different models have been developed around the world. However, these models “have been developed in different time and space using different methods and variables” (Kovacova et al. 2019). Therefore, the question of their validity arises. In addition, it is necessary to mention that information technology has offered new research methods that can be used for developing accurate bankruptcy-prediction models (Veganzones and Severin 2021).

Studies (Kovacova et al. 2019). found that different countries select “different explanatory variables” to develop bankruptcy-prediction models. This shows that general bankruptcy-prediction models are inefficient in specific countries and do not fully explain country specificities. This view is supported by Veganzones and Severin (2021), who point out that different countries have different “juridical and accounting systems” and that each country has “its own corporate failure and accounting rules.” The authors conclude that, when designing bankruptcy -prediction models, the enterprise’s “samples should be from a single country, to ensure their uniform juridical and accounting systems.” This highlights the need to develop country-specific bankruptcy-prediction models.

As Tserng et al. (2011) point out, earlier studies did not explore this problem in single industries, probably due to “the limitedness of defaulted samples”. However, more recently, bankruptcy-prediction models have been developed for different sectors. For example, in the catering (more specifically, restaurant) sector (Becerra-Vicario et al. 2020), in the manufacturing industry (De Andrés et al. 2011c; Liang et al. 2016), in the information and electronic manufacturing sector (Yeh et al. 2010) and in the construction sector (De Andrés et al. 2011a; Tserng et al. 2011; Sánchez-Lasheras et al. 2012; Jang et al. 2021).

This study focuses on enterprises in the construction sector. This selection is based on the following assumptions. Enterprises in the construction sector “have particular characteristics and financial risks” (Tserng et al. 2011). They “are more vulnerable to bankruptcy” due to the “uniqueness of projects and long periods for project completion” (Jang et al. 2021) (which Tserng et al. (2011), Cheng et al. (2014) analyse more deeply) and the significant changes in “the structure of the construction industry” (Jang et al. 2021). Therefore, predicting business failures is essential for such enterprises. More precisely, this study focuses on the construction sector in Lithuania due to “the rapidly increasing number of bankruptcies of the companies in this sector” (Giriūniene et al. 2019).

Numerous studies have been conducted on financial-distress signalling and bankruptcy prediction. However, as Kosmidis and Stavropoulos (2014) point out, thee studies are mainly focused on “large entities or listed corporations.” These studies include those by Altman (1968); Ohlson (1980); Zmijewski (1984); Zavgren (1985); (Lin 2009); Chen and Du (2009); Wu and Hsu (2012); Tinoco and Wilson (2013); Bhattacharjee and Han (2014); Zhang et al. (2016) and Bateni and Asghari (2020).

The issue of bankruptcy prediction becomes more complicated when small and medium-sized enterprises (SMEs) are analysed. While it is recognised that SMEs are essential parts of the economy and their specificities need to be considered, there are substantially fewer models for credit-risk management and bankruptcy prediction focusing on these companies (Tascón et al. 2018; Zhu et al. 2016; Yoshino and Taghizadeh-Hesary 2014; Ciampi and Gordini 2013; Behr and Güttler 2007; Altman and Sabato 2007). This is due to a “lack of data” (Yoshino and Taghizadeh-Hesary 2014; Kosmidis and Stavropoulos 2014; Martínez-Sola et al. 2017), “difficulties in accessing the data to an authentic SME database” (Yoshino and Taghizadeh-Hesary 2014), “lower quality data, lower reliability of information” (Tascón et al. 2018). As Abdullah et al. (2016) highlight, due to the difficulty in obtaining “financial data and other information” on SMEs, very little research has been conducted on these enterprises. On the other hand, it should also be appreciated that “SMEs are generally riskier than large corporations” (Terdpaopong and Mihret 2011). Due to the specificities of SMEs, it is necessary to develop bankruptcy-prediction models that are adapted to these enterprises.

This research analyses the bankruptcy prediction of micro and small enterprises. It is also essential to answer the question of whether, since 2016, in Lithuania, the reduction in information on micro enterprises in financial statements has reduced the accuracy of enterprise-bankruptcy-prediction models.

Therefore, this research is intended to create enterprise-bankruptcy prediction (EBP) models for Lithuanian micro and small enterprises (MiSEs) in the construction sector. The formulation of this aim was drawn from the fact that it is mainly construction enterprises that have gone bankrupt, especially since the world economic crisis, particularly in the current climate of increasing economic uncertainty.

To achieve this aim, two objectives are identified: (i) to examine the usefulness of not only enterprises’ financial ratios, but also other variables (i.e., non-financial, construction-sector and macroeconomic variables) and their contribution to the interpretability of bankruptcy-prediction models; (ii) the creation of models that are not only interpretable, but also accurate. Therefore, we used not only logistic regression (LR) as a statistical model, but also artificial neural networks (ANNs).

The most important contributions of this research are the following findings. Firstly, the developed logistic regression EBP models for MiSEs in the construction sector are characterised by the high level of interpretability of their results, their accuracy and their simplicity. In the enterprise-bankruptcy prediction (EBP) models, the financial variables substantially explain enterprises’ financial statements and performance from different perspectives. This finding can be useful for investors, creditors and other stakeholders in assessing the financial risk of the MiSEs in the construction sector.

The inclusion of enterprises’ non-financial, construction-sector and macroeconomic variables improves the characteristics of the EBP models. The inclusion of macroeconomic variables in these models has a particularly significant impact. This finding can be useful for researchers and practitioners in developing more accurate and reliable EBP models. It can also be useful for policymakers in designing policies and regulations to take appropriate decisions related to the financial stability of the MiSEs in the construction sector.

It can also be stated that the model features flexibility, i.e., stakeholders can assess an enterprise using only financial ratios or other variables.

Second, two-stage hybrid models do not improve bankruptcy prediction. Third, this study develops multilayer perceptions (MLP) and radial basis function (RBF) neural network models based on all sets of independent variables, i.e., the financial ratios, macroeconomic variables, construction-sector variables and non-financial variables of enterprises. The ANN models demonstrate acceptable performance in terms of discrimination. However, ANNs have lower discriminatory power than the logistic regression model based on all the sets of independent variables. Fourth, the multivariate adaptive regression splines (MARS) model demonstrates the best bankruptcy prediction: the MARS model is characterised by outstanding discriminatory power. Hence, a better understanding of the classificatory techniques can be useful for researchers and practitioners in choosing the appropriate modelling approach for bankruptcy prediction and improving the accuracy of EBP models.

This paper consists of an introduction, five main sections and conclusions. Section 2 considers the issue of the compatibility between the accuracy and the interpretability of bankruptcy-prediction models. Section 3 describes the research methodology, i.e., it discusses the data collection and the selection of independent variables and hypotheses, as well as the EBP model’s specifications. Section 4 presents the results of the EBP models for Lithuanian MiSEs in the construction sector. Section 5 presents the concluding remarks.

2. Increasing the Accuracy and Interpretability of Bankruptcy-Prediction Models

In developing bankruptcy-prediction models, the problem of the compatibility between the accuracy and the interpretability of these models is raised. We analyse this issue based on the classification models and variable types used.

We begin to consider this issue by analysing classification models. Advanced models are often used to achieve the highest accuracy in large modern datasets. However, the interpretability of a model, i.e., why it produces a given prediction, may be as crucial as “the prediction accuracy in many applications” (Lundberg and Lee 2017). It should be noted that researchers such as Kumar and Ravi (2007) (as cited by Mai et al. (2019)) distinguish two categories of methods used in bankruptcy-prediction models: statistical models and intelligent models. After their literature review of recent studies on this issue, Mai et al. (2019) provide two observations. Firstly, statistical model development is focused on improving “the model’s prediction accuracy” and providing “more insights in examining distress risk.” Secondly, most of the recent studies on bankruptcy prediction use intelligent methods as they “make fewer assumptions about the data“ and “allow non-linear decision boundaries“; as a result, they are more flexible and “improved classification performance.“ Furthermore, Cao et al. (2020) summarise the review by Mai et al. (2019) and conclude that “methodologically many studies focus on machine learning models due to their estimation precision.“ It should be noted that machine learning is considered a subset of artificial intelligence. Finally, researchers (e.g., Mittelstadt et al. 2019; Cao et al. 2020) divide machine-learning models into two groups: interpretable and non-interpretable. Interpretable models include only simple logistic regression and tree-based models that can serve as benchmarks. By contrast, ANNs are classified as non-interpretable models.

One of the most widely used groups of machine-learning models is ANNs. These are applicable in various areas (Horak et al. 2020). More specifically, Zhang et al. (2016) identify ANNs among five types of credit-risk-evaluation method and agreed that ANNs have “high accuracy.“ For comparison, the average accuracy of multivariate discriminant analysis (MDA), logistic regression and ANNs was 68–76%, 71–77% and close to 85%, respectively (Becerra-Vicario et al. 2020). Although good classification accuracy is an advantage of ANNs, “the difficulty in interpreting the results” could be considered as one of the main limitations of these methods (Figini et al. 2017; Horak et al. 2020). In addition, although neural networks are widely used (Angelini et al. 2008; Zhang et al. 2016; Horak et al. 2020; Becerra-Vicario et al. 2020), they “require more modelling skills to determine proper model parameters and network topologies“ (Zhang et al. 2016).

Logistic regression is a statistical model appropriate for developing bankruptcy-prediction models. This statement is based on the following assumptions. Researchers agree that the statistical models based on logistic regression are widely used in credit-risk analysis and bankruptcy prediction (Crook et al. 2007; Lin 2009; Yap et al. 2011; Crone and Finlay 2012; Nikolic et al. 2013; Zhu et al. 2016; Figini et al. 2017; Kovacova et al. 2019) for their accuracy (West 2000; Crone and Finlay 2012), efficiency (Crone and Finlay 2012; Megan and Circa 2014; Zhu et al. 2016), reliability (Figini et al. 2017; Becerra-Vicario et al. 2020), interpretability (Crone and Finlay 2012; Figini et al. 2017; Han et al. 2018), practicality (Nikolic et al. 2013), simplicity and universality (Han et al. 2018). Furthermore, it is acknowledged that logistic regression is the industry standard (Lessmann et al. 2015), providing “standard benchmarks for the loan default prediction problem” (Olson et al. 2012; Figini et al. 2017). The logistic regression method is used in credit-risk models for small- and medium-sized enterprises (Altman and Sabato 2007; Behr and Güttler 2007; Kosmidis and Stavropoulos 2014; Abdullah et al. 2016; Zhu et al. 2016; Figini et al. 2017). On one hand, in this study, logistic regression is selected because it provides “a suitable balance of accuracy, efficiency and interpretability” in its results (Crone and Finlay 2012; Nikolic et al. 2013), i.e., this model can not only predict bankruptcy, but also provide information on “the variables that are significantly explanatory of bankruptcy” (Becerra-Vicario et al. 2020).

On the other hand, to develop the bankruptcy-prediction model in this study, logistic regression was combined with ANNs. As a consequence, the disadvantage of ANNs, i.e., the difficulty in explaining the classification performed, is eliminated. This solution is based on the following assumptions. The findings by Becerra-Vicario et al. (2020) show that the use of ANNs “exceeds logistic regression in predictive capacity.” For this reason, ANNs are selected as a computational technique to improve the precision accuracy of bankruptcy prediction and they could become new tools for such analyses. It should be noted that ANNs and logistic regression were combined by Lin (2009), Zhu et al. (2016) and Becerra-Vicario et al. (2020).

Researchers (e.g., Al-Sobiei et al. 2005; Jang et al. 2021) have used ANNs for bankruptcy prediction in the construction sector. As Jang et al. (2021) state, most construction-industry studies have focused “on increasing the prediction accuracy of bankruptcy.“ Without prediction accuracy, it is highly relevant to identify “the relationships between input variables and the prediction result.“ Therefore, the combination of ANNs and logistic regression is the appropriate selection for bankruptcy prediction in the construction sector.

Additionally, this study uses MARS as a nonparametric regression technique. This solution is based on the following assumptions. According to Hastie, Tibshirani and Friedman (2003) (as cited by Sánchez-Lasheras et al. (2012)), MARS can be considered as “a generalization of classification and regression trees (CART).” The findings by Lee et al. (2006) (as cited by Yap et al. (2011)) demonstrate that MARS outperforms logistic regression and neural network “approaches in terms of credit scoring accuracy.”

The second question in the issue considered is over the variable types used, i.e., financial ratios and non-financial, business-sector and macroeconomic variables.

In analysing the selection of independent variables for enterprise-bankruptcy prediction and credit-risk-assessment models, researchers typically include financial ratios as explanatory variables (Špicas et al. 2018; Veganzones and Severin 2021), “with the assumption that these ratios contain all relevant information for predicting corporate failure” (Veganzones and Severin 2021). The most commonly used financial variables for analysis are the relative financial ratios calculated from enterprises’ financial statements (the first models included those by Beaver 1966; Altman 1968; Chesser 1974; Ohlson 1980; Zmijewski 1984; Frydman et al. 1985 and Zavgren 1985; current models include those by Bužius et al. 2010; Tseng and Hu 2010; Danėnas et al. 2011; De Andrés et al. 2011c; Pacelli and Azzolini 2011; Mileris 2012; Olson et al. 2012; Wu and Hsu 2012; Gurný and Gurný 2013; Lorca et al. 2014). However, several researchers (e.g., Argenti (1976) (as cited by Veganzones and Severin 2021)) doubt the ability of the model to “predict failure with evidence from only financial ratios.” For example, Tinoco and Wilson (2013) state that “accounting data can only be obtained on an annual basis”; therefore, “there is always the risk of the relying on out dated information.” Thus, this study aims to examine the usefulness of other variables (i.e., non-financial, business sector and macroeconomic variables) and their contribution to the accuracy of bankruptcy-prediction models. Other researchers support the argument that this is a research need. For example, Tinoco and Wilson (2013) point out that very few studies have analysed the effectiveness of these three types of variable in “a statistical financial distress prediction model.”

Non-financial variables are indicators that show an enterprise’s solvency capacity by analysing non-financial sources. Špicas et al. (2018) highlight that the use of these indicators is directly related to external factors, i.e., the information infrastructure and, therefore, that the possibilities of using these indicators vary considerably between countries. Financial and non-financial variables have been combined in bankruptcy-prediction and credit-risk-assessment models by, for example, Špicas et al. (2018) and Becerra-Vicario et al. (2020).

Finally, business-sector and macroeconomic variables are also included in the models: “variations in economic cycles are positively related to failure probability” (Mare 2015) and economic variables can influence “the accuracy of predictive models” (Veganzones and Severin 2021). On one hand, it may be assumed that many explanatory variables can be included in a model. However, on the other hand (as pointed out by Veganzones and Severin (2021)), the inclusion of “irrelevant or redundant” variables can lead “to suboptimal models.” Therefore, the selection of the variables remains a crucial step in model development.

Bankruptcy prediction in the construction sector was analysed by Sueyoshi and Goto (2009) and Sánchez-Lasheras et al. (2012), among others. However, these authors only used financial ratios. Al-Sobiei et al. (2005) used non-financial and economic variables (e.g., overall contractor characteristics, specific contract characteristics and project indicators). Jang et al. (2021) used accounting, construction-market and macroeconomic variables.

The studies by Lithuanian researchers can be divided into two research directions. The first direction involves the evaluation of the applicability of previously developed bankruptcy-prediction models for Lithuanian enterprises. The most widely studied models are the classical statistical bankruptcy-prediction models using linear discriminant analysis (Altman, Springate, Taffler and Tisshaw) and logistic regression (Chesser, Zavgren). Researchers hold differing views on the developed bankruptcy-prediction models. Some express doubts about whether bankruptcy-prediction models developed in different countries are suitable for predicting bankruptcy in Lithuanian enterprises, as Lithuanian companies operate under different conditions (e.g., Purvinis et al. 2005). The second direction is the development of new models for enterprises operating in Lithuania. One of the first Lithuanian researchers to analyse credit-risk-assessment methods in the context of bankruptcy prediction was Grigaravičius (2003), who applied a logistic regression model to predict corporate bankruptcy.

Credit-risk-assessment models are developed for credit institutions—banks (Valvonis 2008; Dzidzevičiūtė 2013) or credit unions (Špicas et al. 2018). Standard credit models are developed by financial institutions for large corporations and are based on large amounts of data. Therefore, these models may not be directly transferred to SMEs. If models are applied to SMEs, then the model-development samples are small (Butkus et al. 2014). Therefore, it is necessary to develop bankruptcy-prediction models for SMEs using large samples of SMEs (studies on this topic in the field of credit-risk assessment include those by Špicas et al. (2018) and Kanapickienė and Špicas (2019).

Small and micro enterprises require special attention. As small enterprises are extremely significant for the socio-economic development of Lithuania, it was decided to simplify the accounting and financial reporting of these enterprises in order to reduce the administrative burden. Since 2016, the structure of financial statements in Lithuania has changed and the amount of information provided in the accounts of micro enterprises has been significantly reduced. Consequently, some of the bankruptcy-prediction models developed specifically for Lithuanian enterprises cannot be applied to these companies and it is therefore important to reassess whether the amount of available financial information is sufficient to predict the probability of the bankruptcy of small and micro enterprises.

3. Research Methodology

The EBP models for Lithuanian MiSEs in the construction sector were formed in this study. The research consisted of the following stages: (1) data collection, (2) selection of independent variables, (3) selection of the classificatory devices.

3.1. Data Collection

Considering the statistics on business bankruptcy and the trends of bankrupt enterprises in Lithuania, enterprises from the construction sector were selected for this study. This selection is based on the following reasons.

Firstly, according to the data of the State Data Agency of the Republic of Lithuania (hereafter referred to as Statistics Lithuania), on 1 January 2021, there were 87,707 enterprises in Lithuania (65,629 on 1 January 2009 and 65,779 on 1 January 2013, respectively). The majority of all operating enterprises worked in the fields of (a) wholesale and retail trade, (b) manufacturing, (c) construction, (d) transportation and storage and (e) professional, scientific and technical activities (the percentages of companies in each field of economic activity in each year were as follows: in 2009, 33.8%, 11.2%, 10.8%, 9.2%, 9.6%; in 2013, 33.0%, 10.3%, 9.2%, 9.8%, 10.8%; in 2021, 27.7%, 9.2%, 10.7%, 9.7%, 12.3%, respectively). Thus, the construction sector is one of the five largest sectors in Lithuania.

Secondly, the statistical data show that, during the 2009–2019 period, bankruptcy processes were initiated in 20,791 enterprises1. Regarding the five major sectors mentioned above, in 2009–2019, most bankruptcy processes were initiated in the (a) wholesale and retail trade, (b) manufacturing, (c) construction and (d) transportation and storage sectors (the percentages of enterprise bankruptcy in each field were as follows: in 2009, 23.2%, 16.9%, 23.6%, 14.9%; in 2013, 30.8%, 10.6%, 16.4%, 11.4%; and in 2019, 28.1%, 8.8%, 17.5%, 10.2%, respectively), i.e., in these four sectors, 67% of all bankruptcies occurred during the 2009–2019 period.

Thirdly, the analysis of the sectors with the highest bankruptcy rates reveals that the construction sector has the highest percentage of initiated bankruptcy processes among all enterprises in the industry (in 2009, 6.1%). This tendency has lasted until the present day (in 2013, 4.2%; in 2019, 3.4%). According to Jang et al. (2021), the reasons for the high level of bankruptcies in this sector can be either (i) internal, i.e., “the uniqueness of projects and long periods for project completion” and (ii) external, i.e., due to the changes in the structure of the construction industry, as the authors argue, as a result of “globalisation, technological advances, increased competition and regulation.”

The latter reason is one of the main factors that led to the selection of this sector for the present study. Finally, it is also worth mentioning that the construction sector can be identified as a growing sector, i.e., during the 2009–2019 period, the number of enterprises increased by 32 percentage points.

To summarise, the reasons discussed above determined the selection of construction enterprises for this study. To continue, the study’s organisation was defined in terms of the period considered, the control period, the population, the sampling and the sample size.

3.1.1. The Period Considered and the Control Period

To create the models, financial and non-financial data of bankrupt and non-bankrupt enterprises during the 2007–2013 period, i.e., the period considered, were investigated.

The reasons for this choice were as follows. The 2008/2009 global financial “crisis and economic downturn have had some serious implications” for the construction sector (Sánchez-Lasheras et al. 2012). Furthermore, Kjosevski et al. (2019) state that the financial crisis period lasted “from September 2008 to December 2009.” Therefore, in this study, the period considered was intended to cover the pre-crisis, crisis and post-crisis periods.

It should be noted that this study investigates enterprises that either (i) went bankrupt or (ii) started bankruptcy processes during the 2009–2013 period. At this point, it is worth explaining that the period considered is two years longer than the period of bankruptcy of the enterprises, as we had two years of pre-bankruptcy information on the enterprises that went bankrupt in 2009.

In this study, the data for the model development was collected and prepared in 2021. Therefore, an additional assessment of the business continuity of non-bankrupt enterprises was performed for the year 2021, i.e., the control period.

3.1.2. The Population

According to the data from Statistics Lithuania, on 1 January 2009, in the construction sector, there were 7091 enterprises in operation; on 1 January 2013, the number was 6033; during the 2009–2013 period, the process of bankruptcy was initiated for 1582 enterprises in the construction sector. As this study focuses on MiSEs, it is necessary to consider the definition of these enterprises, which is problematic for the following reasons.

Firstly, micro and small enterprises are defined by the Republic of Lithuania Law on Small and Medium-Sized Business Development (2017). This legal act states that a micro enterprise is an enterprise that has fewer than ten employees and whose financial data meet any one of the following conditions: (i) the annual revenue of the enterprise does not exceed EUR 2 million; (ii) the value of assets indicated in the statement of financial position does not exceed EUR 2 million. A small enterprise is an enterprise that has fewer than 50 employees and whose financial data meet any one of the following conditions: (i) the annual revenue of the enterprise does not exceed EUR 10 million; (ii) the value of assets indicated in the statement of financial position does not exceed EUR 10 million.

Secondly, it should be noted that the Law on Statements of Entities of the Republic of Lithuania (2017) also provides requirements for the sizes of enterprises; however, these are only valid for financial reporting purposes2. According to this legal act, a micro enterprise is an enterprise with at least two indicators that do not exceed the following amounts on the last day of a financial year: (i) the value of assets indicated in the statement of financial position—EUR 0.35 million; (ii) net sales revenue during a financial reporting year—EUR 0.7 million; (iii) the average annual number of payroll employees during a financial reporting year—10 employees. A small enterprise is an enterprise with at least two indicators that do not exceed the following amounts on the last day of a financial year: (i) the value of assets indicated in the statement of financial position—EUR 4 million; (ii) net sales revenue during a financial reporting year—EUR 8 million; (iii) the average annual number of payroll employees during a financial reporting year—50 employees.

In the context of this study, MiSEs are understood according to the definition in the Law on Statements of Entities of the Republic of Lithuania (2017). However, the requirements of this legal act feature limitations. As only the financial statements of the enterprises under investigation are known (i.e., the number of employees of these enterprises is unknown), the selection of MiSEs was based on the remaining two parameters, i.e., the group of MiSEs included enterprises that met the following criteria: (i) the value of assets indicated in the statement of financial position—EUR 4 million and/or (ii) net sales revenue during a financial reporting year—EUR 8 million. Therefore, a sample of MiSEs was formed from this population to develop the bankruptcy-prediction models.

Thirdly, as stated above, the legislation defines the size of an enterprise in terms of three parameters: (i) assets, (ii) annual revenue and (iii) the number of employees. However, for statistics, enterprises are defined only by the number of employees, i.e., according to Statistics Lithuania, an enterprise is considered micro if it has fewer than ten employees and a small enterprise must have fewer than 50 employees. Therefore, all statistical information about these enterprises is presented according to the definition by Statistics Lithuania.

According to the data from Statistics Lithuania, the number of enterprises in operation3 at the beginning of 2013 in Lithuania with fewer than 50 employees was 63,075 (95.9% of all the enterprises in operation in Lithuania). Moreover, 5701 enterprises employed fewer than 50 persons in the construction sector in 2013 (94.5% of all enterprises in the construction sector). This indicates that in this sector, MiSEs predominate, i.e., they determine the performance of the whole industry. Therefore, research on MiSEs in the construction sector is relevant.

3.1.3. Sampling and Sample Size

In this research, the sample comprised financial and non-financial data from MiSEs in the construction sector during the 2007–2013 period. The sample was formed from two groups of the following enterprises:

• bankrupt enterprises. During the period (2009–2013), these enterprises either (i) went bankrupt or (ii) started bankruptcy processes;
• non-bankrupt enterprises. The enterprises (i) did not go bankrupt or start bankruptcy processes and (ii) continued their activities and showed no indications of activity failure. This means that the enterprises were operational in 2007 and continued their activity in 2021; the enterprises were not reformed, reorganised, restructured or liquidated; they did not participate in reorganisation, separation, etc.

The following additional requirements were applied to non-bankrupt enterprises.

Firstly, the liabilities of the enterprise do not equal or exceed the assets of the enterprise during the period considered. This requirement was based on Grigaravičius (2003)’s assumption that an enterprise is considered to be insolvent if its “debts are equal or exceed the overall asset of a company.”

Secondly, according to Špicas et al. (2018), the specificity of the activities of MiSEs determines that “the cessation of activities without announcing bankruptcy in this target segment can occur more frequently than in the segments of large and medium enterprises.” Therefore, the business-continuity opportunity of these enterprises was additionally assessed. To form the non-bankrupt-enterprise sample only with enterprises “performing real economic and commercial activities,” according to Špicas et al. (2018)’s methodology, enterprises that met any of the following criteria were excluded from the sample: (i) during the period considered, (a) “annual income of the enterprise does not exceed EUR 10,000”, (b) “value of assets indicated in the statement of financial position does not exceed EUR 5000” and (ii) during the control period (i.e., in 2021), the enterprise employed two or fewer employees. It should be noted that these data were collected from the website Rekvizitai.lt (accessed May–July 2021).

In conclusion, the research sample was formed from the following enterprises:

(1)

Three-hundred and twenty-one bankrupt enterprises, i.e., enterprises that (i) went bankrupt or (ii) started bankruptcy processes during the period of 2009–2013.

(2)

Two hundred and sixty non-bankrupt enterprises, i.e., enterprises that (i) did not go bankrupt or start bankruptcy processes during the period considered and (ii) continued their activities and showed no indications of activity failure by the year 2021.

3.2. Selection of Independent Variables

The set of independent variables consisted of enterprises’ financial and non-financial variables, as well as business-sector and macroeconomic variables.

3.2.1. Financial Ratios

Financial ratios are used to evaluate the changes in the position and performance of enterprises. To construct a set of relative financial ratios, about one hundred different credit-risk and bankruptcy-prediction models were analysed (e.g., Altman 1968; Ohlson 1980; Zmijewski 1984; Frydman et al. 1985; Zavgren 1985; Varetto 1998; Pompe and Feelders 1997; Dimitras et al. 1999; Zopoudinis and Doumpos 1999; Grigaravičius 2003; Huang et al. 2004; Min and Lee 2005; Wang et al. 2005; Zhou and Tian 2007; Altman and Sabato 2007; Mori and Umezawa 2007; Angelini et al. 2008; Vasiliauskaitė and Cvilikas 2008; Zhang and Hardle 2010; Chen and Du 2009; Lin 2009; Min and Jeong 2009; Ryser and Denzler 2009; Bužius et al. 2010; Tseng and Hu 2010; Danėnas et al. 2011; De Andrés et al. 2011c; Pacelli and Azzolini 2011; Mileris 2012; Olson et al. 2012; Wu and Hsu 2012; Gurný and Gurný 2013; Lorca et al. 2014). As a result, our research group (Špicas et al. 2015) identified 168 different relative financial ratios. However, according to the legislation of Lithuania, i.e., according to the National Accounting Standards and the Law on Statements of Entities of the Republic of Lithuania, MiSEs are entitled to present financial statements with less-detailed information. Therefore, in Lithuania, MiSEs cannot provide all the aforementioned indicators. These limitations prevented the calculation of more than a hundred ratios for MiSEs. Some examples are as follows. (i) MiSEs may not generate cash-flow statements, i.e., these enterprises cannot calculate cash-flow ratios. (ii) Due to a lack of detail in the statements of financial position (i.e., an abridged statement of financial position can be prepared by small enterprises and a short statement of financial position can be prepared by micro enterprises), the MiSEs cannot calculate ratios containing financial debts. (iii) Due to a lack of detail in the statements of profit or loss, small enterprises cannot calculate ratios containing interest expenses or depreciation. (iv) Since the statements of profit or loss prepared by the National Accounting Standards do not provide earnings before interest and taxes (EBIT), it is problematic to use financial ratios with EBIT (as well as EBITDA). (v) Most Lithuanian MiSEs are joint-stock companies, so estimating market multiples is impossible. In summary, 53 ratios were selected for this study due to these limitations.

In EBP models, an enterprise’s financial performance should be assessed from different perspectives. Therefore, in the development of these models, according to Kanapickienė and Špicas (2019), the selected financial ratios were divided into the following different groups: (i) profitability ratios (this group of ratios is divided into two subgroups: return from sales and return on investment); (ii) liquidity ratios; (iii) solvency ratios; (iv) activity ratios (including three subgroups: (a) assets turnover, (b) equity and liabilities turnover, (c) level of expenses); (v) structure ratios (in which two subgroups are distinguished: (a) total-assets-structure ratios and (b) equity- and liabilities-structure ratios); (vi) other ratios (these ratios indicate the size of an enterprise). For more detail, see Appendix A,

Table A1. Financial variables used to develop the EBP models for Lithuanian MiSEs in the construction sector.

Financial Variable (Financial Ratio)	Calculation Formula
1a. Profitability ratios (return from sales)
Gross profit/sales	GP/S
EBIT/sales	EBIT/S
EBT/sales	EBT/S
Net profit/sales	NP/S
1b. Profitability ratios (return on investment)
Gross profit/total assets	GP/TA
EBIT/total assets	EBIT/TA
EBIT/current liabilities	EBIT/CL
EBT/total assets	EBT/TA
EBT/equity	EBT/Eq
EBT/(equity–current liabilities)	EBT/(Eq-CL)
Net profit/total assets	ROA
Net profit/equity	ROE
2. Liquidity ratios
Current assets/current liabilities	CA/CL
(Current assets–inventories)/current liabilities	(CA-INV)/CL
Inventories/current liabilities	INV/CL
Accounts receivable/total liabilities	AR/TL
Accounts receivable/(total liabilities–cash)	AR/(TL-Cash)
Cash/current liabilities	Cash/CL
(Cash–inventories)/current liabilities	(Cash-INV)/CL
Cash/total liabilities	Cash/TL
Cash/equity	Cash/Eq
Working capital/total assets	WC/TA
Working capital/equity	WC/Eq
(Current liabilities–cash)/total assets	(CL-Cash)/TA
3. Solvency ratios
Total liabilities/total assets	TL/TA
Equity/total assets	Eq/TA
Equity/(equity + long term liabilities)	Eq/(Eq+LTL)
Equity/total liabilities	Eq/TL
Fixed assets/equity	FA/Eq
Current assets/total liabilities	CA/TL
Current assets/(total liabilities–cash)	CA/(TL-Cash)
(Equity− Intangible Assets)/(Total Assets–Intangible Assets–Fixed assets–Cash)	(Eq-IA)/(TA-IA-FA-Cash)
4. Activity ratios
4a. Activity ratios (assets turnover)
Sales/inventories	S/INV
Sales/accounts receivable	S/AR
Sales/fixed assets	S/FA
Sales/current assets	S/CA
Sales/total assets	S/TA
Sales/cash	S/Cash
Sales/working capital	S/WC
4b. Activity ratios (equity and liabilities turnover)
Sales/equity	S/Eq
Sales/capital	S/C
Sales/current liabilities	S/CL
Sales/total liabilities	S/TL
4c. Activity ratios (level of expenses)
Cost of sales/sales	CS/S
Working capital/operating expenses	WC/OE
5a. Structure ratios (total assets structure ratios)
Current assets/total assets	CA/TA
Accounts receivable/inventories	AR/INV
Inventories/total assets	INV/TA
Cash/total assets	Cash/TA
5b. Structure ratios (equity and liabilities structure ratios)
Retained earnings/total assets	RE/TA
Current liabilities/(total liabilities−cash)	CL/(TL-Cash)
6 Other ratios (size of enterprise)
Logarithm of total assets	LogTA
Logarithm of total sales	LogS

. Based on these arguments, Hypothesis 1 was formulated, as follows.

Hypothesis 1 (H1).

In EBP models, the financial variables substantially explain the enterprise’s financial statements and performance from different perspectives.

3.2.2. Non-Financial Variables

This research used the non-financial variables that were collected from public information. These indicators were defined as follows: (i) audit of financial statements (the abbreviation of this indicator is AUDIT), (ii) sole shareholder, i.e., the enterprise has a single or more than one shareholder (SHARE), (iii) the number of records published in the Register of Legal Entities (RECORDS), (iv) late submission of financial statements (SUBMISSION_FS), (v) the age of the enterprise (AGE) (see Appendix A,

Table A2. Non-financial variables used to develop the EBP models for Lithuanian MiSEs in the construction sector.

Abbreviation	Variables	Description	Data Source
AUDIT	Audit of financial statements	Whether the annual financial statements were audited: (i) the audit has been carried out or (ii) the audit has not been carried out (Yes—1; No—0)	SECR 1
SHARE	Sole shareholder	(i) The company has a single shareholder or (ii) more than one shareholder has acquired shares in the company (Yes—1; No—0)	SECR 1
RECORDS	Number of records	The number of records published in the Register of Legal Entities	SECR 1
SUBMISSION_FS	Late submission of financial statements	Financial statements were submitted late (days)	SECR 1
AGE	The age of the enterprise	The difference between the financial year and the enterprise’s establishment year	SECR 1

Source: compiled by the authors. Note: ¹—State Enterprise Centre of Registers (SECR), Register of Legal Entities. Available online: https://www.registrucentras.lt/jar/ (accessed July–August 2021).

).

3.2.3. Construction-Sector Variables

Using the data from Statistics Lithuania, the business-, i.e., construction-sector variables were collected. The selected variables were divided into the two following groups:

(a) Macroeconomic indicators characterising the construction sector. These were divided into six sub-groups, i.e., (i) index of construction work carried out within the country (ICW) and its annual change (ICW_CHG), (ii) construction work carried out within the country at current prices (CW) and its annual change (CW_CHG), (iii) turnover from construction activities in non-financial enterprises (TCA) and its annual change (TCA_CHG), (iv) the share of the construction activity in the country in the total construction-activity revenue (SCAinC) and its annual change (SCAinC_CHG), (v) index of wages and salaries in construction enterprises (IWS) and its annual change (IWS_CHG) and (vi) index of the number of persons employed in construction enterprises (INPE) and its annual change (INPE_CHG)). For more detail, see Appendix A,

Table A3. Macroeconomic indicators characterising the construction sector used to develop the EBP models for Lithuanian MiSEs in the construction sector.

Abbreviation	Full Name, Description
ICW	Index of construction work carried out within the country (2015 = 100)
ICW_CHG	Annual change in index of construction work carried out within the country (2015 = 100) (%); calculation = [X(t)/X(t − 1)] − 1
CW	Construction work carried out within the country at current prices (thousands of EUR)
CW_CHG	Annual change in construction work carried out within the country at current prices (%); calculation = [X(t)/X(t − 1)] − 1
TCA	Turnover from construction activities in non-financial enterprises (thousands of EUR)
TCA_CHG	Annual change in turnover from construction activities in non-financial enterprises (%); calculation = [X(t)/X(t − 1)] − 1
SCAinC	The share of the construction activity in the country in the total construction-activity revenue (at current prices) (%)
SCAinC_CHG	Annual change in the share of the construction activity in the country in the total construction-activity revenue (%); calculation = [X(t)/X(t − 1)] − 1
IWS	Index of wages and salaries in construction enterprises (2015 = 100)
IWS_CHG	Annual change in index of wages and salaries in construction enterprises (2015 = 100) (%); calculation = [X(t)/X(t − 1)] − 1
INPE	Index of number of persons employed in construction enterprises (2015 = 100)
INPE_CHG	Annual change in index of the number of persons employed in construction enterprises (2015 = 100); calculation = [X(t)/X(t − 1)] − 1

. As Jang et al. (2021) state, “the construction industry is a project-based industry”; therefore, construction enterprises “are directly influenced by macroeconomic factors.”

(b) Financial indicators for the construction sector can also help construction enterprises predict their probability of bankruptcy. In this study, these indicators were divided into five sub-groups, i.e., (i) profitability ratios (gross profit margin (GP/S_CS), net profit margin (NP/S_CS), return on assets (ROA_CS), return on equity (ROE_CS)), (ii) liquidity ratio (current ratio (CA/CL_CS)), (iii) solvency ratio (total-liabilities-to-total-assets ratio (TL/TA_CS)); (iv) activity ratios (receivables turnover ratio (S/AR_CS), total asset-turnover ratio (S/TA_CS)); (v) other (change in customer insolvency and late payments over the last three months (CCI_CS)). For more detail, see Appendix A,

Table A4. Financial indicators for the construction sector used to develop the EBP models for Lithuanian MiSEs in the construction sector.

Abbreviation	Variable, Calculation Formula
GP/S_CS	Gross profit margin (%). Calculation: gross profit/sales
NP/S_CS	Net profit margin (%). Calculation: net profit/sales
ROA_CS	Return on assets (ROA) (%)
ROE_CS	Return on equity (ROE) (%)
CA/CL_CS	Current ratio. Calculation: current assets/current liabilities
TL/TA_CS	Total liabilities-to-total assets ratio. Calculation: total liabilities/total assets
S/AR_CS	Receivables turnover ratio (times). Calculation: sales/accounts receivable
S/TA_CS	Total asset turnover (times). Calculation: sales/total assets
CCI_CS	Change in customer insolvency and late payments over the last three months (increasing) (%)

.

3.2.4. Macroeconomic Variables

Based on data from Statistics Lithuania, macroeconomic variables were collected and divided into five following groups: (a) group of GDP variables, which was divided into three sub-groups, i.e., (i) GDP and its annual change (GDP_CHG), (ii) GDP index and its annual change (GDP_index_CHG) and (iii) GDP at market prices (EUR per capita) (GDP(MP)) and its annual change (GDP(MP)_CHG); (b) group of inflation variables (i.e., the harmonised index of consumer prices at constant tax rates (HICP), annual inflation (INF), average annual inflation (INF_A)); (c) group of house-price-index variables (i.e., house -price index (HPI) and its annual change (HPI_CHG)); (d) unemployment rate (UR); (e) construction-input-price index (CIPI). For more detail, see Appendix A,

Table A5. Macroeconomic variables of the country (Lithuania) used to develop the EBP models for Lithuanian MiSEs in the construction sector.

Abbreviation	Full Name, Description
GDP	GDP (at 2010 constant prices)
GDP_CHG	GDP yearly change (at 2010 constant prices) (%); calculation = [X(t)/X(t − 1)] − 1
GDP_index	GDP index (at 2010 constant prices, 2010 = 100)
GDP_index_CHG	GDP index annual change (at 2010 constant prices, 2010 = 100) (%); calculation = [X(t)/X(t − 1)] − 1
GDP(MP)	GDP at market prices (EUR per capita)
GDP(MP)_CHG	Annual change in GDP at market prices (Euro per capita) (%); calculation = [X(t)/X(t − 1)] − 1
HICP	The harmonised index of consumer prices at constant tax rates (2015 = 100)
INF	Annual inflation
INF_A	Average annual inflation
HPI	House-price index (2015 = 100)
HPI_CHG	Annual change of house price index (%); calculation = [X(t)/X(t − 1)] − 1
UR	Unemployment rate
CIPI	Construction-input-price index (CIPI) (%)

.

Finally, based on the arguments presented in Section 2 and the indicators selected in Section 3.2, Hypothesis 2 was formulated, as follows.

Hypothesis 2 (H2).

The inclusion of enterprises’ non-financial, construction-sector and macroeconomic variables substantially improves the characteristics of EBP models.

Finally, 92 independent variables, i.e., the 53 financial ratios, 5 non-financial variables, 12 macroeconomic indicators characterising the construction sector, 9 financial indicators for the construction sector and 13 macroeconomic variables, were selected for the creation of the EBP models. In total 92 (i.e., n = 92) independent variables are analysed in the study.

3.2.5. Pre-Processing Stage: Selection of Statistical Tests

According to some researchers (De Andrés et al. 2011b), in the research process, it is appropriate to consider including a “pre-processing stage” that uses statistical methods as a basic approach for the ratio estimation. As du Jardin (2009) states, variable selection methods also influence the determination of the accuracy of predictions. Therefore, selection of statistical tests is an important stage of model development.

In this stage of research, the selection of independent variables was performed as follows.

Firstly, an analysis of missing values was performed. According to Kanapickienė and Špicas (2019), the number of missing values of independent variables should be analysed. In cases in which the financial ratio could not be calculated because the data required to calculate this ratio were not presented in the financial statements of a significant number of enterprises, the removal of this ratio from the analysis was considered (Špicas et al. 2018). To estimate the effect of missing data appropriately, we carried out an analysis of research about using the statistical methods in practice (i.e., in quantitative research). Discussing the issue of missing values, Madley-Dowd et al. (2019) and Dong and Peng (2013) refer to Schafer (1999), who states that ”when the rate of missing information is small (say, less than 5%) then single-imputation inferences for a scalar estimand may be fairly accurate.” Furthermore, these authors point out that “when the amount of missing data are large (greater than 10%) the results of subsequent statistical analyses may be biased.” Therefore, this study excluded further analysis ratios with missing values above 5%.

Secondly, each independent variable was examined in the sample of bankrupt and non-bankrupt enterprises. Hence, every independent variable k (k = 1, 2, …, n; where n is the number of independent variables analysed in this research) was investigated in two samples: (i) in the sample of the non-bankrupt enterprises (N_k1, N_k2, …, N_ki, … …, N_km, where N_ki is the independent variable k for the non-bankrupt enterprise i and m is the number of the non-bankrupt enterprises) and (ii) in the sample of the bankrupt enterprises (B_k1, B_k2, …, B_kj, …, B_kl, where B_kj is the independent variable k for the bankrupt enterprise j and l is the number of the bankrupt enterprises).

Before selection of a statistical test, it was verified that data were drawn from a normally distributed population. The key test for the assessment of normality is Kolmogorov–Smirnov (K–S) test. The null hypothesis H0 of the K–S test was as follows: the data are drawn from a normally distributed population. The alternate hypothesis H1 was as follows: the data are drawn from a population that is not normally distributed. If the results of the K–S test were significant (p < α, there α = 0.05 (α—level of significance)), rejecting the null hypothesis H0 would mean rejecting the assumption of normality for the distribution, i.e., the data were derived from a population that was not normally distributed.

Depending on the result of the K–S test, the procedure for the selection of further statistical tests was as follows

(1)

If the assumption of normality is violated, the Mann–Whitney U test is used. The null hypothesis H0 of the Mann–Whitney U test was as follows: the distributions of the independent variables of the bankrupt and non-bankrupt enterprises are equal. The alternate hypothesis H1 was as follows: the distributions of the independent variables of the bankrupt and non-bankrupt enterprises are different. The decision was made based on the following provisions: (i) H0 is rejected, distributions of the independent variables are not equal if p < α (α = 0.05); (ii) H0 is not rejected, distributions of the independent variables are equal if p ≥ α.

(2)

If the assumption of normality was valid, we used the t-test. This test was applied in empirical studies (Ravisankar et al. (2011); Pustylnick (2012); Špicas et al. (2015) and others), in which, using the relative financial ratios in the financial statements, prediction of the possibility of bankruptcy was analysed.

We applied the t-test for two independent samples (i.e., the bankrupt and non-bankrupt enterprises’ samples for each independent variable k) when the two samples were selected from populations with normal distributions (N_k ~ N(µ_kN, σ²_N), B_k ~ N(µ_kB, σ²_B)) and equal variances (σ²_N, σ²_B). Furthermore, their averages (µ_kN and µ_kB) and variances (σ²_N and σ²_B) were not known. Therefore, firstly, using Levene’s test, the equality of variances was evaluated. The equality-of-averages hypothesis was thus verified.

Null hypothesis H0: the independent-variable averages in the samples of the non-bankrupt and bankrupt enterprises do not differ (µ_kN = µ_kB). Alternate hypothesis H1: the independent-variable averages in the samples of the non-bankrupt and bankrupt enterprises differ (µ_kN ≠ µ_kB). The decision was made based on the following provisions: (i) H0 is rejected (i.e., the independent-variable averages are not equal if p < α (α = 0.05)); (ii) H0 is not rejected (i.e., the independent-variable averages do not differ if p ≥ α (α = 0.05)).

Thus, aforementioned methods were used to select the independent variables for further investigation.

Finally, the independent variables that showed statistically significant differences between the samples of the non-bankrupt and bankrupt enterprises were divided into the groups that are presented in Section 3.2.1 and Section 3.2.2. When considering which independent variables from each group should be included in the model, a correlation matrix for the variables was developed. The possibility of removing some strongly correlated variables was analysed. The remaining variables were used to compile the logistic regression, ANNs and their combination models. It should also be noted that, as argued by De Andrés et al. (2011c), the studies by Tsai (2009) and Ravisankar and Ravi (2010) show the possibility of using ANNs for the classification stage.

3.3. Classificatory Devices

To create EBP models for Lithuanian MiSEs in the construction sector, we used not only logistic regression, but also ANNs and MARS model.

3.3.1. The Logistic Regression Model

According to Bateni and Asghari (2020), the logistic regression model assumes that for an enterprise with a given set of characteristics, “a definable probability that it will default” can be calculated, i.e., the probability of default depends on these characteristics.

Using the logistic regression model, the probability of default (PD), i.e., the probability that an enterprise will go bankrupt, is calculated as:

$$PD=P\left(Y=1\right)=\frac{1}{1+e^{-z}}$$

(1)

The dependent variable in logistic regression, i.e., PD, is a dummy variable. According to Behr and Güttler (2007), the PD takes the value 1 (Y = 1) if an enterprise declares bankruptcy in the observation period, otherwise 0 (Y = 0). In this study, companies with PD ≥ 50% were classified into the bankruptcy group; companies with PD < 50% were classified into the non-bankruptcy group.

We constructed the multidimensional logistic regression models where the z is determined as:

$$z={\beta }_0+{\sum }_{i=1}^k{\beta }_i{X}_i,$$

(2)

where β₀ is the coefficient of the constant term and β_i represents the particular coefficient in a linear combination of k independent variables (i = 1, …, k) in Equation (2). Independent variables X_i are all potentially relevant parameters that may drive credit/bankruptcy risk (Behr and Güttler 2007). In this research, independent variables X_i are (i) financial ratios, (ii) non-financial variables, (iii) macroeconomic indicators characterising the construction sector, (iv) financial indicators for the construction sector and (v) macroeconomic variables. In addition to the financial variables, this study contained a large set of other variables that could be included as control variables. Therefore, an additional set of control variables was not distinguished.

Furthermore, the independent variables were selected on the basis of stepwise method (forward selection). This method was used, by Lin (2009), Yap et al. (2011) and Gurný and Gurný (2013), among others. Finally, following previous studies (e.g., those by Behr and Güttler (2007); Nikolic et al. (2013); Tserng et al. (2011); Yap et al. (2011); Lorca et al. (2014)), the LR coefficients were estimated using the maximum-likelihood-estimation method.

The model was regarded as appropriate when the following requirements were followed: (i) chi-square-criterion p-value was less than 0.05; (ii) Cox-and-Snell R Square and Nagelkerke R Square were not less than 0.2; (iii) statistically significant variables were present in the model, i.e., Wald’s p-values were less than 0.05.

3.3.2. Artificial Neural Network Model

In order to develop classification tools for identifying potentially bankrupt entities, researchers use a variety of models, i.e., not only single models, but also hybrid models or combinations of classical and intelligent systems. Some examples are provided below.

(1) Researchers use different neural networks, analyse them and compare their results. (i) West (2000) investigated the credit-scoring accuracy of five neural network models: “the traditional multilayer perceptron (MLP) network, the mixture of experts (MOE), RBF, learning vector quantisation (LVQ) and fuzzy adaptive resonance (FAR).” According to theoretical analysis, West (2000) states that “the multilayer perceptron is most accurate” model. However, “results demonstrate that the multilayer perceptron may not be the most accurate neural network model and that both the mixture-of-experts and radial basis function neural network models should be considered for credit scoring applications.” (ii) Horak et al. (2020) used two artificial neural networks (multilayer-perceptron artificial neural networks (MLP) and radial-basis-function artificial neural networks (RBF). The authors suggest five ANN models based on MLPs that are applicable in practice. The performance of these networks was above 80%, i.e., as authors state, the performance seemed very high. (iii) Ciampi and Gordini (2013) used a feed-forward MLP model. (iv) Al-Sobiei et al. (2005) used NeuroShell Predictor software with two different—neural and genetic—training strategies.

(2) Researchers use different models (including neural networks) and compare their results. For example, (a) Becerra-Vicario et al. (2020) used the logistic regression technique and deep recurrent convolutional neural network (DRCNN) for bankruptcy-prediction models in the restaurant industry. (b) According to Becerra-Vicario et al. (2020), Gregova et al. (2020) used logistic regression, a neural network and random-forest models to analyse financial distress of industrial enterprises and neural network models showed the best results. (c) Korol (2019) aimed to develop dynamic bankruptcy-prediction models for European enterprises. The author used four methods—(i) fuzzy sets, (ii) a recurrent artificial neural network, (iii) a multilayer neural network and (iv) decision trees. The findings of that study suggested that the fuzzy-sets model provided superior results for the effectiveness of models, i.e., it was superior to the other developed models. Additionally, it should be noted that the effectiveness of NN models is also high, i.e., they showed 93–95% correct classifications one year before bankruptcy.

(3) De Andrés et al. (2011b) concluded that most applied hybrid systems (HS) improve the results of individual classifiers. Studies confirmed these findings, e.g., (i) results obtained by Sánchez-Lasheras et al. (2012) showed that the proposed hybrid approach (SOM and MARS) is “much more accurate than the benchmark techniques for the identification of the bankrupt companies.” (ii) Zhu et al. (2016) constructed three two-stage hybrid models based on an artificial neural network and logistic regression.

Based on these observations and studies, we decided to use ANN as a distinct approach to bankruptcy-risk analysis and to develop a hybrid model using LR in the first stage and ANN in the second. Within ANN approach, we used multilayer perception (MLP) network and radial-basis-function artificial neural network (RBF) techniques. As already stated by du Jardin (2021): “since all these techniques have been widely presented in the literature, it is not necessary to discuss them once more here.”

3.3.3. Multivariate Adaptive Regression Splines Model

The MARS is a multivariate nonparametric regression technique (De Andrés et al. 2011a); (Sánchez-Lasheras et al. 2012). According to Hastie, Tibshirani and Friedman (2003) (as cited by Sánchez-Lasheras et al. (2012)), MARS can be considered “a generalisation of classification and regression trees (CART).” The advantage of this method is that it “does not require any a priori assumptions about the underlying functional relationship between dependent and independent variables” (Sánchez-Lasheras et al. 2012). Therefore, Lee et al. (2006) (as cited by Yap et al. (2011) demonstrated that MARS outperforms logistic regression and neural networks “in terms of credit scoring accuracy.”

To measure the predictive accuracy of EBP models, the study applies the receiver operating characteristic (ROC) curve, as this analysis is widely used (Behr and Güttler 2007; Figini et al. 2017; Chang et al. 2018). As Tserng et al. (2011) state, the ROC curve “is a useful tool for assessing discriminatory power of the credit scoring model,” as well as a bankruptcy-prediction model. Technically, according to Liang et al. (2016), the ROC curve is “a graphical plot used to illustrate the prediction model as its discrimination threshold is varied.”

Han et al. (2018) state that the area under the curve (AUC) can be deployed as an indicator to quantify “a quantitative performance measure: the area will range from 0.5, for a worthless model, to 1, for a perfect classifier.” Tserng et al. (2011) and Zhu et al. (2016) note the following: if 0.7 ≤ AUC < 0.8, the model has acceptable discriminatory power; if 0.8 ≤ AUC < 0.9, the model has excellent discriminatory power; and if AUC ≥ 0.9, the model has outstanding discriminatory power.

4. Research Results and Findings

4.1. Using Statistical Tests: Estimation of Independent Variables

During the formation of the EBP models, the estimation of independent variables was carried out in the pre-processing stage described in the Methodology (Section 3.2.5).

First, an analysis of the missing values was performed. During this stage, three variables (financial ratios) were removed: Sales/Inventories, Sales/Accounts Receivable and Accounts Receivable/Inventories.

The second stage was the assessment of normality. The Kolmogorov–Smirnov-test results for each financial ratio showed that each financial ratio was derived from a population that was not normally distributed, i.e., the null hypothesis H0 of the K–S test was rejected for each financial ratio. For this reason, the Mann–Whitney U test was used to assess whether the distributions of the independent variables of the bankrupt and non-bankrupt enterprises were equal or different. If the independent variable in these two enterprise groups was not different, this indicator was not used in the final models. This study found no significant difference between the following financial ratios of bankrupt and non-bankrupt enterprises: Accounts Receivable/(Total Liabilities − Cash), Sales/Fixed Assets, Sales/Current Assets, Sales/Capital, Logarithm of Total Assets. This means that the null hypothesis H0 of the Mann–Whitney U test was not rejected (p ≥ α, there α = 0.05) for these financial ratios.

4.2. Logistic Regression EBP Models

Separate multidimensional logistic regression EBP models for Lithuanian MiSEs in the construction sector were developed during this research.

First, different EBP models were created using four groups of variables, i.e., (i) the financial ratios, (ii) macroeconomic variables, (iii) construction-sector variables and (iv) non-financial variables of the enterprises. Varied model variants were created using (1) only financial ratios (Models M1.1 and M1.2), (2) financial ratios and macroeconomic variables (Models M2.1 and M2.2), (3) financial ratios, macroeconomic variables and construction-sector variables (Models M3.1 and M3.2) and (4) financial ratios, macroeconomic variables, construction-sector variables and non-financial variables of the enterprises (Model M4). Logistic regression EBP models were constructed by selecting independent variables and calculating the coefficients of these variables (see

Table 1. Logistic regression EBP models for MiSEs in the construction sector.

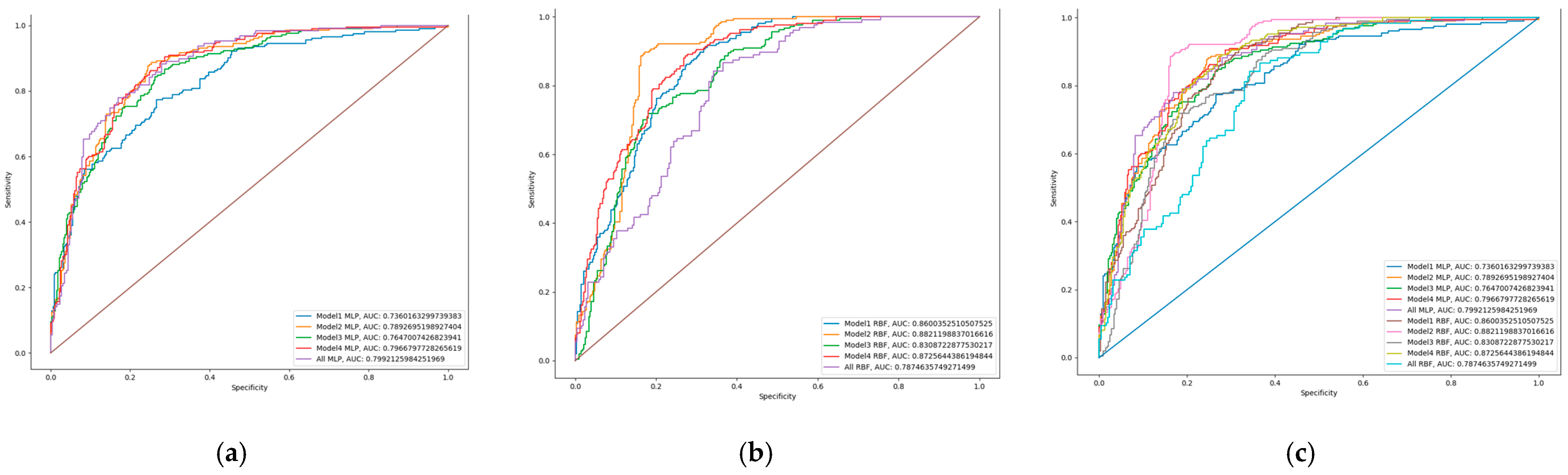
Independent Variables		Model:
		M1.1		M1.2		M2.1		M2.2		M3.1		M3.2		M4
		Coef.	Sign.	Coef.	Sign.	Coef.	Sign.	Coef.	Sign.	Coef.	Sign.	Coef.	Sign.	Coef.	Sign.
Constant		−2.212	0.000	−2.550	0.000	1.271	0.574	2.427	0.205	−3.068	0.023	−0.719	0.748	−2.372	0.567
Financial variables (Financial ratios)
1a. Profitability ratios (return from sales)
EBIT/Sales	EBIT/S							−0.554	0.003
1b. Profitability ratios (return on investment)
Gross Profit/Total Assets	GP/TA	0.504	0.000	1.652	0.000
EBIT/Total Assets	EBIT/TA	1.155	0.000
Net Profit/Total Assets	ROA			1.040	0.000
2. Liquidity ratios
Accounts Receivable/Total Liabilities	AR/TL	0.139	0.000	1.140	0.000									0.268	0.000
(Cash − Inventories)/Current Liabilities	(CASH-INV)/CL					−0.330	0.109
3. Solvency ratios
Total Liabilities/Total Assets	TL/TA	3.334	0.000	4.136	0.000	3.440	0.000	3.532	0.000	3.875	0.000	2.806	0.000	2.720	0.000
4. Activity ratios
4a. Activity ratios (assets turnover)
Sales/Total Assets	S/TA					1.390	0.000					0.306	0.000
4b. Activity ratios (equity and liabilities turnover)
Sales/Current Liabilities	S/CL					−0.453	0.000
Sales/Total Liabilities	S/TL	−0.064	0.003	−0.311	0.000									−0.107	0.000
4c. Activity ratios (Level of expenses)
Cost of Sales/Sales	CS/S	0.911	0.000	1.841	0.000					−0.778	0.002
5a. Structure ratios (total assets structure ratios)
Current Assets/Total Assets	CA/TA	−1.188	0.000	−3.048	0.000	−2.013	0.000	−2.030	0.000	−2.178	0.000	−2.192	0.000	−2.395	0.000
Inventory/Total Assets	INV/TA	2.934	0.000	4.128	0.000	1.265	0.061	3.086	0.000			2.691	0.000
Macroeconomic variables
GDP index	GDP_index											−0.096	0.000
The harmonised index of consumer prices at constant tax rates	HICP					−0.023	0.327	−0.036	0.081
Average annual inflation	INF_A									0.158	0.000	0.251	0.000
Construction-sector variables
Macroeconomic indicators characterising the construction sector
Annual change of index of construction work carried out within the country	ICW_CHG													0.012	0.218
Annual change in the share of the construction activity in the country in the total-construction-activity revenue	SCAinC_CHG													−0.041	0.148
Financial indicators for the construction sector
Gross profit margin	GP/S_CS									0.111	0.089	0.438	0.000	0.311	0.000
Total-asset-turnover ratio (times)	S/TA_CS													−3.575	0.237
Change in customer insolvency and late payments over the last three months	CCI_CS													0.038	0.000
Non-financial variables
The age of the enterprise	AGE													−0.137	0.000
The sole shareholder	SHARE													−0.785	0.000
Chi-square p-value		0.000		0.000		0.000		0.000		0.000		0.000		0.000
Cox-and-Snell R square		0.543		0.583		0.590		0.562		0.570		0.568		0.585
Nagelkerke R square		0.738		0.793		0.803		0.763		0.774		0.771		0.792
Model test sample (dataset):
The total percentage of the model’s correctly classified cases		68.1		75.8		90.4		91.7		69.4		84.2		77.7
The percentage of the model’s correctly classified bankrupt-enterprises cases		82.8		85.7		85.2		80.3		85.7		90.0		89.0
The percentage of the model’s correctly classified non-bankrupt-enterprises cases		59.0		69.7		93.8		98.8		59.3		80.4		70.3
AUC		0.751		0.821		0.952		0.985		0.746		0.907		0.838
Model training sample (dataset):
The total percentage of the model’s correctly classified cases		71.4		79.2		94.2		94.2		75.3		86.2		80.2
The percentage of the model’s correctly classified bankrupt-enterprises cases		84.7		89.8		91.7		85.6		90.6		89.5		90.6
The percentage of the model’s correctly classified non-bankrupt-enterprises cases		63.1		72.6		95.7		99.5		65.8		84.2		73.4
AUC		0.803		0.868		0.988		0.996		0.817		0.935		0.876

Abbreviations used: Coef.—coefficient; Sign.—significance.

).

An analysis of the modelling process led to the following conclusions regarding the inclusion of financial indicators in the models.

(1) All the models first select the Current Assets/Total Assets (CA/TA) ratio, which was included in the structure ratios (total assets structure ratios) group of financial ratios. The coefficient of this ratio was negative, i.e., an improvement in the Current Assets/Total Assets (CA/TA) ratio led to greater stability for the enterprise and, thus, reduced bankruptcy risk. Moreover, the coefficient of this indicator was the largest negative coefficient in all the models. Hence, this ratio’s impact on enterprise stability was the largest in all the models.

(2) The second indicator selected in all the models was the Total Liabilities/Total Assets (TL/TA) ratio, which was included in the solvency ratio group of financial ratios. The coefficient of this indicator was positive, i.e., an increase in the Total Liabilities/Total Assets (TL/TA) ratio led to an increase in bankruptcy risk. Moreover, the coefficient of this ratio was the largest positive coefficient in all the models, which means that the impact of this ratio on the enterprises’ bankruptcy risk was the largest in all the models.

(3) Further, in the models that used not only financial ratios, this stage selected the majority of variables from the other variable groups, i.e., macroeconomic, construction-sector and non-financial variables, depending on which variable groups were used for the model construction.

(4) The Inventory/Total Assets (INV/TA) ratio was the third financial indicator selected in most of the models (i.e., all the models except for Models M3.1 and M4; in these models, the financial ratio was selected from the activity ratio group. The Inventory/Total Assets (INV/TA) ratio belonged to the ’structure ratios (total assets structure ratios)’ group of financial ratios.

(5) Next, the remaining ratios are selected.

The following conclusions can be drawn about the financial ratio groups used to construct the models. (1) All the models use variables from the following two financial ratio groups: (i) solvency ratios and (ii) structural ratios (more precisely, sub-group of total-asset-structure ratios’). (2) In addition, no models used variables from (i) structural ratios sub-group of equity-and-liabilities-structure ratios and (i) the financial ratio group of other ratios. (3) Although the models widely use the variables from different groups of financial ratios, the following consistencies were identified: (i) Models M1.1 and M1.2 use as variables only financial ratios of enterprises and do not use variables from the profitability-ratios sub-group of return of sales. (ii) Models M2.1 and M2.2 exclude financial ratios from the profitability sub-group of return on investment and Model M2.2 does not use the activity ratios. (iii) Models M3.1 and M3.2 exclude profitability and liquidity ratios. (iv) Model M4 does not use profitability ratios.

The group of profitability ratios (return on sales) is characterized by the EBIT/Sales ratio, which, as Kanapickiene and Špicas (2019) note, is one of the most important profitability ratios of an enterprise, as it shows “the profitability of the enterprise during its operating and investment cycles, however, without the evaluation of the financing policy.” This ratio is used in Model M2.2. However, since 2016, due to changes in the structures of the statements of profit or loss, the EBIT/Sales ratio cannot be calculated by micro-enterprises (MiE). Consequently, these enterprises have to select other models.

Return on investment is used to measure an enterprise’s overall ability to generate profit with a given level of assets, equity, or the total capital it employs. The group of profitability ratios (return on investment) is characterized by the Gross Profit/Total Assets, EBIT/Total Assets and Net Profit/Total Assets ratios. The higher the ratios, the more profit is generated by a given level of assets.

Usually, return on assets (ROA) measures the return earned by an enterprise on its assets and calculates a Net Profit/Total Assets ratio. However, net profit is the return to equity holders. At the same time, assets are financed not only by equity holders, but also by creditors. Therefore, interest expenses, i.e., the return to creditors, must be deducted from the net profit. Thus, as Henry et al. (2011) argue, some analysts prefer to calculate “ROA on a pre-interest and pre-tax basis,” i.e., they use the EBIT/Total Assets ratio. Additionally, Model M1.1 uses the Gross Profit/Total Assets ratio, which is used to measure the gross profit earned by an enterprise on its assets. It is important to highlight that no model uses return on equity (ROE), which measures the profit earned by an enterprise using its equity capital.

Liquidity measures an enterprise’s ability to meet its short-term obligations (Henry et al. 2011). Therefore, liquidity is often characterized by the current ratio (Current Assets/Current Liabilities), i.e., the ability of an enterprise to meet its current liabilities using its current assets is assessed. According to Kanapickienė and Špicas (2019), if the enterprise has already experienced difficulties in paying its current liabilities in the past year, the year’s short-term liabilities are likely not to be covered.

In this research, the group of liquidity ratios was characterized by the following two ratios: (i) the Accounts Receivable/Total Liabilities ratio, which shows the ability of an enterprise to meet its current liabilities using its accounts receivable; (ii) and the Cash−Inventories/Current Liabilities ratio, which requires a more detailed discussion. Firstly, this ratio consists of two ratios, i.e., the Cash/Current Liabilities ratio and the Inventories/Current Liabilities ratio. Secondly, the Cash ratio (the Cash/Current Liabilities ratio) is generally a reliable measure of an enterprise’s liquidity in a crisis, i.e., it represents the ability of an enterprise to meet its current liabilities using its cash. The Inventories/Current Liabilities ratio measures the ability of an enterprise to meet its current liabilities using inventories. It should also be noted that inventories can be used to cover a liability when the products produced from them are sold.

Solvency refers to an enterprise’s ability to meet its total liabilities. The group of Solvency ratios is characterized by the Total Liabilities/Total Assets ratio, which measures the percentage of total assets financed with total liabilities. The models are consistent with economic logic: a higher ratio indicates a higher financial risk for an enterprise, i.e., the enterprise has large liabilities that will need to be covered in the future.

The group of Activity ratios (assets turnover) is characterized by the total-asset-turnover ratio, i.e., the Sales/Total Assets ratio, which measures the ability of an enterprise to generate sales with a given level of assets. According to Henry et al. (2011), “a higher ratio indicates greater efficiency.” Conversely, “a low asset turnover ratio can be an indicator of inefficiency or relative capital intensity of the business.” However, the models show that bankruptcy risk increases as total asset turnover rises. This reflects the strategic decision taken by the management of a financially distressed enterprise to use a more capital-intensive approach. On the other hand, the total-asset-turnover ratio includes total assets, i.e., both fixed and current assets, which may not indicate inefficient working-capital management.

The group of Activity ratios (equity and liabilities turnover) is characterized by the Current Liabilities turnover (calculated as Sales/Current Liabilities) and Total Liabilities turnover (calculated as Sales/Total Liabilities) ratios. Low turnover rates can indicate difficulties in making payments on time. The models confirm the following economic logic: decreasing turnover increases bankruptcy risk. Models M1.1 and M1.2 use the Sales/Total Liabilities ratio. However, Model M2.1 prefers the Sales/Current Liabilities ratio.

The group of Activity ratios (level of expenses) is characterized by the Cost of Sales/Sales ratio, which indicates the percentage of sales available to cover the cost of sales expenses. A lower ratio indicates a combination of lower product costs and higher product pricing. On the sales side, according to Henry et al. (2011), “the ability to charge a higher price is constrained by competition.” An enterprise can increase prices if a product has a competitive advantage. On the cost side, a lower cost of sales can indicate that an enterprise has a competitive advantage in terms of product costs. Increases in the Cost of Sales/Sales ratio show an enterprise’s deteriorating market situation.

The group of Structure ratios (total-assets-structure ratios) is characterized by the Current Assets/Total Assets and Inventory/Total Assets ratios.

Finally, it can be observed that the number of financial ratios decreases in models that use more than one financial ratio. For example, while Models M1.1 and M1.2 use eight financial ratios each, Models M3.1, M3.2 and M4 use four financial ratios each.

The following conclusions can be drawn about the other variables (those other than financial ratios) used to develop the models:

(1) The models use the GDP index and inflation as macroeconomic variables. (a) The GDP index is used in Model M3.2. This variable has a statistically significant negative effect on the probability of default. (b) In the models, inflation is described by two variables. (i) Models M2.1 and M2.2 use one macroeconomic variable: HICP (The harmonised index of consumer prices at constant tax rates). The coefficient of this indicator is negative, i.e., a decrease in HICP leads to an increase in bankruptcy risk. In model M2.1, the HICP has statically insignificant effects on the probability of default. As the HICP is used to measure inflation in the EU and to make comparisons between EU Member States, these models can be used in other EU countries. Moreover, this variable is not used in other models. (ii) Models M3.1 and M3.2 use average annual inflation (INF_A). The coefficient of this indicator is positive, i.e., an increase in INF_A leads to an increase in bankruptcy risk. In summary, the impact of inflation on bankruptcy risk is mixed.

(2) Two macroeconomic indicators characterising the construction sector are used in Model 4.1, i.e., ICW_CHG (annual change in index of construction work carried out within the country) and SCAinC_CHG (annual change in the share of the construction activity in the country in the total-construction-activity revenue).

The ICW_CHG4 is used to measure the overall level of construction-sector activity within a country. When this indicator increases, there is more demand for construction services. On one hand, this can positively affect the sales and profitability of construction enterprises; as a consequence, the increased activity may reduce enterprises’ bankruptcy risk. On the other hand, financially weak enterprises cannot manage their expenses and cash flows effectively. Therefore, increases in activity in the sector may increase enterprises’ bankruptcy risk.

Increases in the SCAinC_CHG mean that the construction activity in the country is declining and the pressure to find alternative sources of sales decreases. This can have a positive effect on the sales and profitability of construction enterprises and reduce their bankruptcy risk. In the case of Lithuania, ICW_CHG has a positive and SCAinC_CHG has a negative but statically insignificant effect on bankruptcy risk.

(3) Financial indicators for the construction sector are used in three models: (i) in Models 3.1, 3.2 and M4, the gross profit margin in the construction sector (GP/S_CS) has a positive effect on the bankruptcy risk of enterprises; (ii) the same effect is also found for the variable CCI_CS (change in customer insolvency and late payments over the last three months); (iii) the sector’s total-asset-turnover ratio (S/TA_CS) has a negative but statically insignificant effect on the probability of default.

The indicators’ movement is consistent with economic logic. Firstly, a higher GP/S_CS indicates that enterprises in the construction sector are increasing the prices of construction works/objects or managing their expenses more efficiently, which can lead to an improvement in their financial performance and stability and a reduction in bankruptcy risk. Profitability growth increases competition in the sector; consequently, financially weak firms take on riskier or more complex projects, which may increase their bankruptcy risk. Secondly, a positive CCI_CS can indicate cash-flow problems for construction enterprises. On one hand, a positive CCI_CS can suggest that customers have financial difficulties and, therefore, that enterprises are not able to receive payments for the work carried out. On the other hand, if payments are delayed or customers are unable to make them, enterprises have difficulties in meeting their financial obligations, i.e., their risk of bankruptcy increases. Third, increases in the S/TA_CS indicate that enterprises in the sector are utilising their assets ineffectively to generate sales. Consequently, enterprises’ financial performance deteriorates and their probability of default increases.

(4) Model M4 uses two non-financial variables, i.e., the age of the enterprise and the sole shareholder, which have a statically significant negative effect on the probability of default. Therefore, it can be argued that bankruptcy risk decreases as an enterprise’s lifetime increases. Similarly, bankruptcy risk decreases when a company has a single shareholder. There is a logical explanation for this: the age of a company reflects its experience in business and a single shareholder takes on more responsibility, which gives the enterprise greater stability.

The Wald test for independent variables shows whether the variables included in the models are statistically significant: the majority of the independent variables had a Wald’s p-value of less than 0.05. Significance at the 10% level was demonstrated by the INV/TA (p-value = 0.061 (in model M2.1), HICP (p-value = 0.081 (in model M2.2) and GP/S_CS (p-value = 0.089 (in model M3.1). Four variables are insignificant: one in Model M2.1 (HICP, p-value = 0.327); three in Model M4 (ICW_CHG p-value = 0.218; SCAinC_CHG p-value = 0.148, S/TA_CS p-value = 0.237). In M2.1 and M4, insignificant macroeconomic and industry-sector variables were retained to illustrate their impact on bankruptcy risk.

Using Equations (1) and (2), the probability of default (PD), i.e., the probability that an enterprise will go bankrupt, was calculated. According to the logistic regression models formed, enterprises with PD ≥ 50% were classified as bankrupt and enterprises with PD < 50% were classified as non-bankrupt. According to the logistic regression EBP models formed, the calculation of coefficients z is shown in Table 1.

In addition, the overall fit of the models was appropriate as they complied with the following requirements: (i) the chi-square-criterion p-value is less than 0.05; and (ii) the Cox-and-Snell R Square and Nagelkerke R Square is not less than 0.2. (iii) The models showed the following total percentages of correctly classified cases: 71.4% (Model M1.1)–94.2% (Model 2.2) in the model-training sample; 68.1% (Model M1.1)–91.7% (Model 2.2) in the model-test sample. Therefore, the enterprises were classified more correctly in the model-training sample. (Table 1). Consequently, according to the total of correct classifications in the model-test sample, the following observations were noted. (i) The classification percentage for Models M1.1 and M3.1 was lower (68.1% and 69.4% respectively). (ii) Models M3.2, M2.1 and M2.2 effectively classified the enterprises (84.2%, 90.4% and 91.7%, respectively).

Regarding the construction of credit-risk models, West (2000) notes that “the costs of granting credit to a bad risk candidate, is significantly greater than the cost of denying credit to a good risk candidate.” Zhu et al. (2016) agree with this statement and declare that the improvement of the prediction-accuracy ratio for enterprises with high credit risk is more important than that of the prediction-accuracy ratio for enterprises with low credit risk. In other words, the creditor’s losses are higher in the case of a Type I error, so the aim is usually to reduce the likelihood of this error (Mileris 2009).

In this study, the logistic regression model showed a high percentage of correctly classified bankrupt-enterprise cases, from 80.3% (model M2.2) to 90.0% (model M3.2). According to the correct classification of non-bankrupt enterprises in the model-test sample, the following observations were noted. (i) The classification percentage for Models M1.1, M1.2 and M3.1 was lower (59.0%, 69.7% and 59.3%, respectively). (ii) Models M2.1 and M2.2 classified the non-bankrupt enterprises (93.8% and 98.8%, respectively) more effectively than the bankrupt enterprises.

In conclusion, for all the LR models, the AUC differed from 0.5, i.e., more accurate classifications were achieved with the logistic regression than by chance. Table 1 shows that the LR models demonstrated acceptable (for models M1.1 and M3.1), excellent (for models M1.2 and M4) and outstanding (for models M2.1, M2.2 and M3.2) performance in terms of discrimination. This indicates that the formed models met the accuracy requirement: the majority of the models were characterised by high discriminatory power and the AUC values were over 0.8. These results support the findings for LR models by Nikolic et al. (2013) and Becerra-Vicario et al. (2020) (i.e., AUC > 0.8).

4.3. Two-Stage Hybrid-Model Development

This study developed two-stage hybrid models. In these models, Stage I was based on the LR model and Stage II was based on the ANN models.

For Stage I LR, models that have higher discriminatory power are used, i.e., those with higher AUC values. Therefore, (i) Model M1.2 was selected from the models that use the financial ratios of enterprises as independent variables (AUC (M1.2) = 0.821 is higher than AUC (M1.1) = 0.751). (ii) Model M2.2 was selected from among the models that use financial ratios and macroeconomic variables (AUC (M2.2) = 0.985 is higher than AUC (M2.1) = 0.952). (iii) Model M3.2 was selected from the models that used financial ratios, macroeconomic variables and construction-sector variables (AUC (M3.2) = 0.907 is higher than AUC (M3.1) = 0.746). (iv) Model M4 represented the models that used the financial ratios, macroeconomic variables, construction-sector variables and non-financial variables of enterprises (AUC (M4) = 0.838) (see Table 1). For Stage II, two ANN models were used, i.e., MLP and RBF neural networks. Thus, this study developed eight two-stage hybrid models, i.e., M1.2+ M1 MLP, M1.2+ M1 RBF, M2.2+ M2 MLP, M2.2+ M2 RBF, M3.2+ M3 MLP, M3.2+ M3 RBF, M4+ M4 MLP, M4+ M4 RBF.

According to the total percentage of the cases correctly classified by the models (the accuracy rate), the models showed mixed results. Compared to Stage I, the Stage II accuracy rate increased in Models M1 and M2, using both MLP and RBF neural networks, i.e., the Stage II M1 MLP and M1 RBF accuracy rates were higher than those of the M1.2; the Stage II M4 MLP and M4 RBF accuracy rates were higher than those of the M4. Similarly, but in the opposite direction, the accuracy rate varied in models M2 and M3, i.e., the Stage II M2 MLP and M2 RBF accuracy rates were lower than those of the M2.2 and the Stage II M3 MLP and M3 RBF accuracy rates were lower than those of the M3.2.

In this study, Stage II showed a lower percentage of bankrupt-enterprise cases correctly classified by the majority of the models, except for the model M2.2+ M2 RBF.

According to the percentage of the correctly classified non-bankrupt-enterprise cases (the specificity ratio), the models showed mixed results. In Stage II (both MLP and RBF neuron networks), the non-bankrupt enterprises were classified better by Models M1 and M4, i.e., the Stage II M1 MLP and M1 RBF specificity rates were higher than those with M1.2, while the Stage II M4 MLP and M4 RBF specificity rates were higher than those with M4. Similarly, but in the opposite direction, the specificity rate varied in model M2, i.e., the Stage II M2 MLP and M2 RBF specificity rates were lower than those with M2.2. Furthermore, for Model M3, the MLP neural network improved the specificity rate (from 80.4% in Stage I to 85.3% in Stage II (M3 MLP)), while the RBF neural network worsened the specificity rate (from 80.4% in Stage I to 71.9% in Stage II (M3 RBF)).

For model M1, the MLP and RBF neural network models classified the non-bankrupt enterprises the best. However, for models M2, M3 and M4, the RBF neural network models classified bankrupt enterprises better than non-bankrupt enterprises, whereas the opposite was observed with the MLP neural network models.

Finally, for all the ANN models, the AUC significantly differed from 0.5, i.e., better classifications were achieved with the ANN models than by chance.

Table 2. Two-stage hybrid EBP models for MiSEs in the construction sector.

Model	M1.2+ M1 MLP		M1.2+ M1 RBF		M2.2+ M2 MLP		M2.2+ M2 RBF
Stage	St. I	St. II	St. I	St. II	St. I	St. II	St. I	St. II
	M1.2	M1 MLP	M1.2	M1 RBF	M2.2	M2 MLP	M2.2	M2 RBF
Model-test sample (dataset):
The total percentage of the model’s correctly classified cases (Accuracy rate)	75.8	76.4	75.8	78.1	91.7	80.6	91.7	79.4
The percentage of the model’s correctly classified bankrupt-enterprises cases (Sensitivity)	85.7	61.6	85.7	76.4	80.3	71.9	80.3	92.1
The percentage of the model’s correctly classified non-bankrupt-enterprises cases (Specificity)	69.7	85.6	69.7	79.2	98.8	85.9	98.8	71.6
AUC	0.821	0.736	0.821	0.860	0.985	0.789	0.985	0.882
Model	M3.2+ M3 MLP		M3.2+ M3 RBF		M4+ M4 MLP		M4+ M4 RBF
Stage	St. I	St. II	St. I	St. II	St. I	St. II	St. I	St. II
	M3.2	M3 MLP	M3.2	M3 RBF	M4	M4 MLP	M4	M4 RBF
Model-test sample (dataset):
The total percentage of the model’s correctly classified cases (Accuracy rate)	84.2	78.4	84.2	74.1	77.7	80.6	77.7	79.3
The percentage of the model’s correctly classified bankrupt-enterprises cases (Sensitivity)	90.0	67.6	90.0	77.6	89.0	75.2	89.0	82.4
The percentage of the model’s correctly classified non-bankrupt-enterprises cases (Specificity)	80.4	85.3	80.4	71.9	70.3	84.1	70.3	77.4
AUC	0.907	0.765	0.907	0.831	0.838	0.797	0.838	0.873

Abbreviations used: St.—stage.

shows that, in Stage II, all the MLP neural network models demonstrated acceptable discrimination and all the RBF neural network models showed excellent performance in terms of discrimination.

However, compared to Stage I, based on the LR model, Stage II showed a lower AUC value in the majority of the ANN models, except for the model M1 RBF (i.e., AUC (M1.2) = 0.821 is lower than AUC (M1 RBF) = 0.860) and M4 RBF (i.e., AUC (M4) = 0.838 is lower than AUC (M4 RBF) = 0.873).

Furthermore, Figure 1 shows ROC curves and the AUC is presented in Figure 1 and Table 2.

In this context, it should be noted that two-stage hybrid models do not improve bankruptcy prediction. As Tserng et al. (2011) argue, it is likely that these results are influenced by the construction industry’s special characteristics and financial risks. In contrast, when analysing credit risk in the banking industry, Lin (2009) found that the proposed two-stage hybrid models (i.e., models that integrate the LR and ANN approaches) outperformed logistic regression and artificial neural networks. Similarly, Zhu et al. (2016) stated that the proposed two-stage hybrid model “has the best classification capability to forecast SMEs credit risk” in supply-chain financing.

4.4. MLP and RBF Neural Network Models

This study develops MLP and RBF neural network models—M(ALL.MLP) and M(ALL.RBF)—based on all the sets of independent variables, i.e., the financial ratios, macroeconomic variables, construction-sector variables and non-financial variables of enterprises.

This study compared the performances of these bankruptcy-prediction models and the results of the analysis indicated the following conclusions.

The RBF neural network models classify bankrupt enterprises better than non-bankrupt enterprises (i.e., the model correctly classified 76.4% of the bankrupt and 66.9% of the non-bankrupt enterprises). By contrast, the MLP neural network models classified non-bankrupt (84.1% cases) enterprises better than bankrupt (74.8%) enterprises (see

Table 3. EBP models for MiSEs in the construction sector: MLP and RBF neural network models and the MARS Model.

Model	M(ALL.MLP)	M(ALL.RBF)	M(MARS)
Model-test sample (dataset):
The total percentage of the cases correctly classified by the models	81.6	70.1	93.9
The percentage of the bankrupt-enterprise cases correctly classified by the models	74.8	76.4	93.8
The percentage of the non-bankrupt-enterprise cases correctly classified by the model	84.1	66.9	93.9
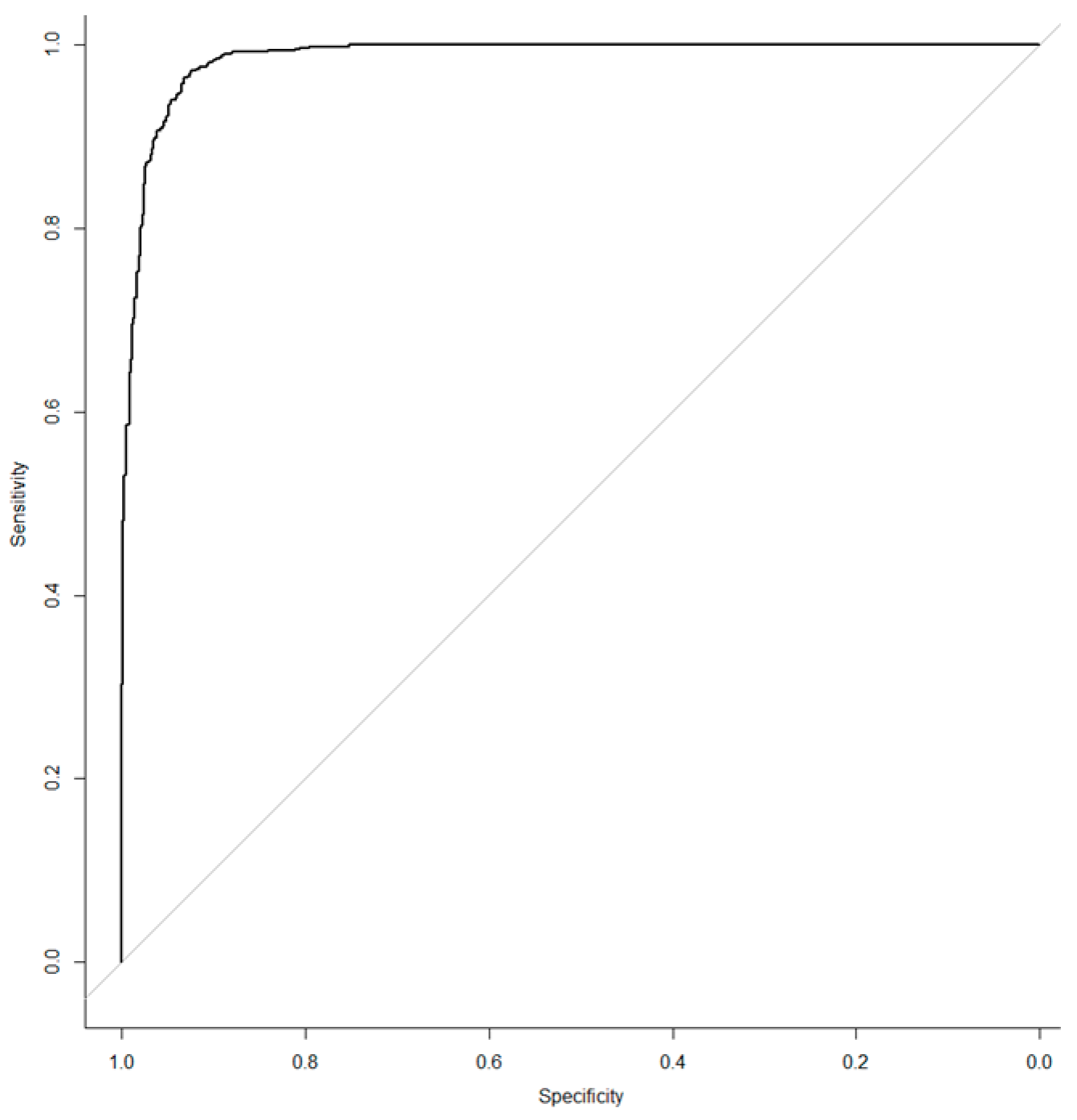
AUC	0.799	0.787	0.987

).

The total percentage of the cases correctly classified by the models was higher for the MLP model (81.6% total enterprises) than for the RBF model (70.1%). (i) The MLP neural network model demonstrated a higher total percentage of correctly classified cases (81.6%) than the LR model M4 (77.7%). (ii) The results of the RBF neural network model were worse (70.1%). However, Table 3 shows that the ANN models demonstrated acceptable performance in terms of discrimination, i.e., AUC (M(ALL.MLP)) = 0.799, AUC (M(ALL.RBF)) = 0.787. It can be concluded that ANNs have lower discriminatory power than the LR model based on all the sets of independent variables, i.e., model M4 (AUC (M4) = 0.838). Furthermore, Figure 1 shows the ROC curves and the AUC. To summarise, it cannot be argued that ANN models are more accurate in predicting bankruptcy. This result differs from the results presented by Becerra-Vicario et al. (2020): their findings showed that the use of ANNs “exceeds logistic regression in a predictive capacity.” Tseng and Hu (2010) compared four bankruptcy-prediction models: (i) the logit model, (ii) the quadratic interval logit model, (iii) the backpropagation MLP and (iv) the RBF network. Their results indicated that the RBF network outperforms the other models. In addition, Tserng et al. (2011) note that “too many input variables add training time to the models”; however, “they do not always improve the predicting performance,” and “sometimes they are even a disturbance and lower the model’s predicting ability.”

4.5. The MARS Model

The MARS model correctly classified 93.8% of the bankrupt and 93.9% of the non-bankrupt enterprises and also had an excellent (93.9%) total percentage of correctly classified cases (see Table 3).

The formed models met the accuracy requirement: the MARS model is characterized by outstanding discriminatory power and the AUC value is over 0.9 (i.e., AUC (M(MARS)) = 0.987). Furthermore, Figure 2 shows the ROC curves and the AUC is presented in Table 3.

To achieve such high credit-risk-prediction accuracy, the model selects and uses ten independent variables (see Appendix A,

Table A6. Variables used to develop the EBP models for Lithuanian MiSEs in the construction sector: LR and MARS models.

Variables		Variable Is Used in
		LR Model	MARS Model
I. Financial Variables
1a. Profitability ratios (return from sales)
EBIT/Sales	EBIT/S	x
1b. Profitability ratios (return on investment)
Gross Profit/Total Assets	GP/TA	x
EBIT/Total Assets	EBIT/TA	x
Net Profit/Total Assets	ROA	x
2. Liquidity ratios
Accounts Receivable/Total Liabilities	AR/TL	x
(Cash−Inventories)/Current Liabilities	(CASH-INV)/CL	x
(Current Liabilities−Cash)/Total Assets	(CL-Cash)/TA		x
3. Solvency ratios
Total Liabilities/Total Assets	TL/TA	x	x
4. Activity ratios
4a. Activity ratios (assets turnover)
Sales/Fixed Assets	S/FA		x
Sales/Total Assets	S/TA	x	x
4b. Activity ratios (equity and liabilities turnover)
Sales/Current Liabilities	S/CL	x
Sales/Total Liabilities	S/TL	x
4c. Activity ratios (level of expenses)
Cost of Sales/Sales	CS/S	x
5a. Structure ratios (total-assets-structure ratios)
Current Assets/Total Assets	CA/TA	x	x
Inventory/Total Assets	INV/TA	x
Cash/Total Assets	Cash/TA		x
II. Macroeconomic Variables
GDP index	GDP_index	x
The harmonised index of consumer prices at constant tax rates	HICP	x	x
Average annual inflation	INF_A	x
House-price index	HPI		x
III. Construction-Sector Variables
Macroeconomic indicators characterising the construction sector
Annual change in index of construction work carried out within the country	ICW_CHG	x
Annual change in the share of the construction activity in the country in the total construction activity revenue	SCAinC_CHG	x
IV. Financial Indicators for the Construction Sector
Gross profit margin (%) Gross profit/sales	GP/S_CS	x
Total-asset-turnover ratio (times) Sales/total assets	S/TA_CS	x
Change in customer insolvency and late payments over the last three months	CCI_CS	x
V. Non-Financial Variables
The age of the enterprise	AGE	x	x
Sole shareholder	SHARE	x
Number of records	RECORDS		x

). (a) The first six are financial ratios, i.e., (i) one liquidity ratio ((Current Liabilities–Cash)/Total Assets), (ii) one solvency ratio (Total Liabilities/Total Assets), (iii) two activity ratios (Sales/Fixed Assets, Sales/Total Assets) and (iv) two structure ratios (Current Assets/Total Assets, Cash/Total Assets). It should be noted that three of these ratios are not used in LR models. (b) In terms of macroeconomic variables, the model uses HICP (the harmonised index of consumer prices at constant tax rates) and HPI (the house-price Index). It should be noted that the HPI is not used in LR models. (c) In terms of the non-financial variables of enterprises, the model uses AGE (the age of the enterprise) and RECORDS (the number of records), which are not used in LR models. To summarise, the MARS model selected five new variables. This suggests that further research is needed to determine this selection of the MARS model and the differences in selection between the MARS and LR models. For comparison, the findings by Sánchez-Lasheras et al. (2012) show that the MARS model’s accuracy is high (99.01%). However, this result was worse those demonstrated with ANNs and the authors concluded that the MARS model is “useless for practical purposes.”

5. Conclusions

The issue of companies’ financial stability has been widely analysed. However, in periods of economic instability, the issues of company solvency and bankruptcy prediction are particularly important, as the inability of a company to continue its activities affects not only the company itself but also other stakeholders (other companies, financial institutions, public authorities, employees, etc.). Therefore, to ensure the continuity of operations and protect the interests of stakeholders, it is essential to continuously assess the financial situations of companies and resolve financial problems before it becomes clear that companies are insolvent. Due to the specific nature of their activities, these issues are particularly acute for small construction companies.

This study developed EBP models for Lithuanian MiSEs in the construction sector. The study also focused on increasing the accuracy and interpretability of bankruptcy-prediction models.

This issue was analysed based on the classification models and types of variable used. The study approached the problem from two perspectives: the selection of the independent variables and the choice of forecasting methods.

Different EBP models were created using four groups of variables, i.e., (i) the financial ratios, (ii) macroeconomic variables, (iii) construction-sector variables and (iv) non-financial variables of enterprises. To develop the bankruptcy-prediction model in this study, logistic regression, ANNs and MARS models were used. In addition, the study developed two-stage hybrid models, i.e., logistic regression was combined with ANNs.

The findings of this study can be formulated as follows.

First, the logistic regression EBP models developed for MiSEs in the construction sector are characterised by the high interpretability of their results, their accuracy and their simplicity. In the EBP models, the financial variables substantially explain enterprises’ financial statements and performance from different perspectives. The inclusion of enterprises’ non-financial, construction-sector and macroeconomic variables improved the characteristics of the EBP models. The inclusion of macroeconomic variables in the models had a particularly significant impact. It can also be stated that the models feature flexibility, i.e., stakeholders can assess enterprises using only financial ratios or other variables.

Second, two-stage hybrid models do not improve bankruptcy prediction.

Third, this study developed MLP and RBF neural network models based on all the sets of independent variables, i.e., the financial ratios, macroeconomic variables, construction-sector variables and non-financial variables of enterprises. The ANN models demonstrated acceptable performance in terms of discrimination. However, the ANNs had lower discriminatory power than the LR model based on all the sets of independent variables.

Fourth, the MARS model demonstrated the best bankruptcy prediction: the MARS model is characterised by outstanding discriminatory power.

In this study, three forecasting methods were used (logistic regression, ANN (more precisely, MLP and RBF neural networks) and MARS). In further research, it will be reasonable to also apply other machine-learning models: random forest (e.g., Mori and Umezawa (2007) and Uddin et al. (2022)), gradient boosting (e.g., Papík and Papíková (2023) tested CatBoost, LightGBM and XGBoost algorithms) and support vector machine (e.g., Tserng et al. 2011).

It was stated in the introduction that when designing bankruptcy-prediction models for an enterprise, “samples should be from a single country, to ensure their uniform juridical and accounting systems” (Veganzones and Severin 2021). However, this could be seen as a limitation of this study. Therefore, the proposed bankruptcy-prediction models should be tested in other countries at a similar economic level, expanding the research sample.