Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review
Abstract
:1. Introduction
- (1)
- What are the main methods used to determine agricultural insurance premiums based on the rainfall index?
- (2)
- How is the rainfall index used in the calculation of agricultural insurance premiums?
- (3)
- What commodities are included in rainfall index-based agricultural insurance?
- (4)
- What meteorological risks are considered in the measurement of the rainfall index?
- (5)
- How is the compensation payment scheme for rainfall index-based agricultural insurance?
2. Materials and Methods
- (1)
- The article was written in English;
- (2)
- The article has reached the final publishing stage;
- (3)
- The publication period is twenty years, from 2005 to 2024.
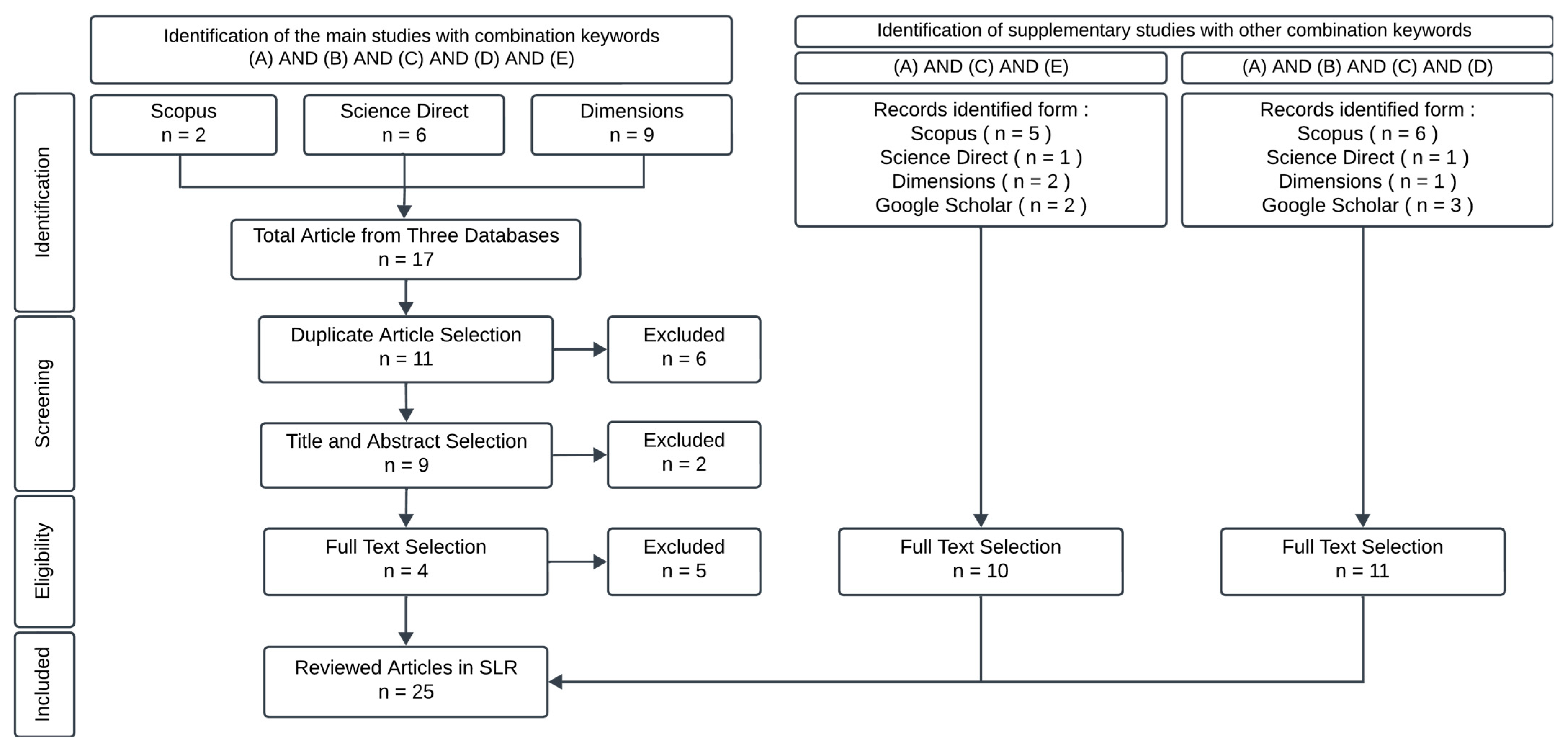
- Duplicate articles were removed from the three databases to ensure accuracy and diversity.
- The selection of articles focused on the title and abstract, which represented the most descriptive part of the entire content. Additionally, this stage also saved time in the selection process. Articles with titles and abstracts that did not relate to the criteria and the research topic were excluded at this stage.
3. Results
3.1. Result of Article Selection Using PRISMA Method
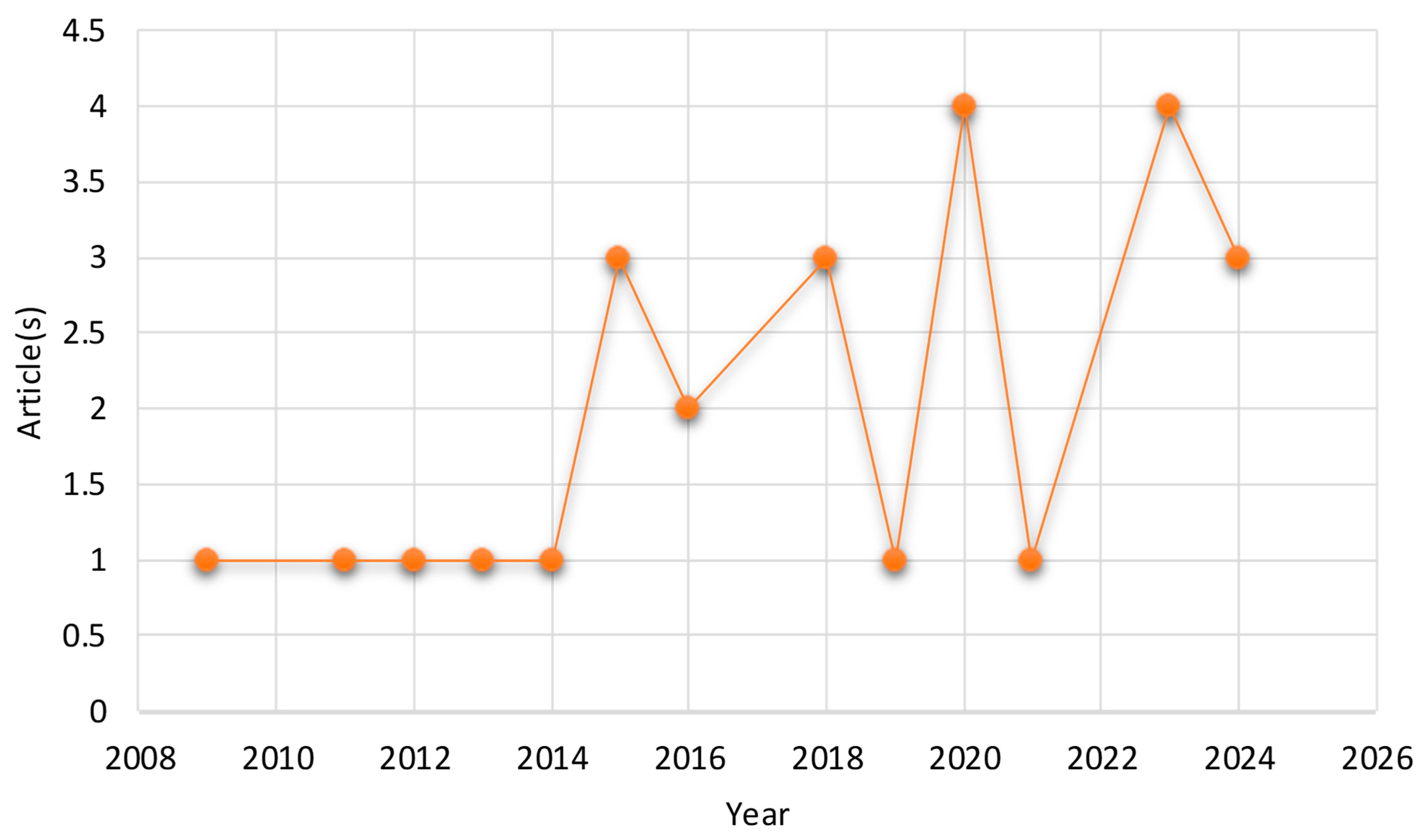
3.2. Bibliometric Analysis of Reviewed Articles
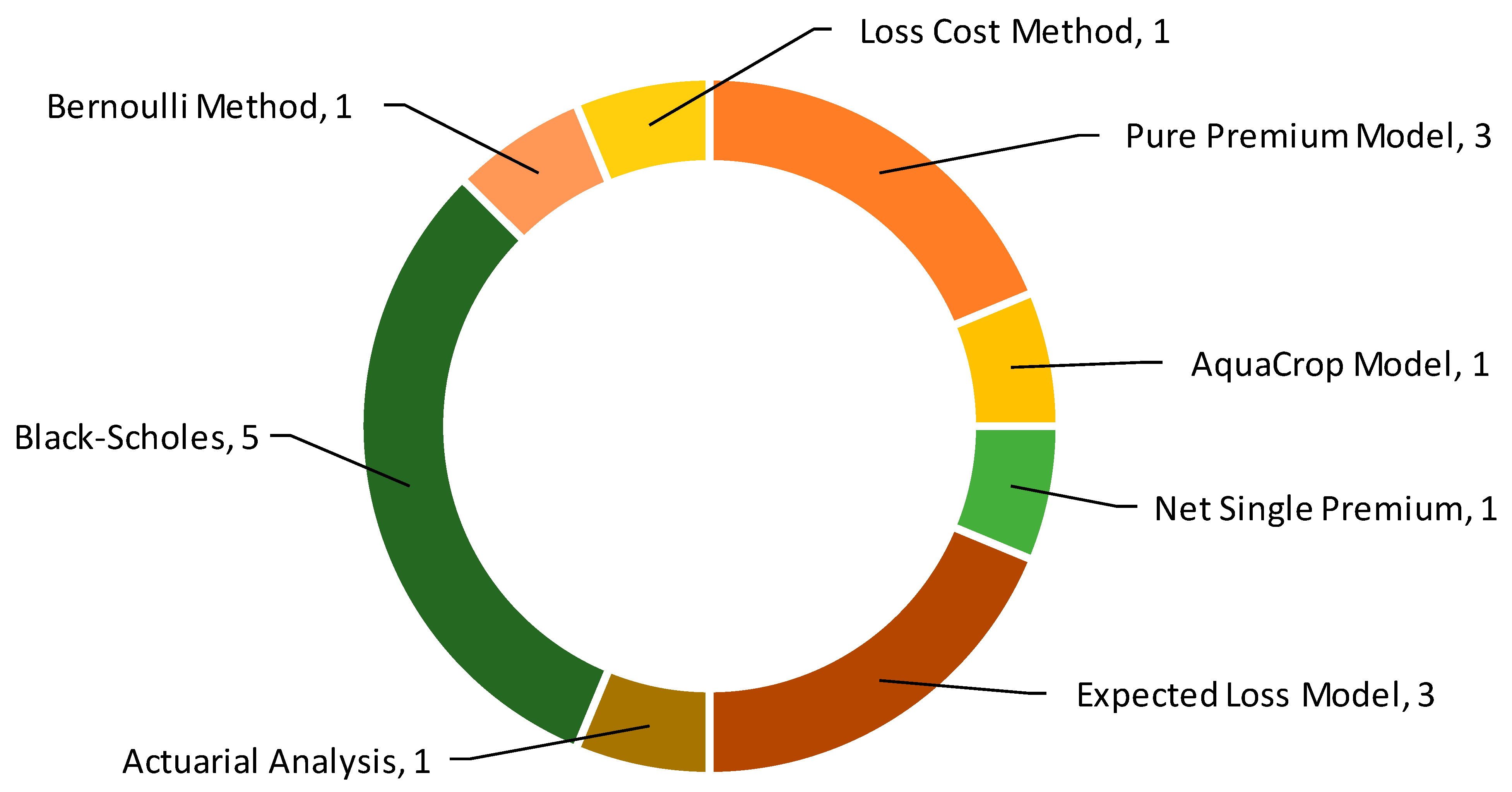
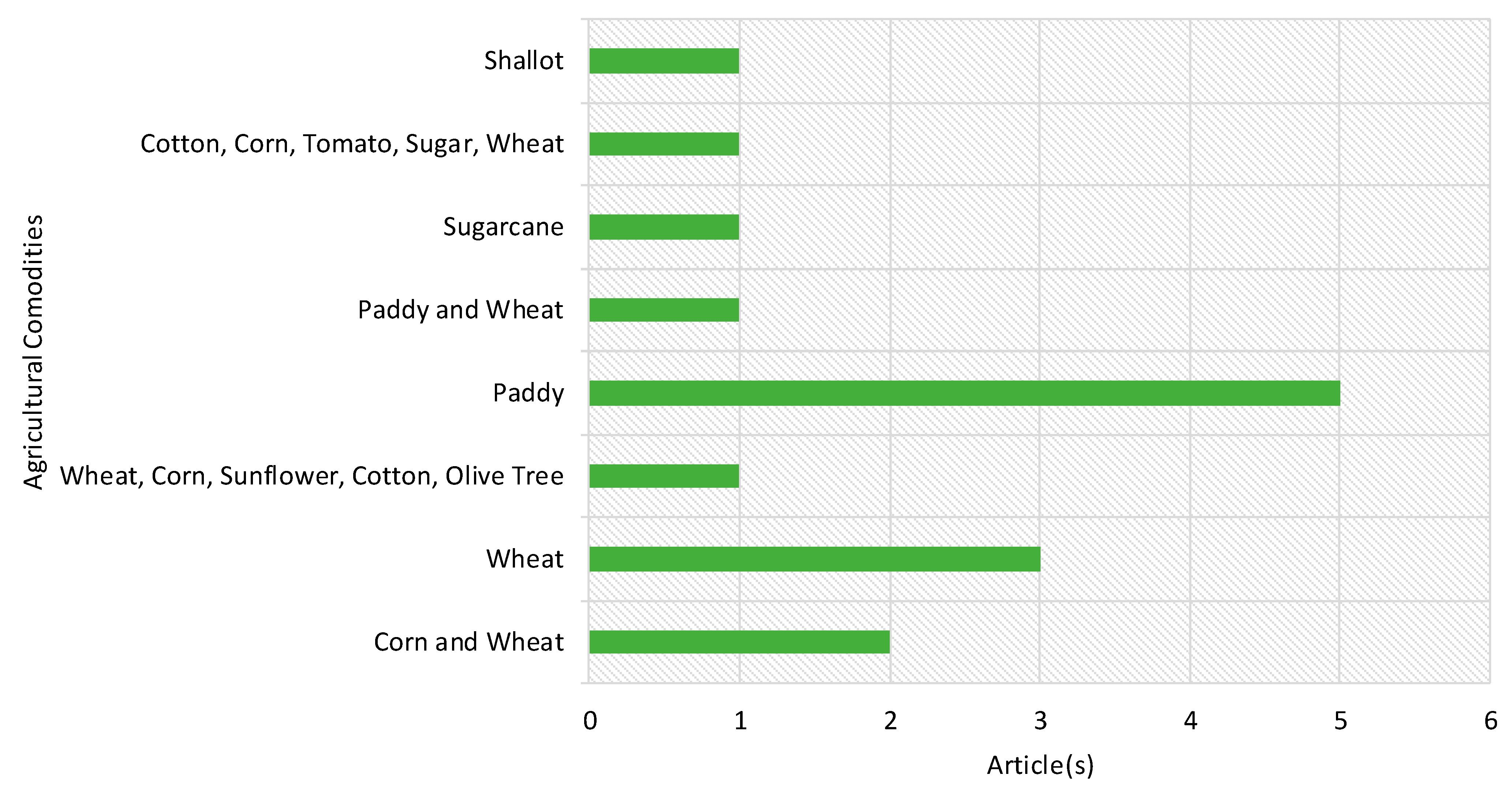
3.3. Analysis of Reviewed Articles Based on Research Question
4. Discussion
4.1. Summary of Reviewed Articles
4.2. Literature Gap Analysis and Future Research
- (1)
- The reference option is a European type that can be exercised at maturity.
- (2)
- The stock price follows a lognormal distributed random pattern with constant stock return variance.
- (3)
- The risk-free interest rate is constant.
- (4)
- There is no dividend payment on the stock during the option’s remaining life.
- (5)
- No taxes and transaction costs in buying or selling options.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Afshar, Mehdi H., Timothy Foster, Thomas P. Higginbottom, Ben Parkes, Koen Hufkens, Sanjay Mansabdar, Francisco Ceballos, and Berber Kramer. 2021. Improving the Performance of Index Insurance Using Crop Models and Phenological Monitoring. Remote Sensing 13: 924. [Google Scholar] [CrossRef]
- Alfandari, Ravit, and Brian J. Taylor. 2022. Systematic Bibliographic Database Searching for Literature Reviews: Case Study on Child Protection Decision-Making. British Journal of Social Work 52: 518–35. [Google Scholar] [CrossRef]
- Ariyanti, Devi, Riaman Riaman, and Iin Irianingsih. 2020. Application of Historical Burn Analysis Method in Determining Agricultural Premium Based on Climate Index Using Black Scholes Method. JTAM Jurnal Teori Dan Aplikasi Matematika 4: 28–38. [Google Scholar] [CrossRef]
- Atanga, Raphael Ane, and Vitus Tankpa. 2021. Climate Change, Flood Disaster Risk and Food Security Nexus in Northern Ghana. Frontiers in Sustainable Food Systems 5: 706721. [Google Scholar] [CrossRef]
- Azka, Muhammad, Fauziyyah, Primadina Hasanah, and Syalam Ali Wira Dinata. 2021. Designing Rainfall Index Insurance for Rubber Plantation in Balikpapan. Paper presented at International Conference on Mathematics, Statistics and Data Science (ICMSDS), Bogor, Indonesia, November 11–12. [Google Scholar]
- Ballotta, Laura, Gianluca Fusai, Ioannis Kyriakou, Nikos C. Papapostolou, and Panos K. Pouliasis. 2020. Risk Management of Climate Impact for Tourism Operators: An Empirical Analysis on Ski Resorts. Tourism Management 77: 104011. [Google Scholar] [CrossRef]
- Banks, Erik. 2004. Alternative Risk Transfer: Integrated Risk Management through Insurance, Reinsurance, and the Capital Markets. Oxford: John Wiley & Sons, Ltd. [Google Scholar]
- Baškot, Bojan, and Stanko Stanić. 2020. Parametric Crop Insurance against Floods: The Case of Bosnia and Herzegovina. Economic Annals 65: 83–100. [Google Scholar] [CrossRef]
- Berry, Elliot M., Sandro Dernini, Barbara Burlingame, Alexandre Meybeck, and Piero Conforti. 2015. Food Security and Sustainability: Can One Exist without the Other? Public Health Nutrition 18: 2293–302. [Google Scholar] [CrossRef]
- Bertranda, Jean-Louis, Xavier Brusseta, and Maxime Fortin. 2015. Assessing and Hedging the Cost of Unseasonal Weather: Case of the Apparel Sector. European Journal of Operational Research 244: 261–76. [Google Scholar] [CrossRef]
- Bobojonov, Ihtiyor, Aden Aw-Hassan, and Rolf Sommer. 2014. Index-Based Insurance for Climate Risk Management and Rural Development in Syria. Climate and Development 6: 166–78. [Google Scholar] [CrossRef]
- Bokusheva, Raushan. 2018. Using Copulas for Rating Weather Index Insurance Contracts. Journal of Applied Statistics 45: 2328–56. [Google Scholar] [CrossRef]
- Chang, Chia-Chien, Wei-Yi Huang, and So-De Shyu. 2012. Pricing Mortgage Insurance with Asymmetric Jump Risk and Default Risk: Evidence in the U.S. Housing Market. Journal of Real Estate Finance and Economics 45: 846–68. [Google Scholar] [CrossRef]
- Chicaíza, Liliana, and David Cabedo. 2009. Using the Black-Scholes Method for Estimating High-Cost Illness Insurance Premiums in Colombia. Innovar: Revista de Ciencias Administrativas y Sociales 19: 119–30. [Google Scholar]
- Coble, Keith H., Terry Hanson, Corey J. Miller, and Saleem Shaik. 2003. Agricultural Insurance as an Environmental Policy Tool. Journal of Agricultutal and Applied Economics 35: 391–405. [Google Scholar] [CrossRef]
- Cogato, Alessia, Franco Meggio, Massimiliano De Antoni Migliorati, and Francesco Marinello. 2019. Extreme Weather Events in Agriculture: A Systematic Review. Sustainability 11: 2547. [Google Scholar] [CrossRef]
- Cramer, Sam, Michael Kampouridis, Alex A. Freitas, and Antonis Alexandridis. 2019. Stochastic Model Genetic Programming: Deriving Pricing Equations for Rainfall Weather Derivatives. Swarm and Evolutionary Computation 46: 184–200. [Google Scholar] [CrossRef]
- Dick, William J. A., and Weijing Wang. 2010. Government Interventions in Agricultural Insurance. Agriculture and Agricultural Science Procedia 1: 4–12. [Google Scholar] [CrossRef]
- Duncan, Tyrone E., Yaozhong Hu, and Bozenna Pasik-Duncan. 2000. Stochastic Calculus for Fractional Brownian Motion. I: Theory. SIAM Journal on Control and Optimization 38: 582–612. [Google Scholar] [CrossRef]
- Edame, Greg E., Anam Bassey Ekpenyong, William M. Fonta, and Emmanuel. J. C. Duru. 2011. Climate Change, Food Security and Agricultural Productivity in Africa: Issues and Policy Directions. International Journal of Humanities and Social Sience 1: 205–23. [Google Scholar]
- Fang, Guochang, Kun Yang, Gang Chen, and Lixin Tian. 2023. Environmental Protection Tax Superseded Pollution Fees, Does China Effectively Abate Ecological Footprints? Journal of Cleaner Production 388: 135846. [Google Scholar] [CrossRef]
- Filiapuspa, M. H., S. F. Sari, and S. Mardiyati. 2019. Applying Black Scholes Method for Crop Insurance Pricing. AIP Conference Proceedings 2168: 020042. [Google Scholar] [CrossRef]
- Firdaniza, Firdaniza, Budi Nurani Ruchjana, Diah Chaerani, and Jaziar Radianti. 2022. Information Diffusion Model in Twitter: A Systematic Literature Review. Information 13: 13. [Google Scholar] [CrossRef]
- Gómez-Limón, José A. 2020. Hydrological Drought Insurance for Irrigated Agriculture in Southern Spain. Agricultural Water Management 240: 106271. [Google Scholar] [CrossRef]
- He, Xin Jiang, and Sha Lin. 2021. A Fractional Black-Scholes Model with Stochastic Volatility and European Option Pricing. Expert Systems with Applications 178: 114983. [Google Scholar] [CrossRef]
- Heimfarth, Leif Erec, and Oliver Musshoff. 2011. Weather Index-Based Insurances for Farmers in the North China Plain: An Analysis of Risk Reduction Potential and Basis Risk. Agricultural Finance Review 71: 218–39. [Google Scholar] [CrossRef]
- Higham, Desmond J. 2004. An Introduction to Financial Option Valuation. New York: Cambridge University Press. [Google Scholar]
- Hohl, Roman Marco. 2019. Agricultural Risk Transfer: From Insurance to Reinsurance to Capital Markets. West Sussex: John Wiley & Sons. [Google Scholar]
- Hu, Yaozhong, and Bernt Oksendal. 2000. Fractional White Noise Calculus and Application to Finance. Infinite Dimensional Analysis 6: 1–32. [Google Scholar] [CrossRef]
- Hull, John C. 2002. Options, Futures, and Other Derivatives. Upper Saddle River: Prentice Hall. [Google Scholar]
- Kajwang, Ben. 2022. Weather Based Index Insurance and Its Role in Agricultural Production. International Journal of Agriculture 7: 13–25. [Google Scholar] [CrossRef]
- Kath, Jarrod, Shahbaz Mushtaq, Ross Henry, Adewuyi Adeyinka, and Roger Stone. 2018. Index Insurance Benefits Agricultural Producers Exposed to Excessive Rainfall Risk. Weather and Climate Extremes 22: 1–9. [Google Scholar] [CrossRef]
- Koprivica, Marija, Jelena Kočović, and Drago Cvijanović. 2024. A Model for Determining Premium Rates in Indexbased Crop Insurance. Ekonomika Poljoprivrede 71: 397–412. [Google Scholar] [CrossRef]
- Lesk, Corey, Pedram Rowhani, and Navin Ramankutty. 2016. Influence of Extreme Weather Disasters on Global Crop Production. Nature 529: 84–87. [Google Scholar] [CrossRef]
- Luenberger, David G. 1998. Investment Science. New York: Oxford University Press. [Google Scholar]
- Mandelbrot, Benoit, and Howard M. Taylor. 1967. On the Distribution of Stock Price Differences. Operations Research 15: 1057–62. [Google Scholar] [CrossRef]
- Markonah, Markonah, Hedwigis Esti Riwayati, and Riska Kumalasari. 2023. The Effect of Premium Income, Expenses Claim, and Underwriting on Profitability of Indonesia Joint Enterprises Insurance Companies. Jurnal Siasat Bisnis 27: 219–34. [Google Scholar] [CrossRef]
- Marola, Geby, Neva Satyahadewi, and Wirda Andani. 2023. Application of The Black Scholes Method for Counting Agricultural Insurance Premium Price Based on Rainfall Index in Kapuas Hulu Regency. BAREKENG: Jurnal Ilmu Matematika Dan Terapan 17: 819–26. [Google Scholar] [CrossRef]
- Melnikov, Alexander, and Shuo Tong. 2013. Efficient Hedging for Equity-Linked Life Insurance Contracts with Stochastic Interest Rate. Risk and Decision Analysis 4: 207–23. [Google Scholar] [CrossRef]
- Meng, Huayue, and Long Qian. 2024. Performances of Different Yield-Detrending Methods in Assessing the Impacts of Agricultural Drought and Flooding: A Case Study in the Middle-and-Lower Reach of the Yangtze River, China. Agricultural Water Management 296: 108812. [Google Scholar] [CrossRef]
- Meng, Li, and Mei Wang. 2010. Comparison of Black-Scholes Formula with Fractional Black-Scholes Formula in the Foreign Exchange Option Market with Changing Volatility. Asia-Pacific Financial Markets 17: 99–111. [Google Scholar] [CrossRef]
- Muin, Fatkhul, and Haris Mubarak. 2024. Protection and Empowerment of Farmers: Legal Policy Framework Beyond Farmer Insurance. Nurani Hukum Jurnal Ilmu Hukum 7: 57–83. [Google Scholar] [CrossRef]
- Nagaraju, Dileep, Bharath Venkatareddy, and G. Kotreshwar. 2021. Innovative Alternatives for Crop Insurance: Rainfall-Index-Based Insurance and Futures. International Journal of Banking, Risk and Insurance 9: 12–19. [Google Scholar]
- Necula, Ciprian. 2002. Option Pricing in a Fractional Brownian Motion Environment. Bucharest: DOFIN, Academy of Economic Studies. [Google Scholar] [CrossRef]
- Nnadi, F. N., J. Chikaire, J. A. Echetama, R. A. Ihenacho, P. C. Umunnakwe, and C. O. Utazi. 2013. Agricultural Insurance: A Strategic Tool for Climate Change Adaptation in the Agricultural Sector. Net Journal of Agricultural Science 1: 1–9. [Google Scholar]
- Page, Matthew J., David Moher, Patrick M. Bossuyt, Isabelle Boutron, Tammy C. Hoffmann, Cynthia D. Mulrow, Larissa Shamseer, Jennifer M. Tetzlaff, Elie A. Akl, Sue E. Brennan, and et al. 2021. PRISMA 2020 Explanation and Elaboration: Updated Guidance and Exemplars for Reporting Systematic Reviews. The BMJ 372: 178–89. [Google Scholar] [CrossRef]
- Pandiangan, Naomi, and Sukono. 2020. Determination of Deposit Insurance Premium (LPS): Merton’ s Option Theory with Co-Insurance Consideration. Operations Research: International Conference Series 1: 44–49. [Google Scholar] [CrossRef]
- Paramita, Aryana, Faizah Sari, Dian Kusumaningrum, and Valantino A. Sutomo. 2023. Pure Premium Calculation of Dry Weather-Based Insurance for Wonogiri Farmers. AIP Conference Proceedings 2877: 030005. [Google Scholar] [CrossRef]
- Peters, Edgar E. 1989. Fractal Structure in the Capital Markets. Financial Analysts Journal 45: 32–37. [Google Scholar] [CrossRef]
- Pingali, Prabhu. 2007. Agricultural Growth and Economic Development: A View through the Globalization Lens. Agricultural Economists 37: 1–12. [Google Scholar] [CrossRef]
- Poudel, M. P., S. E. Chen, and W. C. Huang. 2016. Pricing of Rainfall Index Insurance for Rice and Wheat in Nepal. Journal of Agricultural Science and Technology 18: 291–302. [Google Scholar]
- Prabakaran, Sellamuthu, Isabel C. Garcia, and Jose U. Mora. 2020. A Temperature Stochastic Model for Option Pricing and Its Impacts on the Electricity Market. Economic Analysis and Policy 68: 58–77. [Google Scholar] [CrossRef]
- Prabowo, Agung, Diah Paramita Amitarwati, Agus Sugandha, and Slamet Riyadi. 2023a. Determination of Agricultural Insurance Premium Prices Based on Rainfall Index with the Black-Scholes Model. PESHUM: Jurnal Pendidikan, Sosial Dan Humaniora 2: 895–903. [Google Scholar] [CrossRef]
- Prabowo, Agung, Sukono, and Mustafa Mamat. 2023b. Determination of the Amount of Premium and Indemnity in Shallot Farming Insurance. Universal Journal of Agricultural Research 11: 322–35. [Google Scholar] [CrossRef]
- Prabowo, Agung, Zahrahtul Amani Zakaria, Mustafa Mamat, Sukono, Slamet Riyadi, and Abdul Talib Bon. 2020. Determination of Agricultural Insurance Premium Prices Based on Rainfall Index with Formula Cash-or-Nothing Put Option. Paper presented at 2nd Africa International Conference on Industrial Engineering and Operations Management, Harare, Zimbabwe, December 7–10. [Google Scholar]
- Purwandari, Titi, Yuyun Hidayat, Sukono, Kalfin, Riza Andrian Ibrahim, and Subiyanto. 2024. Development of the Black–Scholes Model for Determining Insurance Premiums to Mitigate the Risk of Disaster Losses Using the Principles of Mutual Cooperation and Regional Economic Growth. Risks 12: 110. [Google Scholar] [CrossRef]
- Putri, Endah R. M., Venansius R. Tjahjono, and Daryono B. Utomo. 2018. An Analytic Valuation of a Deposit Insurance. Matematika 34: 115–28. [Google Scholar] [CrossRef]
- Rahadi, Fabiyan, Dwi Susanti, and Nurfadhlina Binti Abdul Halim. 2023. Determination of Microinsurance Premiums in Cattle Farms Based on Protein Content Index and Milk Production Using the Black-Scholes Method. Operations Research: International Conference Series 4: 72–80. [Google Scholar] [CrossRef]
- Raharjanti, Amalia, Riaman, and Sukono. 2024. Calculation of Rice Farming Insurance Premium Price in Magelang City Based on Rainfall Index with Black-Scholes Method. International Journal of Business, Economics, and Social Development 5: 94–103. [Google Scholar] [CrossRef]
- Riaman, Sukono, Sudradjat Supian, and Noriszura Ismail. 2022. Mapping in the Topic of Mathematical Model in Paddy Agricultural Insurance Based on Bibliometric Analysis: A Systematic Review Approach. Computation 10: 50. [Google Scholar] [CrossRef]
- Ruiz, Jorge, Maria Bielza, Alberto Garrido, and Ana Iglesias. 2015. Dealing with Drought in Irrigated Agriculture through Insurance Schemes: An Application to an Irrigation District in Southern Spain. Spanish Journal of Agricultural Research 13: 1–15. [Google Scholar] [CrossRef]
- Saputra, Jumadil, Suhal Kusairi, and Nur Azura Sanusi. 2021. Determining Equity-Linked Policy Premium for Family Takaful: An Application of Black-Scholes Option Pricing with Escrowed Dynamic Model. Decision Science Letters 10: 247–62. [Google Scholar] [CrossRef]
- Sholikhah, Nufus Mar’Atu, and Dimara Kusuma Hakim. 2024. Forecasting Rainfall in Planting Onion Crops in Brebes District, Brebes District Using Holt-Winters Exponential Smoothing. Jurnal E-Komtek 8: 22–30. [Google Scholar] [CrossRef]
- Silvestre, Prima R., and Felino P. Lansigan. 2015. Drought Risk Management through Rainfall-Based Insurance for Rain-Fed Rice Production in Pangasinan, Philppines. Asia Pacific Journal of Multidisciplinary Research 3: 111–20. [Google Scholar]
- Sukono, Hafizan Juahir, Riza Andrian Ibrahim, Moch Panji Agung Saputra, Yuyun Hidayat, and Igif Gimin Prihanto. 2022. Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics 10: 2668. [Google Scholar] [CrossRef]
- Sun, Baojing, Changhao Guo, and G. Cornelis van Kooten. 2014. Hedging Weather Risk for Corn Production in Northeastern China: The Efficiency of Weather-Indexed Insurance. Agricultural Finance Review 74: 555–72. [Google Scholar] [CrossRef]
- Tang, Wenguang, and Shuhua Chang. 2016. A Semi-Lagrangian Method for the Weather Options of Mean-Reverting Brownian Motion with Jump–Diffusion. Computers & Mathematics with Applications 71: 1045–58. [Google Scholar] [CrossRef]
- Tricco, Andrea C., Erin Lillie, Wasifa Zarin, Kelly K. O’Brien, Heather Colquhoun, Danielle Levac, David Moher, Micah D. J. Peters, Tanya Horsley, Laura Weeks, and et al. 2018. PRISMA Extension for Scoping Reviews (PRISMA-ScR): Checklist and Explanation. Annals of Internal Medicine 169: 467–73. [Google Scholar] [CrossRef]
- Valverde, Raul. 2015. An Insurance Model for the Protection of Corporations against the Bankruptcy of Suppliers. European Journal of Economics, Finance and Administrative Sciences 48: 38–58. [Google Scholar]
- Vyas, Shalika, Tobias Dalhaus, Martin Kropff, Pramod Aggarwal, and Miranda P.M. Meuwissen. 2021. Mapping Global Research on Agricultural Insurance. Environmental Research Letters 16: 103003. [Google Scholar] [CrossRef]
- Wen, Yvonne Wong Jing, Raja Rajeswari Ponnusamy, and Ho Ming Kang. 2019. Application of Weather Index-Based Insurance for Paddy Yield: The Case of Malaysia. International Journal of Advanced and Applied Sciences 6: 51–59. [Google Scholar] [CrossRef]


| Keywords | Search Terms |
|---|---|
| A | (“Insurance”) |
| B | (“Crop” OR “Agriculture” OR “Agricultural”) |
| C | (“Premiums”) |
| D | (“Weather Index” OR “Rainfall Index”) |
| E | (“Black Scholes” OR “Black-Scholes” OR “fractional Black-Scholes” OR “fractional Black Scholes”) |
| Author(s) | Research Objectives |
|---|---|
| Chicaíza and Cabedo (2009) | Calculating high-cost disease insurance premiums in the Colombian health system using Black–Scholes. |
| Chang et al. (2012) | Modeling house price changes in the context of mortgage insurance pricing using Black–Scholes. |
| Melnikov and Tong (2013) | Evaluating equity-linked life insurance contracts with efficient hedging techniques based on Black–Scholes. |
| Valverde (2015) | Estimating insurance premiums that can be used to reduce the risk of supplier bankruptcy using Black–Scholes. |
| Putri et al. (2018) | Evaluating the economic value of deposit insurance using Black–Scholes. |
| Pandiangan and Sukono (2020) | Determining the deposit insurance premium in Indonesia using Black–Scholes. |
| Saputra et al. (2021) | Developing a premium model in Takaful insurance with Sharia principles using Black–Scholes. |
| Fang et al. (2023) | Analyzing the price of environmental insurance using Black–Scholes. |
| Rahadi et al. (2023) | Calculating the price of microinsurance premiums on cattle farms using Black–Scholes. |
| Purwandari et al. (2024) | Developing a natural disaster insurance premium model using Black–Scholes. |
| Heimfarth and Musshoff (2011) | Analyzing weather index-based insurance on maize and wheat farming in the North China Plain. |
| Bobojonov et al. (2014) | Applying index-based insurance for climate risk management using the pure premium model and rural development in Syria. |
| Ruiz et al. (2015) | Evaluating the feasibility of using the AquaCrop model in calculating drought insurance premiums for irrigated agriculture. |
| Silvestre and Lansigan (2015) | Developing a rainfall index-based crop insurance model for rice production in Pangasinan, Philippines, using Net Single Premiums. |
| Poudel et al. (2016) | Estimating rainfall index-based crop insurance premiums for rice and wheat in Nepal using the expected loss model. |
| Kath et al. (2018) | Investigating the financial benefits of excess rainfall index insurance for sugarcane farmers in Tully, Northern Australia, and calculating premiums using the expected loss model. |
| Bokusheva (2018) | Developing a copula-based weather index insurance design methodology that aims to cover extreme weather events. |
| Wen et al. (2019) | Developing a specific model for determining premium rates in index-based crop insurance. |
| Baškot and Stanić (2020) | Determining the premium model for parametric insurance in the agricultural sector of Bosnia and Herzegovina using the Black–Scholes method. |
| Gómez-Limón (2020) | Proposing an index-based hydrological drought insurance scheme for irrigated agriculture and calculated fair premiums through an actuarial analysis. |
| Koprivica et al. (2024) | Determining the suitability of weather index-based agricultural insurance models for each selected rice growing zone in Malaysia. |
| Ariyanti et al. (2020) | Determining the amount of premiums to be paid by farmers using the Black–Scholes method based on the climate index. |
| Prabowo et al. (2023b) | Determining premium rates in rainfall index-based agricultural insurance for shallot crops using Black–Scholes in Central Java. |
| Marola et al. (2023) | Calculating the value of agricultural insurance premiums based on the rainfall index in Kapuas Hulu Regency using the Black–Scholes method. |
| Raharjanti et al. (2024) | Determining the price of agricultural insurance premiums based on the rainfall index in Magelang City using the Black–Scholes method. |
| Author(s) | Premium Calculation Model |
|---|---|
| Heimfarth and Musshoff (2011) | |
| Bobojonov et al. (2014) | |
| Ruiz et al. (2015) | |
| Silvestre and Lansigan (2015) | |
| Poudel et al. (2016) | |
| Kath et al. (2018) | |
| Bokusheva (2018) | |
| Wen et al. (2019) | |
| Baškot and Stanić (2020) | |
| Gómez-Limón (2020) | |
| Koprivica et al. (2024) | |
| Ariyanti et al. (2020); Prabowo et al. (2023b); Marola et al. (2023); and Raharjanti et al. (2024) |
| Variable | Description |
|---|---|
| Premium for agricultural insurance contract | |
| Maximum amount of compensation (indemnity) received | |
| Actual rainfall index | |
| Trigger threshold; i.e., rainfall index at which compensation payments start to be made | |
| Exit threshold; i.e., rainfall index at which maximum payment is made | |
| Exponential constant with value 2.718281828… ≈2.718 | |
| Risk-free interest rate | |
| Period of insurance | |
| Sum of rainfall values from index probability | |
| Amount of compensation at time | |
| Premium rate (in percentage) | |
| Average income of crops | |
| Amount of compensation (indemnity) against drought | |
| Amount of compensation (indemnity) against flood | |
| Probability of indemnity amount against drought protection | |
| Gamma density function of actual rainfall | |
| Probability of each rainfall value level | |
| Expectation of Bernoulli random variable | |
| Standard deviation | |
| Standard normal cumulative distribution function | |
| Expectation of drought protection indemnity variable |
| Author(s) | Risk-Based Compensation Payment Scheme |
|---|---|
| Heimfarth and Musshoff (2011) | |
| Bobojonov et al. (2014) | |
| Ruiz et al. (2015) | - |
| Silvestre and Lansigan (2015) | |
| Poudel et al. (2016) | |
| Kath et al. (2018) | - |
| Bokusheva (2018) | |
| Gómez-Limón (2020) | |
| Ariyanti et al. (2020) | |
| Prabowo et al. (2023b) | |
| Marola et al. (2023) | - |
| Koprivica et al. (2024) | - |
| Raharjanti et al. (2024) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azahra, A.S.; Johansyah, M.D.; Sukono. Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review. Risks 2024, 12, 205. https://doi.org/10.3390/risks12120205
Azahra AS, Johansyah MD, Sukono. Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review. Risks. 2024; 12(12):205. https://doi.org/10.3390/risks12120205
Chicago/Turabian StyleAzahra, Astrid Sulistya, Muhamad Deni Johansyah, and Sukono. 2024. "Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review" Risks 12, no. 12: 205. https://doi.org/10.3390/risks12120205
APA StyleAzahra, A. S., Johansyah, M. D., & Sukono. (2024). Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review. Risks, 12(12), 205. https://doi.org/10.3390/risks12120205






