The Role of Longevity-Indexed Bond in Risk Management of Aggregated Defined Benefit Pension Scheme

Abstract

Defined benefit (DB) pension plans are a primary type of pension schemes with the sponsor assuming most of the risks. Longevity-indexed bonds have been used to hedge or transfer risks in pension plans. Our objective is to study an aggregated DB pension plan’s optimal risk management problem focusing on minimizing the solvency risk over a finite time horizon and to investigate the investment strategies in a market, comprising a longevity-indexed bond and a risk-free asset, under stochastic nominal interest rates. Using the dynamic programming technique in the stochastic control problem, we obtain the closed-form optimal investment strategy by solving the corresponding Hamilton–Jacobi–Bellman (HJB) equation. In addition, a comparative analysis implicates that longevity-indexed bonds significantly reduce solvency risk compared to zero-coupon bonds, offering a strategic advantage in pension fund management. Besides the closed-form solution and the comparative study, another novelty of this study is the extension of actuarial liability (AL) and normal cost (NC) definitions, and we introduce the risk neutral valuation of liabilities in DB pension scheme with the consideration of mortality rate.

1. Introduction and Motivation

There are two primary types of pension schemes: defined contribution (DC) plans and DB plans (Recent works on DC and DB pension plans can be found in Ng and Chong (2023); Guan et al. (2022), respectively). In a DC pension scheme, contributions are deterministic or a percentage of the member’s salary (which may be stochastic), with benefits depending on the accumulation of contributions and investment returns. In this scenario, the individual bears the majority of the inherent risk. Conversely, in a DB pension scheme, the benefits received upon retirement are clearly defined by the plan’s rules (typically related to salary and years of service), with the sponsor assuming most of the risks, including investment, inflation, longevity and solvency risks.

Longevity risk, the concern of policyholders or affiliates outliving insurers’ or pension sponsors’ expectations, has garnered significant academic and practical interest recently. The work of Cox et al. (2013) proposes hedging strategies for managing this risk, yet natural hedging methods cannot mitigate all aspects of longevity risk within nonparametric mortality models; see Zhu and Bauer (2014). Further studies on longevity risk are detailed in subsequent research: Blake and Cairns (2021); Broeders et al. (2021); Rong et al. (2023), etc. To transfer or hedge against longevity risk, the literature extensively discusses products related to longevity. The work of Chen et al. (2023) investigates optimal longevity risk transfer under asymmetric information using indemnity longevity swaps. Moreover, the market offers longevity caps, longevity floors and longevity-indexed bonds; see Bravo and Nunes (2021).

Longevity-indexed bonds are financial instruments linked to mortality rates, bridging financial and actuarial risks. Blake et al. (2006) thoroughly analyzed such assets, with Barbarin (2008) applying the Heath–Jarrow–Morton (HJM) methodology for a more realistic market model of longevity bond prices. Wills and Sherris (2010) focused on the structuring and pricing of longevity securities using mortgage and credit risk techniques. Other works on longevity bond can be found in Bauer et al. (2010); Leung et al. (2018).

Longevity-indexed bonds and other longevity-linked securities are widely studied in stochastic optimal consumption/portfolio decision problems. In order to maximize the terminal utility function for an economic agency, Menoncin (2008) investigated the role of a longevity-indexed bond in optimal portfolios and found that the value function in the market with a longevity bond is equal or greater than that without a longevity bond. By trading a longevity-linked security with continuous rate payments, Biagini et al. (2013) examined the mean-variance hedging for insurance products through longevity-linked securities. Further research on optimal strategies for longevity bonds is documented in various studies; see Kort and Vellekoop (2017); Menoncin and Regis (2017).

However, for pension plans, longevity-indexed bonds and other longevity-linked securities are not comprehensively studied in stochastic optimization problems. Usually, the pension sponsor allocates the fund in financial market consisting of several kinds of risky and risk-less assets; thus, it is important to consider the kind of assets to hold and the number of shares to buy. There are a few works that study the role of longevity bonds and longevity insurances in pension schemes. In DC pension schemes, Zhang (2018) studied optimal investment decisions in a longevity bond, implying the optimal expected utility in the market with a longevity bond is higher than that without it. Berstein and Morales (2021) examined the role of longevity insurances and found that longevity insurances could finance higher pension efficiently. In hybrid pension plans, Liu et al. (2023) examined a longevity bond and revealed that the optimal benefit payment with a longevity-indexed bond is higher than that without it. In DB pension schemes, Cox et al. (2013) investigated optimal investment decisions numerically, but not analytically, and found that longevity bonds can be used to hedge longevity risks, within a discrete time framework.

Our motivation is to find the closed-form investment decisions on longevity bonds within a continuous time framework and examine whether longevity bonds play a positive role or not in a DB pension plan. Theoretically, with the longevity risk increasing, the solvency risk also increases in most cases. As longevity bonds play a positive role and can hedge longevity risks in Zhang (2018); Liu et al. (2023); Cox et al. (2013), we think it is reasonable to suppose that investment in longevity bond may reduce solvency risk in DB pension plans.

This paper considers an optimization problem in an aggregated DB pension plan which pays close attention to solvency risk. It involves continuously adjusting investment weights within a market comprising a longevity bond and a bank account, aiming to minimize terminal solvency risk within a finite time frame.

Our contribution is three-fold. Theoretically, our work offers closed-form investment decisions on a longevity bond. Moreover, this research advances previous work (see Josa-Fombellida and Rincón-Zapatero 2010) by providing an explicit form of optimal solvency risk. Empirically, this work investigates the role of longevity bond in an aggregated DB pension plan. Practically, we extend the definitions of AL and NC in Josa-Fombellida and Rincón-Zapatero (2004, 2010) with the consideration of mortality rate, thereby deriving a new actualization rate.

The remainder of this study is organized as follows: Section 2 introduces the pension model and three assets within a stochastic interest rate framework. Section 3 identifies the optimal investment strategy and the minimum solvency risk with investment in a complete market consisting of a longevity-indexed bond and a risk-free asset. We derive the HJB equation using the dynamic programming approach. Section 4 examines the case replacing the indexed bond with a zero-coupon bond. Section 5 conducts a sensitivity analysis and compares the solvency risks in Section 3 and Section 4. Finally, Section 6 concludes the paper and suggests directions for further research.

2. Model Assumptions and Notations

We let ($\Omega ,\mathcal{F},\mathbb{F},\mathbb{P}$) be a filtered probability space. Filtration $\mathbb{F}={\left\{{\mathcal{F}}_t\right\}}_{t\in [0,T_0]}$ satisfies the usual conditions, i.e., ${\left\{{\mathcal{F}}_t\right\}}_{t\in [0,T_0]}$ is right continuous and ${\mathcal{F}}_0$ contains all the $\mathbb{P}$-negligible events in $\mathcal{F}$. Here, $T_0$ is a constant terminal time (which is shown later in Section 2.2). We let $\mathbb{E}$ be the expectation with respect to probability measure $\mathbb{P}$, and $\mathbb{E}(·|{\mathcal{F}}_t)$ denotes conditional expectation with respect to probability measure $\mathbb{P}$ given by information available up to time t.

2.1. The Pension Model

In an aggregated DB pension plan, with the purpose of delivery of benefits to the affiliates after retirement time, the plan sponsor withdraws time-varying funds continuously. We use the following notations of elements for the pension plan:

• $AL\left(t\right)$: Actuarial liability at time t, that is, the level of reserve to be detained by the pension fund and fixed by the chosen funding method, which is the liability part of the pension plan;
• $F\left(t\right)$: Fund at time t, which is the market value of assets covering the actuarial liability (asset part);
• $UAL\left(t\right)$: Unfunded actuarial liability at time t, which is the difference between the actuarial liability (reserve that we should have) and the fund (reserve that we really have). This amount can be positive (deficit or underfunding) or negative (surplus or overfunding);
• $P\left(t\right)$: Benefits promised to affiliates at time t;
• $C\left(t\right)$: Contribution rate at time t;
• $NC\left(t\right)$: Normal cost at time t;
• $SC\left(t\right)$: Supplementary contribution rate, which satisfies $C\left(t\right)=NC\left(t\right)+SC\left(t\right)$;
• $M\left(x\right)$: Percentage of promised benefits accumulated up to age $x\in [a,d]$, $a,d\in {\mathbb{R}}_{+}$; hence, we have $M\left(a\right)=0$ and $M\left(d\right)=1$. We assume that M is differentiable;
• $m\left(x\right)$: The probability density of M;
• $\delta \left(t\right)$: Technical rate of actualization;
• $\lambda \left(t\right)$: Force of mortality, which is defined by $\lambda \left(t\right)=\underset{\Delta t\to 0}{lim}\frac{P({\tau }_x<t+\Delta t|{\tau }_x>t)}{\Delta t}$, where ${\tau }_x$ is the future residual lifetime of a life who survives to age x.

Remark 1. 

Force of mortality λ is deterministic in the context. There are lots of different assumptions on the form of λ. For simplicity, λ has a form of $\frac{\omega }{\omega -t}$ in Guan and Liang (2014), where ω is the largest survival age.

For analytical tractability, we have two assumptions following in the work of Josa-Fombellida and Rincón-Zapatero (2010) and the work of Liang et al. (2014):

Assumption 1. 

Benefit P follows a drifted Brownian Motion:

$$dP\left(t\right)={\mu }_{P}P\left(t\right)dt+{\sigma }_{P}d{W}_P\left(t\right),$$

(1)

with initial liability $P\left(0\right)=P_0$. ${\mu }_P,{\sigma }_P\in {\mathbb{R}}_{+}$ and $W_P$ is a standard Brownian Motion under probability measure $\mathbb{P}$.

Assumption 2. 

Supplementary contribution is proportional to the unfunded actuarial liability, so the total contribution satisfies

$$C\left(t\right)=NC\left(t\right)+k\left(AL\right(t)-F(t\left)\right),$$

(2)

where $k\in [0,1]$ is a constant.

We extend the definitions of the actuarial functions $AL$ and $NC$ in Josa-Fombellida and Rincón-Zapatero (2004) (with deterministic interest rate) and Josa-Fombellida and Rincón-Zapatero (2010) (with stochastic interest rate), with consideration of mortality rate in Definition 1.

Definition 1. 

For every $t\ge 0$, $AL\left(t\right)$ and $NC\left(t\right)$ are defined as follows:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill AL\left(t\right)& =& \mathbb{E}\left\{{\displaystyle {\int }_a^d{e}^{-{\int }_t^{t+d-x}\delta \left(s\right)ds}M\left(x\right)P{(t+d-x)}_{d-x}{p}_{t}dx|{\mathcal{F}}_t}\right\}\hfill \\ \hfill & =& \mathbb{E}\left\{{\displaystyle {\int }_a^d{e}^{-{\int }_t^{t+d-x}[\delta \left(s\right)+\lambda \left(s\right)]ds}M\left(x\right)P(t+d-x)dx|{\mathcal{F}}_t}\right\};\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill NC\left(t\right)& =& \mathbb{E}\left\{{\displaystyle {\int }_a^d{e}^{-{\int }_t^{t+d-x}\delta \left(s\right)ds}m\left(x\right)P{(t+d-x)}_{d-x}{p}_{t}dx|{\mathcal{F}}_t}\right\}\hfill \\ \hfill & =& \mathbb{E}\left\{{\displaystyle {\int }_a^d{e}^{-{\int }_t^{t+d-x}[\delta \left(s\right)+\lambda \left(s\right)]ds}m\left(x\right)P(t+d-x)dx|{\mathcal{F}}_t}\right\},\hfill \end{array}\end{array}$$

where ${ }_t{p}_x$ is the probability that a life aged x will survive at least t years. $AL\left(t\right)$ is the total expected benefits accumulated by percentage $M\left(x\right)$ with consideration of mortality rate $\lambda \left(t\right)$, discounted at technical rate $\delta \left(t\right)$. Analogous explanation can be given to $NC\left(t\right)$ according to probability density function $m\left(x\right)$.

Remark 2. 

If we set $\lambda =0$ in $AL$ and $NC$ in Definition 1, it degenerates into the case given by Josa-Fombellida and Rincón-Zapatero (2010) without consideration of mortality rate.

Using basic properties of conditional expectation, $AL$ and $NC$ in Definition 1 can be rewritten as

$${\displaystyle AL\left(t\right)={\int }_a^d\mathbb{E}\left\{e^{-{\int }_t^{t+d-x}[\delta \left(s\right)+\lambda \left(s\right)]ds}P(t+d-x)|{\mathcal{F}}_t\right\}M\left(x\right)dx;}$$

$${\displaystyle NC\left(t\right)={\int }_a^d\mathbb{E}\left\{e^{-{\int }_t^{t+d-x}[\delta \left(s\right)+\lambda \left(s\right)]ds}P(t+d-x)|{\mathcal{F}}_t\right\}m\left(x\right)dx.}$$

The identities of $AL$ and $NC$ and the connection between them are given in Proposition 1.

Proposition 1. 

Actuarial functions $AL$ and $NC$ satisfy $AL={\psi }_{AL}P$ and $NC={\psi }_{NC}P$, and the connection of $AL$ and $NC$ is given by

$$\left[{\mu }_P-\delta \left(t\right)-\lambda \left(t\right)+{\displaystyle \frac{{\xi }_{AL}\left(t\right)}{{\psi }_{AL}\left(t\right)}}\right]AL\left(t\right)-NC\left(t\right)+P\left(t\right)=0,$$

where ${\psi }_{AL}$, ${\psi }_{NC}$ and ${\xi }_{AL}$ are the following stochastic processes:

$${\displaystyle {\psi }_{AL}\left(t\right)={\int }_a^d{e}^{-{\int }_t^{t+d-x}[{\mu }_P-\delta \left(u\right)-\lambda \left(u\right)]du}M\left(x\right)dx,}$$

$${\displaystyle {\psi }_{NC}\left(t\right)={\int }_a^d{e}^{-{\int }_t^{t+d-x}[{\mu }_P-\delta \left(u\right)-\lambda \left(u\right)]du}m\left(x\right)dx,}$$

$${\displaystyle {\xi }_{AL}\left(t\right)={\int }_a^d{e}^{-{\int }_t^{t+d-x}{\mu }_P-\delta \left(u\right)-\lambda \left(u\right)du}\left[{\mu }_P-\delta (t+d-x)-\lambda (t+d-x)\right]M\left(x\right)dx-\left({\mu }_P-\delta \left(t\right)-\lambda \left(t\right)\right){\psi }_{AL}\left(t\right).}$$

Moreover, the actuarial liability satisfies

$$dAL\left(t\right)=\left[{\mu }_P+{\displaystyle \frac{{\xi }_{AL}\left(t\right)}{{\psi }_{AL}\left(t\right)}}\right]AL\left(t\right)dt+{\sigma }_{P}AL\left(t\right)d{W}_P\left(t\right),$$

(3)

with $AL\left(0\right)={\psi }_{AL}\left(0\right)P_0\triangleq A{L}_0$.

Proof of Proposition 1. 

The proof is similar to that in the work of Josa-Fombellida and Rincón-Zapatero (2010), so it is omitted here. □

2.2. The Financial Market

We assume that the nominal instantaneous interest rate follows the Vasicek model, which satisfies the stochastic differential equation (henceforth SDE):

$$dr\left(t\right)=(a-br\left(t\right))dt+{\sigma }_{r}d{W}_r\left(t\right),$$

(4)

with initial value $r\left(0\right)=r_0$, where $W_r$ is a standard Brownian Motion under $\mathbb{P}$, and a, b and ${\sigma }_r$ are all positive constants. In the context of this work, we assume that $W_r$ is correlated with $W_P$ and the correlation coefficient is $\rho$, since inflation has effects on both interest rate and salary, and $P\left(t\right)$ is usually related to the salary at the moment of retirement.

Now, we define $W_0\left(t\right)$ such that

$$d{W}_P\left(t\right)=\rho \left(t\right)d{W}_r\left(t\right)+\sqrt{1-{\rho }^2\left(t\right)}d{W}_0\left(t\right),$$

with $W_0\left(0\right)=0$. Thus, $W_r$ and $W_0$ are independent Brownian motions transforming Equations (1) and (3) into the following forms:

$$dP\left(t\right)={\mu }_{P}P\left(t\right)dt+{\sigma }_P\left[\rho \left(t\right)d{W}_r\left(t\right)+\sqrt{1-{\rho }^2\left(t\right)}d{W}_0\left(t\right)\right],$$

$$dAL\left(t\right)=\left[{\mu }_P+{\displaystyle \frac{{\xi }_{AL}\left(t\right)}{{\psi }_{AL}\left(t\right)}}\right]AL\left(t\right)dt+{\sigma }_{P}AL\left(t\right)\left[\rho \left(t\right)d{W}_r\left(t\right)+\sqrt{1-{\rho }^2\left(t\right)}d{W}_0\left(t\right)\right].$$

(5)

We assume that there are three continuously tradable and perfectly divisible underlying instruments in the financial market. Moreover, we suppose that borrowing and short-selling are permitted.

a. A risk-less asset $S_0\left(t\right)$ is modeled by

$${\displaystyle \frac{d{S}_0\left(t\right)}{S_0\left(t\right)}}=r\left(t\right)dt,$$

(6)

with $S_0\left(0\right)=1$.

b. A zero-coupon bond (or a T-bond) pays one dollar at its expiration time $T_0$ which can be thought of as a derivative of interest rate. Its value $B(t,T_0)$ at time t can be written as the expected present value of its future cash flow under the equivalent martingale measure $\mathbb{Q}$, under which the present value process, $e^{-{\int }_0^{t}r\left(u\right)du}B(t,T_0)$, is a local martingale:

$$B(t,T_0)={\mathbb{E}}_{\mathbb{Q}}\left\{e^{-{\int }_t^{T_0}r\left(u\right)du}|{\mathcal{F}}_t\right\},$$

where ${\mathbb{E}}_{\mathbb{Q}}$ denotes the expectation with respect to measure $\mathbb{Q}$.

By the martingale property of the discounted process, $e^{-{\int }_0^{t}r\left(u\right)du}B(t,T_0)$, and following the work of Menoncin (2008), we obtain

$$dB(t,T_0)=B(t,T_0)r\left(t\right)dt+{\displaystyle \frac{\partial B(t,T_0)}{\partial r\left(t\right)}}{\sigma }_{r}d{W}_r^{\mathbb{Q}}\left(t\right),$$

with terminal condition $B(T_0,T_0)=1$, where $W_r^{\mathbb{Q}}\left(t\right)$ is a standard Brownian motion under measure $\mathbb{Q}$. By the Girsanov theorem, we have $d{W}_r^{\mathbb{Q}}\left(t\right)={\zeta }_{r}dt+d{W}_r\left(t\right)$, where ${\zeta }_r$ is the market price for interest rate risk. The corresponding Radon–Nikodym derivative is $\Lambda \left(T_0\right)=d\mathbb{Q}/d\mathbb{P}=exp[-{\zeta }_r{W}_r\left(T_0\right)-\frac{1}{2}{\zeta }_r^2{T}_0]$. Consequently, we have the SDE of $B(t,T_0)$ under physical measure $\mathbb{P}$:

$${\displaystyle \frac{dB(t,T_0)}{B(t,T_0)}}=(r\left(t\right)+{\nabla }_r^B{\sigma }_r{\zeta }_r)dt+{\nabla }_r^B{\sigma }_{r}d{W}_r\left(t\right),$$

where ${\nabla }_r^B=\frac{\partial B(t,T_0)}{\partial r\left(t\right)}\frac{1}{B(t,T_0)}$ is the semi-elasticity of bond price $B(t,T_0)$ with respect to interest rate r. ${\nabla }_r^B$ is negative because bond price usually negatively reacts to fluctuates in interest rate. It has an explicit form of $\frac{e^{-b(T-t)}-1}{b}$ under the Vasicek model given by Equation (4). Thus, ${\zeta }_r$ is negative, because the bond has positive premium compared with the bank account.

Remark 3. 

The explicit formula of the zero-coupon bond process ${\left(B(t,T_0)\right)}_{t\in [0,T_0]}$ with Vasicek’s interest rates is $B(t,T_0)=A_1(t,T_0)e^{-A_2(t,T_0)r\left(t\right)}$, with

$$A_1(t,T_0)=exp\left\{\left[{\displaystyle \frac{a}{b}}-{\displaystyle \frac{{\sigma }_r^2}{2b^2}}\right]\left[A_2(T_0-t)-(T_0-t)\right]-{\displaystyle \frac{{\sigma }_r^2}{4b}}{A}_2{(t,T_0)}^2\right\},$$

and

$$A_2(t,T_0)={\displaystyle \frac{1}{b}}\left(1-e^{-b(T_0-t)}\right).$$

c. A longevity-indexed bond is defined with the same terminal time $T_0$, from which the investor can obtain $l_{T_0}/l_t$ at the maturity time, where $l_t$ is the amount of people of a given population (whose ages are all x at initial time 0) who have survived from time 0 to time t. By the fundamental theorem of asset pricing, we obtain the price of the longevity bond at time t:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill L(t,T_0)& =& {\mathbb{E}}_{\mathbb{Q}}\left\{{\displaystyle \frac{l_{T_0}}{l_t}}{e}^{-{\int }_t^{T_0}r\left(u\right)du}|{\mathcal{F}}_t\right\}={\mathbb{E}}_{\mathbb{Q}}\left\{T_0-t{p}_{x+t}{e}^{-{\int }_t^{T_0}r\left(u\right)du}|{\mathcal{F}}_t\right\}\hfill \\ \hfill & =& {\mathbb{E}}_{\mathbb{Q}}\left\{e^{-{\int }_t^{T_0}\lambda \left(u\right)du}{e}^{-{\int }_t^{T_0}r\left(u\right)du}|{\mathcal{F}}_t\right\}=e^{-{\int }_t^{T_0}\lambda \left(u\right)du}B(t,T_0).\hfill \end{array}\end{array}$$

Following Zhang (2018), we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dL(t,T_0)}{L(t,T_0)}}& =& \lambda \left(t\right)dt+{\displaystyle \frac{dB(t,T_0)}{B(t,T_0)}}\hfill \\ \hfill & =& (\lambda \left(t\right)+r\left(t\right)+{\nabla }_r^B{\sigma }_r{\zeta }_r)dt+{\nabla }_r^B{\sigma }_{r}d{W}_r\left(t\right)\hfill \end{array}$$

(7)

with terminal condition $L(T_0,T_0)=1$. Thus, we obtain a correlation between the prices of a longevity bond and a zero-coupon bond.

Remark 4. 

If we set $\lambda =0$, the SDE of the longevity bond degenerates to the SDE of the zero-coupon bond; thus, the latter can serve as a special case of the former.

Remark 5. 

The market may also consist of stocks or other kind of assets, but the purpose of this work is to investigate the behavior of the longevity bond in solvency risk management, so it makes little sense for our problem.

3. DB Pension Fund Management with Investment of the Longevity Bond

In this section, we attempt to find the optimal proportion of fund assets put into a risk-less asset and a longevity-indexed bond in an aggregated DB pension scheme in order to minimize the solvency risk at terminal time $T(T\le T_0)$.

3.1. Risk-Neutral Valuation of Liabilities

As mentioned in Josa-Fombellida and Rincón-Zapatero (2010), it is significant to derive a fair valuation of the liability by a technical rate of actualization, which can be served as a modification of the short interest rate. It is given in Proposition 2.

Proposition 2. 

The instantaneously technical rate of actualization ${\delta }^L$ satisfies:

$${\delta }^L\left(t\right)=r\left(t\right)+{\mu }_P-{\nu }^L\left(t\right)-\lambda \left(t\right),$$

where ${\nu }^L\left(t\right)={\mu }_P-{\zeta }_r{\sigma }_P\rho \left(t\right)-\lambda \left(t\right){\displaystyle \frac{{\sigma }_P\rho \left(t\right)}{{\nabla }_r^B{\sigma }_r}}$.

Proof of Proposition 2. 

The proof is similar to that of Josa-Fombellida and Rincón-Zapatero (2010), so it is omitted. □

3.2. The Wealth Process and Optimization Problem

The pension plan manager invests the fund wealth in a portfolio consisting of risk-less asset $S_0\left(t\right)$, which is given in Equation (6), and longevity-indexed bond $L(t,T_0)$, which is given in Equation (7), in which case the market is complete. The dynamics of returns on the fund process is

$$dF\left(t\right)={\omega }^L\left(t\right)L(t,T_0){\displaystyle \frac{dL(t,T_0)}{L(t,T_0)}}+\left(F\left(t\right)-{\omega }^L\left(t\right)L(t,T_0)\right){\displaystyle \frac{d{S}_0\left(t\right)}{S_0\left(t\right)}}+\left(C\left(t\right)-P\left(t\right)\right)dt,$$

(8)

with initial value $F\left(0\right)=F_0>0$, where ${\omega }^L\left(t\right)$ is the number of the longevity bond held in the portfolio at time t.

Substituting Equations (2), (6) and (7) into Equation (8), we have

$$\begin{array}{ccc}\hfill dF\left(t\right)& =& [F\left(t\right)r\left(t\right)+{\omega }^L\left(t\right)L(t,T_0)\left(\lambda \left(t\right)+{\nabla }_r^B{\sigma }_r{\zeta }_r\right)+\left[{\displaystyle \frac{{\xi }_{AL}\left(t\right)}{{\psi }_{AL}\left(t\right)}}+{\mu }_P-{\delta }^L\left(t\right)-\lambda \left(t\right)\right]AL\left(t\right)\hfill \\ \hfill & & +k\left(AL\left(t\right)-F\left(t\right)\right)]dt+{\omega }^L\left(t\right)L(t,T_0){\nabla }_r^B{\sigma }_{r}d{W}_r\left(t\right),\hfill \end{array}$$

(9)

with consideration of Proposition 2.

Next, we restrict investment strategy ${\omega }^L$ to fulfill some technical conditions:

Definition 2. 

Strategy ${\omega }^L$ is called admissible if the following three conditions are satisfied:

a. ${\omega }^L\left(t\right)$ is progressively measurable with respect to ${\left\{{\mathcal{F}}_t\right\}}_{t\in [0,T_0]}$;

b. $\mathbb{E}\left\{{\displaystyle {\int }_0^T{\left({\omega }^L\left(t\right)L(t,T_0){\nabla }_r^B{\sigma }_r\right)}^{2}dt}\right\}<\infty ;$

c. Equation (9) has a unique strong solution for the initial value $\left(0,F_0,A{L}_0,r_0\right)$.

The set of all admissible controls is denoted by Π.

By setting $X=F-AL$ and inserting Equation (5) into $dX$, we have

$$\begin{array}{ccc}\hfill dX\left(t\right)& =& \left[(r-k)X\left(t\right)+\left(r-{\delta }^L\left(t\right)-\lambda \left(t\right)\right)AL\left(t\right)+{\omega }^L\left(t\right)L(t,T_0)\left(\lambda \left(t\right)+{\nabla }_r^B{\sigma }_r{\zeta }_r\right)\right]dt\hfill \\ \hfill & & +\left[{\omega }^L\left(t\right)L(t,T_0){\nabla }_r^B{\sigma }_r-{\sigma }_P\rho \left(t\right)AL\left(t\right)\right]d{W}_r\left(t\right)-{\sigma }_P\sqrt{1-{\rho }^2\left(t\right)}AL\left(t\right)d{W}_0\left(t\right),\hfill \end{array}$$

(10)

with initial condition $X\left(0\right)=F_0-A{L}_0\triangleq X_0$.

The preference of the pension fund sponsor is to minimize the terminal solvency risk. The objective function is given by

$$J((X_0,A{L}_0,r_0);{\omega }^L)={\mathbb{E}}_{X_0,A{L}_0,r_0}{X}^2\left(T\right).$$

The dynamic programming approach is used to solve the problem. We denote

$$V(t,X,AL,r)=\underset{\left\{{\omega }^L\in \Pi \right\}}{min}\left\{J((t,X,AL,r);{\omega }^L): \mathrm{subject} \mathrm{to}\left(10\right),\left(5\right),\left(4\right)\right\}$$

as the value function of this optimization problem, which is non-negative and strictly convex (which is shown in Appendix A). In optimal control problem, value function and optimal investment strategy can be obtained by solving the corresponding HJB equation; see Fleming and Soner (1993) or Yong and Zhou (1999):

$$\begin{array}{c}\hfill \underset{\left\{{\omega }^L\in \Pi \right\}}{min}\Psi \left({\omega }^{L}L\right)=0,\end{array}$$

(11)

where

$$\begin{array}{ccc}\hfill \Psi \left({\omega }^{L}L\right)=& & V_t+\left[(r-k)X+(r-{\delta }^L-\lambda )AL+{\omega }^{L}L(\lambda +{\nabla }_r^B{\sigma }_r{\zeta }_r)\right]V_X+\left[{\displaystyle \frac{{\xi }_{AL}}{{\psi }_{AL}}}+{\mu }_P\right]AL{V}_{AL}+(a-br)V_r\hfill \\ \hfill & & +{\displaystyle \frac{1}{2}}\left[{({\omega }^{L}L{\nabla }_r^B{\sigma }_r-{\sigma }_P\rho AL)}^2+{\sigma }_P^2(1-{\rho }^2)A{L}^2\right]V_{XX}+{\displaystyle \frac{1}{2}}{\sigma }_P^{2}A{L}^2{V}_{AL,AL}+{\displaystyle \frac{1}{2}}{{\sigma }_r}^2{V}_{rr}\hfill \\ \hfill & & +\left[{\omega }^{L}L{\nabla }_r^B{\sigma }_r{\sigma }_P\rho AL-{\sigma }_P^{2}A{L}^2\right]V_{X,AL}+{\sigma }_r({\omega }^{L}L{\nabla }_r^B{\sigma }_r-{\sigma }_P\rho AL)V_{X,r}+{\sigma }_r{\sigma }_P\rho AL{V}_{AL,r}=0,\hfill \end{array}$$

(12)

with

$$\begin{array}{c}\hfill V(T,X,AL,r)=X^2,\end{array}$$

(13)

where $V_t$, $V_X$, $V_{AL}$, $V_r$, $V_{XX}$, $V_{AL,AL}$, $V_{rr}$, $V_{X,AL}$, $V_{X,r}$ and $V_{AL,r}$ are the first- and second-order partial derivatives of V with respect to t, X, $AL$ and r, respectively.

${\omega }^{L}L$ is the amount invested in the longevity-indexed bond. Then, $\underset{\left\{{\omega }^L\in \Pi \right\}}{min}\Psi \left({\omega }^{L}L\right)$ can be obtained by utilizing the following two necessary conditions satisfied by the optimal amount ${{\omega }^L}^{*}L$:

$$\begin{array}{ccc}\hfill & & \Psi \left({{\omega }^L}^{*}L\right)=0,\hfill \\ \hfill & & {\displaystyle \frac{d\Psi }{d\left({\omega }^{L}L\right)}}\left({{\omega }^L}^{*}L\right)=0.\hfill \end{array}$$

The optimal investment amount ${{\omega }^L}^{*}L$ in terms of derivatives of the value function is given by

$$\begin{array}{c}\hfill {{\omega }^L}^{*}L=-\left[{\displaystyle \frac{\lambda }{{{\nabla }_r^B}^2{{\sigma }_r}^2}}+{\displaystyle \frac{{\zeta }_r}{{\nabla }_r^B{\sigma }_r}}\right]{\displaystyle \frac{V_X}{V_{XX}}}-{\displaystyle \frac{{\sigma }_P\rho AL}{{\nabla }_r^B{\sigma }_r}}{\displaystyle \frac{V_{X,AL}}{V_{XX}}}-{\displaystyle \frac{1}{{\nabla }_r^B}}{\displaystyle \frac{V_{X,r}}{V_{XX}}}+{\displaystyle \frac{{\sigma }_P\rho AL}{{\nabla }_r^B{\sigma }_r}}.\end{array}$$

(14)

Substituting Equation (14) into Equations (11) and (12), we finally obtain the explicit form of the optimal investment strategy and the minimized solvency risk. The results are shown in the following theorem.

Theorem 1. 

We denote the value function by $V(t,X,AL,r)\triangleq V^L(t,X,AL,r)$ and let $\tau \le T$. The minimum terminal solvency risk is given by

$${\displaystyle V^L(t,X,AL,r)=g^L\left(t\right)e^{{\gamma }^L\left(t\right)r}·X^2+\left[{\int }_t^T{\epsilon }^L(t;\tau )e^{{\eta }^L(t;\tau )r}d\tau \right]{AL}^2.}$$

(15)

The optimal investment strategy is

$${{\omega }^L}^{*}L\left(t\right)=-\left[{\displaystyle \frac{\lambda }{{{\nabla }_r^B}^2{{\sigma }_r}^2}}+{\displaystyle \frac{{\zeta }_r}{{\nabla }_r^B{\sigma }_r}}-{\displaystyle \frac{2}{b}}\left[1-e^{-b(T-t)}\right]{\displaystyle \frac{1}{{\nabla }_r^B}}\right]X+{\displaystyle \frac{{\sigma }_P\rho }{{\nabla }_r^B{\sigma }_r}}AL,$$

(16)

where

$$\begin{array}{ccc}\hfill {\gamma }^L\left(t\right)& =& \frac{2}{b}(1-e^{-b(T-t)});\hfill \\ \hfill g^L\left(t\right)& =& e^{{\int }_t^T{h}^L\left(s\right)ds};\hfill \\ \hfill h^L\left(t\right)& =& -2k-\frac{{(\lambda +{\nabla }_r^B{\sigma }_r{\zeta }_r)}^2}{{{\nabla }_r^B}^2{{\sigma }_r}^2}+\left[a-2{\sigma }_r\left(\frac{\lambda }{{\nabla }_r^B{\sigma }_r}+{\zeta }_r\right)\right]{\gamma }^L\left(t\right)-\frac{1}{2}{{\sigma }_r}^2{{\gamma }^L}^2\left(t\right);\hfill \\ \hfill {\eta }^L(t;\tau )& =& {\gamma }^L\left(\tau \right)e^{-b(\tau -t)};\hfill \\ \hfill {\epsilon }^L(t;\tau )& =& {\sigma }_P^2(1-{\rho }^2)g^L\left(\tau \right)e^{{\int }_t^{\tau }{y}^L(s;\tau )ds};\hfill \\ \hfill y^L(t;\tau )& =& 2\left[{\displaystyle \frac{{\xi }_{AL}}{{\psi }_{AL}}}+{\mu }_P\right]+{\sigma }_P^2+\left(a+2{\sigma }_r{\sigma }_P\rho \right){\eta }^L(t;\tau )+{\displaystyle \frac{1}{2}}{\sigma }_r^2{{\eta }^L}^2(t;\tau ).\hfill \end{array}$$

(17)

Proof. 

See Appendix A. □

Remark 6. 

Note that short-selling is permitted in the context. From Equation (16), ${{\omega }^L}^{*}L\left(t\right)$ might be negative. This may occur when $X\left(t\right)$ is positive, i.e., the pension is overfunded. On one hand, longevity bonds can be used to hedge longevity risks according to Cox et al. (2013), but perhaps it is unnecessary to hedge this kind of risk when it is overfunded. On the other hand, a longevity bond is a kind of risky asset itself. When funds are much larger than liabilities, the pension sponsor may attempt to hold more bank account, say, more that 100% since there is no constraint in the market, thus the amount held in the longevity bond might be negative.

Substituting the optimal investment strategy ${{\omega }^L}^{*}L\left(t\right)$ into $X\left(t\right)$, we obtain the corresponding $X^{*}\left(t\right)$. Here, we offer a possible path of ${{\omega }^L}^{*}L\left(t\right)$ and $X^{*}\left(t\right)$ in Figure 1 and Figure 2, respectively.

4. Special Case: DB Pension Fund Management with Investment of Zero-Coupon Bond

This section considers a similar optimal problem with an absent mortality rate, i.e., $\lambda \equiv 0$, which makes the dynamic of the longevity-indexed bond degenerates to the dynamic of a normal zero-coupon bond. Compared with the work of Josa-Fombellida and Rincón-Zapatero (2010), we find the explicit form of the value function. Here, we abuse the notation $F\left(t\right)$ to represent the pension wealth at time t. The market consisting of a zero-coupon bond and a bank account is again complete. As the counterpart of Proposition 2, we state the technical rate in this special case in Proposition 3 to define a fair liability.

Proposition 3. 

The technical rate of actualization is

$${\delta }^B\left(t\right)=r\left(t\right)+{\mu }_P-{\nu }^B\left(t\right),$$

where ${\nu }^B\left(t\right)={\mu }_P-{\zeta }_r{\sigma }_P\rho \left(t\right)$.

Similarly, the dynamic of the wealth process is

$$\begin{array}{ccc}\hfill dF\left(t\right)& =& {\omega }^B\left(t\right)B(t,T_0){\displaystyle \frac{dB(t,T_0)}{B(t,T_0)}}+\left(F\left(t\right)-{\omega }^B\left(t\right)B(t,T_0)\right){\displaystyle \frac{d{S}_0\left(t\right)}{S_0\left(t\right)}}+\left(C\left(t\right)-P\left(t\right)\right)dt\hfill \\ \hfill & =& \left[\left(r\left(t\right)-k\right)\left(F\left(t\right)-AL\left(t\right)\right)+\left[r\left(t\right)+{\displaystyle \frac{{\xi }_{AL}^B\left(t\right)}{{\psi }_{AL}^B\left(t\right)}}+{\mu }_P-\delta \left(t\right)\right]AL\left(t\right)+{\omega }^B\left(t\right)B(t,T_0){\nabla }_r^B{\sigma }_r{\zeta }_r\right]dt\hfill \\ \hfill & & +{\omega }^B\left(t\right)B(t,T_0){\nabla }_r^B{\sigma }_{r}d{W}_r\left(t\right),\hfill \end{array}$$

with initial value $F\left(0\right)=F_0>0$, where ${\omega }^B$ is the number of the zero-coupon bond held in the portfolio. Here,

$$\begin{array}{ccc}\hfill {\psi }_{AL}^B\left(t\right)& =& {\int }_a^d{e}^{-{\int }_t^{t+d-x}[{\mu }_P-\delta \left(u\right)]du}M\left(x\right)dx,\hfill \\ {\xi }_{AL}^B\left(t\right)& =& {\int }_a^d{e}^{-{\int }_t^{t+d-x}{\mu }_P-\delta \left(u\right)du}\left[{\mu }_P-\delta (t+d-x)\right]M\left(x\right)dx-\left({\mu }_P-\delta \left(t\right)\right){\psi }_{AL}^B\left(t\right).\hfill \end{array}$$

A strategy is called admissible if it satisfies similar conditions in Definition 2, and the set of all admissible controls is again denoted by $\Pi$.

Setting $X=F-AL$, we have

$$\begin{array}{ccc}\hfill dX\left(t\right)& =& \left[(r-k)X\left(t\right)+\left(r-\delta \left(t\right)\right)AL\left(t\right)+{\omega }^B\left(t\right)B(t,T_0){\nabla }_r^B{\sigma }_r{\zeta }_r\right]dt\hfill \\ \hfill & & +\left[{\omega }^B\left(t\right)B(t,T_0){\nabla }_r^B{\sigma }_r-{\sigma }_P\rho \left(t\right)AL\left(t\right)\right]d{W}_r\left(t\right)-{\sigma }_P\sqrt{1-{\rho }^2\left(t\right)}AL\left(t\right)d{W}_0\left(t\right),\hfill \end{array}$$

with $X\left(0\right)=X_0$.

Here, the objective function and the optimal problem are the same as those in Section 3, except that the longevity-indexed bond is changed into a normal zero-coupon bond. Analogously, denoting $V^B(t,X,AL,r)$ as the value function, we offer the optimal results in Theorem 2 without any proof.

Theorem 2. 

We set $\tau \le T$ and denote the value function in Section 4 by $V^B(t,X,AL,r)$. The minimum terminal solvency risk is given by

$$\begin{array}{c}\hfill {\displaystyle V^B(t,X,AL,r)=g^B\left(t\right)e^{{\gamma }^B\left(t\right)r}·X^2+\left[{\int }_t^T{\epsilon }^B(t;\tau )e^{{\eta }^B(t;\tau )r}d\tau \right]{AL}^2.}\end{array}$$

(18)

The optimal investment strategy is

$$\begin{array}{c}\hfill {{\omega }^B}^{*}B\left(t\right)=-\left[{\displaystyle \frac{{\zeta }_r}{{\nabla }_r^B{\sigma }_r}}-{\displaystyle \frac{2}{b}}\left(1-e^{-b(T-t)}\right){\displaystyle \frac{1}{{\nabla }_r^B}}\right]X+{\displaystyle \frac{{\sigma }_P\rho }{{\nabla }_r^B{\sigma }_r}}AL,\end{array}$$

where

$$\begin{array}{ccc}\hfill {\gamma }^B\left(t\right)& =& {\displaystyle \frac{2}{b}}(1-e^{-b(T-t)})={\gamma }^L\left(t\right)\triangleq \gamma \left(t\right);\hfill \\ \hfill g^B\left(t\right)& =& e^{{\int }_t^T{h}^B\left(s\right)ds};\hfill \\ \hfill h^B\left(t\right)& =& -2k-{\zeta }_r^2+(a-2{\sigma }_r{\zeta }_r)\gamma \left(t\right)-{\displaystyle \frac{1}{2}}{{\sigma }_r}^2{\gamma }^2\left(t\right);\hfill \\ \hfill {\eta }^B(t;\tau )& =& {\gamma }^B\left(\tau \right)e^{-b(\tau -t)}={\eta }^L(t;\tau )\triangleq \eta (t;\tau );\hfill \\ \hfill {\epsilon }^B(t;\tau )& =& {\sigma }_P^2(1-{\rho }^2)g^B\left(\tau \right)e^{{\int }_t^{\tau }{y}^B(s;\tau )ds};\hfill \\ \hfill y^B(t;\tau )& =& 2\left[{\displaystyle \frac{{\xi }_{AL}^B}{{\psi }_{AL}^B}}+{\mu }_P\right]+{\sigma }_P^2+(a+2{\sigma }_r{\sigma }_P\rho )\eta (t;\tau )+{\displaystyle \frac{1}{2}}{\sigma }_r^2{\eta }^2(t;\tau ).\hfill \end{array}$$

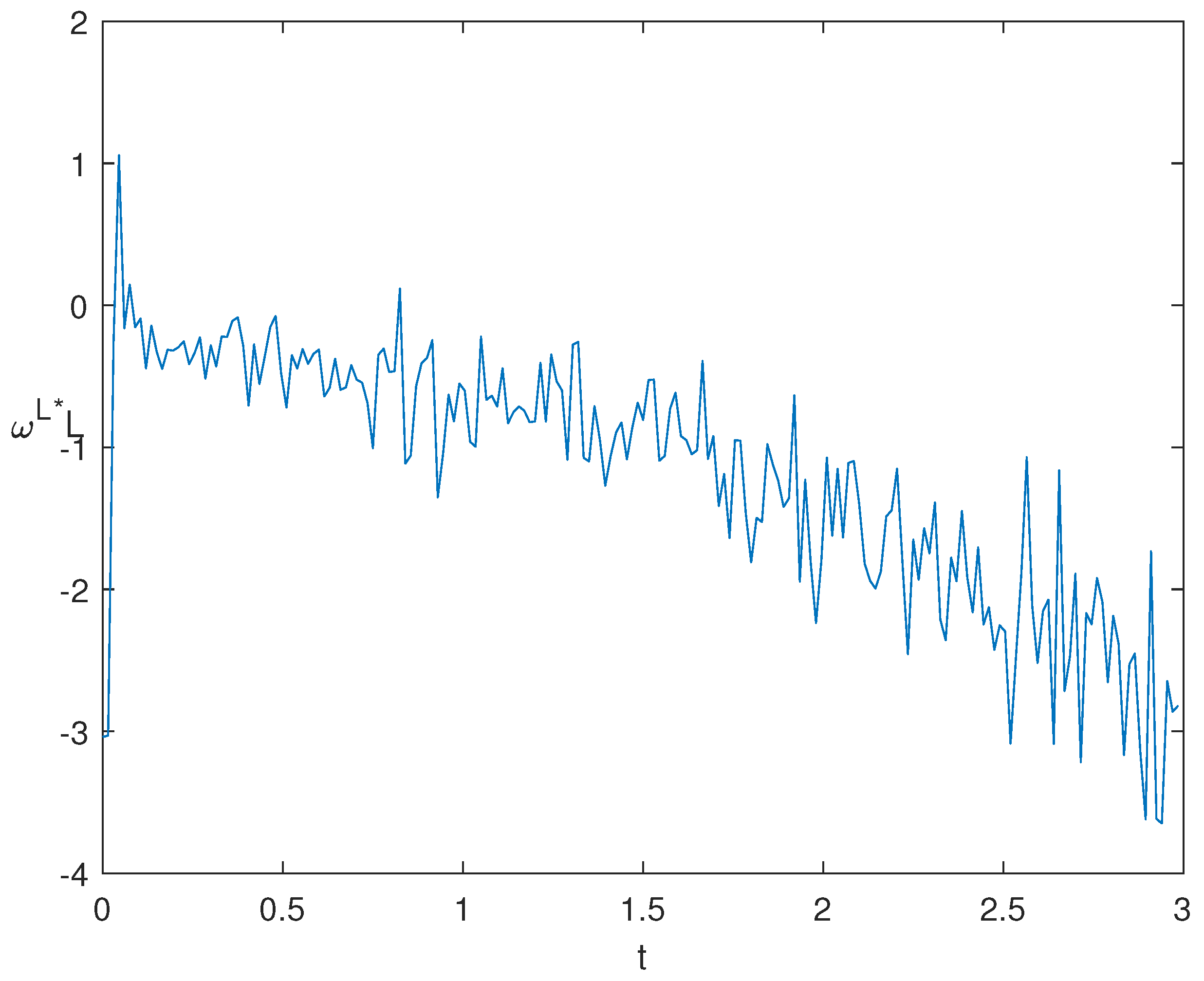
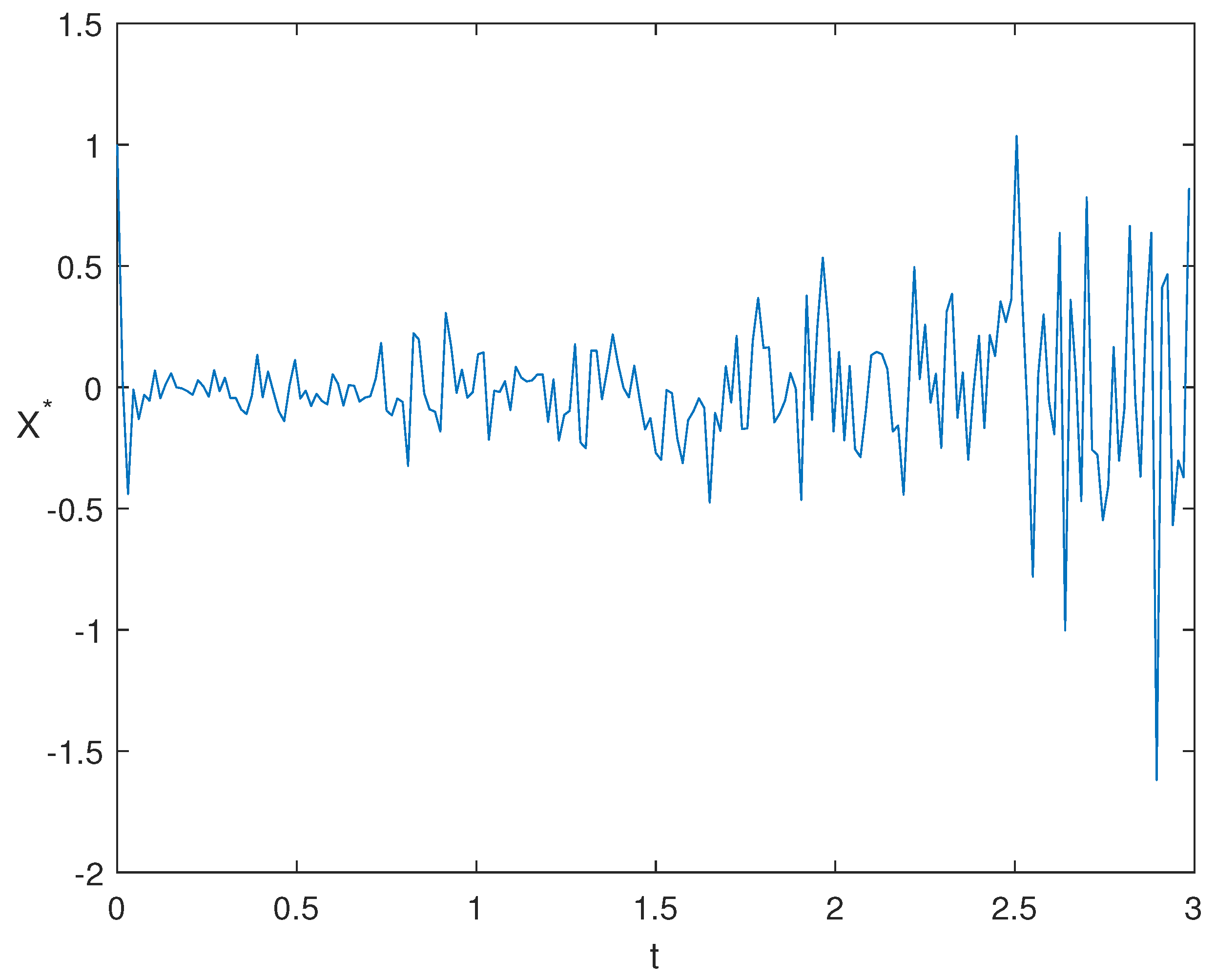
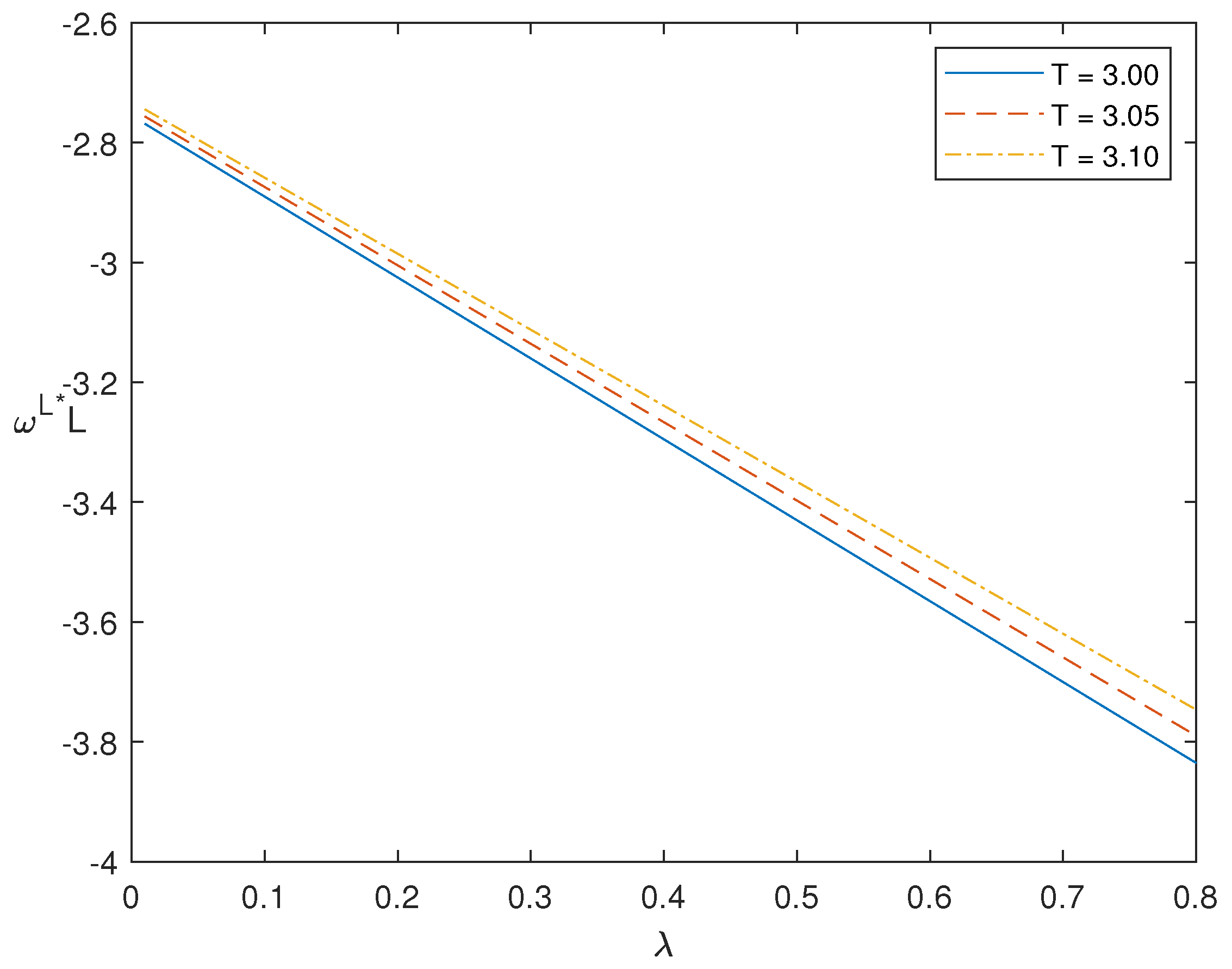
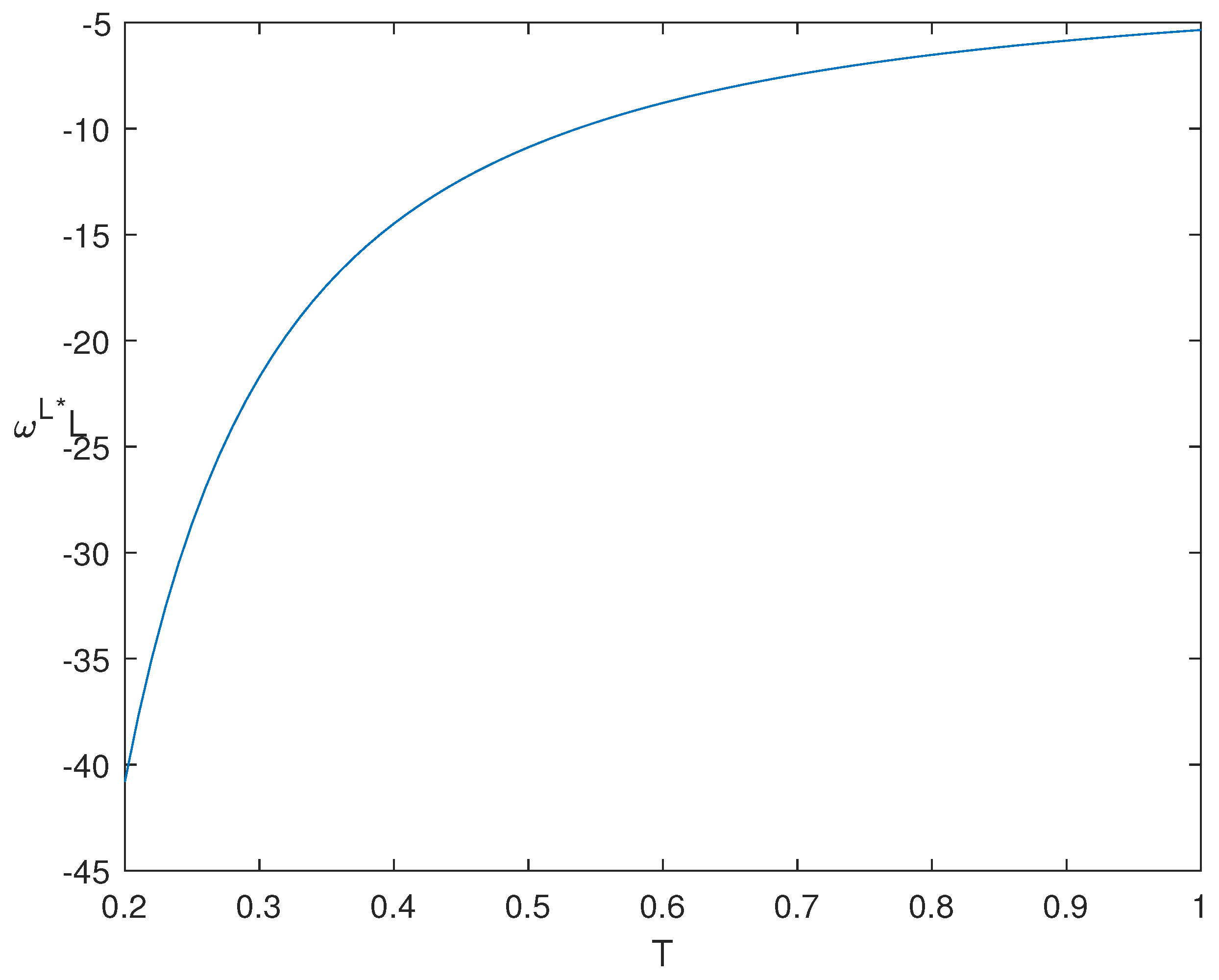
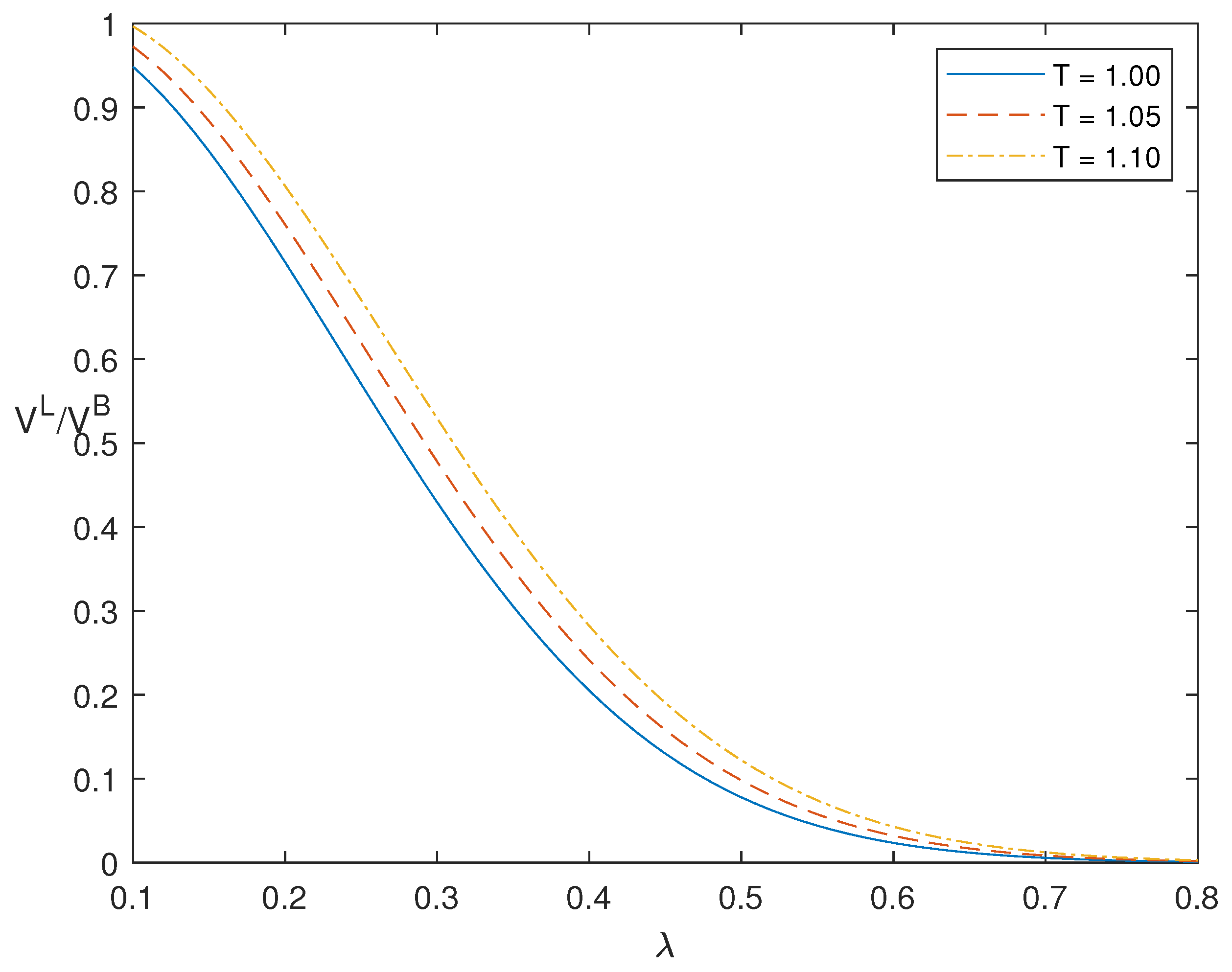
5. Sensitivity Analysis

This section investigates the influence of the employed parameters of the model on optimal control and value function. We mainly explore the impacts of mortality rate $\lambda$ and terminal time T on optimal investment decision ${{\omega }^L}^{*}L$ and value function $V^L$.

In the pension model, $k\in [0,1]$ represents the surplus (or deficit) amortized rate. Here, we choose $0.5$. Parameter ${\sigma }_P(>0)$ is the volatility of benefit, which is $8\%$ in Josa-Fombellida and Rincón-Zapatero (2010). Here, ${\sigma }_P=30\%$, since we try to investigate the influence of the employed parameters under relative high risks. Due to the matching of risks and returns, i.e., appreciation rate growing with volatility increasing, we set ${\mu }_P=0.1$, which is also a bit higher than $0.04$ in Josa-Fombellida and Rincón-Zapatero (2010). Parameter $\rho$ is the correlation coefficient between $W_P$ and $W_r$. In the market, if inflation rate grows, both the nominal interest rate and salary grow, and the promised benefits also grow, since benefits are usually positively correlated with the salary at the moment of retirement. Thus, it is rational to assume that $\rho \in [0,1]$ and here we choose $\rho =0.5$.

In the interest rate model, ${\sigma }_r>0$ is the volatility of interest rate; here, we choose $30\%$ since we attempt to conduct the sensitivity analysis under high risks. Parameter b represents the mean reversion coefficient, while $a/b$ is the long-run mean of interest rate. In the work of Han and Hung (2017), the speed of mean-reversion is 0.0395 and the long-run mean is 0.0369. Here, we choose almost the same speed of mean-reversion, which is 0.03, but a bit higher long-run mean, which is 0.05, since our volatility is also higher than that in Han and Hung (2017). Parameter ${\zeta }_r$ is the market price of interest rate risk, i.e., the bond’s excess return divided by volatility, which should be negative. Theoretically, bonds’ return rate is usually higher than risk-less return rate, for example, $5\%$, and bonds’ volatility should not excess stocks’ volatility. So it is reasonable to assume that, for instance, ${\zeta }_r\in [-0.01,-2]$. The value of ${\zeta }_r$ is $-0.46$ in Menoncin (2008). Here, we choose −0.5 without loss of generality. The parameters are given in

Table 1. Parameters of the model.

${\mathit{X}}_0$	${\mathbf{AL}}_0$	$\mathit{\kappa }$	${\mathit{\mu }}_{\mathit{P}}$	${\mathit{\sigma }}_{\mathit{P}}$	$\mathit{\rho }$	${\mathit{\zeta }}_{\mathit{r}}$	${\mathit{\sigma }}_{\mathit{r}}$	a	b	${\mathit{r}}_0$
1	1	0.5	0.1	0.3	0.5	−0.5	0.3	0.0015	0.03	0.05

.

When the mortality rate is high, the longevity risk is usually low. Likewise, ${{\omega }^L}^{*}L$ might be low because the sponsor may not need a lot of longevity bonds to hedge longevity risk. From another aspect, when the mortality rate is high, the price of longevity bond is low, thus ${{\omega }^L}^{*}L$ might be low, too. To test this point of view, Figure 3 demonstrates the effect of mortality rate $\lambda$ on optimal investment strategy ${{\omega }^L}^{*}L$. When the mortality rate becomes larger, the investment amount becomes smaller. Figure 3 also shows that with the same $\lambda$, ${{\omega }^L}^{*}L$ becomes larger with a longer T. A rational explanation is that the DB pension scheme faces higher risks in the long run, so investment amount in the risky bond (in a short position) becomes smaller in order to reduce risk, which is more clear in Figure 4.

If longevity risk is hedged by the longevity-indexed bond, we may have a lower solvency risk with a lower mortality rate. Figure 5 demonstrates the effect of mortality rate $\lambda$ on value function $V^L$, and it shows that the pension scheme has a lower value function (which means lower solvency risk) with a lower mortality rate (which may cause higher longevity risk). It seems that investments in the longevity bond reduce the solvency risk in a DB pension plan. In addition, Figure 5 also shows that the solvency risk is lower with a smaller $\lambda$ in a longer period. It shows that the hedging strategy is more efficient in the long run.

In addition, if longevity risk is reduced by the longevity bond, we may have a lower solvency risk in the market with the longevity bond than that with a normal zero-coupon bond. $V^L$ and $V^B$ denote the value function in Section 3 (with investment in the longevity bond) and Section 4 (with investment in the zero-coupon bond), respectively. To test this, Figure 6 demonstrates the performance of $V^L/V^B$ with different $\lambda$ values. The ratio $V^L/V^B$ is lower than 1 with $\lambda$ from $0.1$ to $0.8$, implying the solvency risk in Section 3 is lower than that in Section 4.

6. Conclusions

This paper investigates, by means of dynamic programming technique, an optimal control problem for an aggregated DB pension plan in a stochastic interest rate framework. The pension sponsor’s objective is to minimize the terminal solvency risk by managing the fund wealth in finite time horizon through a portfolio comprising a longevity-indexed bond and a risk-less asset. The explicit investment policy is derived by solving the corresponding HJB equation. By replacing the longevity-indexed bond with a normal zero-coupon bond, we find that the value function in the market with a longevity bond is lower than that with a zero-coupon bond, i.e., a longevity bond plays a positive role and has a strategic advantage in hedging solvency risk in such DB pension scheme.

It may be significant to consider the benefit process with the influence of mortality rate in the future, which may generate more realistic sample paths of the benefit. Mortality rate may be stochastic. It is also interesting to consider constrained control variable $\omega \ge 0$, i.e., short-selling is prohibited, which is consistent with some regulations and risk management policies. This makes the value function unsmooth; thus, the technique of viscosity solutions in the dynamic programming approach might be applied. We leave these two points for future study.