COVID-19 and Excess Mortality: An Actuarial Study
Abstract
:1. Introduction
2. Literature Review
3. Methodology
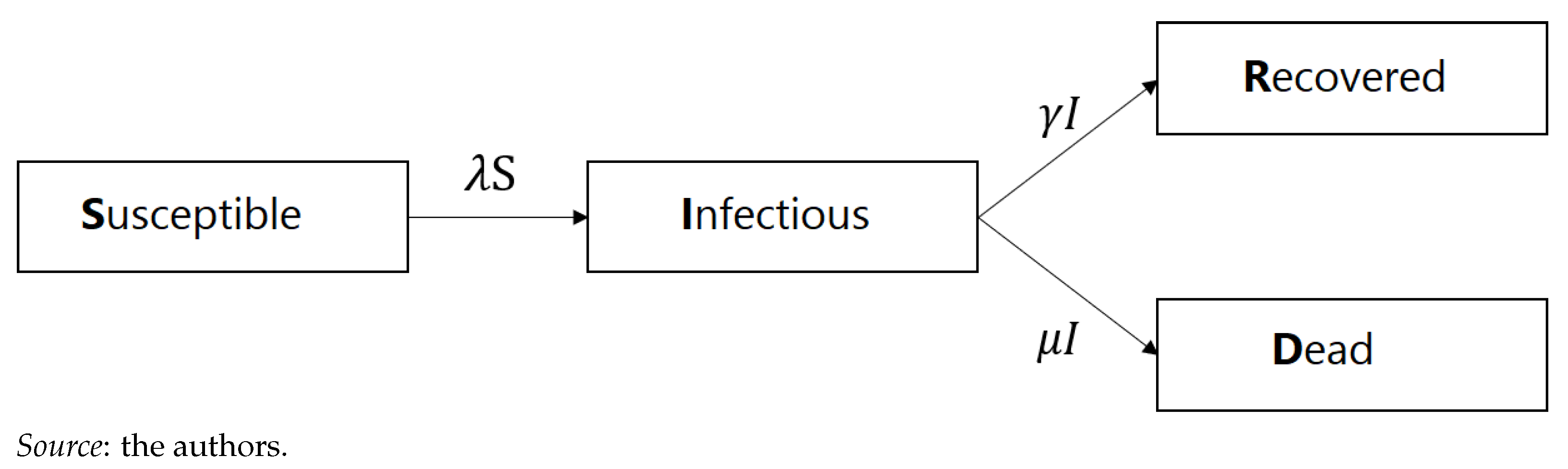
3.1. SIRD Model
- Category 1: Individuals aged 0–24 years;
- Category 2: Individuals aged 25–44 years;
- Category 3: Individuals aged 45–64 years;
- Category 4: Individuals aged 65–74 years;
- Category 5: Individuals aged 75–84 years;
- Category 6: Individuals aged 85+ years.
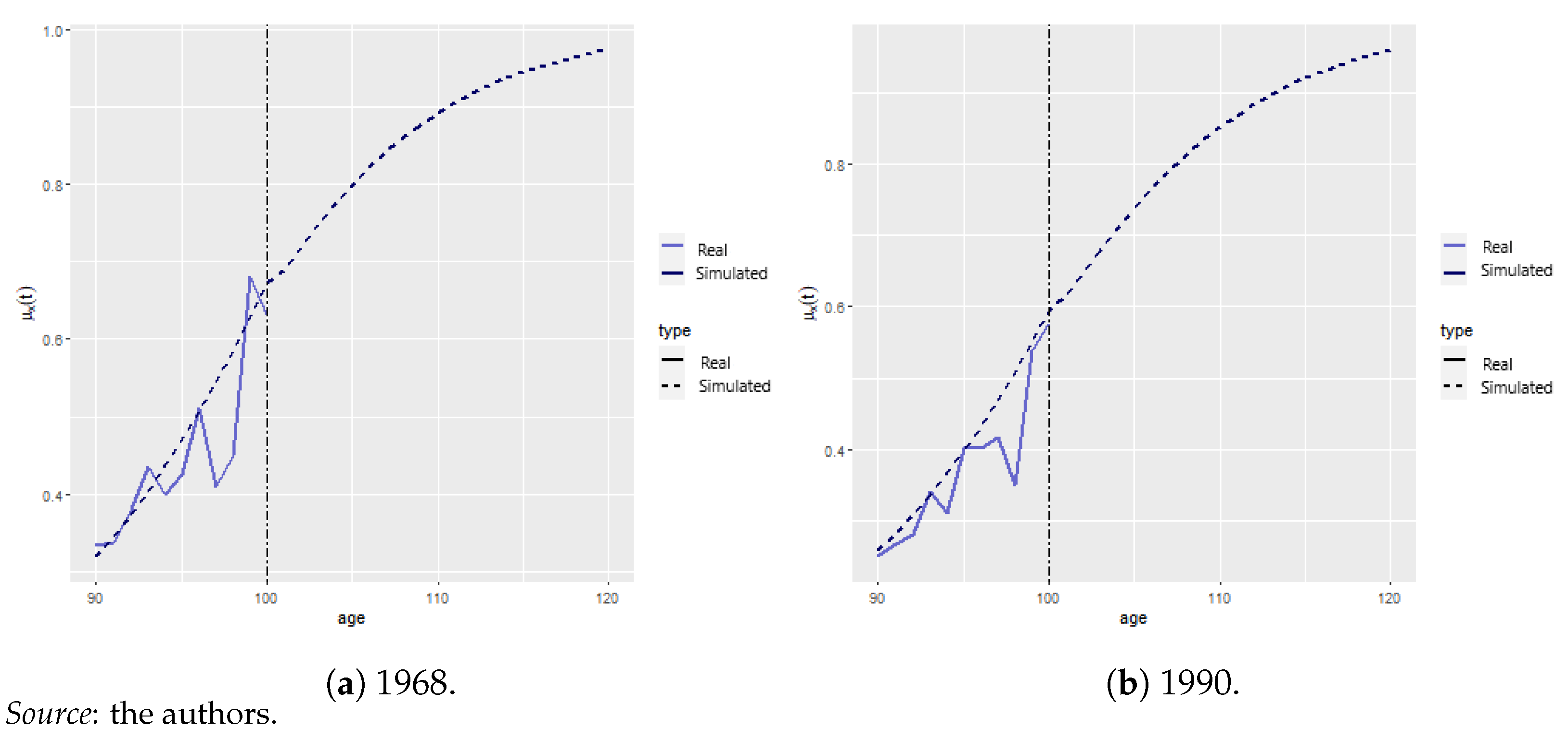
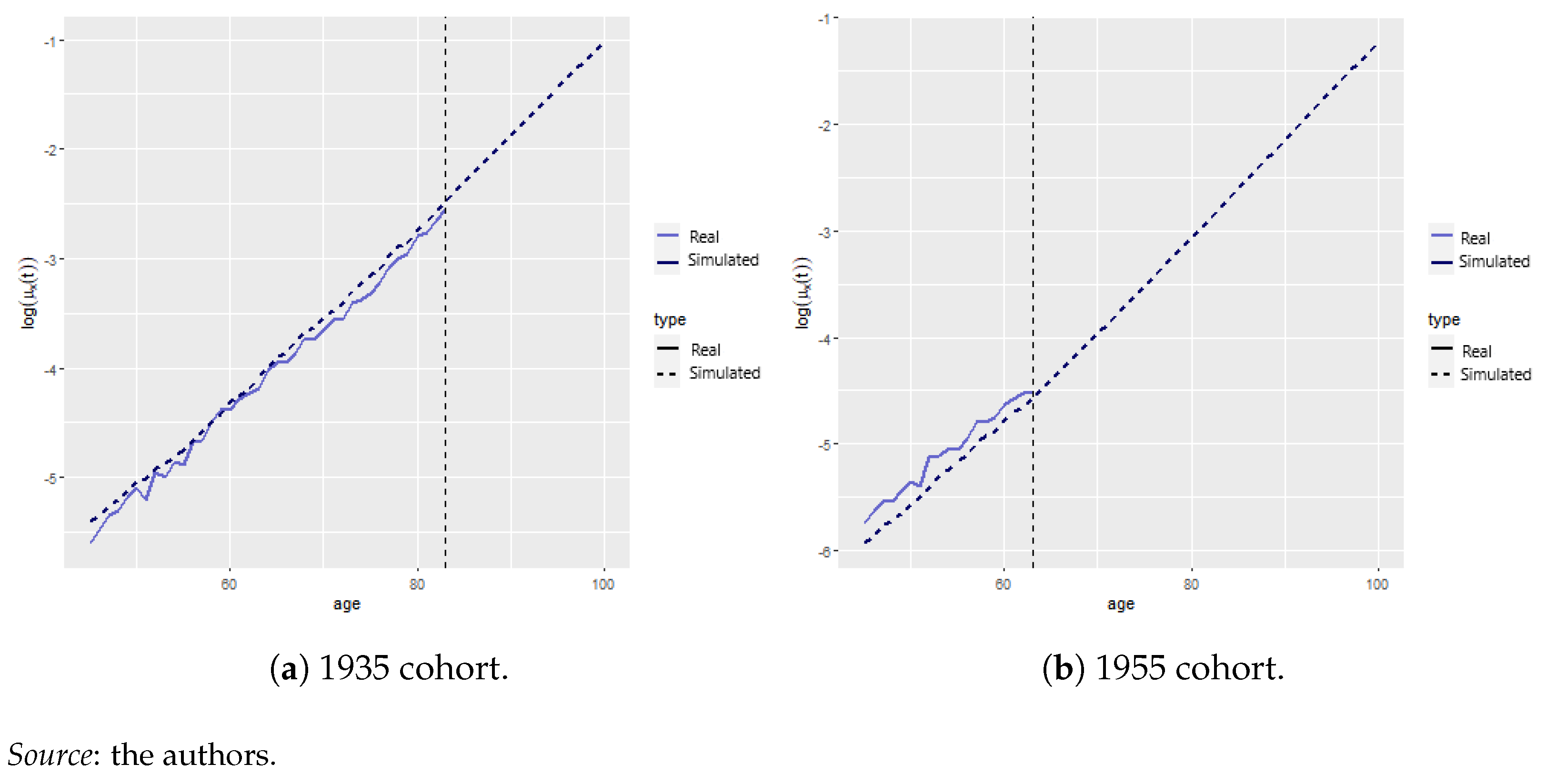
Model Identification
3.2. Cairns, Blake, and Dowd Model
- (intercept) represents the global mortality trend and is generally a decreasing parameter since it improves over time.
- (slope) represents the improvements in mortality and, typically, has a positive slope, indicating that improvements are greater during the first part of the age period considered.
3.3. Final Model
3.4. Actuarial Application
3.4.1. Whole Life Insurance
3.4.2. Life Annuity
4. Numerical Implementation
4.1. Database
4.2. Epidemiological Model
4.2.1. Parameters
- the initial conditions: N, , ;
- the social contract matrix: C;
- COVID-19-related parameters: , , , and .
- corresponds to 1 March 2020, and T corresponds to either for 31 October 2020 for the preliminary model7 and for 31 December 2020 for the model with delay and final model;
- is the daily number of deaths predicted by the model for day, t, and age group, i, given by
- is the real number of daily deaths for time, t, and age group, i.
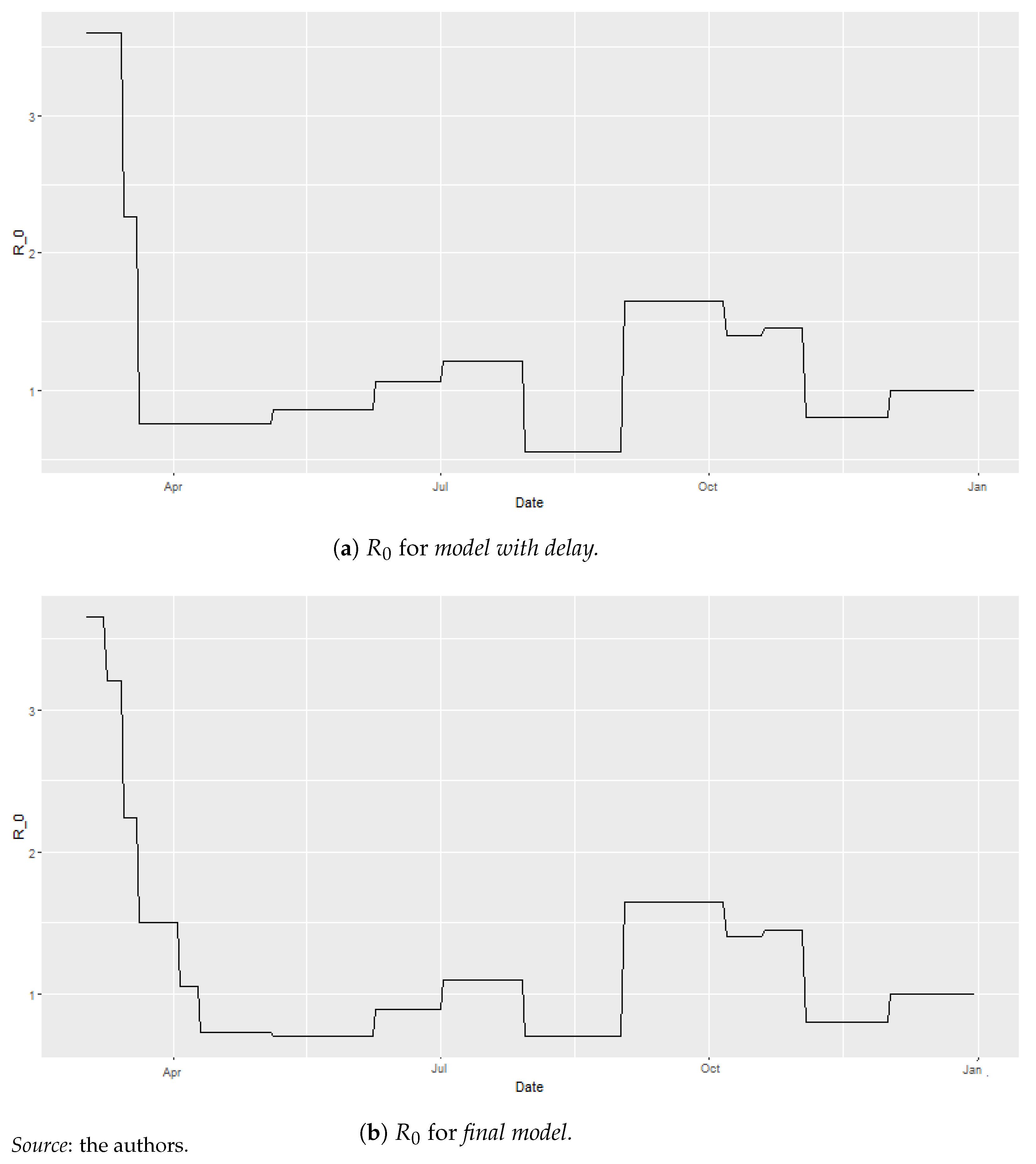
- Model with delay: This model relies on the values that coincide between the two waves but uses , which was estimated for our database;
- Final model: This model relies on the values that differ between the two waves and uses the estimated , which was fine-tuned to the differences observed between the two waves.
- : the Belgian population, as of 1 January 2020 per age category, is given in Table 1:
- : Number of deaths reported until 2 March 2020 (Sciensano 2021);
- : The social contact matrix, which is based on the Socrates tool from Willem et al. (2020);
- : is determined using , according to the following equation:
4.2.2. Preliminary Model
4.2.3. Parameter Calculation
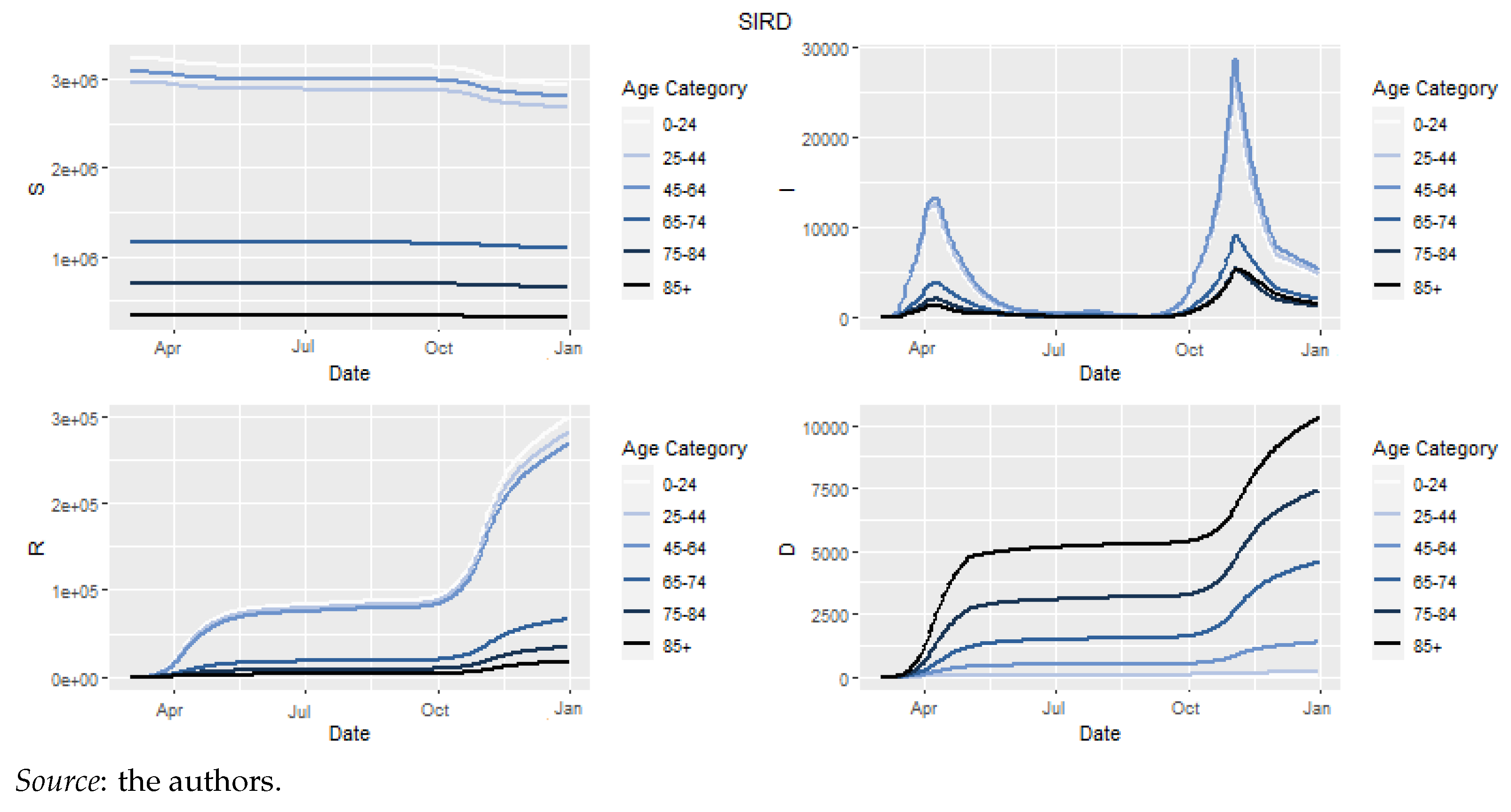
4.2.4. Epidemiological Model: Results
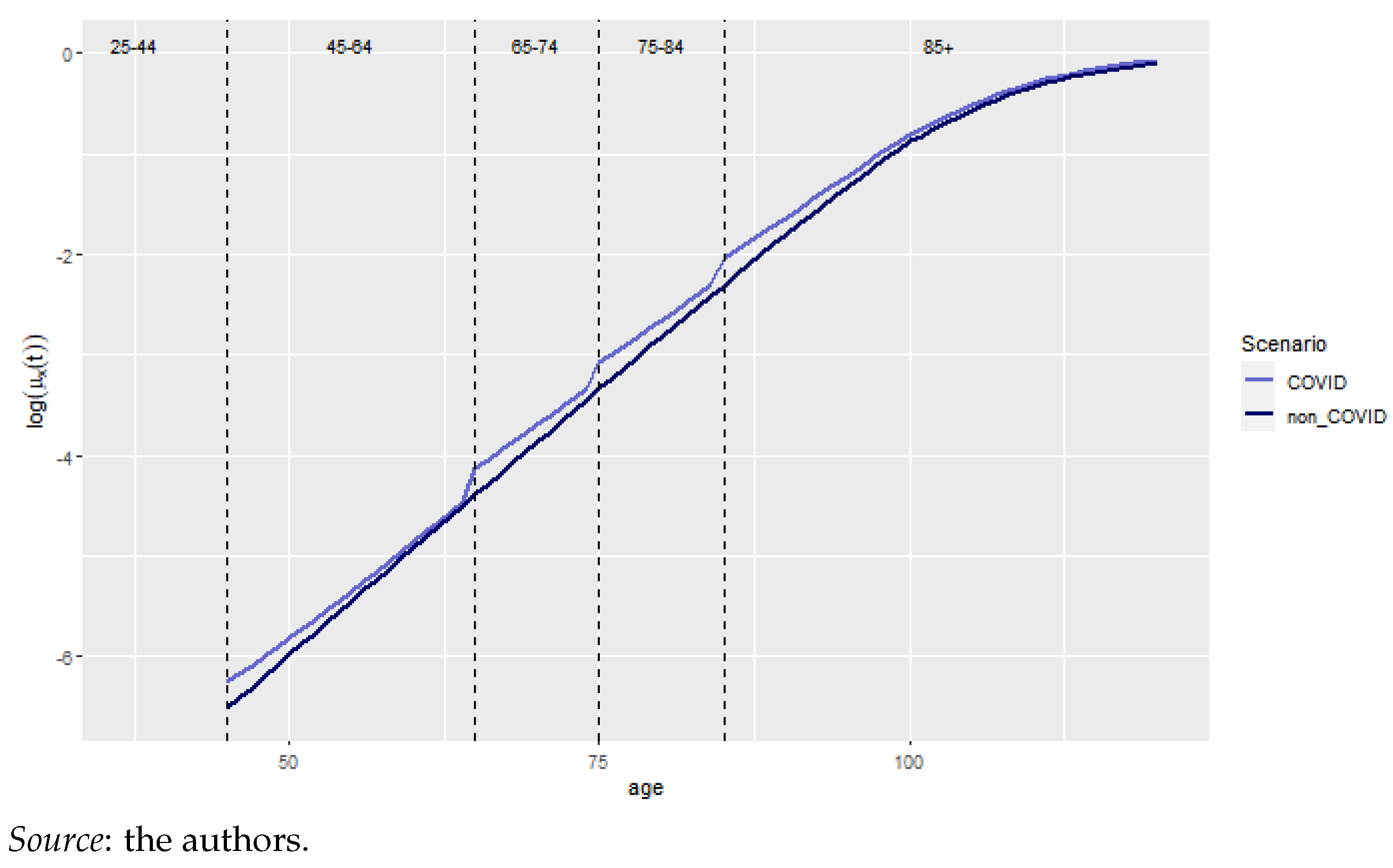
4.3. Cairns-Blake-Dowd Model
4.4. Model Reconciliation
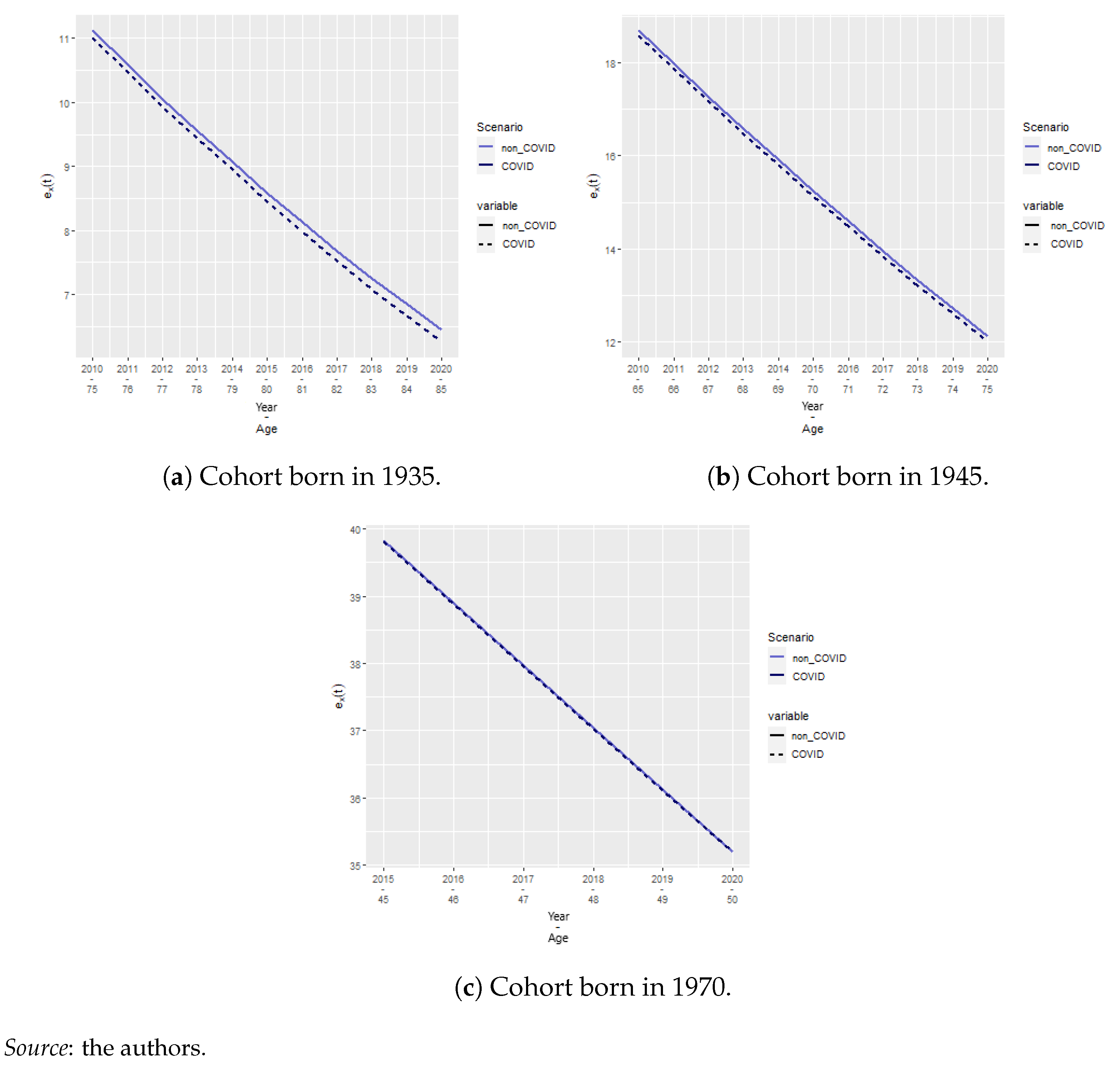
4.5. Actuarial Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Cairns, Blake, and Dowd Estimation and Analysis
Appendix A.1. Estimation
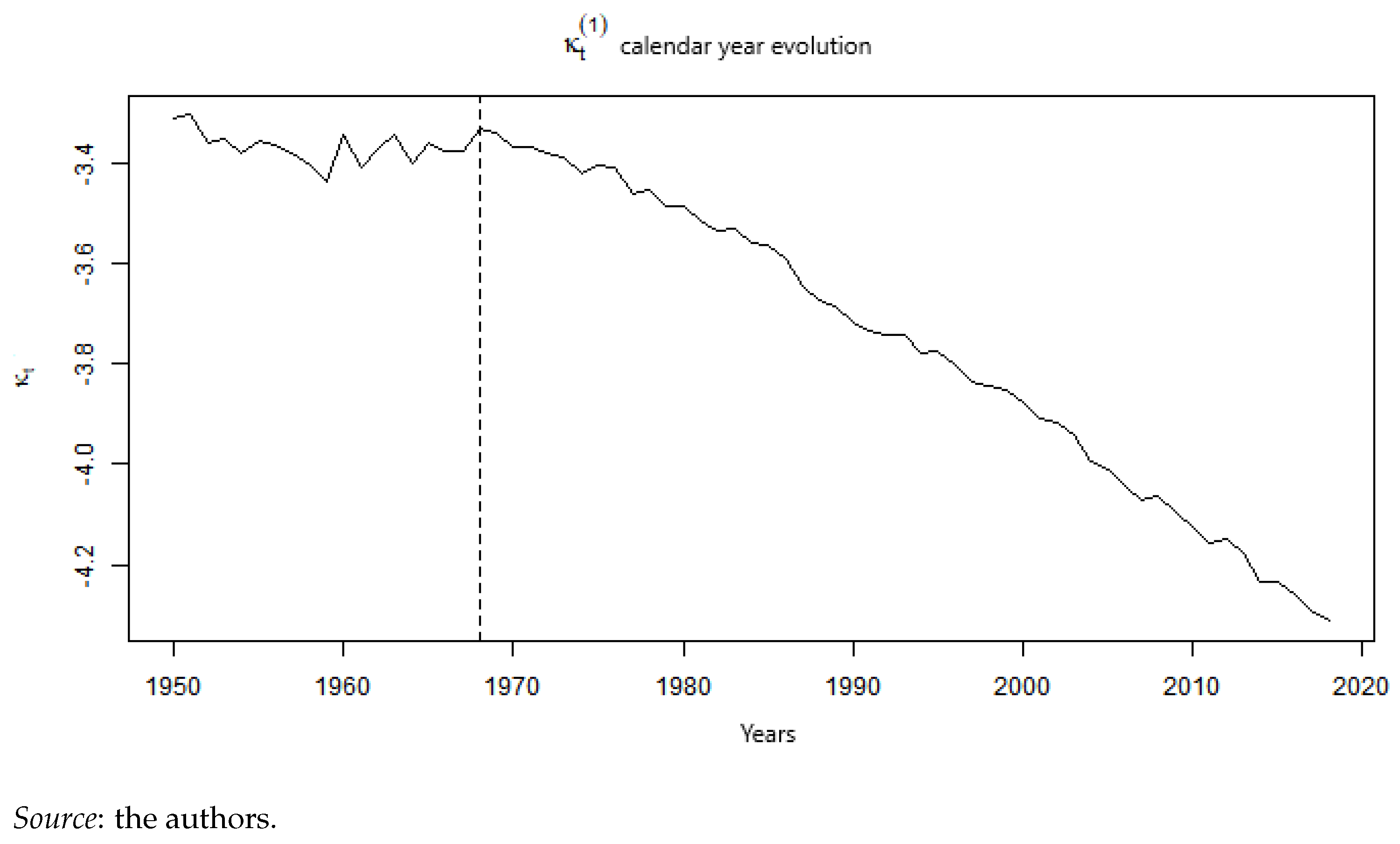
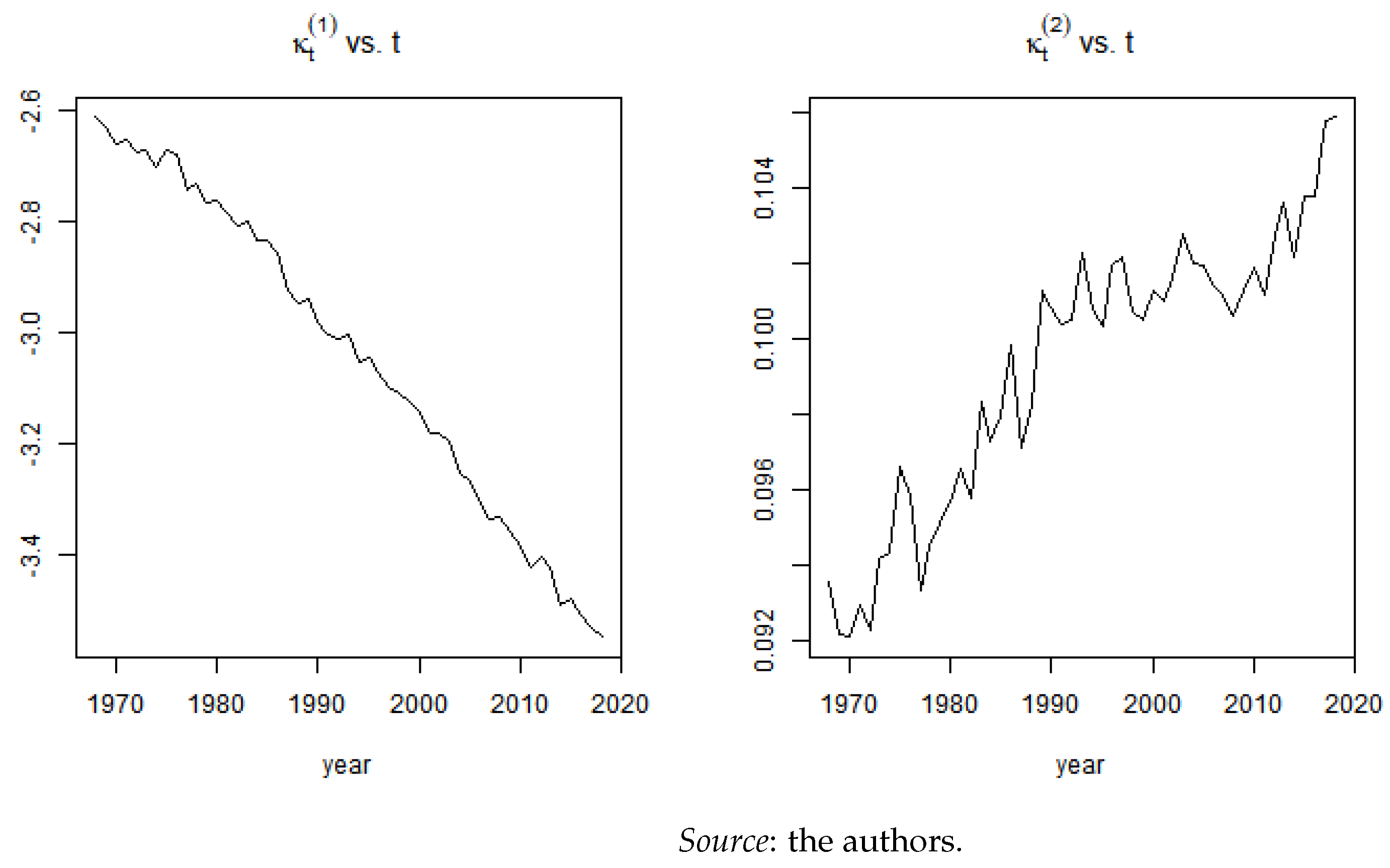
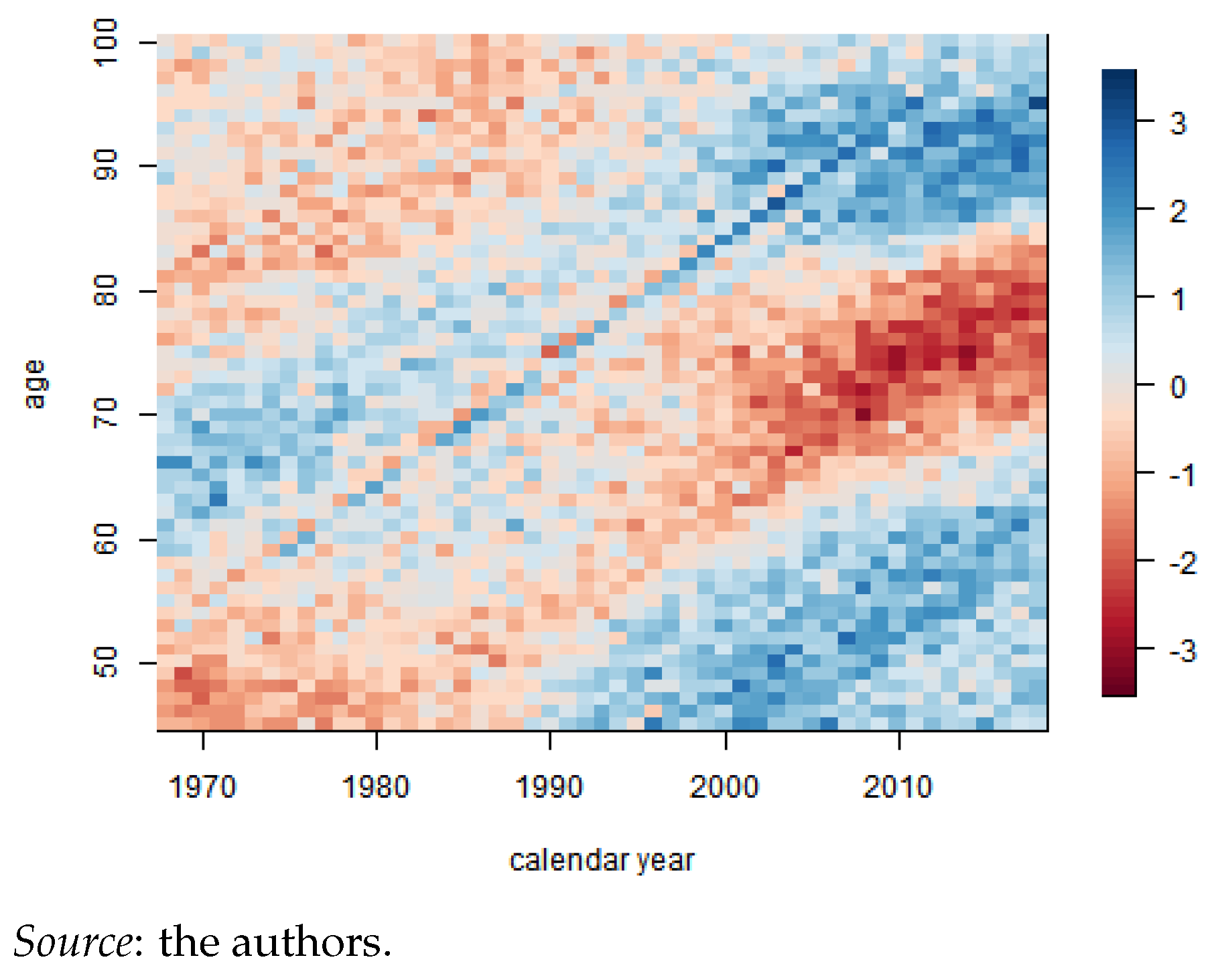
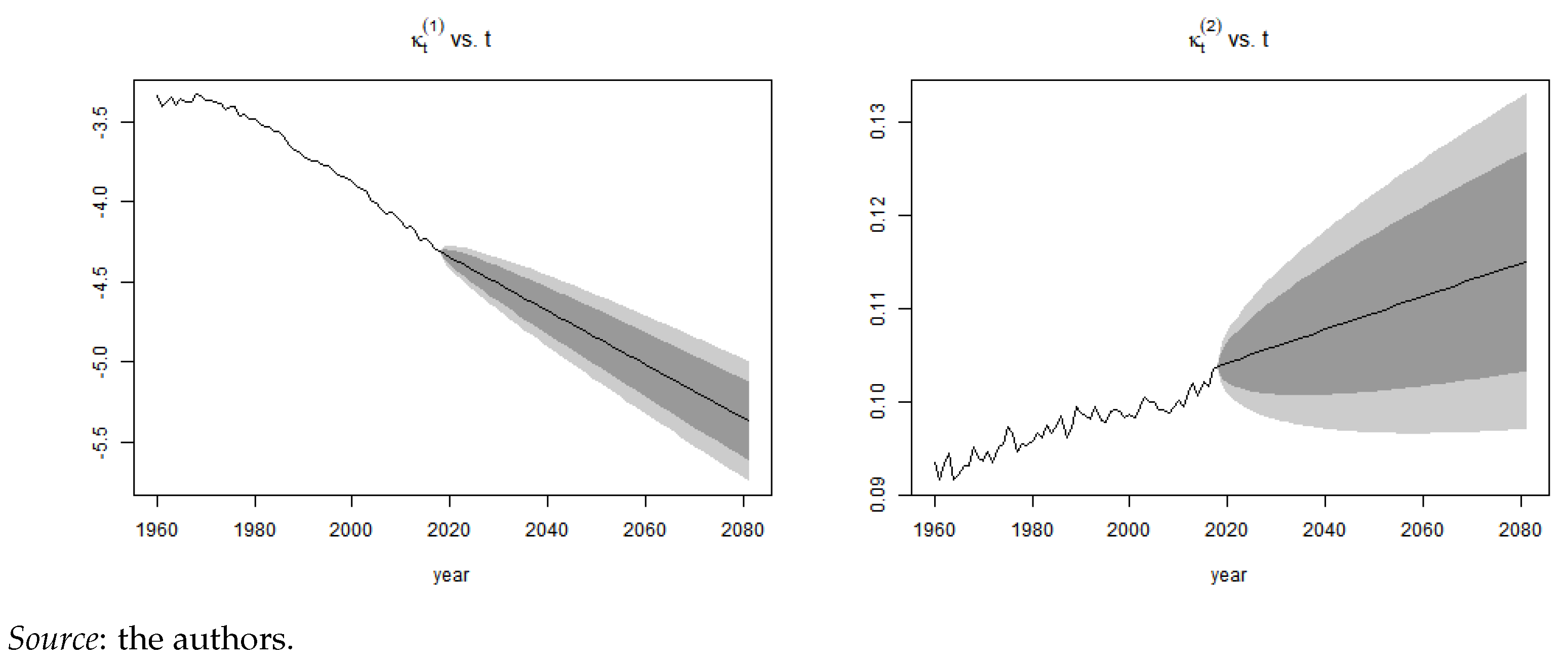
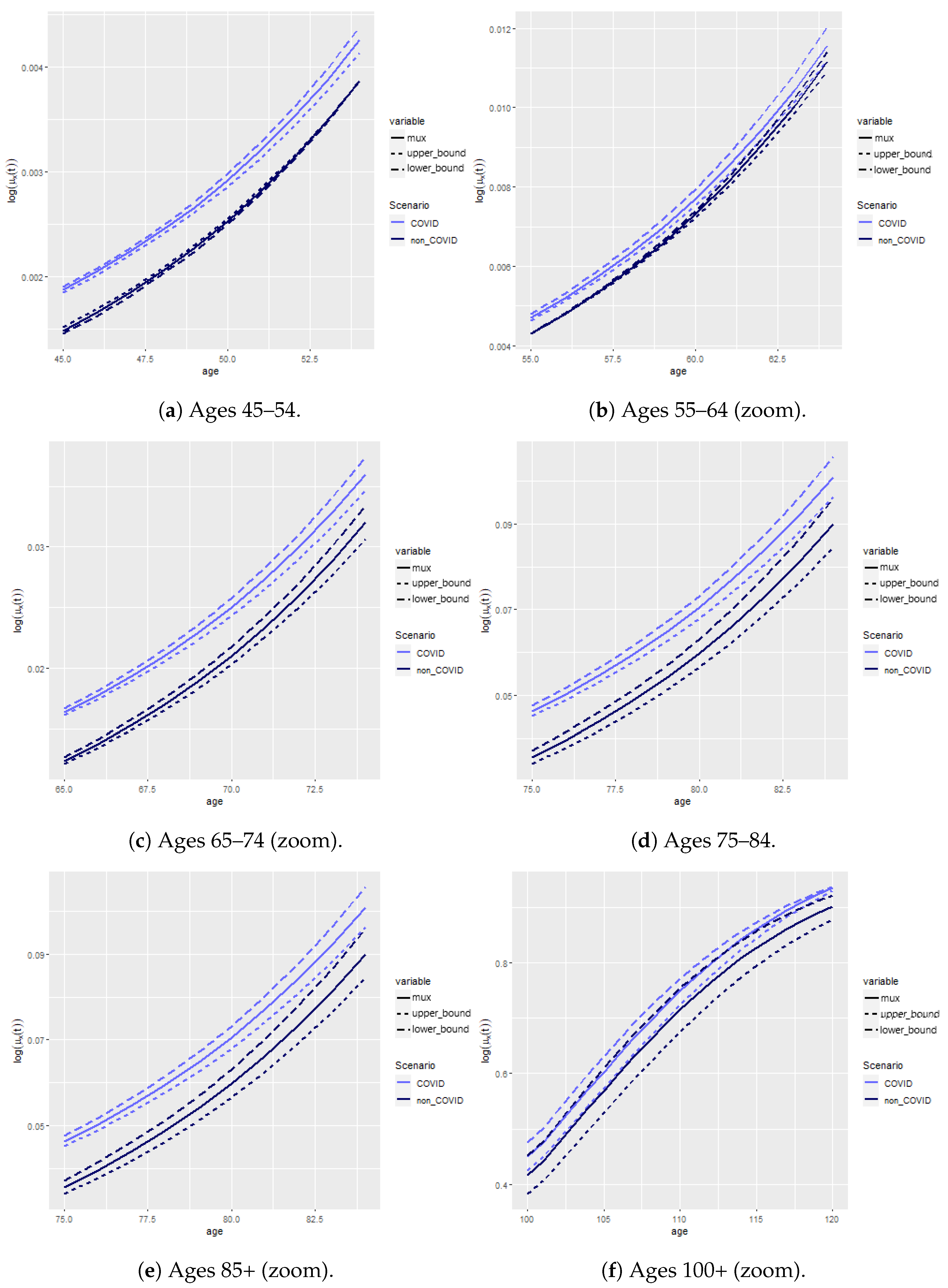
Appendix A.2. Mortality Projection and Extrapolation
| 1 | The yearly seasonal flu does not fall within the scope of our study, being a recurrent sickness. Our aim is to model a one-off pandemic caused by a new virus as distinguished by the CDC. |
| 2 | The SIS model is commonly used to model the common cold or the flu as infection does not provide long-term immunity. |
| 3 | The recovered state is absorbent. This was a reasonable hypothesis in 2020, the year in which the model was parametrized. COVID infection was assumed to provide long-term immunity. The models that allow for recovery could address this but they are outside the scope of this study due to data limitations. |
| 4 | This is in contrast to one-period methodologies, such as the Euler method, which solely refers to a previous point and its derivative to determine the actual value, or the Runge-Kutta method, which uses a few intermediate points but rejects all previous points to obtain a higher-order value. |
| 5 | This package relies on generalized linear models and uses the package gnm to solve for numerous stochastic mortality models that can be expressed within a GLM framework. The algorithm follows two steps. Firstly, the nonlinear parameters are updated, and then the linear parameters are. Secondly, all parameters are updated jointly until convergence is attained. |
| 6 | The Human Mortality Database was created to provide detailed data about population and mortality to researchers, students, journalists, political analysist and individuals interested in the history of human longevity. |
| 7 | |
| 8 | It is time-dependent because the lockdown and quarantine rules have changed according to the evolution of the pandemic. |
| 9 | Mortality rates for Belgium were studied in various studies (Levin et al. 2020; Molenberghs et al. 2020). The meta-study from Levin et al. (2020) finds the relationship . However, these results are not wave-dependent. |
| 10 | This corresponds to the following intervals in the final model: 1/3/2020, 8/3/2020, 14/03/2020, 19/03/2020, 26/03/2020, 2/4/2020, 9/4/2020, 4/5/2020, 8/6/2020, 1/7/2020, 29/07/2020, 1/9/2020, 6/10/2020, 19/10/2020, 2/11/2020, 1/12/2020, 24/12/2020, and 31/12/2020. |
| 11 | Details about the characteristics of the contract are given in Section 4.5. |
| 12 | Obviously, the 1935 and 1955 cohorts were 83 and 63 years old in 2018, whcih is the last observed year according to Human Mortality Database (2021), making it impossible to compare with empirical data beyond these ages. |
| 13 | In reality COVID related mortality will most likely vary within the age category. However, we are unable to extract this trend due to data limitations. |
| 14 | Carannante et al. (2022) only provide point estimates of their insurance product valuation. |
| 15 | Missing values, as wel as NA, are associated zero weight and are hence not included in the fit. |
References
- Abou-Ismail, Anas. 2020. Compartmental models of the COVID-19 pandemic for physicians and physician-scientists. SN Comprehensive Clinical Medicine 2: 852–58. [Google Scholar] [CrossRef] [PubMed]
- Arnold, Séverine, and Michael Sherris. 2013. Forecasting mortality trends allowing for cause-of-death mortality dependence. North American Actuarial Journal 17: 273–82. [Google Scholar] [CrossRef]
- Arnold, Séverine, and Michael Sherris. 2015. Causes-of-death mortality: What do we know on their dependence? North American Actuarial Journal 19: 116–28. [Google Scholar] [CrossRef]
- Balabdaoui, Fadoua, and Dirk Mohr. 2020. Age-stratified discrete compartment model of the COVID-19 epidemic with application to switzerland. Scientific Reports 10: 1–12. [Google Scholar] [CrossRef]
- Boumezoued, Alexandre, Héloïse Labit Hardy, Nicole El Karoui, and Séverine Arnold. 2018. Cause-of-death mortality: What can be learned from population dynamics? Insurance: Mathematics and Economics 78: 301–15. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Calafiore, Giuseppe C., Carlo Novara, and Corrado Possieri. 2020. A modified sir model for the COVID-19 contagion in italy. Paper presented at the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, December 14–18; pp. 3889–94. [Google Scholar]
- Carannante, Maria, Valeria D’Amato, and Steven Haberman. 2022. COVID-19 accelerated mortality shocks and the impact on life insurance: The italian situation. Annals of Actuarial Science 16: 478–97. [Google Scholar] [CrossRef]
- CDC. 2021. 1918 Pandemic (h1n1 Virus). Available online: https://www.cdc.gov/flu/pandemic-resources/1918-pandemic-h1n1.html (accessed on 24 May 2021).
- Chen, Xiaowei, Wing Fung Chong, Runhuan Feng, and Linfeng Zhang. 2021. Pandemic risk management: Resources contingency planning and allocation. Insurance: Mathematics and Economics 101: 359–83. [Google Scholar] [CrossRef] [PubMed]
- Feng, Runhuan, and Jose Garrido. 2011. Actuarial applications of epidemiological models. North American Actuarial Journal 15: 112–36. [Google Scholar] [CrossRef]
- Feng, Runhuan, José Garrido, Longhao Jin, Sooie-Hoe Loke, and Linfeng Zhang. 2022. Epidemic compartmental models and their insurance applications. In Pandemics: Insurance and Social Protection. Edited by María del Carmen Boado-Penas and Julia Eisenberg. Cham: Springer International Publishing, pp. 13–40. [Google Scholar]
- Fernández-Villaverde, Jesús, and Charles I. Jones. 2022. Estimating and simulating a sird model of COVID-19 for many countries, states, and cities. Journal of Economic Dynamics and Control 140: 104318. [Google Scholar] [CrossRef]
- Franco, Nicolas. 2021. COVID-19 belgium: Extended seir-qd model with nursing homes and long-term scenarios-based forecasts. Epidemics 37: 100490. [Google Scholar] [CrossRef] [PubMed]
- Hall, R. Dale, Cynthia S. MacDonald, Peter J. Miller, Achilles N. Natsis, Lisa A. Schilling, Steven C. Siegel, and J. Patrick Wiese. 2020. Society of Actuaries Research Brief: Impact of COVID-19. Technical Report. Itasca: Society of Actuaries. [Google Scholar]
- Hethcote, Herbert W. 2000. The mathematics of infectious diseases. SIAM Review 42: 599–653. [Google Scholar] [CrossRef]
- Hindmarsh, Alan C. 1983. Odepack, a systematized collection of ode solvers. Scientific Computing 1: 55–64. [Google Scholar]
- Huang, Yubei, Lei Yang, Hongji Dai, Fei Tian, and Kexin Chen. 2020. Epidemic situation and forecasting of COVID-19 in and outside china. Bull World Health Organ 10. [Google Scholar] [CrossRef]
- Human Mortality Database. 2021. Life Tables Belgium 1968–2018—Total (Both Sexes). Available online: https://www.mortality.org/ (accessed on 24 May 2021).
- Institute and Faculty of Actuaries. 2015. Longevity Bulletin 6: The Pandemic Edition. Technical Report. Itasca: Institute and Faculty of Actuaries. [Google Scholar]
- Kermack, William Ogilvy, and Anderson G. McKendrick. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 115: 700–21. [Google Scholar]
- Kermack, William Ogilvy, and Anderson G. McKendrick. 1932. Contributions to the mathematical theory of epidemics. ii.—The problem of endemicity. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 138: 55–83. [Google Scholar]
- Levin, Andrew T., William P. Hanage, Nana Owusu-Boaitey, Kensington B. Cochran, Seamus P. Walsh, and Gideon Meyerowitz-Katz. 2020. Assessing the age specificity of infection fatality rates for COVID-19: Systematic review, meta-analysis, and public policy implications. European Journal of Epidemiology 35: 1123–38. [Google Scholar] [CrossRef]
- Li, Han, Hong Li, Yang Lu, and Anastasios Panagiotelis. 2019. A forecast reconciliation approach to cause-of-death mortality modeling. Insurance: Mathematics and Economics 86: 122–33. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2019. Modeling cause-of-death mortality using hierarchical archimedean copula. Scandinavian Actuarial Journal 2019: 247–72. [Google Scholar] [CrossRef]
- Lyu, Pintao, Anja De Waegenaere, and Bertrand Melenberg. 2021. A multi-population approach to forecasting all-cause mortality using cause-of-death mortality data. North American Actuarial Journal 25: S421–S456. [Google Scholar] [CrossRef]
- Molenberghs, Geert, Christel Faes, Johan Verbeeck, Patrick Deboosere, Steven Abrams, Lander Willem, Jan Aerts, Heidi Theeten, Brecht Devleesschauwer, Natalia Bustos Sierra, and et al. 2020. Belgian COVID-19 mortality, excess deaths, number of deaths per million, and infection fatality rates (9 March–28 June 2020). Euro Surveill. 27: 2002060. [Google Scholar]
- O’Driscoll, Megan, Gabriel Ribeiro Dos Santos, Lin Wang, Derek AT Cummings, Andrew S Azman, Juliette Paireau, Arnaud Fontanet, Simon Cauchemez, and Henrik Salje. 2021. Age-specific mortality and immunity patterns of SARS-CoV-2. Nature 590: 140–45. [Google Scholar] [CrossRef]
- Rogers, Andrei, and Kathy Gard. 1991. Applications of the heligman/pollard model mortality schedule. Population Bulletin of the United Nations 30: 79–105. [Google Scholar]
- Saunders-Hastings, Patrick R., and Daniel Krewski. 2016. Reviewing the history of pandemic influenza: Understanding patterns of emergence and transmission. Pathogens 5: 66. [Google Scholar] [CrossRef] [PubMed]
- Schnürch, Simon, Torsten Kleinow, Ralf Korn, and Andreas Wagner. 2022. The impact of mortality shocks on modelling and insurance valuation as exemplified by COVID-19. Annals of Actuarial Science 16: 498–526. [Google Scholar] [CrossRef]
- Sciensano. 2021. COVID-19 Database. Available online: https://epistat.wiv-isp.be/covid/ (accessed on 24 May 2021).
- Spiegelhalter, David. 2020. Use of “normal” risk to improve understanding of dangers of COVID-19. BMJ 370: m3259. [Google Scholar] [CrossRef]
- Statbel. 2021. Population Structure. Available online: https://statbel.fgov.be/fr/themes/population/structure-de-la-population (accessed on 24 May 2021).
- Tabeau, Ewa, Peter Ekamper, Corina Huisman, and Alinda Bosch. 1999. Improving overall mortality forecasts by analysing cause-of-death, period and cohort effects in trends. European Journal of Population/Revue Européenne de Démographie 15: 153–83. [Google Scholar] [CrossRef]
- Tang, Lu, Yiwang Zhou, Lili Wang, Soumik Purkayastha, Leyao Zhang, Jie He, Fei Wang, and Peter X.-K. Song. 2020. A review of multi-compartment infectious disease models. International Statistical Review 88: 462–513. [Google Scholar] [CrossRef]
- Thatcher, A. Roger. 1999. The long-term pattern of adult mortality and the highest attained age. Journal of the Royal Statistical Society: Series A (Statistics in Society) 162: 5–43. [Google Scholar] [CrossRef]
- Villegas, Andrés M., Vladimir K. Kaishev, and Pietro Millossovich. 2018. Stmomo: An r package for stochastic mortality modeling. Journal of Statistical Software 84: 1–38. [Google Scholar] [CrossRef]
- WHO. 2021a. Ebola Virus Disease. Available online: https://www.who.int/csr/disease/ebola/en/ (accessed on 24 May 2021).
- WHO. 2021b. Past Pandemics. Available online: https://www.euro.who.int/en/health-topics/communicable-diseases/influenza/pandemic-influenza/past-pandemics (accessed on 24 May 2021).
- Willem, Lander, Thang Van Hoang, Sebastian Funk, Pietro Coletti, Philippe Beutels, and Niel Hens. 2020. Socrates: An online tool leveraging a social contact data sharing initiative to assess mitigation strategies for COVID-19. BMC Research Notes 13: 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wilmoth, John R. 1996. 13 mortality projections for japan. Health and Mortality among Elderly Populations, 266. [Google Scholar] [CrossRef]
- Zhao, Shilei, and Hua Chen. 2020. Modeling the epidemic dynamics and control of COVID-19 outbreak in china. Quantitative Biology 8: 11–19. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Ming, and John P. Klein. 1995. Estimates of marginal survival for dependent competing risks based on an assumed copula. Biometrika 82: 127–38. [Google Scholar] [CrossRef]
- Zhou, Rui, and Johnny Siu-Hang Li. 2022. A multi-parameter-level model for simulating future mortality scenarios with covid-alike effects. Annals of Actuarial Science 16: 453–77. [Google Scholar] [CrossRef]
- Zittersteyn, Geert, and Jennifer Alonso-García. 2021. Common factor cause-specific mortality model. Risks 9: 221. [Google Scholar] [CrossRef]



| 0–24 | 25–44 | 45–64 | 65–74 | 75–84 | 85+ | |
|---|---|---|---|---|---|---|
| 3,237,498 | 2,968,631 | 3,082,034 | 1,170,399 | 698,940 | 335,139 |
| 0–24 | 25–44 | 45–64 | 65–74 | 75–84 | 85+ | |
|---|---|---|---|---|---|---|
| 5 | 2 | 10 | 1 | 1 | 0 |
| 01/03–13/03 | 14/03–18/03 | 19/03–03/05 | 04/05–07/06 | |
| 4.13 [3.89; 4.39] | 2.24 [2.13; 2.35] | 0.65 [0.61; 0.72] | 0.79 [0.75; 0.83] | |
| 08/06–30/06 | 01/07–28/07 | 29/07–31/08 | 01/09–31/10 | |
| 0.99 [0.91; 1.07] | 1.40 [1.29; 1.53] | 0.75 [0.63; 0.88] | 1.73 [1.62; 1.85] |
| March–April | 0–24 | 25–44 | 45–64 | 65–74 | 75+ |
| 0.0 | 0.02 | 0.21 | 1.85 | 9.25 | |
| April–July | 0–24 | 25–44 | 45–64 | 65–74 | 75+ |
| 0.0 | 0.01 | 0.19 | 1.72 | 7.84 | |
| July- | 0–24 | 25–44 | 45–64 | 65–74 | 75+ |
| 0.0 | 0.01 | 0.08 | 0.86 | 1.89 |
| Period | Level of Restrictions |
|---|---|
| 01/03/2020–13/03/2020 | Pre-lockdown |
| 14/03/2020–18/03/2020 | Schools and leisure closed |
| 19/03/2020–03/04/2020 | Full lockdown |
| 04/04/2020–07/06/2020 | Phase 1–2 |
| 08/06/2020–30/06/2020 | Phase 3 |
| 01/07/2020–28/07/2020 | Phase 4 |
| 29/07/2020–31/08/2020 | Phase 4 bis |
| 01/09/2020–05/10/2020 | Second wave |
| 06/10/2020–18/10/2020 | Limited social contacts |
| 19/10/2020–01/11/2020 | Curfew |
| 02/11/2020–31/11/2020 | (light) Lockdown |
| 01/12/2020–23/12/2020 | Reopening of shops |
| 24/12/2020–31/12/2020 | Public holiday period |
| # Parameter Set | |||||
|---|---|---|---|---|---|
| 6 | 10 | 15,360 | 94,527 | ||
| # de cores | 1 | 14.00 s | 26.21 s | NA | NA |
| 3 | 5.63 s | 15.26 s | NA | NA | |
| 8 | 2.92 s | 5.17 s | 1 h 39 m 50.09 s | 10 h 14 m 23.06 s | |
| First Wave | 0–24 | 25–44 | 45–64 | 65–74 | 75–84 | 85+ |
| Second wave | 0–24 | 25–44 | 45–64 | 65–74 | 75–84 | 85+ |
| Model | Period 1 | Period 2 |
|---|---|---|
| Preliminary model | 402.3329 | NA |
| Model with delay | 393.6614 | 543.0819 |
| Final model | 239.5903 | 525.7816 |
| 0–24 | 25–44 | 45-64 | 65–74 | 75–84 | 85+ | |
|---|---|---|---|---|---|---|
| Model | 0 | 0.005 | 0.039 | 0.400 | 1.081 | 3.390 |
| Empirical | 0 | 0.003 | 0.037 | 0.214 | 0.835 | 3.187 |
| Whole Life Insurance | Lifetime Immediate Annuity | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPV | Standard Deviation (=) | NPV | Standard Deviation (=) | ||||||||||
| Scenario | (%) | Scenario | (%) | Scenario | (%) | Scenario | (%) | ||||||
| COVID | No COVID | COVID | No COVID | COVID | No COVID | COVID | No COVID | ||||||
| Underwriting year: 2000 | |||||||||||||
| Age | 75 | 9492 | 9469 | 0.241 | 3374 | 3379 | −0.148 | 402,980 | 403,932 | −0.235 | 131,879 | 132,138 | −0.196 |
| 85 | 12,225 | 12,203 | 0.180 | 3289 | 3308 | −0.567 | 288,976 | 289,892 | −0.316 | 122,519 | 123,434 | −0.741 | |
| Underwriting year: 2019 | |||||||||||||
| Age | 50 | 7156 | 7151 | 0.064 | 2951 | 2943 | 0.288 | 500,451 | 500,641 | −0.038 | 117,177 | 116,817 | 0.308 |
| 65 | 11,023 | 10,992 | 0.285 | 3309 | 3279 | 0.935 | 339,090 | 340,397 | −0.384 | 126,118 | 124,801 | 1.055 | |
| Whole Life Insurance | Lifetime Immediate Annuity | ||||
|---|---|---|---|---|---|
| VAP 1 (%) | 1 (%) | VAP 1 (%) | 1 (%) | ||
| Underwriting year: 2000 | |||||
| Age | 75 | 2.294 | −1.611 | −2.244 | −2.099 |
| 85 | 1.551 | −5.150 | −2.724 | −6.781 | |
| Underwriting year: 2019 | |||||
| Age | 50 | 0.637 | 2.826 | −0.379 | 3.019 |
| 65 | 2.799 | 8.474 | −3.770 | 9.491 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delbrouck, C.; Alonso-García, J. COVID-19 and Excess Mortality: An Actuarial Study. Risks 2024, 12, 61. https://doi.org/10.3390/risks12040061
Delbrouck C, Alonso-García J. COVID-19 and Excess Mortality: An Actuarial Study. Risks. 2024; 12(4):61. https://doi.org/10.3390/risks12040061
Chicago/Turabian StyleDelbrouck, Camille, and Jennifer Alonso-García. 2024. "COVID-19 and Excess Mortality: An Actuarial Study" Risks 12, no. 4: 61. https://doi.org/10.3390/risks12040061
APA StyleDelbrouck, C., & Alonso-García, J. (2024). COVID-19 and Excess Mortality: An Actuarial Study. Risks, 12(4), 61. https://doi.org/10.3390/risks12040061







