Abstract
In the insurance sector, Zero-Inflated models are commonly used due to the unique nature of insurance data, which often contain both genuine zeros (meaning no claims made) and potential claims. Although active developments in modeling excess zero data have occurred, the use of Bayesian techniques for parameter estimation in Zero-Inflated Poisson models has not been widely explored. This research aims to introduce a new Bayesian approach for estimating the parameters of the Zero-Inflated Poisson model. The method involves employing Gamma and Beta prior distributions to derive closed formulas for Bayes estimators and predictive density. Additionally, we propose a data-driven approach for selecting hyper-parameter values that produce highly accurate Bayes estimates. Simulation studies confirm that, for small and moderate sample sizes, the Bayesian method outperforms the maximum likelihood (ML) method in terms of accuracy. To illustrate the ML and Bayesian methods proposed in the article, a real dataset is analyzed.
1. Introduction
The high occurrence of zero-valued observations in insurance claim data is a well-documented phenomenon. Traditional count models, such as Poisson or Negative Binomial, struggle to accurately represent insurance claim data due to the excessive dispersion caused by the observed frequency of zeros surpassing expectations based on these models. Perumean-Chaney et al. (2013) emphasized the importance of considering the excess zeros to achieve satisfactory modeling of both zero and non-zero counts. In the statistical literature, two main approaches have been developed to address datasets with a large number of zeros: Hurdle models and Zero-Inflated models. Hurdle models, initially proposed by Mullahy (1986), adopt a truncated-at-zero approach, as seen in truncated Poisson and Negative Binomial models. Zero-Inflated models, introduced by Lambert (1992), utilize a mixture model approach, separating the population into two groups—one with only zero outcomes and the other with non-zero outcomes. Notable examples include Zero-Inflated Poisson and Negative Binomial regressions.
The generic Zero-Inflated distribution is defined as:
where p denotes the probability of extra zeros and can be any count distribution, such as Poisson or Negative Binomial. If follows a Poisson distribution, this model simplifies to the Zero-Inflated Poisson (ZIP) model, expressed by the density:
In cases where covariates are linked with both the probability p of a structural zero and the mean function of the Poisson model, logistic regression is used to model p, and log-linear regression is applied to model . This analytical framework is referred to as ZIP regression, which, while not the primary focus of this study, serves as a foundation for our exploration.
In the insurance sector, the adoption of Zero-Inflated models is widespread, reflecting the distinctive characteristics of insurance data, which often comprise both actual zeros (indicating no claims) and potential claims. Various studies exemplify this application trend: Mouatassim and Ezzahid (2012) applied Zero-Inflated Poisson regression to a private health insurance dataset using the EM algorithm to maximize the log-likelihood function. Chen et al. (2019) introduced a penalized Poisson regression for subgroup analysis in claim frequency data, implementing an ADMM algorithm for optimization. Zhang et al. (2022) developed a multivariate zero-inflated hurdle model for multivariate count data with extra zeros, employing the EM algorithm for parameter estimation.
Ghosh et al. (2006) delved into a Bayesian analysis of Zero-Inflated power series ZIPS () regression models, employing the log link function to correlate the mean of the power series with covariates and the logit function for modeling p. They proposed Beta () and power series-specific priors for the unknown parameters p and , respectively, overcoming analytical challenges through Monte Carlo simulation-based techniques. Their findings highlighted the superiority of the Bayesian approach over traditional methods.
Recent trends also show an inclination towards integrating machine learning techniques with Zero-Inflated models. Zhou et al. (2022) proposed modeling Tweedie’s compound Poisson distribution using EMTboost. Lee (2021) used cyclic coordinate descent optimization for Zero-Inflated Poisson regression, addressing saddle points with Delta boosting. Meng et al. (2022) introduced innovative approaches using Gradient Boosted Decision Trees for training Zero-Inflated Poisson regression models.
To the best of our knowledge, the most recent Bayesian analysis was conducted by Angers and Biswas (2003). In their study, the authors discussed a Zero-Inflated generalized Poisson model that includes three parameters, namely p, , and . The Bayesian analysis employs a conditional uniform prior for the parameters p and , given , while Jeffreys’ prior is used for . The authors concluded that analytical integration was not feasible, leading to the use of Monte-Carlo integration with importance sampling for parameter estimation. In contrast, our study utilizes beta and gamma priors to provide enhanced flexibility in the shapes of prior distributions, offering closed formulas for Bayes estimators, predictive density, and predictive expected values. This approach diverges from the regression-centric literature on the ZIP model. Boucher et al. (2007) presents models that consist of generalizations of count distributions with time dependency where the dependence between contracts of the same insureds can be modeled with Bayesian and frequentist models, based on a generalization of Poisson and negative binomial distributions.
The structure of the paper is organized as follows: In Section 2, we present the deviations for Maximum Likelihood Estimators (MLEs). Section 3 employs gamma and beta distributions as prior distributions for the parameters and p, respectively. This section also elaborates on the derivation of the predictive density , the conditional expectation , and an approximation for the percentile of the predictive distribution. Here, signifies a random sample from a Zero-Inflated Poisson () distribution, and z represents an observed value of . Section 4 summarizes the outcomes of the simulation studies and introduces a data-driven approach for selecting hyper-parameter values of the prior distribution. Section 5 is devoted to the analysis of a real dataset, demonstrating the Bayesian inference methodology introduced in this work. Finally, Section 6 offers brief concluding remarks about the study. The Mathematica code utilized for the simulation studies and the computations performed on the real data are available upon request from the authors.
2. Maximum Likelihood Estimation
The probability mass function of the Zero-Inflated Poisson (ZIP) distribution, denoted as ZIP, is given by
where , , , and p is the probability that reflects the degree of zero inflation. It can be shown that
Let be a random sample from ZIP. Without a loss of generality, consider the corresponding sorted sample
for some positive integers
The likelihood function is
The log of the likelihood function can be written as
To find the Maximum Likelihood Estimators (MLEs) of and p, the following equations need to be solved simultaneously:
After some algebraic manipulations, it can be demonstrated that the MLEs are solutions to the equations
where represents the average of the non-zero observations. It is important to note that the equation is nonlinear in . To solve for , one can employ Mathematica’s ‘FindRoot’ function, which iteratively seeks the root of the equation. The function can be invoked as follows:
where is an initial “good” guess for the solution. This equation is guaranteed to have a unique solution under appropriate conditions. Once the MLE for has been determined, the MLE for p can subsequently be computed.
3. Bayesian Inference
This section delineates a Bayesian methodology for the computation of Bayes estimates for the parameters, the formulation of the predictive density, and the approximation of percentiles for the predictive distribution.
3.1. Bayes Estimates of Parameters
Applying the Binomial expansion,
the likelihood function , as presented in Section 2, can be expressed as
where c is a normalizing constant and it does not need to be found, as it will be canceled out once the posterior PDF has been formulated. .
For the parameters and p, respectively, we consider the gamma and beta conjugate prior distributions. The choice of the gamma distribution as a prior for is due to its flexibility in shaping the probability density function (pdf) for a positive random variable like , given the selection of parameter values. Similarly, the beta distribution is chosen as a prior for p because its support matches the possible range of p values, and like the gamma distribution, it offers flexibility in shaping its pdf for a range of parameter values. Employing the gamma and beta prior distributions, we define
Utilizing Equations (2) and (3), the joint posterior distribution of can be expressed as follows:
However, it is necessary that
Therefore, utilizing
the joint posterior is
Since
the marginal posteriors are
Under the squared-error loss function, the Bayes estimates of and p are the expected values of the corresponding priors. Therefore,
The Bayes estimators presented in Equation (5) are expressed as closed-form solutions, obviating the need for numerical integration. This represents a significant advantage of our methodology over that presented in Angers and Biswas (2003).
3.2. Predictive pdf and Expected Value E
One of the predictive measures of interest is the expected value of a new observation z from the Zero-Inflated Poisson (ZIP) distribution, given a set of observations : . To calculate the expected value, it is necessary to derive the predictive probability density function (pdf) , expressed as
For the case, we have,
After multiplying and dividing the above integrands by appropriate terms to convert them into PDFs, and then integrating, we obtain,
For ,
After applying the appropriate conversions to PDFs and integrating them,
Note that the term inside the first square bracket on the left side of the sum corresponds to the PMF of a Negative Binomial distribution with the parameters . Consequently, the predictive density can be expressed as
where . Therefore, the predictive density is
For example, for , , , , , , and , the numerical values of for are given below.
For instance, if y represents the number of claims per month, then based on the observed sample , we would predict that the number of claims z in the upcoming month would be zero with a probability of 0.773, one with a probability of 0.052, and so forth. The probabilities detailed above can be visually represented in a bar chart, as depicted in Figure 1. The x-axis is labeled as z, and the y-axis is labeled as .
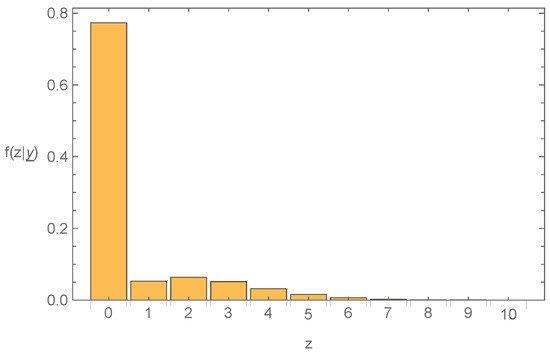
Figure 1.
Graph of the predictive density.
The conditional expected value is derived via the predictive density.
Recall that . Also, the term represents the expected value of a Negative Binomial distribution with parameters and q. Hence,
Consequently, the conditional expected value in the closed form is given by
It should be noted that the objective of formulating the predictive density and the corresponding computations is for predictive purposes. However, to accomplish this, Bayes estimates of the parameters should be computed.
3.3. Approximate Percentile for the Predictive Distribution
Recall that the value of the predictive pdf , derived in Section 3.2,
is independent of z. For instance, utilizing the same parameter values for m, S, n, , , , and specified in Section 3.2, we calculate . Let us define the cumulative distribution function (CDF) as
Note, the expression within the square brackets corresponds to for , as previously established in Section 3.2. To determine an approximate 95th percentile for the predictive distribution, we require that
Mathematica can be utilized to enumerate the values of , starting with , and to identify the interval that encloses 0.95. Employing the same input values for m, n, S, …, we obtain:
Since 0.95 is within the interval , corresponding to , it can be inferred that, based on the observed sample and the specified hyper-parameter values, the forthcoming value of z would not exceed 4 with approximately 0.95 probability.
4. Simulation
Simulation studies were conducted to evaluate the accuracy of Bayesian and Maximum Likelihood estimators for the parameters and p. The simulation studies proceeded as follows:
- Step 1: Generate samples of size , and 100, respectively, from the Zero-Inflated Poisson distribution using selected “true” values of the parameters and p listed in the tables.
- Step 2: For each set of “true” parameter values of and p, as outlined in Section 2, the MLEs are determined using the equations
- Step 3: Selecting optimal hyper-parameter values is crucial for obtaining accurate Bayes estimates.
Recall that the conjugate prior distribution for is a gamma distribution. Given that
we let , or in other words, . This ensures that the prior distribution of is centered at the selected “true” value for . By substituting this into the formula, we can deduce that, to achieve high accuracy for the Bayes estimate of , the hyper-parameters and should be selected in such a way that they are consistent with the expected value and variance of . Since , we therefore choose a large value for to ensure that is small, and let to ensure that . It is noted that there is no unique pair of hyper-parameter values for and ; any pair that meets the above criteria should suffice. However, simulation studies confirm that a larger value of provides a more accurate Bayes estimate.
Recall that p follows a beta distribution which is also considered a conjugate prior. A similar rationale is used for selecting the hyper-parameters and . We have
By substituting into and after a few algebraic manipulations, we obtain
Note that is a decreasing function of . Therefore, for a given value of p, to make small, we choose a large value for .
The goal is to select and such that the true selected value of p in simulation studies is closely approximated by its expected value. That is, , or , and a large value for to minimize . Although multiple pairs of hyper-parameter values can meet these conditions, larger values of have been shown to yield more accurate Bayes estimates of p.
- Step 4: Bayes estimates are computed as detailed in Section 3.
- Step 5: The simulation involves calculating the average of the estimates and the square root of the Average Square Error (ASE) based on simulated samples.
In simulation studies, it is important to note that n and the “true” values of and p should be selected so that the nonlinear Equation (9) has a solution. Recall from Section 2, the equations
for finding MLEs of and p. The first equation is nonlinear in and can written as
where is the sample mean of non-zero values in the data, and . Mathematica can be used to find its unique solution.
Recall that the expected value of Y is given by
By equating the first population moment of Zip( to the first sample moment, we obtain , which reduces to
The above relationship between n, , and p provides guidance for selecting the “true” values for in simulation studies. For small values of n and , a large value for p must be selected. For example, if , we expect to have substantial zeros in the data, as is very small. This means p, the percentage of zeros in the data, must be large. The value of p depends on S, the sum of non-zero values in the data. Using the same values for , if (a reasonable value, as ), then , but if (not expected, as ), we obtain , which is not an accepted value.
Simulation studies have confirmed that when n and are small, but the selected value of p is also small, Equation (9) fails to have a solution.
Furthermore, the mean and square root of the Average Square Error () for each parameter are detailed in Table 1, Table 2, Table 3 and Table 4. For instance, for the MLE of is defined as
As previously discussed, there are multiple options for selecting hyper-parameter values. In Table 1, Table 2, Table 3 and Table 4, two sets of hyper-parameter values are utilized, following the proposed method for their selection. These tables demonstrate that as the sample size increases, the Average Squared Error (ASE) for the Maximum Likelihood Estimator (MLE) decreases, as anticipated. Notably, for smaller sample sizes, the Bayes estimator exhibits superior accuracy compared to the MLE. Furthermore, for larger values of and , the accuracies of Bayes estimators for p and are enhanced. For instance, in Table 1, with true parameters and , two sets of hyper-parameters are selected. Set 1: , , , The for is 0.02014 and for p is 0.00475 when . Set 2: , , , results in for of 0.00504 and for p of 0.00134 when . It is important to note that the Bayes estimators’ formulas (8) include n in their denominators. Thus, for a larger sample size n, the Average Squared Error for both Bayes estimators somewhat increases, yet they still significantly surpass the MLE in terms of accuracy, as measured by the Average Squared Error (ASE).

Table 1.
Comparison of the ML and Bayesian estimates with different pairs of hyper-parameters.

Table 2.
Comparison of the ML and Bayesian estimates with different pairs of hyper-parameters.

Table 3.
Comparison of the ML and Bayesian estimates with different pairs of hyper-parameters.

Table 4.
Comparison of the ML and Bayesian estimates with different pairs of hyper-parameters.
- Sensitivity Test
A sensitivity analysis, https://www.investopedia.com/terms/s/sensitivityanalysis.asp (accessed on 15 April 2024), tests how independent variables, under a set of assumptions, influence the outcome of a dependent variable. This section theoretically demonstrates that the accuracy of Bayesian estimates, as measured by , improves with larger values of and . The simulation results, presented in Table 1, Table 2, Table 3 and Table 4, align with our theoretical assertions, utilizing two distinct sets of hyper-parameters. To corroborate these findings further, a sensitivity test was executed for a specific set of “true” parameter values: , , and . Under these stipulations, we considered small hyper-parameter values
and large hyper-parameter values
yielding samples of size from the ZIP model with and . The outcomes of the sensitivity test are summarized in Table 5, revealing a substantial decrease in both for estimates of and p, when transitioning from smaller to larger values of hyper-parameters. For example, from a small values to a large values , changes from 0.04149 to 0.01198 for and from 0.01414 to 0.00470 for p. This trend is also evident within each group. For the smaller hyper-parameter group, the for diminishes from 0.04149 to 0.04058, and the for p from 0.01414 to 0.01377 corresponding to hyper-parameters and , as the hyper-parameter values incrementally increase by approximately 0.7% for on each step (from 271 to 273) and 0.9% for on each step (from 211 to 213). A similar pattern is observed for the larger group, even though the increments for and are about 0.17% on each step ( from 1146 to 1148) and 0.25% on each step ( from 796 to 798), respectively. This sensitivity analysis validates that the precision of Bayesian estimates is contingent upon the choice of hyper-parameters, with larger and values enhancing estimate accuracy in terms of As shown in Table 5, there is a gradual increase in hyper-parameters and a corresponding steady decrease in For the practical application of the proposed method, it is advisable to establish a stopping rule for the increment in the hyper-parameters. Specifically, the increase in hyper-parameters should continue until no significant reduction in is observed.

Table 5.
Sensitivity test for accuracy of Bayesian estimates by selecting hyper-parameters.
5. Numerical Example
5.1. The Synthetic Auto Telematics Dataset
This section focuses on the practical application of the ML and Bayesian methods discussed in the article, using a real dataset.
5.1.1. Data and Basic Descriptive Statistics
The dataset selected for our analysis is the synthetic auto telematics dataset, accessible at http://www2.math.uconn.edu/~valdez/data.html (accessed on 20 January 2024). Using real-world insurance datasets frequently presents significant challenges due to the need to maintain the confidentiality of individual customer information. The synthetic dataset developed by So et al. (2021) was designed to closely mimic genuine telematics auto data originally sourced from a Canadian-based insurer, which offered a UBI program that was launched in 2013 to its automobile insurance policyholders. It was created to be openly accessible to researchers for their studies, enabling them to work with data that closely resembles real-world scenarios while ensuring privacy protection. Therefore, to evaluate the practical relevance of the proposed models, we decided to use this synthetic dataset instead of real data.
The synthetic dataset consists of 100,000 policies with a total of 52 variables, which includes the NB_Claim variable representing the number of claims. For further information on the 52 variables, please refer to So et al. (2021). Figure 2 displays a histogram that visualizes the descriptive statistics for the number of claims in the synthetic auto telematics dataset. The average number of claims is 0.04494, with the minimum number of claims being zero, with a frequency of 95,728, and a maximum number of claims reaching three, with a frequency of 11. The respective frequencies for one and two claims are 4061 and 200. Furthermore, the standard deviation of the number of claims stands at 0.21813, indicating a wide dispersion across the dataset. The skewness of the number of claims, valued at 5.1138, demonstrates that the data are right-skewed. Moreover, a kurtosis of the number of claims of 31.538 signifies the presence of a heavy tail in the data distribution. Notably, the histogram reveals an exceptionally high frequency of zero claims, characteristic of Zero-Inflated model data, underscoring the limitation of regular distributions such as the Poisson or Negative Binomial in effectively modeling the number of claims.
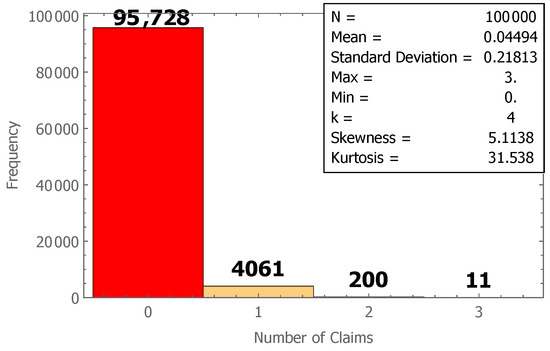
Figure 2.
Histogram of the synthetic auto telematics dataset.
5.1.2. Goodness-of-Fit of the Synthetic Auto Telematics Dataset
Chi-Square Goodness-Fit-Test
To assess the suitability of the Zero Inflated Poisson model for the synthetic auto telematics dataset, we consider the hypotheses:
H0:
The data are generated from a Zero-Inflated Poisson distribution.
Ha:
The data are not generated from a Zero-Inflated Poisson distribution.
Klugman et al. (2012) have suggested that the Kolmogorov–Smirnov and Anderson–Darling tests apply solely to individual datasets. Hence, for a grouped dataset like the synthetic auto telematics dataset, the Chi-Square goodness-of-fit test is utilized to ascertain if a categorical variable conforms to a hypothesized frequency distribution. The degrees of freedom for the test statistic are given by , where k is the number of categories.
Given that two parameters, and p, are estimated, the Chi-square test formula is represented as:
where denotes the observed frequencies, and refers to the expected frequencies based on the model.
Applying this approach to the specific dataset, we have:
Given that we have four categories (zero, one, two, and greater than or equal to three), we determine the degrees of freedom () to be 1. At significance levels of or , the null hypothesis is rejected if the statistic,
exceeds or , respectively. Therefore, a smaller value of the statistic indicates stronger support for , implying a better fit of the data to the Zero-Inflated Poisson model.
Score Test
The score test, https://en.wikipedia.org/wiki/Score_test (accessed on 17 April 2024), is utilized to evaluate the constraints of parameters within a statistical model. The process of formulating the score test is detailed as follows:
The hypotheses are defined by:
The test statistic is given as:
where
The critical values are and . Reject if .
The distribution under test is defined as:
Considering the hypotheses versus , which are equivalent to:
Using from Section 2, for testing versus , we obtain:
As a result, the Score test can be expressed as:
where n is the sample size, and m is the number of zeros in the sample. To compute , replace with its MLE under , that is, . The score test is asymptotically distributed as Chi-square with 1 degree of freedom. Thus, the larger the value of , the stronger the evidence in support of , indicating a better fit for the Zero-Inflated Poisson model.
As previously mentioned, determining the optimal hyper-parameter values poses a significant challenge. Given that the “true” values of parameters and p are unknown in practice, we propose a data-driven approach to determine hyper-parameter values, utilizing their Maximum Likelihood Estimates (MLEs), as discussed in the Simulation section.
Note that in real practice, unlike in simulations, the “true” values of parameters are unknown. However, we are still required to choose the “best” values for the hyper-parameters. This can be accomplished through the MLEs of and p. The method proposed here for selecting hyper-parameter values has also been employed by Deng and Aminzadeh (2023) and Aminzadeh and Deng (2022), where the authors use MLEs to choose hyper-parameter values.
The following steps are proposed for selecting hyper-parameter values for “real” data:
- Apply a goodness-of-fit test to assess how well the data fits the Zero-Inflated Poisson distribution. Goodness-of-fit tests extensively developed in the literature for ZIP() include the Score and Chi-square tests considered in this article.
- Compute the MLEs and , as detailed in Section 2.
- Choose a large value for and let .
- Choose a large value for and let , or if selecting first.
This approach ensures the selection of hyper-parameter values that best fit the given real data under the assumption of a Zero-Inflated Poisson distribution.
The table indicates that the Zero-Inflated Poisson model provides a good fit to the data according to the Maximum Likelihood (ML) estimation method. Given the large sample size (), the Bayesian method does not significantly outperform the ML method. The findings presented in Table 6 align with our expectations: larger hyper-parameter values enhance the model’s fit to the data. Utilizing the Chi-square test with a critical value of , Table 6 demonstrates that the ZIP model, employing ML estimates as well as Bayes 4 and Bayes 5 sets of hyper-parameters, adequately fits the data.

Table 6.
Goodness-of-fit tests of the ML and Bayesian estimates with different pairs of hyper-parameters.
The score test yields a value of 3.67026, which exceeds . Consequently, we reject the null hypothesis (that the data follows a Poisson distribution) in favor of the alternative hypothesis, affirming that the ZIP model better suits the dataset at a significance level of 0.10.
5.2. A Simulated Data from ZIP Model
In this section, a random sample of size 200 from a ZIP model with and is generated. The summary of the generated data is presented in Figure 3.
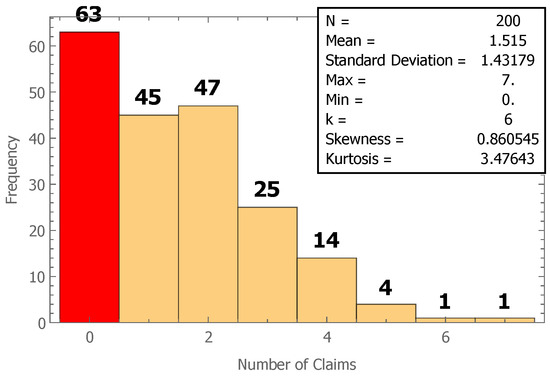
Figure 3.
Histogram of the sample generated from ZIP with and .
There are six categories (zero, one, two, three, four, and greater than or equal to five). The sample mean is 1.515, and the sample standard deviation is 1.41179. The maximum value observed is seven, and the minimum is zero. The skewness = 0.86055 which indicates that the data are right-skewed, and the Kurtosis = 3.47643 which indicates that the data have a heavy tail. The histogram confirms the high frequency of zeros. We use the same test statistics as in Section 5.1. The observed values are as follows:
The expected frequencies are
where are estimates of , respectively.
The table was prepared using the same method described in the Simulation Section. That is, for a selected value of , we let , and for a selected , we let .
Table 7 reveals that all of the ZIP models (with different hyper-parameter values) are a good fit for the dataset, as all the test values are smaller than . Additionally, the value based on ML is larger than those based on the Bayesian method, suggesting that the Bayesian method provides a better fit for the data than the ML method. Both the ML and Bayesian approaches confirm that the data fit the ZIP model well, as expected.

Table 7.
Goodness-of-fit test of simulated data with different pairs of hyper-parameters. we confirm it is correct, There are different ways to select other hyper-parameters.
The calculated score test value is greater than the critical value of 3.841. Therefore, we reject the null hypothesis that the data follow a Poisson distribution and accept the alternative hypothesis that the Zero-Inflated Poisson (ZIP) model is a better fit for the dataset.
Table 8 uses a similar approach to Section 5.1 for selecting hyper-parameter values. That is, for a selected value of , we let , and for a selected , we let . showing that all of the ZIP models fit the dataset well as the critical value is 7.815. Based on the MLE method, the test value of 0.71024 is slightly smaller than other Bayes-based test values. We noticed that, since MLE estimates of and p are used to determine the hyper-parameters, the Bayesian estimates of and p are somewhat underestimated. Additionally, the larger the values of the hyper-parameters, the better the model fits the data.

Table 8.
Goodness-of-fit test of simulated data with different pairs of hyper-parameters.
Table 7 and Table 8 demonstrate that as hyper-parameter values increase, the Chi-square test values decrease, suggesting a better fit for the data. However, a notable exception is observed with a small pair of hyper-parameters in Table 7, where the Chi-square test value is larger than those obtained from MLE. Specifically, in Table 7, the entry “Bayes 6”, which utilizes very small hyper-parameters, has a Chi-square value of 1.10954, significantly higher than other values in the table. This observation confirms that larger hyper-parameters result in a better fit.
6. Conclusions
Many insurance claims datasets exhibit a high frequency of no claims. To analyze such data, researchers have proposed the use of Zero-Inflated models. These models incorporate parameters with covariates using link functions and are referred to as Zero-Inflated Regression Models. Various methods, including Maximum Likelihood (ML), Bayesian, and Decision Tree, among others, have been employed to fit the data. A significant distinction of this research from prior studies is the introduction of a novel Bayesian approach for the Zero-Inflated Poisson model without covariates. This study aims to develop the statistical ZIP model by estimating the unknown parameters and p. To our knowledge, similar research has not been documented in the literature. We derive analytical solutions for the Maximum Likelihood estimators of the unknown parameters and p. Additionally, we present analytical closed-form solutions for Bayesian Estimators of these parameters by selecting conjugate prior distributions: Gamma for and Beta for p, respectively. The comparison between the ML and Bayesian methods indicates that the Bayesian method, utilizing a data-driven approach (which employs MLEs of parameters p and to select hyper-parameter values), surpasses the ML method in accuracy. We derived the predictive distribution based on the posterior distribution, predicting possible future observations from past observed values and calculating percentiles. Furthermore, we demonstrate that larger values of the hyper-parameters and enhance the accuracy of the Bayesian estimates. Our findings are confirmed through a sensitivity test. The real-life data from the synthetic auto telematics dataset and simulated data from a specified Zero-Inflated Poisson model, using the methods proposed in this paper, validated the goodness-of-fit (GOF) to the ZIP model based on both Chi-square and Score tests. However, the simulation has limitations, including 1. Ensuring the data adequately fit the Zero-Inflated Poisson model in real applications. 2. The sample size is sufficiently large so that the MLEs of parameters p and are accurate. 3. The selection of hyper-parameter values aligns with the MLEs, as elaborated in Section 4 (Step 3). Future research could explore non-traditional discrete Time Series modeling for Zero-Inflated data to forecast the number of claims at specific future points and extend the Bayesian analysis to the Zero-Inflated Negative Binomial (ZINB) model without covariates. Furthermore, in this article the parameters and p are assumed to be independent. A future line of improvement would consist of introducing some copula that allows contemplating the dependence between the parameters, as a small value of corresponds to a large value of p.
Author Contributions
Conceptualization, M.D., M.S.A. and B.S.; Methodology, M.D. and M.S.A.; Software, M.D., M.S.A. and B.S.; Validation, M.S.A.; Formal analysis, M.D. and M.S.A.; Investigations, M.D., M.S.A. and B.S.; Resources, M.D., M.S.A. and B.S.; Data curation, B.S.; writing—original draft preparation, M.D., M.S.A. and B.S.; writing—review and editing, M.D., M.S.A. and B.S.; visualization, M.D. and M.S.A. supervision, Not applicable; project administration, Not applicable; funding acquisition, Not applicable. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors are grateful for the editors’ and reviewers’ invaluable time and suggestions to enhance the article’s presentation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aminzadeh, Mostafa S., and Min Deng. 2022. Bayesian Estimation of Renewal Function Based on Pareto-distributed Inter-arrival Times via an MCMC Algorithm. Variance 15: p1–p15. [Google Scholar]
- Angers, Jean-François, and Atanu Biswas. 2003. A Bayesian analysis of zero-inflated generalized Poisson model. Computational Statistics & Data Analysis 42: 37–46, ISSN 0167-9473. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillén. 2007. Risk Classification for Claim Counts A Comparative Analysis of Various Zero-inflated Mixed Poisson and Hurdle Models. North American Actuarial Journal 11: 110–31. [Google Scholar] [CrossRef]
- Chen, Kun, Rui Huang, Ngai Hang Chan, and Chun Yip Yau. 2019. Subgroup analysis of Zero-Inflated Poisson regression model with applications to insurance data. Insurance: Mathematics and Economics 86: 8–18. [Google Scholar] [CrossRef]
- Deng, Min, and Mostafa S. Aminzadeh. 2023. Bayesian Inference for the Loss Models via Mixture Priors. Risks 11: 156. [Google Scholar] [CrossRef]
- Ghosh, Sujit K., Pabak Mukhopadhyay, and Jye-Chyi Lu. 2006. Bayesian analysis of zero-inflated regression models. Journal of Statal Planning & Inference 136: 1360–75. [Google Scholar]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models from Data to Decisions, 3rd ed. New York: John Wiley. [Google Scholar]
- Lambert, Diane. 1992. Zero-Inflated Poisson regression, with an application to defects in manufacturing. Technometrics 34: 1–14. [Google Scholar] [CrossRef]
- Lee, Simon C. 2021. Addressing imbalanced insurance data through Zero-Inflated Poisson regression with boosting. ASTIN Bulletin: The Journal of the IAA 51: 27–55. [Google Scholar] [CrossRef]
- Meng, Shengwang, Yaqian Gao, and Yifan Huang. 2022. Actuarial intelligence in auto insurance: Claim frequency modeling with driving behavior features and improved boosted trees. Insurance: Mathematics and Economics 106: 115–27. [Google Scholar] [CrossRef]
- Mouatassim, Younès, and El Hadj Ezzahid. 2012. Poisson regression and Zero-Inflated Poisson regression: Applica- tion to private health insurance data. European Actuarial Journal 2: 187–204. [Google Scholar] [CrossRef]
- Mullahy, John. 1986. Specification and testing of some modified count data models. Journal of Econometrics 33: 341–65. [Google Scholar] [CrossRef]
- Perumean-Chaney, Suzanne E., Charity Morgan, David McDowall, and Inmaculada Aban. 2013. Zero-inflated and overdispersed: What’s one to do? Journal of Statistical Computation and Simulation 83: 1671–83. [Google Scholar] [CrossRef]
- So, Banghee, Jean-Philippe Boucher, and Emiliano A. Valdez. 2021. Synthetic dataset generation of driver telematics. Risks 9: 58. [Google Scholar] [CrossRef]
- Zhang, Pengcheng, David Pitt, and Xueyuan Wu. 2022. A new multivariate zero-inflated hurdle model with applications in automobile insurance. ASTIN Bulletin: The Journal of the IAA 52: 393–416. [Google Scholar] [CrossRef]
- Zhou, He, Wei Qian, and Yi Yang. 2022. Tweedie gradient boosting for extremely unbalanced zero-inflated data. Communications in Statistics-Simulation and Computation 51: 5507–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).