Towards Examining the Volatility of Top Market-Cap Cryptocurrencies Throughout the COVID-19 Outbreak and the Russia–Ukraine War: Empirical Evidence from GARCH-Type Models
Abstract
:1. Introduction
2. Literature Review
2.1. The Transformation of the Cryptocurrency Market: Adoption, Volatility, and Market Behavior
2.2. Prior Literature Towards Volatility in Cryptocurrencies: Insights from Market Forces, Speculation, and Global Events
2.3. Understanding Cryptocurrency Volatility Through the Lens of GARCH Models
2.4. Earlier Studies on Volatility Dynamics in Cryptocurrencies: GARCH and Emerging Methodologies
3. Research Hypotheses
4. Empirical Methodology
4.1. Selected Data
4.2. Quantitative Framework
4.2.1. ARCH Model Framework
4.2.2. GARCH(1,1) Model Framework
4.2.3. EGARCH(1,1) Model Framework
4.2.4. TGARCH(1,1) Model Framework
4.2.5. DCC GARCH(1,1) Model Framework
5. Empirical Results
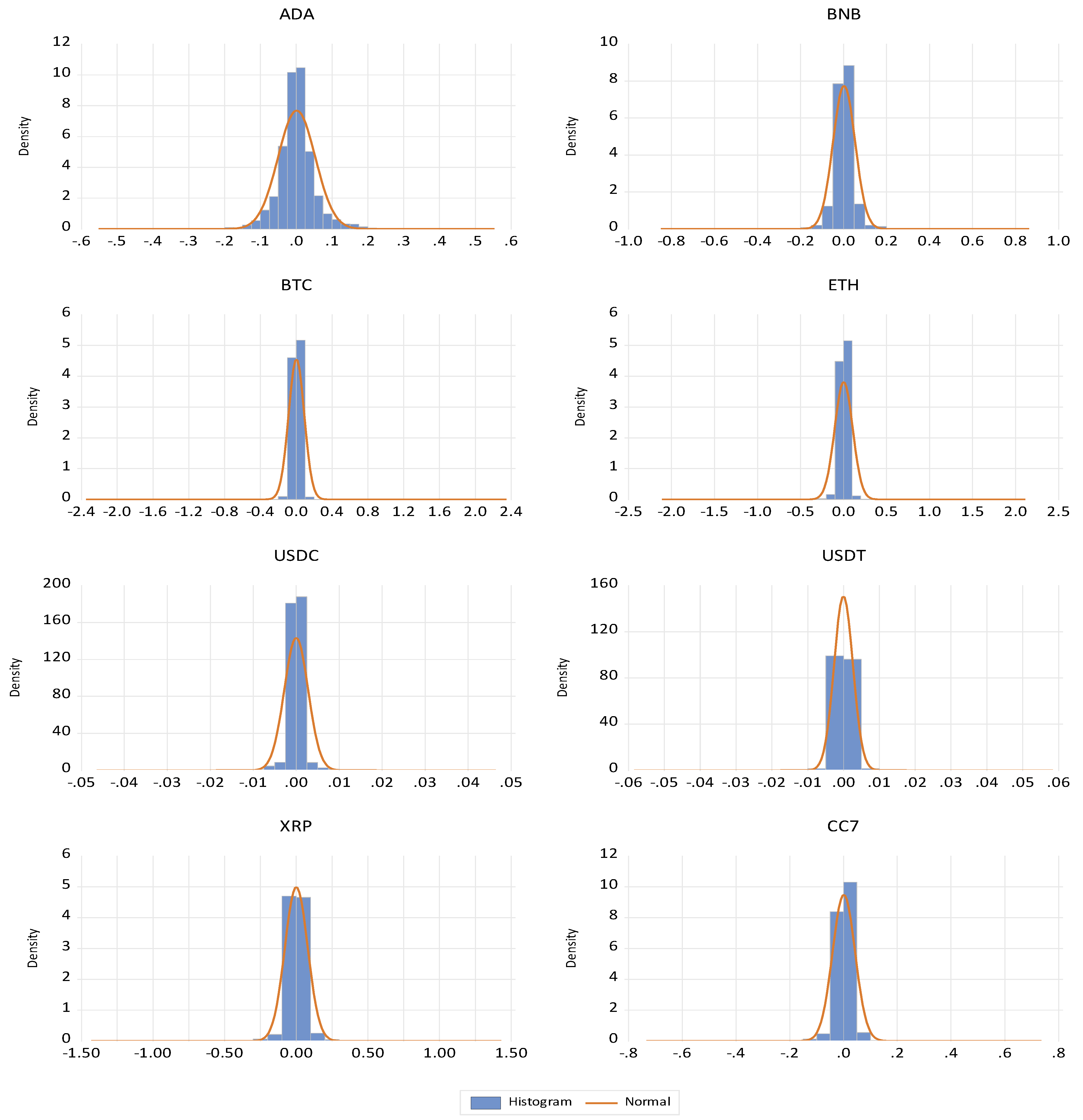
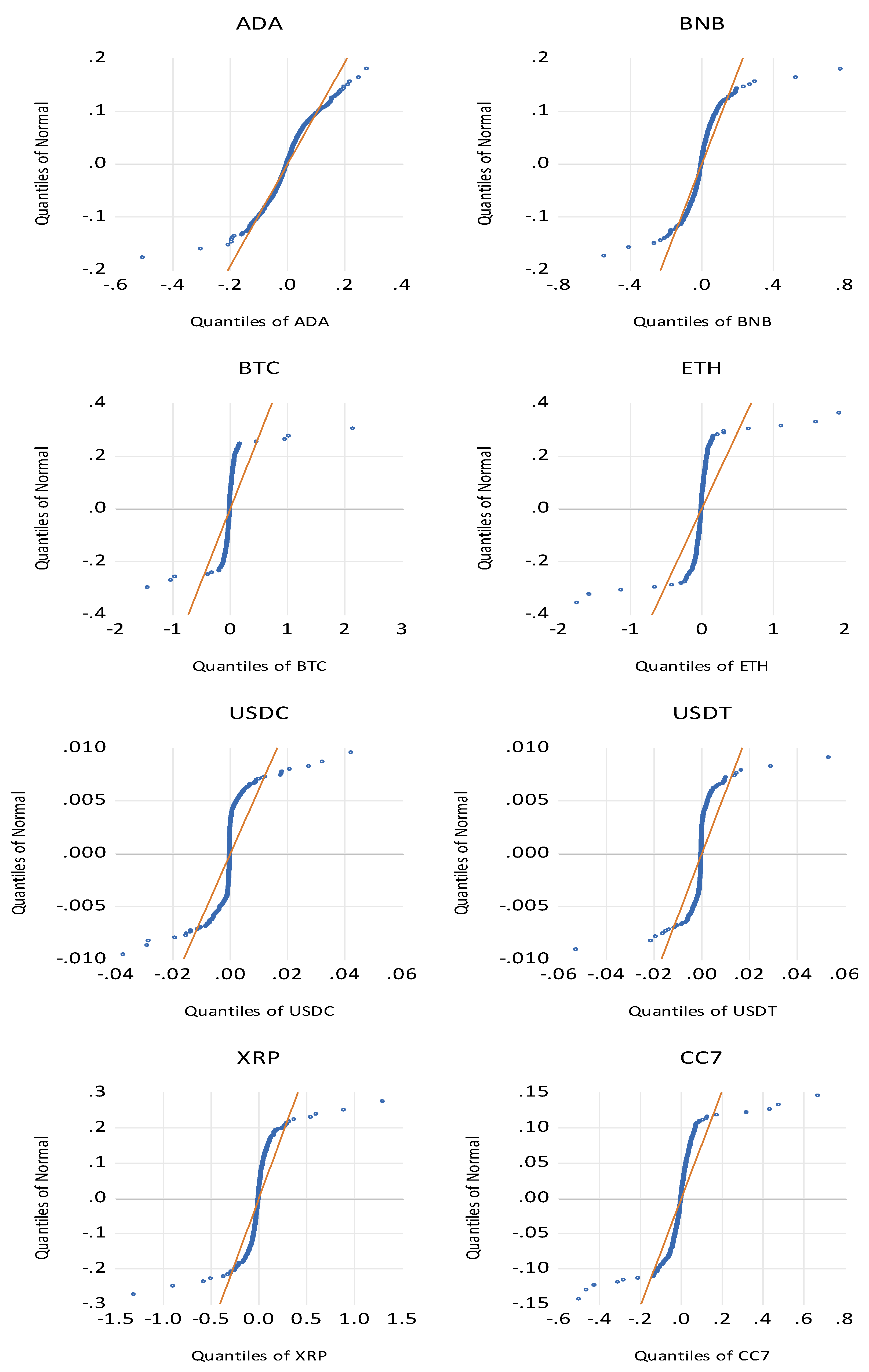
5.1. Descriptive Statistics
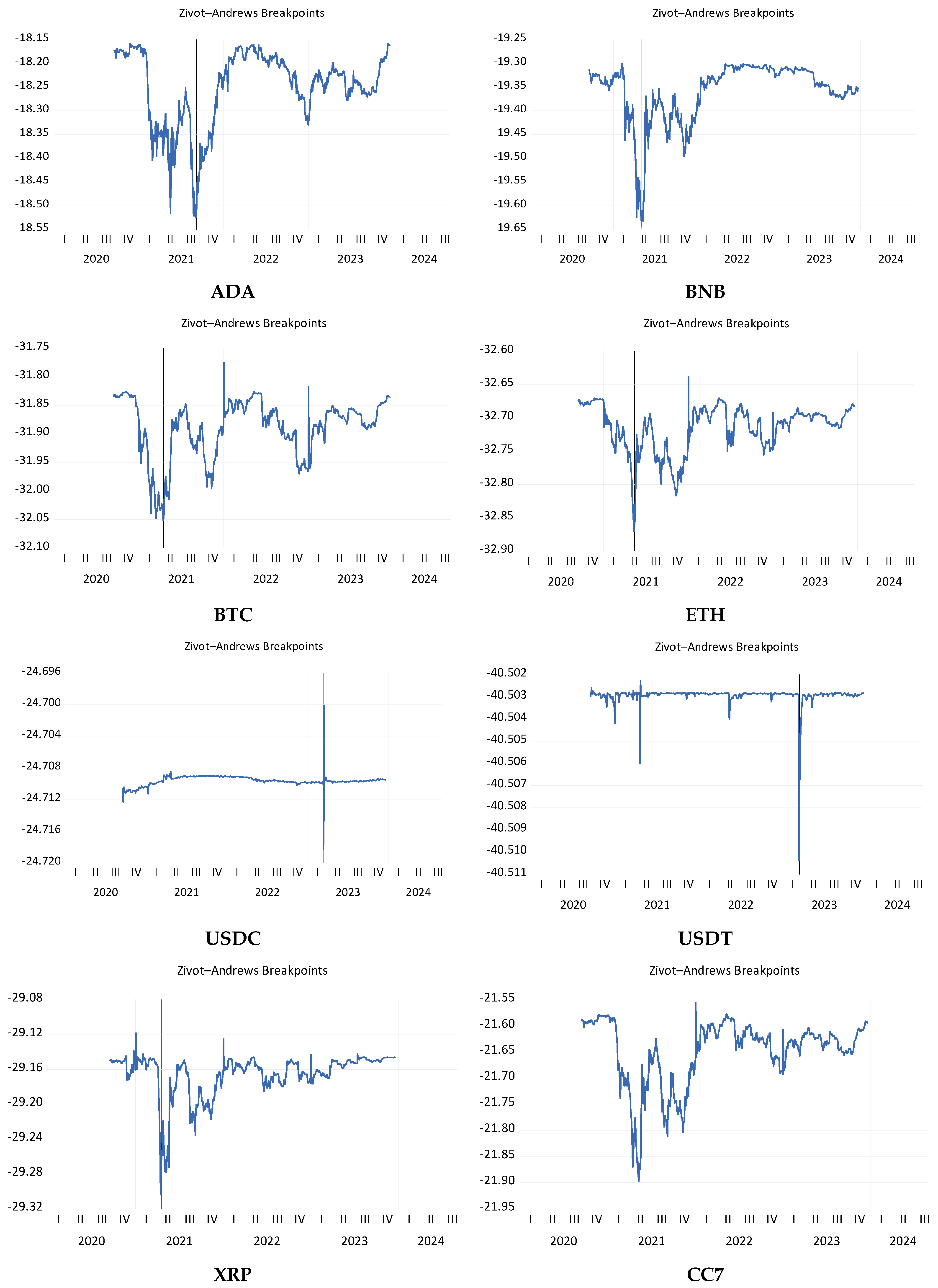
5.2. Stationarity Investigation
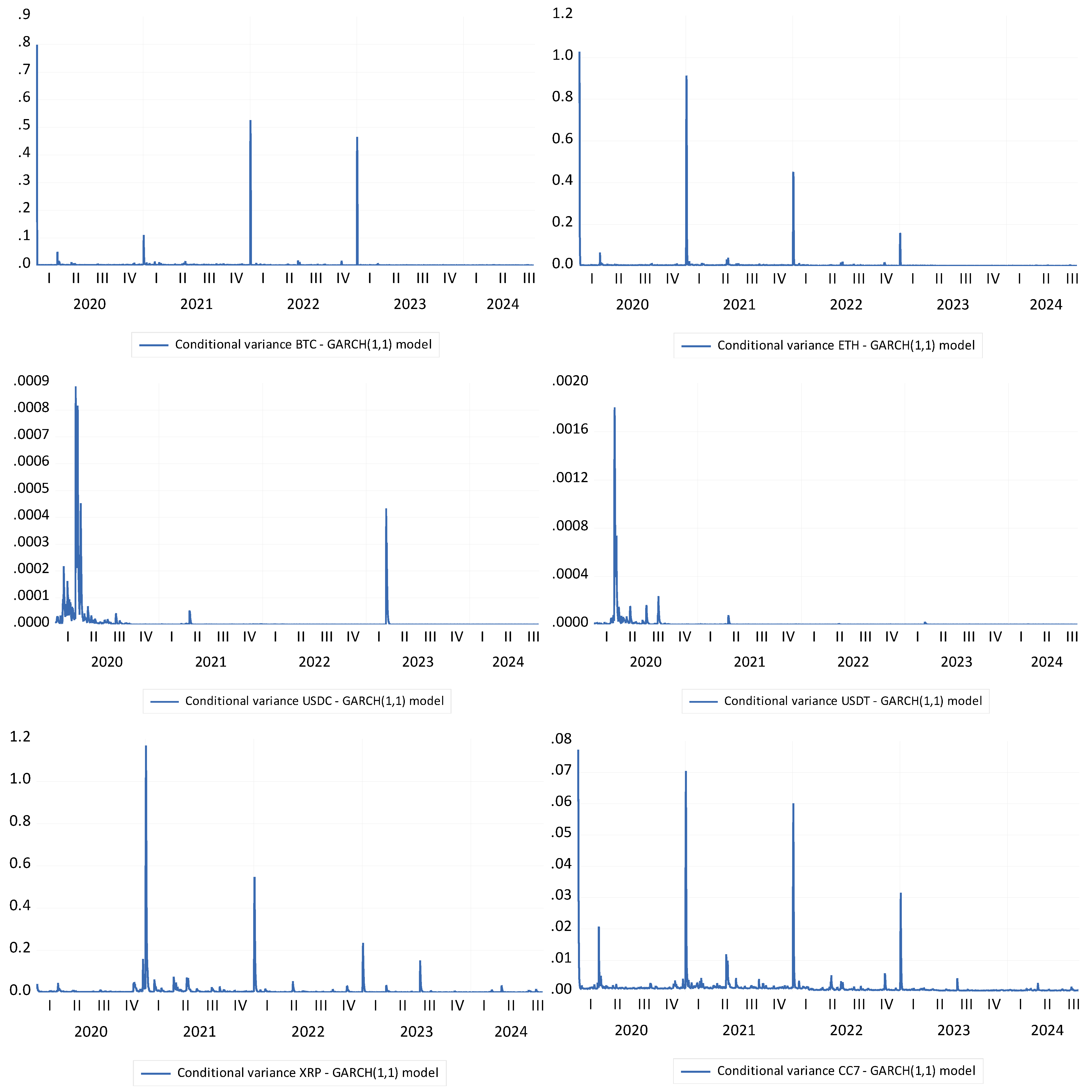
5.3. Outcomes of GARCH(1,1) Model
- H1.2 (volatility persistence during financial crises) is confirmed. The persistence of volatility, particularly during periods of crisis like COVID-19, is evident from the significant ARCH and GARCH coefficients across major cryptocurrencies (BTC, ETH, USDC, and CC7). This persistence indicates that shocks from these crises had a lasting effect on market volatility, which is consistent with the existing literature on volatility clustering during turbulent periods.
- H2.2 (amplified volatility during negative price shocks) is partially confirmed. While cryptocurrencies like BTC and ETH exhibited significant volatility increases during negative price shocks such as COVID-19, this effect was not uniform across all assets. For instance, stablecoins such as USDC and USDT showed minimal or no amplification, which suggests that, while negative shocks can heighten volatility for many digital assets, their impact may vary depending on the asset type and market dynamics.
- H3.2 (COVID-19’s stronger impact on volatility compared to the Russia–Ukraine war) is confirmed. The COVID-19 pandemic had a more widespread and pronounced effect on cryptocurrency volatility compared to the Russia–Ukraine war. Significant increases in volatility for assets like BTC, ETH, and USDC during the pandemic highlight the global economic shockwaves it generated, in contrast to the more localized impact of geopolitical instability from the war, which showed negative correlations with volatility in certain assets.
- H4.2 (stablecoins as risk-hedging instruments) is partially confirmed. While stablecoins such as USDC and USDT exhibited relative stability during the COVID-19 crisis, their role as effective risk-hedging instruments was somewhat limited. This limitation stems from issues like liquidity concerns and the reliance on traditional financial systems that could restrict their utility in extreme market conditions. Despite their relatively stable prices, stablecoins may not offer the full protection expected from traditional safe-haven assets.
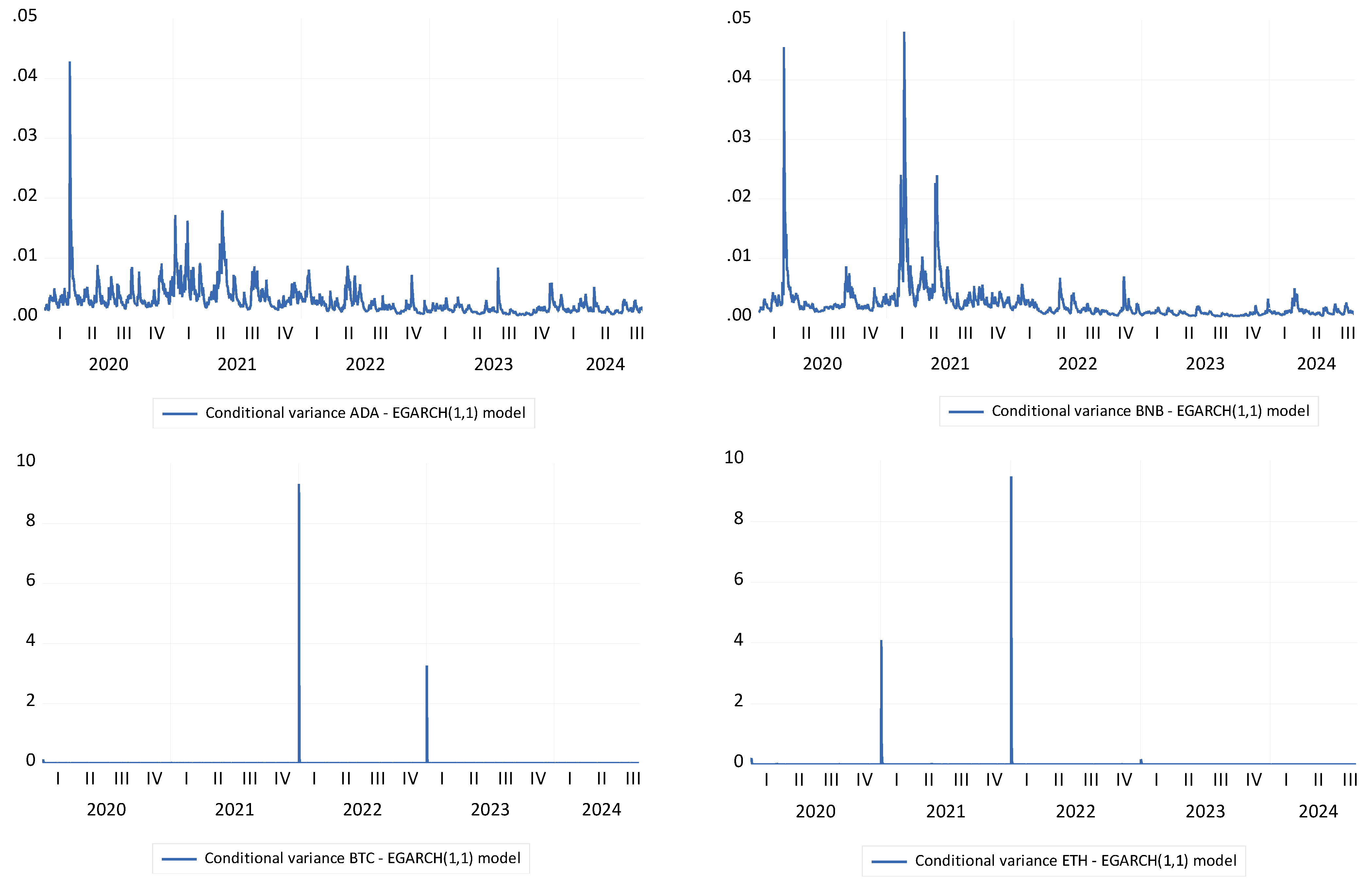
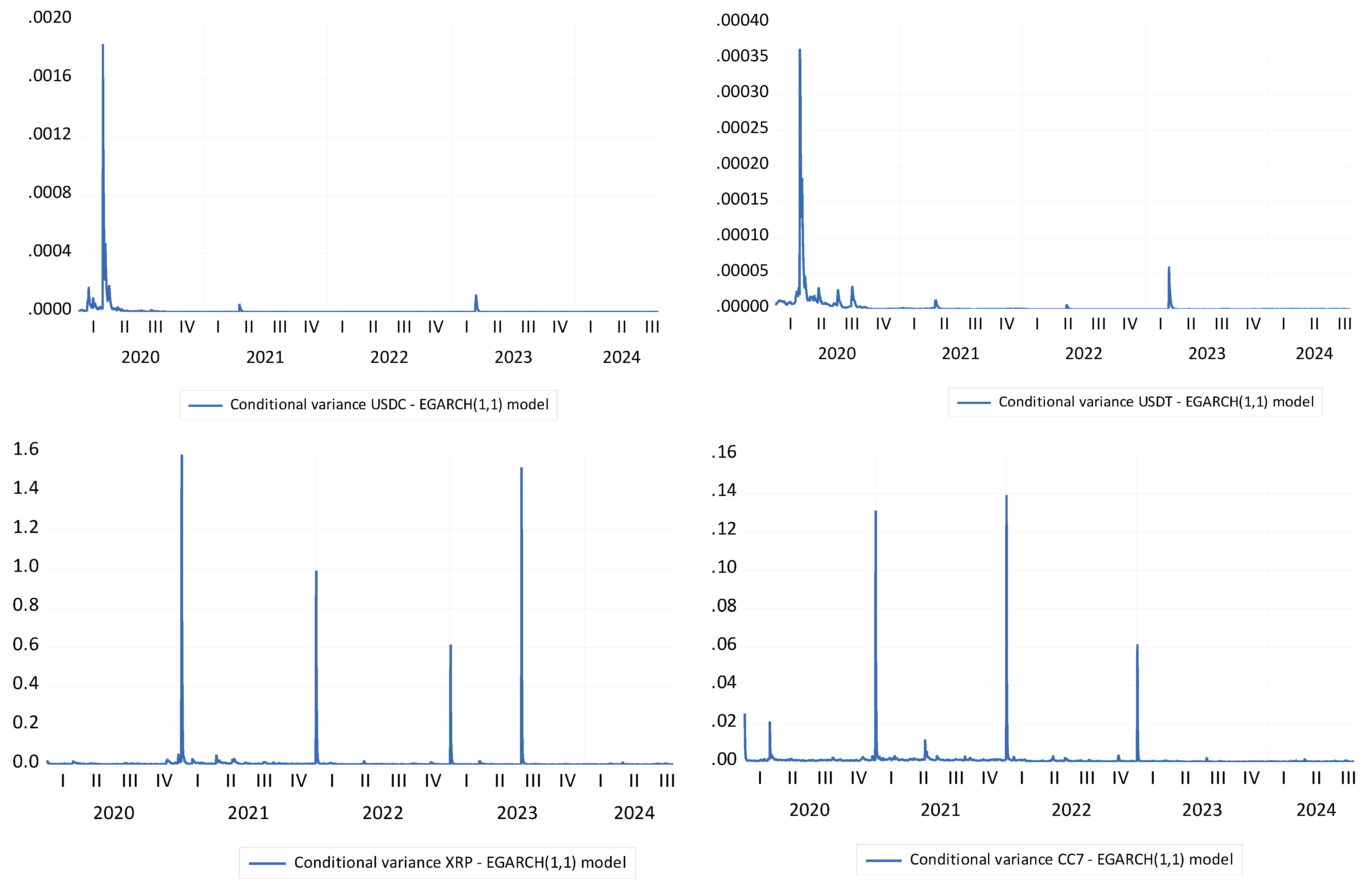
5.4. Outcomes of EGARCH(1,1) Model
- The results support H1.2, showing significant positive coefficients for lagged volatility terms (C(4) and C(6)), indicating that volatility persists over time. High volatility tends to follow high volatility, especially during crises like the COVID-19 pandemic, confirming volatility clustering.
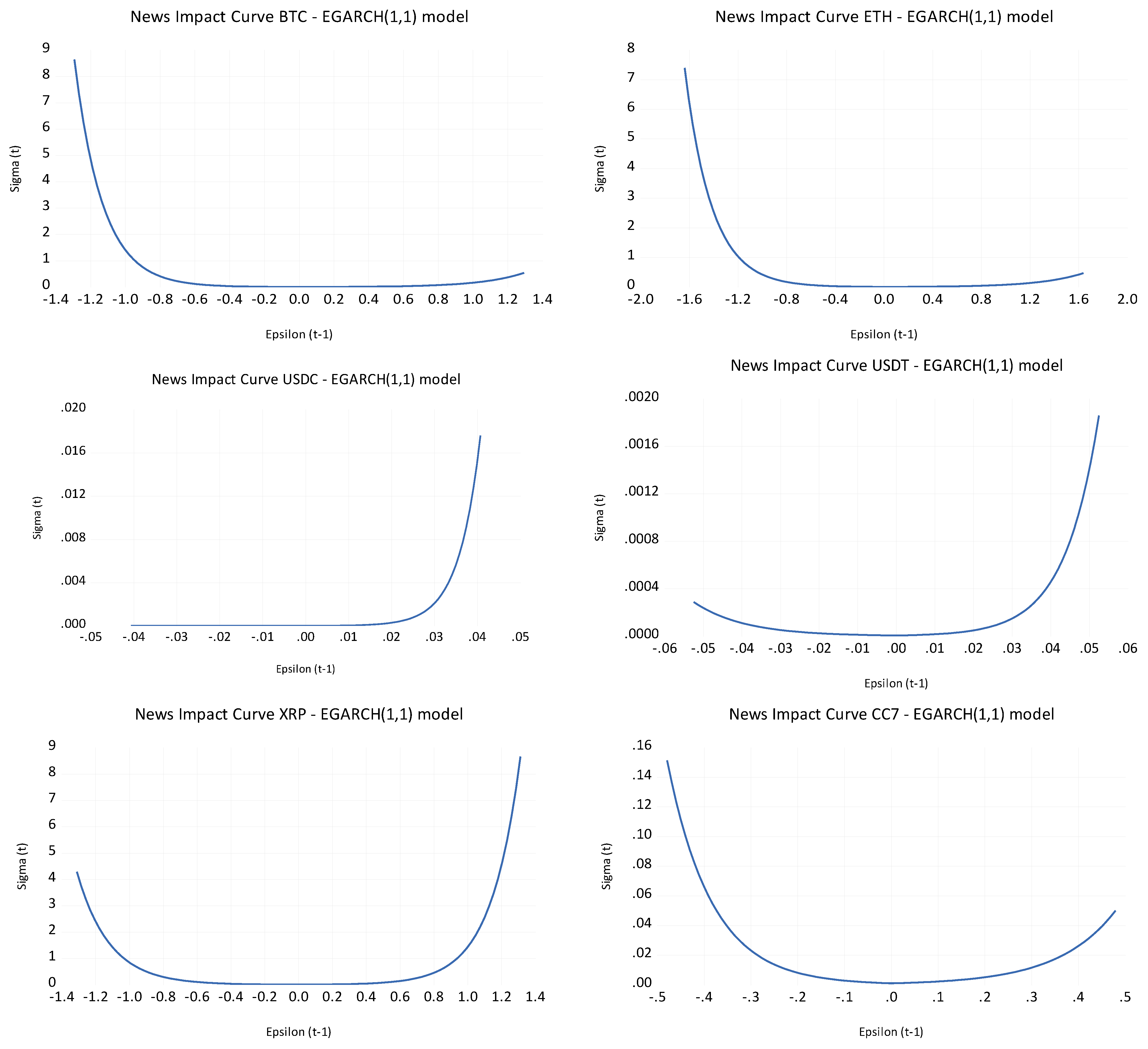
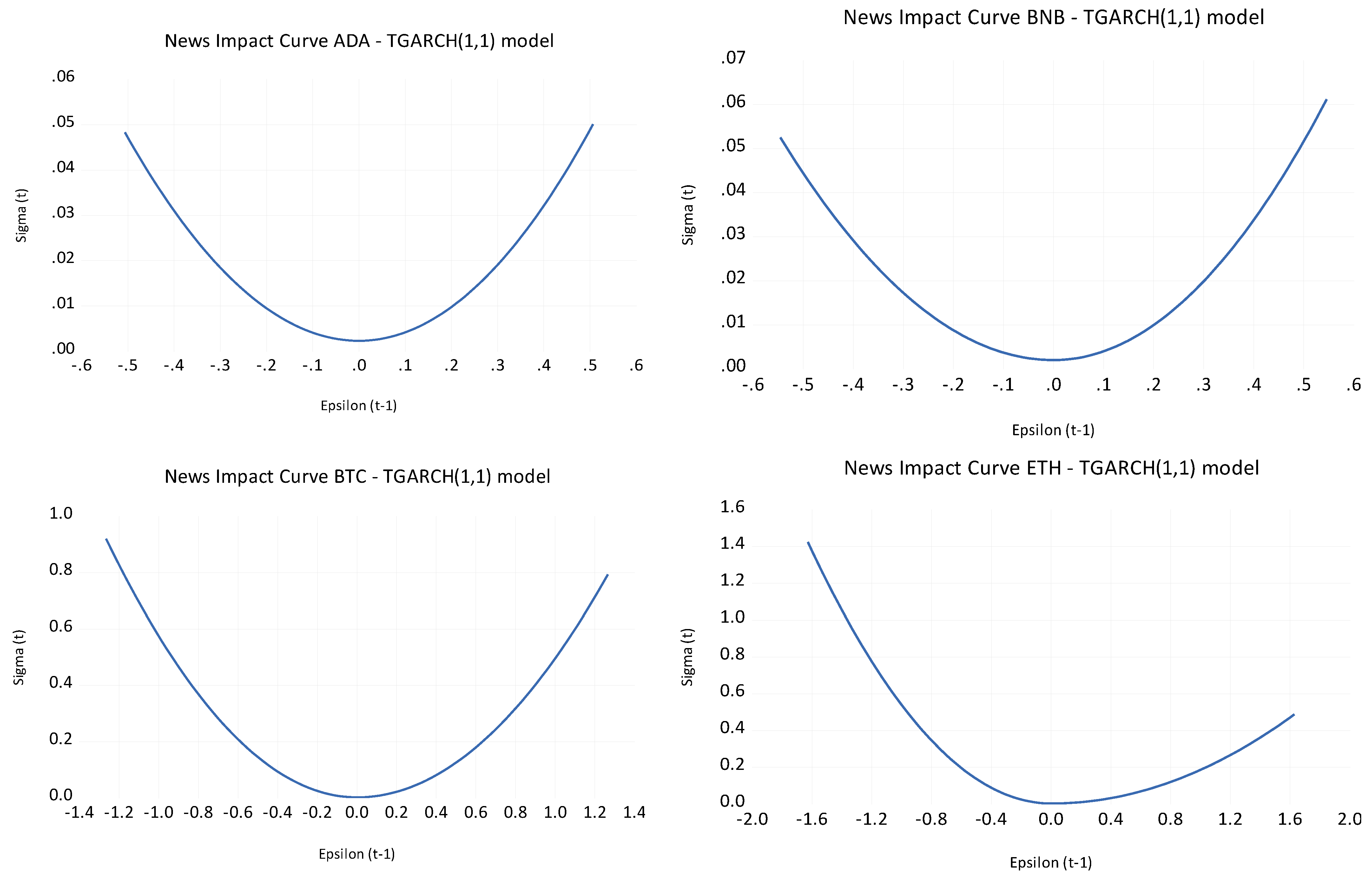
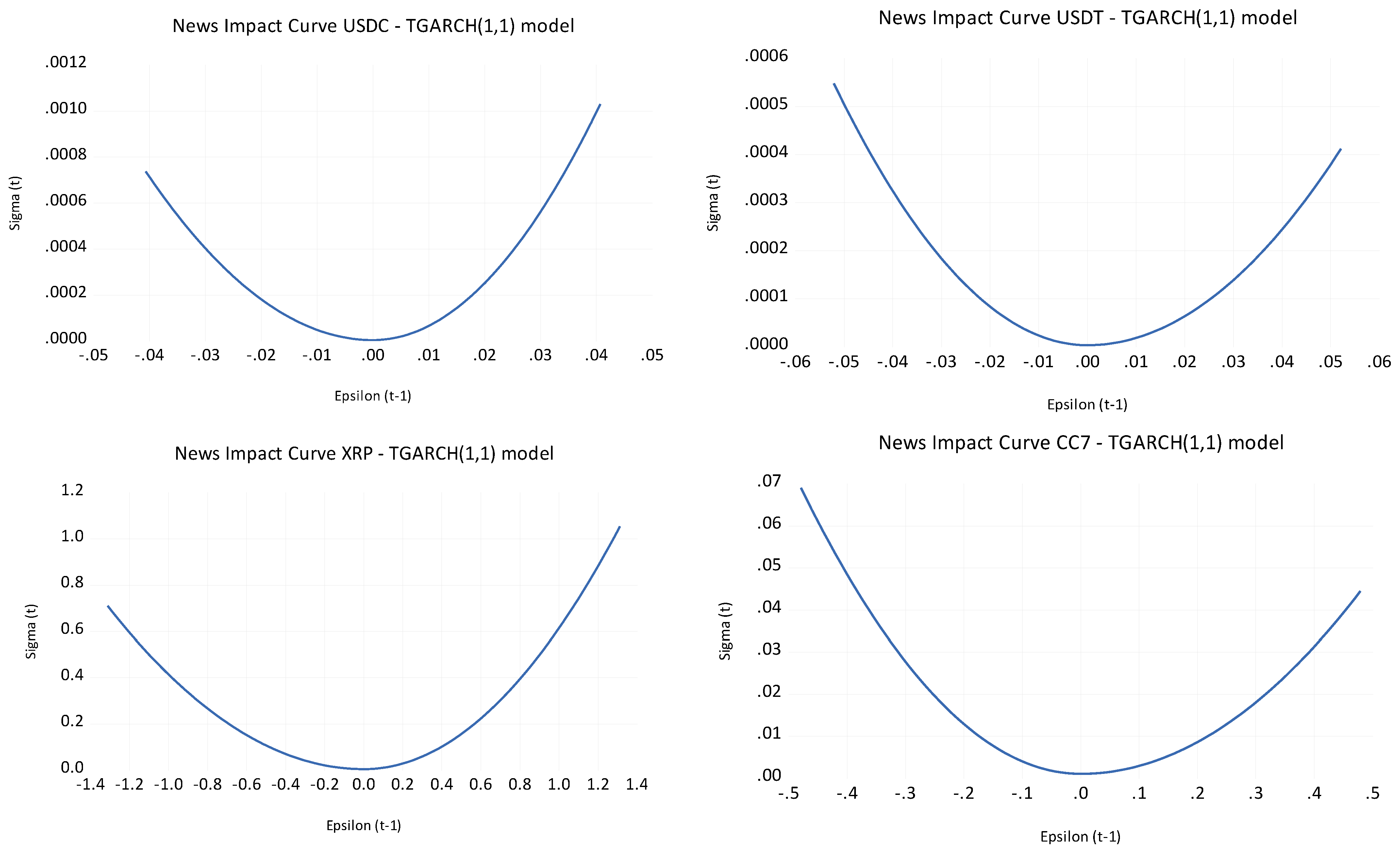
- H2.2 is confirmed by the negative and significant leverage effect (C(3)), which shows that negative shocks lead to higher volatility than positive shocks of equal magnitude. The news impact curves also reinforce this, highlighting that negative news has a stronger effect on volatility, especially for BTC, ETH, and CC7.
- The COVID-19 dummy (C(7)) has a stronger impact on volatility than the Russia–Ukraine war, supporting H3.2. The pandemic had a broader, more significant effect on market volatility, particularly for BTC and ETH, while the war’s impact was more localized.
- The results partially support H4.2. While USDC and USDT exhibit lower volatility than other cryptocurrencies; their lack of significant growth trends suggests they may not fully function as risk hedges, with liquidity being a limiting factor.
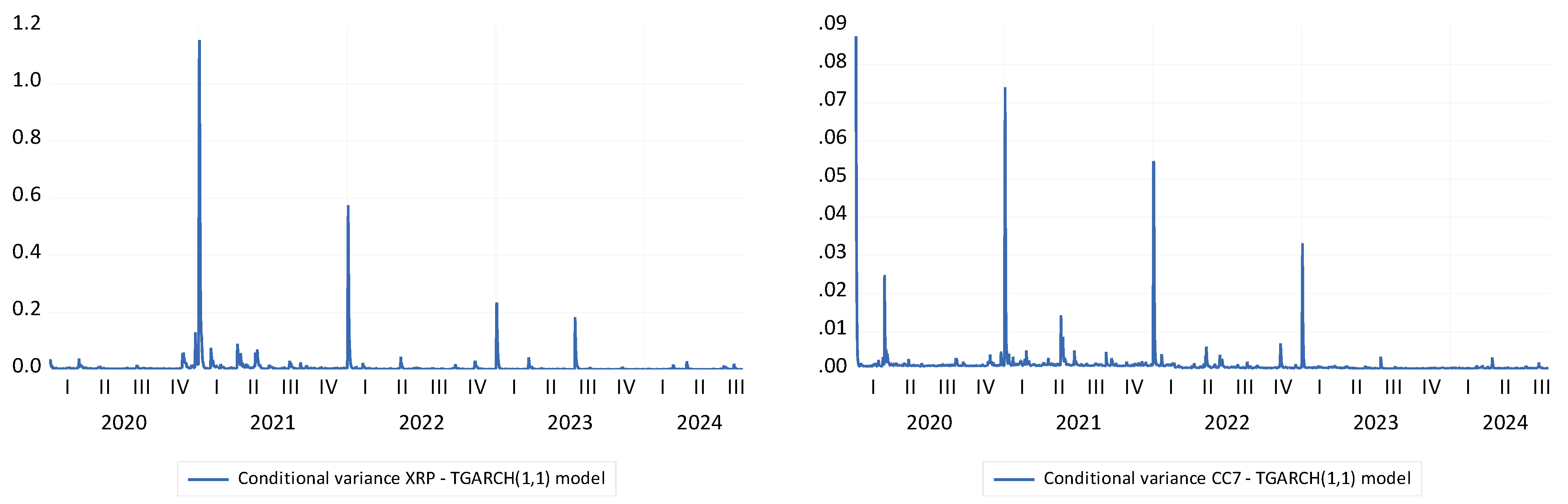
5.5. Outcomes of TGARCH(1,1) Model
- H1.2 is validated based on the significant GARCH term (GARCH(−1)) across most cryptocurrencies (except for BTC) and suggests volatility persistence. This means that past volatility influences future volatility, particularly in periods of market stress such as the COVID-19 pandemic and geopolitical tensions (WAR). The TGARCH(1,1) model shows that volatility clustering is a strong feature across assets, indicating that the persistence of volatility during crises is indeed observed.
- H2.2 is partially validated since the significant leverage effect observed for ETH (and partially for other cryptocurrencies) confirms that negative shocks tend to cause larger volatility spikes than positive shocks. This asymmetry is consistent with behavioral finance theories, where negative news or market shocks trigger more significant market reactions, especially in speculative assets like BTC, ETH, and CC7. However, for BTC and XRP, no significant leverage effect was observed, suggesting a more symmetric response to shocks in these assets, which means the hypothesis is partially supported.
- H3.2 is validated considering that the COVID-19 variable is statistically significant for BTC and ETH, confirming that the pandemic had a more substantial impact on these cryptocurrencies’ volatility than the geopolitical tensions arising from the Russia–Ukraine war. For most cryptocurrencies, the COVID-19 variable shows a positive and significant impact, further supporting this hypothesis.
- H4.2 is partially validated as the results suggest that stablecoins like USDC and USDT exhibit less volatility during positive returns, implying their role as safer assets. However, their volatility still rises during negative market events, but not to the extent seen in more volatile cryptocurrencies. This aligns with the hypothesis that stablecoins are more stable in times of market turbulence, but with the limitation that their volatility does increase, albeit to a lesser extent. Therefore, while the hypothesis is partially validated, it does not fully hold during extreme market stress.
5.6. Outcomes of DCC-GARCH Model
- H1.2 is validated because of the high persistence of volatility, especially with [beta1] values close to 1, which indicates that past volatility plays a significant role in predicting future volatility. This supports the hypothesis that volatility persists during financial crises, such as the COVID-19 outbreak and the Russia–Ukraine war.
- H2.2 is partially validated since the results show that short-term volatility shocks (alpha1) are significant for assets like BTC (0.7470) and ETH (0.4732), indicating higher sensitivity to shocks for these assets. However, cryptocurrencies like USDT and USDC show lower sensitivity, meaning this effect is not universally observed across all assets.
- H3.2 is not strongly supported for the reason that the dummies for COVID-19 (mxreg1) and the Russia–Ukraine war (mxreg2) generally show no significant impact on returns for most assets, except for a few cases (e.g., BTC). While the events may have influenced volatility, their direct impact on returns seems less pronounced.
- H4.2 is partially validated because while USDT and USDC exhibit lower volatility sensitivity to short-term shocks (alpha1), they show relatively higher shape parameters (indicating more extreme returns). This suggests that stablecoins might be more volatile in extreme market conditions, limiting their role as stable risk-hedging instruments. This result is consistent with the partial validation of H4.2.
6. Discussion of Empirical Findings
7. Concluding Remarks and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Aalborg, Halvor Aarhus, Peter Molnár, and Jon Erik de Vries. 2019. What can explain the price, volatility and trading volume of Bitcoin? Finance Research Letters 29: 255–65. [Google Scholar] [CrossRef]
- Apergis. 2022. COVID-19 and cryptocurrency volatility: Evidence from asymmetric modelling. Finance Research Letters 47: 102659. [Google Scholar] [CrossRef] [PubMed]
- Assaf, Ata, Avishek Bhandari, Husni Charif, and Ender Demir. 2022. Multivariate long memory structure in the cryptocurrency market: The impact of COVID-19. International Review of Financial Analysis 82: 102132. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, Steven J. Davis, and Stephen J. Terry. 2020. COVID-Induced Economic Uncertainty. NBER Working Paper No. 26983. Cambridge, MA: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Elie Bouri, Rangan Gupta, and David Roubaud. 2017. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Economic Modelling 64: 74–81, ISSN 0264-9993. [Google Scholar] [CrossRef]
- Bariviera, Aurelio F. 2017. The inefficiency of Bitcoin revisited: A dynamic approach. Economics Letters 161: 1–4. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas Dimpfl. 2018. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Baur, Dirk G., KiHoon Hong, and Adrian D. Lee. 2018. Bitcoin: Medium of exchange or speculative assets? Journal of International Financial Markets, Institutions and Money 54: 177–89. [Google Scholar] [CrossRef]
- Ben-Ahmed, K., S. Theiri, and N. Kasraoui. 2023. Short-term effect of COVID-19 pandemic on cryptocurrency markets: A DCC-GARCH model analysis. Helyion 9: e18847. [Google Scholar] [CrossRef]
- Beneki, Christina, Alexandros Koulis, Nikolaos A. Kyriazis, and Stephanos Papadamou. 2019. Investigating volatility transmission and hedging properties between Bitcoin and Ethereum. Research in International Business and Finance 48: 219–27. [Google Scholar] [CrossRef]
- Bentouir, N., A. Bendob, El Amine M. Abdelli, B. S. Maliki, M. Kertous, and A. Khalil. 2022. How the Cryptocurrencies React to Covid-19 Pandemic? An Empirical Study Using DCC GARCH Model (2019–2021). In Digital Economy, Business Analytics, and Big Data Analytics Applications. Edited by G. S. Yaseen. Studies in Computational Intelligence. Cham: Springer, vol. 1010. [Google Scholar] [CrossRef]
- Bergsli, Lykke Øverland, Andrea Falk Lind, Peter Molnár, and Michał Polasik. 2022. Forecasting volatility of Bitcoin. Research in International Business and Finance 59: 101540. [Google Scholar] [CrossRef]
- Bouoiyour, J., and R. Selmi. 2015. Bitcoin Price: Is it Really that New Round of Volatility Can Be on Way? MPRA Paper No. 65580, CATT. Pau: University of Pau. Available online: https://mpra.ub.uni-muenchen.de/65580/ (accessed on 1 August 2024).
- Brière, Marie, Kim Oosterlinck, and Ariane Szafarz. 2015. Virtual currency, tangible return: Portfolio diversification with bitcoin. Journal of Asset Management 16: 365–73. [Google Scholar] [CrossRef]
- Brini, Alessio, and Jimmie Lenz. 2022. Assessing the resiliency of investors against cryptocurrency market crashes through the leverage effect. Economics Letters 220: 110885. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, and Timur Zekokh. 2019. Modelling volatility of cryptocurrencies using Markov-Switching models. Research in International Business and Finance 48: 143–55. [Google Scholar] [CrossRef]
- Chi, Yeguang, and Wenyan Hao. 2021. Volatility models for cryptocurrencies and applications in the options market. Journal of International Financial Markets, Institutions & Money 75: 101421. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Stephen Chan, Saralees Nadarajah, and Joerg Osterrieder. 2017. GARCH modelling of cryptocurrencies. Journal of Risk and Financial Management 10: 17. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Miroslava Rajcaniova, and d’Artis Kancs. 2016. The Economics of BitCoin Price Formation. Applied Economics 48: 1799–815. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Miroslava Rajcaniova, and d’Artis Kancs. 2018. Virtual relationships: Short and long-run evidence from Bitcoin and altcoin markets. Journal of International Financial Markets, Institutions and Money 52: 173–95. [Google Scholar] [CrossRef]
- Conlon, Thomas, and Richard McGee. 2020. Safe Haven or Risky Hazard? Bitcoin during the COVID-19 Bear Market. Finance Research Letters 35: 101607. [Google Scholar] [CrossRef] [PubMed]
- Conrad, Christian, Anessa Custovic, and Eric Ghysels. 2018. Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. Journal of Risk and Financial Management 11: 23. [Google Scholar] [CrossRef]
- Corbet, Shaen, Andrew Meegan, Charles Larkin, Brian Lucey, and Larisa Yarovaya. 2018. Exploring the dynamic relationships between cryptocurrencies and other financial assets. Economics Letters 165: 28–34. [Google Scholar] [CrossRef]
- Corbet, Shaen, Yang (Greg) Hou, Yang Hu, Charles Larkin, Brian Lucey, and Les Oxley. 2022. Cryptocurrency liquidity and volatility interrelationships during the COVID-19 pandemic. Finance Research Letters 45: 102137, ISSN 1544-6123. [Google Scholar] [CrossRef] [PubMed]
- Cryptomus. 2024. How Many Cryptocurrencies Are There? Cryptomus. Available online: https://cryptomus.com/blog/how-many-cryptocurrencies-are-there (accessed on 1 August 2024).
- Dwyer, Gerald P. 2015. The economics of Bitcoin and similar private digital currencies. Journal of Financial Stability 17: 81–91. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016a. Bitcoin, gold and the dollar—A GARCH volatility analysisBitcoin, gold and the dollar-A GARCH volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016b. Hedging capabilities of bitcoin. Is it the virtual gold? Finance Research Letters 16: 139–44. [Google Scholar] [CrossRef]
- Engle, Robert F., and Tim Bollerslev. 1986. Modelling the persistence of conditional variances. Econometric Reviews 5: 1–50. [Google Scholar] [CrossRef]
- Fang, Yi, and Zhiquan Shao. 2022. The Russia-Ukraine conflict and volatility risk of commodity markets. Finance Research Letters 50: 103264. [Google Scholar] [CrossRef]
- Ferreira, Marisa, Francisco J. F. Silva, and Gualter Couto. 2024. How risky are cryptocurrencies? Applied Economics 56: 8320–31. [Google Scholar] [CrossRef]
- Forbes. 2022. Bitcoin Price Falls After Russia Attacks Ukraine. Available online: https://edition.cnn.com/2022/02/24/business/bitcoin-price-drops-ukraine-russia-attack/index.html?utm_source=chatgpt.com (accessed on 1 August 2024).
- Foroutan, Parisa, and Salim Lahmiri. 2022. The effect of COVID-19 pandemic on return-volume and return-volatility relationships in cryptocurrency markets. Chaos, Solitons & Fractals 162: 112443. [Google Scholar] [CrossRef]
- Fung, Kennard, Jiin Jeong, and Javier Pereira. 2022. More to cryptos than bitcoin: A GARCH modelling of heterogeneous cryptocurrencies. Finance Research Letters 47: 102544. [Google Scholar] [CrossRef]
- Grinberg, Reuben. 2011. Bitcoin: An innovative alternative digital currency. Hastings Science & Technology Law Journal 4: 160–207. [Google Scholar]
- Hampl, Filip, Dagmar Vágnerová Linnertová, and Matúš Horváth. 2024. Crypto havens during war times? Evidence from the Russian invasion of Ukraine. The North American Journal of Economics and Finance 71: 106294. [Google Scholar] [CrossRef]
- Hattori, Takahiro. 2020. A forecast comparison of volatility models using realized volatility: Evidence from the Bitcoin market. Applied Economics Letters 27: 591–95. [Google Scholar] [CrossRef]
- Huang, Jing-Zhi, Jun Ni, and Li Xu. 2022. Leverage effect in cryptocurrency markets. Pacific-Basin Finance Journal 73: 101773. [Google Scholar] [CrossRef]
- James, Nick, Max Menzies, and Jennifer Chan. 2021. Changes to the extreme and erratic behaviour of cryptocurrencies during COVID-19. Physica A: Statistical Mechanics and Its Applications 565: 125581. [Google Scholar] [CrossRef]
- Kamal, Md Rajib, and Ranik Raaen Wahlstrøm. 2023. Cryptocurrencies and the threat versus the act event of geopolitical risk. Finance Research Letters 57: 104224. [Google Scholar] [CrossRef]
- Karagiannopoulou, Sofia, Konstantina Ragazou, Ioannis Passas, Alexandros Garefalakis, and Nikolaos Sariannidis. 2023. The Impact of the COVID-19 Pandemic on the Volatility of Cryptocurrencies. International Journal of Financial Studies 11: 50. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2019. An empirical investigation of volatility dynamics in the cryptocurrency market. An empirical investigation of volatility dynamics in the cryptocurrency market. Research in International Business and Finance 50: 322–35. [Google Scholar] [CrossRef]
- Khan, Mrestyal, and Maaz Khan. 2021. Cryptomarket Volatility in Times of COVID-19 Pandemic: Application of GARCH Models. Economic Research Guardian 11: 170–81. [Google Scholar]
- Kim, Jong-Min, Chulhee Jun, and Junyoup Lee. 2021. Forecasting the Volatility of the Cryptocurrency Market by GARCH and Stochastic Volatility. Mathematics 9: 1614. [Google Scholar] [CrossRef]
- Klein, Tony, Hien Pham Thu, and Thomas Walther. 2018. Bitcoin is not the New Gold—A comparison of volatility, correlation, and portfolio performance. International Review of Financial Analysis 59: 105–6. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2015. What are the Main Drivers of the Bitcoin Price?: Evidence from Wavelet Coherence Analysis. PLoS ONE 10: e0123923. [Google Scholar] [CrossRef]
- Kyriazis, Νikolaos A., Kalliopi Daskalou, Marios Arampatzis, Paraskevi Prassa, and Evangelia Papaioannou. 2019. Estimating the volatility of cryptocurrencies during bearish markets by employing GARCH models. Heliyon 5: e02239. [Google Scholar] [CrossRef]
- Long, Huaigang, Ender Demir, Barbara Będowska-Sójka, Adam Zaremba, and Syed Jawad Hussain Shahzad. 2022. Is geopolitical risk priced in the cross-section of cryptocurrency returns? Finance Research Letters 49: 103131. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1990. Stationarity and Persistence in the GARCH(1,1) Model. Econometric Theory 6: 318–34. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Polasik, Michal, Anna Iwona Piotrowska, Tomasz Piotr Wisniewski, Radoslaw Kotkowski, and Geoffrey Lightfoot. 2015. Price Fluctuations and the Use of Bitcoin: An Empirical Inquiry. International Journal of Electronic Commerce 20: 9–49. [Google Scholar] [CrossRef]
- Pratas, Tiago E., Filipe R. Ramos, and Lihki Rubio. 2024. Forecasting bitcoin volatility: Exploring the potential of deep learning. Eurasian Economic Review 13: 285–305. [Google Scholar] [CrossRef]
- Salisu, Afees A., and Ahamuefula E. Ogbonna. 2022. The return volatility of cryptocurrencies during the COVID-19 pandemic: Assessing the news effect. Global Finance Journal 54: 100641. [Google Scholar] [CrossRef]
- Satoshi, N. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/en/bitcoin-paper (accessed on 1 August 2024).
- Symitsi, Efthymia, and Konstantinos J. Chalvatzis. 2018. Return, volatility and shock spillovers of Bitcoin with energy and technology companies. Economics Letters 170: 127–30. [Google Scholar] [CrossRef]
- Taera, Edosa Getachew, Budi Setiawan, Adil Saleem, Andi Sri Wahyuni, Daniel K.S. Chang, Robert Jeyakumar Nathan, and Zoltan Lakner. 2023. The impact of COVID-19 and Russia–Ukraine war on the financial asset volatility: Evidence from equity, cryptocurrency and alternative assets. Journal of Open Innovation: Technology, Market, and Complexity 9: 100116. [Google Scholar] [CrossRef]
- Tan, Chia-Yen, You-Beng Koh, Kok-Haur Ng, and Kooi-Huat Ng. 2021. Dynamic volatility modelling of Bitcoin using time-varying transition probability Markov-switching GARCH model. North American Journal of Economics and Finance 56: 101377. [Google Scholar] [CrossRef]
- Theiri, T. Saliha, Ramzi Nekhili, and Jahangir Sultan. 2023. Cryptocurrency liquidity during the Russia–Ukraine war: The case of Bitcoin and Ethereum. Journal of Risk Finance 24: 59–71. [Google Scholar] [CrossRef]
- TheStreet. 2025. Crypto Market Sees $2 Billion in Liquidations, Worse Than COVID and FTX Crashes. Available online: https://www.thestreet.com/crypto/markets/crypto-market-sees-2-billion-in-liquidations-worse-than-covid-and-ftx-crashes- (accessed on 1 August 2024).
- Tiwari, Aviral Kumar, Satish Kumar, and Rajesh Pathak. 2019. Modelling the dynamics of Bitcoin and Litecoin: GARCH versus stochastic volatility models. Applied Economics 51: 4073–82. [Google Scholar] [CrossRef]
- Urquhart, Andrew. 2016. The inefficiency of Bitcoin. Economics Letters 148: 80–82. [Google Scholar] [CrossRef]
- Wang, Changlin. 2021. Different GARCH model analysis on returns and volatility in Bitcoin. Data Science in Finance and Economics 1: 37–59. [Google Scholar] [CrossRef]
- Yarovaya, Larisa, Roman Matkovskyy, and Akanksha Jalan. 2022. The COVID-19 Black Swan Crisis: Reaction and Recovery of Various Financial Markets. Research in International Business and Finance 59: 101521. [Google Scholar] [CrossRef]
- Yermack, David. 2013. Is Bitcoin a Real Currency? An Economic Appraisal. The National Bureau of Economic Research 36: 31–43. [Google Scholar]
- Yi, Shuyue, Zishuang Xu, and Gang-Jin Wang. 2018. Volatility connectedness in the cryptocurrency market: Is Bitcoin a dominant cryptocurrency? International Review of Financial Analysis 60: 98–114. [Google Scholar] [CrossRef]
- Yıldırım, Hakan, and Festus Victor Bekun. 2023. Predicting volatility of bitcoin returns with ARCH, GARCH and EGARCH models. Future Business Journal 9: 75. [Google Scholar] [CrossRef]
- Zhang, Pengcheng, Kunpeng Xu, and Jiayin Qi. 2023. The impact of regulation on cryptocurrency market volatility in the context of the COVID-19 pandemic—Evidence from China. Economic Analysis and Policy 80: 222–46. [Google Scholar] [CrossRef]




| Digital Asset | Abbreviation | Description |
|---|---|---|
| Bitcoin | BTC | The world’s first decentralized digital currency, introduced in 2009 by an anonymous person or group using the pseudonym Satoshi Nakamoto. It operates on a peer-to-peer network without the need for intermediaries like banks or governments. Satoshi (2008) argued that a peer-to-peer electronic cash system enables direct online payments between parties without the need for a financial institution. Transactions are verified by network nodes through cryptography and recorded on a public, immutable blockchain ledger. |
| Ethereum | ETH | A decentralized, open-source blockchain platform that enables the creation of smart contracts and decentralized applications (DApps). It was proposed in 2013 by Vitalik Buterin and launched in 2015. Unlike Bitcoin, which primarily serves as a digital currency, Ethereum is designed to be a programmable blockchain that supports a wide range of applications, including DeFi (Decentralized Finance), NFTs (Non-Fungible Tokens), and DAOs (Decentralized Autonomous Organizations). |
| Tether | USDT | A stablecoin that is pegged to the value of the U.S. dollar (USD) on a 1:1 basis. It was launched in 2014 by the company Tether Limited and operates on multiple blockchain networks. USDT is designed to provide the stability of fiat currency while maintaining the efficiency and transparency of blockchain technology. |
| BNB | BNB | The native cryptocurrency of the Binance ecosystem, originally launched in 2017 as an ERC-20 token on the Ethereum blockchain. Later, it migrated to its own blockchain, the BNB Chain (formerly Binance Smart Chain and Binance Chain). BNB was created by Binance, one of the world’s largest cryptocurrency exchanges, to be used for transaction fees, trading, and various applications within the Binance ecosystem. |
| USDC | USDC | A stablecoin pegged to the U.S. dollar (USD) at a 1:1 ratio. It was launched in 2018 by Circle in partnership with Coinbase, operating under the Centre Consortium. USDC is backed by fiat reserves, including cash and short-term U.S. government bonds, making it a reliable digital equivalent of the dollar. It is widely used in decentralized finance (DeFi), cross-border payments, and cryptocurrency trading. |
| XRP | XRP | A digital asset and the native cryptocurrency of the XRP Ledger (XRPL), an open-source, decentralized blockchain designed for fast and efficient cross-border payments. It was created in 2012 by Ripple Labs (San Francisco, CA, USA) to facilitate instant, low-cost international transactions for banks, financial institutions, and payment providers. Unlike Bitcoin and Ethereum, XRP does not rely on mining; instead, it uses a unique consensus mechanism for transaction validation. |
| Cardano | ADA | A decentralized, open-source blockchain platform designed for scalability, security, and sustainability. It was founded in 2017 by Charles Hoskinson, one of the co-founders of Ethereum, and is developed by Input Output Global (IOG). Cardano aims to improve upon previous blockchain networks by using a scientific, research-driven approach to development. |
| Date Meaning | Price (USD) | BTC | ETH | XRP | BNB | USDC | USDT | ADA |
|---|---|---|---|---|---|---|---|---|
| Type | ||||||||
| Cryptocurrency | Token | Cryptocurrency | Cryptocurrency | Stablecoin | Stablecoin | Cryptocurrency | ||
| Onset of the sample | 1 January 2020 | 29,260 | 730 | 0.238 | 14 | 1.0041 | 0.99984 | 0.0335 |
| WHO declaration of COVID-19 | 11 March 2020 | 7859 | 193 | 0.207 | 17 | 0.9973 | 0.99881 | 0.0396 |
| Commencement of the Russia–Ukraine war | 24 February 2022 | 38,400 | 2636 | 0.703 | 361 | 1.0000 | 1.00064 | 0.8534 |
| WHO officially declared the end of COVID-19 as a global health emergency | 5 May 2023 | 29,525 | 1990 | 0.467 | 327 | 1.0000 | 1.00102 | 0.3947 |
| End of the sample | 1 September 2024 | 58,419 | 2502 | 0.5600 | 513 | 1.0000 | 1.0000 | 0.3317 |
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| Mean | 0.001265 | 0.002583 | 0.001665 | 0.001856 | −7.28E-06 | −3.79E-06 | 0.000501 | 0.001123 |
| Median | 0.000442 | 0.001398 | 0.000888 | 0.001739 | 2.00E-06 | −6.00E-06 | −0.00014 | 0.001875 |
| Maximum | 0.279436 | 0.780889 | 2.147523 | 1.931678 | 0.042439 | 0.053393 | 1.304429 | 0.672576 |
| Minimum | −0.50364 | −0.54281 | −1.43616 | −1.73876 | −0.03723 | −0.05257 | −1.30652 | −0.49785 |
| Std. Dev. | 0.051889 | 0.051413 | 0.087432 | 0.104477 | 0.00278 | 0.002641 | 0.079804 | 0.042004 |
| Skewness | −0.22739 | 1.81669 | 6.087529 | 1.088167 | 1.16401 | 0.554669 | 0.086384 | 1.244048 |
| Kurtosis | 11.13653 | 51.81022 | 296.5039 | 194.2136 | 90.67 | 208.7554 | 110.7716 | 87.92355 |
| Jarque–Bera | 4717.871 | 170,190.2 | 6,130,383 | 2,597,807 | 546,413.4 | 3,007,656 | 825,131.3 | 512,792.9 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 1705 | 1705 | 1705 | 1705 | 1705 | 1705 | 1705 | 1705 |
| Covariance | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
| ADA | 0.002691 | |||||||
| BNB | 0.001531 | 0.002642 | ||||||
| BTC | 0.000840 | 0.002014 | 0.007640 | |||||
| ETH | 0.001239 | 0.002267 | 0.008068 | 0.010909 | ||||
| USDC | −9.41E-06 | −1.56E-05 | −1.29E-05 | −1.60E-05 | 7.72E-06 | |||
| USDT | −1.85E-05 | −2.27E-05 | −1.41E-05 | −1.76E-05 | 5.38E-06 | 6.97E-06 | ||
| XRP | 0.001451 | 0.001277 | 0.003700 | 0.005815 | −4.29E-06 | −5.41E-06 | 0.006365 | |
| CC7 | 0.001103 | 0.001385 | 0.003176 | 0.004038 | −6.45E-06 | −9.41E-06 | 0.002657 | 0.001763 |
| Correlation | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
| ADA | 1.000000 | |||||||
| BNB | 0.574123 | 1.000000 | ||||||
| BTC | 0.185249 | 0.448377 | 1.000000 | |||||
| ETH | 0.228708 | 0.422240 | 0.883799 | 1.000000 | ||||
| USDC | −0.065253 | −0.109378 | −0.053134 | −0.055296 | 1.000000 | |||
| USDT | −0.134843 | −0.167139 | −0.061049 | −0.063768 | 0.733904 | 1.000000 | ||
| XRP | 0.350640 | 0.311444 | 0.530526 | 0.697901 | −0.019356 | −0.025702 | 1.000000 | |
| CC7 | 0.506554 | 0.641528 | 0.865425 | 0.920644 | −0.055298 | −0.084890 | 0.793073 | 1.000000 |
| Variables | Lag Number | AC | PAC | Q-Stat | Prob |
|---|---|---|---|---|---|
| ADA | 36 | −0.0430 | −0.0420 | 74.5000 | 0.0000 |
| BNB | 36 | 0.0070 | 0.0030 | 73.6710 | 0.0000 |
| BTC | 36 | 0.0020 | 0.0100 | 298.8900 | 0.0000 |
| ETH | 36 | −0.0030 | 0.0080 | 307.5800 | 0.0000 |
| USDC | 36 | 0.1790 | 0.0620 | 736.9900 | 0.0000 |
| USDT | 36 | 0.1360 | 0.0060 | 807.1100 | 0.0000 |
| XRP | 36 | −0.0470 | −0.0450 | 185.6600 | 0.0000 |
| CC7 | 36 | −0.0160 | −0.0010 | 186.0200 | 0.0000 |
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| t-Statistic | −44.29567 | −28.6233 | −31.839 | −32.637 | −16.9532 | −18.2710 | −29.1545 | −62.3745 |
| Prob | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.00000 | 0.0001 |
| Lag Length Schwarz info criterion | 0 | 1 | 2 | 2 | 10 | 18 | 2 | 0 |
| AIC | −3.0860 | −3.2551 | −2.9027 | −2.3062 | −9.3204 | 0.96476 | −2.3089 | −3.7837 |
| F-statistic Prob (F-statistic) | 1962.106 0.000000 | 1020.889 0.000000 | 1221.906 0.000000 | 1288 0.000000 | 467.650 0.000000 | 389.813 0.000000 | 1013.220 0.000000 | 3890.588 0.000000 |
| Test critical values | ||||||||
| 1% | −3.433984 | |||||||
| 5% | −2.863032 | |||||||
| 10% | −2.567612 | |||||||
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| t-Statistic | −18.52625 | −19.64573 | −32.05270 | −32.87102 | −24.71840 | −40.51040 | −29.30377 | −21.89878 |
| Prob | 0.000217 | 0.000104 | 0.000320 | 0.001111 | 0.008155 | 0.067926 | 0.005545 | 0.000116 |
| Chosen lag length | 4 | 3 | 2 | 2 | 4 | 2 | 2 | 3 |
| Chosen break point | 4 September 2021 | 4 May 2021 | 16 April 2021 | 13 May 2021 | 13 March 2023 | 13 March 2023 | 16 April 2021 | 10 May 2021 |
| Critical Values | ||||||||
| 1% | −5.34 | |||||||
| 5% | −4.93 | |||||||
| 10% | −4.58 | |||||||
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| Mean Equation | ||||||||
| C | −0.0004 | 0.0012 | 0.0011 | 0.0018 | 0.0000 | 0.0000 | −0.0003 | 0.0016 |
| Prob | 0.6254 | 0.0533 | 0.0531 | 0.0090 | 0.8817 | 0.6402 | 0.6323 | 0.0006 |
| Dependent Variable(−1) | −0.0715 | −0.0832 | −0.0775 | −0.0666 | −0.4143 | −0.3134 | −0.1079 | −0.0681 |
| Prob | 0.0037 | 0.0000 | 0.0009 | 0.0058 | 0.0000 | 0.0000 | 0.0000 | 0.0058 |
| Variance Equation | ||||||||
| C | 0.0004 | 0.0003 | 0.0020 | 0.0021 | 0.0000 | 0.0000 | 0.0009 | 0.0004 |
| Prob | 0.0006 | 0.0006 | 0.0004 | 0.0000 | 0.0001 | 0.0001 | 0.0023 | 0.0000 |
| RESID(−1)^2 | 0.1839 | 0.1866 | 0.4948 | 0.3530 | 0.5287 | 0.6089 | 0.5013 | 0.2453 |
| Prob | 0.0000 | 0.0000 | 0.0024 | 0.0002 | 0.0000 | 0.0000 | 0.0008 | 0.0000 |
| GARCH(−1) | 0.7319 | 0.7577 | −0.0050 | 0.1386 | 0.5890 | 0.5998 | 0.5566 | 0.4259 |
| Prob | 0.0000 | 0.0000 | 0.3247 | 0.0428 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| COVID-19 | 0.0001 | 0.0000 | 0.0004 | 0.0008 | 0.0000 | 0.0000 | 0.0002 | 0.0001 |
| Prob | 0.2021 | 0.0922 | 0.0289 | 0.0003 | 0.5874 | 0.0008 | 0.1667 | 0.0170 |
| WAR | −0.0002 | −0.0002 | −0.0011 | −0.0015 | 0.0000 | 0.0000 | −0.0005 | −0.0003 |
| Prob | 0.0046 | 0.0022 | 0.0028 | 0.0001 | 0.0005 | 0.0047 | 0.0203 | 0.0001 |
| T-DIST. DOF | 4.0505 | 3.3443 | 2.5064 | 2.7636 | 3.4263 | 3.0047 | 2.4873 | 3.2213 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Information Criteria | ||||||||
| Akaike info criterion | −3.4190 | −3.8963 | −4.1350 | −3.6800 | −13.0358 | −12.5976 | −3.5886 | −4.6334 |
| Schwarz criterion | −3.3934 | −3.8708 | −4.1095 | −3.6544 | −13.0102 | −12.5720 | −3.5631 | −4.6078 |
| Hannan–Quinn criterion | −3.4095 | −3.8868 | −4.1256 | −3.6705 | −13.0263 | −12.5881 | −3.5792 | −4.6239 |
| Residual Diagnostics | ||||||||
| Correlogram of Standardized Residuals | ||||||||
| AC(5) | −0.013 | 0.002 | −0.017 | 0.016 | −0.0020 | −0.003 | −0.009 | 0.01 |
| PAC(5) | −0.018 | −0.005 | −0.018 | 0.017 | −0.0020 | −0.005 | −0.01 | 0.011 |
| Q-Stat(5) | 10.274 | 14.382 | 6.5463 | 6.2781 | 5.6698 | 7.2255 | 2.2811 | 6.0096 |
| Prob | 0.068 | 0.013 | 0.257 | 0.28 | 0.3400 | 0.204 | 0.809 | 0.305 |
| AC(10) | 0.018 | 0.017 | −0.006 | −0.026 | −0.0140 | −0.024 | −0.004 | 0.002 |
| PAC(10) | 0.016 | 0.017 | −0.007 | −0.029 | −0.0140 | −0.025 | −0.004 | 0.001 |
| Q-Stat(10) | 22.216 | 18.842 | 8.4463 | 10.454 | 6.1290 | 10.497 | 3.9181 | 7.3358 |
| Prob | 0.014 | 0.042 | 0.585 | 0.402 | 0.8040 | 0.398 | 0.951 | 0.693 |
| AC(20) | 0.004 | −0.037 | −0.02 | 0.005 | 0.0070 | −0.003 | −0.006 | 0.007 |
| PAC(20) | −0.003 | −0.038 | −0.017 | 0.005 | 0.0070 | −0.006 | −0.008 | 0.01 |
| Q-Stat(20) | 30.328 | 27.208 | 14.685 | 14.551 | 9.0969 | 16.768 | 6.8351 | 14.306 |
| Prob | 0.065 | 0.13 | 0.794 | 0.801 | 0.9820 | 0.668 | 0.997 | 0.815 |
| Correlogram of Standardized Residuals Squared | ||||||||
| AC(5) | 0.0060 | 0.0070 | −0.0020 | −0.0020 | −0.0010 | −0.0030 | −0.0070 | −0.0060 |
| PAC(5) | 0.0060 | 0.0080 | −0.0020 | −0.0020 | −0.0010 | −0.0030 | −0.0070 | −0.0060 |
| Q-Stat(5) | 2.8133 | 6.3805 | 0.0371 | 0.0426 | 0.0051 | 0.0422 | 0.2163 | 0.3614 |
| Prob | 0.7290 | 0.2710 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9990 | 0.9960 |
| AC(10) | −0.0050 | −0.0120 | −0.0020 | 0.0110 | −0.0010 | −0.0030 | 0.0020 | 0.0050 |
| PAC(10) | −0.0050 | −0.0100 | −0.0020 | 0.0110 | −0.0010 | −0.0030 | 0.0020 | 0.0050 |
| Q-Stat(10) | 4.7305 | 7.5681 | 0.0926 | 0.2864 | 0.0106 | 0.0998 | 0.3348 | 0.7488 |
| Prob | 0.9080 | 0.6710 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| AC(20) | −0.0130 | −0.0210 | 0.0020 | 0.0030 | −0.0010 | −0.0030 | 0.0060 | 0.0120 |
| PAC(20) | −0.0160 | −0.0220 | 0.0010 | 0.0030 | −0.0010 | −0.0030 | 0.0060 | 0.0110 |
| Q-Stat(20) | 11.8160 | 11.2410 | 0.1679 | 0.3937 | 0.0202 | 0.1778 | 0.7526 | 1.3534 |
| Prob | 0.9220 | 0.9400 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| ARCH + GARCH Terms | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
|---|---|---|---|---|---|---|---|---|
| RESID(−1)^2 + GARCH (−1) | 0.9158 | 0.9443 | 0.4898 | 0.4916 | 1.1177 | 1.2087 | 1.0579 | 0.6712 |
| ARCH LM Test (Lag = 1) | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
|---|---|---|---|---|---|---|---|---|
| F-statistic | 0.3611 | 0.2443 | 0.0002 | 0.0003 | 0.0009 | 0.0000 | 0.0072 | 0.0389 |
| Prob(F-statistic) | 0.5480 | 0.6212 | 0.9897 | 0.9863 | 0.9767 | 0.9999 | 0.9323 | 0.8437 |
| Obs*R-squared | 0.3614 | 0.2446 | 0.0002 | 0.0003 | 0.0009 | 0.0000 | 0.0072 | 0.0389 |
| Prob. Chi-Square | 0.5477 | 0.6209 | 0.9897 | 0.9863 | 0.9767 | 0.9999 | 0.9322 | 0.8436 |
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| Mean Equation | ||||||||
| C | −0.0003 | 0.0013 | 0.0009 | 0.0016 | 0.0000 | 0.0000 | −0.0003 | 0.0014 |
| Prob | 0.7293 | 0.0405 | 0.1192 | 0.0233 | 0.3812 | 0.5618 | 0.7071 | 0.0032 |
| Dependent Var(−1) | −0.0748 | −0.0829 | −0.0668 | −0.0523 | −0.4092 | −0.3089 | −0.0990 | −0.0582 |
| Prob | 0.0020 | 0.0000 | 0.0017 | 0.0221 | 0.0000 | 0.0000 | 0.0000 | 0.0166 |
| Variance Equation | ||||||||
| C(3) | −0.8512 | −0.6691 | −2.4537 | −1.8860 | −0.5414 | −0.5348 | −1.1759 | −2.0915 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| C(4) | 0.3290 | 0.3207 | 0.3453 | 0.3322 | 0.2771 | 0.2265 | 0.4288 | 0.3538 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| C(5) | 0.0110 | 0.0139 | −0.0725 | −0.0765 | 0.2360 | 0.0425 | 0.0209 | −0.0439 |
| Prob | 0.6880 | 0.5907 | 0.1068 | 0.0235 | 0.0000 | 0.0137 | 0.5415 | 0.1901 |
| C(6) | 0.8946 | 0.9247 | 0.6304 | 0.7249 | 0.9727 | 0.9657 | 0.8284 | 0.7361 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| C(7) | 0.0271 | 0.0198 | 0.1183 | 0.1764 | −0.0404 | −0.0962 | 0.0421 | 0.0999 |
| Prob | 0.2978 | 0.3542 | 0.0450 | 0.0008 | 0.0043 | 0.0000 | 0.2360 | 0.0331 |
| C(8) | −0.0847 | −0.0842 | −0.2363 | −0.2100 | −0.1018 | −0.1248 | −0.1208 | −0.2158 |
| Prob | 0.0047 | 0.0025 | 0.0005 | 0.0002 | 0.0000 | 0.0000 | 0.0023 | 0.0002 |
| T-DIST. DOF | 4.1216 | 3.3678 | 2.5132 | 2.8338 | 3.2478 | 2.9373 | 2.5043 | 3.2895 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Information Criteria | ||||||||
| Akaike info criterion | −3.4196 | −3.8921 | −4.1333 | −3.6885 | −12.9972 | −12.5621 | −3.5874 | −4.6381 |
| Schwarz criterion | −3.3908 | −3.8634 | −4.1046 | −3.6598 | −12.9684 | −12.5334 | −3.5586 | −4.6094 |
| Hannan–Quinn criterion | −3.4089 | −3.8815 | −4.1227 | −3.6778 | −12.9865 | −12.5515 | −3.5767 | −4.6275 |
| Residual Diagnostics | ||||||||
| Correlogram of Standardized Residuals | ||||||||
| AC(5) | −0.014 | 0.005 | 0.001 | 0.008 | 0.0010 | −0.007 | −0.009 | −0.013 |
| PAC(5) | −0.019 | −0.003 | 0.001 | 0.008 | 0.0010 | −0.01 | −0.011 | −0.014 |
| Q-Stat(5) | 10.919 | 15.656 | 3.0811 | 4.2577 | 0.6970 | 10.045 | 3.0769 | 6.001 |
| Prob | 0.053 | 0.008 | 0.687 | 0.513 | 0.9830 | 0.074 | 0.688 | 0.306 |
| AC(10) | 0.016 | 0.016 | 0.000 | −0.021 | −0.0080 | −0.023 | −0.013 | −0.007 |
| PAC(10) | 0.014 | 0.016 | −0.001 | −0.023 | −0.0080 | −0.023 | −0.013 | −0.008 |
| Q-Stat(10) | 23.133 | 19.777 | 3.9312 | 7.1781 | 0.8668 | 13.677 | 6.775 | 8.0002 |
| Prob | 0.01 | 0.031 | 0.95 | 0.709 | 1.0000 | 0.188 | 0.747 | 0.629 |
| AC(20) | 0.006 | −0.034 | 0.01 | 0.008 | 0.0020 | 0.001 | −0.01 | −0.019 |
| PAC(20) | −0.001 | −0.036 | 0.012 | 0.008 | 0.0020 | −0.003 | −0.014 | −0.017 |
| Q-Stat(20) | 31.756 | 27.871 | 11.489 | 10.627 | 1.6696 | 18.876 | 9.3528 | 14.028 |
| Prob | 0.046 | 0.112 | 0.933 | 0.955 | 1.0000 | 0.53 | 0.978 | 0.829 |
| Correlogram of Standardized Residuals Squared | ||||||||
| AC(5) | 0.0070 | 0.0070 | −0.0020 | −0.0020 | −0.0010 | −0.0030 | −0.0070 | −0.0050 |
| PAC(5) | 0.0070 | 0.0080 | −0.0020 | −0.0020 | −0.0010 | −0.0030 | −0.0070 | −0.0050 |
| Q-Stat(5) | 2.7261 | 5.8385 | 0.0415 | 0.0620 | 0.0027 | 0.0413 | 0.2045 | 0.2582 |
| Prob | 0.7420 | 0.3220 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9990 | 0.9980 |
| AC(10) | −0.0030 | −0.0090 | −0.0020 | 0.0060 | −0.0010 | −0.0030 | 0.0050 | 0.0020 |
| PAC(10) | −0.0030 | −0.0070 | −0.0020 | 0.0060 | −0.0010 | −0.0030 | 0.0050 | 0.0020 |
| Q-Stat(10) | 5.0459 | 7.1726 | 0.0891 | 0.1769 | 0.0059 | 0.0964 | 0.4031 | 0.4993 |
| Prob | 0.8880 | 0.7090 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| AC(20) | −0.0130 | −0.0200 | 0.0010 | 0.0020 | −0.0010 | −0.0030 | 0.0040 | 0.0080 |
| PAC(20) | −0.0150 | −0.0220 | 0.0010 | 0.0020 | −0.0010 | −0.0030 | 0.0040 | 0.0080 |
| Q-Stat(20) | 12.0220 | 10.7310 | 0.1454 | 0.2663 | 0.0120 | 0.1913 | 0.8413 | 0.9213 |
| Prob | 0.9150 | 0.9530 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| ARCH LM Test (Lag = 1) | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
|---|---|---|---|---|---|---|---|---|
| F-statistic | 0.1988 | 0.0406 | 0.0065 | 0.0088 | 0.0002 | 0.0015 | 0.0212 | 0.0142 |
| Prob(F-statistic) | 0.6557 | 0.8404 | 0.9358 | 0.9252 | 0.9889 | 0.9686 | 0.8844 | 0.9052 |
| Obs*R-squared | 0.1991 | 0.0406 | 0.0065 | 0.0088 | 0.0002 | 0.0015 | 0.0212 | 0.0142 |
| Prob. Chi-Square | 0.6555 | 0.8403 | 0.9358 | 0.9251 | 0.9889 | 0.9686 | 0.8843 | 0.9051 |
| ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 | |
|---|---|---|---|---|---|---|---|---|
| Mean Equation | ||||||||
| C | −0.0004 | 0.0013 | 0.0011 | 0.0016 | 0.0000 | 0.0000 | −0.0002 | 0.0015 |
| Prob | 0.6410 | 0.0446 | 0.0546 | 0.0224 | 0.6664 | 0.5606 | 0.7895 | 0.0011 |
| Dependent Variable(−1) | −0.0720 | −0.0837 | −0.0801 | −0.0580 | −0.4136 | −0.4389 | −0.1077 | −0.0658 |
| Prob | 0.0034 | 0.0000 | 0.0006 | 0.0167 | 0.0000 | 0.0000 | 0.0000 | 0.0078 |
| Variance Equation | ||||||||
| C | 0.0004 | 0.0003 | 0.0022 | 0.0020 | 0.0000 | 0.0000 | 0.0009 | 0.0005 |
| Prob | 0.0006 | 0.0007 | 0.0015 | 0.0000 | 0.0001 | 0.0000 | 0.0028 | 0.0000 |
| RESID(−1)^2 | 0.1862 | 0.1987 | 0.4940 | 0.1828 | 0.6197 | 0.1503 | 0.6093 | 0.1893 |
| Prob | 0.0001 | 0.0001 | 0.0139 | 0.0149 | 0.0000 | 0.0000 | 0.0029 | 0.0077 |
| RESID(−1)^2*(RESID(−1) < 0) | −0.0070 | −0.0291 | 0.0793 | 0.3532 | −0.1768 | 0.0501 | −0.1997 | 0.1072 |
| Prob | 0.8894 | 0.5598 | 0.6988 | 0.0120 | 0.1962 | 0.0615 | 0.2127 | 0.2265 |
| GARCH(−1) | 0.7335 | 0.7627 | −0.0051 | 0.1479 | 0.5903 | 0.5995 | 0.5603 | 0.4094 |
| Prob | 0.0000 | 0.0000 | 0.4252 | 0.0157 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| COVID-19 | 0.0001 | 0.0000 | 0.0004 | 0.0008 | 0.0000 | 0.0000 | 0.0002 | 0.0001 |
| Prob | 0.2017 | 0.0908 | 0.0383 | 0.0002 | 0.5904 | 0.0000 | 0.1667 | 0.0161 |
| WAR | −0.0002 | −0.0002 | −0.0012 | −0.0014 | 0.0000 | 0.0000 | −0.0004 | −0.0003 |
| Prob | 0.0047 | 0.0025 | 0.0054 | 0.0000 | 0.0005 | 0.0000 | 0.0244 | 0.0001 |
| T-DIST. DOF | 4.0497 | 3.3451 | 2.4586 | 2.8354 | 3.4151 | 20.0000 | 2.4775 | 3.2554 |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Information Criteria | ||||||||
| Akaike info criterion | −3.4178 | −3.8953 | −4.1340 | −3.6829 | −13.0359 | −12.2407 | −3.5888 | −4.6331 |
| Schwarz criterion | −3.3891 | −3.8666 | −4.1052 | −3.6542 | −13.0071 | −12.2120 | −3.5600 | −4.6044 |
| Hannan–Quinn criterion | −3.4072 | −3.8847 | −4.1233 | −3.6723 | −13.0252 | −12.2301 | −3.5781 | −4.6225 |
| Residual Diagnostics | ||||||||
| Correlogram of Standardized Residuals | ||||||||
| AC(5) | −0.0140 | 0.0010 | 0.0100 | 0.0190 | −0.0010 | 0.0000 | −0.0110 | −0.0160 |
| PAC(5) | −0.0180 | −0.0060 | 0.0110 | 0.0210 | −0.0010 | −0.0060 | −0.0120 | −0.0160 |
| Q-Stat(5) | 10.2900 | 14.3350 | 5.9341 | 6.7967 | 4.7094 | 25.7060 | 2.2776 | 6.3285 |
| Prob | 0.0670 | 0.0140 | 0.3130 | 0.2360 | 0.4520 | 0.0000 | 0.8100 | 0.2760 |
| AC(10) | 0.0170 | 0.0170 | 0.0020 | −0.0270 | −0.0130 | −0.0480 | −0.0040 | −0.0050 |
| PAC(10) | 0.0160 | 0.0170 | 0.0010 | −0.0290 | −0.0130 | −0.0500 | −0.0040 | −0.0060 |
| Q-Stat(10) | 22.2500 | 18.9560 | 7.2554 | 11.4880 | 5.1181 | 34.6120 | 4.0323 | 8.1580 |
| Prob | 0.0140 | 0.0410 | 0.7010 | 0.3210 | 0.8830 | 0.0000 | 0.9460 | 0.6130 |
| AC(20) | 0.0040 | −0.0370 | 0.0070 | 0.0070 | 0.0070 | 0.0060 | −0.0050 | −0.0200 |
| PAC(20) | −0.0030 | −0.0390 | 0.0100 | 0.0070 | 0.0070 | −0.0040 | −0.0080 | −0.0180 |
| Q-Stat(20) | 30.4320 | 27.2550 | 14.3940 | 15.7910 | 7.7829 | 48.6840 | 6.9948 | 14.4320 |
| Prob | 0.0630 | 0.1280 | 0.8100 | 0.7300 | 0.9930 | 0.0000 | 0.9970 | 0.8080 |
| Correlogram of Standardized Residuals Squared | ||||||||
| AC(5) | 0.006 | 0.007 | −0.002 | −0.002 | −0.0010 | −0.003 | −0.007 | −0.006 |
| PAC(5) | 0.006 | 0.009 | −0.002 | −0.002 | −0.0010 | −0.003 | −0.007 | −0.006 |
| Q-Stat(5) | 2.795 | 6.738 | 0.037 | 0.058 | 0.0045 | 0.102 | 0.203 | 0.417 |
| Prob | 0.731 | 0.241 | 1.000 | 1.000 | 1.0000 | 1.000 | 0.999 | 0.995 |
| AC(10) | −0.005 | −0.013 | −0.002 | 0.011 | −0.0010 | −0.002 | 0.002 | 0.005 |
| PAC(10) | −0.006 | −0.012 | −0.002 | 0.011 | −0.0010 | −0.002 | 0.002 | 0.005 |
| Q-Stat(10) | 4.729 | 8.145 | 0.092 | 0.319 | 0.0096 | 0.181 | 0.325 | 0.788 |
| Prob | 0.909 | 0.615 | 1.000 | 1.000 | 1.0000 | 1.000 | 1.000 | 1.000 |
| AC(20) | −0.013 | −0.021 | 0.001 | 0.003 | −0.0010 | −0.003 | 0.007 | 0.011 |
| PAC(20) | −0.016 | −0.023 | 0.001 | 0.003 | −0.0010 | −0.003 | 0.006 | 0.011 |
| Q-Stat(20) | 11.816 | 11.562 | 0.166 | 0.421 | 0.0186 | 0.242 | 0.744 | 1.361 |
| Prob | 0.922 | 0.930 | 1.000 | 1.000 | 1.0000 | 1.000 | 1.000 | 1.000 |
| ARCH LM Test (Lag = 1) | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
|---|---|---|---|---|---|---|---|---|
| F-statistic | 0.3478 | 0.2227 | 0.0001 | 0.0122 | 0.0006 | 0.0609 | 0.0050 | 0.0801 |
| Prob(F-statistic) | 0.5554 | 0.6370 | 0.9913 | 0.9122 | 0.9804 | 0.8051 | 0.9436 | 0.7772 |
| Obs*R-squared | 0.3481 | 0.2230 | 0.0001 | 0.0122 | 0.0006 | 0.0610 | 0.0050 | 0.0802 |
| Prob. Chi-Square | 0.5552 | 0.6368 | 0.9913 | 0.9121 | 0.9804 | 0.8050 | 0.9436 | 0.7771 |
| CC7-ADA | ||||||
| Estimate | Std. Error | t Value | Pr(>|t|) | Information Criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3138 | 0.0009 | Akaike | −8.7088 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4834 | 0.6288 | Bayes | −8.6514 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8566 | 0.0043 | Shibata | −8.7090 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7771 | 0.0055 | Hannan–Quinn | −8.6876 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.1191 | 0.0018 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1530.5181 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0908 | 26.8747 | 0.0000 | ||
| [ADA].mu | 0.0023 | 0.0025 | 0.9382 | 0.3482 | ||
| [ADA].mxreg1 | −0.0012 | 0.0019 | −0.6268 | 0.5308 | ||
| [ADA].mxreg2 | −0.0030 | 0.0023 | −1.3038 | 0.1923 | ||
| [ADA].omega | 0.0001 | 0.0001 | 2.5372 | 0.0112 | ||
| [ADA].alpha1 | 0.1974 | 0.0423 | 4.6626 | 0.0000 | ||
| [ADA].beta1 | 0.7812 | 0.0422 | 18.5006 | 0.0000 | ||
| [ADA].shape | 3.9196 | 0.4884 | 8.0260 | 0.0000 | ||
| [Joint]dcca1 | 0.0847 | 0.0293 | 2.8850 | 0.0039 | ||
| [Joint]dccb1 | 0.9123 | 0.0317 | 28.7833 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.3912 | 10.2251 | 0.0000 | ||
| CC7−BNB | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3214 | 0.0009 | Akaike | −9.0572 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4841 | 0.6283 | Bayes | −8.9998 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8608 | 0.0042 | Shibata | −9.0575 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7009 | 0.0069 | Hannan–Quinn | −9.0360 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.1629 | 0.0016 | ||
| [CC7].beta1 | 0.9890 | 0.0007 | 1511.6378 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0843 | 28.9319 | 0.0000 | ||
| [BNB].mu | 0.0033 | 0.0020 | 1.6522 | 0.0985 | ||
| [BNB].mxreg1 | 0.0003 | 0.0013 | 0.1979 | 0.8431 | ||
| [BNB].mxreg2 | −0.0030 | 0.0019 | −1.5802 | 0.1141 | ||
| [BNB].omega | 0.0001 | 0.0000 | 2.7688 | 0.0056 | ||
| [BNB].alpha1 | 0.2175 | 0.0505 | 4.3034 | 0.0000 | ||
| [BNB].beta1 | 0.7815 | 0.0411 | 19.0348 | 0.0000 | ||
| [BNB].shape | 3.3055 | 0.3257 | 10.1483 | 0.0000 | ||
| [Joint]dcca1 | 0.1108 | 0.0137 | 8.1135 | 0.0000 | ||
| [Joint]dccb1 | 0.8821 | 0.0156 | 56.6239 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.2644 | 15.1295 | 0.0000 | ||
| CC7−BTC | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3210 | 0.0009 | Akaike | −9.5012 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4839 | 0.6284 | Bayes | −9.4438 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8587 | 0.0043 | Shibata | −9.5014 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7904 | 0.0053 | Hannan–Quinn | −9.4800 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.1534 | 0.0016 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1532.9520 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0810 | 30.1285 | 0.0000 | ||
| [BTC].mu | 0.0029 | 0.0015 | 1.9018 | 0.0572 | ||
| [BTC].mxreg1 | −0.0005 | 0.0012 | −0.4001 | 0.6891 | ||
| [BTC].mxreg2 | −0.0022 | 0.0013 | −1.6678 | 0.0954 | ||
| [BTC].omega | 0.0019 | 0.0008 | 2.3340 | 0.0196 | ||
| [BTC].alpha1 | 0.7470 | 0.4425 | 1.6880 | 0.0914 | ||
| [BTC].beta1 | 0.0000 | 0.0017 | 0.0000 | 1.0000 | ||
| [BTC].shape | 2.3521 | 0.2194 | 10.7231 | 0.0000 | ||
| [Joint]dcca1 | 0.0350 | 0.0167 | 2.0990 | 0.0358 | ||
| [Joint]dccb1 | 0.9650 | 0.0164 | 58.8945 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.1729 | 23.1330 | 0.0000 | ||
| CC7−ETH | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3291 | 0.0009 | Akaike | −9.2377 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4844 | 0.6281 | Bayes | −9.1803 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8643 | 0.0042 | Shibata | −9.2379 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7016 | 0.0069 | Hannan–Quinn | −9.2164 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.1652 | 0.0016 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1530.8940 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0793 | 30.7797 | 0.0000 | ||
| [ETH].mu | 0.0041 | 0.0022 | 1.8743 | 0.0609 | ||
| [ETH].mxreg1 | 0.0000 | 0.0016 | 0.0020 | 0.9984 | ||
| [ETH].mxreg2 | −0.0032 | 0.0020 | −1.6021 | 0.1091 | ||
| [ETH].omega | 0.0008 | 0.0015 | 0.5264 | 0.5986 | ||
| [ETH].alpha1 | 0.4732 | 0.4584 | 1.0324 | 0.3019 | ||
| [ETH].beta1 | 0.4685 | 0.6000 | 0.7809 | 0.4349 | ||
| [ETH].shape | 2.6430 | 0.4058 | 6.5134 | 0.0000 | ||
| [Joint]dcca1 | 0.0512 | 0.0108 | 4.7458 | 0.0000 | ||
| [Joint]dccb1 | 0.9488 | 0.0107 | 89.0135 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.3039 | 13.1618 | 0.0000 | ||
| CC7−USDC | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3236 | 0.0009 | Akaike | −17.0190 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4839 | 0.6284 | Bayes | −16.9620 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8626 | 0.0042 | Shibata | −17.0200 |
| [CC7].omega | 0.0000 | 0.0000 | 2.8509 | 0.0044 | Hannan–Quinn | −16.9980 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.1618 | 0.0016 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1795.8015 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0651 | 37.4670 | 0.0000 | ||
| [USDC].mu | 0.0000 | 0.0000 | −0.6815 | 0.4956 | ||
| [USDC].mxreg1 | 0.0000 | 0.0000 | 0.9921 | 0.3212 | ||
| [USDC].mxreg2 | 0.0000 | 0.0000 | 0.4514 | 0.6517 | ||
| [USDC].omega | 0.0000 | 0.0000 | 0.0338 | 0.9730 | ||
| [USDC].alpha1 | 0.0533 | 0.0054 | 9.8875 | 0.0000 | ||
| [USDC].beta1 | 0.8952 | 0.0110 | 81.1157 | 0.0000 | ||
| [USDC].shape | 3.9340 | 0.0827 | 47.5494 | 0.0000 | ||
| [Joint]dcca1 | 0.0054 | 0.0094 | 0.5668 | 0.5708 | ||
| [Joint]dccb1 | 0.6962 | 0.8488 | 0.8202 | 0.4121 | ||
| [Joint]mshape | 4.0000 | 0.6464 | 6.1884 | 0.0000 | ||
| CC7−USDT | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3217 | 0.0009 | Akaike | −16.7700 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4837 | 0.6286 | Bayes | −16.7120 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8603 | 0.0042 | Shibata | −16.7700 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7793 | 0.0054 | Hannan–Quinn | −16.7490 |
| [CC7].alpha1 | 0.0066 | 0.0020 | 3.2304 | 0.0012 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1668.3132 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0077 | 318.1613 | 0.0000 | ||
| [USDT].mu | 0.0000 | 0.0000 | −0.1770 | 0.8595 | ||
| [USDT].mxreg1 | 0.0000 | 0.0000 | 0.4620 | 0.6441 | ||
| [USDT].mxreg2 | 0.0000 | 0.0000 | −0.1277 | 0.8984 | ||
| [USDT].omega | 0.0000 | 0.0000 | 0.0104 | 0.9917 | ||
| [USDT].alpha1 | 0.2333 | 0.0263 | 8.8566 | 0.0000 | ||
| [USDT].beta1 | 0.6928 | 0.0383 | 18.1051 | 0.0000 | ||
| [USDT].shape | 6.7669 | 2.6822 | 2.5229 | 0.0116 | ||
| [Joint]dcca1 | 0.0074 | 0.0028 | 2.6665 | 0.0077 | ||
| [Joint]dccb1 | 0.9912 | 0.0039 | 255.6924 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.3379 | 11.8378 | 0.0000 | ||
| CC7−XRP | ||||||
| Estimate | Std. Error | t value | Pr(>|t|) | Information criteria | ||
| [CC7].mu | 0.0045 | 0.0013 | 3.3215 | 0.0009 | Akaike | −8.9836 |
| [CC7].mxreg1 | −0.0005 | 0.0010 | −0.4838 | 0.6285 | Bayes | −8.9261 |
| [CC7].mxreg2 | −0.0035 | 0.0012 | −2.8639 | 0.0042 | Shibata | −8.9838 |
| [CC7].omega | 0.0000 | 0.0000 | 2.7275 | 0.0064 | Hannan–Quinn | −8.9623 |
| [CC7].alpha1 | 0.0066 | 0.0021 | 3.0986 | 0.0019 | ||
| [CC7].beta1 | 0.9890 | 0.0006 | 1541.8189 | 0.0000 | ||
| [CC7].shape | 2.4403 | 0.0866 | 28.1887 | 0.0000 | ||
| [XRP].mu | 0.0011 | 0.0019 | 0.5624 | 0.5738 | ||
| [XRP].mxreg1 | −0.0009 | 0.0016 | −0.5742 | 0.5659 | ||
| [XRP].mxreg2 | −0.0014 | 0.0017 | −0.7953 | 0.4265 | ||
| [XRP].omega | 0.0005 | 0.0001 | 5.3408 | 0.0000 | ||
| [XRP].alpha1 | 0.4161 | 0.0951 | 4.3729 | 0.0000 | ||
| [XRP].beta1 | 0.5829 | 0.0425 | 13.7317 | 0.0000 | ||
| [XRP].shape | 2.6522 | 0.1983 | 13.3772 | 0.0000 | ||
| [Joint]dcca1 | 0.0649 | 0.0182 | 3.5602 | 0.0004 | ||
| [Joint]dccb1 | 0.9351 | 0.0216 | 43.3735 | 0.0000 | ||
| [Joint]mshape | 4.0000 | 0.2597 | 15.4024 | 0.0000 | ||
| Variables | Key Findings | Interpretation |
|---|---|---|
| [CC7].mu | Significant across all models (p < 0.01) | Indicates a consistent positive mean return for the CC7 index across different cryptocurrencies. |
| [CC7].mxreg1 | Generally insignificant (p > 0.05) | Suggests no strong external factors influencing the returns of CC7. |
| [CC7].mxreg2 | Significant for some pairs (p < 0.05) | Indicates the influence of specific market factors on certain cryptocurrencies. |
| [CC7].omega | Significant (p < 0.05) for all models | Suggests positive volatility clustering in the market, implying periods of high volatility. |
| [CC7].alpha1 | Significant (p < 0.01) | Represents high short-term volatility persistence across cryptocurrencies. |
| [CC7].beta1 | Significant (p < 0.01) | Shows strong long-term volatility persistence, especially for the CC7 index. |
| [CC7].shape | Significant (p < 0.01) | Indicates positive skewness in the distribution of returns. |
| Cryptocurrency-specific variables (e.g., [ADA], [BNB], [BTC]) | Varies by cryptocurrency; some coefficients significant (e.g., [ADA].alpha1 and [BNB].alpha1) | Specific cryptocurrencies, such as ADA and BNB, exhibit stronger short-term volatility persistence. |
| Joint dcca1 | Significant for all models (p < 0.05) | Indicates significant dynamic correlations between the CC7 index and individual cryptocurrencies. |
| Joint dccb1 | Significant (p < 0.01) | Highlights a strong positive correlation between cryptocurrencies, emphasizing interdependencies. |
| Joint mshape | Significant (p < 0.01) | Reflects a stable distribution model, confirming the overall market structure. |
| Feature | ADA | BNB | BTC | ETH | USDC | USDT | XRP | CC7 |
|---|---|---|---|---|---|---|---|---|
| Influence of Past Fluctuations | Limited influence | High persistence | Limited persistence | Moderate persistence | Moderate persistence | High persistence | Moderate persistence | Moderate persistence |
| Leverage Effect Observed | Leverage effect observed | Leverage effect observed | Leverage effect observed | Leverage effect observed | No leverage effect | No leverage effect | No leverage effect | Leverage effect observed |
| EGARCH: Volatility Response to Shocks | Asymmetric response, negative shocks amplify volatility | Strong asymmetry, persistent volatility | Limited asymmetry, mild amplification | Asymmetric response, higher volatility after negative shocks | Symmetric response, moderate persistence | Symmetric response, low volatility | Asymmetric response, sharp amplification | Moderate asymmetry, prolonged volatility |
| Impact of COVID-19 | Limited effect, not statistically significant | Limited effect, not statistically significant | Significant positive impact, statistically significant | Strong significant positive impact, statistically significant | No impact | No impact | Limited impact, low significance | Moderate impact, statistically significant |
| Impact of WAR | Negative impact, limited effect, low significance | Negative impact, limited effect, low significance | Negative impact, moderate effect, statistically significant | Negative impact, strong effect, statistically significant | No impact | No impact | Negative impact, limited effect, low significance | Negative impact, moderate effect, statistically significant |
| Dynamic Correlation | Moderate dynamic correlation | High dynamic correlation | Limited dynamic correlation | High dynamic correlation | Strong dynamic correlation | Strong dynamic correlation | Moderate dynamic correlation | Moderate dynamic correlation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gherghina, Ș.-C.; Constantinescu, C.-A. Towards Examining the Volatility of Top Market-Cap Cryptocurrencies Throughout the COVID-19 Outbreak and the Russia–Ukraine War: Empirical Evidence from GARCH-Type Models. Risks 2025, 13, 57. https://doi.org/10.3390/risks13030057
Gherghina Ș-C, Constantinescu C-A. Towards Examining the Volatility of Top Market-Cap Cryptocurrencies Throughout the COVID-19 Outbreak and the Russia–Ukraine War: Empirical Evidence from GARCH-Type Models. Risks. 2025; 13(3):57. https://doi.org/10.3390/risks13030057
Chicago/Turabian StyleGherghina, Ștefan-Cristian, and Cristina-Andreea Constantinescu. 2025. "Towards Examining the Volatility of Top Market-Cap Cryptocurrencies Throughout the COVID-19 Outbreak and the Russia–Ukraine War: Empirical Evidence from GARCH-Type Models" Risks 13, no. 3: 57. https://doi.org/10.3390/risks13030057
APA StyleGherghina, Ș.-C., & Constantinescu, C.-A. (2025). Towards Examining the Volatility of Top Market-Cap Cryptocurrencies Throughout the COVID-19 Outbreak and the Russia–Ukraine War: Empirical Evidence from GARCH-Type Models. Risks, 13(3), 57. https://doi.org/10.3390/risks13030057








