Fuzzy Non-Payment Risk Management Rooted in Optimized Household Consumption Units
Abstract
:1. Introduction
Literature Review
2. Data and Methods
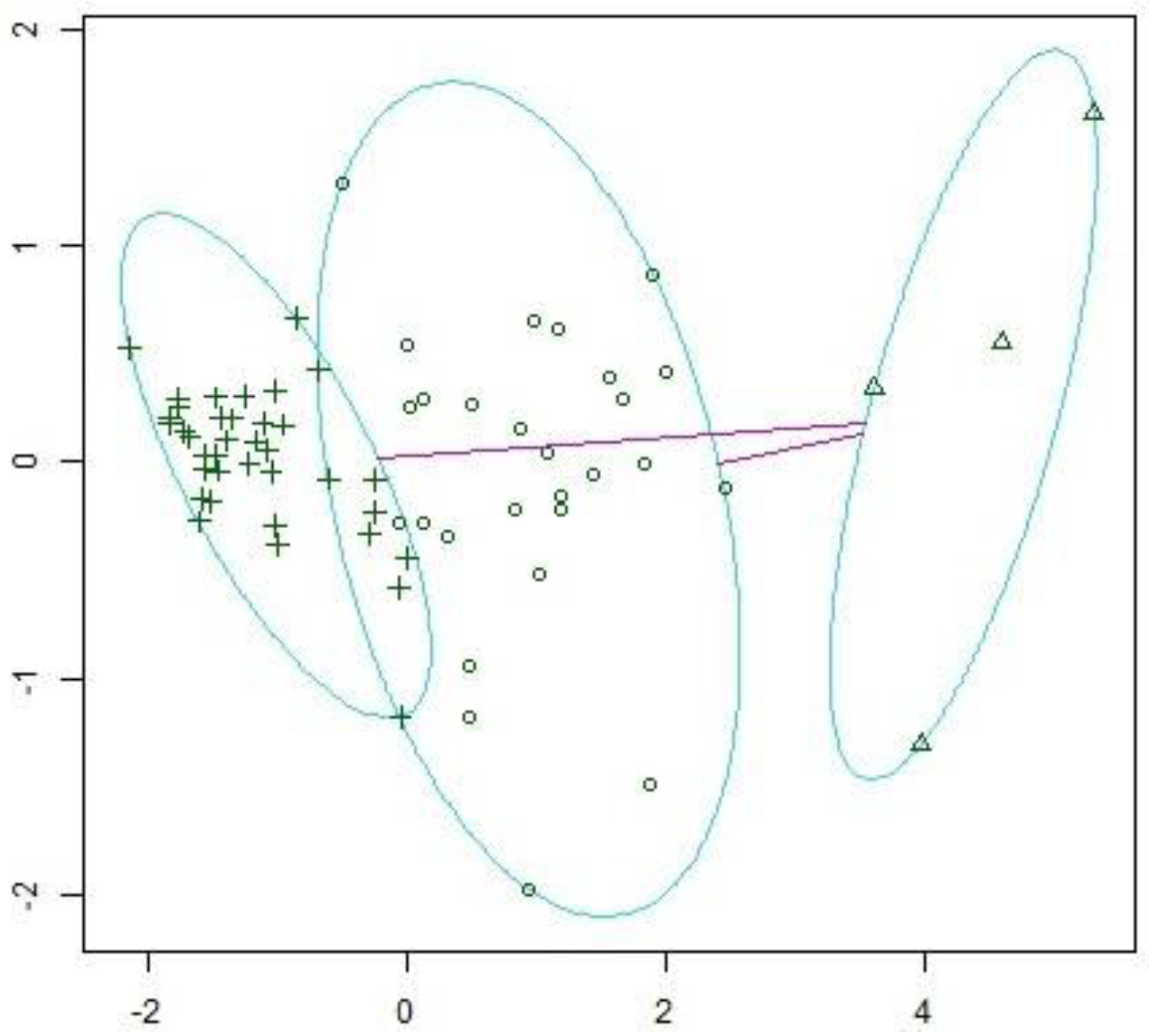
3. Results and Analysis
3.1. Optimizing Household Equivalization by Age Groups
3.2. Fuzzy Modeling to Estimate Household Credit Risk
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alonso Moral, Jose Maria, Ciro Castiello, Luis Magdalena, and Corrado Mencar. 2021. Explainable Fuzzy Systems: Paving the Way from Interpretable Fuzzy Systems to Explainable AI Systems. Studies in Computational Intelligence. Cham: Springer International Publishing, vol. 970. [Google Scholar] [CrossRef]
- Ampountolas, Apostolos, Titus Nyarko Nde, Paresh Date, and Corina Constantinescu. 2021. A Machine Learning Approach for Micro-Credit Scoring. Risks 9: 50. [Google Scholar] [CrossRef]
- Bacci, Silvia, and Bruno Chiandotto. 2019. Introduction to Statistical Decision Theory: Utility Theory and Causal Analysis. New York: Chapman and Hall/CRC. [Google Scholar] [CrossRef]
- Bahoo, Salman, Marco Cucculelli, Xhoana Goga, and Jasmine Mondolo. 2024. Artificial Intelligence in Finance: A Comprehensive Review through Bibliometric and Content Analysis. SN Business & Economics 4: 23. [Google Scholar] [CrossRef]
- Balestra, Carlotta, and Friderike Oehler. 2023. Measuring the Joint Distribution of Household Income, Consumption and Wealth at the Micro-Level: Methodological Issues and Experimental Results: 2023 Edition. Luxembourg: Publications Office of the European Union. [Google Scholar]
- Baser, Furkan, Oguz Koc, and Ayşe Sevtap Selcuk-Kestel. 2023. Credit Risk Evaluation Using Clustering Based Fuzzy Classification Method. Expert Systems with Applications 223: 119882. [Google Scholar] [CrossRef]
- Băban, Marius, and Călin Florin Băban. 2025. Patterns of Open Innovation Between Industry and University: A Fuzzy Cluster Analysis Based on the Antecedents of Their Collaboration. Mathematics 13: 772. [Google Scholar] [CrossRef]
- Beck, Amir. 2023. Introduction to Nonlinear Optimization: Theory, Algorithms, and Applications with Python and MATLAB, 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics. [Google Scholar] [CrossRef]
- Bermudez Vera, Ivan Mauricio, Jaime Mosquera Restrepo, and Diego Fernando Manotas-Duque. 2025. Data Mining for the Adjustment of Credit Scoring Models in Solidarity Economy Entities: A Methodology for Addressing Class Imbalances. Risks 13: 20. [Google Scholar] [CrossRef]
- Besharov, Douglas J., and Kenneth A. Couch. 2012. Counting the Poor: New Thinking about European Poverty Measures and Lessons for the United States. Oxford and New York: Oxford University Press. [Google Scholar]
- Bessis, Joël. 2015. Risk Management in Banking, 4th ed. ProQuest Ebook Central. Chichester: Wiley. ISBN 978-1-118-66021-8. [Google Scholar]
- Brown, Paul O., Meng Ching Chiang, Shiqing Guo, Yingzi Jin, Carson K. Leung, Evan L. Murray, Adam G. M. Pazdor, and Alfredo Cuzzocrea. 2022. Mahalanobis Distance Based K-Means Clustering. In Big Data Analytics and Knowledge Discovery. Edited by Robert Wrembel, Johann Gamper, Gabriele Kotsis, A. Min Tjoa and Ismail Khalil. Cham: Springer International Publishing, pp. 256–62. [Google Scholar] [CrossRef]
- Brygała, Magdalena. 2022. Consumer Bankruptcy Prediction Using Balanced and Imbalanced Data. Risks 10: 24. [Google Scholar] [CrossRef]
- Brzezicka, Justyna. 2021. Towards a Typology of Housing Price Bubbles: A Literature Review. Housing, Theory and Society 38: 320–42. [Google Scholar] [CrossRef]
- Chang, Victor, Sharuga Sivakulasingam, Hai Wang, Siu Tung Wong, Meghana Ashok Ganatra, and Jiabin Luo. 2024. Credit Risk Prediction Using Machine Learning and Deep Learning: A Study on Credit Card Customers. Risks 12: 174. [Google Scholar] [CrossRef]
- Chen, Ning, Bernardete Ribeiro, and An Chen. 2016. Financial Credit Risk Assessment: A Recent Review. Artificial Intelligence Review 45: 1–23. [Google Scholar] [CrossRef]
- Černevičienė, Jurgita, and Audrius Kabašinskas. 2024. Explainable Artificial Intelligence (XAI) in Finance: A Systematic Literature Review. Artificial Intelligence Review 57: 216. [Google Scholar] [CrossRef]
- Eiselt, H. A., and Carl-Louis Sandblom, eds. 2019. Methods for Nonlinearly Constrained Problems. In Nonlinear Optimization. Cham: Springer International Publishing, vol. 282, pp. 243–78. [Google Scholar] [CrossRef]
- Eurostat. 2020. The Comparability of the EU-SILC Income Variable: Reviews and Recommendations: 2020 Edition. Luxembourg: Publications Office of the European Union. [Google Scholar]
- Eurostat. 2022. Improving the Measurement of Poverty and Social Exclusion in Europe: Reducing Non Sampling Errors: 2022 Edition. Luxembourg: Publications Office of the European Union. [Google Scholar]
- Ferraro, Maria Brigida. 2024. Fuzzy k-Means: History and Applications. Econometrics and Statistics 30: 110–23. [Google Scholar] [CrossRef]
- Ferraro, Maria Brigida, Paolo Giordani, and Alessio Serafini. 2019. Fclust: An R Package for Fuzzy Clustering. The R Journal 11: 198. [Google Scholar] [CrossRef]
- Fisher, Jonathan D. 2019. Who Files for Personal Bankruptcy in the United States? Journal of Consumer Affairs 53: 2003–26. [Google Scholar] [CrossRef]
- Fritz-Morgenthal, Sebastian, Bernhard Hein, and Jochen Papenbrock. 2022. Financial Risk Management and Explainable, Trustworthy, Responsible AI. Frontiers in Artificial Intelligence 5: 779799. [Google Scholar] [CrossRef]
- Hashemi, Seyed Hossein, Seyed Ali Mousavi Dehghani, Seyed Ehsan Samimi, Mahmood Dinmohammad, and Seyed Abdolrasoul Hashemi. 2020. Performance Comparison of GRG Algorithm with Evolutionary Algorithms in an Aqueous Electrolyte System. Modeling Earth Systems and Environment 6: 2103–10. [Google Scholar] [CrossRef]
- Ignatius, Joshua, Adel Hatami-Marbini, Amirah Rahman, Lalitha Dhamotharan, and Pegah Khoshnevis. 2018. A Fuzzy Decision Support System for Credit Scoring. Neural Computing and Applications 29: 921–37. [Google Scholar] [CrossRef]
- Izquierdo Llanes, Gregorio, and Antonio Salcedo. 2023. Why Does Equivalization Matter? An Application to the Monetary Poverty in the Sustainable Development Goals Framework. Quality & Quantity 57: 2575–89. [Google Scholar] [CrossRef]
- Jahn, Johannes. 2020. Introduction to the Theory of Nonlinear Optimization. Cham: Springer International Publishing. [Google Scholar] [CrossRef]
- Jakubik, Petr, and Saida Teleu. 2025. Improving Credit Risk Assessment in Uncertain Times: Insights from IFRS 9. Risks 13: 38. [Google Scholar] [CrossRef]
- Kerre, Etienne, and John Mordeson. 2018. Fuzzy Mathematics. Basel: MDPI. [Google Scholar] [CrossRef]
- Leland, Hayne E. 2012. Predictions of Default Probabilities in Structural Models of Debt. In The Credit Market Handbook, 1st ed. Edited by H. Gifford Fong. Hoboken: Wiley, pp. 39–64. [Google Scholar] [CrossRef]
- Li, Weiping. 2016. Probability of Default and Default Correlations. Journal of Risk and Financial Management 9: 7. [Google Scholar] [CrossRef]
- Majumder, Amita, and Ranjan Ray. 2020. National and Subnational Purchasing Power Parity: A Review. Decision 47: 103–24. [Google Scholar] [CrossRef]
- Mazzini, Gabriele, and Filippo Bagni. 2023. Considerations on the Regulation of AI Systems in the Financial Sector by the AI Act. Frontiers in Artificial Intelligence 6: 1277544. [Google Scholar] [CrossRef] [PubMed]
- Milana, Carlo, and Arvind Ashta. 2021. Artificial Intelligence Techniques in Finance and Financial Markets: A Survey of the Literature. Strategic Change 30: 189–209. [Google Scholar] [CrossRef]
- Mussabayev, Rustam. 2024. Optimizing Euclidean Distance Computation. Mathematics 12: 3787. [Google Scholar] [CrossRef]
- Nahar, Janifer, Md Atiqur Rahaman, Md Alauddin, and Farhana Zaman Rozony. 2024. Big Data in Credit Risk Management: A Systematic Review of Transformative Practices and Future Directions. International Journal of Management Information Systems and Data Science 1: 68–79. [Google Scholar] [CrossRef]
- Nkambule, Dumisani Selby, Bhekisipho Twala, and Jan Harm Christiaan Pretorius. 2024. Effective Machine Learning Techniques for Dealing with Poor Credit Data. Risks 12: 172. [Google Scholar] [CrossRef]
- OECD. 2013. OECD Framework for Statistics on the Distribution of Household Income, Consumption and Wealth. Paris: OECD. [Google Scholar] [CrossRef]
- Piao, Ying’ai, Meiru Li, Hongyuan Sun, and Ying Yang. 2023. Income Inequality, Household Debt, and Consumption Growth in the United States. Sustainability 15: 3910. [Google Scholar] [CrossRef]
- Salazar, Fabian Leandro Moreno, and Juan Carlos Figueroa-García. 2025. Fuzzy Theory in Credit Scoring: A Literature Review. In Advanced Research in Technologies, Information, Innovation and Sustainability. Edited by Teresa Guarda, Filipe Portela and Maria Fernanda Augusto. Cham: Springer Nature Switzerland, vol. 2348, pp. 55–68. [Google Scholar] [CrossRef]
- Sanchez-Roger, Marc, María Dolores Oliver-Alfonso, and Carlos Sanchís-Pedregosa. 2019. Fuzzy Logic and Its Uses in Finance: A Systematic Review Exploring Its Potential to Deal with Banking Crises. Mathematics 7: 1091. [Google Scholar] [CrossRef]
- Saulo, Helton, Roberto Vila, Giovanna V. Borges, Marcelo Bourguignon, Víctor Leiva, and Carolina Marchant. 2023. Modeling Income Data via New Parametric Quantile Regressions: Formulation, Computational Statistics, and Application. Mathematics 11: 448. [Google Scholar] [CrossRef]
- Sisodia, Bhupendra Veer Singh, and Dhirendra Singh. 2020. Calibration Approach-Based Estimators for Finite Population Mean in Multistage Stratified Random Sampling. In Statistical Methods and Applications in Forestry and Environmental Sciences. Edited by Girish Chandra, Raman Nautiyal and Hukum Chandra. Singapore: Springer, pp. 105–23. [Google Scholar] [CrossRef]
- Stundziene, Alina, Vaida Pilinkiene, Jurgita Bruneckiene, Andrius Grybauskas, Mantas Lukauskas, and Irena Pekarskiene. 2024. Future Directions in Nowcasting Economic Activity: A Systematic Literature Review. Journal of Economic Surveys 38: 1199–1233. [Google Scholar] [CrossRef]
- Takawira, Oliver, and John W. Muteba Mwamba. 2022. Sovereign Credit Ratings Analysis Using the Logistic Regression Model. Risks 10: 70. [Google Scholar] [CrossRef]
- Tiwari, Kuldeep Kumar, Sandeep Bhougal, and Sunil Kumar. 2022. A Comparative Study of Ratio Estimators with Regression Estimator. Journal of Statistics Applications & Probability Letters 9: 101–4. [Google Scholar] [CrossRef]
- UNECE. 2017. Guide on Poverty Measurement. e-ISBN: 9789213627907. Available online: https://digitallibrary.un.org/record/3931399/files/ECECESSTAT20174.pdf (accessed on 4 February 2025).
- Vagaská, Alena, and Miroslav Gombár. 2021. Mathematical Optimization and Application of Nonlinear Programming. In Algorithms as a Basis of Modern Applied Mathematics. Edited by Šárka Hošková-Mayerová, Cristina Flaut and Fabrizio Maturo. Cham: Springer International Publishing, pp. 461–86. [Google Scholar] [CrossRef]
- Wang, Hao, Anthony Bellotti, Rong Qu, and Ruibin Bai. 2024. Discrete-Time Survival Models with Neural Networks for Age–Period–Cohort Analysis of Credit Risk. Risks 12: 31. [Google Scholar] [CrossRef]
- Wang, Xingqi, and Zhenhua Mao. 2023. Research on the Impact of Digital Inclusive Finance on the Financial Vulnerability of Aging Families. Risks 11: 209. [Google Scholar] [CrossRef]
- Weber, Patrick, K. Valerie Carl, and Oliver Hinz. 2024. Applications of Explainable Artificial Intelligence in Finance—A Systematic Review of Finance, Information Systems, and Computer Science Literature. Management Review Quarterly 74: 867–907. [Google Scholar] [CrossRef]
- Wilhelmina Afua Addy, Chinonye Esther Ugochukwu, Adedoyin Tolulope Oyewole, Onyeka Chrisanctus Ofodile, Omotayo Bukola Adeoye, and Chinwe Chinazo Okoye. 2024. Predictive Analytics in Credit Risk Management for Banks: A Comprehensive Review. GSC Advanced Research and Reviews 18: 434–49. [Google Scholar] [CrossRef]
- Wójcicka-Wójtowicz, Aleksandra, and Krzysztof Piasecki. 2021. Application of the Oriented Fuzzy Numbers in Credit Risk Assessment. Mathematics 9: 535. [Google Scholar] [CrossRef]
- Zhang, Shixiao, Peisong Han, and Changbao Wu. 2023. Calibration Techniques Encompassing Survey Sampling, Missing Data Analysis and Causal Inference. International Statistical Review 91: 165–92. [Google Scholar] [CrossRef]
- Zhao, Xianbo, Bon-Gang Hwang, and Sui Pheng Low. 2015. Risk Management and Enterprise Risk Management. In Enterprise Risk Management in International Construction Operations. Edited by Xianbo Zhao, Bon-Gang Hwang and Sui Pheng Low. Singapore: Springer, pp. 33–83. [Google Scholar] [CrossRef]
| Type of Household | 2023 | 2020 | 2017 | 2014 | 2011 | 2008 |
|---|---|---|---|---|---|---|
| 1 Adult64− | 16.4 | 15.0 | 14.2 | 14.2 | 13.2 | 12.0 |
| 2 Adults64− | 13.9 | 15.1 | 14.8 | 15.9 | 16.3 | 16.0 |
| 1 Adult65+ | 12.0 | 11.4 | 11.4 | 10.6 | 9.8 | 10.2 |
| 2 Adults65+ | 9.4 | 9.3 | 9.2 | 8.7 | 8.0 | 7.3 |
| 3 Adults64− | 8.6 | 8.8 | 8.7 | 8.4 | 8.5 | 9.0 |
| 4 Adults64− | 6.6 | 6.5 | 6.1 | 6.1 | 6.4 | 7.2 |
| 2 Adults64−, 1 Child | 5.7 | 6.6 | 7.4 | 7.8 | 8.1 | 7.8 |
| 1 Adult64−, 1 Adult65+ | 4.8 | 5.1 | 5.6 | 5.2 | 4.9 | 4.7 |
| 2 Adults64−, 2 Children | 4,6 | 6.0 | 6.4 | 6.7 | 6.8 | 6.5 |
| 1 Adult64−, 2 Adults65+ | 2.7 | 2.4 | 2.3 | 2.2 | 2.3 | 2.2 |
| 3 Adults64−, 1 Child | 2.5 | 2.8 | 3.3 | 3.1 | 3.5 | 3.4 |
| 2 Adults64−, 1 Adult65+ | 2.4 | 2.1 | 1.9 | 2.1 | 2.1 | 2.1 |
| 5 Adults64− | 1.4 | 0.9 | 0.9 | 0.9 | 1.1 | 1.7 |
| 3 Adults64−, 1 Adult65+ | 1.0 | 0.8 | 0.8 | 0.8 | 1.0 | 1.2 |
| 2 Adults64−, 3 Children | 1.0 | 0.8 | 1.0 | 1.0 | 0.9 | 0.8 |
| 4 Adults64−, 1 Child | 0.9 | 0.7 | 0.8 | 1.0 | 1.2 | 1.1 |
| Year | α1 | α2 | α3 | α4 |
|---|---|---|---|---|
| 2023 | 0.50 | 0.42 | 0.31 | 0.90 |
| 2020 | 0.50 | 0.36 | 0.33 | 0.85 |
| 2017 | 0.50 | 0.36 | 0.27 | 0.93 |
| 2014 | 0.50 | 0.40 | 0.24 | 0.92 |
| 2011 | 0.50 | 0.28 | 0.24 | 0.91 |
| 2008 | 0.50 | 0.19 | 0.21 | 0.94 |
| Year | (1) Total Monetary Expenditure | (2) Monetary Expenditure Mean (1 Adult64−) | (3) Consumption Units (Millions) | (4) Deviation (%) | ||
|---|---|---|---|---|---|---|
| OECD Scale | Optimized Scale | OECD Scale | Optimized Scale | |||
| 2023 | 496.70 | 16,604 | 32.50 | 30.09 | +8.6% | +0.6% |
| 2020 | 386.73 | 13,873 | 31.68 | 28.21 | +13.6% | +1.2% |
| 2017 | 432.34 | 15,100 | 31.05 | 28.59 | +8.4% | −0.1% |
| 2014 | 385.90 | 13,499 | 30.88 | 28.44 | +8.0% | −0.5% |
| 2011 | 409.20 | 14,947 | 30.83 | 27.39 | +12.6% | 0.0% |
| 2008 | 435.73 | 16,542 | 30.12 | 26.42 | +14.3% | +0.3% |
| Type of Household | Observed Monetary Consumption Mean | OECD Modified Scale | Optimized Scale | |||
|---|---|---|---|---|---|---|
| 2023 | 2014 | 2023 | 2014 | 2023 | 2014 | |
| 1 Adult64− | 16,604 | 13,499 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 Adult65+ | 14,012 | 10,804 | +18.5 | +24.9 | +9.9 | +13.4 |
| 2 Adults64− | 26,747 | 22,499 | −6.9 | −10.0 | −10.6 | −12.9 |
| 2 Adults65+ | 23,275 | 18,457 | +7.0 | +9.7 | −7.2 | −6.9 |
| 1 Adult64−, 1 Adult65+ | 23,693 | 18,711 | +5.1 | +8.2 | −3.9 | −1.7 |
| 2 Adults64−, 1 Adult65+ | 28,128 | 24,666 | +18.1 | +9.5 | +6.2 | −1.2 |
| 2 Adults64−, 1 Child | 28,996 | 22,962 | +3.1 | +5.8 | −2.3 | −2.1 |
| 1 Adult64−, 2 Adults65+ | 27,454 | 20,677 | +21.0 | +30.6 | +4.7 | +12.1 |
| 2 Adults64−, 2 Children | 34,344 | 26,650 | +1.5 | +6.4 | −4.9 | −5.0 |
| 3 Adults64− | 31,569 | 25,940 | +5.2 | +4.1 | −1.9 | −1.5 |
| 3 Adults64−, 1 Child | 33,199 | 25,256 | +15.0 | +22.9 | +6.3 | +12.2 |
| 4 Adults64− | 38,601 | 30,913 | +7.5 | +9.2 | −1.9 | +1.5 |
| Region | Disposable Income Quartile | Cluster 1 (High) | Cluster 2 (Medium) | Cluster 3 (Low) |
|---|---|---|---|---|
| Basque Country | Q1 | 0.76 | 0.18 | 0.06 |
| Balearic I. | Q1 | 0.81 | 0.12 | 0.06 |
| Asturias | Q1 | 0.06 | 0.89 | 0.05 |
| C. Valenciana | Q2 | 0.03 | 0.70 | 0.27 |
| Galicia | Q2 | 0.03 | 0.43 | 0.54 |
| Castilla y León | Q2 | 0.03 | 0.24 | 0.73 |
| Canary I. | Q3 | 0.07 | 0.59 | 0.34 |
| C. Madrid | Q3 | 0.03 | 0.63 | 0.34 |
| Cataluña | Q3 | 0.03 | 0.31 | 0.66 |
| Navarra | Q4 | 0.02 | 0.06 | 0.92 |
| Aragón | Q4 | 0.01 | 0.03 | 0.96 |
| Extremadura | Q4 | 0.00 | 0.01 | 0.99 |
| Mortgage or Rental Payments | Utility Bills | Other | |
|---|---|---|---|
| Cluster 1 (High) | 21.5 | 18.1 | 10.0 |
| Cluster 2 (Medium) | 11.2 | 6.6 | 5.8 |
| Cluster 3 (Low) | 3.2 | 1.9 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izquierdo Llanes, G.; Salcedo, A. Fuzzy Non-Payment Risk Management Rooted in Optimized Household Consumption Units. Risks 2025, 13, 74. https://doi.org/10.3390/risks13040074
Izquierdo Llanes G, Salcedo A. Fuzzy Non-Payment Risk Management Rooted in Optimized Household Consumption Units. Risks. 2025; 13(4):74. https://doi.org/10.3390/risks13040074
Chicago/Turabian StyleIzquierdo Llanes, Gregorio, and Antonio Salcedo. 2025. "Fuzzy Non-Payment Risk Management Rooted in Optimized Household Consumption Units" Risks 13, no. 4: 74. https://doi.org/10.3390/risks13040074
APA StyleIzquierdo Llanes, G., & Salcedo, A. (2025). Fuzzy Non-Payment Risk Management Rooted in Optimized Household Consumption Units. Risks, 13(4), 74. https://doi.org/10.3390/risks13040074





