Abstract
Longevity risk constitutes an important risk factor for life insurance companies, and it can be managed through longevity-linked securities. The market of longevity-linked securities is at present far from being complete and does not allow finding a unique pricing measure. We propose a method to estimate the maximum market price of longevity risk depending on the risk margin implicit within the calculation of the technical provisions as defined by Solvency II. The maximum price of longevity risk is determined for a survivor forward (S-forward), an agreement between two counterparties to exchange at maturity a fixed survival-dependent payment for a payment depending on the realized survival of a given cohort of individuals. The maximum prices determined for the S-forwards can be used to price other longevity-linked securities, such as q-forwards. The Cairns–Blake–Dowd model is used to represent the evolution of mortality over time that combined with the information on the risk margin, enables us to calculate upper limits for the risk-adjusted survival probabilities, the market price of longevity risk and the S-forward prices. Numerical results can be extended for the pricing of other longevity-linked securities.
1. Introduction
Currently, one of the main risks affecting pension funds and insurance companies selling annuity products is longevity risk, i.e., the risk to experience unexpected improvements in lifetime duration. Longevity risk implications are represented by the extension of the average period of the annuity payment, corresponding to unexpectedly higher actuarial liabilities. In the technical specifications released by EIOPA (2014a) “Longevity risk is associated with the risk of loss, or of adverse change in the value of insurance liabilities, resulting from changes in the level, trend, or volatility of mortality rates, where a decrease in the mortality rate leads to an increase in the value of insurance liabilities”. According to the report on fifth Quantitative Impact Study EIOPA (2011), in the Solvency II life underwriting risk module, longevity risk is (together with the lapse risk) the main risk for life insurance companies.
Longevity risk can be hedged in several ways. One of the most appealing solutions is to transfer longevity risk to capital markets through the so-called longevity-linked securities, financial contracts that have payoffs linked to the level of a survivor index of a reference population. Over the past few years, considerable attention was paid to longevity risk securitization on behalf of major investment banks, pension funds and reinsurers. Several longevity-linked securities have been proposed in the literature: e.g., longevity bonds, q -forwards, survivor swaps and longevity caps and floors (see, e.g., Blake et al. (2006) for a detailed description), but only some of them were issued in the market.
One of the main obstacles that slows down the development of a worldwide longevity market is determining the price of these instruments. The longevity market is currently incomplete and makes it impossible to estimate a unique market price of longevity risk, i.e., the premium that a life insurer or pension plan might be willing to pay to release such a risk. Many authors have addressed the question of how to price longevity-linked securities, but the calibration of the market price of longevity risk remains an open question (see Bauer et al. (2010) for a review and comparison of different pricing approaches). Some authors explored the possibility to link the price of longevity-linked securities to the amount that the insurer should hold to cover unexpected losses. In particular, Börger (2010) asserts that the risk margin under Solvency II can be considered as the “maximum price” that a life insurer would be willing to pay to transfer longevity risk via securitization. In the same context, Stevens et al. (2009) determine the “maximum price” of a portfolio of survivor swaps as the difference between the buffer (asset value in excess of the best estimate liabilities) sufficient to cover all future liabilities with a certain probability with and without a survivor swap. The work in Meyricke and Sherris (2014) analyzes the trade off between the costs and benefits of hedging longevity risk, where “the benefits arise from reduction in the Solvency Capital Requirement that would otherwise have to be held against longevity risk under Solvency II”.
Under this approach, we propose a method to estimate the maximum price of longevity risk from the risk margin for longevity implicit in the market-consistent evaluation of technical provisions under Solvency II legislation. According to Solvency II, insurance liabilities that cannot be hedged, e.g., the ones deriving from longevity risk, are calculated as the sum of a best estimate plus a risk margin (RM), which is the market value of the uncertainty on insurance obligations. The RM is determined by the cost of capital approach based on future solvency capital requirements (SCR). The overall SCR is then calculated by aggregating capital requirements from individual risk modules (longevity risk and other risk factors), using the relevant correlation matrices. As pointed out by Börger (2010), a shortcoming of the approach to estimating a market price of longevity risk is that the maximum price an insurer is willing to pay may be different due to diversification effects with other risks than longevity. Diversification can be achieved by natural hedging, i.e., by combining products that have negative correlation, in order to lower the insurer’s overall risk exposure. However, the insurer has its own specific portfolio and tailored natural hedging strategies that would clearly differ from insurer to insurer. Consequently, since the aim of the paper is to find the maximum price of longevity risk for a generic insurer, natural hedging between longevity and mortality (as well as other risk diversification strategies) cannot be included in the model. If the capital associated with longevity, risk was evaluated in light of the capital allocation of the total diversified SCR; the view on the “maximum price” would change. Although it is generally correct to take account of diversification effects, the paper focuses on the situation of an insurer that wishes to hedge a net longevity position considering the SCR for the stand-alone longevity risk, net of diversification effects accordingly.
The longevity risk can be mitigated and the SCR for longevity risk reduced, if the insurer enters into a longevity-linked security. If an insurer is completely hedged from longevity risk after entering a longevity-linked security, SCR for longevity risk reduces to zero, and so does the corresponding RM. Therefore, the risk margin measures the benefit to the insurer from longevity risk hedging obtained through securitization. In other words, the insurer is interested in securitization if its cost is less than the saving of RM that he/she could obtain from its use; otherwise, he/she gives up to cover the longevity risk and holds the regulatory capital necessary to address it. Therefore, the RM for longevity risk can be considered an estimation of the maximum price that the insurer would be willing to pay to transfer longevity risk.
Note that we provide estimates of the maximum acceptable price of longevity risk, without taking into account the minimum price. From the insurer’s point of view, on which the paper focuses, there is no minimum price of longevity risk below which he/she would not transfer the risk to the capital markets. The minimum price can only be determined from the point of view of the longevity insurance seller, but if this entity is not an insurance/reinsurance undertaking and therefore not regulated by Solvency II, a methodological framework based on the RM is not usable to determine the minimum price. When available, upper and lower bounds for the risk premium specify a “price range for negotiation between sellers and buyers” (Cui 2008) and “any price within this range can be an acceptable transaction price” (Barrieu and Loubergé 2013).
The approach we propose could also be applied to insurers subject to other solvency regimes, e.g., to those subject to the Swiss Solvency Test that provides a market value margin calculated with the cost of capital approach (similarly to Solvency II) that would be reduced to zero in the case of perfect hedging. We will not deal with this aspect here. For further information on the Swiss Solvency Test, the reader can refer to the Swiss Federal Office of Private Insurance SWISS (2006) and Eling et al. (2008).
However, longevity-linked securities are affected by the counterparty default risk that can increase their costs and implies a specific capital charge for the insurer entering in the transaction (see Biffis et al. (2016) for an analysis of counterparty default risk in longevity swaps). The calculation of the risk margin for counterparty default risk in longevity-linked securities is beyond the scope of this paper. If the counterparty default risk were introduced, it would reduce the SCR savings achieved by the longevity risk hedging and would increase the cost of hedging. If such risk is taken into account, the “maximum price” should be less.
Existing literature (see, e.g., Li and Hardy (2011)) shows that the longevity hedge is affected by basis risk, the risk caused by the difference between the reference population of the hedging instrument and the insured population. The presence of basis risk decreases the hedge effectiveness of the hedging instrument, and a larger solvency capital requirement is necessary to cover future liabilities. However, in this paper, we do not take into account basis risk, as we assume that the insurer’s reference population is the same as the longevity-linked instruments.
To determine the maximum price of longevity risk, we consider a survivor forward (S-forward), an agreement between two counterparties to exchange at maturity a fixed survival-dependent payment for a payment depending on the realized survival of a given cohort of individuals. An insurer wishing to hedge longevity risk may enter into a portfolio of S-forwards taking a long position, i.e., assuming an obligation to pay fixed payments in return for variable payments. The S-forward premium is measured as the difference between the fixed and the expected value of future cash flows and can be represented by a spread. We propose a method to determine the maximum spread that the longevity risk hedger is willing to pay to cover unexpected losses. It is calculated such that, at inception, the RM of a given insurance contract hedged by the S-forward is equal to the RM of the contract without longevity hedging, so that the two solutions are indifferent. We conduct the analysis by considering three different calculation methods of the SCR allowed under the Solvency II project: the standard formula, the value at risk (VaR) approach and the stressed-trend approach, so that the assessment is consistent with the measurement of the SCR and RM chosen by the insurance company.
Mortality dynamics are modeled via a stochastic projection model to take into account the uncertainty in the future evolution of mortality. To find the model that best fits Italian data, we compare the performances of seven different models. The Cairns–Blake–Dowd model (Cairns et al. 2006a) with a cohort effect is the model that best fits the data. Our results show that the maximum spread increases with the starting age of the S-forward underlying cohort, as well as with the maturity, due to the increasing uncertainty of survival probabilities for older ages and longer time. For example, under the standard formula approach, the maximum risk premium accepted by insurers for an S-forward written on a cohort of Italian males aged 65 at the issue of the annuity is 0.3% for five-year maturity and 15.4% for a 20-year maturity.
We estimate the maximum price of longevity risk according to a risk-neutral pricing framework that includes a risk adjustment into the real-world probability distribution. In the risk-neutral valuation, the mortality dynamics is specified under a risk-adjusted measure that is equivalent to the real-world measure, and the expected cash flows can be discounted to the risk-free rate. Once having defined the mortality model under the real-world probability measure, we use the RM approach to calculate the maximum value of the risk-neutral survival probabilities and find the maximum market price of longevity risk minimizing the squared errors between this value and the real-world survival probabilities. In the same pricing framework, the upper limit of the longevity risk market price can be used to price other and more complex longevity-linked securities, such as survivor swaps and q-forwards. To determine the longevity risk premium, Milevsky et al. (2005) proposed the Sharpe ratio approach based on both expected value and the volatility of payments. Under this approach, the expected return on the longevity-linked securities is equal to the risk-free rate plus the Sharpe ratio multiplied three times its standard deviation. The work in Milevsky et al. (2006) stated that for the longevity market, the Sharpe ratio can be set equal to that from the S&P500 index, i.e., 0.25.
In this context, we firstly determine the maximum price of a set of q-forwards through our model based on the RM approach and then estimate the implied maximum Sharpe ratio that can be considered acceptable by an annuity provider for hedging longevity risk.
Although the use of RM to price the longevity-linked securities has been suggested in the literature, the method we propose is original, as it provides an exact measurement of the maximum price of these hedging instruments, allowing insurers to assess their actual convenience to longevity risk securitization and thus promoting the longevity market development.
The paper is organized as follows. Section 2 describes the features of S-forwards. In Section 3, we present the method to determine the maximum price of an S-forward contract from the RM in the Solvency II framework, as well as the procedure to estimate the corresponding market price of longevity risk. Section 4 describes the mortality model adopted in the paper and provides the results of the model fitting applied to the Italian male population. The risk-neutral version of the model necessary for pricing S-forwards is also shown. Section 5 gives numerical results for the “maximum price” of S-forwards written on the Italian population for different cohorts and maturities and the underlying market price of longevity risk. Conclusions are given in Section 6.
2. S-Forwards: Definition and Notation
Consider the situation of an insurer with a portfolio of pure endowments paying a lump sum at maturity T, if the insured is still alive.
We assume the same sum insured for all of the policyholders. In this regard, where the sums insured are different, their heterogeneity may affect the riskiness of the insurance portfolio. Actually, a stronger dispersion in the insured amounts leads to a higher capital requirement due to random fluctuations in mortality. Otherwise, as pointed out by Pitacco et al. (2009) (see page 317 for further details), longevity risk is independent of the heterogeneity of the portfolio. Therefore, as our paper focuses on longevity risk, we do not consider the effect of the heterogeneity of the insured amounts on the portfolio’s riskiness.
Suppose that he/she decides to transfer the longevity risk arising from this portfolio to the capital market through a set of S-forwards, as a static hedge. An S-forward is an agreement between two counterparties to exchange at a fixed maturity T an amount equal to the realized survival probability of a given population cohort (floating rate payment), in return for a fixed survival probability agreed at the inception of the contract (fixed rate payment). Among the longevity-linked securities we have chosen the S-forwards for several reasons: they are certainly very promising instruments thanks to their lower transactions costs, high flexibility and easiness to be canceled, and they require only the will of the counterparties to transfer their death exposure without the need of a liquid market. Further, they involve lower basis risk compared with other derivatives. As stated in the Introduction, we assume that the insurer’s reference population is the same as the S-forward’s one.
Consider a cohort of identical policyholders, , all aged x at initial Time 0. For easiness of representation, lump sums are fixed to one monetary unit (m.u.). At maturity T, the number of survivors to age (both realized and expected) is:
where is the survival rate of an individual aged x at Time 0 to be alive at age , is the expectation operator associated with real world probability measure P and . If the difference between the realized and the expected survivor at time T is positive, i.e., , the insurer experiences a portfolio loss at time T.
Let be the fixed leg of the S-forward at time T, where is the fixed proportional risk premium required by investors to take on longevity risk and the floating leg. At payment date T, the cash-flow is equal to the difference between the fixed leg and the floating leg (Figure 1).
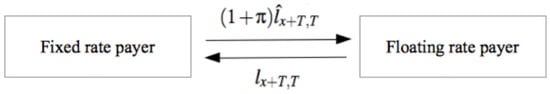
Figure 1.
S-forward cash flows.
As observed in the Introduction, the pricing of longevity-linked securities is far from being trivial. The existing literature on this topic is quite extensive, and there is a lively debate concerning the performance of different approaches for pricing such securities. Actually, there are at least three pricing approaches for longevity-linked securities: the Wang transform, the instantaneous Sharpe ratio and the risk-neutral approach.
The first one is the distortion approach based on the Wang transform Wang (2002) providing a distortion operator that transforms the death probability distribution to generate risk-adjusted death probabilities discounted by risk-free interest rates (e.g., see Lin and Cox (2005)). The Wang transform has been criticized by many authors (see, e.g., Siu-Hang Li and Cheuk-Yin Ng (2011); Bauer et al. (2010)) because it is not a linear functional and, therefore, yields arbitrage opportunities that do not lead to a price consistent with the arbitrage-free price. Moreover, as pointed out by Cairns et al. (2006b), it is not clear “how different transforms for different cohorts and terms to maturity relate to one another and form a coherent whole”. All of the aforementioned authors conclude that the Wang distortion approach does not provide a universal framework for pricing longevity-linked securities and is not a suitable choice in a framework with multiple cohorts.
As briefly described in the Introduction, the second approach applies the Sharpe ratio rule assuming that the risk premium required by investors to take on longevity risk is equal to the Sharpe ratio for other undiversifiable financial instruments Milevsky et al. (2005). This approach corresponds to a change of the probability measure from the real-world measure to a risk-adjusted measure provided by a constant market price of risk Bauer et al. (2010). As mentioned in the Introduction, Milevsky et al. (2006) propose for the longevity market a 0.25 level of the Sharpe ratio according to stock market data. However, Bauer et al. (2010) stated that “empirical studies show that the risk premium for stocks is considerably higher than for other securities”. The Sharpe ratio can be alternatively calibrated to a suitable annuity quote, but again, the question relies on the adequacy of the annuity market to price longevity-linked securities. In this regard, it should be kept in mind that the annuity provider, in addition to longevity risk, is also subject to other sources of risk, and the resulting risk premium should be greater than the risk premium for a longevity-linked security.
The third approach consists of adapting the risk-neutral pricing framework developed for interest-rate derivatives to longevity-linked securities (for example, see Dahl (2004); Cairns et al. (2006a); Biffis et al. (2010)). As pointed out by Barrieau et al. Barrieu and Loubergé (2013) “the main underlying assumption of this approach is that it is possible to replicate cash flows of a given transaction dynamically using basic traded securities in a highly liquid market”. Therefore, the application of a risk-neutral approach requires a highly liquid underlying market that is necessary to build a replicating strategy. Nevertheless, the longevity market at present is far from being liquid, and the specification of the risk-neutral measure is difficult due to the limited data on the market price of longevity risk.
Our model allows estimating the maximum market price of longevity risk from the information enclosed in the RM calculated with the Solvency II standard formula. Therefore, it allows applying the risk-neutral approach that can be generally considered the most adequate methodology because it is suited for multiple cohorts and ages; unlike the Sharpe ratio approach, it is able to capture the dependence between different cohorts Meyricke and Sherris (2014) and, unlike, the Wang transform, provides a uniquely-defined price and then a universal framework for pricing longevity-linked securities.
We define a risk-neutral probability measure Q that is equivalent to the current real-world measure P, and we assume that the interest rate is independent of the mortality rate. We set in such a way that the S-forward value is zero at the inception date: we are assuming that the market values of the fixed and floating legs are equal. Therefore, the following condition holds:
where is the price at Time 0 of a zero-coupon bond paying a fixed amount of one at time T. From Equations (1) and (2), we can find the fixed proportional S-forward premium, , as follows:
Note that can be written as , where is the spread required by the floating leg payer expressed as a continuously compounding rate. Hence, is given by:
3. Pricing S-Forwards via the Risk Margin
Under the Solvency II project, the market value of the liabilities related to unhedgeable risks is set equal to the sum of its best estimate (BE) and a risk margin (RM), representing a risk adjustment of the BE. The RM is then determined by a cost-of-capital (CoC) approach, i.e., by the cost of providing an amount of capital equal to the SCR necessary to fulfill the insurance obligations over time.
In the definition proposed by Solvency II, the SCR at Time 0 is the capital required to cover, with probability, the unexpected losses on a one-year time horizon. The CoC rate represents the average spread over the risk-free rate, which the market requires as earning on insurance companies’ equity. As observed by Zhou and Li (2013), the profit margin, which an insurance company taking on risk must include in its insurance premiums, should typically be no less than the risk margin. However, an exact computation of the RM would require the determination of , conditional on the mortality evolution up to time t (see Christiansen and Niemeyer (2014) for the SCR definitions for future points in time). For practical purposes, the computation of SCR future values is too complex, so that simplifications are needed Börger (2010). In the EIOPA Guidelines on the valuation of technical provisions EIOPA (2014b), some approximations are listed (see Guidelines 62). In the following, we will consider the approximation of the by assuming a mortality evolution up to time t according to its best estimate. In the formula, the RM at time t is defined as:
where the CoC rate is set to 6% as fixed in the current Solvency II standard formula, the is the SCR for year i and is the discount factor calculated with the risk-free interest rate term structure.
Solvency II provides several methods to calculate the SCR: full internal model, standard formula and partial internal model, standard formula with undertaking-specific parameters, standard formula simplification. In the following, we will consider the standard formula, as well as two partial internal models. The estimates derived from the partial internal models are compatible with the overall calibration objectives for the standard formula (i.e., a value at risk with a confidence level over a one-year time horizon) as required by Solvency II.
- (a)
- SCR under the standard formula:The Solvency II project suggests a standard formula to compute the above-defined SCR. If we just consider the SCR related to longevity risk and assume no other risk exists, the SCR required at t for an insurance company with a portfolio of pure endowments is equal to:where denotes the change in the value of its basic own funds at time t due to a longevity shock; is the value of the technical provisions after experiencing a longevity shock; and is the BE of the technical provisions. The longevity shock in the standard formula is a permanent reduction by 20% of the BE of the mortality rates at each age EIOPA (2014a).
- (b)
- SCR under the VaR measure:Instead of the standard formula that sets a deterministic longevity shock, a more appropriate model to capture the insurer risk can be based on the calculation of in a stochastic setting as a function of value at risk (VaR) of liabilities given a fixed confidence level. In general form, the VaR measures the potential loss in value of a risky asset or liability over a defined time horizon for a given confidence level, say 99.5% (i.e., with a 0.5% ruin probability). The can be defined as:where is the quantiles at the 99.5% confidence level of technical provisions.
- (c)
- SCR under the stressed-trend approach:As longevity risk arises from the uncertainty in changes of the long-term mortality trend, Richards et al. (2013) argue that a stressed-trend approach is the most appropriate way to investigate longevity trend risk. This trend is the result of an accumulation of small changes over many years; therefore, technical provisions should be calculated via a long-term stress projection from a stochastic mortality model, under a stressed-trend approach. There has been plenty of feedback from QIS4 and QIS5 participants on the adequacy of the one-off shock approach for longevity risk recommended by the standard formula. “As the current shock was only a shock on the level, it failed to adequately take into account trend risk: undertakings felt a stress on the future improvement rates would be more appropriate” EIOPA (2011). We define the SCR under the stressed-trend approach, , as:where is the technical provision calculated by the stressed-trend mortality projection obtained by deducting the projection standard error from the central projection, where is the cumulative distribution function of a normal (0,1) (see Richards et al. (2013) for further details). The projection standard error here encloses parameter risk and not process risk, i.e., the risk arising from the variability of the time processes used to represent the biometric trends. It is usually denoted as the risk of random fluctuations and is a diversifiable risk, because it decreases, in relative terms, by increasing the portfolio size.
Observe that, while the standard formula is based on a deterministic approach, the computation of the SCR for longevity risk via the VaR approach and the stressed-trend approach requires a stochastic mortality model.
Under a given approach (a, b or c) and assuming a mortality evolution up to time t according to its best estimate, the for a portfolio of pure endowments is given by:
where is the BE of survival probabilities and are the survival probabilities at time t calculated according to a defined approach (a, b or c):
where are the quantiles at the 99.5% confidence level of the stochastic survival probabilities that an individual alive at t at age will be alive at T at age and are the stressed-trend survival probabilities.
Assuming that an insurer is completely hedged against longevity risk, by assumption the only risk source, there is no need for the company to set any solvency capital aside. Both the SCR and the RM reduce to zero. Reasonably, we can assume that an insurer might be interested in securitizing his/her longevity risk if the transaction price is lower or equal to the present value of the future CoC required upon longevity risk. Following this point of view, the RM can be considered as the “maximum price” that an insurance company would pay for longevity risk securitization (see Börger (2010)). As argued in the Introduction, if we take into account the counterparty default risk, we should include the RM for such a risk. In this case, the “maximum price” should be less.
Consider an insurance company entering an S-forward with maturity T. The SCR at time t after the hedging is equal to:
where and are the survivors in the portfolio of pure endowments and those underlying the S-forward, respectively. Note that if these two quantities coincide, , then . Substituting Equations (9) and (11) in Equation (5), we derive the following values of the RM in before and after the hedging, respectively:
The difference between the RM before and after the longevity hedging () provides a measure of the amount of RM saved by the insurer hedging the longevity risk through an S-forward:
Clearly, when , the RM saved by the insurer exactly matches the RM for longevity risk (see Equation (12)). We assume that such savings corresponds to the maximum premium that an insurer would pay for hedging longevity risk. This leads to:
where . From Equations (14) and (15), we can obtain the “maximum price” for the S-forward fixed payer (or the corresponding spread required by the floating leg payer, ):
This result is valid for basic instruments with a single maturity, as an S-forward. At present, the market of S-forwards is far from being developed. Therefore, (or the spread ), calculated through the RM, can be used for pricing these derivatives. Thus, the hedger should not be interested in entering into a transaction if the price is higher than that calculated with this approach. Besides, the calculated on different maturities can be used to find the “maximum price” of vanilla survivor swaps.
3.1. The Market Price of Longevity Risk
Given a stochastic mortality model with n factors, the dynamics of the model under the risk-adjusted pricing measure Q depends on a vector of the market price of longevity risk , associated with the n factors. Assuming that and reminding about the relation between and the ratio between risk-neutral and real-world survival probabilities (see Equation (3)), we obtain a “maximum” value for :
Now, we can find the market price of longevity risk minimizing the squared errors between the maximum value of the risk-neutral survival probabilities calculated via the RM approach, , and the risk-neutral survival probabilities depending on the mortality, model, , so that:
where m is the number of S-forwards the model is calibrated to and and are respectively the maturity and the age at issue of the reference population of the j-th S-forward.
Note that the values of could be used to find the “maximum price” of more complex longevity-linked securities. In the next section, we describe the mortality model we use in the paper.
4. The Mortality Model
We define as the deaths occurring during year t at age x, assumed to follow a Poisson distribution, the exposed-to-risk aged x during year t so that the central death rate at age x and time t are estimated as . Let be the probability to die in year t for an individual aged x and the corresponding survival probability. We make the usual assumption that the force of mortality remains constant over each year of integer age and over each calendar year. This implies that the relationship between and is given by .
Various stochastic mortality models have been set forth in recent years. We select the model among seven stochastic models that best fits our data according to the Bayes information criterion (BIC), an objective model selection criterion based on the statistical quality of fit 1.The seven models we compared are taken from the paper of Cairns et al. (2009) and include the Lee–Carter model (LC), its extension proposed by Renshaw and Haberman (RH), the age-period-cohort model introduced by Currie, the Cairns–Blake–Dowd model (CBD) and three extensions that add a cohort effect, a quadratic term to the age effect and a different form of the cohort effect, respectively. We fit the seven models to the mortality data of the Italian population downloaded from the Human Mortality Database HMD (2010), related to the age range 60–90 and the period 1974–2007 for males. Data start from year 1974 as the first year of available time series on mortality tables, annually processed by the Italian National Institute of Statistics (ISTAT) according to a uniform methodology. The fitting results are shown in Table 1 where the extension of the Cairns–Blake–Dowd model including a cohort component, here indicated as the CBD-1, is characterized by the highest value of the BIC statistic. In order to ensure completeness, we included the corresponding maximum log-likelihood (MLL) estimates for all of the analyzed models. The CBD-1 model is described by the following equation:
where is the average of the ages used in the dataset, and reflect period-related effects and represents the cohort-related effect, with . To avoid any identifiability problems, two constraints were introduced: and , where C is the set of cohort years of birth that have been included in the analysis (1884–1947).

Table 1.
Maximum log-likelihood estimates, BIC statistic and rank for each model calculated on mortality rates of Italian males, ages 60–90, years 1974–2007.
In Figure 2 we show the maximum-likelihood estimates of , and . We can see a distinctive cohort effect in the parameter , showing that cohort mortality is rising at a higher rate for males born after 1920. In the estimation of the cohort effect, we excluded cohorts for which there were less than five observations: cohorts’ birth in 1884–1887 and 1944–1947.
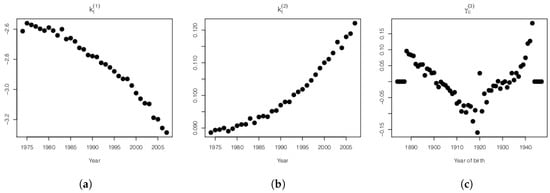
Figure 2.
Estimated parameters of the CBD-1 model, Italian male population, ages 60–90, years 1974–2007. (a) Parameter ; (b) Parameter ; (c) Parameter .
4.1. Mortality Projections
In order to make forecasts of the CBD-1 model, we select a multivariate ARIMA model for the three processes of the estimated parameters , and . In more general notation, the multivariate ARIMA model can be described as:
where is the vector of parameters , and at step s, where s indicates the time t or the cohort c according to the case; is the vector of parameters of the autoregressive part of the model; is a 3 × 1 vector of the drifts of the model; C is a 3 × 3 constant upper triangular matrix so that is the covariance matrix; and Z is a 3 × 1 vector of standard normal random variables.
Balancing between the best selected ARIMA models fitting the parameters 2 and the desire to deal with a simple model, we chose an ARIMA(0,1,0) to describe the first two parameters, and , and an ARIMA(1,1,0) for the cohort parameter . We assume the existence of correlation between parameter and , while we adopt the usual assumption that is independent of the others. Results of the fitting procedure on Italian data are reported in Table 2.

Table 2.
Fitted parameters of the ARIMA models.
The fitted matrix C is as follows:
Note that under the stressed-trend approach, the mortality model is given by , where is the mortality rate from the central projection and is the volatility arising from the uncertainty originating from the ARIMA parameters estimate.
4.2. The Risk-Neutral Mortality Model
In the following, we specify the risk-neutral approach to the mortality model described in the previous subsection, which so far was defined under the real-world probability measure P. For the multivariate ARIMA model specified by Equation (21) under the risk-neutral measure Q, we propose:
where the vector is the market price of longevity risk associated with processes , and under the measure Q, respectively. Following Cairns et al. (2006a), in the absence of complete market price data, we assume that is constant over time.
Vector should be calibrated on the market price of longevity-linked securities when available. The market of longevity-linked securities being incomplete, it is not always possible to find real market data. Following the approach proposed in Section 3, we find the market price of longevity risk, according to Equation (19). To solve the minimization problem in such an equation, we have used the optim() function in the statistical computing software R (R Core Team (2015)).
The market price of longevity risk affects the logit of death probabilities under the risk-neutral measure in the following way (see Figure 3):
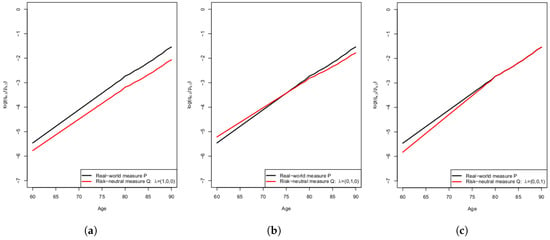
Figure 3.
Logit of projected death probabilities (year 2023) under the real-world probability measure and risk-neutral probability measure with different values. (a) ; (b) ; (c) .
- : positive values produce a downward shift and a lower slope of the curve (the latter effect is due to the presence of a positive correlation between parameters and );
- : positive values produce a lower slope of the curve and a rotation around the point ;
- : if we consider cohort data, positive values produce a downward shift of the curve only for future cohorts, while in the case of cross-sectional data, positive values increase the slope of the curve for future cohorts, while the slope does not change for historical cohorts.
5. Numerical Results
In this section, we show the results of the numerical application of our model for the Italian population. Table 3, Table 4 and Table 5 show the values of evaluated in the year 2008 for the cohorts of individuals aged 65, 70, 75, 80, 85 and for different maturities T, according to the three specifications of the SCR.

Table 3.
Values of for different cohorts and maturities. Standard formula approach.

Table 4.
Values of for different cohorts and maturities. VaR approach.

Table 5.
Values of for different cohorts and maturities. Stressed-trend approach.
Values of do not increase linearly with the S-forward maturity (see Figure 4 for the VaR approach; plots for other approaches are similar) as a natural consequence of the increasing uncertainty of survival probabilities for longer time horizons. Moreover, increases with the starting age of the underlying cohort due to the increasing uncertainty of survival probabilities for older ages. This means that hedgers are disposed to accept a higher spread when the cohort is older or the maturity is longer.
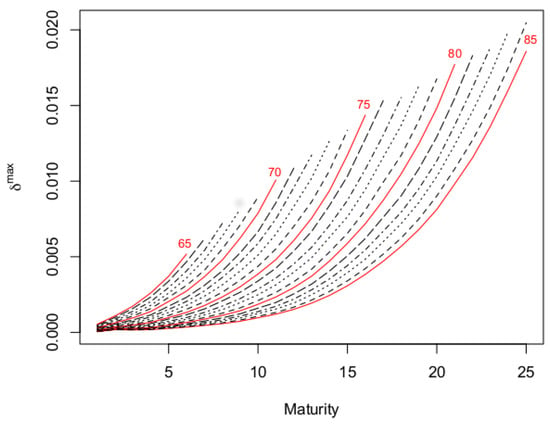
Figure 4.
Values of for the cohorts aged 65–85 in 2008 and all of the maturities. Red lines: cohorts aged 65, 70, 75, 80 and 85.
To better understand the differences in the maximum price among the considered approaches, in Figure 5, we plot the survival probabilities, , implied in the calculation for five cohorts (aged 65, 70, 75, 80, 85 in year 2008). For example, if we consider the cohort born in 1933, we can observe that the five-year survival probability under the shock approach is higher than the corresponding survival probability calculated using VaR and stress-trend approaches. This causes a higher in the shock approach for S-forwards with a five-year maturity compared to the other approaches. The opposite scenario occurs if we look at the 15-year survival probability.
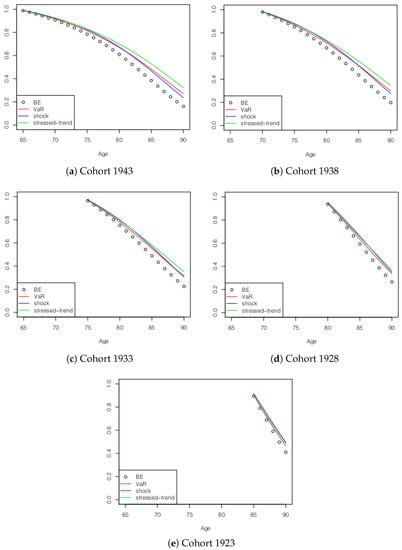
Figure 5.
Values of , and for different cohorts.
As described in Section 3.1, we obtain the vector of the market price of longevity risk minimizing the squared errors between the risk-neutral survival probabilities and the corresponding value calculated via the RM approach (see Equation (19)). The vector is calibrated on the maximum S-forward prices evaluated in 2008 considering the set of ages 65–85 and the maturities from 5–25 years. Results are given in Table 6.

Table 6.
Market price of longevity risk .
The heat map of the relative percentage error (RPE), , is plotted in Figure 6. It helps to identify the difference between the risk-neutral probabilities by age (vertical lines) and maturity (horizontal lines) with light grey areas indicating positive values, while dark grey areas show negative values. In all of the graphs of Figure 6, the most negative values are found for older ages and smaller maturities, while the most positive values are found for the younger ages and larger maturity. This implies that the model underestimates the risk-neutral probabilities for contracts with smaller maturities and older cohorts, and conversely, it overestimates the risk-neutral probabilities for contracts with larger maturities and younger cohorts.
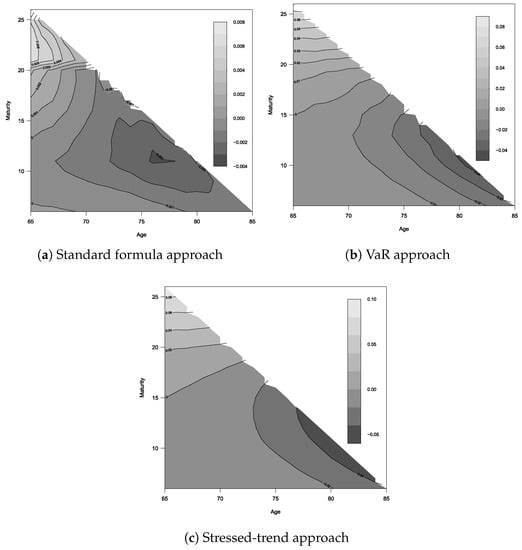
Figure 6.
Values of according to different approaches.
We also analyzed the behavior of and when the CoC rate varies in the range of 4– for each of the approaches here considered. Obviously, values show an increase/decrease proportional to the increase/decrease of the CoC rate (see Equation (16)). From the values, we then estimated the vector satisfying Equation (19) (results are shown in Figure 7).
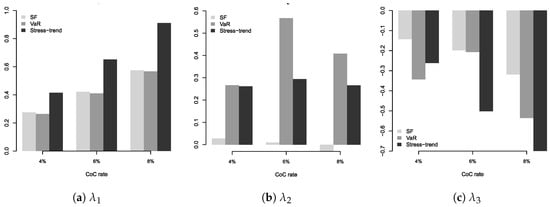
Figure 7.
Values of according to different approaches and different cost-of-capital (CoC) (4%, 6%, 8%).
In Figure 8, we study the impact of different CoC rates on the transform of death probabilities (evaluated in 2008) and on the transform of projected death probabilities (evaluated in year 2023) under both the real-world and risk-neutral probability measure. Results show that an increase in the CoC rate produces, within the standard formula approach, a downward shift of the under the risk-neutral measure. This shift is mainly obtained by an increase of ; however, a change in also produces a rotation around the point that is compensated by a reduction of . Under the standard formula approach, has minor changes. A similar behavior, but at a greater level, is observed under the stressed-trend approach. Conversely, under the VaR approach, an increase of the CoC rate involves a downward shift of the under the risk-neutral measure accompanied by a decrease in the slope for cohorts prior to 1943 (age less than 80 years in 2023). In these cases, has negative values, decreasing along with the CoC rates.
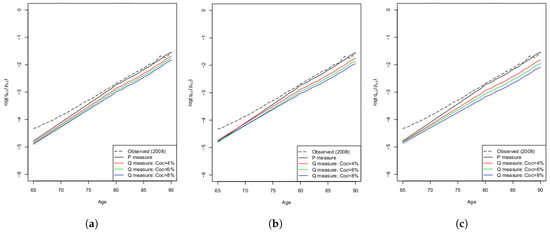
Figure 8.
Logit transform of projected death probabilities (year 2023) under the real-world probability measure and risk-neutral probability measure with different CoC values. (a) Standard formula approach; (b) VaR approach; (c) Stressed-trend approach.
5.1. q-Forward Pricing
As mentioned above, the market price of longevity risk provided by our model could be used to price other longevity-linked securities. Up to now, a wide range of longevity-linked securities has been proposed on the market, e.g., longevity bonds, longevity or survivor swaps and q-forwards. Among these, q-forwards have several advantages: they are based on standardized indices reflecting the experience of a large population, and they are less difficult to price, less expensive and more liquid. For these reasons, we decided to focus our analysis on q-forwards. A q-forward is a zero-coupon swap that involves the exchange at maturity date of a fixed amount for a random amount that is proportional to a mortality index for the reference population at maturity. The fixed payment is proportional to the forward mortality rate for the reference population and is set so that the q-forward value is zero at inception (see Coughlan et al. (2007) for further details on the mechanism of q-forwards). The payoff of q-forwards usually depends on the average mortality rate for age-buckets of five or 10 years.
In our model, we obtain the values of q-forwards as the risk-neutral expectation, while their prices are usually calculated according to the Sharpe ratio approach (see, e.g., the LifeMetrics technical document Coughlan et al. (2007)), as follows:
where T is the time to maturity, is the required annualized Sharpe ratio and is the historical standard deviation of changes in the mortality rate.
We consider a set of three q-forwards for age-buckets of five years, from age 65 up to age 79 with different maturities. Results obtained with our model are shown in Figure 9 compared with the expected mortality rate . q-forwards values calculated under both the standard formula and VaR approaches are quite similar, while they are lower under the stressed-trend approach, consistent with the results in Figure 5.
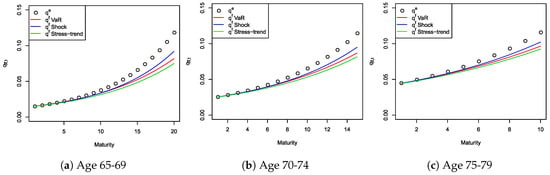
Figure 9.
Q-forward prices by different age groups.
Now, we can estimate the implied maximum Sharpe ratio, , that an annuity provider should be willing to pay to hedge longevity risk from the q-forward prices reported in Figure 9. The Sharpe ratio values for the set of three q-forwards with a 10-year maturity are reported in Table 7. Results differ from one approach to the other, but the standard formula and VaR approaches produce values that are quite similar to 0.25, usually suggested in the literature (see, e.g., Milevsky et al. (2006); Loeys et al. (2007)).

Table 7.
Sharpe ratio.
6. Conclusions
In this paper, we have investigated the possibility to price S-forwards using the information enclosed in the risk margin and the standard formula under the Solvency II project. Our approach provides estimates of the “maximum price” that the fixed payer is disposed to pay for hedging longevity risk. If the required S-forward price were higher, the annuity provider would have the convenience of keeping longevity risk. The “maximum price” is calculated under the Solvency II standard formula and two partial internal models (one based on the VaR and the other one on the stressed-trend approach) for different ages and maturities, as well as for different levels of CoC rate.
Once a mortality projection model is defined under the real-world probability measure, we calibrate the upper limit of market price of longevity risk, , associated with the risk-neutral mortality model. In the same pricing framework, values can be used to find the “maximum price” of other longevity-linked securities. Specifically, we price q-forwards, and we calibrate the implied maximum Sharpe ratio that an annuity provider should be willing to pay to hedge longevity risk. The prices provided by our model seem consistent with those obtained by other commonly-used approaches (e.g., the Sharpe ratio) and offer a point of reference for insurance companies or pension funds in defining longevity risk hedging policies through longevity-linked securities. In fact, these prices represent the threshold above which it is not convenient to use these hedging tools, and risk retention requiring an appropriate level of solvency capital becomes preferable.
In the numerical example here provided, only the Cairns–Blake–Dowd (with cohort effect) mortality projection model is used. It would be interesting to analyze the effects of different mortality models on the market price of longevity risk, taking into consideration the model risk in the pricing. This aspect will be object of future research.
One shall notice that the approach suggested in this paper depends on two fundamental assumptions. First of all, we adopt the CoC method to calculate RM, while one might consider other methods and assess whether the results obtained were similar to the CoC method both numerically and in terms of the considered variables. Secondly, we assume that all insurance companies accept the same market price of longevity risk implicit in the RM calculation under Solvency II. However, diversification effects, strategic reasons and attitude toward risk could induce the insurer to accept a different market price of longevity risk (see Börger (2010)). Moreover, we have not considered the counterparty default risk that would increase the costs of longevity-linked securities and require a specific capital charge for the insurer. The effect of this risk on the risk margin and the maximum price of longevity risk should be the object of further research.
Finally, it should be kept in mind that the proposed methodology highly depends on the individual situation of the insurance company and that the paper aims to establish a maximum price for the market of longevity-linked securities, tailored to the insurer’s specific portfolio. Although our approach has some limitations, it has the advantage of working in the known and possibly standardized framework of Solvency II, and the RM can be considered a possible tool to estimate a maximum value for the market price of longevity risk.
Acknowledgments
The authors thank the anonymous referees for helpful comments.
Author Contributions
The two authors have equally contributed to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barrieu, Pauline, and Henri Loubergé. 2013. Reinsurance and securitisation of life insurance risk: The impact of regulatory constraints. Insurance: Mathematics and Economics 52: 135–44. [Google Scholar] [CrossRef]
- Bauer, Daniel, Börger Matthias, and Jochen Ruß. 2010. On the pricing of longevity-linked securities. Insurance: Mathematics and Economics 46: 139–49. [Google Scholar] [CrossRef]
- Biffis, Enrico, Denuit Michel, and Pierre Devolder. 2010. Stochastic Mortality Under Measure Changes. Scandinavian Actuarial Journal 4: 284–311. [Google Scholar] [CrossRef]
- Biffis, Enrico, Blake David, Pitotti Lorenzo, and Ariel Sun. 2016. The Cost of Counterparty Risk and Collateralization in Longevity Swaps. The Journal of Risk and Insurance 83: 387–419. [Google Scholar] [CrossRef]
- Blake, David, Cairns Andrew J. G., and Kevin Dowd. 2006. Living with Mortality: Longevity Bonds and Other Mortality-Linked Securities. British Actuarial Journal 12: 153–228. [Google Scholar] [CrossRef]
- Börger, M. 2010. Deterministic Shock vs. Stochastic Value-at-Risk—An Analysis of the Solvency II Standard Model Approach to Longevity Risk. Blaẗter der DGVFM 31: 225–59. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., Blake David, and Kevin Dowd. 2006a. A Two-Factor Model for Stochastic Mortality with Parameter Uncertainty: Theory and Calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., Blake David, and Kevin Dowd. 2006b. Pricing death: Frameworks for the valuation and securitization of mortality risk. ASTIN Bulletin 36: 79–120. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., Blake David, Kevin Dowd, Coughlan Guy D., Epstein David, Ong Alen, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Christiansen, Marcus C., and Andreas Niemeyer. 2014. Fundamental definition of the Solvency Capital Requirement in Solvency II. Astin Bulletin 44: 501–33. [Google Scholar] [CrossRef]
- Coughlan, Guy D., Epstein David, Sinha David, and Honig, Paul Amit. 2007. q-Forwards: Derivatives for Transferring Longevity and Mortality Risk. Available online: https://www.researchgate.net/publication/256109844_q-Forwards_Derivatives_for_Transferring_Longevity_and_Mortality_Risks (accessed on 8 February 2016).
- Cui, Jiajia. 2008. Longevity Risk Pricing. Available online: http://dx.doi.org/10.2139/ssrn.972038 (accessed on 15 March 2017).
- Dahl, Mikkel. 2004. Stochastic mortality in life insurance: market reserves and mortality-linked insurance contracts. Insurance: Mathematics and Economics 35: 113–36. [Google Scholar] [CrossRef]
- EIOPA. 2011. EIOPA Report on the fifth Quantitative Impact Study (QIS5) for Solvency II. EIOPA-TFQIS5-11/001. Frankfurt: EIOPA. [Google Scholar]
- EIOPA. 2014a. Technical Specifications for the Solvency II Preparatory Phase (part I). Available online: https://eiopa.europa.eu/Publications/Standards/A_-_Technical_Specification_for_the_Preparatory_Phase_Part_I_.pdf (accessed on 8 February 2017).
- EIOPA. 2014b. Guidelines on Valuation of Technical Provisions. Available online: https://eiopa.europa.eu/Publications/Guidelines/TP_Final_document_EN.pdf (accessed on 6 April 2017).
- Eling, M., N. Gatzert, and H. Schmeiser. 2008. The swiss solvency test and its market implications. The Geneva Papers on Risk and Insurance Issues and Practice 33: 418–39. [Google Scholar] [CrossRef]
- Human Mortality Database. University of California, Berkeley (USA) and Max Planck Institute for Demographic Research (Germany). Available online: http://www.mortality.org (accessed on 16 February 2016).
- Li, Johnny S. H., and Mary R. Hardy. 2011. Measuring Basis Risk Involved in Longevity Hedges. North American Actuarial Journal 15: 177–200. [Google Scholar] [CrossRef]
- Lin, Yijia, and Samuel H. Cox. 2005. Securitization of Mortality Risks in Life Annuities. The Journal of Risk and Insurance 72: 227–52. [Google Scholar] [CrossRef]
- Loeys, Jan, Panigirtzoglou Nikolaos, and Ruy M. Ribeiro. 2007. Longevity: A Market in the Making. J.P. London: Morgan’s Global Market Strategy. [Google Scholar]
- Meyricke, Ramona, and Michael Sherris. 2014. Longevity risk, cost of capital and hedging for life insurers under Solvency II. Insurance: Mathematics and Economics 55: 147–55. [Google Scholar] [CrossRef]
- Milevsky, Moshe A., Promislow S. David, and Virginia R. Young. 2005. Financial Valuation of Mortality Risk via the Instantaneous Sharpe Ratio: Applications to Pricing Pure Endowments. Working Paper. Ann Arbor: Department of Mathematics, University of Michigan. [Google Scholar]
- Milevsky, Moshe A., Promislow S. David, and Virginia R. Young. 2006. Killing the law of large numbers: mortality risk premiums and the Sharpe ratio. Journal of Risk and Insurance 73: 673–86. [Google Scholar] [CrossRef]
- Pitacco, Ermanno, Denuit Michel, and Steven Haberman. 2009. Modelling Longevity Dynamics for Pensions and Annuity Business. Oxford: Oxford University Press. [Google Scholar]
- R Core Team. 2015. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Richards, Stephen J., I. D. Currie, and G. P. Ritchie. 2013. A Value at Risk framework for longevity trend risk. British Actuarial Journal 19: 116–39. [Google Scholar] [CrossRef]
- Siu-Hang Li, Johnny, and Andrew Cheuk-Yin Ng. 2011. Canonical Valuation of Mortality-Linked Securities. Journal of Risk and Insurance 78: 853–84. [Google Scholar] [CrossRef]
- Stevens, Ralph, Anja De Waegenaere, and Bertrand Melenberg. Longevity Risk and Hedge Effects in a Portfolio of Life Insurance Products with Investment Risk. Paper presented at the AFIR/LIFE Colloquium, 6–11 September 2009, Munich, Germany.
- Swiss Federal Office of Private Insurance (FOPI). 2006. Technical Document on the Swiss Solvency Test. Available online: www.finma.ch (accessed on 7 September 2016).
- Wang, Shaun S. 2002. A universal framework for pricing financial and insurance risks. ASTIN Bulletin 32: 213–34. [Google Scholar] [CrossRef]
- Zhou, Rui, and Johnny Siu-Hang Li. 2013. A cautionary note on pricing longevity index-swaps. Scandinavian Actuarial Journal 1: 1–23. [Google Scholar] [CrossRef]
| 1. | The BIC is defined as: , where is the log likelihood function, is the set of parameters to be estimated with the likelihood function, is the maximum likelihood estimate of the parameters vector, N is the number of observations and K the effective number of estimated parameters. The log likelihood function of the model is defined as: . |
| 2. | The goodness of fit is assessed through both the maximum log-likelihood function and Akaike’s information criterion , where l is the log likelihood function and K the effective number of estimated parameters. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).