Abstract
Two insurance companies with reserves compete for customers, such that in a suitable differential game the smaller company with aims at minimizing by using the premium as control and the larger at maximizing by using . Deductibles are fixed but may be different. If and is the leader choosing its premium first, conditions for Stackelberg equilibrium are established. For gamma-distributed rates of claim arrivals, explicit equilibrium premiums are obtained, and shown to depend on the running reserve difference. The analysis is based on the diffusion approximation to a standard Cramér-Lundberg risk process extended to allow investment in a risk-free asset.
1. Introduction
Insurance premiums are typically calculated based on the expected loss, with an added loading depending on distributional properties of the risk (the expected value principle, variance principle, utility premium, etc.). An alternative to these static premium principles is to consider the premium as a dynamic control variable of the insurance company, as suggested in Asmussen et al. (2013) and Thøgersen (2016). In this approach, the individual customer’s problem of deciding whether or not to insure at any given premium offered is modelled explicitly, and the premium is chosen optimally by the insurance company, balancing the resulting portfolio size against revenue per customer in order to minimize ruin probability. The analysis is based on the diffusion approximation to a standard Cramér-Lundberg risk process, extended to allow investment in a risk-free asset. In Asmussen et al. (2019), this idea is extended to a situation where insurance companies compete against each other, and Nash equilibria in premium controls of the resulting stochastic differential game are determined under suitable conditions. However, in some cases, no Nash equilibrium exists.
In the present paper, we present a parallel to this analysis dealing with product differentiation, with insurance companies offering different deductibles, and accounting for the possibility of Stackelberg equilibria. Two insurance companies compete against each other such that one company is the leader, choosing its premium first, and the other company is the follower, choosing its premium in response to the leader’s. The setting is slightly modified relative to that in Asmussen et al. (2019), in that we do not consider search and switching costs when modelling the customer’s choice between insurance products. Our main contributions are, first, to establish the existence of Stackelberg equilibrium under suitable conditions on this strategic game between insurance companies, and to identify the restrictions under which this reduces to the special case of Nash equilibrium. To our best knowledge, this adds at least the following new features to the literature on game theory in insurance: an example of Stackelberg equilibrium in premium controls; a finding of dependence of optimal premiums on reserves; and an occurrence of the phenomenon of adverse selection in a stochastic differential game between insurance companies, i.e., a lower premium charged increases portfolio size but leaves the average customer riskier to the company.
In the literature following Taylor (1986), the individual insurance company is frequently modelled as setting its premium in response to the aggregate insurance market, without explicitly considering the analogous behavior of the other companies constituting this market and the resulting strategic interactions. Examples include Taylor (1987) on marginal expense rates, Emms and Haberman (2005) generalizing the deterministic discrete-time analysis of Taylor to a stochastic continuous-time model, Pantelous and Passalidou (2013, 2015) using stochastic demand functions in discrete time, and Emms (2007) and Emms et al. (2007), adopting stochastic processes for the market average premium and demand conditions in continuous time. Pantelous and Passalidou (2017) recently found the optimal premium to depend on the company’s reserve in a competitive environment in the sense of this literature, but, again, this is not explicitly a game-theoretic equilibrium in the sense of Nash or Stackelberg, which is where we obtain dependence on reserves.
Game-theoretic aspects arise if the other insurers in the market in fact do react to the policy of the individual insurer, with the latter explicitly taking this into account in setting its policy. Market reaction to the individual insurer’s premium is considered by Emms (2011). Explicit games between insurance companies have been studied using non-cooperative game theory, where Cournot games involve volume controls, see, e.g., Powers et al. (1998), whereas premium controls correspond to Bertrand games, e.g., the one-period games in Polborn (1998) and Dutang et al. (2013), who note that one aspect missing in their analysis is adverse selection among policyholders—our analysis includes this. Emms (2012) and Boonen et al. (2018) do consider continuous-time differential games in premium controls, but again based on Taylor (1986) type demand functions of own and market average premium. Boonen et al. (2018) in addition present a continuous-time extension of a one-period aggregate game of Wu and Pantelous (2017), involving a price elasticity of demand or market power parameter, and the individual insurer’s payoff depending on own premium and an aggregate of market premiums. The models are deterministic and open-loop Nash equilibria are determined. In contrast, rather than assuming demand functions, we model the customer’s choice of where to insure directly and find closed-loop or feedback Nash and Stackelberg equilibria in the resulting continuous-time strategic stochastic differential game between insurance companies. The roles of product differentiation via deductibles, adverse selection, and separating equilibrium in our solution are reminiscent of Rothschild and Stiglitz (1976), one of the first applications of game theory to competition in insurance premiums.
Besides competition in premiums, game theory has found several other applications in insurance, starting with Borch (1962) on risk transfer. Zeng (2010), Taksar and Zeng (2011), and Jin et al. (2013) consider Nash equilibria of stochastic differential games between insurance companies in reinsurance strategies. The analysis has been extended to non-zero sum games and additional investment controls by Bensoussan et al. (2014), nonlinear risk processes by Meng et al. (2015), ambiguity-aversion by Pun and Wong (2016), and insurance companies with different levels of trust in information by Yan et al. (2017). Stackelberg-type equilibria of stochastic differential games have been studied in Lin et al. (2012), where an insurance company selects an investment strategy while the market (or nature) selects a worst-case probability scenario, and in Chen and Shen (2018), where the game is between insurer and reinsurer, but not as here in a game between insurance companies. For some more remote references, see Asmussen et al. (2019). Stackelberg games were introduced by von Stackelberg (1934), and the theory of stochastic differential Stackelberg games is considered by Yong (2002), Bensoussan et al. (2015), and Shi et al. (2016).
Premium competition between insurance companies is likely to arise because the premium charged may affect both portfolio size and revenue per customer. Without market frictions or product differentiation, it might be expected that all customers would simply insure at the company offering the lowest premium. However, this may not be the case in the presence of market frictions. Thus, when choosing which insurance company to contact, customers may face different costs of search and switching, transportation, or information acquisition, or they may simply exhibit differences in preferences. Search frictions have been studied in economics by Diamond (1982), Mortensen (1982), Mortensen and Pissarides (1994), and others. Brown and Goolsbee (2002) studied the effect of internet search on life insurance premiums in US data. Information frictions have been modelled as differences in the cost of obtaining information, e.g., by Salop and Stiglitz (1977). In Asmussen et al. (2019) we study premium competition between insurance companies in the presence of market frictions. In the present paper, we consider instead product differentiation, and for simplicity abstract from market frictions. With the leading example of car insurance in mind, product differentiation may come in several forms. Here, we focus on different deductibles. Other possibilities would be bonus-malus systems, see Denuit et al. (2007), or proportional compensation in deductibles, similar to reinsurance arrangements, see Albrecher et al. (2017).
We consider the case of two insurance companies, referred to as and . We allow for product differentiation by letting offer an insurance contract with fixed deductible for a premium , . The deductible measures the quality of the insurance product, so the company offering the lower deductible will be able to charge a higher premium.
We assume that there is a financial market consisting of a single risk-free asset with dynamics , where r is the risk-free interest rate. All excess wealth of customers and reserve of insurers is invested in this asset. There are N customers in the insurance market. We assume that all customers must insure at either or and focus the analysis on the choice between the two companies. This involves several characteristics of both customer and insurance product. We pay special attention to product differentiation and customer risk.
The characteristics of an individual customer are unknown to the insurance companies, but their probability distribution known. Based on this distribution, the companies can determine the expected portfolio sizes and average claim frequencies in their portfolios as functions of the premiums offered. The gross premium rate of is then , and the aggregate claim frequency is .
Let be the initial reserve of company i. For given premiums , the reserve of is governed by the dynamics
where and are independent Wiener processes, and
The random variable Z represents claim sizes, assumed to be independent and identically distributed. Thus, (1) can be considered as a diffusion approximation to the Cramér-Lundberg process extended to the case where the insurance companies have access to investment in a risk-free asset. Such diffusion approximations have been used widely, based on the arguments of Iglehart (1969).
The aim is to derive value functions for the insurance companies, and determine game-theoretic equilibria. We consider here what we call push-pull competition. We assume that the largest company in terms of initial capital, , selects its premium to try to push the small company away, while the small company tries to pull closer to the large company. For and the leader choosing its premium first, we derive conditions for a Stackelberg equilibrium. The stronger feature of a Nash equilibrium may also occur, and we give conditions for that, but our numerical examples indicate that Stackelberg is the more typical case. Subsequently, for completeness, we briefly sketch the solution in the opposite case, . The claim frequencies of individual customers are considered random to the insurance company, and we obtain explicit solutions for equilibrium premiums in the case of gamma-distributed claim frequencies.
The structure of the paper is as follows. In Section 2 we analyze the customer’s problem. We proceed to portfolio characteristics in Section 3. In Section 4, we use the portfolio characteristics to find the strategies of and . In Section 5, we obtain explicit solutions in the case of gamma-distributed claim frequencies, and provide numerical examples. Section 6 concludes. Some calculations and proofs are deferred to Appendix A.
2. Customer’s Problem
The customer has access to the risk-free asset paying interest at rate r. This is the customer’s only source of income, and he/she invests all his/her wealth in this. The customer is exposed to a risk , modelled as a compound Poisson process , where is a Poisson process with claim frequency , and are the claim sizes, assumed to be independent of . The customer will then reduce this risk by buying insurance. If the customer insures at , then he/she will continuously pay the premium , and in return have the claim sizes reduced to at most . The wealth of the customer when insuring at company i thus has dynamics
where is the compound Poisson process , and the customer’s initial wealth.
We here use similar evaluation criteria and subsequent arguments as in Thøgersen (2016), which we refer to for a more exhaustive treatment. The first step is to realize that the expected present discounted wealth when insuring at can be evaluated as
where is a subjective discount rate. If the customer were risk-neutral, he/she would simply choose the insurance company generating maximum expected present discounted wealth. Thus, he/she would prefer over if
However, an existence criterion for the insurance industry is that customers are risk averse, and this requires modification of (2). If , the customer will be facing an excess claim size risk when insuring at the company with the higher deductible. Let this additional (or reduced) risk be denoted when insuring at rather than . Please note that corresponds to the last factor in (2), and is positive if , and vice versa. Let denote the risk aversion of the customer. By standard arguments of insurance, due to the risk aversion, the customer will be willing to pay a fee to avoid the additional risk. We will take this into account by introducing a personal safety loading that the customer is willing to pay to avoid the excess risk present when . This is incorporated in (2) by multiplying the excess risk by . The more risk averse the customer, the higher the safety loading, i.e., is non-negative and increasing in , with . Thus, including risk aversion, the customer will prefer over if
and conversely, over if
In the next section, we use these relations to evaluate the portfolio sizes and average claim frequencies of the respective companies. We remark, however, at this place that in Asmussen et al. (2019) we have presented an in part more sophisticated approach to the customer’s problem involving a finite decision horizon with varying interpretations, but for the sake of simplicity, we have not pursued this aspect here.
3. Portfolio Characteristics
The claim frequencies of the customers will be considered as random to the firm and denoted by A for a given customer. The case (3) then corresponds to the event
and (4) to the complementary event .
For the expected portfolio size and the average claim frequency take the form
where N is the market size. Vice versa for , where
Letting
the probability of (5) can for (corresponding to ) be evaluated as
so, the portfolio sizes are
The average claim frequency for is the conditional expected value of the random claim frequency A given that the customer insures at , i.e.,
and likewise, for ,
if . Otherwise, and if . The criterion for obtaining information from the customers’ choices stems from the assumption , which indicates that offers a better product than , and therefore the premium should not exceed . Otherwise, every customer would obviously choose to insure at .
In case , which means that offers a better insurance product, i.e., a lower deductible, , then by symmetry
if . Otherwise, if , then would offer a lower premium for a better product, and would hence win the entire market of customers.
4. The Strategies of the insurance Companies—Push and Pull
We now consider the optimization problems of the insurance companies. A control is a set of premium strategies where denote the premiums set by the companies at time t. As in much of stochastic control theory, we will only consider Markovian (also called feedback) strategies , meaning that only depend on the current value of the difference between the corresponding controlled reserve processes . That is, we can write , for suitable functions . Since the (uncontrolled) reserves have the dynamics (1), this makes a diffusion process,
where
and is again a Wiener process. Without loss of generality, we take , i.e., is the large company and the small. The large company seeks to maximize the reserve difference (to push the competitor further away), while the small company seeks to minimize the same (to pull closer to the competitor), each taking the current reserve difference as the state variable. The optimality criterion is to consider a fixed interval with and let
Then the large company chooses to maximize the probability to exit at the upper boundary, and the small chooses to minimize , or equivalently to maximize the probability to exit at the lower boundary.
Remark 1.
The feedback assumption implies that this is equivalent to maximizing (minimizing) for all .
Given that deductibles are different, one of the firms offers a product of higher quality (lower deductible) than the other. Therefore, the sequence of the game matters, and so a Stackelberg game is considered, where the companies compete sequentially. The sequence of the game is that at any time t
- The insurance company with the better product (i.e., lower deductible) is the leader and thus plays first.
- The insurance company with the lower quality product is the follower, and plays second, instantly after observing the leader’s choice.
If (the smallest firm) is the leader and the follower (i.e., ), then a Stackelberg equilibrium is defined as a strategy pair satisfying
where . This case, , is relevant when the company offering the lower deductible is not able to attract sufficiently many high-risk customers (who need this extra protection) to become the largest company. We briefly discuss the opposite case below, in Remark 6.
The Stackelberg equilibrium concept involves backward induction. First, the optimal response of the follower is determined as a reaction function. Next, the leader inserts the reaction function of the follower into its optimization problem, and solves for the best first move. As the game evolves in continuous time, the reserve difference changes. At each instant, each firm reconsiders its strategy, taking the running reserve difference as the state variable, and taking into account the future strategies of both companies, as long as the reserve difference remains in . The criteria for a Stackelberg equilibrium are less strict than the ones for the more common Nash equilibrium, defined as a strategy pair satisfying
i.e., neither firm has an incentive to deviate from its strategy unilaterally. We later specify the specific (second order) criteria for our solution for both types of equilibrium.
We next quote from Asmussen et al. (2019) some results that will allow replacing optimization problems in the space of functions by the more elementary problem of pointwise maximization/minimization of the real-valued ratio
between the drift and variance of the reserve difference process in (10).
Lemma 1.
Let be bounded and measurable functions on an interval such that and let be defined on a suitable probability space such that W is a standard Brownian motion and
for some . Define further ,
and . Then:
(i) .
(ii) For a given function κ on and a given , let denote the r.h.s. in (i). Then implies .
By slight abuse of notation, define
To ease notation here and in the following subsections, we use the notation
for partial derivatives, where the number of primes indicates the number of times the function is differentiated, and the subscript specifies with respect to which variable. 1
Now consider the resulting drift and variance of the reserves in (1), focusing on the case . Writing and , it follows from (1) and Section 3 that the drift and variance for the reserve of can be written as
and for ,
with y given by (6). These expressions show that the denominator in (15) depends on the controls because so does y and implies (if then reduces to ). Therefore, we need to optimize over the entire function (15) and not just the difference in drifts as in Asmussen et al. (2019).
From (6), by lowering the premium , (with a high deductible in their product) can increase y and thereby portfolio size , for given , but at the expense of simultaneously increasing average claim rate , leaving the combined effect on the drift in (1) of sign that may go either way in general. Thus, there is a tradeoff, reflecting the adverse selection problem, cf. Rothschild and Stiglitz (1976), i.e., lowering the premium brings more but riskier customers. In contrast, by lowering its premium for given , (offering the lower deductible) can lower y and thereby simultaneously increase portfolio size and reduce average claim rate , but the combined effect on the drift of the reserve difference in (10) is nevertheless of ambiguous sign, and further modelling indeed required.
By (i) of Lemma 1, takes the form , and combination of (ii) of the lemma and Remark 1 allows characterizing a Stackelberg equilibrium with as the leader and the follower. It shows that the optimization problem is local: We can just consider maximization or minimization of separately at each . This yields Proposition 1 below, in which we find the explicit (local) conditions for a Stackelberg equilibrium in (11) in terms of the function from (15). For a solution to exist, the maximizing company should be facing a (locally, at least) concave problem structure, and the minimizing company a convex one. Existence cannot be guaranteed in general, but needs to be verified when considering a specific distribution of A, and hence a specific . For the standard assumption of a gamma-distributed heterogeneity, we see in Section 5 that an equilibrium does in fact exist and is unique. Although multiple solutions do not occur in this example, they cannot be excluded in general, so that the equilibrium may not be unique. The approach with backward induction should be the same, though giving a set of solutions. As multiple equilibria do not arise in the gamma case, we do not discuss them in more depth, except noting that uniqueness is guaranteed if the (local) concavity and convexity properties exploited in the following proposition extend globally.
For a fixed , write for the optimal premium for given follows a strategy with premium at level .
Proposition 1.
In a Stackelberg equilibrium , the optimal set , of premiums at level δ is a solution to
The first order conditions for are
and the second order conditions are
where is the Hessian of .
Proof.
Condition (16) follows from the definition of Stackelberg equilibrium, see (11), and the local character of the problem discussed above. Choosing the best given means that takes as , so satisfies
The problem is facing is then to minimize so is the zero of the function
At a Stackelberg equilibrium we have . We therefore get
and the second order condition means
Now (20) implies that the first term in (22) vanishes, and using (20) again, we arrive at (17). Furthermore, differentiating (20) gives
and thus in (23) vanishes. So does the second term, by (20), and hence (23) reduces to
where the first equality follows from (24). Combination with (21) produces (19). □
Corollary 1.
Proof.
Follows from Asmussen et al. (2019). □
It is clear from Proposition 1 and Corollary 1 that the Stackelberg equilibrium concept is more general than Nash equilibrium. In particular, by (18) and (25), the diagonal entries of the relevant Hessian are of opposite sign in Nash equilibrium, so (19) is automatic. Furthermore, since (18) and (19) are the general conditions for a (local) saddlepoint of , any saddlepoint of this function gives rise to a (local) Stackelberg equilibrium. Geometrically, such a saddlepoint need not be parallel to the axes corresponding to the controls (premiums). In case the cross-partial (equivalently, the policy of does not depend on that of at the optimum), then the saddlepoint is parallel to the axes and, indeed, gives rise to a (local) Nash equilibrium. Again, the conditions are only necessary, whereas sufficient conditions would involve global concavity/convexity.
Heuristically, because the premium controls of the companies are equally powerful and act in opposite directions, they should split customers evenly. This is formalized in the next proposition.
Proposition 2.
In Stackelberg equilibrium, and share the market equally, i.e., .
Proof.
Suppressing for notational convenience, let and denote the numerator and denominator, respectively, of in (15). Simple calculations show that the partial derivatives satisfy the relations
with y from (6). Following Proposition 1, we find the first order condition for ,
which can be reduced to
From this equation, the optimal response function is deduced. Similarly, the first order condition for can be reduced to
Using the relation (26) between the partial derivatives yields
which in combination with (27) yields . Hence, in Stackelberg equilibrium y should be the median of A, and from (7), . □
5. Gamma-Distributed Claim Frequencies
For modelling purposes, we assume that the claim frequencies are distributed according to , with c.d.f. where
are the Gamma function, and the lower resp. upper incomplete Gamma function. The gamma distribution is standard for modelling unobserved heterogeneity in a Poissonian setting (in insurance, a classical case is credibility theory, see Bühlmann and Gisler (2006); in general Bayesian modelling, the gamma has the role of a conjugate prior greatly facilitating calculations, see Robert (2007)). However, the outline calculations can easily be paralleled for other distributions, though the amount of analytic details may be considerable.
The portfolio characteristics (7)–(9) can then be written explicitly as
if and which, as explained in Section 3, is equivalent to and .
Theorem 1.
Assume that , and let denote the median of . Then a Stackelberg equilibrium exists at
where
provided
and
with
Remark 2.
As we discussed in Asmussen et al. (2019), there are arguments that motivate to remove condition (31) of non-negative premiums or to tighten it to premiums never below net levels . However, since now depends on y from (6) and hence on premiums unlike in the Nash equilibrium occurring there, this route leads to an implicit condition and is not pursued further here. See; however, the discussion following (37) below.
Proof.
Using the portfolio characteristics (28) and the notation from the proof of Proposition 2, we can write the numerator of the criterion to be optimized (15) as
using the relations and . Similarly, for the denominator,
The derivatives of the incomplete Gamma functions are
and by the definition (6) of y, we have . Hence, and have partial derivatives
confirming (26) in this case. By Proposition 2, y must be the median of the gamma distribution, namely, the value that solves . From the definition (6) of y it then follows that is chosen to satisfy
Thus, when evaluated at , the optimal response by is . We may now evaluate the expressions
Substitute these into (27) and solve for to get
The second order conditions, (18) and (19), are verified in Appendix A such that the first order conditions yield the types of optima desired.
We have without loss of generality assumed that , i.e., by (6), charges the highest premium. This is reasonable because it offers the best product (). Indeed, there cannot be an equilibrium in the region , since here, the criterion to be optimized would be , which is decreasing in . Since seeks to minimize, it would increase until again . □
Corollary 2.
If, in addition to (32), the premiums in (29) satisfy
then furthermore meets the conditions of a Nash equilibrium.
Proof.
Follows from Corollary 1 and calculations in the Appendix A. □
Remark 3.
The median is not analytically available, but can be solved for numerically. Banneheka and Ekanayake (2009) argue that the median for can be approximated as . Further to this, note that by scaling properties of the gamma distribution, is the median of a distribution. Evidently, equilibrium premiums scale in proportion to a.
Remark 4.
If , the gamma distribution reduces to the exponential with parameter and median . In this case, the expressions for equilibrium premiums simplify to
Remark 5.
Without product differentiation, , premiums coincide, . With product differentiation, the difference between equilibrium premiums is increasing in excess risk and safety loading .
Remark 6.
In case , i.e., the large firm offers the highest-quality insurance product (lowest deductible), then for a gamma-distributed claim frequency, the criterion to be optimized is by symmetry instead
In this case, will be the leader of the Stackelberg game, and the follower. Recall here that because we have . The same approach as in the proof of Theorem 1 then yields the equilibrium
We have again that , (this follows as in the proof of Proposition 2 and as in that case does not depend on the assumption of gamma-distributed heterogeneity). The case is relevant if the company offering best protection (lowest deductible) and therefore charging highest premiums is able to more than cover the extra cost associated with the high-risk customers willing to pay such higher premiums, and thus become the largest company.
Returning to Theorem 1 and the discussion of how the Stackelberg equilibrium evolves over time, note that due to interest rates, the strategy of the leader (here, , with strategy ) changes in an affine fashion with . Although indicates the difference in initial reserves, the companies may reoptimize at any point in time. The game is repeated every instant, and each new equilibrium in the feedback version of the game takes the same form, with premiums set as in Theorem 1, and the running difference in reserves. As functions of , the Stackelberg equilibrium premiums, and , remain time-invariant. In game-theoretic terms, the equilibrium is time-consistent. Furthermore, the portfolio characteristics actually remain constant through time. The reason is that the difference between premiums, , clearly is constant over time, not dependent on the reserve difference , and by Section 3, portfolio sizes and average claim frequencies for the companies only depend on the difference in premiums.
Numerical Illustration
We have aimed for examples with parameters that are somehow realistic in car insurance, taking the time unit as a year and the monetary unit as one €. For gamma-distributed unobserved heterogeneity there are some studies (see Bichsel (1964)) with b very close to 1, so for the sake of illustration, we take . Furthermore, an average claim frequency of order 0.05–0.10 is common in Western countries, so we took . A gamma(0.1,1)-distribution has median . Examples of gamma-distributed claim frequencies across customers are illustrated in Figure 1 for different values of the parameters a and b. The combinations of parameters are chosen to maintain an average claim frequency of 0.1.
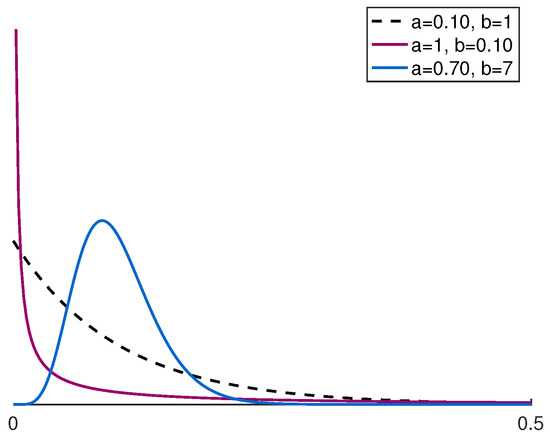
Figure 1.
The gamma distribution of the claim frequencies for different a and b.
Assuming for simplicity that the claim sizes are exponentially distributed with parameter , then we additionally have that
for , together with excess risk
Aiming for an average claim size of 5000 €, we choose €. We consider a deductible for of of the average claim size, that is . Similarly for with of the claim size giving . Note in particularly that . For these parameter values, we get
Assume further that there are customers with identical personal safety loadings of and that the risk-free interest rate is . To get an indicator of the level of the reserves, we find a starting point, R, based on a Value at Risk (VaR) principle. As N is rather large, the distribution of the sum can be approximated by the normal distribution N . Solving for the R that satisfies
using the inverse of the N cdf, yields . Next, is assumed to have a reserve somewhat more than R, and somewhat less. More specifically, we let
which leads to an initial reserve difference of . Choosing e.g., we get a difference of . Since the analytic results do not depend on the bounds on the reserve, and , their particular values do not matter, and we just need that the interval contains the chosen . Given this value, the graph of the criterion to be optimized, , appears in Figure 2, and the corresponding contour diagram in Figure 3.
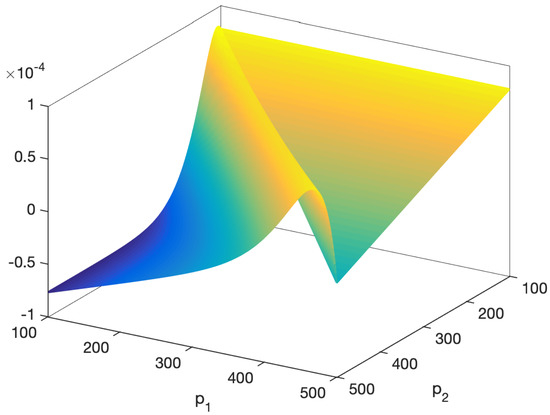
Figure 2.
Graph of .
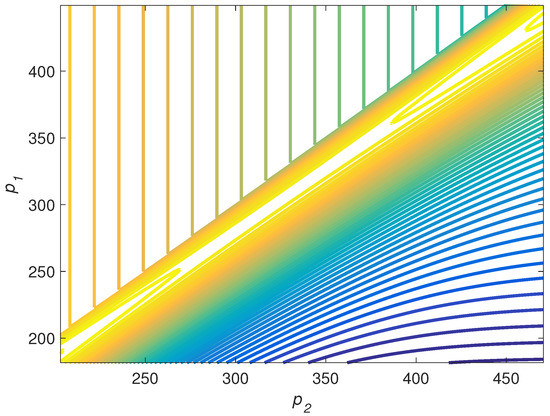
Figure 3.
Contour diagram of .
Recall that we here consider the case where offers the better product () and chooses its premium first. Given this, maximizes by seeking toward the ridge that appears diagonally when choosing . The market leader, , takes this response function of into account, and minimizes along the ridge, by choice of . The optimum provides the Stackelberg equilibrium, at the saddle point. However, in this case the saddle is located diagonally, not parallel to the axes, and there is no Nash equilibrium. In particular, given , would benefit from increasing , moving away from the ridge (toward cooler colors in the figures). While this precludes Nash equilibrium, the analysis demonstrates that it is possible to obtain an equilibrium in finite premiums by having commit to some at the given , then letting respond, i.e., a Stackelberg equilibrium. This is also verified by the value
which tells us that condition (32) is satisfied, whereas (34) is not, as , i.e., greater than in this case.
From Theorem 1, we compute the Stackelberg equilibrium premiums
at the current reserve difference . These are to be compared with the net premiums
so that pursuing solely the competition aspects would lead to a likely loss for at the current reserve difference. This is not necessarily a paradox since the perspective of control and game theory is to focus solely on a one-eyed goal. Larger means is lagging more behind the large firm , and this gives greater incentive to compete for customers by lowering its premium, with responding by letting premiums move in lockstep. Thus, in equilibrium, always receives a higher premium than , reflecting the higher quality product (lower deductible). This type of product is attractive to “bad” customers, that is, customers with high claim frequency, as seen in Figure 4. These customers are expected to experience more losses than “good” customers, and are therefore willing to pay extra for better coverage, yielding a separating equilibrium, with customers’ choices revealing their type, as in Rothschild and Stiglitz (1976). Still, may remain the smallest company, due to the higher risk of its customers.
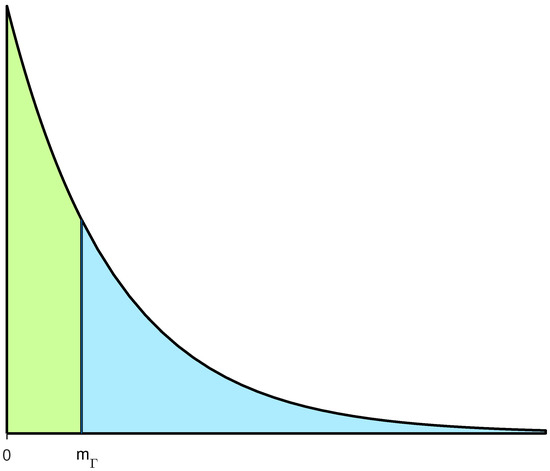
Figure 4.
Distribution of customers in equilibrium, where customers with claim frequencies in the green (blue) area insure at ().
In Figure 5 and Figure 6, exhibiting aspects of D, we take a closer graphical look at the second order criteria. Starting with Figure 5, we plot D as a function of . All other parameters remain the same as above. Values for for which are plotted in green to indicate that the equilibrium is of Stackelberg type. Values that yield , and hence equilibrium of Nash-type, are plotted in blue. Finally, the values plotted with red give , which tells us that there is no equilibrium. Here we see that D is indeed a linearly increasing function of , as it should be according to (30) and (33). Hence, for small -values we get a Stackelberg equilibrium (green). For a small spectrum in the middle we get a Nash equilibrium (blue), and, finally, for large values of there is no equilibrium. The same color codes are used in Figure 6, which shows the color plateaus of D, and not the actual values, as depending on the deductibles, and . As we restrict the analysis to the case where , it is only the lower triangular part that is illustrated. For simultaneously large values (above ) of and , there appears an area (red) where there is no equilibrium. However, is ten times the average claim size of 5000 and obviously an unrealistically large value of the deductibles. For and being close, i.e., along the diagonal, there is then an equilibrium of Stackelberg type (green area) for smaller values. Moving away from the diagonal, the equilibrium type will change from Stackelberg to Nash (blue area). However, in the most realistic region of deductibles being below the mean claim size it is always Stackelberg.
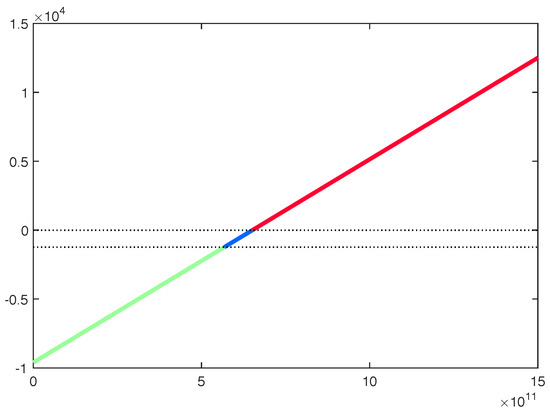
Figure 5.
D as a function of . Green indicates Stackelberg equilibrium, blue indicates Nash equilibrium, and red indicates neither.
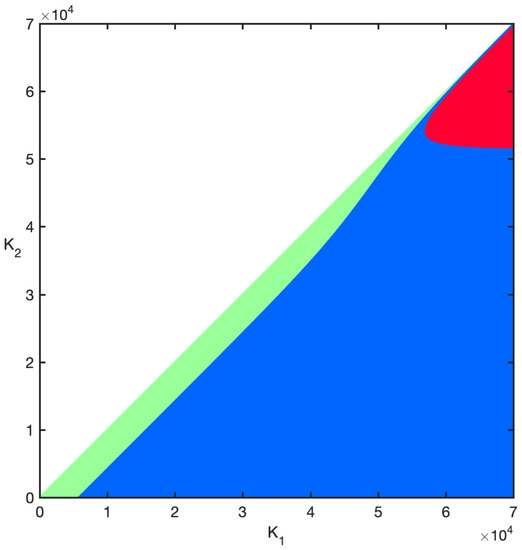
Figure 6.
D as a function of and for . Green indicates Stackelberg equilibrium, blue indicates Nash equilibrium, and red indicates neither.
6. Conclusions
We have considered a non-life insurance market in which two insurance companies compete for customers by choice of premium strategies. Each company chooses its strategy to balance revenue against portfolio size, taking into account the strategy of the other company. We pay special attention to product differentiation and customer risk, while abstracting for simplicity from market frictions. For product differentiation, we focus on different deductibles, noting that alternatives would include bonus-malus systems, and proportional compensation in deductibles. The analysis is carried out in continuous time using stochastic differential game techniques. Adverse selection implies that a change in premium alters the risk composition of the portfolio. With claim arrival rates following a gamma distribution across customers, Stackelberg equilibrium premiums are derived. Conditions under which a Nash equilibrium exists are also established, but our numerical examples indicate that Stackelberg is the more typical case. Equilibrium premiums depend in an affine fashion on the running difference between the reserves of the companies, each modelled using the diffusion approximation to a standard Cramér-Lundberg risk process, extended to allow investment in a risk-free asset. Numerical illustrations of both types of equilibrium are provided.
Overall, the managerial implications are that insurance companies should consider the premium as an active means to control portfolio size and revenue per customer in competition with other companies, as opposed to merely pooling individual risks and setting the premium based on conventional principles. Future research could consider three or more companies competing for market shares, to account explicitly for the risk of ruin or the possibility that some potential customers choose not to insure, or to pursue the more sophisticated ideas of Asmussen et al. (2019) on the customer’s problem.
Author Contributions
Conceptualization, S.A., B.J.C., and J.T.; methodology, S.A. and J.T.; software, J.T.; validation, S.A., B.J.C., and J.T.; formal analysis, J.T.; writing–original draft preparation, S.A., B.J.C., and J.T.; writing–review and editing, B.J.C. and J.T.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Second Order Derivative Tests for Theorem 1
Since we only need to consider a fixed , we write for notational convenience instead of . Please note that the first order conditions, in the present case (17), can be written as
and consider the second order partial derivatives
In optimum the critical point must satisfy the first order condition (27), which reduces the second order partial derivatives to
From the links between the first order derivatives in the proof of Theorem 1,
where . The second order derivative test on the Hessian in (19),
then confirms a saddle point, provided we can show the condition (18). For this, we need to be more specific and find the actual second order derivatives and evaluate them in equilibrium. Differentiating and with respect to yields
Evaluating at the equilibrium premiums,
Multiplying by the positive constant , the criterion can be written in reduced form explicitly as
Inserting the optimal premium,
we can reduce the condition to
which is the same as (32).
The condition (25) for a Nash equilibrium can also be found more explicitly by using the link in (A2) between the second order derivatives. The condition can be rewritten as
which, using the same approach as above, can be written as
where
which combined yields (34).
References
- Albrecher, Hansjörg, Jozef L. Teugels, and Jan Beirlant. 2017. Reinsurance: Actuarial and Statistical Aspects. Hoboken: John Wiley & Sons. [Google Scholar]
- Asmussen, Søren, Bent Jesper Christensen, and Michael Taksar. 2013. Portfolio size as function of the premium: Modelling and optimization. Stochastics 85: 575–88. [Google Scholar] [CrossRef]
- Asmussen, Søren, Bent Jesper Christensen, and Julie Thøgersen. 2019. Equilibrium premium strategies for push-pull competition in a non-life insurance market. Insurance: Mathematics and Economics. In press. Available online: https://doi.org/10.1016/j.insmatheco.2019.02.002 (accessed on 16 April 2019).
- Banneheka, B. M. S. G., and G. E. M. U. P. D. Ekanayake. 2009. New point estimator for the median of gamma distribution. Vidyodaya Journal of Science 14: 95–103. [Google Scholar]
- Bensoussan, Alain, Shaokuan Chen, and Suresh P Sethi. 2015. The maximum principle for global solutions of stochastic stackelberg differential games. SIAM Journal on Control and Optimization 53: 1956–81. [Google Scholar] [CrossRef]
- Bensoussan, Alain, Chi Chung Siu, Sheung Chi Phillip Yam, and Hailiang Yang. 2014. A class of non-zero-sum stochastic differential investment and reinsurance games. Automatica 50: 2025–37. [Google Scholar] [CrossRef]
- Bichsel, F. 1964. Erfahrungstarifierung in der motorfahrzeug-haftphlichtversicherung. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker 64: 119–30. [Google Scholar]
- Boonen, Tim J., Athanasios A. Pantelous, and Renchao Wu. 2018. Non-cooperative dynamic games for general insurance markets. Insurance: Mathematics and Economics 78: 123–35. [Google Scholar] [CrossRef]
- Borch, Karl Henrik. 1962. Application of game theory to some problems in automobile insurance. ASTIN Bulletin 2: 208–21. [Google Scholar] [CrossRef]
- Brown, Jeffrey R., and Austan Goolsbee. 2002. Does the internet make markets more competitive? evidence from the life insurance industry. Journal of Political Economy 110: 481–507. [Google Scholar] [CrossRef]
- Bühlmann, Hans, and Alois Gisler. 2006. A Course in Credibility Theory and Its Applications. Berlin: Springer. [Google Scholar]
- Chen, Lv, and Yang Shen. 2018. On a new paradigm of optimal reinsurance: A stochastic stackelberg differential game between an insurer and a reinsurer. ASTIN Bulletin 48: 905–60. [Google Scholar] [CrossRef]
- Denuit, Michel, Xavier Maréchal, Sandra Pitrebois, and Jean-François Walhin. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. Hoboken: John Wiley & Sons. [Google Scholar]
- Diamond, Peter A. 1982. Wage determination and efficiency in search equilibrium. The Review of Economic Studies 49: 217–27. [Google Scholar] [CrossRef]
- Dutang, Christophe, Hansjoerg Albrecher, and Stéphane Loisel. 2013. Competition among non-life insurers under solvency constraints: A game-theoretic approach. European Journal of Operational Research 231: 702–11. [Google Scholar] [CrossRef]
- Emms, Paul. 2007. Dynamic pricing of general insurance in a competitive market. ASTIN Bulletin 37: 1–34. [Google Scholar] [CrossRef]
- Emms, Paul. 2011. Pricing general insurance in a reactive and competitive market. Journal of Computational and Applied Mathematics 236: 1314–32. [Google Scholar] [CrossRef][Green Version]
- Emms, Paul. 2012. Equilibrium pricing of general insurance policies. North American Actuarial Journal 16: 323–49. [Google Scholar] [CrossRef]
- Emms, Paul, and Steven Haberman. 2005. Pricing general insurance using optimal control theory. ASTIN Bulletin 35: 427–53. [Google Scholar] [CrossRef]
- Emms, Paul, Steven Haberman, and Irene Savoulli. 2007. Optimal strategies for pricing general insurance. Insurance: Mathematics and Economics 40: 15–34. [Google Scholar] [CrossRef]
- Iglehart, Donald L. 1969. Diffusion approximations in collective risk theory. Journal of Applied Probability 6: 285–92. [Google Scholar] [CrossRef]
- Jin, Zhuo, George Yin, and Fuke Wu. 2013. Optimal reinsurance strategies in regime-switching jump diffusion models: Stochastic differential game formulation and numerical methods. Insurance: Mathematics and Economics 53: 733–46. [Google Scholar] [CrossRef]
- Lin, Xiang, Chunhong Zhang, and Tak Kuen Siu. 2012. Stochastic differential portfolio games for an insurer in a jump-diffusion risk process. Mathematical Methods of Operations Research 75: 83–100. [Google Scholar] [CrossRef]
- Meng, Hui, Shuanming Li, and Zhuo Jin. 2015. A reinsurance game between two insurance companies with nonlinear risk processes. Insurance: Mathematics and Economics 62: 91–97. [Google Scholar] [CrossRef]
- Mortensen, Dale T. 1982. Property rights and efficiency in mating, racing, and related games. The American Economic Review 72: 968–79. [Google Scholar]
- Mortensen, Dale T., and Christopher A. Pissarides. 1994. Job creation and job destruction in the theory of unemployment. The Review of Economic Studies 61: 397–415. [Google Scholar] [CrossRef]
- Pantelous, Athanasios A., and Eudokia Passalidou. 2013. Optimal premium pricing policy in a competitive insurance market environment. Annals of Actuarial Science 7: 175–91. [Google Scholar] [CrossRef]
- Pantelous, Athanasios A., and Eudokia Passalidou. 2015. Optimal premium pricing strategies for competitive general insurance markets. Applied Mathematics and Computation 259: 858–74. [Google Scholar] [CrossRef]
- Pantelous, Athanasios A., and Eudokia Passalidou. 2017. Optimal strategies for a non-linear premium-reserve model in a competitive insurance market. Annals of Actuarial Science 11: 1–19. [Google Scholar] [CrossRef]
- Polborn, Mattias K. 1998. A model of an oligopoly in an insurance market. The Geneva Papers on Risk and Insurance Theory 23: 41–48. [Google Scholar] [CrossRef]
- Powers, Michael R., Martin Shubik, and Shun Tian Yao. 1998. Insurance market games: Scale effects and public policy. Journal of Economics 67: 109–34. [Google Scholar] [CrossRef]
- Pun, Chi Seng, and Hoi Ying Wong. 2016. Robust non-zero-sum stochastic differential reinsurance game. Insurance: Mathematics and Economics 68: 169–77. [Google Scholar]
- Robert, Christian. 2007. The Bayesian Choice: from Decision-Theoretic Foundations to Computational Implementation. Berlin: Springer. [Google Scholar]
- Rothschild, Michael, and Joseph Stiglitz. 1976. Equilibrium in competitive insurance markets: An essay on the economics of imperfect information. The Quarterly Journal of Economics 90: 629–49. [Google Scholar] [CrossRef]
- Salop, Steven, and Joseph Stiglitz. 1977. Bargains and ripoffs: A model of monopolistically competitive price dispersion. The Review of Economic Studies 44: 493–510. [Google Scholar] [CrossRef]
- Shi, Jingtao, Guangchen Wang, and Jie Xiong. 2016. Leader–follower stochastic differential game with asymmetric information and applications. Automatica 63: 60–73. [Google Scholar] [CrossRef]
- Taksar, Michael, and Xudong Zeng. 2011. Optimal non-proportional reinsurance control and stochastic differential games. Insurance: Mathematics and Economics 48: 64–71. [Google Scholar] [CrossRef]
- Taylor, Gregory C. 1986. Underwriting strategy in a competitive insurance environment. Insurance: Mathematics and Economics 5: 59–77. [Google Scholar] [CrossRef]
- Taylor, Gregory C. 1987. Expenses and underwriting strategy in competition. Insurance: Mathematics and Economics 6: 275–87. [Google Scholar] [CrossRef]
- Thøgersen, Julie. 2016. Optimal premium as a function of the deductible: Customer analysis and portfolio characteristics. Risks 4: 42. [Google Scholar] [CrossRef]
- von Stackelberg, Heinrich. 1934. Marktform und Gleichgewicht. Berlin: Verlag von Julius Springer. [Google Scholar]
- Wu, Renchao, and Athanasios A Pantelous. 2017. Potential games with aggregation in non-cooperative general insurance markets. ASTIN Bulletin 47: 269–302. [Google Scholar] [CrossRef]
- Yan, Ming, Fanyi Peng, and Shuhua Zhang. 2017. A reinsurance and investment game between two insurance companies with the different opinions about some extra information. Insurance: Mathematics and Economics 75: 58–70. [Google Scholar] [CrossRef]
- Yong, Jiongmin. 2002. A leader-follower stochastic linear quadratic differential game. SIAM Journal on Control and Optimization 41: 1015–41. [Google Scholar] [CrossRef]
- Zeng, Xudong. 2010. A stochastic differential reinsurance game. Journal of Applied Probability 47: 335–49. [Google Scholar] [CrossRef]
| 1 | The standard notation avoids the primes and considers the subscript as sufficient, but we want to emphasize the differentiation here in order to avoid confusion with other notation in the paper, e.g., and . |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).