The Investigation of a Forward-Rate Mortality Framework
Abstract
:1. Introduction
2. Forward Mortality Framework
2.1. Longevity Bond Pricing
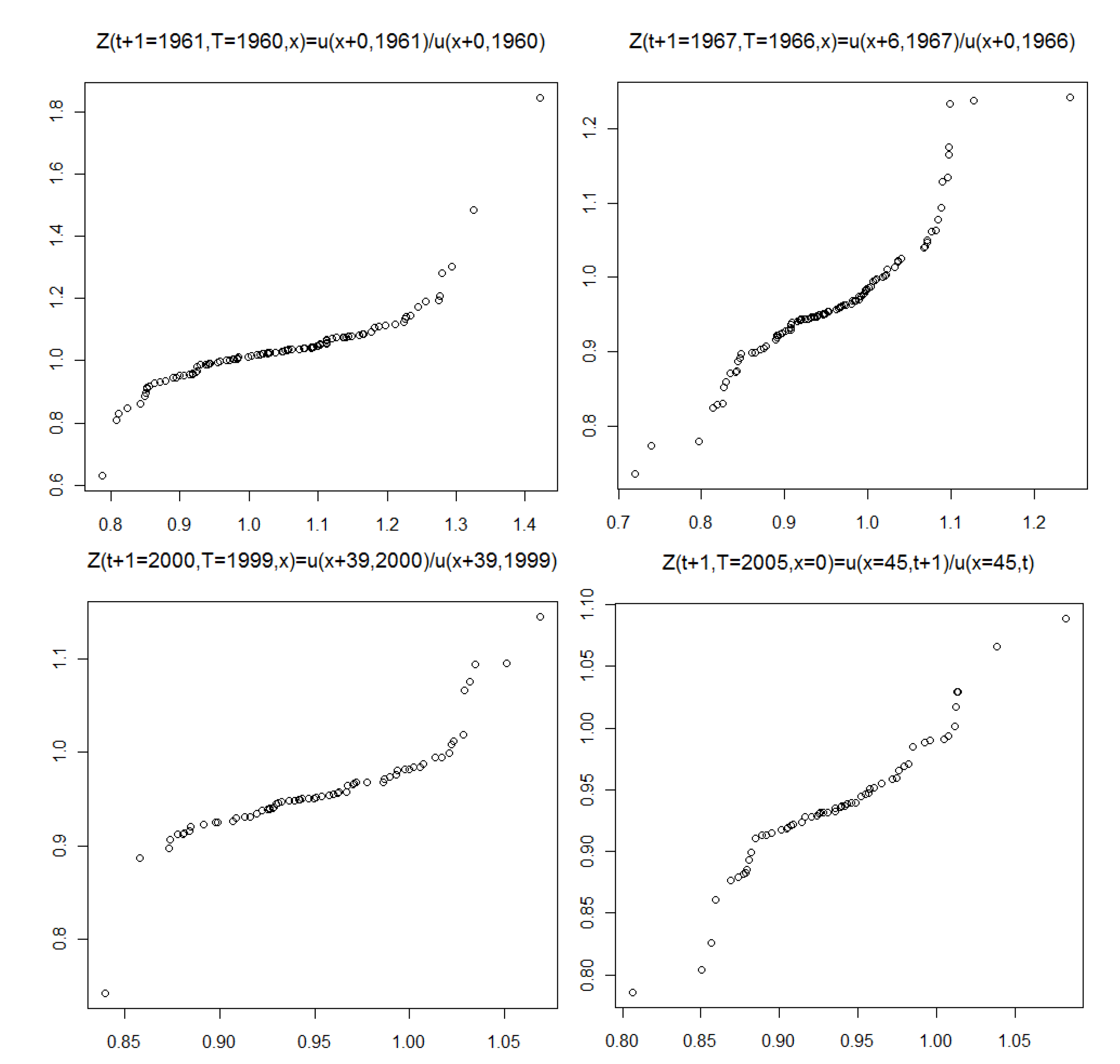
2.2. The Olivier–Smith Model
2.3. Univariate Tweedie Generalization
3. Model Assessment
3.1. Independent Distributions
3.1.1. Correlation Analysis
3.1.2. Principal Component Analysis
3.2. Identical Distributions
3.3. Appropriate Parametric Distribution
- The Anderson–Darling statistic , given by
- The Kolmogorov statistic D, given by , where
- The Cramér–von Mises statistic , given by
4. Multivariate Generalization
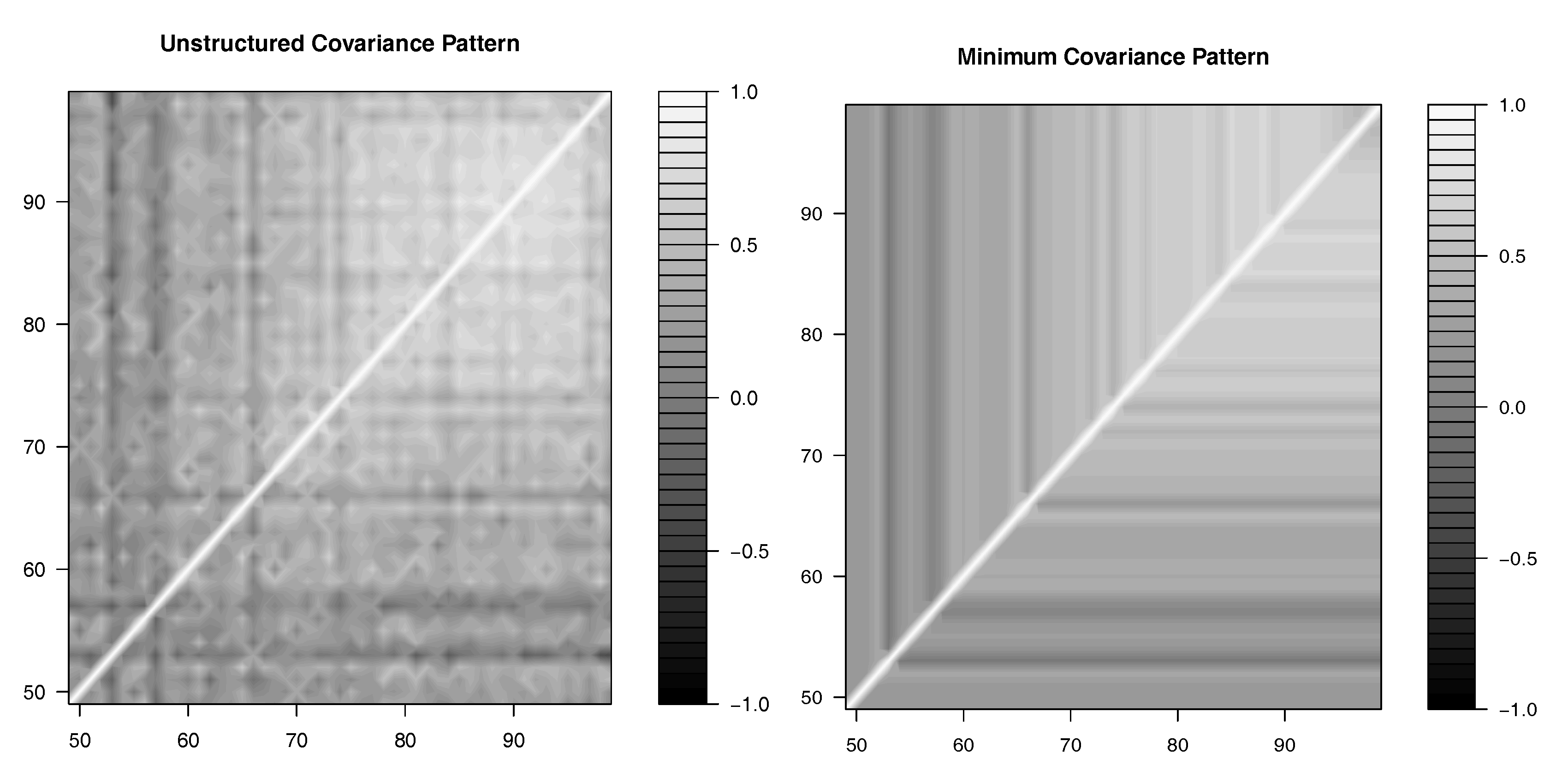
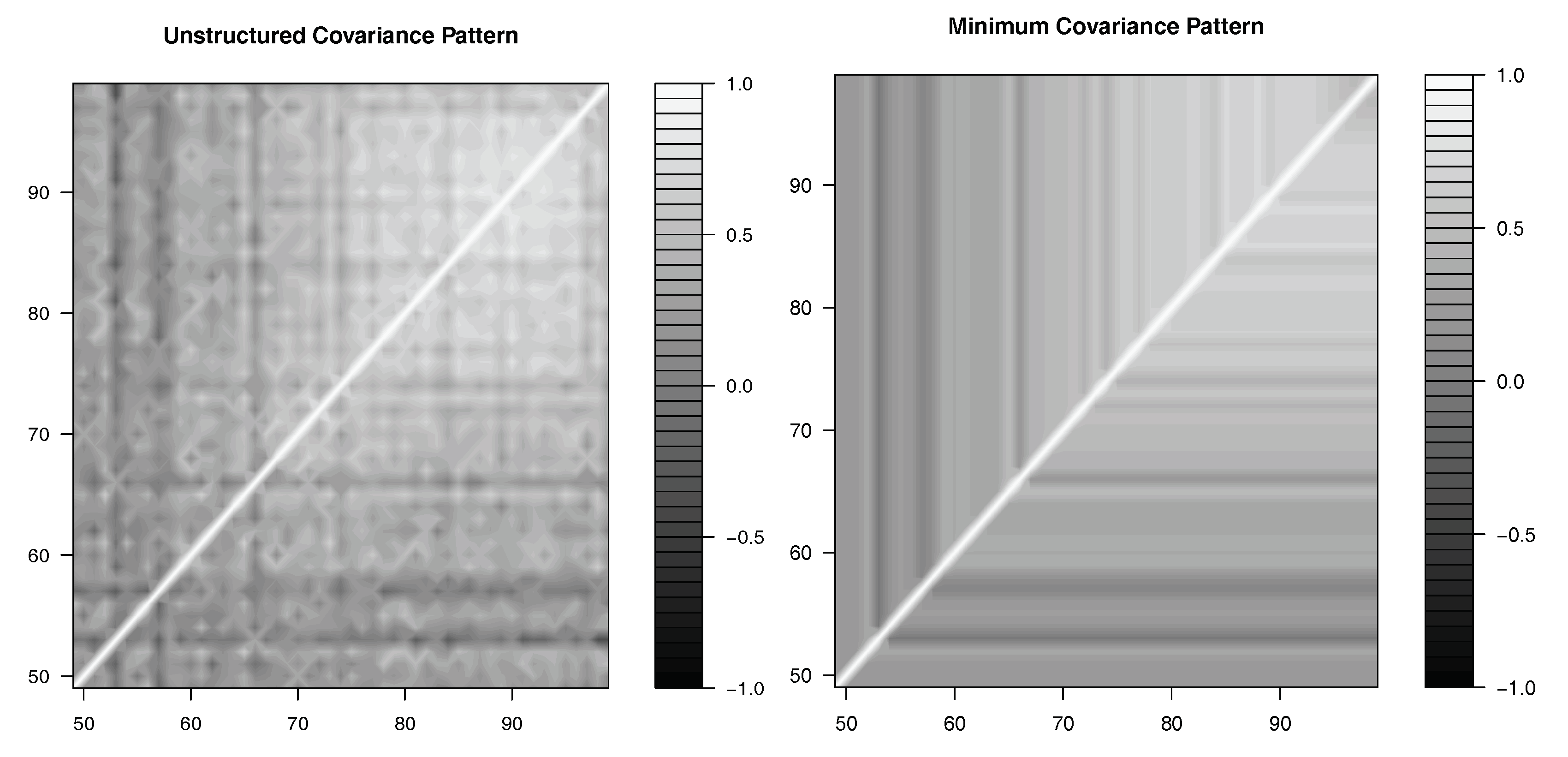
4.1. Minimum Covariance Pattern
4.2. Capturing Dependence with Copulas
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aalen, Odd O. 1992. Modelling heterogeneity in survival analysis by the compound Poisson distribution. Annals of Applied Probability 2: 951–72. [Google Scholar] [CrossRef]
- Akaike, Hirotugu. 1974. A new look at the statistical model identification. IEEE Transaction on Automatic Control 19: 716–23. [Google Scholar] [CrossRef]
- Bauer, Daniel. 2006. An Arbitrage-Free Family of Longevity Bonds. Ulm: University of Ulm. [Google Scholar]
- Bauer, Daniel, and Jochen Ruß. 2006. Pricing longevity bonds using implied survival probabilities. Paper presented at Meeting of the American Risk and Insurance Association (ARIA), Washington, DC, USA, August 6. [Google Scholar]
- Biffis, Enrico. 2005. Affine processes for dynamic mortality and actuarial valuations. Insurance: Mathematics and Economics 37: 443–68. [Google Scholar] [CrossRef]
- Blackburn, Craig, and Michael Sherris. 2013. Consistent dynamic affine mortality models for longevity risk applications. Insurance: Mathematics and Economics 53: 64–73. [Google Scholar] [CrossRef]
- Blake, David, Andrew J. G. Cairns, and Kevin Dowd. 2006. Living with mortality: Longevity bonds and other mortality-linked securities. British Actuarial Journal 12: 153–97. [Google Scholar] [CrossRef]
- Breymann, Wolfgang, Alexandra Dias, and Paul Embrechts. 2003. Dependence structures for multivariate high-frequency data in finance. Quantitative Finance 3: 1–14. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G. 2007. A multifactor generalisation of the Olivier-Smith model for stochastic mortality. Paper presented at 1st IAA Life Colloquium, Stockholm, Sweden, June 10–13. [Google Scholar]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. Pricing death: Frameworks for the valuation and securitization of mortality risk. ASTIN Bulletin 36: 79–120. [Google Scholar] [CrossRef]
- Cherubini, Umberto, Elisa Luciano, and Walter Vecchiato. 2004. Copula Methods in Finance. Hoboken: Wiley Finance Series. [Google Scholar]
- CMI. 2005. Projecting Future Mortality: Towards a Proposal for a Stochastic Methodology. Working Paper 15 of the Continuous Mortality Investigation. London: The Faculty of Actuaries and Institute of Actuaries. [Google Scholar]
- Cox, John C., Jonathan E. Ingersoll Jr., and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica: Journal of the Econometric Society 53: 385–407. [Google Scholar] [CrossRef]
- D’Agostino, Ralph B., and Michael A. Stephens. 1986. Goodness-of-fit techniques. In Statistics: Textbooks and Monographs. New York: Dekker. [Google Scholar]
- Embrechts, Paul, Alexander McNeil, and Daniel Straumann. 2002. Correlation and dependence in risk management: Properties and pitfalls. In Risk Management: Value at Risk and Beyond. Cambridge: Cambridge University Press, pp. 176–223. [Google Scholar]
- Fang, Hong-Bin, Kai-Tai Fang, and Samuel Kotz. 2002. The meta-elliptical distributions with given marginals. Journal of Multivariate Analysis 82: 1–16. [Google Scholar] [CrossRef]
- Frahm, Gabriel, Markus Junker, and Alexander Szimayer. 2003. Elliptical copulas: Applicability and limitations. Statistics and Probability Letters 63: 275–86. [Google Scholar] [CrossRef]
- Furman, Edward, and Zinoviy Landsman. 2010. Multivariate Tweedie distributions and some related capital-at-risk analysis. Insurance: Mathematics and Economics 46: 351–61. [Google Scholar]
- Hult, Henrik, and Filip Lindskog. 2002. Multivariate extremes, aggregation and dependence in elliptical distributions. Advances in Applied Probability 34: 587–608. [Google Scholar] [CrossRef]
- Human Mortality Database. 2013. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org or www.humanmortality.de (accessed on 8 March 2013).
- Ignatieva, Katja, Andrew Song, and Jonathan Ziveyi. 2018. Fourier space time-stepping algorithm for valuing guaranteed minimum withdrawal benefits in variable annuities under regime-switching and stochastic mortality. ASTIN Bulletin 48: 139–69. [Google Scholar] [CrossRef]
- Jevtić, Petar, Elisa Luciano, and Elena Vigna. 2013. Mortality surface by means of continuous time cohort models. Insurance: Mathematics and Economics 53: 122–33. [Google Scholar] [CrossRef]
- Joe, Harry. 1990. Multivariate concordance. Journal of Multivariate Analysis 35: 12–30. [Google Scholar] [CrossRef] [Green Version]
- Joe, Harry. 1997. Multivariate Models and Dependence Concepts. London: Chapman & Hall. [Google Scholar]
- Jørgensen, Bent. 1997. The Theory of Dispersion Models. London: Chapman & Hall. [Google Scholar]
- Jørgensen, Bent, and Marta C. Paes De Souza. 1994. Fitting Tweedie’s compound Poisson model to insurance claims data. Scandinavian Actuarial Journal 1: 69–93. [Google Scholar] [CrossRef]
- Kaas, Rob. 2005. Compound Poisson Distributions and GLM’s—Tweedie’s Distribution. Brussels: Royal Flemish Academy of Belgium for Science and the Arts. [Google Scholar]
- Liu, Xiaoming. 2008. Stochastic Mortality Modelling. Ph.D. thesis, University of Toronto, Toronto, ON, Canada. [Google Scholar]
- Luciano, Elisa, and Elena Vigna. 2005. Non Mean Reverting Affine Processes for Stochastic Mortality. Torino: International Centre for Economic Research. [Google Scholar]
- MacLeish, Donald L., and Christopher G. Small. 1988. The Theory and Applications of Statistical Inference Functions. New York: Springer. [Google Scholar]
- McCullagh, Peter, and John A. Nelder. 1989. Generalized Linear Models, 2nd ed. London: Chapman & Hall. [Google Scholar]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management. Princeton: Princeton Series in Finance. [Google Scholar]
- Norberg, Ragnar. 2010. Forward mortality and other vital rates—Are they the way forward? Insurance: Mathematics and Economics 47: 105–12. [Google Scholar] [CrossRef]
- Olivier, Phillip, and Tony Jeffery. 2004. Stochastic Mortality Models. Presentation to the Society of Actuaries of Ireland. Available online: www.actuaries.ie/Resources/eventspapers/PastCalendarListing.htm (accessed on 13 February 2019).
- Russo, Vincenzo, Rosella Giacometti, Sergio Ortobelli, Svetlozar Rachev, and Frank J. Fabozzi. 2010. Calibrating Affine Stochastic Mortality Models Using Insurance Contracts Premiums. Technical Report. Karlsruhe: University of Karlsruhe. [Google Scholar]
- Smith, Andrew D. 2005. Stochastic mortality modelling. Paper presented at Workshop on the Interface between Quantitative Finance and Insurance, Edinburgh, Scotland, April 4–8; Available online: www.icms.org.uk/archive/meetings/2005/quantfinance/ (accessed on 13 February 2019).
- Stephens, Michael A. 1974. EDF statistics for goodness of fit and some comparisons. Journal of the American Statistical Association 69: 730–37. [Google Scholar] [CrossRef]
- Tweedie, Maurice C. K. 1984. An index which distinguishes some important exponential families. In Statistics: Applications and New Directions. Edited by Jayanta K. Ghosh and Jogabrata Roy. Calcutta: Indian Statistical Institute, pp. 579–604. [Google Scholar]
- Wills, Samuel, and Michael Sherris. 2010. Securitization, structuring and pricing of longevity risk. Insurance: Mathematics and Economics 46: 173–85. [Google Scholar] [CrossRef]
- Ziveyi, Jonathan, Craig Blackburn, and Michael Sherris. 2013. Pricing european options on deferred annuities. Insurance: Mathematics and Economics 52: 300–11. [Google Scholar] [CrossRef]

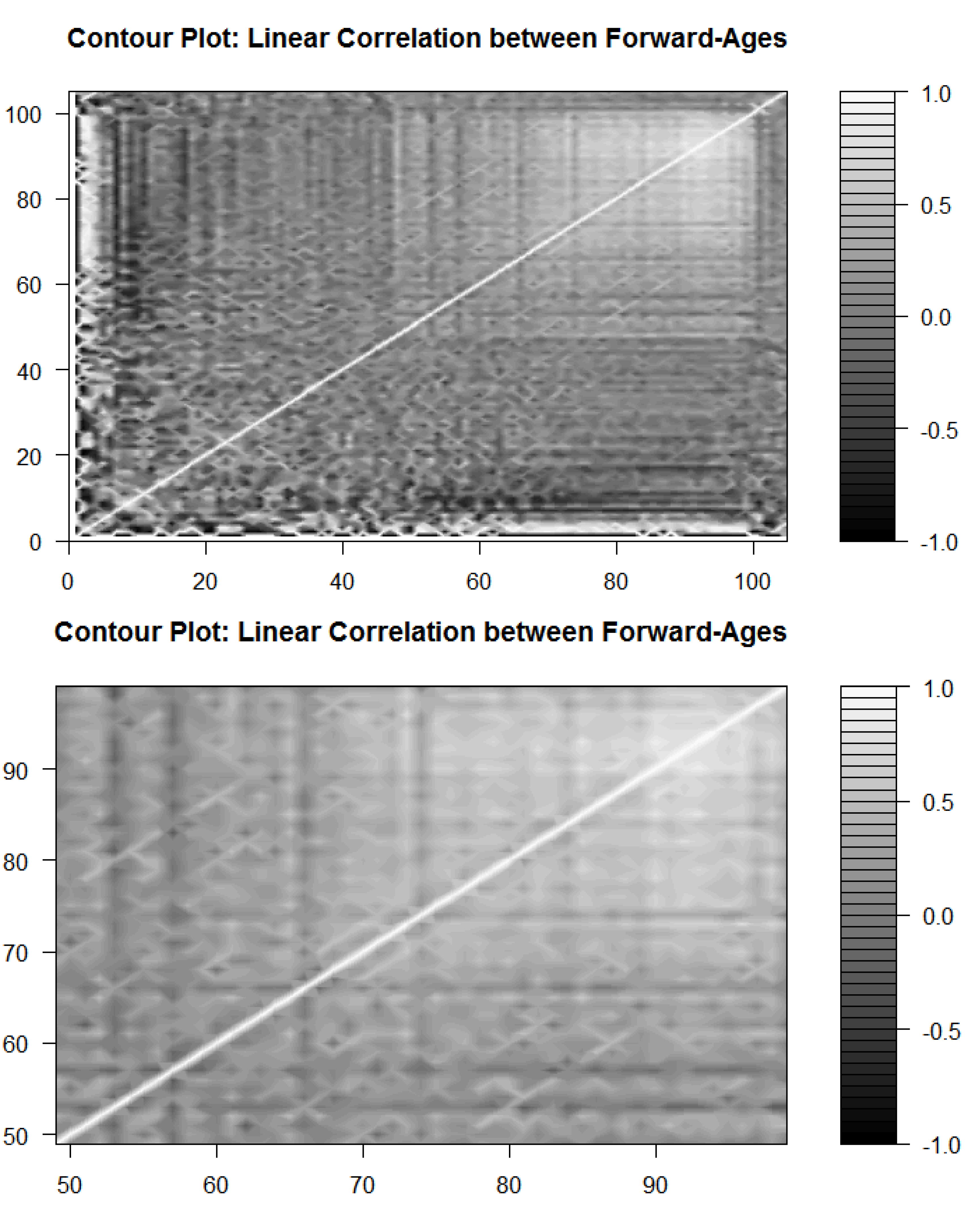
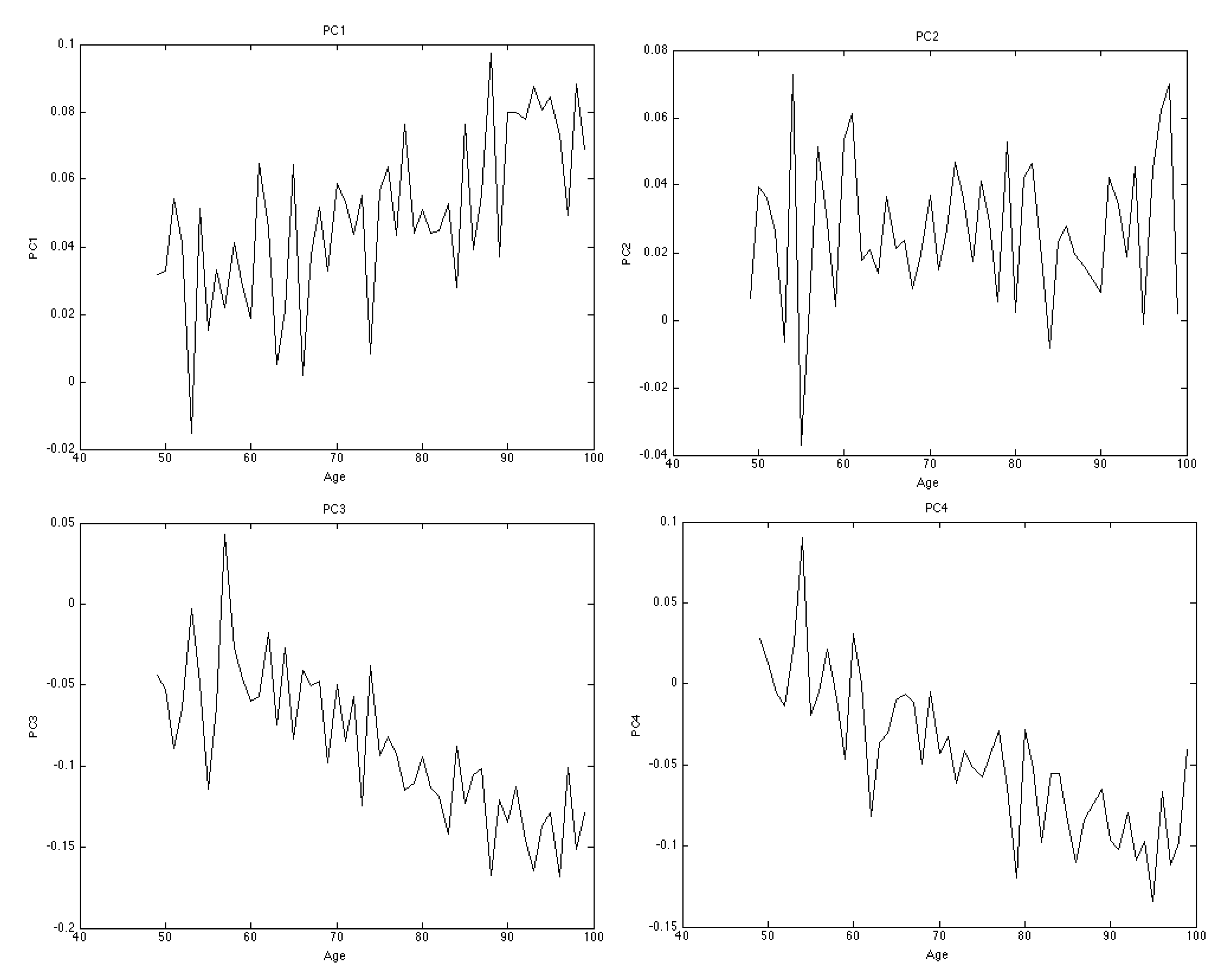


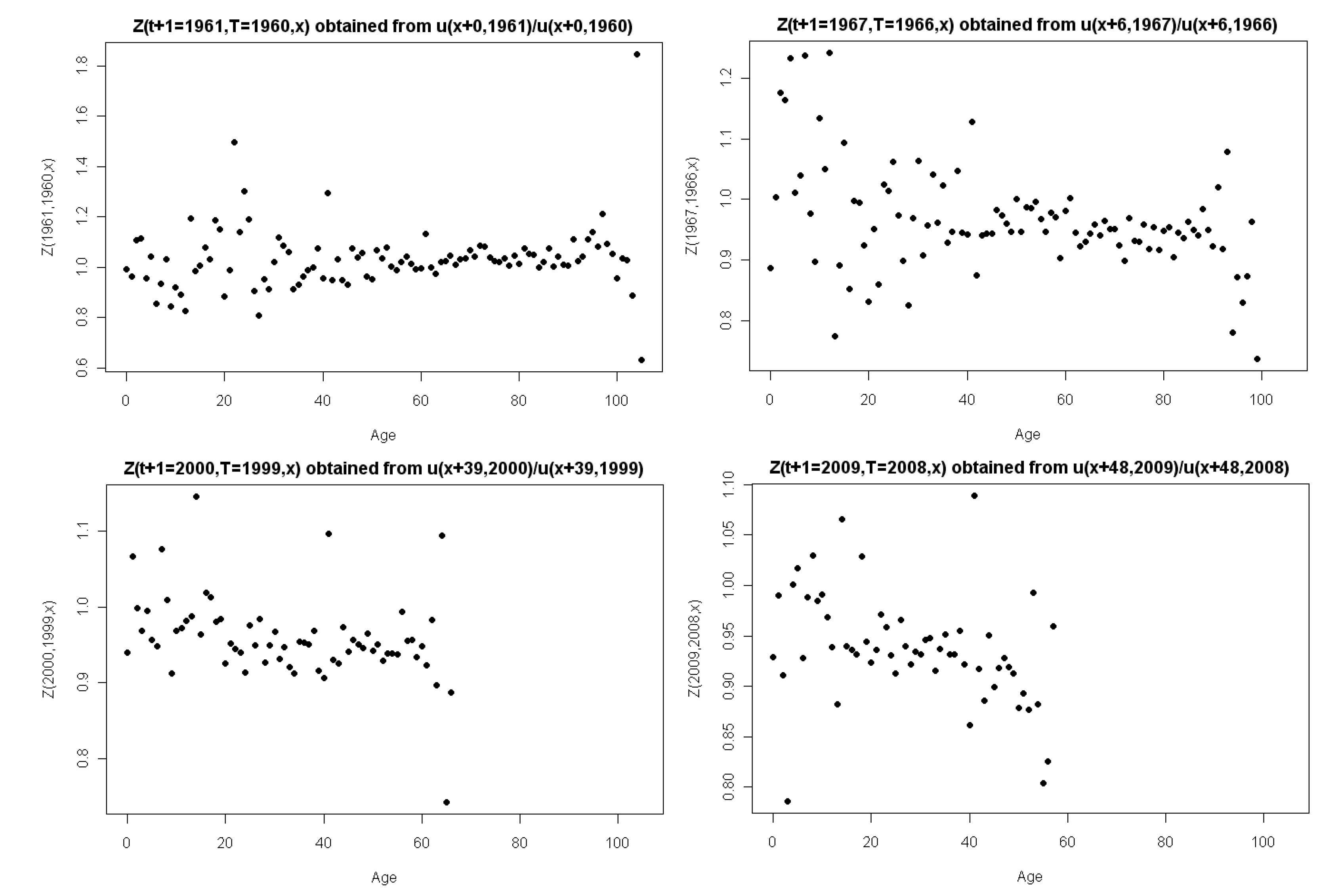
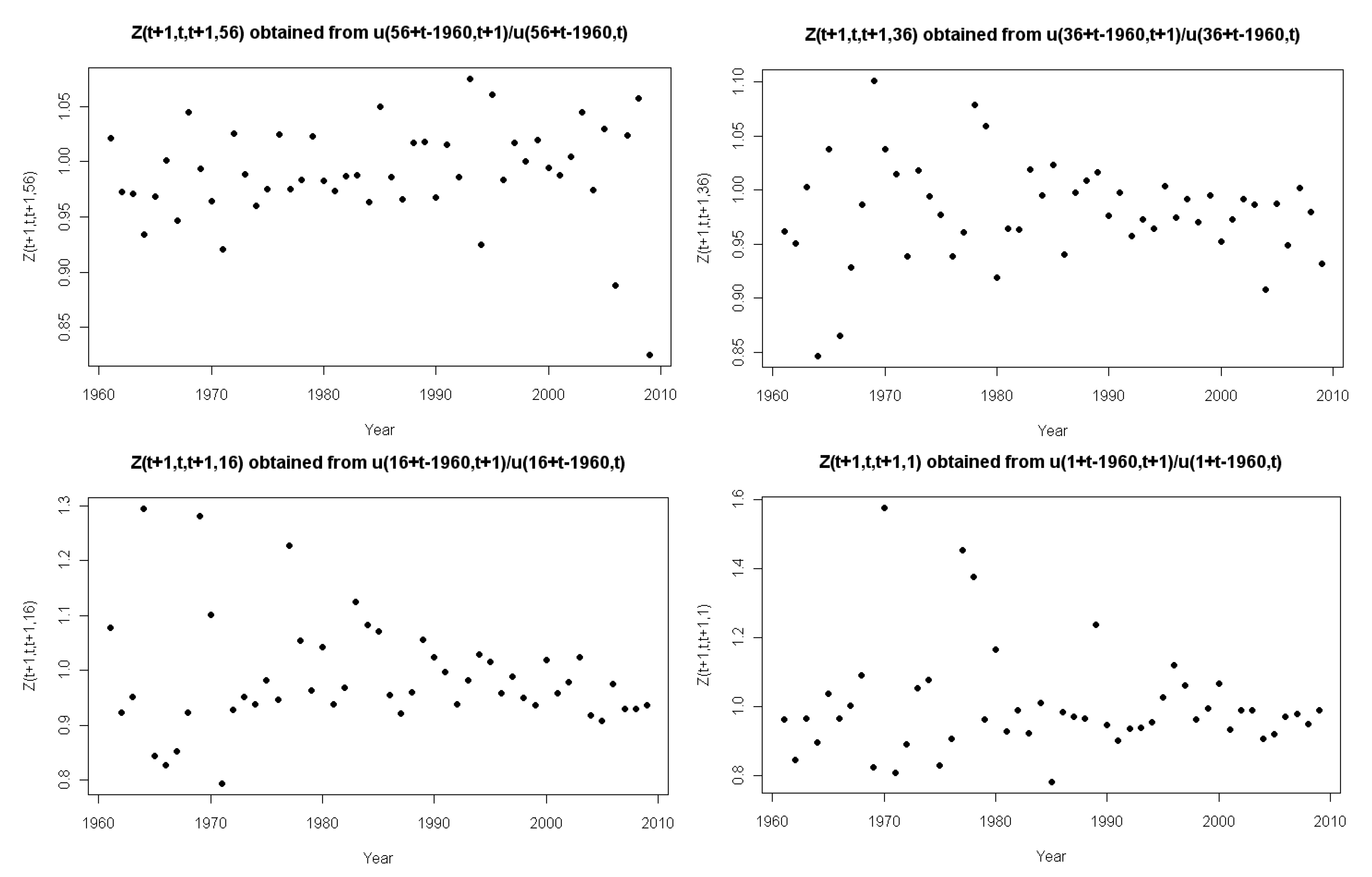




| Eigenvalue | Individual Variance | Cumulative Variance |
|---|---|---|
| 0.2818 | 0.2818 | |
| 0.2096 | 0.4915 | |
| 0.1416 | 0.6331 | |
| 0.1028 | 0.7359 | |
| 0.0434 | 0.7793 | |
| 0.0312 | 0.8104 | |
| 0.0214 | 0.8319 | |
| 0.0167 | 0.8485 | |
| 0.0156 | 0.8641 | |
| 0.0138 | 0.8779 | |
| 0.0122 | 0.8901 | |
| 0.0112 | 0.9013 | |
| 0.0103 | 0.9116 | |
| 0.0096 | 0.9213 | |
| 0.0074 | 0.9287 | |
| 0.0068 | 0.9355 |
| Stat. | Crit.5% | Crit.1% |
|---|---|---|
| 2.492 | 3.857 | |
| D | 1.358 | 1.628 |
| 0.461 | 0.743 |
| D | |||||
|---|---|---|---|---|---|
| Panel A: The Stochastic Mortality Component over Time t for Fixed x | |||||
| 12.943646 | 12.624253 | ** | ** | ** | |
| 415.72498 | 421.08874 | ** | ** | ** | |
| 452.03843 | 458.56811 | ** | ** | ** | |
| 331.04846 | 335.43804 | ** | ** | ** | |
| Panel B: The Stochastic Mortality Component over Age x for Fixed t | |||||
| 71.337103 | 69.005897 | * | * | ||
| 127.56511 | 132.22064 | * | ** | ** | |
| 312.29324 | 325.31700 | * | ** | * | |
| 297.92308 | 317.92973 | ** | ** | ** | |
| Panel C: The Stochastic Mortality Component for Fixed Year-of-Birth | |||||
| 497.3803 | 502.4013 | ** | ** | ** | |
| 444.92502 | 454.13746 | ** | ** | ** | |
| 107.80345 | 109.21021 | ** | ** | ** | |
| 53.05649 | 53.04923 | * | * | * | |
| Forward-Ages | Gaussian Copula | Student’s t Copula | ||
|---|---|---|---|---|
| Gaussian | Gamma | Gaussian | Gamma | |
| 49–59 | −5.95 | −7.29 | −3.93 | −5.26 |
| 59–69 | −23.45 | −27.46 | −21.44 | −25.43 |
| 69–79 | −145.26 | −154.93 | −143.23 | −152.91 |
| 79–89 | −223.68 | −241.29 | −246.88 | −266.26 |
| 89–99 | −403.88 | −410.02 | −405.27 | −410.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alai, D.H.; Ignatieva, K.; Sherris, M. The Investigation of a Forward-Rate Mortality Framework. Risks 2019, 7, 61. https://doi.org/10.3390/risks7020061
Alai DH, Ignatieva K, Sherris M. The Investigation of a Forward-Rate Mortality Framework. Risks. 2019; 7(2):61. https://doi.org/10.3390/risks7020061
Chicago/Turabian StyleAlai, Daniel H., Katja Ignatieva, and Michael Sherris. 2019. "The Investigation of a Forward-Rate Mortality Framework" Risks 7, no. 2: 61. https://doi.org/10.3390/risks7020061
APA StyleAlai, D. H., Ignatieva, K., & Sherris, M. (2019). The Investigation of a Forward-Rate Mortality Framework. Risks, 7(2), 61. https://doi.org/10.3390/risks7020061





