Hospital Proximity and Mortality in Australia
Abstract
:1. Introduction
2. Data
2.1. Notation
- x age next birthday, for ,
- r region, for ,
- city within region r,
- h hospital,
- age dependent mortality for age x,
- number of deaths at age x in region r,
- number of exposed lives at age x in region r,
- population of city contained in region r,
- the distance (in degrees) from to the nearest hospital
2.2. A General Model
- is the strength of age-based hospital proximity effects;
- the population-weighted distance to the nearest hospital;
- is a variance term (see below);
- is a normal error term with constant variance.
3. The Model with Heteroscedasticity
3.1. The Model without Proximity or Regionality
3.2. The Model with Regionality but Not Proximity
A Regionalized Model
4. The Model with Proximity
5. Diagnostics
6. Indigenity
- their lifestyle and culture leads to riskier outcomes (a racist argument); or
- their remoteness from health care.
7. Conclusions
Funding
Conflicts of Interest
Appendix A. Assessing the Impact of Rural Areas
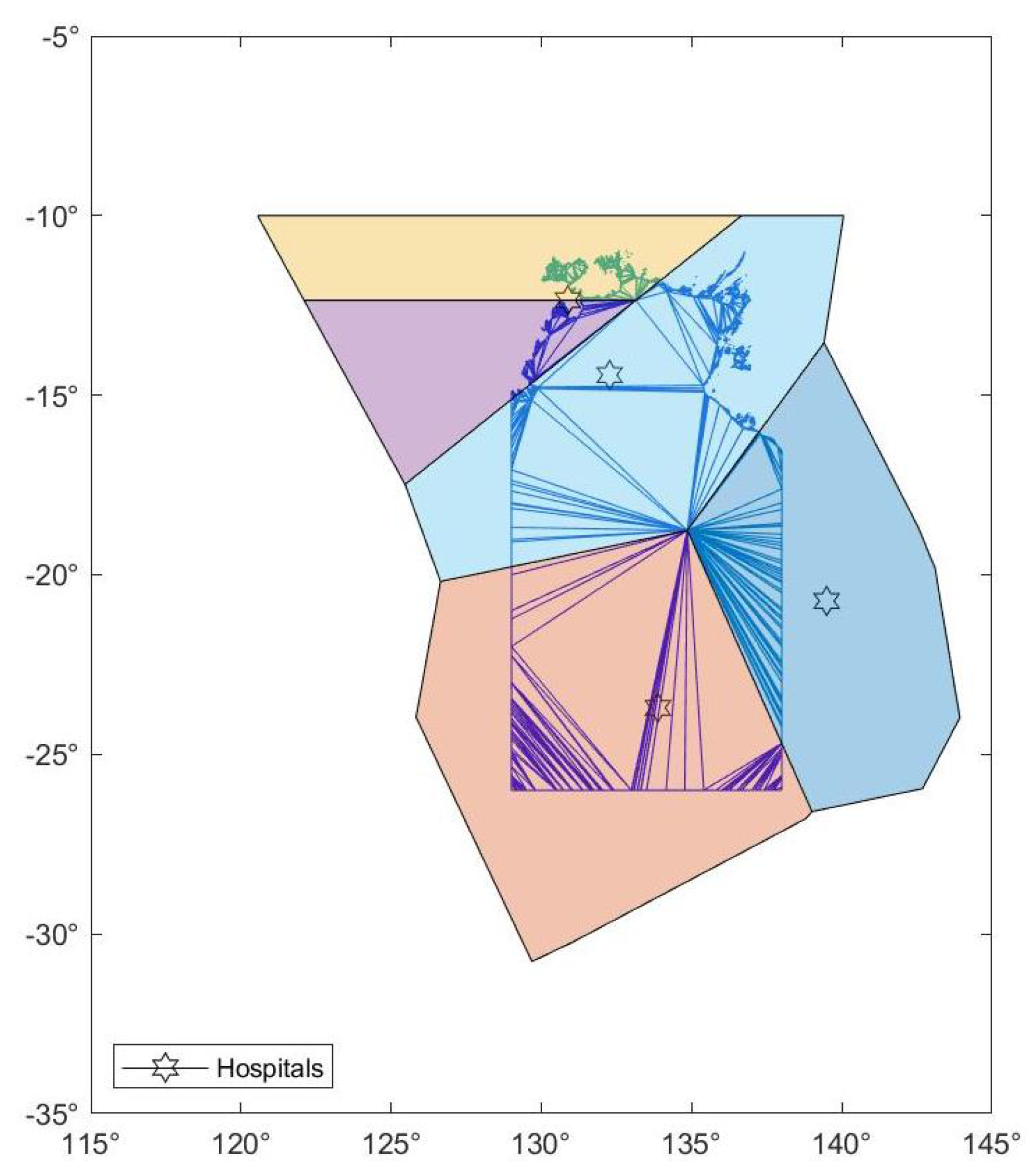
- The ‘catchment area’ of each hospital is calculated. This is a polygon whose interior consists of points, all of which have the given hospital as its nearest. The polygon may be constructed by drawing a line segment between a given hospital, and all other hospitals, and then taking a perpendicular through the midpoint of each line segment, The perpendiculars establish the catchment area of each hospital. By definition, the catchment areas cannot intersect. The process is illustrated in Figure A1 below for SD = 58, which includes numerous outlying islands.
- Each SD is divided into catchment areas for the various hospitals. It should be noted that a hospital need not actually be in a SD, as some remote regions have their nearest hospital in another SD.
- The intersection of SDs and catchment areas is polygons which themselves may not be simply connected. Thus, for the purpose of assessing average nearest distance, a triangulation of each polygon must be made. Integration over the triangles comprising each polygon may then be undertaken to calculate average nearest distance. The results for each SD are set out in Table 1.
Appendix B. The Model with Proximity
Appendix C
| SD | Statistical Division | 1–5 | 6–10 | 11–15 | 16–20 | 21–25 | 26–30 | 31–35 | 36–40 | 41–45 | 46–50 | 51–55 | 56–60 | 61–65 | 66–70 | 71–75 | 76–80 | 81–85 | ≥ 86 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sydney | 1.9% | 1.1% | 0.8% | 5.4% | 3.6% | 2.2% | 1.9% | 2.6% | 2.4% | 1.5% | 0.7% | 0.8% | 0.6% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.5% |
| 2 | Hunter | 13.4% | 7.7% | 5.5% | 28.9% | 23.9% | 18.2% | 15.1% | 18.5% | 16.2% | 9.7% | 4.8% | 4.8% | 3.5% | 3.1% | 1.9% | 1.1% | 0.6% | −0.1% | 2.7% |
| 3 | Illawarra | 6.1% | 3.1% | 2.2% | 13.9% | 11.4% | 8.5% | 6.8% | 8.6% | 7.0% | 4.1% | 2.0% | 2.0% | 1.4% | 1.1% | 0.7% | 0.4% | 0.2% | −0.1% | 1.1% |
| 4 | Richmond-Tweed | 6.2% | 3.1% | 2.1% | 13.4% | 13.3% | 10.0% | 7.6% | 8.7% | 6.9% | 3.6% | 1.7% | 1.7% | 1.4% | 1.1% | 0.6% | 0.3% | 0.2% | 0.0% | 0.9% |
| 5 | Mid-North-Coast | 17.9% | 9.3% | 6.2% | 34.7% | 37.2% | 29.4% | 22.9% | 25.3% | 20.2% | 11.5% | 5.4% | 5.3% | 3.7% | 3.0% | 1.8% | 1.0% | 0.6% | −0.1% | 2.8% |
| 6 | Northern (NSW) | 19.2% | 11.4% | 8.3% | 40.2% | 37.9% | 30.3% | 25.1% | 28.9% | 25.2% | 15.5% | 7.7% | 7.5% | 5.5% | 4.7% | 3.0% | 2.0% | 1.2% | −0.3% | 4.8% |
| 7 | North-Western | 31.1% | 19.9% | 15.1% | 60.1% | 58.0% | 46.9% | 40.2% | 44.7% | 40.0% | 27.0% | 15.1% | 14.7% | 10.9% | 9.3% | 6.3% | 3.8% | 2.7% | −0.7% | 9.9% |
| 8 | Central-West | 14.6% | 8.3% | 6.1% | 31.3% | 29.1% | 22.1% | 18.0% | 21.8% | 18.9% | 11.3% | 5.5% | 5.4% | 4.1% | 3.5% | 2.2% | 1.4% | 0.8% | −0.2% | 3.4% |
| 9 | South-Eastern | 17.2% | 9.8% | 6.8% | 36.3% | 35.3% | 26.4% | 20.6% | 23.0% | 19.4% | 11.5% | 5.7% | 5.5% | 4.1% | 3.5% | 2.3% | 1.4% | 0.8% | −0.2% | 3.6% |
| 10 | Murrumbidgee | 14.8% | 8.1% | 6.0% | 30.3% | 27.4% | 21.2% | 18.0% | 21.8% | 18.8% | 11.5% | 5.9% | 6.1% | 4.8% | 3.8% | 2.4% | 1.4% | 0.8% | −0.2% | 3.7% |
| 11 | Murray | 23.1% | 13.8% | 9.5% | 44.7% | 42.8% | 32.0% | 27.5% | 32.0% | 27.8% | 16.9% | 8.4% | 8.5% | 6.5% | 5.3% | 3.4% | 1.9% | 1.1% | −0.3% | 5.1% |
| 12 | Far-West | 50.6% | 37.0% | 28.8% | 74.7% | 73.0% | 64.9% | 57.8% | 62.9% | 56.9% | 40.6% | 23.7% | 22.7% | 19.6% | 16.8% | 10.1% | 5.4% | 4.0% | −1.2% | 15.5% |
| 13 | Melbourne | 1.3% | 0.8% | 0.6% | 3.5% | 2.3% | 1.5% | 1.3% | 1.7% | 1.6% | 1.0% | 0.5% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 14 | Barwon | 6.3% | 3.4% | 2.3% | 14.6% | 12.4% | 8.8% | 6.9% | 8.6% | 7.5% | 4.4% | 2.1% | 2.1% | 1.6% | 1.4% | 0.8% | 0.5% | 0.2% | −0.1% | 1.2% |
| 15 | Western-District | 27.0% | 14.1% | 9.7% | 46.0% | 44.7% | 35.7% | 29.2% | 33.2% | 28.4% | 18.3% | 9.1% | 9.3% | 7.4% | 6.3% | 3.8% | 2.2% | 1.2% | −0.3% | 5.5% |
| 16 | Centra- | 6.1% | 3.2% | 2.2% | 13.2% | 11.4% | 8.9% | 7.1% | 8.6% | 7.2% | 4.3% | 1.9% | 2.0% | 1.5% | 1.3% | 0.8% | 0.5% | 0.3% | −0.1% | 1.2% |
| 17 | Wimmera | 30.6% | 16.9% | 11.8% | 51.7% | 51.4% | 41.5% | 34.8% | 37.4% | 31.5% | 19.3% | 10.3% | 9.9% | 7.8% | 6.1% | 3.5% | 2.0% | 1.2% | −0.3% | 5.3% |
| 18 | Mallee | 35.2% | 21.5% | 16.0% | 60.6% | 59.0% | 47.0% | 41.9% | 45.4% | 41.5% | 27.9% | 15.6% | 15.8% | 12.3% | 10.0% | 6.6% | 3.5% | 2.0% | −0.5% | 9.1% |
| 19 | Loddon | 7.1% | 3.5% | 2.4% | 15.5% | 14.3% | 11.0% | 8.5% | 9.8% | 8.2% | 4.4% | 2.1% | 2.1% | 1.6% | 1.4% | 0.9% | 0.5% | 0.3% | −0.1% | 1.3% |
| 20 | Goulburn | 9.5% | 5.1% | 3.5% | 22.3% | 22.1% | 16.3% | 12.2% | 13.7% | 11.9% | 6.9% | 3.3% | 3.3% | 2.4% | 2.1% | 1.3% | 0.8% | 0.4% | −0.1% | 2.0% |
| 21 | Ovens-Murray | 21.2% | 12.3% | 8.3% | 39.1% | 38.7% | 30.4% | 24.6% | 28.2% | 24.0% | 15.0% | 7.4% | 7.6% | 6.0% | 5.1% | 3.5% | 1.9% | 1.1% | −0.3% | 4.9% |
| 22 | East-Gippsland | 20.6% | 11.5% | 7.8% | 39.9% | 38.7% | 29.3% | 25.2% | 27.8% | 23.9% | 13.7% | 6.3% | 6.0% | 4.4% | 3.5% | 2.3% | 1.3% | 0.8% | −0.2% | 3.6% |
| 23 | Gippsland | 8.5% | 4.1% | 2.8% | 17.4% | 16.9% | 12.7% | 9.9% | 11.2% | 9.3% | 5.3% | 2.5% | 2.4% | 1.8% | 1.5% | 0.9% | 0.5% | 0.3% | −0.1% | 1.4% |
| 24 | Brisbane | 3.2% | 1.9% | 1.4% | 8.3% | 5.8% | 4.0% | 3.3% | 4.5% | 4.2% | 2.6% | 1.2% | 1.2% | 1.0% | 1.0% | 0.7% | 0.4% | 0.2% | 0.0% | 0.9% |
| 25 | Gold-Coast | 1.7% | 1.0% | 0.7% | 4.4% | 3.1% | 2.0% | 1.7% | 2.3% | 2.1% | 1.2% | 0.6% | 0.6% | 0.4% | 0.4% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 26 | Sunshine-Coast | 3.3% | 1.7% | 1.2% | 8.3% | 7.5% | 5.2% | 3.8% | 4.7% | 3.9% | 2.1% | 1.0% | 1.0% | 0.7% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.5% |
| 27 | West-Moreton | 9.3% | 4.9% | 3.3% | 22.7% | 22.8% | 16.9% | 12.3% | 13.5% | 10.9% | 6.6% | 3.1% | 2.9% | 2.1% | 1.8% | 1.3% | 0.9% | 0.5% | −0.1% | 2.1% |
| 28 | Wide-Bay-Burnett | 16.3% | 8.6% | 5.8% | 35.4% | 34.1% | 25.8% | 20.4% | 22.9% | 19.5% | 11.3% | 5.4% | 4.8% | 3.2% | 2.6% | 1.8% | 1.1% | 0.7% | −0.2% | 2.9% |
| 29 | Darling | 12.5% | 7.3% | 5.1% | 29.3% | 24.8% | 19.4% | 16.0% | 19.4% | 17.4% | 10.4% | 5.1% | 5.2% | 3.8% | 3.3% | 2.1% | 1.3% | 0.7% | −0.2% | 3.1% |
| 30 | South-West | 43.7% | 31.1% | 28.2% | 76.0% | 70.9% | 59.1% | 52.7% | 59.4% | 55.7% | 41.4% | 27.0% | 26.5% | 22.3% | 20.2% | 13.3% | 9.0% | 7.4% | −1.4% | 20.2% |
| 31 | Fitzroy | 17.5% | 10.6% | 7.6% | 39.0% | 32.7% | 24.6% | 21.1% | 25.3% | 22.2% | 14.0% | 7.5% | 8.1% | 6.6% | 6.0% | 4.0% | 2.5% | 1.6% | −0.4% | 5.9% |
| 32 | Central-West | 53.8% | 42.4% | 39.3% | 81.1% | 75.7% | 67.7% | 62.4% | 67.5% | 64.4% | 51.1% | 30.5% | 34.2% | 25.3% | 22.2% | 14.6% | 9.7% | 6.7% | −1.7% | 22.3% |
| 33 | Mackay | 35.1% | 22.7% | 17.3% | 62.7% | 53.4% | 41.2% | 36.5% | 42.0% | 39.0% | 26.8% | 15.1% | 16.4% | 13.8% | 13.5% | 10.1% | 6.3% | 4.0% | −1.1% | 13.6% |
| 34 | Northern (QLD) | 40.5% | 26.9% | 20.2% | 64.5% | 55.5% | 46.7% | 42.5% | 49.8% | 47.7% | 34.3% | 20.3% | 20.8% | 17.9% | 16.2% | 11.9% | 7.5% | 4.4% | −1.1% | 15.8% |
| 35 | Far- | 24.7% | 15.8% | 11.7% | 53.1% | 46.8% | 34.4% | 28.1% | 33.2% | 30.4% | 20.3% | 10.8% | 11.1% | 9.2% | 8.7% | 6.1% | 4.2% | 2.5% | −0.6% | 8.9% |
| 36 | North-West | 56.3% | 43.2% | 39.3% | 82.9% | 75.0% | 64.9% | 61.3% | 69.3% | 68.2% | 57.1% | 40.6% | 41.7% | 35.7% | 39.7% | 29.9% | 24.9% | 19.5% | −6.4% | 40.2% |
| 37 | Adelaide | 0.6% | 0.4% | 0.2% | 1.5% | 1.1% | 0.7% | 0.6% | 0.8% | 0.7% | 0.4% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 38 | Outer-Adelaide | 14.0% | 7.3% | 5.1% | 28.5% | 29.2% | 22.0% | 16.4% | 17.6% | 14.9% | 8.5% | 4.3% | 4.2% | 3.2% | 2.7% | 1.8% | 1.1% | 0.6% | −0.1% | 2.6% |
| 39 | Yorke | 24.4% | 13.0% | 9.4% | 46.0% | 45.2% | 35.8% | 30.3% | 31.1% | 25.0% | 15.6% | 7.1% | 6.7% | 4.4% | 3.6% | 2.3% | 1.3% | 0.8% | −0.2% | 3.6% |
| 40 | Murray-Lands | 25.3% | 14.7% | 10.4% | 47.7% | 45.6% | 34.6% | 28.3% | 30.4% | 27.9% | 17.4% | 8.8% | 8.7% | 6.4% | 5.6% | 3.5% | 2.1% | 1.2% | −0.3% | 5.4% |
| 41 | South-East | 36.7% | 22.6% | 16.4% | 61.2% | 56.0% | 44.6% | 39.6% | 42.3% | 39.1% | 26.6% | 14.7% | 15.4% | 12.9% | 11.4% | 7.6% | 4.1% | 2.5% | −0.6% | 10.3% |
| 42 | Eyre | 46.8% | 29.2% | 22.4% | 70.5% | 66.1% | 55.6% | 49.3% | 52.8% | 50.1% | 34.9% | 19.7% | 20.6% | 16.0% | 14.7% | 10.3% | 5.7% | 3.3% | −0.8% | 13.6% |
| 43 | Northern SA | 44.6% | 28.7% | 22.8% | 69.4% | 66.6% | 54.8% | 48.4% | 52.9% | 47.8% | 34.9% | 20.8% | 21.0% | 16.4% | 13.8% | 9.9% | 6.3% | 4.2% | −1.0% | 14.6% |
| 44 | Perth | 1.5% | 0.9% | 0.6% | 3.6% | 2.6% | 1.8% | 1.6% | 2.0% | 1.8% | 1.1% | 0.5% | 0.5% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.4% |
| 45 | South-West | 23.4% | 13.1% | 9.0% | 44.6% | 43.5% | 32.7% | 27.0% | 29.7% | 26.0% | 16.4% | 8.5% | 8.4% | 6.3% | 5.1% | 3.3% | 2.0% | 1.2% | −0.3% | 5.2% |
| 46 | Lower | 42.2% | 26.7% | 20.6% | 66.6% | 66.6% | 54.3% | 48.9% | 52.5% | 45.8% | 32.7% | 17.9% | 18.1% | 15.1% | 12.4% | 8.3% | 5.2% | 3.0% | −0.8% | 12.4% |
| 47 | Upper-Great-Southern | 29.9% | 18.7% | 15.6% | 63.3% | 57.2% | 43.0% | 34.6% | 38.5% | 36.4% | 23.0% | 12.0% | 12.2% | 9.6% | 9.0% | 6.6% | 4.0% | 2.9% | −0.5% | 9.0% |
| 48 | Midlands | 29.2% | 16.6% | 12.6% | 57.5% | 54.6% | 43.3% | 34.2% | 36.7% | 30.8% | 20.4% | 10.7% | 10.0% | 7.7% | 6.5% | 4.6% | 3.1% | 2.1% | −0.6% | 7.7% |
| 49 | South-Eastern | 53.4% | 38.5% | 33.2% | 80.2% | 72.3% | 60.4% | 55.2% | 61.2% | 59.8% | 48.3% | 32.6% | 34.5% | 31.9% | 32.2% | 27.6% | 22.1% | 17.3% | −4.3% | 34.5% |
| 50 | Central | 52.4% | 36.0% | 29.9% | 77.6% | 75.3% | 64.3% | 56.8% | 61.4% | 57.9% | 44.3% | 27.1% | 27.7% | 23.5% | 20.2% | 15.3% | 9.3% | 7.2% | −2.3% | 22.5% |
| 51 | Pilbara | 68.9% | 56.9% | 53.9% | 90.3% | 85.6% | 74.7% | 68.4% | 75.1% | 74.7% | 63.8% | 48.9% | 55.5% | 60.9% | 69.1% | 74.3% | 62.7% | 58.9% | −41.0% | 65.2% |
| 52 | Kimberley | 62.9% | 48.5% | 45.9% | 86.7% | 80.2% | 70.0% | 66.1% | 72.7% | 73.3% | 61.7% | 44.6% | 51.4% | 47.6% | 47.0% | 42.2% | 41.2% | 32.4% | −9.5% | 50.6% |
| 53 | Greater-Hobart | 2.3% | 1.4% | 1.0% | 5.8% | 4.5% | 3.4% | 2.8% | 3.5% | 3.0% | 1.7% | 0.8% | 0.8% | 0.6% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.5% |
| 54 | Southern | 13.7% | 8.0% | 5.7% | 33.6% | 33.3% | 24.3% | 17.3% | 18.7% | 16.1% | 8.9% | 4.1% | 3.8% | 2.7% | 2.6% | 1.8% | 1.3% | 0.8% | −0.3% | 3.2% |
| 55 | Northern (TAS) | 6.6% | 3.6% | 2.5% | 15.8% | 13.4% | 10.1% | 8.1% | 9.3% | 8.1% | 4.5% | 2.2% | 2.1% | 1.6% | 1.4% | 0.9% | 0.5% | 0.3% | −0.1% | 1.3% |
| 56 | Mersey-Lyell | 20.0% | 12.0% | 8.5% | 42.4% | 41.4% | 30.8% | 25.4% | 28.3% | 24.1% | 15.4% | 7.6% | 7.7% | 5.6% | 4.7% | 3.1% | 2.0% | 1.1% | −0.3% | 4.7% |
| 57 | Darwin | 3.0% | 2.0% | 1.4% | 9.8% | 6.4% | 3.9% | 3.2% | 4.4% | 4.0% | 2.5% | 1.2% | 1.3% | 1.2% | 1.3% | 1.2% | 0.9% | 0.7% | −0.2% | 1.6% |
| 58 | Northern-Territory | 55.2% | 40.1% | 34.7% | 79.9% | 74.6% | 65.0% | 61.1% | 67.8% | 67.3% | 56.1% | 39.4% | 43.5% | 41.0% | 44.8% | 47.1% | 36.9% | 32.7% | −15.1% | 48.2% |
| 59 | Canberra | 0.7% | 0.4% | 0.3% | 1.8% | 1.1% | 0.8% | 0.7% | 1.0% | 0.9% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.2% |
| Total | 10.4% | 6.2% | 4.4% | 24.1% | 18.7% | 13.1% | 11.0% | 13.9% | 12.6% | 7.7% | 3.9% | 3.9% | 3.1% | 2.7% | 1.8% | 1.0% | 0.6% | −0.1% | 2.5% |
| SD | Statistical Division | 1–5 | 6–10 | 11–15 | 16–20 | 21–25 | 26–30 | 31–35 | 36–40 | 41–45 | 46–50 | 51–55 | 56–60 | 61–65 | 66–70 | 71–75 | 76–80 | 81–85 | ≥ 86 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sydney | 1.5% | 0.1% | 1.1% | 2.4% | 1.4% | 1.8% | 1.9% | 2.1% | 2.2% | 1.5% | 0.9% | 0.9% | 0.6% | 0.7% | 0.5% | 0.2% | 0.1% | 0.0% | 0.3% |
| 2 | Hunter | 11.2% | 0.8% | 6.9% | 14.8% | 11.0% | 15.3% | 15.8% | 15.6% | 15.1% | 10.0% | 6.4% | 6.0% | 3.8% | 4.1% | 2.6% | 1.2% | 0.5% | 0.0% | 1.8% |
| 3 | Illawarra | 4.8% | 0.3% | 2.8% | 6.5% | 4.9% | 7.1% | 7.1% | 6.9% | 6.3% | 4.1% | 2.6% | 2.5% | 1.5% | 1.5% | 1.0% | 0.5% | 0.2% | 0.0% | 0.7% |
| 4 | Richmond-Tweed | 5.1% | 0.3% | 2.7% | 6.4% | 5.9% | 8.1% | 7.6% | 6.8% | 6.1% | 3.7% | 2.2% | 2.3% | 1.5% | 1.5% | 0.9% | 0.4% | 0.2% | 0.0% | 0.6% |
| 5 | Mid-North-Coast | 15.9% | 1.0% | 7.9% | 18.4% | 19.4% | 24.3% | 22.9% | 20.3% | 18.0% | 11.4% | 7.3% | 6.8% | 4.0% | 4.2% | 2.7% | 1.4% | 0.6% | 0.0% | 2.0% |
| 6 | Northern | 16.2% | 1.2% | 10.2% | 21.8% | 18.6% | 25.0% | 25.3% | 24.5% | 23.2% | 15.8% | 10.5% | 9.8% | 6.2% | 6.4% | 4.5% | 2.3% | 1.0% | −0.1% | 3.2% |
| 7 | North-Western | 26.4% | 2.2% | 18.5% | 38.7% | 32.7% | 38.7% | 40.2% | 38.3% | 38.0% | 27.9% | 19.6% | 18.6% | 12.4% | 13.2% | 8.9% | 5.0% | 2.2% | −0.2% | 7.0% |
| 8 | Central-West | 12.3% | 0.8% | 7.3% | 16.1% | 13.6% | 18.9% | 18.9% | 18.3% | 17.2% | 11.9% | 7.5% | 7.0% | 4.4% | 4.8% | 3.1% | 1.6% | 0.7% | −0.1% | 2.2% |
| 9 | South-Eastern | 14.7% | 1.0% | 8.2% | 19.4% | 17.7% | 21.9% | 20.9% | 18.4% | 17.8% | 11.9% | 7.6% | 7.1% | 4.4% | 5.0% | 3.5% | 1.8% | 0.8% | −0.1% | 2.6% |
| 10 | Murrumbidgee | 11.7% | 0.8% | 7.3% | 16.0% | 12.8% | 17.6% | 18.3% | 18.4% | 17.6% | 12.1% | 7.9% | 7.9% | 5.1% | 5.1% | 3.4% | 1.7% | 0.7% | −0.1% | 2.4% |
| 11 | Murray | 19.4% | 1.5% | 12.0% | 25.4% | 21.0% | 27.5% | 28.5% | 26.8% | 26.1% | 17.2% | 11.4% | 11.1% | 7.1% | 7.2% | 4.9% | 2.4% | 1.0% | −0.1% | 3.5% |
| 12 | Far-West | 46.1% | 5.0% | 33.3% | 57.5% | 51.9% | 58.4% | 58.4% | 57.9% | 55.1% | 41.3% | 30.8% | 29.8% | 20.8% | 21.0% | 13.3% | 6.5% | 3.6% | −0.2% | 9.9% |
| 13 | Melbourne | 1.1% | 0.1% | 0.7% | 1.6% | 0.9% | 1.2% | 1.3% | 1.3% | 1.5% | 1.0% | 0.6% | 0.6% | 0.4% | 0.5% | 0.3% | 0.1% | 0.1% | 0.0% | 0.2% |
| 14 | Barwon | 5.3% | 0.3% | 3.1% | 6.9% | 5.2% | 7.2% | 7.3% | 7.0% | 6.8% | 4.4% | 2.7% | 2.6% | 1.7% | 1.8% | 1.1% | 0.5% | 0.2% | 0.0% | 0.8% |
| 15 | Western-District | 20.7% | 1.5% | 12.6% | 26.0% | 24.9% | 30.1% | 30.6% | 28.2% | 26.3% | 18.5% | 12.3% | 12.1% | 8.0% | 8.2% | 5.3% | 2.6% | 1.0% | −0.1% | 3.5% |
| 16 | Centra- | 5.1% | 0.3% | 2.9% | 6.1% | 4.7% | 7.1% | 7.4% | 6.7% | 6.6% | 4.3% | 2.6% | 2.6% | 1.7% | 1.9% | 1.2% | 0.5% | 0.2% | 0.0% | 0.8% |
| 17 | Wimmera | 25.1% | 1.8% | 14.3% | 32.3% | 31.5% | 34.3% | 35.0% | 31.9% | 30.5% | 20.8% | 13.8% | 13.3% | 8.1% | 8.3% | 5.3% | 2.4% | 1.0% | −0.1% | 3.4% |
| 18 | Mallee | 31.9% | 2.5% | 19.0% | 38.6% | 35.9% | 41.0% | 42.2% | 40.3% | 39.2% | 29.1% | 20.7% | 19.8% | 13.2% | 13.4% | 8.9% | 4.3% | 1.8% | −0.2% | 6.2% |
| 19 | Loddon | 5.6% | 0.3% | 3.0% | 7.1% | 5.8% | 8.9% | 8.7% | 7.7% | 7.1% | 4.6% | 2.8% | 2.7% | 1.8% | 2.0% | 1.3% | 0.6% | 0.3% | 0.0% | 0.9% |
| 20 | Goulburn | 8.4% | 0.5% | 4.5% | 11.0% | 10.0% | 12.5% | 12.2% | 11.0% | 10.6% | 7.2% | 4.4% | 4.2% | 2.7% | 3.0% | 1.9% | 1.0% | 0.4% | 0.0% | 1.3% |
| 21 | Ovens-Murray | 17.9% | 1.2% | 10.5% | 22.6% | 20.5% | 25.6% | 25.3% | 23.3% | 22.1% | 14.9% | 9.9% | 9.6% | 6.4% | 7.2% | 4.7% | 2.3% | 1.0% | −0.1% | 3.2% |
| 22 | East-Gippsland | 17.3% | 1.2% | 9.5% | 21.0% | 20.6% | 25.7% | 25.6% | 23.3% | 21.4% | 13.6% | 8.2% | 7.6% | 4.9% | 5.0% | 3.5% | 1.8% | 0.8% | −0.1% | 2.6% |
| 23 | Gippsland | 6.5% | 0.4% | 3.5% | 8.4% | 7.0% | 10.0% | 10.0% | 9.2% | 8.5% | 5.4% | 3.3% | 3.1% | 1.9% | 2.1% | 1.4% | 0.7% | 0.3% | 0.0% | 1.0% |
| 24 | Brisbane | 2.7% | 0.2% | 1.7% | 3.7% | 2.2% | 3.2% | 3.5% | 3.6% | 3.8% | 2.6% | 1.6% | 1.6% | 1.1% | 1.4% | 0.9% | 0.4% | 0.2% | 0.0% | 0.6% |
| 25 | Gold-Coast | 1.4% | 0.1% | 0.9% | 2.0% | 1.2% | 1.7% | 1.8% | 1.8% | 1.8% | 1.2% | 0.7% | 0.7% | 0.4% | 0.5% | 0.4% | 0.2% | 0.1% | 0.0% | 0.2% |
| 26 | Sunshine-Coast | 2.9% | 0.2% | 1.5% | 3.8% | 3.1% | 4.3% | 4.0% | 3.6% | 3.2% | 2.1% | 1.3% | 1.2% | 0.7% | 0.8% | 0.6% | 0.3% | 0.1% | 0.0% | 0.4% |
| 27 | West-Moreton | 8.4% | 0.4% | 4.0% | 10.4% | 9.8% | 12.9% | 12.1% | 10.5% | 9.8% | 6.7% | 4.2% | 3.7% | 2.4% | 2.8% | 2.1% | 1.2% | 0.5% | 0.0% | 1.6% |
| 28 | Wide-Bay-Burnett | 13.5% | 0.8% | 7.4% | 18.6% | 16.2% | 20.3% | 20.3% | 18.0% | 16.8% | 11.3% | 6.9% | 6.0% | 3.6% | 4.0% | 2.9% | 1.6% | 0.7% | −0.1% | 2.3% |
| 29 | Darling | 10.2% | 0.7% | 6.4% | 14.7% | 11.3% | 16.0% | 16.5% | 15.9% | 15.8% | 10.5% | 6.8% | 6.5% | 4.1% | 4.6% | 3.0% | 1.6% | 0.7% | 0.0% | 2.1% |
| 30 | South-West | 40.3% | 4.0% | 33.5% | 61.5% | 44.6% | 52.3% | 52.4% | 52.0% | 52.3% | 42.8% | 35.2% | 33.8% | 25.1% | 24.8% | 19.6% | 11.1% | 5.7% | −0.5% | 15.5% |
| 31 | Fitzroy | 14.5% | 1.0% | 9.0% | 20.6% | 15.5% | 20.2% | 21.0% | 21.3% | 20.5% | 14.8% | 10.3% | 10.8% | 7.4% | 8.3% | 5.7% | 3.1% | 1.4% | −0.1% | 4.2% |
| 32 | Central-West | 53.3% | 5.8% | 43.1% | 65.3% | 48.7% | 56.6% | 62.6% | 61.7% | 59.5% | 51.7% | 39.3% | 41.1% | 29.4% | 30.9% | 24.6% | 14.7% | 7.3% | −0.7% | 20.0% |
| 33 | Mackay | 29.4% | 2.5% | 19.6% | 39.6% | 29.7% | 36.1% | 37.4% | 37.0% | 36.5% | 27.6% | 20.1% | 21.0% | 15.7% | 19.0% | 13.4% | 7.7% | 3.7% | −0.3% | 10.1% |
| 34 | Northern | 33.9% | 3.3% | 23.9% | 42.4% | 32.1% | 40.8% | 43.5% | 44.2% | 44.7% | 34.8% | 25.8% | 26.0% | 19.3% | 21.8% | 15.8% | 8.6% | 3.9% | −0.3% | 11.6% |
| 35 | Far- | 20.3% | 1.6% | 14.1% | 30.9% | 24.0% | 27.5% | 28.0% | 27.8% | 28.0% | 20.5% | 14.2% | 14.8% | 10.5% | 13.0% | 9.9% | 5.4% | 2.4% | −0.2% | 7.0% |
| 36 | North-West | 47.4% | 5.9% | 43.1% | 68.0% | 51.2% | 56.4% | 60.8% | 65.2% | 66.9% | 58.4% | 49.9% | 51.4% | 41.7% | 53.5% | 41.9% | 28.1% | 18.0% | −1.7% | 34.9% |
| 37 | Adelaide | 0.5% | 0.0% | 0.3% | 0.7% | 0.4% | 0.6% | 0.7% | 0.7% | 0.7% | 0.4% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 38 | Outer-Adelaide | 12.1% | 0.7% | 6.4% | 15.1% | 14.3% | 18.3% | 16.1% | 14.0% | 13.2% | 9.0% | 5.7% | 5.2% | 3.3% | 3.9% | 2.7% | 1.3% | 0.6% | 0.0% | 1.8% |
| 39 | Yorke | 20.6% | 1.4% | 11.0% | 27.3% | 26.9% | 31.2% | 30.7% | 24.8% | 23.2% | 15.5% | 9.7% | 8.5% | 4.7% | 5.3% | 3.4% | 1.8% | 0.8% | −0.1% | 2.5% |
| 40 | Murray-Lands | 21.0% | 1.5% | 12.0% | 28.9% | 25.0% | 29.6% | 29.8% | 26.7% | 25.8% | 18.4% | 11.7% | 10.5% | 7.4% | 7.5% | 5.2% | 2.7% | 1.0% | −0.1% | 3.6% |
| 41 | South-East | 29.6% | 2.4% | 19.6% | 40.2% | 34.0% | 39.0% | 40.6% | 37.5% | 38.0% | 27.6% | 19.4% | 20.2% | 13.4% | 14.0% | 10.0% | 5.0% | 2.2% | −0.2% | 6.8% |
| 42 | Eyre | 40.1% | 3.5% | 26.8% | 50.9% | 44.8% | 48.9% | 49.8% | 47.9% | 47.6% | 35.3% | 26.0% | 25.2% | 16.8% | 20.2% | 14.6% | 6.6% | 3.0% | −0.2% | 9.4% |
| 43 | Northern | 38.8% | 3.5% | 25.8% | 49.7% | 42.0% | 47.8% | 48.9% | 47.4% | 47.5% | 37.3% | 26.5% | 25.5% | 17.2% | 19.1% | 13.6% | 7.2% | 3.5% | −0.3% | 10.3% |
| 44 | Perth | 1.2% | 0.1% | 0.8% | 1.6% | 1.0% | 1.5% | 1.6% | 1.6% | 1.6% | 1.1% | 0.6% | 0.7% | 0.5% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 45 | South-West | 19.6% | 1.4% | 11.4% | 25.1% | 22.9% | 27.8% | 26.8% | 24.5% | 23.6% | 16.6% | 11.1% | 10.4% | 6.7% | 7.1% | 5.0% | 2.6% | 1.3% | −0.1% | 4.0% |
| 46 | Lower | 35.1% | 3.2% | 24.1% | 46.4% | 44.4% | 48.5% | 48.8% | 44.9% | 43.6% | 32.0% | 23.1% | 22.9% | 15.8% | 16.7% | 11.9% | 6.4% | 2.9% | −0.2% | 9.0% |
| 47 | Upper-Great-Southern | 24.0% | 1.9% | 17.8% | 41.0% | 32.6% | 36.5% | 39.1% | 34.5% | 36.8% | 23.4% | 16.4% | 15.6% | 11.6% | 11.3% | 9.0% | 5.4% | 1.9% | −0.1% | 6.0% |
| 48 | Midlands | 23.2% | 1.7% | 15.3% | 38.6% | 32.0% | 35.8% | 33.4% | 30.7% | 30.0% | 21.1% | 13.2% | 12.4% | 8.3% | 9.4% | 7.7% | 4.5% | 2.1% | −0.2% | 6.0% |
| 49 | South-Eastern | 43.8% | 4.9% | 36.5% | 59.8% | 49.3% | 53.6% | 55.1% | 57.1% | 58.5% | 51.2% | 40.7% | 44.3% | 37.1% | 42.9% | 35.2% | 23.5% | 12.2% | −1.1% | 27.3% |
| 50 | Central | 44.9% | 4.5% | 32.7% | 58.5% | 52.5% | 56.0% | 57.6% | 55.8% | 55.1% | 45.0% | 34.4% | 35.0% | 25.7% | 28.7% | 21.2% | 14.2% | 7.5% | −0.7% | 18.8% |
| 51 | Pilbara | 57.5% | 9.1% | 55.8% | 77.9% | 65.6% | 67.7% | 68.3% | 71.5% | 74.6% | 68.5% | 60.3% | 68.1% | 69.1% | 80.3% | 79.1% | 73.3% | 52.3% | −12.9% | 64.7% |
| 52 | Kimberley | 53.0% | 7.3% | 50.2% | 71.1% | 56.9% | 62.5% | 66.6% | 68.5% | 71.3% | 63.8% | 54.2% | 60.3% | 53.4% | 63.7% | 61.8% | 47.9% | 45.7% | −3.8% | 50.3% |
| 53 | Greater-Hobart | 2.0% | 0.1% | 1.3% | 2.6% | 1.8% | 2.7% | 2.9% | 2.8% | 2.7% | 1.7% | 1.0% | 1.0% | 0.7% | 0.8% | 0.5% | 0.2% | 0.1% | 0.0% | 0.3% |
| 54 | Southern | 10.9% | 0.7% | 6.8% | 17.5% | 15.9% | 18.6% | 16.8% | 14.8% | 14.0% | 8.8% | 5.4% | 4.6% | 3.2% | 4.0% | 3.1% | 1.9% | 0.9% | −0.1% | 2.5% |
| 55 | Northern | 5.5% | 0.4% | 3.2% | 7.6% | 5.4% | 8.0% | 8.2% | 7.6% | 7.5% | 4.7% | 2.9% | 2.7% | 1.7% | 1.9% | 1.3% | 0.6% | 0.3% | 0.0% | 0.9% |
| 56 | Mersey-Lyell | 18.0% | 1.3% | 10.7% | 23.8% | 20.5% | 24.9% | 25.6% | 23.3% | 23.0% | 15.7% | 10.1% | 9.5% | 6.1% | 6.7% | 4.5% | 2.4% | 0.9% | −0.1% | 3.2% |
| 57 | Darwin | 2.2% | 0.2% | 1.7% | 4.2% | 2.6% | 2.9% | 3.2% | 3.4% | 3.7% | 2.5% | 1.6% | 1.8% | 1.5% | 2.3% | 2.2% | 1.3% | 0.7% | −0.1% | 1.5% |
| 58 | Northern-Territory | 48.8% | 5.8% | 39.0% | 61.5% | 49.5% | 56.5% | 60.4% | 62.6% | 66.1% | 56.8% | 46.6% | 53.0% | 46.2% | 56.7% | 53.5% | 43.2% | 31.2% | −3.7% | 44.3% |
| 59 | Canberra | 0.6% | 0.0% | 0.4% | 0.8% | 0.4% | 0.6% | 0.7% | 0.8% | 0.8% | 0.5% | 0.3% | 0.3% | 0.2% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| Total | 8.3% | 0.6% | 5.3% | 11.5% | 7.7% | 10.2% | 10.9% | 10.9% | 11.1% | 7.5% | 4.8% | 4.7% | 3.2% | 3.6% | 2.3% | 1.1% | 0.5% | 0.0% | 1.6% |
Appendix D
| SD | Statistical Division | 1–5 | 6–10 | 11–15 | 16–20 | 21–25 | 26–30 | 31–35 | 36–40 | 41–45 | 46–50 | 51–55 | 56–60 | 61–65 | 66–70 | 71–75 | 76–80 | 81–85 | ≥ 86 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sydney | 0.6% | 0.4% | 0.3% | 1.8% | 1.2% | 0.7% | 0.6% | 0.8% | 0.8% | 0.5% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 2 | Hunter | 1.2% | 0.7% | 0.5% | 2.6% | 2.1% | 1.6% | 1.4% | 1.7% | 1.5% | 0.9% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 3 | Illawarra | 1.4% | 0.7% | 0.5% | 3.2% | 2.6% | 2.0% | 1.6% | 2.0% | 1.6% | 0.9% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 4 | Richmond-Tweed | 1.0% | 0.5% | 0.3% | 2.2% | 2.2% | 1.7% | 1.3% | 1.4% | 1.2% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 5 | Mid-North Coast | 3.0% | 1.6% | 1.0% | 5.8% | 6.2% | 4.9% | 3.8% | 4.2% | 3.4% | 1.9% | 0.9% | 0.9% | 0.6% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.5% |
| 6 | Northern (NSW) | 1.0% | 0.6% | 0.4% | 2.1% | 1.9% | 1.5% | 1.3% | 1.5% | 1.3% | 0.8% | 0.4% | 0.4% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 7 | North Western | 0.8% | 0.5% | 0.4% | 1.5% | 1.4% | 1.2% | 1.0% | 1.1% | 1.0% | 0.7% | 0.4% | 0.4% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 8 | Central West | 1.0% | 0.6% | 0.4% | 2.1% | 2.0% | 1.5% | 1.2% | 1.5% | 1.3% | 0.8% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.1% | 0.0% | 0.2% |
| 9 | South Eastern | 1.7% | 1.0% | 0.7% | 3.6% | 3.5% | 2.6% | 2.0% | 2.3% | 1.9% | 1.1% | 0.6% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.4% |
| 10 | Murrumbidgee | 1.1% | 0.6% | 0.5% | 2.3% | 2.1% | 1.6% | 1.4% | 1.6% | 1.4% | 0.9% | 0.4% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 11 | Murray | 1.4% | 0.8% | 0.6% | 2.7% | 2.6% | 1.9% | 1.7% | 1.9% | 1.7% | 1.0% | 0.5% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 12 | Far West | 1.5% | 1.1% | 0.9% | 2.3% | 2.2% | 2.0% | 1.7% | 1.9% | 1.7% | 1.2% | 0.7% | 0.7% | 0.6% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.5% |
| 13 | Melbourne | 0.5% | 0.3% | 0.2% | 1.4% | 1.0% | 0.6% | 0.5% | 0.7% | 0.6% | 0.4% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 14 | Barwon | 0.8% | 0.4% | 0.3% | 1.9% | 1.6% | 1.1% | 0.9% | 1.1% | 1.0% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 15 | Western District | 3.9% | 2.0% | 1.4% | 6.7% | 6.5% | 5.2% | 4.2% | 4.8% | 4.1% | 2.7% | 1.3% | 1.3% | 1.1% | 0.9% | 0.5% | 0.3% | 0.2% | 0.0% | 0.8% |
| 16 | Central Highlands | 0.7% | 0.4% | 0.3% | 1.6% | 1.4% | 1.1% | 0.9% | 1.0% | 0.9% | 0.5% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 17 | Wimmera | 2.6% | 1.4% | 1.0% | 4.4% | 4.3% | 3.5% | 2.9% | 3.2% | 2.7% | 1.6% | 0.9% | 0.8% | 0.7% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.5% |
| 18 | Mallee | 2.0% | 1.2% | 0.9% | 3.5% | 3.4% | 2.7% | 2.4% | 2.6% | 2.4% | 1.6% | 0.9% | 0.9% | 0.7% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.5% |
| 19 | Loddon | 1.0% | 0.5% | 0.3% | 2.1% | 2.0% | 1.5% | 1.2% | 1.3% | 1.1% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 20 | Goulburn | 1.3% | 0.7% | 0.5% | 3.0% | 3.0% | 2.2% | 1.6% | 1.9% | 1.6% | 0.9% | 0.5% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 21 | Ovens-Murray | 2.2% | 1.3% | 0.9% | 4.1% | 4.1% | 3.2% | 2.6% | 3.0% | 2.5% | 1.6% | 0.8% | 0.8% | 0.6% | 0.5% | 0.4% | 0.2% | 0.1% | 0.0% | 0.5% |
| 22 | East Gippsland | 1.8% | 1.0% | 0.7% | 3.5% | 3.4% | 2.5% | 2.2% | 2.4% | 2.1% | 1.2% | 0.6% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 23 | Gippsland | 1.5% | 0.7% | 0.5% | 3.1% | 3.0% | 2.3% | 1.8% | 2.0% | 1.7% | 0.9% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 24 | Brisbane | 1.3% | 0.8% | 0.6% | 3.4% | 2.3% | 1.6% | 1.4% | 1.8% | 1.7% | 1.0% | 0.5% | 0.5% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.4% |
| 25 | Gold Coast | 0.8% | 0.5% | 0.3% | 2.1% | 1.4% | 1.0% | 0.8% | 1.1% | 1.0% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 26 | Sunshine Coast | 1.3% | 0.7% | 0.4% | 3.1% | 2.9% | 2.0% | 1.5% | 1.8% | 1.5% | 0.8% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 27 | West Moreton | 1.3% | 0.7% | 0.5% | 3.2% | 3.2% | 2.4% | 1.7% | 1.9% | 1.5% | 0.9% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 28 | Wide Bay-Burnett | 1.2% | 0.6% | 0.4% | 2.5% | 2.4% | 1.8% | 1.4% | 1.6% | 1.4% | 0.8% | 0.4% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 29 | Darling Downs | 0.6% | 0.4% | 0.3% | 1.5% | 1.2% | 1.0% | 0.8% | 1.0% | 0.9% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 30 | South West | 0.8% | 0.6% | 0.5% | 1.4% | 1.3% | 1.1% | 1.0% | 1.1% | 1.0% | 0.7% | 0.5% | 0.5% | 0.4% | 0.4% | 0.2% | 0.2% | 0.1% | 0.0% | 0.4% |
| 31 | Fitzroy | 0.7% | 0.4% | 0.3% | 1.5% | 1.3% | 0.9% | 0.8% | 1.0% | 0.9% | 0.5% | 0.3% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 32 | Central West | 0.8% | 0.6% | 0.6% | 1.2% | 1.1% | 1.0% | 0.9% | 1.0% | 0.9% | 0.7% | 0.4% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 33 | Mackay | 1.2% | 0.8% | 0.6% | 2.2% | 1.9% | 1.5% | 1.3% | 1.5% | 1.4% | 0.9% | 0.5% | 0.6% | 0.5% | 0.5% | 0.4% | 0.2% | 0.1% | 0.0% | 0.5% |
| 34 | Northern | 1.6% | 1.0% | 0.8% | 2.5% | 2.1% | 1.8% | 1.6% | 1.9% | 1.8% | 1.3% | 0.8% | 0.8% | 0.7% | 0.6% | 0.5% | 0.3% | 0.2% | 0.0% | 0.6% |
| 35 | Far North | 0.4% | 0.3% | 0.2% | 1.0% | 0.8% | 0.6% | 0.5% | 0.6% | 0.6% | 0.4% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 36 | North West | 1.3% | 1.0% | 0.9% | 1.9% | 1.7% | 1.5% | 1.4% | 1.6% | 1.6% | 1.3% | 0.9% | 1.0% | 0.8% | 0.9% | 0.7% | 0.6% | 0.4% | −0.1% | 0.9% |
| 37 | Adelaide | 0.5% | 0.3% | 0.2% | 1.1% | 0.8% | 0.6% | 0.5% | 0.6% | 0.5% | 0.3% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 38 | Outer Adelaide | 1.2% | 0.6% | 0.4% | 2.4% | 2.4% | 1.8% | 1.4% | 1.5% | 1.2% | 0.7% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 39 | Yorke and Lower North | 1.7% | 0.9% | 0.7% | 3.2% | 3.2% | 2.5% | 2.1% | 2.2% | 1.8% | 1.1% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 40 | Murray Lands | 1.4% | 0.8% | 0.6% | 2.7% | 2.6% | 2.0% | 1.6% | 1.7% | 1.6% | 1.0% | 0.5% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 41 | South East | 3.8% | 2.3% | 1.7% | 6.3% | 5.8% | 4.6% | 4.1% | 4.4% | 4.0% | 2.7% | 1.5% | 1.6% | 1.3% | 1.2% | 0.8% | 0.4% | 0.3% | −0.1% | 1.1% |
| 42 | Eyre | 0.9% | 0.6% | 0.4% | 1.4% | 1.3% | 1.1% | 0.9% | 1.0% | 1.0% | 0.7% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 43 | Northern (QLD) | 0.6% | 0.4% | 0.3% | 1.0% | 1.0% | 0.8% | 0.7% | 0.8% | 0.7% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.1% | 0.0% | 0.2% |
| 44 | Perth | 0.6% | 0.3% | 0.2% | 1.3% | 1.0% | 0.7% | 0.6% | 0.7% | 0.7% | 0.4% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 45 | South West | 1.9% | 1.1% | 0.7% | 3.7% | 3.6% | 2.7% | 2.2% | 2.5% | 2.2% | 1.4% | 0.7% | 0.7% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.4% |
| 46 | Lower Great Southern | 2.2% | 1.4% | 1.1% | 3.4% | 3.4% | 2.8% | 2.5% | 2.7% | 2.4% | 1.7% | 0.9% | 0.9% | 0.8% | 0.6% | 0.4% | 0.3% | 0.2% | 0.0% | 0.6% |
| 47 | Upper Great Southern | 0.9% | 0.6% | 0.5% | 1.9% | 1.7% | 1.3% | 1.1% | 1.2% | 1.1% | 0.7% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 48 | Midlands | 0.9% | 0.5% | 0.4% | 1.8% | 1.8% | 1.4% | 1.1% | 1.2% | 1.0% | 0.7% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.1% | 0.0% | 0.2% |
| 49 | South Eastern | 0.7% | 0.5% | 0.5% | 1.1% | 1.0% | 0.8% | 0.8% | 0.8% | 0.8% | 0.7% | 0.4% | 0.5% | 0.4% | 0.4% | 0.4% | 0.3% | 0.2% | −0.1% | 0.5% |
| 50 | Central | 0.7% | 0.5% | 0.4% | 1.1% | 1.1% | 0.9% | 0.8% | 0.9% | 0.8% | 0.6% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 51 | Pilbara | 0.9% | 0.8% | 0.7% | 1.2% | 1.2% | 1.0% | 0.9% | 1.0% | 1.0% | 0.9% | 0.7% | 0.8% | 0.8% | 0.9% | 1.0% | 0.9% | 0.8% | −0.6% | 0.9% |
| 52 | Kimberley | 0.6% | 0.5% | 0.4% | 0.8% | 0.8% | 0.7% | 0.6% | 0.7% | 0.7% | 0.6% | 0.4% | 0.5% | 0.5% | 0.5% | 0.4% | 0.4% | 0.3% | −0.1% | 0.5% |
| 53 | Greater Hobart | 0.9% | 0.5% | 0.4% | 2.2% | 1.7% | 1.3% | 1.1% | 1.3% | 1.2% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.2% |
| 54 | Southern | 1.2% | 0.7% | 0.5% | 2.8% | 2.8% | 2.0% | 1.5% | 1.6% | 1.4% | 0.8% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 55 | Northern (TAS) | 0.6% | 0.3% | 0.2% | 1.4% | 1.2% | 0.9% | 0.7% | 0.9% | 0.7% | 0.4% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 56 | Mersey-Lyell | 1.3% | 0.8% | 0.6% | 2.8% | 2.7% | 2.0% | 1.7% | 1.9% | 1.6% | 1.0% | 0.5% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 57 | Darwin | 0.5% | 0.3% | 0.2% | 1.6% | 1.0% | 0.6% | 0.5% | 0.7% | 0.7% | 0.4% | 0.2% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.3% |
| 58 | Northern Territory - Bal | 1.0% | 0.8% | 0.7% | 1.5% | 1.4% | 1.2% | 1.1% | 1.3% | 1.3% | 1.1% | 0.7% | 0.8% | 0.8% | 0.8% | 0.9% | 0.7% | 0.6% | −0.3% | 0.9% |
| 59 | Canberra | 0.4% | 0.3% | 0.2% | 1.1% | 0.7% | 0.5% | 0.4% | 0.6% | 0.6% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| SD | Statistical Division | 1–5 | 6–10 | 11–15 | 16–20 | 21–25 | 26–30 | 31–35 | 36–40 | 41–45 | 46–50 | 51–55 | 56–60 | 61–65 | 66–70 | 71–75 | 76–80 | 81–85 | ≥86 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sydney | 0.5% | 0.0% | 0.4% | 0.8% | 0.5% | 0.6% | 0.6% | 0.7% | 0.7% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 2 | Hunter | 1.0% | 0.1% | 0.6% | 1.3% | 1.0% | 1.4% | 1.4% | 1.4% | 1.4% | 0.9% | 0.6% | 0.5% | 0.3% | 0.4% | 0.2% | 0.1% | 0.0% | 0.0% | 0.2% |
| 3 | Illawarra | 1.1% | 0.1% | 0.6% | 1.5% | 1.1% | 1.6% | 1.6% | 1.6% | 1.5% | 1.0% | 0.6% | 0.6% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.2% |
| 4 | Richmond-Tweed | 0.9% | 0.1% | 0.4% | 1.1% | 1.0% | 1.3% | 1.3% | 1.1% | 1.0% | 0.6% | 0.4% | 0.4% | 0.2% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 5 | Mid-North Coast | 2.7% | 0.2% | 1.3% | 3.1% | 3.2% | 4.1% | 3.8% | 3.4% | 3.0% | 1.9% | 1.2% | 1.1% | 0.7% | 0.7% | 0.4% | 0.2% | 0.1% | 0.0% | 0.3% |
| 6 | Northern | 0.8% | 0.1% | 0.5% | 1.1% | 1.0% | 1.3% | 1.3% | 1.3% | 1.2% | 0.8% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 7 | North Western | 0.7% | 0.1% | 0.5% | 1.0% | 0.8% | 1.0% | 1.0% | 1.0% | 0.9% | 0.7% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 8 | Central West | 0.8% | 0.1% | 0.5% | 1.1% | 0.9% | 1.3% | 1.3% | 1.2% | 1.2% | 0.8% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 9 | South Eastern | 1.4% | 0.1% | 0.8% | 1.9% | 1.7% | 2.1% | 2.1% | 1.8% | 1.7% | 1.2% | 0.7% | 0.7% | 0.4% | 0.5% | 0.3% | 0.2% | 0.1% | 0.0% | 0.3% |
| 10 | Murrumbidgee | 0.9% | 0.1% | 0.6% | 1.2% | 1.0% | 1.3% | 1.4% | 1.4% | 1.3% | 0.9% | 0.6% | 0.6% | 0.4% | 0.4% | 0.3% | 0.1% | 0.1% | 0.0% | 0.2% |
| 11 | Murray | 1.2% | 0.1% | 0.7% | 1.5% | 1.3% | 1.7% | 1.7% | 1.6% | 1.6% | 1.0% | 0.7% | 0.7% | 0.4% | 0.4% | 0.3% | 0.1% | 0.1% | 0.0% | 0.2% |
| 12 | Far West | 1.4% | 0.2% | 1.0% | 1.7% | 1.6% | 1.8% | 1.8% | 1.7% | 1.7% | 1.2% | 0.9% | 0.9% | 0.6% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.3% |
| 13 | Melbourne | 0.4% | 0.0% | 0.3% | 0.6% | 0.4% | 0.5% | 0.5% | 0.6% | 0.6% | 0.4% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 14 | Barwon | 0.7% | 0.0% | 0.4% | 0.9% | 0.7% | 0.9% | 0.9% | 0.9% | 0.9% | 0.6% | 0.4% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 15 | Western District | 3.0% | 0.2% | 1.8% | 3.8% | 3.6% | 4.4% | 4.4% | 4.1% | 3.8% | 2.7% | 1.8% | 1.8% | 1.2% | 1.2% | 0.8% | 0.4% | 0.1% | 0.0% | 0.5% |
| 16 | Central Highlands | 0.6% | 0.0% | 0.3% | 0.7% | 0.6% | 0.9% | 0.9% | 0.8% | 0.8% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 17 | Wimmera | 2.1% | 0.2% | 1.2% | 2.7% | 2.7% | 2.9% | 3.0% | 2.7% | 2.6% | 1.8% | 1.2% | 1.1% | 0.7% | 0.7% | 0.5% | 0.2% | 0.1% | 0.0% | 0.3% |
| 18 | Mallee | 1.8% | 0.1% | 1.1% | 2.2% | 2.1% | 2.4% | 2.4% | 2.3% | 2.2% | 1.7% | 1.2% | 1.1% | 0.8% | 0.8% | 0.5% | 0.2% | 0.1% | 0.0% | 0.4% |
| 19 | Loddon | 0.8% | 0.0% | 0.4% | 1.0% | 0.8% | 1.2% | 1.2% | 1.1% | 1.0% | 0.6% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 20 | Goulburn | 1.1% | 0.1% | 0.6% | 1.5% | 1.4% | 1.7% | 1.7% | 1.5% | 1.4% | 1.0% | 0.6% | 0.6% | 0.4% | 0.4% | 0.3% | 0.1% | 0.1% | 0.0% | 0.2% |
| 21 | Ovens-Murray | 1.9% | 0.1% | 1.1% | 2.4% | 2.2% | 2.7% | 2.7% | 2.5% | 2.3% | 1.6% | 1.0% | 1.0% | 0.7% | 0.8% | 0.5% | 0.2% | 0.1% | 0.0% | 0.3% |
| 22 | East Gippsland | 1.5% | 0.1% | 0.8% | 1.8% | 1.8% | 2.2% | 2.2% | 2.0% | 1.9% | 1.2% | 0.7% | 0.7% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 23 | Gippsland | 1.2% | 0.1% | 0.6% | 1.5% | 1.2% | 1.8% | 1.8% | 1.6% | 1.5% | 1.0% | 0.6% | 0.6% | 0.3% | 0.4% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 24 | Brisbane | 1.1% | 0.1% | 0.7% | 1.5% | 0.9% | 1.3% | 1.4% | 1.5% | 1.5% | 1.0% | 0.7% | 0.6% | 0.5% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.2% |
| 25 | Gold Coast | 0.7% | 0.0% | 0.4% | 0.9% | 0.6% | 0.8% | 0.8% | 0.9% | 0.9% | 0.6% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 26 | Sunshine Coast | 1.1% | 0.1% | 0.6% | 1.4% | 1.2% | 1.6% | 1.5% | 1.4% | 1.2% | 0.8% | 0.5% | 0.5% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.2% |
| 27 | West Moreton | 1.2% | 0.1% | 0.6% | 1.5% | 1.4% | 1.8% | 1.7% | 1.5% | 1.4% | 1.0% | 0.6% | 0.5% | 0.3% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 28 | Wide Bay-Burnett | 1.0% | 0.1% | 0.5% | 1.3% | 1.1% | 1.4% | 1.4% | 1.3% | 1.2% | 0.8% | 0.5% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 29 | Darling Downs | 0.5% | 0.0% | 0.3% | 0.7% | 0.6% | 0.8% | 0.8% | 0.8% | 0.8% | 0.5% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 30 | South West | 0.7% | 0.1% | 0.6% | 1.1% | 0.8% | 0.9% | 0.9% | 0.9% | 0.9% | 0.8% | 0.6% | 0.6% | 0.5% | 0.4% | 0.4% | 0.2% | 0.1% | 0.0% | 0.3% |
| 31 | Fitzroy | 0.6% | 0.0% | 0.3% | 0.8% | 0.6% | 0.8% | 0.8% | 0.8% | 0.8% | 0.6% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 32 | Central West | 0.8% | 0.1% | 0.6% | 1.0% | 0.7% | 0.8% | 0.9% | 0.9% | 0.9% | 0.8% | 0.6% | 0.6% | 0.4% | 0.5% | 0.4% | 0.2% | 0.1% | 0.0% | 0.3% |
| 33 | Mackay | 1.0% | 0.1% | 0.7% | 1.4% | 1.1% | 1.3% | 1.3% | 1.3% | 1.3% | 1.0% | 0.7% | 0.7% | 0.6% | 0.7% | 0.5% | 0.3% | 0.1% | 0.0% | 0.4% |
| 34 | Northern | 1.3% | 0.1% | 0.9% | 1.6% | 1.2% | 1.6% | 1.7% | 1.7% | 1.7% | 1.3% | 1.0% | 1.0% | 0.7% | 0.8% | 0.6% | 0.3% | 0.2% | 0.0% | 0.4% |
| 35 | Far North | 0.4% | 0.0% | 0.3% | 0.6% | 0.4% | 0.5% | 0.5% | 0.5% | 0.5% | 0.4% | 0.3% | 0.3% | 0.2% | 0.2% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 36 | North West | 1.1% | 0.1% | 1.0% | 1.6% | 1.2% | 1.3% | 1.4% | 1.5% | 1.5% | 1.3% | 1.1% | 1.2% | 1.0% | 1.2% | 1.0% | 0.6% | 0.4% | 0.0% | 0.8% |
| 37 | Adelaide | 0.4% | 0.0% | 0.2% | 0.5% | 0.3% | 0.5% | 0.5% | 0.5% | 0.5% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% |
| 38 | Outer Adelaide | 1.0% | 0.1% | 0.5% | 1.3% | 1.2% | 1.5% | 1.3% | 1.2% | 1.1% | 0.8% | 0.5% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.2% |
| 39 | Yorke and Lower North | 1.5% | 0.1% | 0.8% | 1.9% | 1.9% | 2.2% | 2.2% | 1.8% | 1.6% | 1.1% | 0.7% | 0.6% | 0.3% | 0.4% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 40 | Murray Lands | 1.2% | 0.1% | 0.7% | 1.6% | 1.4% | 1.7% | 1.7% | 1.5% | 1.5% | 1.0% | 0.7% | 0.6% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 41 | South East | 3.0% | 0.3% | 2.0% | 4.1% | 3.5% | 4.0% | 4.2% | 3.9% | 3.9% | 2.8% | 2.0% | 2.1% | 1.4% | 1.4% | 1.0% | 0.5% | 0.2% | 0.0% | 0.7% |
| 42 | Eyre | 0.8% | 0.1% | 0.5% | 1.0% | 0.9% | 0.9% | 1.0% | 0.9% | 0.9% | 0.7% | 0.5% | 0.5% | 0.3% | 0.4% | 0.3% | 0.1% | 0.1% | 0.0% | 0.2% |
| 43 | Northern | 0.6% | 0.1% | 0.4% | 0.7% | 0.6% | 0.7% | 0.7% | 0.7% | 0.7% | 0.5% | 0.4% | 0.4% | 0.2% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 44 | Perth | 0.5% | 0.0% | 0.3% | 0.6% | 0.4% | 0.5% | 0.6% | 0.6% | 0.6% | 0.4% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 45 | South West | 1.6% | 0.1% | 0.9% | 2.1% | 1.9% | 2.3% | 2.2% | 2.0% | 2.0% | 1.4% | 0.9% | 0.9% | 0.6% | 0.6% | 0.4% | 0.2% | 0.1% | 0.0% | 0.3% |
| 46 | Lower Great Southern | 1.8% | 0.2% | 1.2% | 2.4% | 2.3% | 2.5% | 2.5% | 2.3% | 2.2% | 1.6% | 1.2% | 1.2% | 0.8% | 0.9% | 0.6% | 0.3% | 0.1% | 0.0% | 0.5% |
| 47 | Upper Great Southern | 0.7% | 0.1% | 0.5% | 1.3% | 1.0% | 1.1% | 1.2% | 1.1% | 1.1% | 0.7% | 0.5% | 0.5% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 48 | Midlands | 0.7% | 0.1% | 0.5% | 1.2% | 1.0% | 1.2% | 1.1% | 1.0% | 1.0% | 0.7% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.1% | 0.0% | 0.2% |
| 49 | South Eastern | 0.6% | 0.1% | 0.5% | 0.8% | 0.7% | 0.7% | 0.8% | 0.8% | 0.8% | 0.7% | 0.6% | 0.6% | 0.5% | 0.6% | 0.5% | 0.3% | 0.2% | 0.0% | 0.4% |
| 50 | Central | 0.6% | 0.1% | 0.5% | 0.8% | 0.7% | 0.8% | 0.8% | 0.8% | 0.8% | 0.6% | 0.5% | 0.5% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.3% |
| 51 | Pilbara | 0.8% | 0.1% | 0.8% | 1.1% | 0.9% | 0.9% | 0.9% | 1.0% | 1.0% | 0.9% | 0.8% | 0.9% | 0.9% | 1.1% | 1.1% | 1.0% | 0.7% | −0.2% | 0.9% |
| 52 | Kimberley | 0.5% | 0.1% | 0.5% | 0.7% | 0.5% | 0.6% | 0.6% | 0.7% | 0.7% | 0.6% | 0.5% | 0.6% | 0.5% | 0.6% | 0.6% | 0.5% | 0.4% | 0.0% | 0.5% |
| 53 | Greater Hobart | 0.8% | 0.1% | 0.5% | 1.0% | 0.7% | 1.0% | 1.1% | 1.1% | 1.0% | 0.6% | 0.4% | 0.4% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.0% | 0.1% |
| 54 | Southern | 0.9% | 0.1% | 0.6% | 1.5% | 1.3% | 1.6% | 1.4% | 1.2% | 1.2% | 0.7% | 0.5% | 0.4% | 0.3% | 0.3% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 55 | Northern | 0.5% | 0.0% | 0.3% | 0.7% | 0.5% | 0.7% | 0.7% | 0.7% | 0.7% | 0.4% | 0.3% | 0.3% | 0.2% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
| 56 | Mersey-Lyell | 1.2% | 0.1% | 0.7% | 1.6% | 1.4% | 1.6% | 1.7% | 1.5% | 1.5% | 1.0% | 0.7% | 0.6% | 0.4% | 0.4% | 0.3% | 0.2% | 0.1% | 0.0% | 0.2% |
| 57 | Darwin | 0.4% | 0.0% | 0.3% | 0.7% | 0.4% | 0.5% | 0.5% | 0.6% | 0.6% | 0.4% | 0.3% | 0.3% | 0.3% | 0.4% | 0.4% | 0.2% | 0.1% | 0.0% | 0.2% |
| 58 | Northern Territory - Bal | 0.9% | 0.1% | 0.7% | 1.2% | 0.9% | 1.1% | 1.1% | 1.2% | 1.2% | 1.1% | 0.9% | 1.0% | 0.9% | 1.1% | 1.0% | 0.8% | 0.6% | −0.1% | 0.8% |
| 59 | Canberra | 0.4% | 0.0% | 0.2% | 0.5% | 0.3% | 0.4% | 0.5% | 0.5% | 0.5% | 0.3% | 0.2% | 0.2% | 0.1% | 0.2% | 0.1% | 0.1% | 0.0% | 0.0% | 0.1% |
References
- Australian Bureau of Statistics. 2010. ERP by Sex by Single Year of Age Deaths by Sex by Single Year of Age (Private Communication ABS); Canberra: Australian Bureau of Statistics.
- Australian Government Actuary. 2009. Australian Life Tables 2005–2007. Available online: http://www.aga.gov.au/publications/life_tables_2005-07/downloads/Australian_Life_Tables_2005-07.pdf (accessed on 13 July 2019).
- Australian Institute of Health and Welfare. 2017. Hospital Contact Details. November 21. Available online: http://www.aihw.gov.au/ (accessed on 6 December 2017).
- Bentham, Graham. 1986. Proximity to hospital and mortality from motor vehicle traffic accidents. Social Science Medicine 23: 1021–26. [Google Scholar] [CrossRef]
- Brockett, Patrick L. 1991. Information theoretic approach for actuarial science. Transactions of the Society of Actuaries 43: 173–35. [Google Scholar]
- Fung, Man Chung, Gareth W. Peters, and Pavel V. Shevchenko. 2017. A unified approach to mortality modelling using state-space framework: Characterisation, identification, estimation and forecasting. Annals of Actuarial Science 11: 343–389. [Google Scholar] [CrossRef]
- Haining, Robert. 2017. Estimation with heteroscedastic and correlated errors: A spatial analysis of intra-urban mortality data. The Journal of the RSAI 70: 223–41. [Google Scholar]
- Ilienko, Andrii. 2013. Continuous counterparts of poisson and binomial distributions and their properties. Annales Universitatis Scientiarium Budapestinensis Sect. Comp. 39: 137–47. [Google Scholar]
- Karra, Mahesh, Günther Fink, and David Canning. 2017. Facility distance and child mortality: A multi-country study of health facility access, service utilization, and child health outcomes. International Journal of Epidemiology 46: 817–26. [Google Scholar] [CrossRef] [PubMed]
- Kemp, Adrienne W., and C.D. Kemp. 2005. Encyclopedia of Biostatistics. Hoboken: John Wiley and Sons. [Google Scholar]
- Nicholl, Jon, James West, Steve Goodacre, and Janette Turner. 2007. The relationship between distance to hospital and patient mortality in emergencies: An observational study. Emergency Medicine Journal 24: 665–68. [Google Scholar] [CrossRef] [PubMed]
- Venter, Gary G. 2001. Mortality Trend Models. Casualty Actuarial Society E-Forum. Available online: https://pdfs.semanticscholar.org/7d00/d6ba5d1cbc74d78d07816be12bbcd8f26f92.pdf (accessed on 13 July 2019).
| 1 | For example, with the use of standard Matlab functions. |
| 2 | A continuity adjustment may be used for practical applications. |
| 3 | The constants are and X. |
| 4 | Strictly speaking, this is half the usual definition of . It also excludes the term resulting from which is constant across all models. |
| 5 |







| SD | Statistical Division | Area | Male Population | Female Population | No. of Towns * | Ruralization | No. of Hospitals | Average Hospital Distance |
|---|---|---|---|---|---|---|---|---|
| 1 | Sydney | 1.180 | 2,112,861 | 2,169,127 | 54 | 6% | 61 | 0.165 |
| 2 | Hunter | 2.779 | 306,840 | 310,712 | 73 | 13% | 10 | 0.603 |
| 3 | Illawarra | 0.819 | 205,886 | 208,818 | 46 | 11% | 11 | 0.235 |
| 4 | Richmond-Tweed | 0.949 | 113,390 | 116,673 | 36 | 29% | 5 | 0.322 |
| 5 | Mid-North Coast | 2.397 | 146,638 | 150,213 | 72 | 28% | 7 | 0.324 |
| 6 | Northern (NSW) | 9.323 | 89,820 | 90,387 | 39 | 33% | 3 | 1.054 |
| 7 | North Western | 18.868 | 58,670 | 57,641 | 27 | 32% | 1 | 2.164 |
| 8 | Central West | 6.105 | 89,913 | 88,718 | 38 | 28% | 3 | 0.800 |
| 9 | South Eastern | 5.138 | 104,421 | 102,955 | 46 | 40% | 4 | 0.551 |
| 10 | Murrumbidgee | 6.297 | 77,592 | 76,454 | 36 | 26% | 4 | 0.715 |
| 11 | Murray | 8.868 | 58,048 | 57,389 | 31 | 26% | 3 | 0.896 |
| 12 | Far West | 13.887 | 11,421 | 11,500 | 5 | 12% | 1 | 1.793 |
| 13 | Melbourne | 0.788 | 1,848,781 | 1,894,234 | 44 | 6% | 71 | 0.131 |
| 14 | Barwon | 0.921 | 133,285 | 136,406 | 20 | 32% | 4 | 0.419 |
| 15 | Western District | 2.344 | 50,956 | 51,549 | 25 | 34% | 4 | 0.372 |
| 16 | Central Highlands | 1.219 | 72,583 | 74,984 | 21 | 23% | 3 | 0.450 |
| 17 | Wimmera | 3.413 | 24,938 | 25,215 | 19 | 32% | 1 | 0.639 |
| 18 | Mallee | 3.953 | 45,699 | 46,029 | 24 | 32% | 2 | 0.942 |
| 19 | Loddon | 1.463 | 86,199 | 88,719 | 31 | 27% | 4 | 0.393 |
| 20 | Goulburn | 2.752 | 101,682 | 100,753 | 52 | 34% | 4 | 0.398 |
| 21 | Ovens-Murray | 1.773 | 47,753 | 48,358 | 29 | 29% | 2 | 0.510 |
| 22 | East Gippsland | 3.238 | 41,661 | 41,255 | 24 | 37% | 2 | 0.621 |
| 23 | Gippsland | 1.125 | 81,531 | 83,970 | 44 | 31% | 3 | 0.303 |
| 24 | Brisbane | 0.543 | 900,397 | 919,365 | 24 | 5% | 25 | 0.133 |
| 25 | Gold Coast | 0.122 | 256,603 | 261,575 | 3 | 22% | 4 | 0.115 |
| 26 | Sunshine Coast | 0.283 | 144,723 | 150,361 | 19 | 26% | 8 | 0.143 |
| 27 | West Moreton | 1.086 | 36,611 | 36,070 | 26 | 54% | 0 | 0.382 |
| 28 | Wide Bay-Burnett | 4.360 | 134,483 | 135,056 | 48 | 49% | 7 | 0.762 |
| 29 | Darling Downs | 7.057 | 112,598 | 114,543 | 33 | 28% | 5 | 1.075 |
| 30 | South West | 29.092 | 13,580 | 12,786 | 12 | 37% | 1 | 2.991 |
| 31 | Fitzroy | 10.440 | 102,989 | 97,396 | 33 | 26% | 4 | 1.410 |
| 32 | Central West | 35.074 | 5922 | 5640 | 8 | 33% | 0 | 3.701 |
| 33 | Mackay | 7.869 | 83,572 | 76,228 | 32 | 73% | 2 | 1.528 |
| 34 | Northern (QLD) | 6.909 | 106,422 | 103,480 | 27 | 17% | 2 | 1.407 |
| 35 | Far North | 23.008 | 125,711 | 121,584 | 60 | 26% | 4 | 2.971 |
| 36 | North West | 26.434 | 17,680 | 15,533 | 10 | 18% | 1 | 2.355 |
| 37 | Adelaide | 0.180 | 559,635 | 586,177 | 14 | 5% | 22 | 0.073 |
| 38 | Outer Adelaide | 1.153 | 64,537 | 64,233 | 43 | 41% | 0 | 0.649 |
| 39 | Yorke and Lower North | 1.988 | 23,031 | 22,463 | 28 | 40% | 0 | 0.765 |
| 40 | Murray Lands | 4.742 | 35,435 | 34,048 | 22 | 44% | 1 | 0.956 |
| 41 | South East | 2.157 | 32,733 | 31,759 | 15 | 32% | 2 | 0.523 |
| 42 | Eyre | 6.963 | 17,994 | 16,834 | 12 | 36% | 0 | 2.805 |
| 43 | Northern (SA) | 75.032 | 40,688 | 38,321 | 26 | 19% | 3 | 3.766 |
| 44 | Perth | 0.514 | 758,396 | 760,352 | 24 | 9% | 17 | 0.147 |
| 45 | South West | 2.783 | 111,608 | 108,400 | 32 | 18% | 4 | 0.651 |
| 46 | Lower Great Southern | 3.804 | 28,455 | 27,314 | 12 | 32% | 1 | 1.048 |
| 47 | Upper Great Southern | 4.430 | 9761 | 9017 | 13 | 45% | 0 | 1.772 |
| 48 | Midlands | 10.451 | 27,918 | 25,446 | 33 | 46% | 0 | 1.680 |
| 49 | South Eastern | 71.362 | 29,501 | 25,832 | 10 | 36% | 1 | 3.923 |
| 50 | Central | 54.304 | 32,009 | 29,355 | 18 | 84% | 2 | 3.789 |
| 51 | Pilbara | 44.214 | 24,665 | 19,424 | 14 | 14% | 1 | 3.980 |
| 52 | Kimberley | 35.757 | 16,732 | 15,196 | 14 | 26% | 0 | 5.628 |
| 53 | Greater Hobart | 0.150 | 99,799 | 105,682 | 19 | 14% | 4 | 0.143 |
| 54 | Southern | 2.651 | 18,720 | 17,411 | 23 | 62% | 0 | 0.641 |
| 55 | Northern (Tas) | 2.150 | 68,556 | 70,146 | 34 | 24% | 3 | 0.591 |
| 56 | Mersey-Lyell | 2.434 | 54,481 | 55,156 | 25 | 28% | 2 | 0.817 |
| 57 | Darwin | 0.259 | 60,551 | 53,811 | 6 | 11% | 2 | 0.330 |
| 58 | Northern Territory - Bal | 115.970 | 48,764 | 47,501 | 51 | 44% | 2 | 2.871 |
| 59 | Canberra | 0.080 | 165,151 | 168,688 | 2 | 3% | 4 | 0.087 |
| Total | 695.403 | 10,280,979 | 10,414,242 | 1661 | 347 |
| Model | Males | Females |
|---|---|---|
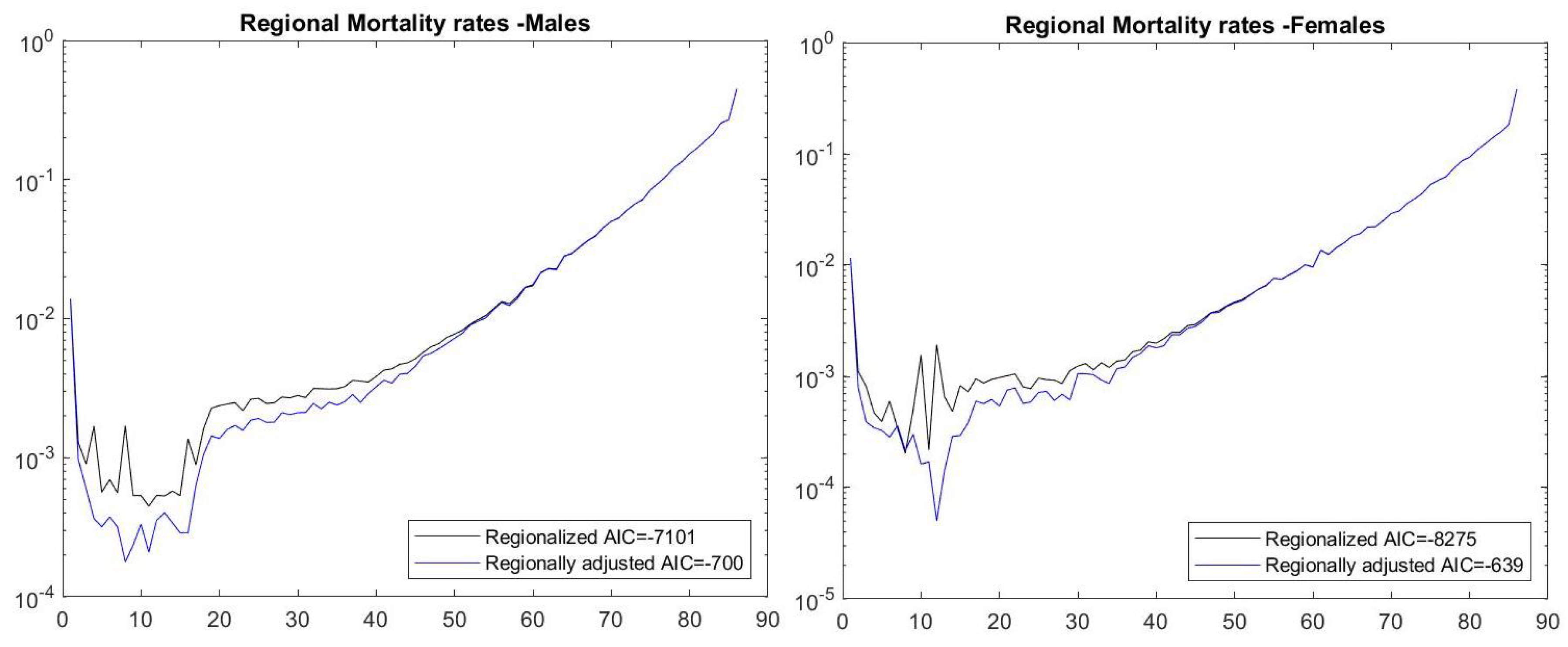
| No regionality | −3768 | −5120 |
| Regionalized | −7101 | −8271 |
| Proximity | −7262 | −8952 |
| Proximity NB | −7796 | −9077 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leung, A. Hospital Proximity and Mortality in Australia. Risks 2019, 7, 81. https://doi.org/10.3390/risks7030081
Leung A. Hospital Proximity and Mortality in Australia. Risks. 2019; 7(3):81. https://doi.org/10.3390/risks7030081
Chicago/Turabian StyleLeung, Andrew. 2019. "Hospital Proximity and Mortality in Australia" Risks 7, no. 3: 81. https://doi.org/10.3390/risks7030081
APA StyleLeung, A. (2019). Hospital Proximity and Mortality in Australia. Risks, 7(3), 81. https://doi.org/10.3390/risks7030081





