Do We Need Stochastic Volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing Squared End-Of-Day Returns on FTSE
Abstract
:1. Introduction
2. Previous Work and Econometric Models
2.1. Stochastic Volatility
2.2. ARCH and GARCH
2.3. Realised Volatility
2.4. Historical-Volatility Model
2.5. Heterogeneous Autoregressive Model (HAR)
2.6. Quantile Regression
3. Analysis Results
3.1. Preliminary Analysis
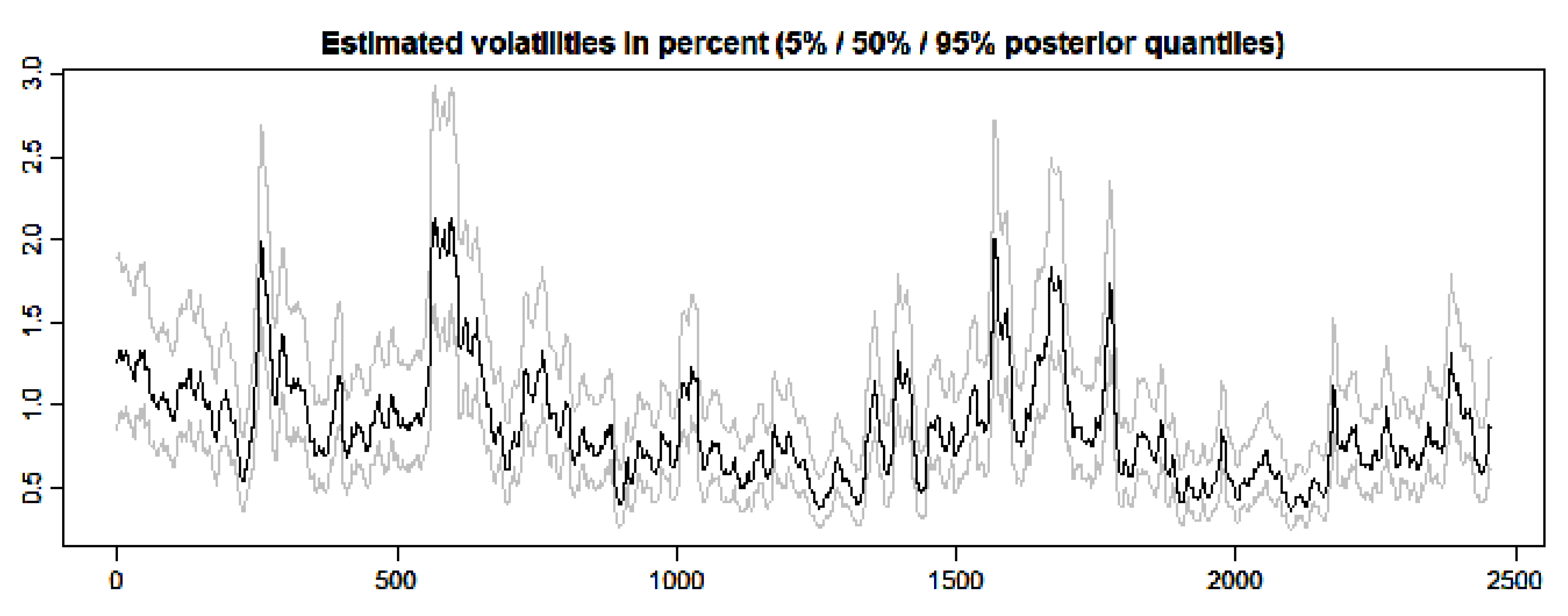
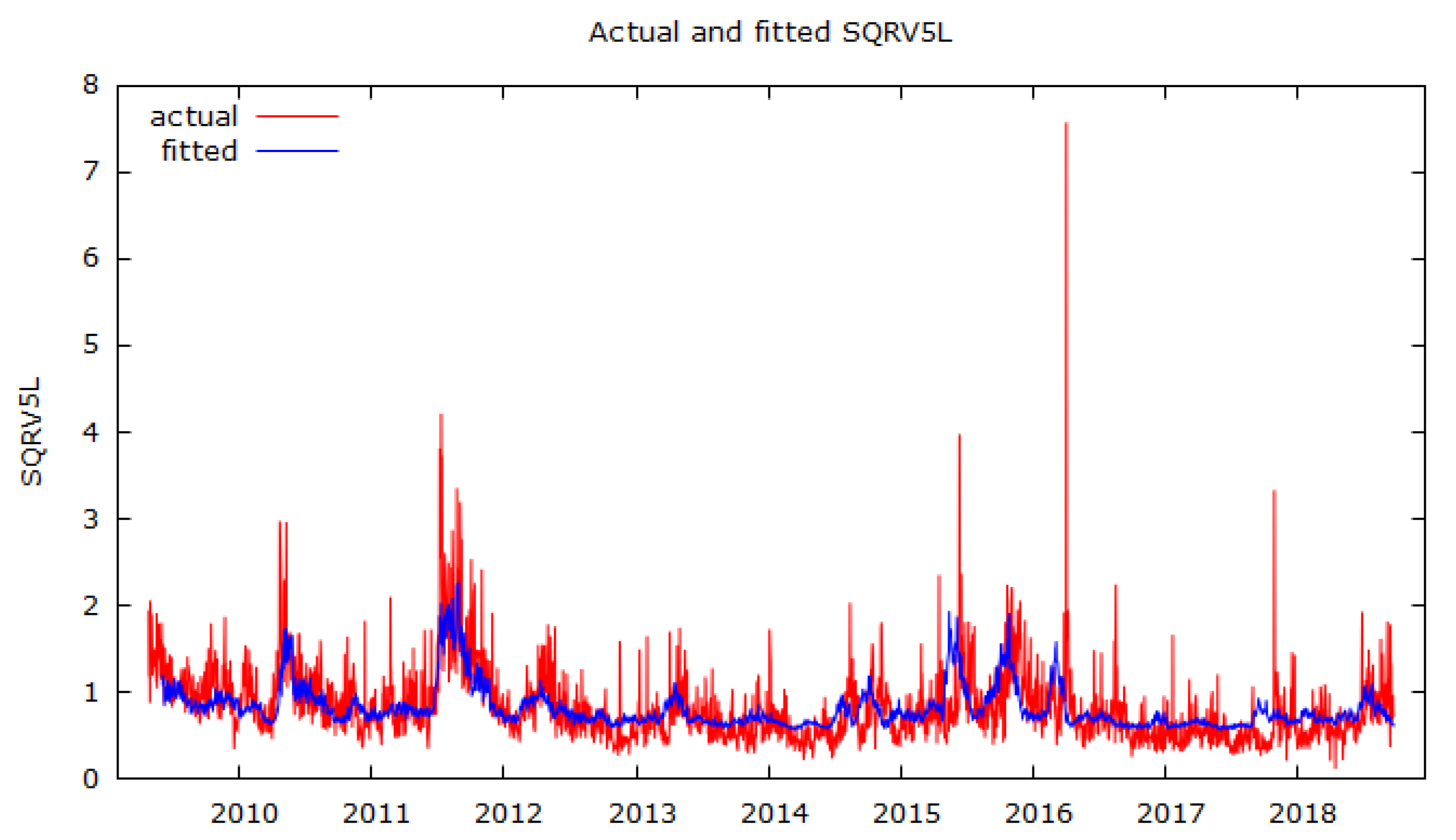
3.2. SV and GARCH Estimates
3.3. Quantile-Regression Results
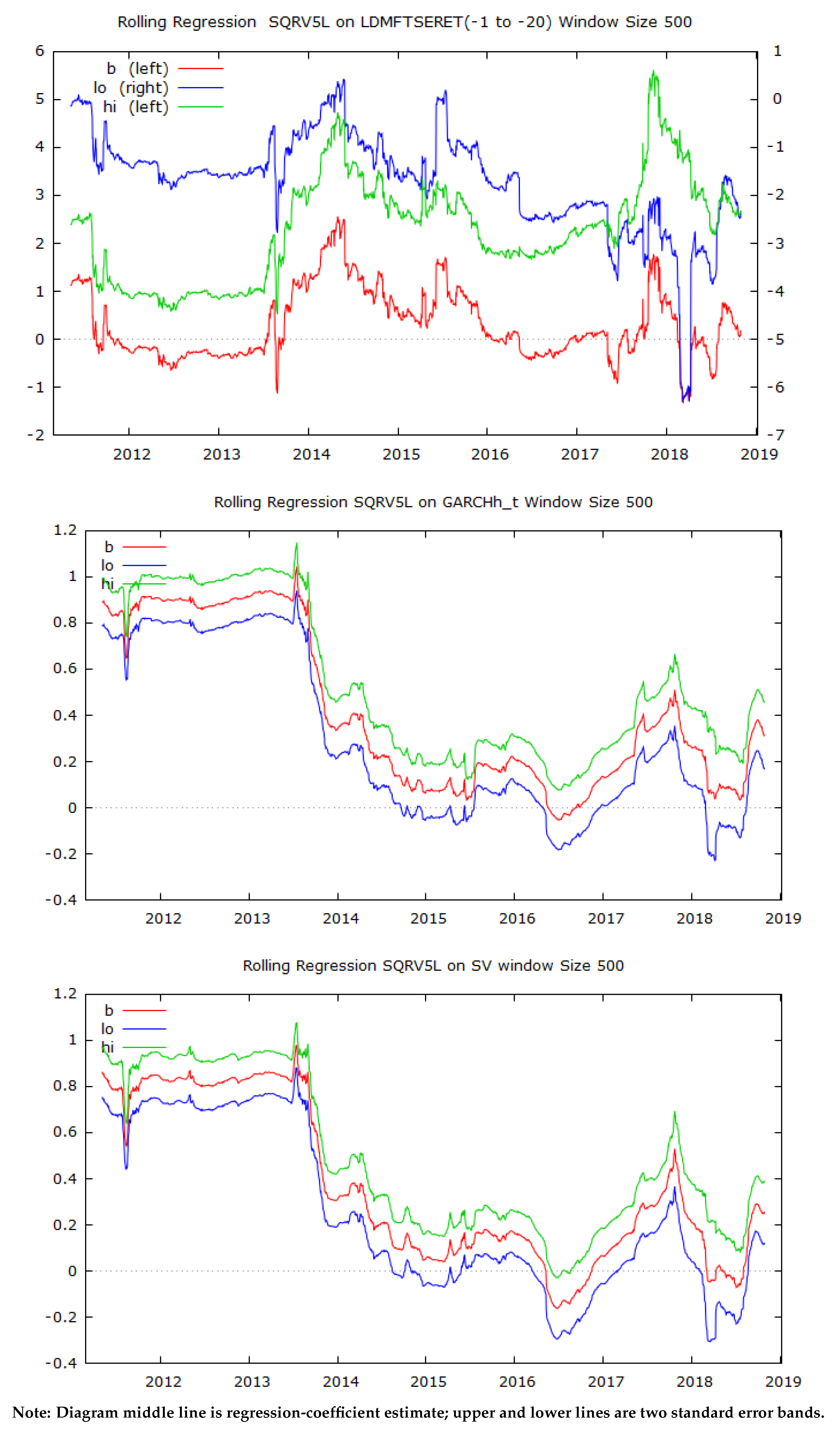
3.4. Rolling-Regression Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Allen, David E., Ron Amram, and Michael McAleer. 2013. Volatility spillovers from the Chinese stock market to economic neighbours. Mathematics and Computers in Simulation 94: 238–57. [Google Scholar] [CrossRef] [Green Version]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001. The distribution of realized stock return volatility. Journal of Financial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 529–626. [Google Scholar] [CrossRef] [Green Version]
- Asai, Manabu, Michael McAleer, and Jun Yu. 2006. Multivariate stochastic volatility: A review. Econometric Reviews 25: 145–75. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002. Econometric analysis of realised volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society, Series B 63: 253–80. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2003. Realized power variation and stochastic volatility models. Bernoulli 9: 243–65. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef] [Green Version]
- Bos, Charles S. 2012. Relating stochastic volatility estimation methods. In Handbook of Volatility Models and Their Applications. Edited by Luc Bauwens, Christian Hafner and Sebastien Laurent. New York: John Wiley & Sons, pp. 147–74. [Google Scholar]
- Christensen, Bent J., and Nagpurnanand R. Prabhala. 1998. The relation between implied and realized volatility. Journal of Financial Economics 37: 125–50. [Google Scholar] [CrossRef]
- Clark, Peter K. 1973. A subordinated stochastic process model with finite variance for speculative prices. Econometrica 41: 135–55. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- Dacorogna, Michel M., Ulrich A. Müller, Olivier V. Pictet, and Richard B. Olsen. 1998. Modelling short term volatility with GARCH and HARCH. Edited by Christian Dunis and Bin Zhou. Nonlinear Modelling of High Frequency Financial Time Series; Chichester: Wiley. [Google Scholar]
- Engle, Robert F. 1982. Autoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Ghysels, Eric, Andrew C. Harvey, and Eric Renault. 1996. Stochastic volatility. In Statistical Methods in Finance, Volume 14, Handbook of Statistics. Edited by Gangadharrao Soundalyarao Maddala and Calyampudi Radhakrishna Rao. Amsterdam: Elsevier, pp. 119–91. [Google Scholar]
- Heber, Gerd, Asger Lunde, Neil Shephard, and Kevin Sheppard. 2009. Oxford-Man Institute’s Realized Library. Oxford: Oxford-Man Institute, University of Oxford. [Google Scholar]
- Jacquier, Eric, Nicholas G. Polson, and Peter E. Rossi. 1994. Bayesian analysis of stochastic volatility models. Journal of Business & Economic Statistics 12: 371–89. [Google Scholar]
- Kastner, Gregor, and Sylvia Frühwirth-Schnatter. 2014. Ancillarity-sufficiency interweaving strategy (ASIS) for boosting MCMC estimation of stochastic volatility models. Computational Statistics and Data Analysis 76: 408–23. [Google Scholar] [CrossRef] [Green Version]
- Kastner, Gregor. 2016. Dealing with stochastic volatility in time series using the R package stochvol. Journal of Statistical Software 69: 1–30. [Google Scholar] [CrossRef] [Green Version]
- Kim, Sangjoon, Neil Shephard, and Siddhartha Chib. 1998. Stochastic volatility: Likelihood inference and comparison with ARCH models. Review of Economic Studies 65: 361–93. [Google Scholar] [CrossRef]
- Koenker, Roger, and Kevin F. Hallock. 2001. Quantile regression. Journal of Economic Perspectives 15: 143–56. [Google Scholar] [CrossRef]
- McAleer, Michael. 2005. Automated inference and learning in modeling financial volatility. Econometric Theory 21: T232–61. [Google Scholar] [CrossRef] [Green Version]
- McCausland, William J., Shirley Miller, and Denis Pelletier. 2011. Simulation smoothing for state-space models: A computational efficiency analysis. Computational Statistics and Data Analysis 55: 199–212. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive W. J. Granger. 2003. Forecasting volatility in financial markets: A review. Journal of Economic Literature 41: 478–539. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive Granger. 2005. Practical issues in forecasting volatility. Financial Analysts Journal 61: 45–56. [Google Scholar] [CrossRef] [Green Version]
- Poterba, James M., and Lawrence H. Summers. 1986. The persistence of volatility and stock market fluctuations. American Economic Review 76: 1124–41. [Google Scholar]
- Rue, Håvard. 2001. Fast sampling of Gaussian Markov random fields. Journal of the Royal Statistical Society Series B 63: 325–38. [Google Scholar] [CrossRef]
- Schwert, G. William. 1989. Why does stock market volatility change over time? Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Shephard, Neil, and Kevin Sheppard. 2010. Realising the future: Forecasting with high-frequency-based volatility (HEAVY) models. Journal of Applied Econometrics 25: 197–231. [Google Scholar] [CrossRef] [Green Version]
- Taylor, Stephen John. 1982. Financial Returns Modelled by the Product of Two Stochastic Processes: A Study of Daily Sugar Prices 1691–79. Edited by Torben Anderson. Time Series Analysis: Theory and Practice 1. Cheltenham: Edward Elgar, pp. 203–26. [Google Scholar]
- Taylor, Stephen J. 1994. Modeling stochastic volatility: A review and comparative study. Mathematical Finance 4: 183–204. [Google Scholar] [CrossRef]
- Taylor, Stephen J., and Xinzhong Xu. 1997. The incremental volatility information in one million foreign exchange quotations. Journal of Empirical Finance 4: 317–40. [Google Scholar] [CrossRef]
- Tauchen, George E., and Mark Pitts. 1983. The price variability-volume relationship on speculative markets. Econometrica 5: 485–505. [Google Scholar] [CrossRef] [Green Version]
- Tsay, Ruey S. 1987. Conditional heteroscedastic time series models. Journal of the American Statistical Association 82: 590–604. [Google Scholar] [CrossRef]
- Yu, Yaming, and Xiao-Li Meng. 2011. To center or not to center: That is not the question—An ancillarity-suffiency interweaving strategy (ASIS) for boosting MCMC efficiency. Journal of Computational and Graphical Statistics 20: 531–70. [Google Scholar] [CrossRef]








| Summary statistics using 27 April 2009–16 April 2019 observations for FTSERET variable (2454 valid observations) | |||
|---|---|---|---|
| Mean | Median | Minimum | Maximum |
| 0.00022266 | 0.00050198 | −0.047798 | 0.050323 |
| Std. Dev. | C.V. | Skewness | Ex. kurtosis |
| 0.0097220 | 43.663 | −0.13603 | 2.1367 |
| 5% | 95% | IQ Range | Missing obs. |
| −0.015687 | 0.016056 | 0.010418 | 0 |
| Summary Statistics, using27 April 2009–16 April 2019 observations for RV5 variable (2454 valid observations) | |||
| Mean | Median | Minimum | Maximum |
| 8.6261 × 10 | 5.1600 × 10 | 1.3300 × 10 | 0.0057390 |
| Std. Dev. | C.V. | Skewness | Ex. kurtosis |
| 0.00016097 | 1.8661 | 19.805 | 633.01 |
| 5% | 95% | IQ Range | Missing obs. |
| 1.4275 × 10 | 0.00025567 | 6.8100 × 10 | 0 |
| Summary of 1000 Markov chain Monte Carlo (MCMC) draws after burn-in of 1000 | |||||
|---|---|---|---|---|---|
| Prior distributions | |||||
| mean = 0 | S.D. = 100 | ||||
| Posterior draws thinning = 1 | |||||
| Mean | S.D. | 5% | 50% | 95% | |
| −9.5938 | 0.11914 | −9.7831 | −9.5944 | −9.3963 | |
| 0.9577 | 0.01051 | 0.9389 | 0.9586 | 0.9734 | |
| 0.2342 | 0.02868 | 0.1915 | 0.2321 | 0.2851 | |
| 0.0083 | 0.00049 | 0.0075 | 0.0083 | 0.0091 | |
| 0.0557 | 0.01378 | 0.0367 | 0.0539 | 0.0813 | |
| Summary statistics using 27 April 2009–16 April 2019 observations for SV variable (2454 valid observations) | |||
|---|---|---|---|
| Mean | Median | Minimum | Maximum |
| 0.87152 | 0.80112 | 0.37146 | 2.1388 |
| Std. Dev. | C.V. | Skewness | Ex. kurtosis |
| 0.32600 | 0.37405 | 1.2754 | 1.9519 |
| 5% | 95% | IQ Range | Missing obs. |
| 0.45723 | 1.5217 | 0.38324 | 0 |
| Summary statistics using 27 April 2009–16 April 2019 observations for garchh variable_t (2454 valid observations) | |||
| Mean | Median | Minimum | Maximum |
| 0.92405 | 0.84738 | 0.51430 | 2.3305 |
| Std. Dev. | C.V. | Skewness | Ex. kurtosis |
| 0.30490 | 0.32996 | 1.6654 | 3.3669 |
| 5% | 95% | IQ Range | Missing obs. |
| 0.59248 | 1.5934 | 0.32905 | 0 |
| Summary statistics using 27 April 2009–16 April 2019 observations for SQRV5L variable (2454 valid observations) | |||
| Mean | Median | Minimum | Maximum |
| 0.81989 | 0.71837 | 0.11543 | 7.5756 |
| Std. Dev. | C.V. | Skewness | Ex. kurtosis |
| 0.43644 | 0.53231 | 3.3736 | 29.966 |
| 5% | 95% | IQ Range | Missing obs. |
| 0.37737 | 1.5990 | 0.44676 | 0 |
| Coefficients | Standard Error | T Statistic | |
|---|---|---|---|
| mu | 1.360 × 10 | 1.601 × 10 | 0.850 |
| omega | 3.406 × 10 | 8.087 × 10 | 4.211 *** |
| alpha1 | 1.199 × 10 | 1.728 × 10 | 6.939 *** |
| beta1 | 8.443 × 10 | 2.240 × 10 | 37.688 *** |
| Ordinary least squares (OLS) using 27 April 2009–16 April 2019 observations (T = 2454). Dependent variable: SQRV5L. | ||||
|---|---|---|---|---|
| Coefficient | Std. Error | t-ratio | p-value | |
| const | 0.305752 | 0.0225825 | 13.54 | 0.0000 |
| SV | 0.589930 | 0.0242700 | 24.31 | 0.0000 |
| Mean dependent var | 0.819888 | S.D. dependent var | 0.436435 | |
| Sum squared resid | 376.5133 | S.E. of regression | 0.391859 | |
| 0.194171 | Adjusted | 0.193842 | ||
| 590.8287 | p-value(F) | 4.1 × 10 | ||
| Log-likelihood | −1182.037 | Akaike criterion | 2368.075 | |
| Schwarz criterion | 2379.686 | Hannan–Quinn | 2372.294 | |
| 0.503365 | Durbin–Watson | 0.991133 | ||
| OLS using 27 April 2009–16 April 2019 observations ( = 2454). Dependent variable: SQRV5L. | ||||
| Coefficient | Std. Error | t-ratio | p-value | |
| const | 0.223766 | 0.0251093 | 8.912 | 0.0000 |
| garchh_t | 0.645116 | 0.0258051 | 25.00 | 0.0000 |
| Mean dependent var | 0.819888 | S.D. dependent var | 0.436435 | |
| Sum squared resid | 372.3346 | S.E. of regression | 0.389678 | |
| 0.203114 | Adjusted | 0.202789 | ||
| 624.9784 | p-value(F) | 4.6 × 10 | ||
| Log-likelihood | −1168.344 | Akaike criterion | 2340.687 | |
| Schwarz criterion | 2352.298 | Hannan–Quinn | 2344.906 | |
| 0.490865 | Durbin–Watson | 1.015052 | ||
| OLS using 4 June 2009–16 April 2019 observations ( = 2426). Dependent variable: SQRV5L. | ||||
| Coefficient | Std. Error | t-ratio | p-value | |
| const | 0.544629 | 0.0111890 | 48.68 | 0.0000 |
| LSQDMFTSE_1 | 0.433934 | 0.414977 | 1.046 | 0.2958 |
| LSQDMFTSE_2 | 0.515250 | 0.419102 | 1.229 | 0.2190 |
| LSQDMFTSE_3 | 1.18029 | 0.420051 | 2.810 | 0.0050 |
| LSQDMFTSE_4 | 0.839649 | 0.421807 | 1.991 | 0.0466 |
| LSQDMFTSE_5 | 1.35951 | 0.423013 | 3.214 | 0.0013 |
| LSQDMFTSE_6 | 0.102526 | 0.422970 | 0.2424 | 0.8085 |
| LSQDMFTSE_7 | 0.663505 | 0.423177 | 1.568 | 0.1170 |
| LSQDMFTSE_8 | 0.242477 | 0.421954 | 0.5747 | 0.5656 |
| LSQDMFTSE_9 | 1.58351 | 0.423249 | 3.741 | 0.0002 |
| LSQDMFTSE_10 | 0.715148 | 0.422994 | 1.691 | 0.0910 |
| LSQDMFTSE_11 | 1.72472 | 0.421790 | 4.089 | 0.0000 |
| LSQDMFTSE_12 | 2.43111 | 0.422496 | 5.754 | 0.0000 |
| LSQDMFTSE_13 | 2.11699 | 0.422470 | 5.011 | 0.0000 |
| LSQDMFTSE_14 | 0.667181 | 0.422379 | 1.580 | 0.1143 |
| LSQDMFTSE_15 | 2.04957 | 0.422271 | 4.854 | 0.0000 |
| LSQDMFTSE_16 | 0.438659 | 0.422071 | 1.039 | 0.2988 |
| LSQDMFTSE_17 | 0.994273 | 0.421786 | 2.357 | 0.0185 |
| LSQDMFTSE_18 | 0.430727 | 0.420974 | 1.023 | 0.3063 |
| LSQDMFTSE_19 | 1.06033 | 0.420799 | 2.520 | 0.0118 |
| LSQDMFTSE_20 | 0.0170270 | 0.421031 | 0.04044 | 0.9677 |
| LSQDMFTSE_21 | 1.03750 | 0.419658 | 2.472 | 0.0135 |
| LSQDMFTSE_22 | 0.303899 | 0.420813 | 0.7222 | 0.4703 |
| LSQDMFTSE_23 | 0.842299 | 0.420028 | 2.005 | 0.0450 |
| LSQDMFTSE_24 | 1.12694 | 0.419905 | 2.684 | 0.0073 |
| LSQDMFTSE_25 | 0.834749 | 0.418637 | 1.994 | 0.0463 |
| LSQDMFTSE_26 | 0.746605 | 0.416243 | 1.794 | 0.0730 |
| LSQDMFTSE_27 | 1.92539 | 0.415125 | 4.638 | 0.0000 |
| LSQDMFTSE_28 | 2.02831 | 0.411577 | 4.928 | 0.0000 |
| Mean dependent var | 0.812434 | S.D. dependent var | 0.432184 | |
| Sum squared resid | 312.0871 | S.E. of regression | 0.360831 | |
| 0.310989 | Adjusted | 0.302940 | ||
| 38.63918 | p-value(F) | 6.2 × 10 | ||
| Log-likelihood | −954.8254 | Akaike criterion | 1967.651 | |
| Schwarz criterion | 2135.677 | Hannan–Quinn | 2028.745 | |
| 0.429918 | Durbin–Watson | 1.139917 | ||
| Variable | Tau | Coefficient | Std. Error | t-Ratio |
|---|---|---|---|---|
| SV(-1) | 0.05 | 0.00179384 | 0.000194807 | 9.20827 *** |
| SV(-1) | 0.25 | 0.00386922 | 0.000179883 | 21.5097 *** |
| SV(-1) | 0.50 | 0.00558958 | 0.000199581 | 28.0066 *** |
| SV(-1) | 0.75 | 0.00746445 | 0.000279415 | 26.7146 *** |
| SV(-1) | 0.95 | 0.0117519 | 0.000798124 | 14.7245 *** |
| GARCHh_t(-1) | 0.05 | 0.00159755 | 0.000195806 | 8.15884 *** |
| GARCHh_t(-1) | 0.25 | 0.00420579 | 0.000191819 | 21.9259 *** |
| GARCHh_t(-1) | 0.50 | 0.00627205 | 0.000204113 | 30.7283 *** |
| GARCHh_t(-1) | 0.75 | 0.00873417 | 0.000334193 | 26.1351 *** |
| GARCHh_t(-1) | 0.95 | 0.0135944 | 0.000860269 | 15.8025 *** |
| DMSQFTSERET(-1) | 0.05 | 0.0132912 | 0.00310350 | 4.28266 *** |
| DMSQFTSERET(-1) | 0.25 | 0.0322416 | 0.00350232 | 9.20578 *** |
| DMSQFTSERET(-1) | 0.50 | 0.0402209 | 0.00311836 | 12.8981 *** |
| DMSQFTSERET(-1) | 0.75 | 0.0522737 | 0.00566966 | 9.21991 *** |
| DMSQFTSERET(-1) | 0.95 | 0.0737864 | 0.0140149 | 5.26486 *** |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allen, D.E.; McAleer, M. Do We Need Stochastic Volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing Squared End-Of-Day Returns on FTSE. Risks 2020, 8, 12. https://doi.org/10.3390/risks8010012
Allen DE, McAleer M. Do We Need Stochastic Volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing Squared End-Of-Day Returns on FTSE. Risks. 2020; 8(1):12. https://doi.org/10.3390/risks8010012
Chicago/Turabian StyleAllen, David E., and Michael McAleer. 2020. "Do We Need Stochastic Volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing Squared End-Of-Day Returns on FTSE" Risks 8, no. 1: 12. https://doi.org/10.3390/risks8010012
APA StyleAllen, D. E., & McAleer, M. (2020). Do We Need Stochastic Volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing Squared End-Of-Day Returns on FTSE. Risks, 8(1), 12. https://doi.org/10.3390/risks8010012






