Abstract
In this paper, we propose a novel framework for estimating systemic risk measures and risk allocations based on Markov Chain Monte Carlo (MCMC) methods. We consider a class of allocations whose jth component can be written as some risk measure of the jth conditional marginal loss distribution given the so-called crisis event. By considering a crisis event as an intersection of linear constraints, this class of allocations covers, for example, conditional Value-at-Risk (CoVaR), conditional expected shortfall (CoES), VaR contributions, and range VaR (RVaR) contributions as special cases. For this class of allocations, analytical calculations are rarely available, and numerical computations based on Monte Carlo (MC) methods often provide inefficient estimates due to the rare-event character of the crisis events. We propose an MCMC estimator constructed from a sample path of a Markov chain whose stationary distribution is the conditional distribution given the crisis event. Efficient constructions of Markov chains, such as the Hamiltonian Monte Carlo and Gibbs sampler, are suggested and studied depending on the crisis event and the underlying loss distribution. The efficiency of the MCMC estimators is demonstrated in a series of numerical experiments.
1. Introduction
In portfolio risk management, risk allocation is an essential step to quantifying the risk of each unit of a portfolio by decomposing the total risk of the whole portfolio. One of the most prevalent rules to determine risk allocations is the Euler princple, proposed by Tasche (1995) and justified from various viewpoints, such as the RORAC compatibility (Tasche (1995) and Tasche (2008)) and cooperative game theory (Denault (2001)). For the popular risk measures, such as VaR, RVaR, and ES, Euler allocations take the form of conditional expectations of the underlying loss random vector given a certain rare event on the total loss of the portfolio; see Tasche (2001) for derivations. We call this rare event the crisis event.The decomposition of risks is also required in the context of systemic risk measurement. Systemic risk is the risk of financial distress of an entire economy as a result of the failure of individual components of the financial system. To quantify such risks, various systemic risk measures have been proposed in the literature, such as conditional VaR (CoVaR) (Adrian and Brunnermeier (2016)), conditional expected shortfall (CoES) (Mainik and Schaanning (2014)), and marginal expected shortfall (MES) (Acharya et al. (2017)). These three measures quantify the risk of individuals by taking the VaR, ES, and expectation of the individual loss, respectively, under some stressed scenario—that is, given the crisis event. Chen et al. (2013), Hoffmann et al. (2016), and Kromer et al. (2016) proposed an axiomatic characterization of systemic risk measures, where the risk of the aggregated loss in a financial system is first measured and then decomposed into the individual economic entities. Due to the similarity of risk allocations with the derivation of systemic risk measures, we refer to both of them as systemic risk allocations. In fact, MES coincides with the Euler allocation of ES, and other Euler allocations can be regarded as special cases of systemic risk measures considered in Gourieroux and Monfort (2013).
Calculating systemic risk allocations given an unconditional joint loss distribution is generally challenging, since analytical calculations often require knowledge of the joint distribution of the marginal and aggregated loss. Furthermore, MC estimation suffers from the rare-event character of the crisis event. For computing CoVaR, CoES, and MES, Mainik and Schaanning (2014), Bernardi et al. (2017), and Jaworski (2017) derived formulas based on the copula of the marginal and aggregated loss; Asimit and Li (2018) derived asymptotic formulas based on the extreme value theory; and Girardi and Ergün (2013) estimated CoVaR under a multivariate GARCH model. Vernic (2006), Chiragiev and Landsman (2007), Dhaene et al. (2008), and Furman and Landsman (2008) calculated Euler allocations for specific joint distributions. Asimit et al. (2011) derived asymptotic formulas for risk allocations. Furman and Zitikis (2009) and Furman et al. (2018) calculated weighted allocations, which include Euler allocations as special cases, under a Stein-type assumption. Concerning the numerical computation of Euler allocations, Glasserman (2005), Glasserman and Li (2005), and Kalkbrener et al. (2004) considered importance sampling methods, and Siller (2013) proposed the Fourier transform Monte Carlo method, all specifically for credit portfolios. For general copula-based dependence models, analytical calculations of systemic risk allocations are rarely available, and an estimation method is, to the best of our knowledge, only addressed in Targino et al. (2015), where sequential Monte Carlo (SMC) samplers are applied.
We address the problem of estimating systemic risk allocations under general copula-based dependent risks in the case where the copula between the marginal and aggregated losses are not necessarily available. We consider a general class of systemic risk allocations in the form of risk measures of a conditional loss distribution given a crisis event, which includes CoVaR, CoES, MES, and Euler allocations as special cases. In our proposed method, the conditional loss distribution, called the target distribution , is simulated by a Markov chain whose stationary distribution is the desired distribution by sequentially updating the sample path based on the available information from . While this MCMC method resembles the SMC in Targino et al. (2015), the latter requires a more complicated implementation involving the choice of forward and backward kernels, resampling and move steps, and even MCMC in the move steps. Our suggested approach directly constructs a single sophisticated Markov chain depending on the target distribution of interest. Applications of MCMC to estimating risk allocations have been studied in Koike and Minami (2019), specifically for VaR contributions. Our paper explores and demonstrates the applicability of MCMC methods to a more general class of systemic risk allocations.
Almost all MCMC methods used in practice are of the Metropolis–Hastings (MH) type (Metropolis et al. (1953) and Hastings (1970)), where the so-called proposal distribution q generates a candidate of the next state based on the current state. This candidate is then accepted or rejected according to the so-called acceptance probability to adjust the stationary distribution to be the target distribution . As explained in Section 3.1 below, the resulting Markov chain has serial correlation, which adversarially affects the efficiency of the estimator. An efficient MCMC of MH type is such that the proposal distribution generates a candidate which exhibits low correlation with the current state with sufficiently large acceptance probability. The main difficulty in constructing such an efficient MCMC estimator for systemic risk allocations is that the support of the target distribution is subject to constraints determined by the crisis event. For such target distributions, simple MCMC methods, such as random walk MH, are not efficient since a candidate is immediately rejected if it violates the constraints; see Section 3.2 for details.
To tackle this problem, we consider two specific MCMC methods, Hamiltonian Monte Carlo (HMC) (Duane et al. (1987)) and the Gibbs sampler (GS) (Geman and Geman (1984) and Gelfand and Smith (1990)). In the HMC method, a candidate is generated according to the so-called Hamiltonian dynamics, which leads to a high acceptance probability and low correlation with the current state by accurately simulating the dynamics of sufficiently long length; see Neal et al. (2011) and Betancourt (2017) for an introduction to HMC. Moreover, the HMC candidates always belong to the crisis event by reflecting the dynamics when the chain hits the boundary of the constraints; see Ruján (1997), Pakman and Paninski (2014), Afshar and Domke (2015), Yi and Doshi-Velez (2017), and Chevallier et al. (2018) for this reflection property of the HMC method. An alternative method to handle the constraints is the GS, in which the chain is updated in each component. Since all the components except the updated one remain fixed, a componentwise update is typically subject to weaker constraints. As long as such componentwise updates are feasible, the GS candidates belong to the crisis event, and the acceptance probability is always 1; see Geweke (1991), Gelfand et al. (1992), and Rodriguez-Yam et al. (2004) for the application of the GS to constrained target distributions, and see Gudmundsson and Hult (2014) and Targino et al. (2015) for applications to estimating risk contributions.
Our findings include efficient MCMC estimators of systemic risk allocations achieved via HMC with reflection and GSs. We assume that the unconditional joint loss density is known, possibly through its marginal densities and copula density. Depending on the supports of the marginal loss distributions and the crisis event, different MCMC methods are applicable. We find that if the marginal loss distributions are one-sided, that is, the supports are bounded from the left, then the crisis event is typically a bounded set and HMC shows good performance. On the other hand, if the marginal losses are two-sided, that is, they have both right and left tails, the crisis event is often unbounded and the GSs perform better, provided that the random number generators of the conditional copulas are available. Based on the samples generated by the MC method, we propose heuristics to determine the parameters of the HMC and GS methods, for which no manual interaction is required. Since, in the MCMC method, the conditional loss distribution of interest is directly simulated, in contrast to MC where rejection is applied based on the unconditional loss distribution, the MCMC method generally outperforms the MC method in terms of the sample size, and thus the standard error. This advantage of MCMC becomes more pronounced as the probability of the crisis event becomes smaller. We demonstrate this efficiency of the MCMC estimators of systemic risk allocations by a series of numerical experiments.
This paper is organized as follows. The general framework of the estimation problem of systemic risk allocations is introduced in Section 2. Our class of systemic risk allocations is proposed in Section 2.1, and their estimation via the MC method is presented in Section 2.2. Section 3 is devoted to MCMC methods for estimating systemic risk allocations. After a brief review of MCMC methods in Section 3.1, we formulate our problem of estimating systemic risk allocations in terms of MCMC in Section 3.2. HMC and GS for constrained target distributions are then investigated in Section 3.3 and Section 3.4, respectively. In Section 4, numerical experiments are conducted, including simulation and empirical studies, and a detailed comparison of MC and our introduced MCMC methods is provided. Section 5 concludes with practical guidance and limitations of the presented MCMC methods. An R script reproducing the numerical experiments is available as Supplementary Material.
2. Systemic Risk Allocations and Their Estimation
In this section, we define a broad class of systemic risk allocations, including Euler allocations, CoVaR, and CoES as special cases. Then, the MC method is described to estimate systemic risk allocations.
2.1. A Class of Systemic Risk Allocations
Let be an atomless probability space, and let , be random variables on this space. The random vector can be interpreted as losses of a portfolio of size d, or losses of d economic entities in an economy over a fixed time period. Throughout the paper, a positive value of a loss random variable represents a financial loss, and a negative loss is interpreted as a profit. Let denote the joint cumulative distribution function (cdf) of with marginal distributions . Assume that admits a probability density function (pdf) with marginal densities . Sklar’s theorem (Nelsen (2006)) allows one to write
where is a copula of . Assuming the density c of the copula C to exist, can be written as
An allocation is a map from a random vector to . The sum can be understood as the capital required to cover the total loss of the portfolio or the economy. The jth component , is then the contribution of the jth loss to the total capital . In this paper, we consider the following class of allocations
where is a map from a random variable to called the jth marginal risk measure for , and is a set called the crisis event. The conditioning set is simply written as if there is no confusion. As we now explain, this class of allocations covers well-known allocations as special cases. For a random variable , we define the Value-at-Risk (VaR) of X at confidence level by
Range Value-at-Risk (RVaR) at confidence levels is defined by
and, if it exists, expected shortfall (ES) at confidence level is defined by . Note that ES is also known as C(onditional)VaR, T(ail)VaR, A(verage)VaR and C(onditional)T(ail)E(expectation). These risk measures are law-invariant in the sense that they depend only on the distribution of X. Therefore, we sometimes write instead of .
We now define various crisis events and marginal risk measures. A typical form of the crisis event is an intersection of a set of linear constraints
Several important special cases of the crisis event of Form (2) are provided in the following.
Definition 1
(VaR, RVaR, and ES crisis events). For , the VaR, RVaR and ES crisis events are defined by
respectively, where is the d-dimensional vector of ones.
Definition 2
(Risk contributions and conditional risk measures). For , we call of
- 1.
- risk contribution-type if ;
- 2.
- CoVaR type if for ;
- 3.
- CoRVaR type if for ; and
- 4.
- CoES-type if for .
The following examples show that coincides with popular allocations for some specific choices of marginal risk measure and crisis event.
Example 1
(Special cases of ).
- (1)
- Risk contributions. If the crisis event is chosen to be , or , the allocations of the risk contribution type reduce to the VaR, RVaR, or ES contributions defined byrespectively. These results are derived by allocating the total capital , and according to the Euler principle; see Tasche (1995). The ES contribution is also called the MES and used as a systemic risk measure; see Acharya et al. (2017).
- (2)
- Conditional risk measures. CoVaR and CoES are systemic risk measures defined byfor ; see Mainik and Schaanning (2014) and Bernardi et al. (2017). Our CoVaR and CoES-type allocations with crisis events or coincide with those defined in the last displayed equations.
Remark 1
(Weighted allocations). For a measurable function , Furman and Zitikis (2008) proposed the weighted allocation with the weight function w being defined by . By taking an indicator function as weight function and provided that , the weighted allocation coincides with the risk contribution-type systemic allocation .
2.2. Monte Carlo Estimation of Systemic Risk Allocations
Even if the joint distribution of the loss random vector is known, the conditional distribution of given , denoted by , is typically too complicated to analytically calculate the systemic risk allocations . An alternative approach is to numerically estimate them by the MC method, as is done in Yamai and Yoshiba (2002) and Fan et al. (2012). To this end, assume that one can generate i.i.d. samples from . If , the MC estimator of , is constructed as follows:
- (1)
- Sample from : For a sample size , generate .
- (2)
- Estimate the crisis event: If the crisis event contains unknown quantities, replace them with their estimates based on . Denote by the estimated crisis event.
- (3)
- Sample from the conditional distribution of given : Among , determine such that for all .
- (4)
- Construct the MC estimator: The MC estimate of is where is the empirical cdf (ecdf) of the ’s.
For an example of (2), if the crisis event is , then and are unknown parameters, and thus they are replaced by and , where is the ecdf of the total loss for . By the law of large numbers (LLN) and the central limit theorem (CLT), the MC estimator of is consistent, and the approximate confidence interval of the true allocation can be constructed based on the asymptotic normality; see Glasserman (2005).
The MC cannot handle VaR crisis events if S admits a pdf, since , and thus, no subsample is picked in (3) above. A possible remedy (although the resulting estimator suffers from an inevitable bias) is to replace with for sufficiently small , so that .
The main advantage of MC for estimating systemic risk allocations is that only a random number generator for is required for implementing the method. Furthermore, MC is applicable for any choice of the crisis event as long as . Moreover, the main computational load is simulating in (1) above, which is typically not demanding. The disadvantage of the MC method is its inefficiency concerning the rare-event characteristics of and . To see this, consider the case where and for and . If the MC sample size is , there are subsamples resulting from (3). To estimate RVaR in (4) based on this subsample, only samples contribute to computing the estimate, which is generally not enough for statistical inference. This effect of sample size reduction is relaxed if ES and/or ES crisis events are considered, but is more problematic for the VaR crisis event since there is a trade-off concerning reducing bias and MC error when choosing ; see Koike and Minami (2019).
3. MCMC Estimation of Systemic Risk Allocations
To overcome the drawback of the MC method for estimating systemic risk allocations, we introduce MCMC methods, which simulate a given distribution by constructing a Markov chain whose stationary distribution is . In this section, we first briefly review MCMC methods, including the MH algorithm as a major subclass of MCMC methods, and then study how to construct an efficient MCMC estimator for the different choices of crisis events.
3.1. A Brief Review of MCMC
Let be a set and be a -algebra on E. A Markov chain is a sequence of E-valued random variables satisfying the Markov property for all , , and . A Markov chain is characterized by its stochastic kernel given by . A probability distribution satisfying for any and is called stationary distribution. Assuming has a density , the detailed balance condition (also known as the reversibility) with respect to is given by
and is known as a sufficient condition for the corresponding kernel K to have the stationary distribution ; see Chib and Greenberg (1995). MCMC methods simulate a distribution as a sample path of a Markov chain whose stationary distribution is the desired one. For a given distribution , also known as target distribution, and a functional , the quantity of interest is estimated by the MCMC estimator where is the empirical distribution constructed from a sample path of the Markov chain whose stationary distribution is . Under regularity conditions, the MCMC estimator is consistent and asymptotically normal; see Nummelin (2002), Nummelin (2004), and Meyn and Tweedie (2012). Its asymptotic variance can be estimated from by, for instance, the batch means estimator; see Jones et al. (2006), Geyer (2011) and Vats et al. (2015) for more details. Consequently, one can construct approximate confidence intervals for the true quantity based on a sample path of the Markov chain.
Since the target distribution is determined by the problem at hand, the problem is to find the stochastic kernel K having as the stationary distribution such that the corresponding Markov chain can be easily simulated. One of the most prevalent stochastic kernels is the Metropolis–Hastings (MH) kernel, defined by , where is the Dirac delta function; ; is a function called a proposal density such that is measurable for any and is a probability density for any ;
and . It can be shown that the MH kernel has stationary distribution ; see Tierney (1994). Simulation of the Markov chain with this MH kernel is conducted by the MH algorithm given in Algorithm 1.
| Algorithm 1 Metropolis–Hastings (MH) algorithm. |
| Require: Random number generator of the proposal density q(x,·) for all x ∈ E, x(0) ∈ supp(π) and the ratio π(y)/π(x) for x, y ∈ E, where π is the density of the stationary distribution. |
| Input: Sample size , proposal density q, and initial value . |
| Output: Sample path of the Markov chain. |
| for do |
| (1) Generate . |
| (2) Calculate the acceptance probability |
| (3) Generate and set . |
| end for |
An advantage of the MCMC method is that a wide variety of distributions can be simulated as a sample path of a Markov chain even if generating i.i.d. samples is not directly feasible. The price to pay is an additional computational cost to calculate the acceptance probability (4), and a possibly higher standard deviation of the estimator compared to the standard deviation of estimators constructed from i.i.d. samples. This attributes to the serial dependence among MCMC samples, which can be seen as follows. Suppose first that the candidate is rejected (so occurs). Then , and thus, the samples are perfectly dependent. The candidate is more likely to be accepted if the acceptance probability is close to 1. In this case, and are expected to be close to each other (otherwise, and thus can be small). Under the continuity of , and are expected to be close and thus dependent with each other. An efficient MCMC method is such that the candidate is sufficiently far from with the probability being as close to as possible. The efficiency of MCMC can indirectly be inspected through the acceptance rate (ACR) and the autocorrelation plot (ACP); ACR is the percentage of times a candidate is accepted among the N iterations, and ACP is the plot of the autocorrelation function of the generated sample path. An efficient MCMC method shows high ACR and steady decline in ACP; see Chib and Greenberg (1995) and Rosenthal et al. (2011) for details. Ideally, the proposal density q is constructed only based on , but typically, q is chosen among a parametric family of distributions. For such cases, simplicity of the choice of tuning parameters of q is also important.
3.2. MCMC Formulation for Estimating Systemic Risk Allocations
Numerous choices of proposal densities q are possible to construct an MH kernel. In this subsection, we consider how to construct an efficient MCMC method for estimating systemic risk allocations depending on the choice of the crisis event . Our goal is to directly simulate the conditional distribution by constructing a Markov chain whose stationary distribution is
provided . Samples from this distribution can directly be used to estimate systemic risk allocations with crisis event and arbitrary marginal risk measures . Other potential applications are outlined in Remark 2.
Remark 2
(Gini shortfall allocation). Samples from the conditional distribution can be used to estimate, for example, the tail-Gini coefficient for , and the Gini shortfall allocation (Furman et al. (2017)) , more efficiently than by applying the MC method. Another application is to estimate risk allocations derived by optimization, given a constant economic capital; see Laeven and Goovaerts (2004) and Dhaene et al. (2012).
We now construct an MH algorithm with target distribution (5). To this end, we assume that
- the ratio can be evaluated for any , and that
- the support of is or .
Regarding Assumption 1, the normalization constant of and the probability are not necessary to be known, since they cancel out in the numerator and the denominator of . In Assumption 2, the loss random vector refers to the profit&loss (P&L) if , and to pure losses if . Note that the case , is essentially included in the case of pure losses as long as the marginal risk measures are law invariant and translation invariant, and the crisis event is the set of linear constraints of Form (2). To see this, define , , and . Then and , where is the set of linear constraints with parameters and . By law invariance and translation invariance of ,
Therefore, the problem of estimating reduces to that of estimating for the shifted loss random vector (such that ) and the modified crisis event of the same form.
For the P&L case, the RVaR and ES crisis events are the set of linear constraints of Form (2) with the number of constraints and 1, respectively. In the case of pure losses, additional d constraints , are imposed, where is the jth d-dimensional unit vector. Therefore, the RVaR and ES crisis events are of Form (2) with and , respectively. For the VaR crisis event, , and thus, (5) cannot be properly defined. In this case, the allocation depends on the conditional joint distribution , but is completely determined by its first variables , since . Estimating systemic risk allocations under the VaR crisis event can thus be achieved by simulating the target distribution
where and the last equation is derived from the linear transformation with unit Jacobian. Note that other transformations are also possible; see Betancourt (2012). Under Assumption 1, the ratio can be evaluated and is not required to be known. In the case of pure losses, the target distribution is subject to d linear constraints , and , where the first constraints come from the non-negativity of the losses and the last one is from the indicator in (6). Therefore, the crisis event for is of Form (2). In the case of P&L, and holds for any . Therefore, the target distribution (6) is free from any constraints and the problem reduces to constructing an MCMC method with target distribution , . In this paper, the P&L case with VaR crisis event is not investigated further, since our focus is the simulation of constrained target distributions; see Koike and Minami (2019) for an MCMC estimation in the P&L case.
MCMC methods to simulate constrained target distributions require careful design of the proposal density q. A simple MCMC method is Metropolis–Hastings with rejection in which the support of the proposal density q may not coincide with that of the target distribution, which is the crisis event , and a candidate is immediately rejected when it violates the constraints. This construction of MCMC is often inefficient due to a low acceptance probability, especially around the boundary of . In this case, an efficient MCMC method can be expected only when the probability mass of is concentrated near the center of . In the following sections, we introduce two alternative MCMC methods for the constrained target distributions of interest, the HMC method and the GS. Each of them is applicable and can be efficient for different choices of the crisis event and underlying loss distribution functions .
3.3. Estimation with Hamiltonian Monte Carlo
We find that if the HMC method is applicable, it is typically the most preferable method to simulate constrained target distributions because of its efficiency and ease of handling constraints. In Section 3.3.1, we briefly present the HMC method with a reflection for constructing a Markov chain supported on the constrained space. In Section 3.3.2, we propose a heuristic for determining the parameters of the HMC method based on the MC presamples.
3.3.1. Hamiltonian Monte Carlo with Reflection
For the possibly unnormalized target density , consider the potential energy , kinetic energy , and the Hamiltonian defined by
with position variable , momentum variable , and kinetic energy density such that . In this paper, the kinetic energy distribution is set to be the multivariate standard normal with and ; other choices of are discussed in Appendix B.2. In the HMC method, a Markov chain augmented on the state space with the stationary distribution is constructed and the desired samples from are obtained as the first -dimensional margins. A process , on is said to follow the Hamiltonian dynamics if it follows the ordinary differential equation (ODE)
Through the Hamiltonian dynamics, the Hamiltonian H and the volume are conserved, that is, and the map has a unit Jacobian for any ; see Neal et al. (2011). Therefore, the value of the joint target density remains unchanged by the Hamiltonian dynamics, that is,
In practice, the dynamics (7) are discretized for simulation by, for example, the so-called leapfrog method summarized in Algorithm 2; see Leimkuhler and Reich (2004) for other discretization methods.
| Algorithm 2 Leapfrog method for Hamiltonian dynamics. |
| Input: Current states , stepsize , gradients and . |
| Output: Updated position . |
| (1) . |
| (2) . |
| (3) . |
Note that the evaluation of does not require the normalization constant of to be known, since . By repeating the leapfrog method T times with stepsize , the Hamiltonian dynamics are approximately simulated with length . Due to the discretization error, the Hamiltonian is not exactly preserved, while it is expected to be almost preserved for which is small enough. The discretization error is called the Hamiltonian error.
All the steps of the HMC method are described in Algorithm 3. In Step (1), the momentum variable is first updated from to , where follows the kinetic energy distribution so that the value of the Hamiltonian changes. In Step (3), the current state is moved along the level curve of by simulating the Hamiltonian dynamics.
| Algorithm 3 Hamiltonian Monte Carlo to simulate . |
| Require: Random number generator of FK, x(0) ∈ supp(π), π(y)/π(x), x, y ∈ E and FK(p’)/FK(p), p, p’ ∈ ℝd. |
| Input: Sample size , kinetic energy density , target density , gradients of the potential and kinetic energies and , stepsize , integration time and initial position . |
| Output: Sample path of the Markov chain. |
| for do |
| (1) Generate . |
| (2) Set . |
| (3) for ,
|
| end for |
| (4) . |
| (5) Calculate . |
| (6) Set for . |
| end for |
By flipping the momentum in Step (4), the HMC method is shown to be reversible w.r.t. (c.f. (3)) and thus to have the stationary distribution ; see Neal et al. (2011) for details. Furthermore, by the conservation property of the Hamiltonian dynamics, the acceptance probability in Step (5) is expected to be close to 1. Moreover, by taking T as sufficiently large, the candidate is expected to be sufficiently decorrelated from the current position . Consequently, the resulting Markov chain is expected to be efficient.
The remaining challenge for applying the HMC method to our problem of estimating systemic risk allocations is how to handle the constraint . As we have seen in Section 2.1 and Section 3.2, is assumed to be an intersection of linear constraints with parameters , describing hyperplanes. Following the ordinary leapfrog method, a candidate is immediately rejected when the trajectory of the Hamiltonian dynamics penetrates one of these hyperplanes. To avoid it, we modify the leapfrog method according to the reflection technique introduced in Afshar and Domke (2015) and Chevallier et al. (2018). As a result, the trajectory is reflected when it hits a hyperplane and the Markov chain moves within the constrained space with probability one. Details of the HMC method with the reflection for our application are described in Appendix A.
3.3.2. Choice of Parameters for HMC
HMC requires as input two parameters, the stepsize , and the integration time T. As we now explain, neither of them should be chosen too large nor too small. Since the stepsize controls the accuracy of the simulation of the Hamiltonian dynamics, needs to be small enough to approximately conserve the Hamiltonian; otherwise, the acceptance probability can be much smaller than 1. On the other hand, an which is too small requires the integration time T to be large enough for the trajectory to reach a farther distance, which is computationally costly. Next, the integration time T needs to be large enough to decorrelate the candidate state with the current state. Meanwhile, the trajectory of the Hamiltonian dynamics may make a U-turn and come back to the starting point if the integration time T is too long; see Neal et al. (2011) for an illustration of this phenomenon.
A notable characteristic of our problem of estimating systemic risk allocations is that the MC sample from the target distribution is available but its sample size may not be sufficient for statistical inference, and, in the case of the VaR crisis event, the samples only approximately follow the target distribution. We utilize the information of this MC presample to build a heuristic for determining the parameters ; see Algorithm 4.
In this heuristic, the initial stepsize is set to be for some constant , say, . This scale was derived in Beskos et al. (2010) and Beskos et al. (2013) under certain assumptions on the target distribution. We determine through the relationship with the acceptance probability. In Step (2-2-2-1) of Algorithm 4, multiple trajectories are simulated, starting from each MC presample with the current stepsize . In the next Step (2-2-2-2), we monitor the acceptance probability and the distance between the starting and ending points while extending the trajectories. Based on the asymptotic optimal acceptance probability 0.65 (c.f. Gupta et al. (1990) and Betancourt et al. (2014)) as , we set the target acceptance probability as
The stepsize is gradually decreased in Step (2-1) of Algorithm 4 until the minimum acceptance probability calculated in Step (2-3) exceeds . To prevent the trajectory from a U-turn, in Step (2-2-2-3), each trajectory is immediately stopped when the distance begins to decrease. The resulting integration time is set to be the average of these turning points, as seen in Step (3). Note that other termination conditions of extending trajectories are possible; see Hoffman and Gelman (2014) and Betancourt (2016).
| Algorithm 4 Heuristic for determining the stepsize and integration time T. |
| Input: MC presample , gradients and , target acceptance probability , initial constant and the maximum integration time ( and are set as default values). |
| Output: Stepsize and integration time T. |
| (1) Set and . |
| (2) while |
| (2-1) Set . |
| (2-2) for |
| (2-2-1) Generate . |
| (2-2-2) for |
| (2-2-2-1) Set for . |
| (2-2-2-2) Calculate
|
| (2-2-2-3) if and , break and set . |
| end for |
| end for |
| (2-3) Compute . |
| end while |
| (3) Set . |
At the end of this section, we briefly revisit the choice of the kinetic energy distribution , which is taken to be a multivariate standard normal throughout this work. As discussed in Neal et al. (2011), applying the HMC method with target distribution and kinetic energy distribution is equivalent to applying HMC with the standardized target distribution and , where L is the Cholesky factor of such that . By taking to be the covariance matrix of , the standardized target distribution becomes uncorrelated with unit variances. In our problem, the sample covariance matrix calculated based on the MC presample is used alternatively. The new target distribution where denotes the Jacobian of , is almost uncorrelated with unit variances, and thus the standard normal kinetic energy fits well; see Livingstone et al. (2019). If the crisis event consists of the set of linear constraints , , then the standardized target density is also subject to the set of linear constraints , . Since the ratio can still be evaluated under Assumption 1, we conclude that the problem remains unchanged after standardization.
Theoretical results of the HMC method with normal kinetic energy are available only when is bounded (Cances et al. (2007) and Chevallier et al. (2018)), or when is unbounded and the tail of is roughly as light as that of the normal distribution (Livingstone et al. (2016) and Durmus et al. (2017)). Boundedness of holds for VaR and RVaR crisis events with pure losses; see Koike and Minami (2019). As is discussed in this paper, convergence results of MCMC estimators are accessible when the density of the underlying joint loss distribution is bounded from above on , which is typically the case when the underlying copula does not admit lower tail dependence. For other cases where is unbounded or the density explodes on , no convergence results are available. Potential remedies for the HMC method to deal with heavy-tailed target distributions are discussed in Appendix B.2.
3.4. Estimation with Gibbs Sampler
As discussed in Section 3.3.2, applying HMC methods to heavy-tailed target distributions on unbounded crisis events is not theoretically supported. To deal with this case, we introduce the GS in this section.
3.4.1. True Gibbs Sampler for Estimating Systemic Risk Allocations
The GS is a special case of the MH method in which the proposal density q is completely determined by the target density via
where is the -dimensional vector that excludes the components from , is the conditional density of the jth variable of given all the other components, is the so-called index set, and is the index probability distribution such that . For this choice of q, the acceptance probability is always equal to 1; see Johnson (2009). The GS is called deterministic scan (DSGS) if and . When the index set is the set of permutations of , the GS is called random permulation (RPGS). Finally, the random scan GS (RSGS) has the proposal (8) with and with probabilities such that . These three GSs can be shown to have as stationary distribution; see Johnson (2009).
Provided that the full conditional distributions , can be simulated, the proposal distribution (8) can be simulated by first selecting an index with probability and then replacing the jth component of the current state with a sample from sequentially for . The main advantage of the GS is that the tails of are naturally incorporated via full conditional distributions, and thus the MCMC method is expected to be efficient even if is heavy-tailed. On the other hand, the applicability of the GS is limited to target distributions such that is available. Moreover, fast simulators of , , are required, since the computational time linearly increases w.r.t. the dimension d.
In our problem of estimating systemic risk allocations, we find that the GS is applicable when the crisis event is of the form
The RVaR crisis event is obviously a special case of (9), and the ES crisis event is included as a limiting case for . Furthermore, the full conditional copulas of the underlying joint loss distribution and their inverses are required to be known as we now explain. Consider the target density . For its jth full conditional density , notice that
and thus, for , , we obtain the cdf of as
for . Denoting the denominator of (10) by , we obtain the quantile function
Therefore, if and its quantile function are available, one can simulate the full conditional target densities with the inversion method; see Devroye (1985). Availability of and its inverse typically depends on the copula of . By Sklar’s theorem (1), the jth full conditional distribution of can be written as
where , and is the jth full conditional copula defined by
where D denotes the operator of partial derivatives with respect to the components given as subscripts and . Assuming the full conditional copula and its inverse are available, one can simulate via
Examples of copulas for which the full conditional distributions and their inverses are available include normal, Student t, and Clayton copulas; see Cambou et al. (2017). In this case, the GS is also applicable to the corresponding survival (-rotated) copula , since
by the relationship for . In a similar way, one can also obtain full conditional copulas and their inverses for other rotated copulas; see Hofert et al. (2018) Section 3.4.1 for rotated copulas.
In the end, we remark that even if the full conditional distributions and their inverses are not available, can be simulated by, for example, the acceptance and rejection method, or even the MH algorithm; see Appendix B.3.
3.4.2. Choice of Parameters for GS
As discussed in Section 3.3.2, we use information from the MC presamples to determine the parameters of the Gibbs kernel (8). Note that standardization of the variables as applied in the HMC method in Section 3.3.2 is not available for the GS, since the latter changes the underlying joint loss distribution, and since the copula after rotating variables is generally not accessible, except for in the elliptical case; see Christen et al. (2017). Among the presented variants of GSs, we adopt RSGS, since determining d probabilities is relatively easy, whereas RPGS requires probabilities to be determined. To this end, we consider the RSGS with the parameters determined by a heuristic described in Algorithm 5.
| Algorithm 5 Random scan Gibbs sampler (RSGS) with heuristic to determine . |
| Require: Random number generator of πj|−j and x(0) ∈ supp(π). |
| Input: MC presample , sample size , initial state , sample size of the pre-run and the target autocorrelation ( and are set as default values). |
| Output:N sample path of the Markov chain. |
| (1) Compute the sample covariance matrix based on . |
| (2) Set and . |
| (3) for |
| (3-1) Generate with probability . |
| (3-2) Update and . |
| end for |
| (4) Set
|
| (5) for , |
| (5-1) Generate with probability . |
| (5-2) Update and . |
| end for |
The RSGS kernel is simulated in Steps (3) and (5) of Algorithm 5. To determine the selection probabilities , consider a one-step update of the RSGS from to with and the one-step kernel
Liu et al. (1995, Lemma 3) implies that
where is the kth moment of .
For the objective function , its minimizer under the constraint satisfies
While this optimizer can be computed based on the MC presamples, we observed that its stable estimation is as computationally demanding as estimating the risk allocations themselves. Alternatively, we calculate (11) under the assumption that follows an elliptical distribution. Under this assumption, (11) is given by
where is the covariance matrix of and , is the submatrix of with indices in . As seen in Step (2) of Algorithm 5, is replaced by its estimate based on the MC presamples.
As shown in Christen et al. (2017), Gibbs samplers require a large number of iterations to lower the serial correlation when the target distribution has strong dependence. To reduce serial correlations, we take every Tth sample in Step (5-2), where is called the thinning interval of times. Note that we use the same notation T as that of the integration time in HMC, since they both represent a repetition time of some single step. Based on the preliminary run with length in Step (3) in Algorithm 5, T is determined as the smallest lag h such that the marginal autocorrelations with lag h are all smaller than the target autocorrelation ; see Step (4) in Algorithm 5.
4. Numerical Experiments
In this section, we demonstrate the performance of the MCMC methods for estimating systemic risk allocations by a series of numerical experiments. We first conduct a simulation study in which true allocations or their partial information are available. Then, we perform an empirical study to demonstrate that our MCMC methods are applicable to a more practical setup. Finally, we make more detailed comparisons between the MC and MCMC methods in various setups. All experiments were run on a MacBook Air with 1.4 GHz Intel Core i5 processor and 4 GB 1600 MHz of DDR3 RAM.
4.1. Simulation Study
In this simulation study, we compare the estimates and standard errors of the MC and MCMC methods under the low-dimensional risk models described in Section 4.1.1. The results and discussions are summarized in Section 4.1.2.
4.1.1. Model Description
We consider the following three-dimensional loss distributions:
- (M1)
- generalized Pareto distributions (GPDs) with parameters and survival Clayton copula with parameter so that Kendall’s tau equals ;
- (M2)
- multivariate Student t distribution with degrees of freedom, location vector , and dispersion matrix , where and for , .
Since the marginals are homogeneous and the copula is exchangeable, the systemic risk allocations under the loss distribution (M1) are all equal, provided that the crisis event is invariant under the permutation of the variables. For the loss distribution (M2), by ellipticality of the joint distribution, analytical formulas of risk contribution-type systemic risk allocations are available; see McNeil et al. (2015) Corollary 8.43. The parameters of the distributions (M1) and (M2) take into account the stylized facts that the loss distribution is heavy-tailed and extreme losses are positively dependent.
We consider the VaR, RVaR, and ES crisis events with confidence levels , and , respectively. For each crisis event, the risk contribution, VaR, RVaR, and ES-type systemic risk allocations are estimated by the MC and MCMC methods, where the parameters of the marginal risk measures VaR, RVaR, and ES are set to be , and , respectively.
We first conduct the MC simulation for the distributions (M1) and (M2). For the VaR crisis event, the modified event with is used to ensure that . Based on these MC presamples, the Markov chains are constructed as described in Section 3.3 and Section 3.4. For the MCMC method, (M1) is the case of pure losses and (M2) is the case of P&L. Therefore, the HMC method is applied to the distribution (M1) for the VaR and RVaR crisis events, the GS is applied to (M1) for the ES crisis event and the GS is applied to the distribution (M2) for the RVaR and ES crisis events. The target distribution of (M2) with VaR constraint is free from constraints and was already investigated in Koike and Minami (2019); we thus omit this case and consider the five remaining cases.
Note that 99.8% of the MC samples from the unconditional distribution are discarded for the VaR crisis event and a further 97.5% of them are wasted to estimate the RVaR contributions. Therefore, MC samples are required to obtain one MC sample from the conditional distribution. Taking this into account, the sample size of the MC estimator is set to be . The sample size of the MCMC estimators is free from such constraints and thus is chosen to be . Initial values for the MCMC methods are taken as the mean vector calculated from the MC samples. Biases are computed only for the contribution-type allocations in the distribution (M2) since the true values are available in this case. For all the five cases, the MC and the MCMC standard errors are computed according to Glasserman (2013) Chapter 1, for MC, and Jones et al. (2006) for MCMC. Asymptotic variances of the MCMC estimators are estimated by the batch means estimator with batch length and batch size . The results are summarized in Table 1 and Table 2.

Table 1.
Estimates and standard errors for the MC and HMC estimators of risk contribution, RVaR, VaR, and ES-type systemic risk allocations under (I) the VaR crisis event, and (II) the RVaR crisis event for the loss distribution (M1). The sample size of the MC method is , and that of the HMC method is . The acceptance rate (ACR), stepsize , integration time T, and run time are ACR , , , and run time mins in Case (I), and ACR , , , and run time mins in Case (II).

Table 2.
Estimates and standard errors for the MC and the GS estimators of risk contribution, VaR, RVaR, and ES-type systemic risk allocations under (III) distribution (M1) and the ES crisis event, (IV) distribution (M2), and the RVaR crisis event, and (V) distribution (M2) and ES crisis event. The sample size of the MC method is and that of the GS is . The thinning interval of times T, selection probability and run time are , and run time secs in Case (III), , and run time secs in Case (IV) and , and run time secs in Case (V).
4.1.2. Results and Discussions
Since a fast random number generators are available for the joint loss distributions (M1) and (M2), the MC estimators are computed almost instantly. On the other hand, the MCMC methods cost around 1.5 min for simulating the MCMC samples, as reported in Table 1 and Table 2. For the HMC method, the main computational cost consists of calculating gradients times for the leapfrog method, and calculating the ratio of target densities N times in the acceptance/rejection step, where N is the length of the sample path and T is the integration time. For the GS, simulating an N-sample path requires random numbers from the full conditional distributions, where T here is the thinning interval of times. Therefore, the computational time of the GS linearly increases w.r.t. the dimension d, which can become prohibitive for the GS in high dimensions. To save computational time, MCMC methods generally require careful implementations of calculating the gradients and the ratio of the target densities for HMC, and of simulating the full conditional distributions for GS.
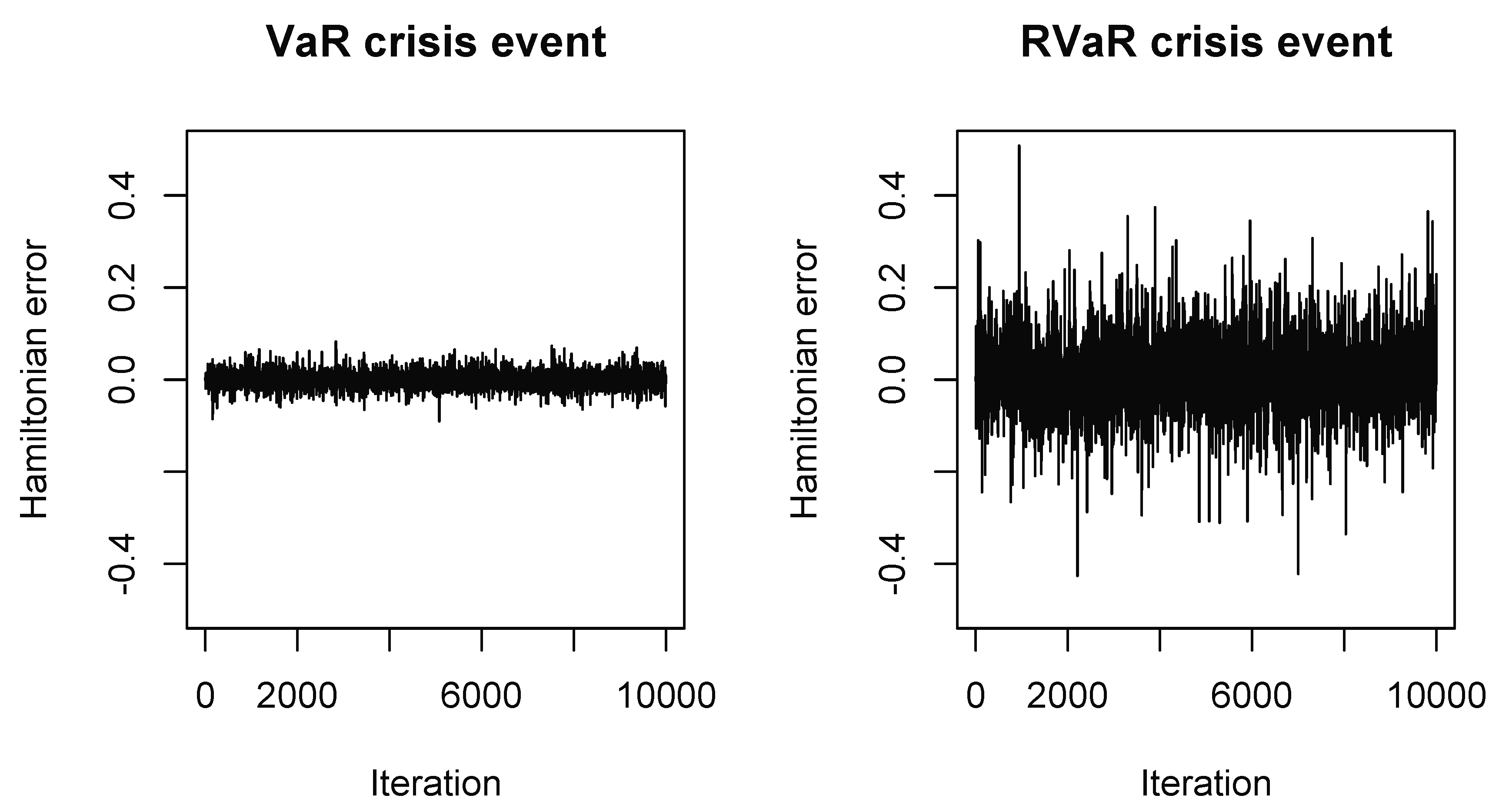
Next, we inspect the performance of the HMC and GS methods. We observed that the autocorrelations of all sample paths steadily decreased below 0.1 if lags were larger than 15. Together with the high ACRs, we conclude that the Markov chains can be considered to be converged. According to the heuristic in Algorithm 4, the stepsize and integration time for the HMC method are selected to be in Case (I) and in Case (II). As indicated by the small Hamiltonian errors in Figure 1, the acceptance rates in both cases are quite close to 1.
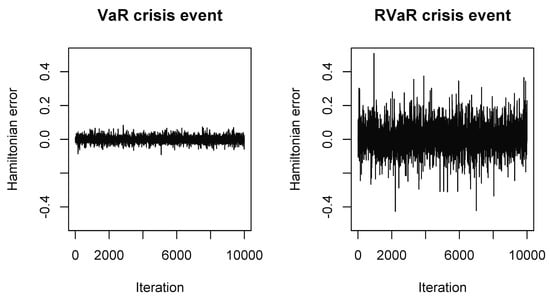
Figure 1.
Hamiltonian errors of the HMC methods for estimating systemic risk allocations with VaR (left) and RVaR (right) crisis events for the loss distribution (M1). The stepsize and integration time are set to be in Case (I) and in Case (II).
For the GS, the thinning interval of times T and the selection probability are determined as and in Case (III), and in Case (IV) and and in Case (V). For biases of the estimators, observe that in all cases ((I) to (V)), the estimates of the MC method and the MCMC method are close to each other. In Cases (I), (II), and (III), the true allocations are the homogeneous allocations, whereas their exact values are not known. From the estimates in Table 1 and Table 2, the MCMC estimates are, on average, more equally allocated compared to those of the MC method, especially in Case (III) where heavy-tailedness may lead to quite slow convergence rates of the MC method. Therefore, lower biases of the MCMC estimators are obtained, compared to those of the MC estimators. In the case of risk contributions in Case (IV) and (V), exact biases are computed based on ellipticality, and they show that the GS estimator has a smaller bias than the one of the MC estimator.
Although the MC sample size is 10 times larger than that of the MCMC method, the standard error of the latter is, in most cases, smaller than the MC standard error. This improvement becomes larger as the probability of the crisis event becomes smaller. The largest improvement is observed in Case (I) with the VaR crisis event, and the smallest one is in Cases (III) and (V) with the ES crisis event. MCMC estimates of the risk contribution-type allocations have consistently smaller standard errors than the MC ones. For the RVaR, VaR, and ES-type allocations, the improvement of standard error varies according to the loss models and the crisis event. A notable improvement is observed for ES-type allocation in Case (III), although a stable statistical inference is challenging due to the heavy-tailedness of the target distribution.
Overall, the simulation study shows that the MCMC estimators outperform the MC estimators due to the increased effective sample size and its insusceptibility to the probability of the crisis event. The MCMC estimators are especially recommended when the probability of the crisis event is too small for the MC method to sufficiently simulate many samples for a meaningful statistical analysis.
Remark 3
(Joint loss distributions with negative dependence in the tail). In the above simulation study, we only considered joint loss distributions with positive dependence. Under the existence of positive dependence, the target density puts more probability mass around its mean, and the probability decays as the point moves away from the mean, since positive dependence among prevents them from going in opposite directions (i.e., one component increases and another one decreases) under the sum constraint; see Koike and Minami (2019) for details. This phenomenon leads to the target distributions being more centered and elliptical, which in turn facilitates efficient moves of Markov chains. Although it may not be realistic, joint loss distributions with negative dependence in the tail are also possible. In this case, the target distribution has more variance, heavy tails, and is even multimodal, since two components can move in opposite directions under the sum constraint. For such cases, constructing efficient MCMC methods becomes more challenging; see Lan et al. (2014) for a remedy for multimodal target distributions with Riemannian manifold HMC.
4.2. Empirical Study
In this section, we illustrate our suggested MCMC methods for estimating risk allocations from insurance company indemnity claims. The dataset consists of 1500 liability claims provided by the Insurance Services Office. Each claim contains an indemnity payment and an allocated loss adjustment expense (ALAE) ; see Hogg and Klugman (2009) for a description. The joint distribution of losses and expenses is studied, for example, in Frees and Valdez (1998) and Klugman and Parsa (1999). Based on Frees and Valdez (1998), we adopt the following parametric model:
(M3) univariate marginals are and with and , and the copula is the survival Clayton copula with parameter (which corresponds to Spearman’s rho ).
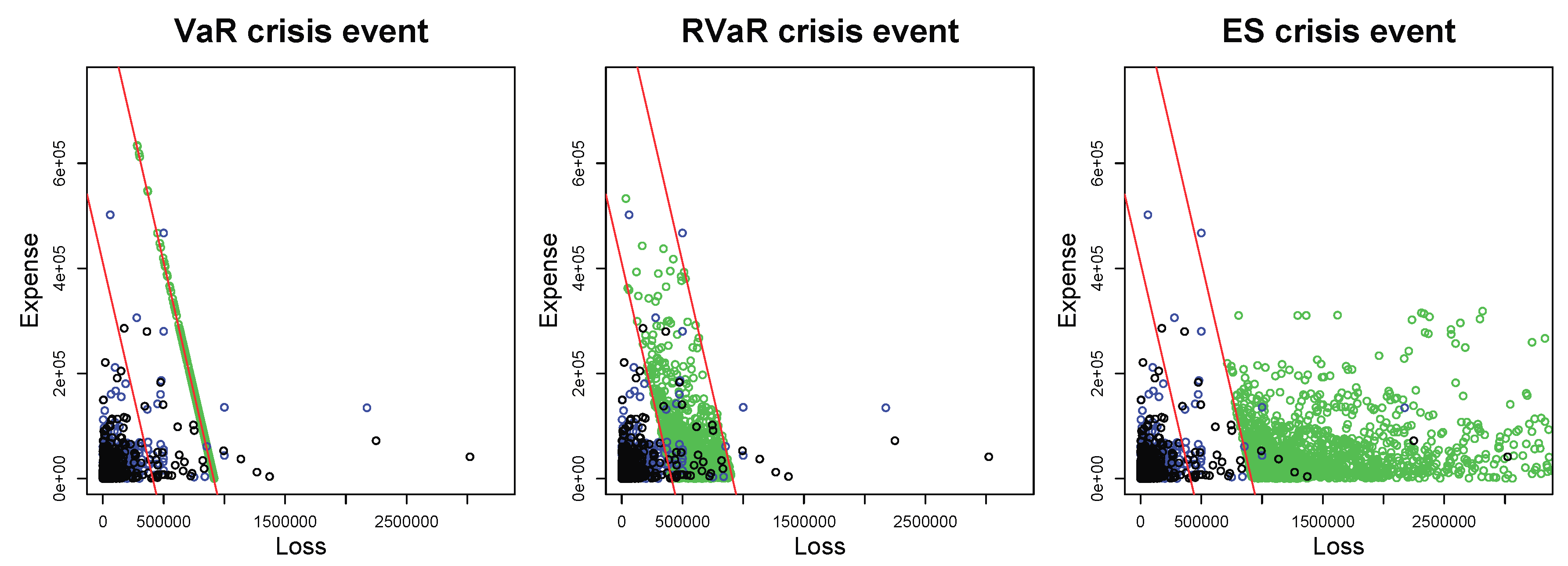
Note that in the loss distribution (M3), the Gumbel copula used in Frees and Valdez (1998) is replaced by the survival Clayton copula, since both of them have the same type of tail dependence and the latter possesses more computationally tractable derivatives. The parameter of the survival Clayton copula is determined so that it reaches the same Spearman’s rho observed in Frees and Valdez (1998). Figure 2 illustrates the data and samples from the distribution (M3). Our goal is to calculate the VaR, RVaR, and ES-type allocations with VaR, RVaR, and ES crisis events for the same confidence levels as in Section 4.1.1. We apply the HMC method to all three crisis events since, due to the infinite and finite variances of and , respectively, the optimal selection probability of the second variable calculated in Step 2 of Algorithm 5 is quite close to 0, and thus the GS did not perform well. The simulated HMC samples are illustrated in Figure 2. The results of estimating the systemic risk allocations are summarized in Table 3.
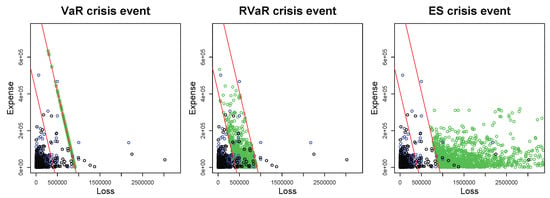
Figure 2.
Plots of MCMC samples (green) with VaR (left), RVaR (center), and ES (right) crisis events. All plots include the data and the MC samples with sample size in black and blue dots, respectively. The red lines represent and where and are the MC estimates of and , respectively, for and .

Table 3.
Estimates and standard errors for the MC and HMC estimators of RVaR, VaR, and ES-type systemic risk allocations under the loss distribution (M3) with the (I) VaR crisis event, (II) RVaR crisis event, and (III) ES crisis event. The MC sample size is , and that of the HMC method is . The acceptance rate (ACR), stepsize , integration time T, and run time are ACR , , and run time min in Case (I), ACR , , and run time min in Case (II), ACR , , and run time min in Case (III).
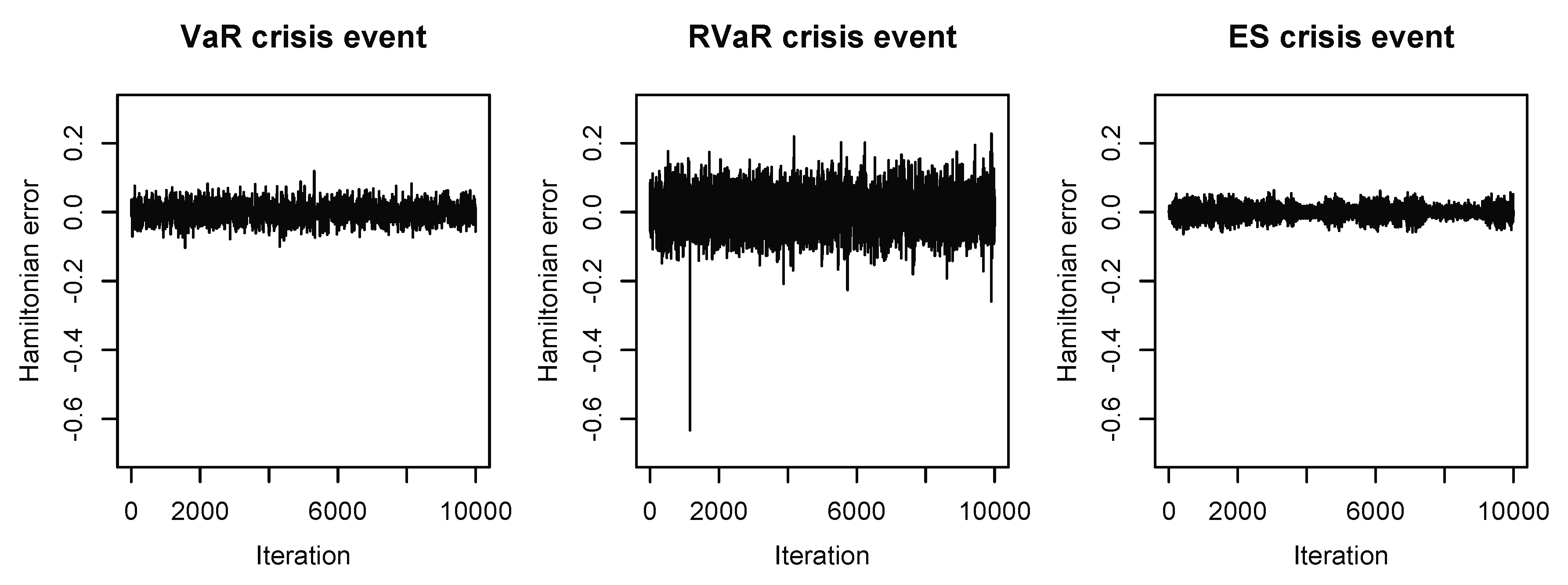
The HMC samples shown in Figure 2 indicate that the conditional distributions of interest are successfully simulated from the desired regions. As displayed in Figure 3, the Hamiltonian errors of all three HMC methods are sufficiently small, which led to the high ACRs of , , and , as listed in Table 3. We also observed that autocorrelations of all sample paths steadily decreased below 0.1 if lags were larger than 80. Together with the high ACRs, we conclude that the Markov chains can be considered to be converged. Due to the heavy-tailedness of the target distribution in the case of the ES crisis event, the stepsize is very small and the integration time is very large compared to the former two cases of the VaR and RVaR crisis events. As a result, the HMC algorithm in this case has a long run time.
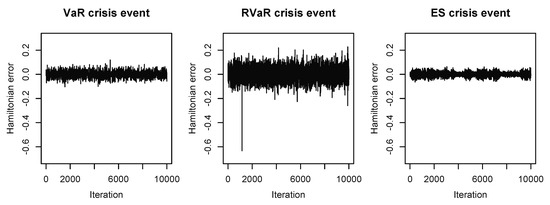
Figure 3.
Hamiltonian errors of the HMC methods for estimating systemic risk allocations with VaR, RVaR, and ES crisis events for the loss distribution (M3). The stepsize and the integration time are chosen as , and , respectively.
The estimates of the MC and HMC methods are close in all cases, except Case (III). In Case (III), the HMC estimates are smaller than the MC ones in almost all cases. Based on the much smaller standard errors of HMC, one could infer that the MC estimates are likely overestimating the allocations due to a small number of extremely large losses, although the corresponding conditional distribution is extremely heavy-tailed, and thus no estimation method might be reliable. In terms of the standard error, the estimation of systemic risk allocations by the HMC method were improved in Cases (I) and (III) compared to that of the MC method; the MC standard errors are slightly smaller than those of HMC in Case (II). All results considered, we conclude from this empirical study that the MCMC estimators outperform the MC estimators in terms of standard error. On the other hand, as indicated by the theory of HMC with normal kinetic energy, the HMC method is not recommended for heavy-tailed target distributions due to the long computational time caused by a small stepsize and large integration time determined by Algorithm 5.
4.3. Detailed Comparison of MCMC with MC
In the previous numerical experiments, we fixed the dimensions of the portfolios and confidence levels of the crisis events. Comparing the MC and MCMC methods after balancing against computational time might be more reasonable, although one should keep in mind that run time depends on various external factors, such as the implementation, hardware, workload, programming language, or compiler options (and our implementation was not optimized for any of these factors). In this section, we compare the MC and MCMC methods with different dimensions, confidence levels, and parameters of the HMC methods in terms of bias, standard error, and the mean squared error (MSE), adjusted by run time.
In this experiment, we fix the sample size of the MC and MCMC methods as . In addition, we assume , that is, the joint loss follows the multivariate Student t distribution with degrees of freedom, location vector , and dispersion matrix P, which is the correlation matrix with all off-diagonal entries equal to . The dimension d of the loss portfolio will vary for comparison. We consider only risk contribution-type systemic risk allocations under VaR, RVaR, and ES crisis events, as true values of these allocations are available to compare against; see McNeil et al. (2015), Corollary 8.43. If b and denote the bias and standard deviation of the MC or MCMC estimator and S the run time, then (under the assumption that run time linearly increases by sample size) we define the time-adjusted MSEs by
We can then compare the MC and MCMC estimators in terms of bias, standard error, and time-adjusted MSE under the following three scenarios:
- (A)
- VaR, RVaR, and ES contributions are estimated by the MC, HMC, and GS methods for dimensions . Note that the GS is applied only to RVaR and ES contributions, not to VaR contributions (same in the other scenarios).
- (B)
- For , VaR, RVaR and ES contributions are estimated by the MC, HMC, and GS methods for confidence levels , and .
- (C)
- For , VaR, RVaR and ES contributions are estimated by the MC and HMC methods with the parameters (determined by Algorithm 4) and .
In the MC method, the modified VaR contribution with is computed. Moreover, if the size of the conditional sample for estimating RVaR and ES contributions is less than 100, then the lower confidence level of the crisis event is subtracted by 0.01, so that at least 100 MC presamples are guaranteed. For the sample paths of the MCMC methods, ACR, ACP, and Hamiltonian errors for the HMC methods were inspected and the convergences of the chains were checked, as in Section 4.1 and Section 4.2.
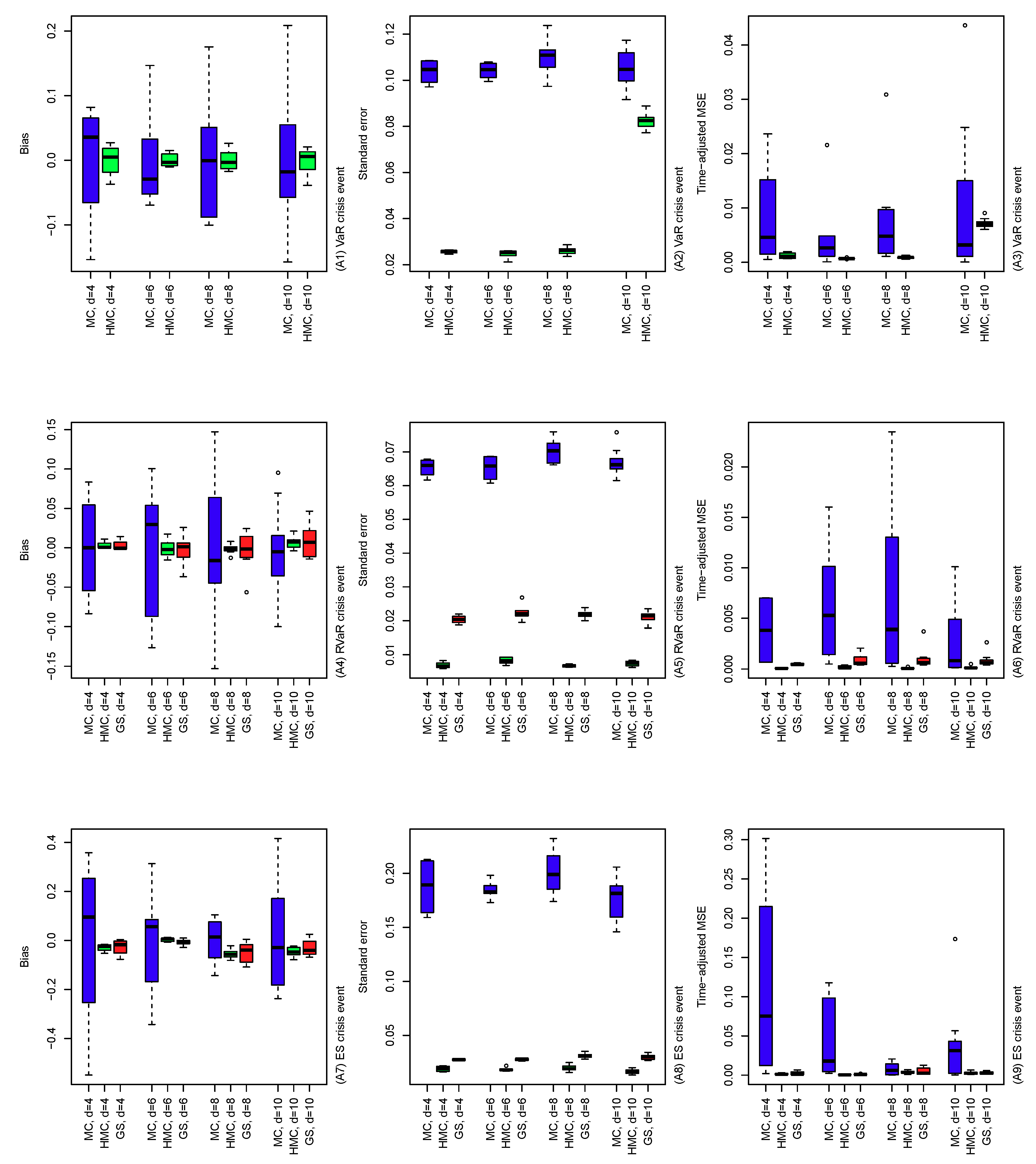
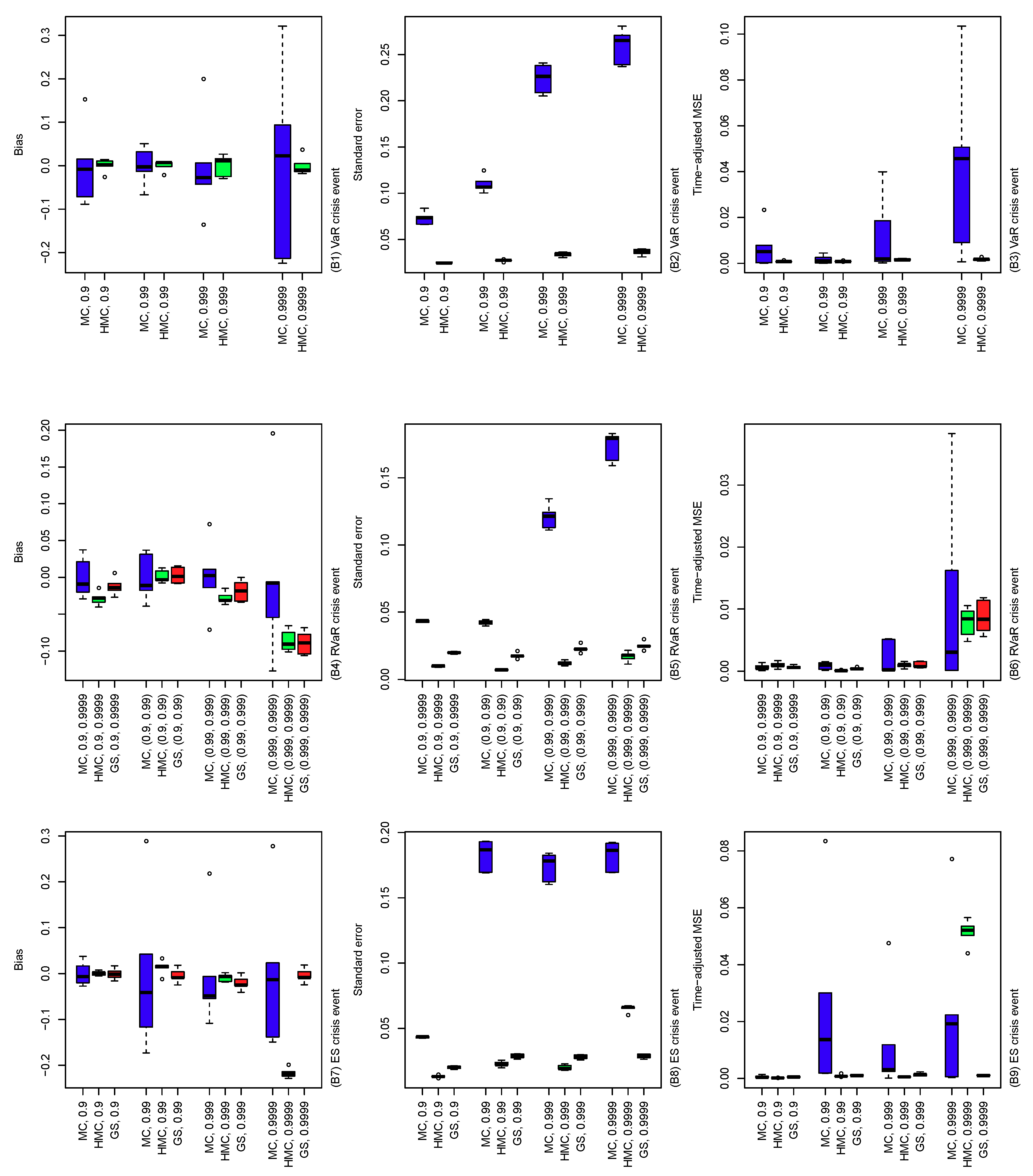
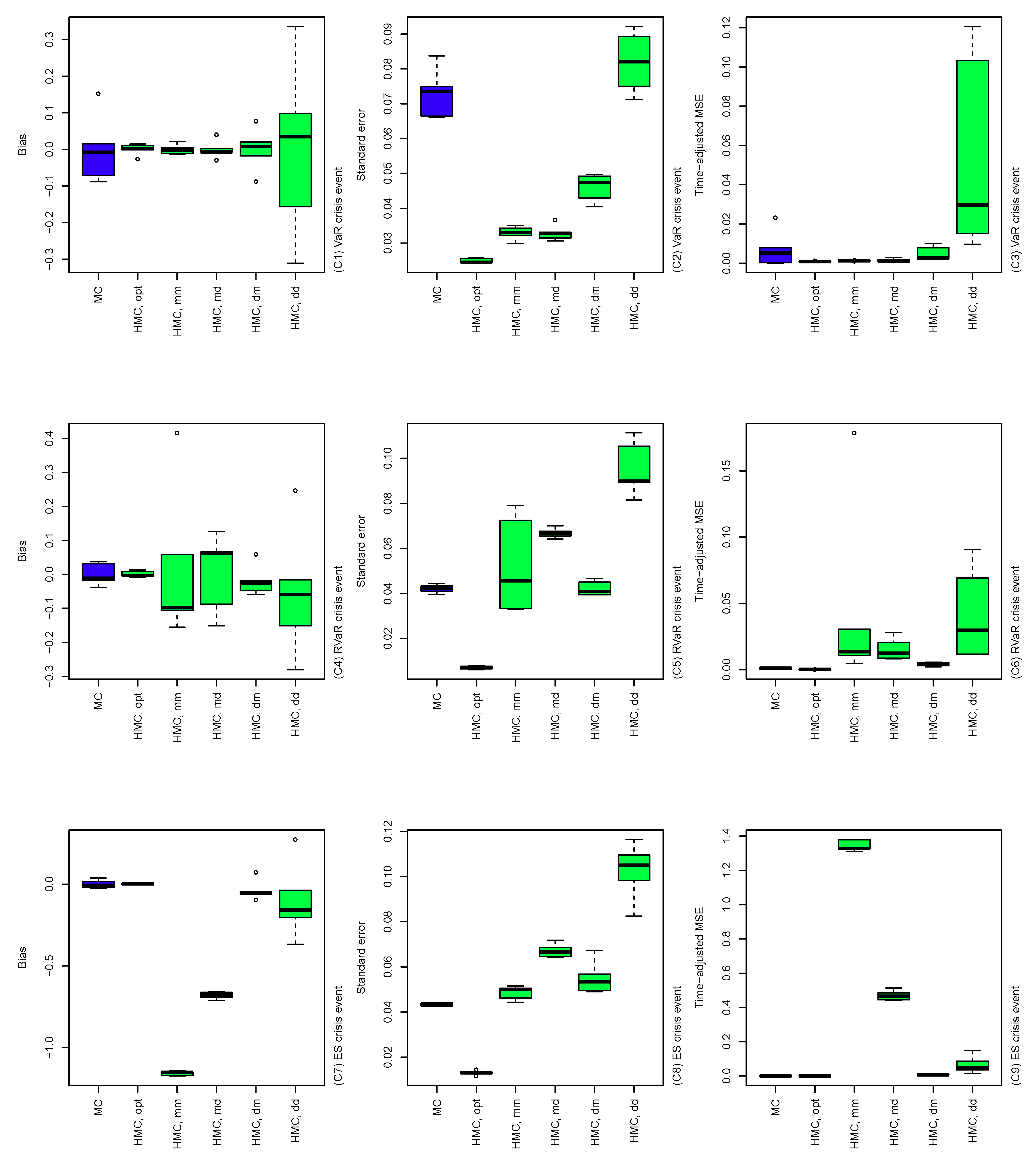
The results of the comparisons of (A), (B), and (C) are summarized in Figure 4, Figure 5 and Figure 6. In Figure 4, the performance of the MC, HMC, and GS estimators is roughly similar across dimensions from 4 to 10. For all crisis events, the HMC and GS estimators outperform MC in terms of bias, standard error, and time-adjusted MSE. From (A5) and (A8), standard errors of the GS estimators are slightly higher than those of the HMC ones, which result in slightly improved performance of the HMC estimator over the GS in terms of MSE. In Figure 5, bias, standard error, and MSE of the MC estimator tend to increase as the probability of the conditioning set decreases. This is simply because the size of the conditional samples in the MC method decreases proportionally to the probability of the crisis event. On the other hand, the HMC and GS estimators provide a stably better performance than MC since such sample size reduction does not occur. As seen in (B4) to (B9) in the cases of RVaR and ES, however, if the probability of the conditioning event is too small and/or the distribution of the MC presample is too different from the original conditional distribution of interest, then the parameters of the HMC method determined by Algorithm 4 can be entirely different from the optimal, which leads to a poor performance of the HMC method, as we will see in the next scenario (C). In Figure 6, the HMC method with optimally determined parameters from Algorithm 4 is compared to non-optimal parameter choices. First, the optimal HMC estimator outperforms MC in terms of bias, standard error, and time-adjusted MSE. On the other hand, from the plots in Figure 6, we see that some of the non-optimal HMC estimators are significantly worse than MC. Therefore, a careful choice of the parameters of the HMC method is required to obtain an improved performance of the HMC method compared to MC.
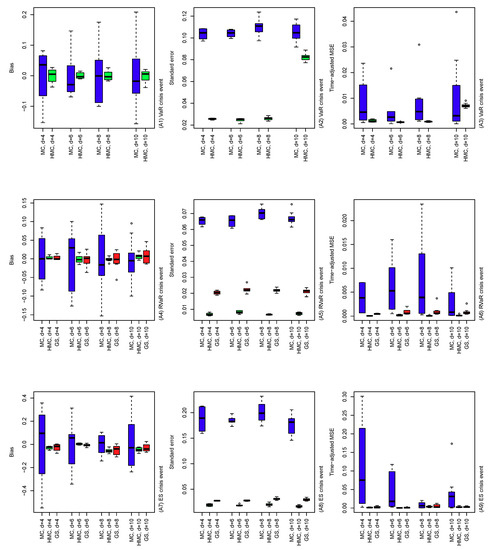
Figure 4.
Bias (left), standard error (middle) and time-adjusted mean squared error (right) of the MC, HMC, and GS estimators of risk contribution-type systemic risk allocations under VaR (top), RVaR (middle), and ES (bottom) crisis events. The underlying loss distribution is , where , and for portfolio dimensions . Note that the GS method is applied only to RVaR and ES contributions.
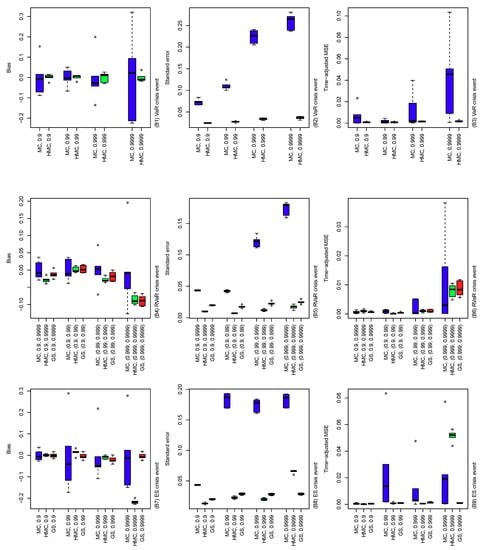
Figure 5.
Bias (left), standard error (middle), and time-adjusted mean squared error (right) of the MC, HMC, and GS estimators of risk contribution-type systemic risk allocations with the underlying loss distribution , where , , and . The crisis event is taken differently, as VaR (top), RVaR (middle) and ES (bottom) for confidence levels , , and . Note that the GS method is applied only to RVaR and ES contributions.
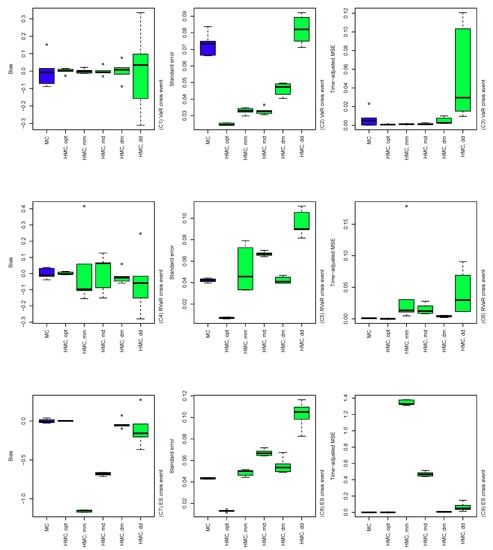
Figure 6.
Bias (left), standard error (middle), and time-adjusted mean squared error (right) of the MC and HMC estimators of risk contribution-type systemic risk allocations under VaR, RVaR, and ES crisis events. The underlying loss distribution is , where , , and . The parameters of the HMC method are taken as determined by Algorithm 4 and . In the labels of the x-axes, each of the five cases and is denoted by HMC.opt, HMC.mm, HMC.md, HMC.dm, and HMC.dd, respectively.
5. Conclusion, Limitations and Future Work
Efficient calculation of systemic risk allocations is a challenging task, especially when the crisis event has a small probability. To solve this problem for models where a joint loss density is available, we proposed MCMC estimators where a Markov chain is constructed with the conditional loss distribution, given the crisis event as the target distribution. By using HMC and GS, efficient simulation methods from the constrained target distribution were obtained and the resulting MCMC estimator was expected to have a smaller standard error compared to that of the MC estimator. Sample efficiency is significantly improved, since the MCMC estimator is computed from samples generated directly from the conditional distribution of interest. Another advantage of the MCMC method is that its performance is less sensitive to the probability of the crisis event, and thus to the confidence levels of the underlying risk measures. We also proposed a heuristic for determining the parameters of the HMC method based on the MC presamples. Numerical experiments demonstrated that our MCMC estimators are more efficient than MC in terms of bias, standard error, and time-adjusted MSE. Stability of the MCMC estimation with respect to the probability of the crisis event and efficiency of the optimal parameter choice of the HMC method were also investigated in the experiments.
Based on the results in this paper, our MCMC estimators can be recommended when the probability of the crisis event is too small for MC to sufficiently simulate many samples for a statistical analysis and/or when unbiased systemic risk allocations under the VaR crisis event are required. The MCMC methods are likely to perform well when the dimension of the portfolio is less than or around 10, losses are bounded from the left, and the crisis event is of VaR or RVaR type; otherwise, heavy-tailedness and computational time can become challenging. Firstly, a theoretical convergence result of the HMC method is typically not available when the target distribution is unbounded and heavy-tailed, which is the case when the losses are unbounded and/or the crisis event is of ES type; see the case of the ES crisis event in the empirical study in Section 4.2. Secondly, both the HMC and GS methods suffer from high-dimensional target distributions since the algorithms contain parts of steps where the computational cost linearly increases in dimension. We observed that, in this case, although the MCMC estimator typically improves bias and standard error compared to MC, the improvement vanishes in terms of time-adjusted MSE due to the long computational time of the MCMC method. Finally, multimodality of joint loss distributions and/or the target distribution is also an undesirable feature since full conditional distributions and their inverses (which are required to implement the GS) are typically unavailable in the former case, and the latter case prevents the HMC method from efficiently exploring the entire support of the target distribution. Potential remedies for heavy-tailed and/or high-dimensional target distributions are the HMC method with a non-normal kinetic energy distribution and roll-back HMC; see Appendix B for details. Further investigation of HMC methods and faster methods for determining the HMC parameters are left for future work.
Supplementary Materials
An R script for reproducing the numerical experiments conducted in this paper is available at http://www.mdpi.com/2227-9091/8/1/6/s1.
Author Contributions
Conceptualization, T.K.; methodology, T.K.; formal analysis, T.K.; investigation, T.K. and M.H.; resources, T.K.; data curation, T.K.; writing—original draft preparation, T.K.; writing—review and editing, M.H.; visualization, T.K. and M.H.; supervision, M.H.; project administration, T.K.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSERC through Discovery Grant RGPIN-5010-2015.
Acknowledgments
We wish to thank to an associate editor and anonymous referees for their careful reading of the manuscript and their insightful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| i.i.d. | Independent and identically distributed |
| Probability distribution function | |
| cdf | Cumulative distribution function |
| ecdf | Empirical cdf |
| GPD | Generalized Pareto distribution |
| MSE | Mean squared error |
| LLN | Law of large numbers |
| CLT | Central limit theorem |
| VaR | Value-at-Risk |
| RVaR | Range VaR |
| ES | Expected shortfall |
| MES | Marginal expected shortfall |
| CoVaR | Conditional VaR |
| CoES | Conditional ES |
| MC | Monte Carlo |
| SMC | Sequential Monte Carlo |
| MCMC | Markov chain Monte Carlo |
| ACR | Acceptance rate |
| ACP | Autocorrelation plot |
| MH | Metropolis–Hastings |
| GS | Gibbs sampler |
| MGS | Metropolized Gibbs sampler |
| DSGS | Deterministic scan GS |
| RPGS | Random permutation GS |
| RSGS | Random scan GS |
| HMC | Hamiltonian Monte Carlo |
| RBHMC | Roll-back HMC |
| RMHMC | Riemannian manifold HMC |
| ALAE | Allocated loss adjustment expense |
| P&L | Profit and loss |
Appendix A. Hamiltonian Dynamics with Boundary Reflection
In this appendix, we describe details of the HMC method with boundary reflection, as mentioned in Section 3.3.1. Let be the hyperplane which the trajectory of the Hamiltonian dynamics hit at . At this time, is immediately replaced by where is the reflected momentum defined by
where and are such that and and are parallel and perpendicular to the hyperplane , respectively. Afshar and Domke (2015) and Chevallier et al. (2018) showed that the map preserves the volume and the Hamiltonian, and that this modified HMC method has the stationary distribution . As long as the initial position belongs to , the trajectory of the HMC method never violates the constraint . The algorithm of this HMC method with reflection is obtained by replacing the Leapfrog function call in Step (3) of Algorithm 3 by Algorithm A1. Accordingly, the parameters of the hyperplanes need to be passed as input to Algorithm 3.
In Step (3-1) of Algorithm A1 the time at which the trajectory hits the boundary is computed. If for some , then the chain hits the boundary during the dynamics with length . At the smallest time among such hitting times, the chain reflects from to against the corresponding boundary as described in Step (3-2-1) of Algorithm A1. The remaining length of the dynamics is and Step (3) is repeated until the remaining length becomes zero. Other techniques of reflecting the dynamics are discussed in Appendix B.1.
| Algorithm A1 Leapfrog method with boundary reflection. |
| Input: Current state , stepsize , gradients and , and constraints , . |
| Output: Updated state . |
| (1) Update . |
| (2) Set , . |
| (3) while |
| (3-1) Compute
|
| (3-2) if for any , |
| (3-2-1) Set
|
| (3-2-2) Set . |
| else |
| (3-2-3) Set and . |
| end if |
| end while |
| (4) Set and . |
Appendix B. Other MCMC Methods
In this appendix, we introduce some advanced MCMC techniques potentially applicable to the problem of estimating systemic risk allocations.
Appendix B.1. Roll-Back HMC
Yi and Doshi-Velez (2017) proposed roll-back HMC (RBHMC), in which the indicator function in the target distribution (5) is replaced by a smooth sigmoid function so that the Hamilotonian dynamics naturally move back inwards when the trajectory violates the constraints. HMC with reflection presented in Section 3.3.1 requires to check M boundary conditions at every iteration of the Hamiltonian dynamics. In our problem the number M linearly increases with the dimension d in the case of pure losses, which leads to a linear increase in the computational cost. The RBHMC method avoids such explicit boundary checks, and thus can reduce the computational cost of the HMC method with constrained target distributions. Despite saving computational time, we observed that the RBHMC method requires a careful choice of the stepsize and the smoothness parameter of the sigmoid function involved, and we could not find any guidance on how to choose them to guarantee a stable performance.
Appendix B.2. Riemannian Manifold HMC
Livingstone et al. (2019) indicated that non-normal kinetic energy distributions can potentially deal with heavy-tailed target distributions. In fact, the kinetic energy distribution can even be dependent on the position variable . For example, when for a positive definite matrix and , the resulting HMC method is known as Riemannian manifold HMC (RMHMC) since this case is equivalent to applying HMC on the Riemannian manifold with metric ; see Girolami and Calderhead (2011). Difficulties in implementing RMHMC are in the choice of metric G and in the simulation of the Hamiltonian dynamics. Due to the complexity of the Hamiltonian dynamics, simple discretization schemes such as the leapfrog method are not applicable, and the trajectory is updated implicitly by solving some system of equations; see Girolami and Calderhead (2011). Various choices of the metric G are studied in Betancourt (2013), Lan et al. (2014) and Livingstone and Girolami (2014) for different purposes. Simulation of RMHMC is studied, for example, in Byrne and Girolami (2013).
Appendix B.3. Metropolized Gibbs Samplers
Müller (1992) introduced the Metropolized Gibbs sampler (MGS) in which the proposal density q in the MH kernel is set to be where has the same marginal distributions as but a different copula for which and are available so that the GS can be applied to simulate this proposal. This method can be used when the inversion method is not feasible since or are not available. Following the MH algorithm, the candidate is accepted with the acceptance probability (4), which can be simply written as
As an example of the MGS, suppose C is the Gumbel copula, for which the full conditional distributions cannot be inverted analytically. One could then choose the survival Clayton copula as the proposal copula above. For this choice of copula, is available by the inversion method as discussed in Section 3.4.1. Furthermore, the acceptance probability is expected to be high especially on the upper tail part because the upper threshold copula of C defined as , , , is known to converge to that of a survival Clayton copula when , ; see Juri and Wüthrich (2002), Juri and Wüthrich (2003), Charpentier and Segers (2007) and Larsson and Nešlehová (2011).
References
- Acharya, Viral V., Lasse H. Pedersen, Thomas Philippon, and Matthew Richardson. 2017. Measuring systemic risk. The Review of Financial Studies 30: 2–47. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. Covar. The American Economic Review 106: 1705. [Google Scholar] [CrossRef]
- Afshar, Hadi Mohasel, and Justin Domke. 2015. Reflection, refraction, and hamiltonian monte carlo. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 3007–15. [Google Scholar]
- Asimit, Alexandru V., Edward Furman, Qihe Tang, and Raluca Vernic. 2011. Asymptotics for risk capital allocations based on conditional tail expectation. Insurance: Mathematics and Economics 49: 310–24. [Google Scholar] [CrossRef]
- Asimit, Alexandru V., and Jinzhu Li. 2018. Systemic risk: An asymptotic evaluation. ASTIN Bulletin: The Journal of The IAA 48: 673–98. [Google Scholar] [CrossRef]
- Bernardi, Mauro, Fabrizio Durante, and Piotr Jaworski. 2017. Covar of families of copulas. Statistics & Probability Letters 120: 8–17. [Google Scholar]
- Beskos, Alexandros, Natesh Pillai, Gareth Roberts, Jesus-Maria Sanz-Serna, and Andrew Stuart. 2010. The acceptance probability of the hybrid monte carlo method in high-dimensional problems. AIP Conference Proceedings 1281: 23–6. [Google Scholar]
- Beskos, Alexandros, Natesh Pillai, Gareth Roberts, Jesus-Maria Sanz-Serna, and Andrew Stuart. 2013. Optimal tuning of the hybrid monte carlo algorithm. Bernoulli 19: 1501–34. [Google Scholar] [CrossRef]
- Betancourt, Michael. 2012. Cruising the simplex: Hamiltonian monte carlo and the dirichlet distribution. AIP Conference Proceedings 1443: 157–64. [Google Scholar]
- Betancourt, Michael. 2013. A general metric for riemannian manifold hamiltonian monte carlo. In International Conference on Geometric Science of Information. New York: Springer, pp. 327–34. [Google Scholar]
- Betancourt, Michael. 2016. Identifying the optimal integration time in hamiltonian monte carlo. arXiv arXiv:1601.00225. [Google Scholar]
- Betancourt, Michael. 2017. A conceptual introduction to hamiltonian monte carlo. arXiv arXiv:1701.02434. [Google Scholar]
- Betancourt, Michael, Simon Byrne, and Mark Girolami. 2014. Optimizing the integrator step size for hamiltonian monte carlo. arXiv arXiv:1411.6669. [Google Scholar]
- Byrne, Simon, and Mark Girolami. 2013. Geodesic monte carlo on embedded manifolds. Scandinavian Journal of Statistics 40: 825–45. [Google Scholar] [CrossRef] [PubMed]
- Cambou, Mathieu, Marius Hofert, and Christiane Lemieux. 2017. Quasi-random numbers for copula models. Statistics and Computing 27: 1307–29. [Google Scholar] [CrossRef]
- Cances, Eric, Frédéric Legoll, and Gabriel Stoltz. 2007. Theoretical and numerical comparison of some sampling methods for molecular dynamics. ESAIM: Mathematical Modelling and Numerical Analysis 41: 351–89. [Google Scholar] [CrossRef]
- Charpentier, Arthur, and Johan Segers. 2007. Lower tail dependence for archimedean copulas: Characterizations and pitfalls. Insurance: Mathematics and Economics 40: 525–32. [Google Scholar] [CrossRef]
- Chen, Chen, Garud Iyengar, and Ciamac C. Moallemi. 2013. An axiomatic approach to systemic risk. Management Science 59: 1373–88. [Google Scholar] [CrossRef]
- Chevallier, Augustin, Sylvain Pion, and Frédéric Cazals. 2018. Hamiltonian Monte Carlo With Boundary Reflections, and Application To Polytope Volume Calculations. Available online: https://hal.archives-ouvertes.fr/hal-01919855/ (accessed on 8 January 2020).
- Chib, Siddhartha, and Edward Greenberg. 1995. Understanding the Metropolis–Hastings algorithm. The American Statistician 49: 327–35. [Google Scholar]
- Chiragiev, Arthur, and Zinoviy Landsman. 2007. Multivariate pareto portfolios: Tce-based capital allocation and divided differences. Scandinavian Actuarial Journal 2007: 261–80. [Google Scholar] [CrossRef]
- Christen, J. Andrés, Colin Fox, and Mario Santana-Cibrian. 2017. Optimal direction gibbs sampler for truncated multivariate normal distributions. Communications in Statistics-Simulation and Computation 46: 2587–600. [Google Scholar] [CrossRef]
- Denault, Michel. 2001. Coherent allocation of risk capital. Journal of Risk 4: 1–34. [Google Scholar] [CrossRef]
- Devroye, Luc. 1985. Non-Uniform Random Variate Generation. New York: Springer. [Google Scholar]
- Dhaene, Jan, Luc Henrard, Zinoviy Landsman, Antoine Vandendorpe, and Steven Vanduffel. 2008. Some results on the cte-based capital allocation rule. Insurance: Mathematics and Economics 42: 855–63. [Google Scholar] [CrossRef]
- Dhaene, Jan, Andreas Tsanakas, Emiliano A. Valdez, and Steven Vanduffel. 2012. Optimal capital allocation principles. Journal of Risk and Insurance 79: 1–28. [Google Scholar] [CrossRef]
- Duane, Simon, Anthony D. Kennedy, Brian J. Pendleton, and Duncan Roweth. 1987. Hybrid monte carlo. Physics Letters B 195: 216–22. [Google Scholar] [CrossRef]
- Durmus, Alain, Eric Moulines, and Eero Saksman. 2017. On the convergence of hamiltonian monte carlo. arXiv arXiv:1705.00166. [Google Scholar]
- Fan, Guobin, Yong Zeng, and Woon K. Wong. 2012. Decomposition of portfolio var and expected shortfall based on multivariate copula simulation. International Journal of Management Science and Engineering Management 7: 153–60. [Google Scholar] [CrossRef]
- Frees, Edward W., and Emiliano A. Valdez. 1998. Understanding relationships using copulas. North American Actuarial Journal 2: 1–25. [Google Scholar] [CrossRef]
- Furman, Edward, Alexey Kuznetsov, and Ričardas Zitikis. 2018. Weighted risk capital allocations in the presence of systematic risk. Insurance: Mathematics and Economics 79: 75–81. [Google Scholar] [CrossRef]
- Furman, Edward, and Zinoviy Landsman. 2008. Economic capital allocations for non-negative portfolios of dependent risks. ASTIN Bulletin: The Journal of the IAA 38: 601–19. [Google Scholar] [CrossRef][Green Version]
- Furman, Edward, Ruodu Wang, and Ričardas Zitikis. 2017. Gini-type measures of risk and variability: Gini shortfall, capital allocations, and heavy-tailed risks. Journal of Banking & Finance 83: 70–84. [Google Scholar]
- Furman, Edward, and Ričardas Zitikis. 2008. Weighted risk capital allocations. Insurance: Mathematics and Economics 43: 263–9. [Google Scholar] [CrossRef]
- Furman, Edward, and Ričardas Zitikis. 2009. Weighted pricing functionals with applications to insurance: An overview. North American Actuarial Journal 13: 483–96. [Google Scholar] [CrossRef]
- Gelfand, Alan E., and Adrian F. M. Smith. 1990. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association 85: 398–409. [Google Scholar] [CrossRef]
- Gelfand, Alan E., Adrian F. M. Smith, and Tai-Ming Lee. 1992. Bayesian analysis of constrained parameter and truncated data problems using gibbs sampling. Journal of the American Statistical Association 87: 523–32. [Google Scholar] [CrossRef]
- Geman, Stuart, and Donald Geman. 1984. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6: 721–41. [Google Scholar] [CrossRef]
- Geweke, John. 1991. Efficient simulation from the multivariate normal and student-t distributions subject to linear constraints and the evaluation of constraint probabilities. In Computing Science and Statistics: Proceedings of the 23rd Symposium on the Interface. Fairfax: Interface Foundation of North America, Inc., pp. 571–8. [Google Scholar]
- Geyer, Charles. 2011. Introduction to markov chain monte carlo. In Handbook of Markov Chain Monte Carlo. New York: Springer, pp. 3–47. [Google Scholar]
- Girardi, Giulio, and A. Tolga Ergün. 2013. Systemic risk measurement: Multivariate garch estimation of covar. Journal of Banking & Finance 37: 3169–80. [Google Scholar]
- Girolami, Mark, and Ben Calderhead. 2011. Riemann manifold langevin and hamiltonian monte carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73: 123–214. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2005. Measuring marginal risk contributions in credit portfolios. Journal of Computational Finance 9: 1–41. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2013. Monte Carlo Methods in Financial Engineering. New York: Springer. [Google Scholar]
- Glasserman, Paul, and Jingyi Li. 2005. Importance sampling for portfolio credit risk. Management Science 51: 1643–56. [Google Scholar] [CrossRef]
- Gourieroux, Christian, and Alain Monfort. 2013. Allocating systemic risk in a regulatory perspective. International Journal of Theoretical and Applied Finance 16: 1350041. [Google Scholar] [CrossRef]
- Gudmundsson, Thorbjörn, and Henrik Hult. 2014. Markov chain monte carlo for computing rare-event probabilities for a heavy-tailed random walk. Journal of Applied Probability 51: 359–76. [Google Scholar] [CrossRef]
- Gupta, Sourendu, A. Irbäc, Frithjof Karsch, and Bengt Petersson. 1990. The acceptance probability in the hybrid monte carlo method. Physics Letters B 242: 437–43. [Google Scholar] [CrossRef]
- Hastings, W. Keith. 1970. Monte carlo sampling methods using markov chains and their applications. Biometrika 57: 97–109. [Google Scholar] [CrossRef]
- Hofert, Marius, Ivan Kojadinovic, Martin Mächler, and Jun Yan. 2018. Elements of Copula Modeling with R. New York: Springer Use R! Series. [Google Scholar] [CrossRef]
- Hoffman, Matthew D., and Andrew Gelman. 2014. The no-u-turn sampler: Adaptively setting path lengths in hamiltonian monte carlo. Journal of Machine Learning Research 15: 1593–623. [Google Scholar]
- Hoffmann, Hannes, Thilo Meyer-Brandis, and Gregor Svindland. 2016. Risk-consistent conditional systemic risk measures. Stochastic Processes and Their Applications 126: 2014–37. [Google Scholar] [CrossRef]
- Hogg, Robert V., and Stuart A. Klugman. 2009. Loss Distributions. Hoboken: John Wiley & Sons, Volume 249. [Google Scholar]
- Jaworski, Piotr. 2017. On conditional value at risk (covar) for tail-dependent copulas. Dependence Modeling 5: 1–19. [Google Scholar] [CrossRef]
- Johnson, Alicia A. 2009. Geometric Ergodicity of Gibbs Samplers. Available online: https://conservancy.umn.edu/handle/11299/53661 (accessed on 8 January 2020).
- Jones, Galin L., Murali Haran, Brian S. Caffo, and Ronald Neath. 2006. Fixed-width output analysis for markov chain monte carlo. Journal of the American Statistical Association 101: 1537–47. [Google Scholar] [CrossRef]
- Juri, Alessandro, and Mario V. Wüthrich. 2002. Copula convergence theorems for tail events. Insurance: Mathematics and Economics 30: 405–20. [Google Scholar] [CrossRef]
- Juri, Alessandro, and Mario V. Wüthrich. 2003. Tail dependence from a distributional point of view. Extremes 6: 213–46. [Google Scholar] [CrossRef]
- Kalkbrener, Michael, Hans Lotter, and Ludger Overbeck. 2004. Sensible and efficient capital allocation for credit portfolios. Risk 17: S19–S24. [Google Scholar]
- Klugman, Stuart A., and Rahul Parsa. 1999. Fitting bivariate loss distributions with copulas. Insurance: Mathematics and Economics 24: 139–48. [Google Scholar] [CrossRef]
- Koike, Takaaki, and Mihoko Minami. 2019. Estimation of risk contributions with mcmc. Quantitative Finance 19: 1579–97. [Google Scholar] [CrossRef]
- Kromer, Eduard, Ludger Overbeck, and Konrad Zilch. 2016. Systemic risk measures on general measurable spaces. Mathematical Methods of Operations Research 84: 323–57. [Google Scholar] [CrossRef]
- Laeven, Roger J. A., and Marc J. Goovaerts. 2004. An optimization approach to the dynamic allocation of economic capital. Insurance: Mathematics and Economics 35: 299–319. [Google Scholar] [CrossRef]
- Lan, Shiwei, Jeffrey Streets, and Babak Shahbaba. 2014. Wormhole hamiltonian monte carlo. In Twenty-Eighth AAAI Conference on Artificial Intelligence. Available online: https://www.aaai.org/ocs/index.php/AAAI/AAAI14/paper/viewPaper/8437 (accessed on 8 January 2020).
- Larsson, Martin, and Johanna Nešlehová. 2011. Extremal behavior of archimedean copulas. Advances in Applied Probability 43: 195–216. [Google Scholar] [CrossRef]
- Leimkuhler, Benedict, and Sebastian Reich. 2004. Simulating Hamiltonian Dynamics. Cambridge: Cambridge University Press, Volume 14. [Google Scholar]
- Liu, Jun S., Wing H. Wong, and Augustine Kong. 1995. Covariance structure and convergence rate of the gibbs sampler with various scans. Journal of the Royal Statistical Society: Series B (Methodological) 57: 157–69. [Google Scholar] [CrossRef]
- Livingstone, Samuel, Michael Betancourt, Simon Byrne, and Mark Girolami. 2016. On the geometric ergodicity of hamiltonian monte carlo. arXiv arXiv:1601.08057. [Google Scholar]
- Livingstone, Samuel, Michael F. Faulkner, and Gareth O. Roberts. 2019. Kinetic energy choice in hamiltonian/hybrid monte carlo. Biometrika 106: 303–19. [Google Scholar] [CrossRef]
- Livingstone, Samuel, and Mark Girolami. 2014. Information-geometric markov chain monte carlo methods using diffusions. Entropy 16: 3074–102. [Google Scholar] [CrossRef]
- Mainik, Georg, and Eric Schaanning. 2014. On dependence consistency of covar and some other systemic risk measures. Statistics & Risk Modeling 31: 49–77. [Google Scholar]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Metropolis, Nicholas, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, and Edward Teller. 1953. Equation of state calculations by fast computing machines. The Journal of Chemical Physics 21: 1087–92. [Google Scholar] [CrossRef]
- Meyn, Sean P., and Richard L. Tweedie. 2012. Markov Chains and Stochastic Stability. New York: Springer. [Google Scholar]
- Müller, Peter. 1992. Alternatives to the Gibbs Sampling Scheme. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.48.5613 (accessed on 8 January 2020).
- Neal, Radford M. 2011. Mcmc using hamiltonian dynamics. Handbook of Markov Chain Monte Carlo 2: 2. [Google Scholar]
- Nelsen, Roger B. 2006. An Introduction to Copulas. New York: Springer. [Google Scholar]
- Nummelin, Esa. 2002. Mc’s for mcmc’ists. International Statistical Review 70: 215–40. [Google Scholar] [CrossRef]
- Nummelin, Esa. 2004. General Irreducible Markov Chains and Non-Negative Operators. Cambridge: Cambridge University Press. [Google Scholar]
- Pakman, Ari, and Liam Paninski. 2014. Exact hamiltonian monte carlo for truncated multivariate gaussians. Journal of Computational and Graphical Statistics 23: 518–42. [Google Scholar] [CrossRef]
- Rodriguez-Yam, Gabriel, Richard A. Davis, and Louis L. Scharf. 2004. Efficient gibbs sampling of truncated multivariate normal with application to constrained linear regression. Unpublished manuscript. [Google Scholar]
- Rosenthal, Jeffrey S. 2011. Optimal proposal distributions and adaptive mcmc. In Handbook of Markov Chain Monte Carlo. Edited by Steve Brooks, Andrew Gelman, Galin Jones and Xiao-Li Meng. Boca Raton: CRC Press. [Google Scholar]
- Ruján, Pál. 1997. Playing billiards in version space. Neural Computation 9: 99–122. [Google Scholar] [CrossRef]
- Siller, Thomas. 2013. Measuring marginal risk contributions in credit portfolios. Quantitative Finance 13: 1915–23. [Google Scholar] [CrossRef]
- Targino, Rodrigo S., Gareth W. Peters, and Pavel V. Shevchenko. 2015. Sequential monte carlo samplers for capital allocation under copula-dependent risk models. Insurance: Mathematics and Economics 61: 206–26. [Google Scholar] [CrossRef]
- Tasche, Dirk. 1995. Risk Contributions and Performance Measurement. Working Paper. München: Techische Universität München. [Google Scholar]
- Tasche, Dirk. 2001. Conditional expectation as quantile derivative. arXiv arXiv:math/0104190. [Google Scholar]
- Tasche, Dirk. 2008. Capital allocation to business units and sub-portfolios: The euler principle. In Pillar II in the New Basel Accord: The Challenge of Economic Capital. Edited by Andrea Resti. London: Risk Books, pp. 423–53. [Google Scholar]
- Tierney, Luke. 1994. Markov chains for exploring posterior distributions. The Annals of Statistics 1994: 1701–28. [Google Scholar] [CrossRef]
- Vats, Dootika, James M. Flegal, and Galin L. Jones. 2015. Multivariate output analysis for markov chain monte carlo. arXiv arXiv:1512.07713. [Google Scholar]
- Vernic, Raluca. 2006. Multivariate skew-normal distributions with applications in insurance. Insurance: Mathematics and Economics 38: 413–26. [Google Scholar] [CrossRef]
- Yamai, Yasuhiro, and Toshinao Yoshiba. 2002. Comparative analyses of expected shortfall and value-at-risk: Their estimation error, decomposition, and optimization. Monetary and Economic Studies 20: 87–121. [Google Scholar]
- Yi, Kexin, and Finale Doshi-Velez. 2017. Roll-back hamiltonian monte carlo. arXiv arXiv:1709.02855. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).