No-Arbitrage Principle in Conic Finance

Abstract

In a one price economy, the Fundamental Theorem of Asset Pricing (FTAP) establishes that no-arbitrage is equivalent to the existence of an equivalent martingale measure. Such an equivalent measure can be derived as the normal unit vector of the hyperplane that separates the attainable gain subspace and the convex cone representing arbitrage opportunities. However, in two-price financial models (where there is a bid–ask price spread), the set of attainable gains is not a subspace anymore. We use convex optimization, and the conic property of this region to characterize the “no-arbitrage” principle in financial models with the bid–ask price spread present. This characterization will lead us to the generation of a set of price factor random variables. Under such a set, we can find the lower and upper bounds (supper-hedging and sub-hedging bounds) for the price of any future cash flow. We will show that for any given cash flow, for which the price is outside the above range, we can build a trading strategy that provides one with an arbitrage opportunity. We will generalize this structure to any two-price finite-period financial model.

1. Introduction

It has been known for a long time (Harrison and Kreps 1979; Harrison and Pliska 1981; Delbaen and Schachermayer 1994) that no-arbitrage opportunity in a one price economy is equivalent to the existence of an equivalent martingale measure. This result is usually referred to as the Fundamental Theorem of Asset Pricing (FTAP). Rogers (1994) used a directional derivative argument to provide a discrete-time proof for FTAP. The case of trading continuously, in particular, was discussed by Harrison and Pliska (1981).

In practice, the law of one price often does not hold. Recently, the literature on transaction costs and the study of no-arbitrage in the presence of bid–ask spreads has been expanding (Jouini and Kallal 1995; Bion-Nadal 2009; Guasoni et al. 2011). Madan (2012) considers financial equilibrium where there are two separate prices at which one may buy from or sell to the market known as ask and bid prices. This is a realistic situation in financial markets. Inside an efficient market, at a given time, a financial security trades at a unique price. The equilibrium conditions that are needed to provide a unique price all depend on arbitrage opportunities that are quickly exploited. A wide category of financial securities trade in vast and diverse markets and few of them meet the equilibrium conditions we mentioned earlier. Market clearing becomes troubling, which leads to prices that are not unique for equivalent securities in different markets. Whenever the above conditions are not satisfied, the “law of one price“ fails to hold. On the other hand, an incomplete market can also take place even under the assumption of “one price”. Incomplete condition explains that there exists the presence of some residual risks that can not be eliminated regardless of the existence of the best hedging (Eberlein et al. 2009; Jacka 1992). In addition, the markets establish a phenomenon that is not anticipated in the one price theory called illiquidity. Illiquidity can be explained as the lack of ability of the market to establish a unique price, that is, to eliminate the spread between the bid and ask prices. This happens when there is an absence of information and/or a lack of interested parties. In these situations, the bid and ask prices are the only real market information that can be observed. Thus, the theoretical framework that has been used to explain the one price market is not accurate enough to deal with many situations one faces in practice.

We adopt the framework of “conic finance“ in this paper. Some earlier studies that use the theory of conic finance include Madan (2012); Cherny and Madan (2010); Eberlein and Madan (2009, 2012); Eberlein et al. (2011). The direction of trade is what distinguishes the theory of two-price economies from that of one price economy. Now there are two types of prices, one price is used for buying from the market called the ask price, and the other price is used for selling to the market called the bid price. In the situation of one price economy, the market plays the role of an auctioneer, who clears the trades and decides the prices. However, in the two-price economy, the financial market plays a role of a passive counterparty to all transactions, who buys at the ask price and sells at the bid price. The spread that is between the bid and ask prices becomes a measure of illiquidity. It also evaluates the principal required to support a position and the cost of unraveling a position.

We also find it necessary to mention that the one-period case discussed in this paper was included in the book by Carr and Zhu (2018) with reference to this paper (a working paper back then).

1.1. Bid–Ask Spreads

A collection of theoretical approaches exists that are trying to model bid–ask spreads. Cherny and Madan (2010) offer a few of the current approaches that have been used to model bid–ask spreads. Copeland and Galai (1983) have discussed the order processing and inventory costs of providers of liquidity. Constantinides (1986) and Jouini and Kallal (1995) investigated the spreads that involve transaction costs of trading in liquid markets. However, the researches mentioned above are comparatively satisfactory to liquid markets where a transaction cost can happen at a price that a contrary trade direction can take place with no price effect. The price-spreads that are related to the theory of two-price economies are discussed in Carr et al. (2001) and Cherny and Madan (2010). These are mostly related to locating actual long-term counterparties that are ready to establish a position for an extended period of time. The spread between the bid and ask prices can be observed as a holding of the charge-exerted while the market does not clear rapidly, as to find a counterparty is going to require time and effort because there is no possibility of doing trades in both directions at any transaction price being observed. Specifically, there is not any possibility of complete replication. In addition, the spread between the bid and ask prices becomes a reflection of the cost of holding the residual risk (Eberlein et al. 2011). Therefore, transactions happen close to or at either the ask price or the bid price, conditional on the direction of the trade. The conic finance is trying to model the bid–ask spread by applying the concept of acceptable cash flows to the market (Madan 2015). However, it is assumed that the market requires a minimal level of acceptability for a position to be profitable. As a result of the market competition, the bid-price is being raised, and the asked-price is being lowered to establish an acceptable position. Therefore the bid–ask spread is tried to be narrowed so that the risk of a position will be minimized. This spread can be seen as the cost of unraveling a position.

1.2. Two-Price Economy

In a two-price economy, a comparatively classical view of markets consistent with its role in the traditional competitive breakdown, where markets play the role of counterparties to transactions, is being assumed. The only difference from the traditional aspect is that the length of a trade depends on the direction of the trade, while the market is buying at the bid price and selling at the ask price. Now regard the classical market when trading is performed in either direction at the current price. The market is always willing to sell at a higher price or similarly buy at a lower price and welcomes all zero-cost random cash streams that have a positive expectation under the equilibrium pricing essentials. Notice that this creates a very large set of market risks that are accepted by the classical financial market within a risk-neutral measure. The two-price financial market is more antagonistic as to which trades it will accept. The collection of zero-cost risks acceptable to the financial market is much smaller as a set. A modeling process of this set of acceptable risks can be observed at Artzner et al. (1999), that was further expanded in Cherny and Madan (2009) and Cherny and Madan (2010). Especially, the set of zero-cost risks that are acceptable to the financial market as a set of random variables is being modeled as a convex cone, including all the non-negative random variables. The theoretical structure required for supporting the two-price economy has been given a huge amount of attention in the past few years. The theory was popularized into the field of mathematical finance by Constantinides (1986) and was introduced as coherent risk measures by Artzner et al. (1999). The research that connects the theory of two-price economies to concave distortions was performed by Cherny and Madan (2009) and Cherny and Madan (2010). They are the researches that gave a perceptive of how to establish the bid–ask prices admissible to the theory of two-prices. After that, the theory of two-prices was given the name “conic finance”, for example Madan and Schoutens (2011) and Madan and Schoutens (2012). In the following sections, we present the theory of two-prices in an abstract manner as it was set out in Madan (2015).

The rest of this paper is structured as follows. In Section 2 we introduce the model, starting by definitions of sets of zero cost and attainable cash flows. We also characterize the utility maximization of trading cash flows. In Section 3 the Fundamental Theorem of Asset Pricing in conic finance (two-price economy) will be stated and proved (all proofs will be in Appendix A), using the pricing factor generated by a solution of the dual problem. In Section 4 we use take advantage of the existence of pricing factors and define price bounds for any attainable cash flow. Additionally, in concrete examples, we will illustrate the trading strategies in the presence of arbitrage opportunities for 1 and 2-period models, along with the super-hedging theorem for the 1-period case. In Lemma 1 a computation complexity will be given, in presence of all possible zero cost bonds. Finally in Section 5 the multi-period case will be discussed where only the one-period bonds and assets will be considered through an iterative process.

2. The Model (Multi-Period)

In this section, we first define the general multi-period model along with all of the necessary components of the model. We establish the FTAP theorem for the multi-period model in conic finance (two-price economy) by considering a utility maximization problem and its dual. We also explain the relation between solutions to our primal and dual problems, along with the price factors derived from the solution of the dual problem, by considering a utility maximization problem and its dual. We use this price factor to find a super-hedging and sub-hedging for any acceptable cash flow.

2.1. The Model Definitions

We start by defining the general model and its components following Madan (2015).

Definition 1.

Let $\mathbb{F}=\left\{\left\{\varnothing ,\Omega \right\}={\mathcal{F}}_0\subset {\mathcal{F}}_1\subset \dots \subset {\mathcal{F}}_T=\mathcal{F}\right\}$ be an information filtration on the probability space $\left(\Omega ,\mathcal{F},P\right),$ where $\Omega =\left\{{\omega }_1,{\omega }_2,\dots ,{\omega }_N\right\}$ is a finite sample space, representing the economic states. We consider a T-period financial model where $T\ge 1$ and for any $0\le t\le T$, cash flows (in∖out) are being traded at time t.

Definition 2.

Let $\mathcal{X}$ denote the space of all $\mathcal{F}$-adapted cash flows $x={\left(x_t\right)}_{t=0}^T$ with the inner product

$$<x,y>=E\left[\sum _{t=o}^T{x}_t{y}_t\right]$$

Then $\mathcal{X}$ is a finite dimensional Hilbert space.

The market consists of M risky assets $S^m\in \mathcal{X},m=1,2,\dots ,M$ and T risk-free zero coupon bonds $1^u,u=1,2,\dots ,T$ where $1_u^u=1$ and $1_t^u=0$ for $t\ne u$. At time t, there is a bid and ask price pair $b_t^i\le a_t^i$. Paying $a_t^i$, one will receive the income flow ${\left(S_t^i\right)}_{s=t+1}^T$ and receiving $b_t^i$ one will get the income flow ${\left(-S_t^i\right)}_{s=t+1}^T$. For risk-less bonds, the bid and ask prices of $1^u$, paid/received at time $t<u$ is denoted by $g_t^u\le h_t^u\le 1$. There are two zero cost cash flows associated with each pair of bid and ask prices.

$S_s^{it}=\left\{\begin{array}{cc}0& s<t\\ -a_t^i& s=t\\ S_s^i& s>t\end{array}\right.$   and   ${\tilde{S}}_s^{it}=\left\{\begin{array}{cc}0& s<t\\ b_t^i& s=t\\ -S_s^i& s>t\end{array}\right.$

Similarly the bond maturing at time u, creates two zero cost cash flows as below:

$1_s^{ut}=\left\{\begin{array}{cc}0& s\ne u,t\\ -h_t^u& s=t\\ 1& s=u\end{array}\right.$   and   ${\tilde{1}}_s^{ut}=\left\{\begin{array}{cc}0& s\ne u,t\\ g_t^u& s=t\\ -1& s=u\end{array}\right.$

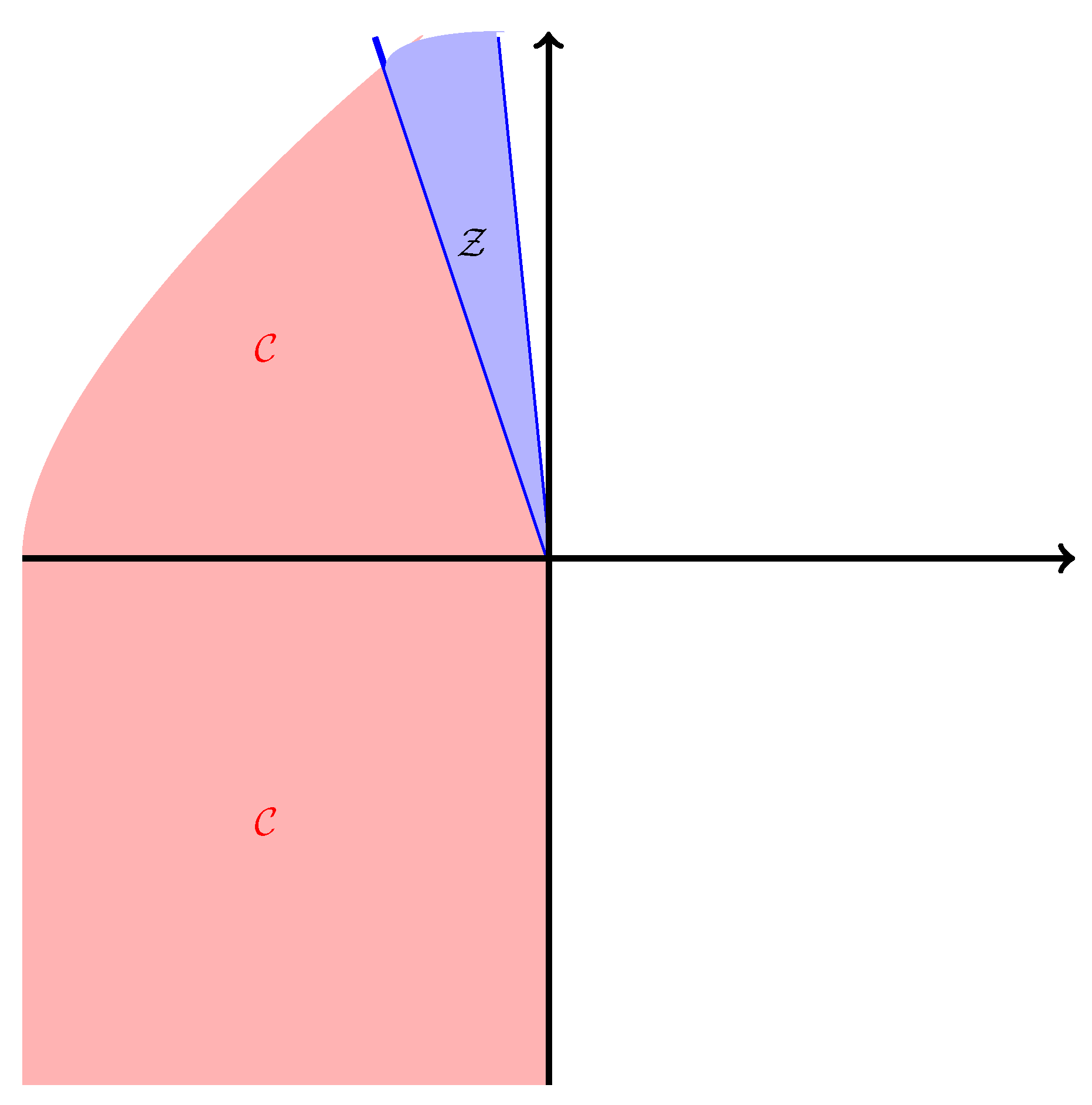
2.2. Set of Zero-Cost Cash Flows

Assuming that one can trade any non-negative multiple of above zero-cost cash flows, and suppose ${\alpha }_t^i,{\tilde{\alpha }}_t^i,{\beta }_t^u,{\tilde{\beta }}_t^u,\mathrm{for}i=1,\dots ,M,u=1,\dots ,T$ are non-negative $\mathcal{F}$-adapted random variables, then $\mathcal{Z}$ is defined to be the set of all zero cost cash flows of the form

$$z=\sum _{t=0}^T\left[\sum _{i=1}^M\left({\alpha }_t^i{S}^{it}+{\tilde{\alpha }}_t^i{\tilde{S}}^{it}\right)+\sum _{u=1}^T\left({\beta }_t^u{1}_s^{ut}+{\tilde{\beta }}_t^u{\tilde{1}}_s^{ut}\right)\right]$$

(1)

It can be seen from the definition that $\mathcal{Z}$ is a cone. Define $\mathcal{C}$ to be the set of all cash flows $c\in \mathcal{X}$ such that there is $z\in \mathcal{Z}$ with $z\ge c$. Then $\mathcal{C}$ is the set of adapted processes, super-replicable at zero cost. It is clear that $\mathcal{C}$ a closed convex cone and $\mathcal{Z}\subset \mathcal{C}$.

Figure 1 is a geometrical demonstration (in ${\mathbb{R}}^2$) of a cone $\mathcal{Z}$ and the convex cone $\mathcal{C}$, set of all vectors dominated by some elements of $\mathcal{Z}$ ($z\ge c$).

2.3. The Characterization of No-Arbitrage

We now define arbitrage and will be characterizing no-arbitrage using a utility maximization problem.

Definition 3.

We say that a cash flow $c={\left(c_t\right)}_{t=0}^T\in \mathcal{C}\setminus \left\{0\right\}$ is an arbitrage if $c_t\ge 0$ for all $t=0,1,\dots ,T$.

Definition 4.

(Utility Function) An extended real valued function $u:\mathbb{R}\to \mathbb{R}\cup \{+\infty \}$ is called a utility function if it satisfies the following three characteristics:

(1)

(Risk Aversion) u is strictly concave,

(2)

(Profit Seeking) u is strictly increasing and ${\displaystyle \underset{t\to +\infty }{lim}u\left(t\right)=+\infty }$,

(3)

(Bankruptcy Forbidden) for any $t<0,u\left(t\right)=-\infty$.

Let ${\mathcal{X}}^{+}$ denote the non-negative cone in $\mathcal{X}$, also $w_0\in {\mathcal{X}}^{+}$ be the initial endowment and ${\displaystyle {\left(c_t\right)}_{t=0}^T=(c_0,c_1,\dots ,c_T)\in \mathcal{C}}$ be a cash flow. Consider the following optimal trading problem

$$p=max\left\{E\left[\sum _{t=0}^{T}u\left(c_t\right)\right];c={\left(c_t\right)}_{t=0}^T\in w_0+\mathcal{C}\right\}$$

where u is a utility function. We are able to characterize the no-arbitrage principle in terms of this utility maximization problem.

Theorem 1

(Characterization of Utility Maximization). The financial market has no-arbitrage opportunity if and only if the optimal trading problem above has a finite value $p<\infty$.

Proof. 

In Appendix A.  □

3. FTAP for Multi-Period Model

In this section, we establish FTAP for conic finance model, characterizing no-arbitrage in terms of the extension of pricing factors. A first version of this theorem was proven by Harrison and Kreps (1979). More general versions of the theorem were proven in 1981 by Harrison and Pliska (1981) and in 1994 by Delbaen and Schachermayer (1994).

Theorem 2

(The First Fundamental Theorem of Asset Pricing). A financial market with time horizon T and price processes of the risky asset and risk-less bond given by $S_1,\dots ,S_T$ and $S_1^0,\dots ,S_T^0$, respectively, is arbitrage-free under the probability P if and only if there exists another probability measure Q such that

i. For any event A, $P\left(A\right)=0$ if and only if $Q\left(A\right)=0$ (We say in this case that P and P are equivalent probability measures).

ii. The discounted price process, $X_1:=\frac{S_1}{S_1^0},\dots ,XT:=\frac{S_T}{S_T^0}$ is a martingale under Q. A measure Q that satisfies (i) and (ii) is known as a risk neutral measure.

We now start by considering dual of the utility maximization problem in Section 2. First, we rephrase the utility maximization problem in Section 2 as an abstract convex programming problem.

For $x={\left(x_t\right)}_{t=0}^T\in \mathcal{X}$, define $g\left(x\right)={\iota }_{w_0+\mathcal{C}}\left(x\right)$ and ${\displaystyle f\left(x\right)=E\left[\sum _{t=0}^T(-u)\left(x_t\right)\right]}$. Then we can rewrite the optimal trading problem in Equation (1) as

$$\begin{array}{cc}\hfill p& {\displaystyle =-min\left\{E\left[\sum _{t=0}^T(-u)\left(c_t\right)\right]{|c=\left(c\right)}_{t=0}^T\in w_0+\mathcal{C}\right\}}\hfill \\ \hfill & {\displaystyle =-\underset{x\in \mathcal{X}}{min}\left\{E\left[\sum _{t=0}^T(-u)\left(x_t\right)\right]+{\iota }_{w_0+\mathcal{C}}\left(x\right)\right\}}\hfill \\ \hfill & {\displaystyle =-\underset{x\in \mathcal{X}}{min}\left\{f\left(x\right)+g\left(x\right)\right\}}\hfill \end{array}$$

The dual representation of the problem above gives us an extension of the Fundamental Theorem of Asset Pricing (FTAP) in conic finance. We approach FTAP via a utility optimization problem.

Definition 5

(Pricing Factor). For $t<u\le T$, we say $f_t^u$ is a pricing factor from time t to time u and compatible with financial market, if the two following conditions are satisfied

$$g_t^u\le {\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^u{1}_s^{ut}\right]\le h_t^u,$$

(2)

and also for $1\le i\le M$

$$b_t^i\le {\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^u{S}_t^i\right]\le a_t^i.$$

Theorem 3.

(FTAP in conic finance) Let $u\left(t\right)$ be a utility function and consider a two-price financial market consisting of price processes of the risky assets and risk-free bonds. Then the market is arbitrage-free under the probability P if and only if there exists a pricing factor.

Proof. 

In Appendix A. □

Remark 1.

Through the proof of Theorem 3, there are a few things we would like to point out here:

(1)

Pricing factor is not unique. This is clear since the existence of a pricing factor in FTAP comes from the existence of a solution to the dual problem, and we know the dual problem does not necessary have a unique solution.

(2)

The pricing factor is related to the utility function u via the duality. In fact we saw specifically that $\overline{z}\in -\partial (-u)\left(\overline{x}\right)$.

(3)

The pricing factors can be used to generate prices for cash flows $c\in \mathcal{C}$ with no-arbitrage existing. We will explain this more in detail on the coming sub-section.

4. Price Bounds and Their Estimates

A distinct feature of conic finance is that prices of assets are not unique. In fact, we see that every price factor will provide a non-arbitrage price. We will see that the set of price factors will provide us price bounds, outside of which arbitrage arises.

4.1. Definition of the Bounds

Define $\mathcal{PF}$ to be the set of all price factors $f_t^s$ that are compatible with the financial market which is

$$\mathcal{PF}=\left\{f_t^s|g_t^u\le {\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^u{1}_s^{ut}\right]\le h_t^u,b_t^i\le {\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^s{S}_s^i\right]\le a_t^i\right\}$$

(3)

Let $c=\left(c_t\right)\in \mathcal{C}$. We define

$$u_t\left(c\right)=sup\left\{{\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^s{c}_s\right]|f_t^s\in \mathcal{PF}\right\}$$

(4)

and

$$l_t\left(c\right)=inf\left\{{\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^s{c}_s\right]|f_t^s\in \mathcal{PF}\right\}$$

(5)

Remark 2.

The values of $u_t\left(c\right)$ and $l_t\left(c\right)$ are the lower and upper bounds for bid and ask prices of the cash flow $c=\left(c_t\right)\in \mathcal{C}$, equivalent to existing no-arbitrage. Equivalently, $[l_t\left(c\right),u_t\left(c\right)]$ is the no-arbitrage region for the price of a given cash flow $c=\left(c_t\right)\in \mathcal{C}.$

Remark 3.

As we know, any of $f_t^u\in \mathcal{PF}$ has a one to one correspondence relation to a solution of the dual problem say $\overline{z}\in {\mathcal{C}}^o$ so that ${\displaystyle {\overline{z}}_t={\Gamma }_t{M}_t={\Gamma }_t\frac{Q}{P}}$, where Q is a P-equivalent martingale measure defined as $Q=M_{t}P$. Since $f_t^u$ are in direct relation to the solution of dual problem, this leads to

$${\displaystyle {\mathbf{E}}_t\left[\sum _{s=t+1}^T{\overline{z}}_s{c}_s\right]={\mathbf{E}}_t\left[{\overline{z}}_t\sum _{s=t+1}^T\frac{{\overline{z}}_s}{{\overline{z}}_t}{c}_s\right]={\overline{z}}_t{\mathbf{E}}_t\left[\sum _{s=t+1}^T{f}_t^s{c}_s\right]}$$

which is a linear combination in terms of the pricing factor we defined above, so that the corresponding maximization and minimization above (and later in our text) becomes a linear programming problem.

A question that one can ask is, if the market (bid and ask) prices of a cash flow $c=\left(c_t\right)\in \mathcal{C}$, are outside of the no-arbitrage region $[l_t\left(c\right),u_t\left(c\right)]$, will any arbitrage opportunity become possible? We will answer this question in the next section.

4.2. Computations in One-Period

To illustrate the general pattern, we start with a simple example.

Example 1.

Consider a one-period model ($T=1$) with a sample space $\Omega =\left\{{\omega }_1,{\omega }_2\right\}$ containing only two elements and let $M=1$ (only one risky asset, $S^1=S$). Additionally, consider a bond

$$1^{1,0}=(-h_0^1,1){\tilde{1}}^{1,0}=(g_0^1,-1)$$

where the ask and prices are $h_0^1=0.9$ and $g_0^1=0.8$, respectively. Assume the asset $S_t$ over times $t=0,1$ has standard initial price 1 and payoff as following

Now consider the following primal maximization problem

$$p_1:=\left\{\begin{array}{c}{\displaystyle u_0=max\mathbf{E}\left[f_0^1{S}_1\right]}\\ {\displaystyle g_0^1\le \mathbf{E}\left[f_0^1\right]\le h_0^1}\end{array}\right.=\left\{\begin{array}{c}{u}_0=max\left[{\displaystyle f_0^1\left({\omega }_1\right)P\left({\omega }_1\right)S_1\left({\omega }_1\right)+f_0^1\left({\omega }_2\right)P\left({\omega }_2\right)S_1\left({\omega }_2\right)}\right]\\ {\displaystyle g_0^1\le f_0^1\left({\omega }_1\right)P\left({\omega }_1\right)+f_0^1\left({\omega }_2\right)P\left({\omega }_2\right)\le h_0^1}\end{array}\right.$$

(6)

For simplicity we let ${\displaystyle r_1:=f_0^1\left({\omega }_1\right)P\left({\omega }_1\right)}$ and ${\displaystyle r_2:=f_0^1\left({\omega }_2\right)P\left({\omega }_2\right)}$ so that the linear programming problem in Equation (6) becomes

$$p_1=\left\{\begin{array}{c}{u}_0=max\left[{\displaystyle r_1{S}_1\left({\omega }_1\right)+r_2{S}_1\left({\omega }_2\right)}\right]\\ {\displaystyle g_0^1\le r_1+r_2\le h_0^1}\end{array}\right.$$

$$=\left\{\begin{array}{c}{u}_0=max\left[{\displaystyle r_1{S}_1\left({\omega }_1\right)+r_2{S}_1\left({\omega }_2\right)}\right]\\ {\displaystyle r_1+r_2\le h_0^1}\\ -r_1-r_2\le -g_0^1\end{array}\right.$$

(7)

A systematical way of deriving the arbitrage strategy is to use linear programming duality. By using the linear programming duality, we can write the dual problem to Equation (7) as

$$d_1:=\left\{\begin{array}{c}{u}_0=min\left(-g_0^1{t}_1+h_0^1{t}_2\right)\\ t_2-t_1\ge S_1\left({\omega }_1\right)\\ t_2-t_1\ge S_1\left({\omega }_2\right)\\ t_1,t_2\ge 0\end{array}\right.$$

$$=\left\{\begin{array}{c}{u}_0=min\left(-g_0^1{t}_1+h_0^1{t}_2\right)\\ {\displaystyle t_2\ge t_1+\underset{\omega \in \Omega }{max}{S}_1\left(\omega \right)}\\ t_1,t_2\ge 0\end{array}\right.$$

(8)

If we use the constraint condition in Equation (8) and substitute in the objective function, we have

$${\displaystyle u_0=\underset{t_1\ge 0}{min}\left[-g_0^1{t}_1+h_0^1\left(t_1+\underset{\omega \in \Omega }{max}{S}_1\left(\omega \right)\right)\right]=\underset{t_1\ge 0}{min}\left[t_1\left(h_0^1-g_0^1\right)+h_0^1\underset{\omega \in \Omega }{max}{S}_1\left(\omega \right)\right]}$$

but since $h_0^1-g_0^1\ge 0,$ minimum happens when $t_1=0$ so that

$${\displaystyle u_0=h_0^1\left(\underset{\omega \in \Omega }{max}{S}_1\left(\omega \right)\right)=0.9\left(2\right)=1.8}$$

(9)

Therefore 1.8 is the highest ask price for $S_1$ offered at time $t=0$ under no-arbitrage condition. That means for any offered price higher than 1.8 one should be able to build a portfolio creating an arbitrage.

In fact for a bid price $b_0>1.8$, since the solution to Equation (8) is $t_1=0,t_2=2$, one can buy 2 unites of bond $1^{1,0}=(-0.9,1)$ at time $t=0$ for the price of 1.8 and receive 2 at time $t=1$ so that $S_1$ can be delivered and still making a profit of ${\displaystyle \frac{b_0-1.8}{0.9}>0}$.

Similarly we can find a lowest bid price $l_0$ for which one can construct a portfolio providing arbitrage if any ask price lower than $l_0$ is available.

The approach illustrated above can also be used in financial market that involves both bonds and stocks. A general result is summarized in the following theorem. We will use the set of all possible pricing factors corresponding to all solutions of the dual problem to provide a no-arbitrage region for a given cash flow. We state the result for super-hedging, i.e., upper bound for no-arbitrage. Sub-hedging can be discussed similarly.

Theorem 4

(Super-Hedging). Suppose that $(c_0,c_1)\in \mathcal{C}$ is an acceptable cash flow, then

$$u_0=\underset{f_0^1\in \mathcal{PF}}{sup}\left\{{\displaystyle \mathbf{E}\left[f_0^1{c}_1\right]}\right\}$$

$$=\underset{{\left(\Lambda ,\gamma \right)}_0\in {\mathbb{R}}_{+}^{2M+2}}{min}\left\{-p_0\left({\left(\Lambda ,\gamma \right)}_0\right)+\underset{\omega \in \Omega }{sup}\left[g_0^1\left(c_1\left(\omega \right)-p_1\left({\left(\Lambda ,\gamma \right)}_0\right)\left(\omega \right)\right)\right]\right\}$$

is a super-hedging bound, where

$$\left\{\begin{array}{l}{p}_0\left({\left(\Lambda ,\gamma \right)}_0\right)=-{\gamma }_0^1{h}_0^1+{\tilde{\gamma }}_0^1{g}_0^1+\sum _{i=1}^M\left[-{\lambda }_0^i{a}_0^i+{\tilde{\lambda }}_0^i{b}_0^i\right]\\ p_1\left({\left(\Lambda ,\gamma \right)}_0\right)={\gamma }_0^1-{\tilde{\gamma }}_0^1+\sum _{i=1}^M\left[{\lambda }_0^i-{\tilde{\lambda }}_0^i\right]S_1^i\end{array}\right.$$

If $b_0$ is a bid price that exceeds a super-hedging bound $u_0$, then the solution to the minimization problem (dual) is a trading strategy ${\left(\overline{\Lambda },\overline{\gamma }\right)}_0\in {\mathbb{R}}_{+}^{2M+2}$ for which if we acquire the zero cost cash flows $\left(p_0\left({\left(\overline{\Lambda },\overline{\gamma }\right)}_0\right),p_1\left({\left(\overline{\Lambda },\overline{\gamma }\right)}_0\right)\right)$, then our portfolio has an arbitrage opportunity.

Proof. 

In Appendix A.  □

We can see that a super-hedging bound $u_0$ can be represented as the value of a pair of dual linear programming problems. The primal provides an easy way of evaluating $u_0$ with the help of price factor in set $\mathcal{P}$. The dual solution, provides us a super-hedging portfolio which guarantees an arbitrage in case of existence of a favorable price for the cash flow $c\in \mathcal{C}$

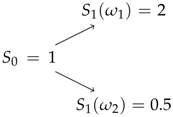
4.3. Two-Period Examples

Before we start setting up the problem for a two-period model, first we aim to explain a simple example for a two-period case. We will discuss and illustrate this two-period model with only one risky asset.

4.3.1. Involving Only 1-Period Bonds

Example 2.

Let $\Omega =\left\{{\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4\right\}$ and consider a two-period model with $T=2$ and $t=0$ and the information structure ${\mathcal{F}}_0\subset {\mathcal{F}}_1\subset {\mathcal{F}}_2$ where for $k=0,1,2$, the σ-algebra ${\mathcal{F}}_k$ is generated by the set ${\mathcal{P}}_k$ which are defined as ${\mathcal{P}}_0=\left\{B_{0,1}\right\},{\mathcal{P}}_1=\{B_{1,1},B_{1,2}\},{\mathcal{P}}_2=\{B_{2,1},B_{2,2},B_{2,3},B_{2,4}\}$. The sets $B_{i,j}$ are all subsets of Ω and they are defined as in the following diagram

Additionally, consider the bonds

$$1^{1,0}=(-h_0^1,1,0){\tilde{1}}^{1,0}=(g_0^1,-1,0)$$

$$1^{2,0}=(-h_0^2,0,1){\tilde{1}}^{2,0}=(g_0^2,0,-1)$$

$$1^{2,1}=(0,-h_1^2,1){\tilde{1}}^{2,1}=(0,g_1^2,-1)$$

where $h_0^1=0.95,g_0^1=0.9,h_0^2=0.9,g_0^2=0.8$ and also $h_1^2\left(B_{1,1}\right)=0.9,h_1^2\left(B_{1,2}\right)=0.95,g_1^2\left(B_{1,1}\right)=0.85,$$g_1^2\left(B_{1,2}\right)=0.9$.

Let $S^1=S$ be our only risky asset with the above price diagram corresponding to zero-cost cash flows

$$S^{i0}=(-a_0^2,S_1,S_2){\tilde{S}}^{i0}=(b_0^2,-S_1,-S_2)$$

$$S^{i1}=(0,-a_1^2,S_2){\tilde{S}}^{i1}=(0,b_1^2,-S_2)$$

We aim to find the highest ask price while no-arbitrage exists. We need to mention here that we are assuming there is no 2-period bond $(-h_0^2,0,1)$ is available. We are going to treat the problem as two consecutive 1-period problems. For this reason, first we try to find the best ask price $u_1^2$ (a ${\mathcal{F}}_1$-measurable random variable) of having $S_2$ being paid at time $t=1$. Therefore for $i=1,2$ we construct the following maximization problem

$$p:\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,i}\right)=max{\mathbf{E}}_1\left[f_1^2{S}_2\right]\left(B_{1,i}\right)}\\ {\displaystyle g_1^2\left(B_{1,i}\right)\le {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2\left(B_{1,i}\right)}\end{array}\right.$$

(10)

and by definition 2.2 we have

$$p:\left\{\begin{array}{c}{\displaystyle u_1^2=max<f_1^2,S_2>}\\ {\displaystyle g_1^2\le {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2}\end{array}\right.$$

(11)

for which the Lagrangian becomes

$$\mathcal{L}(f_1^2,t)=<f_1^2,S_2>+t_1\left(h_1^2-<f_1^2,S_2>\right)+t_2\left(<f_1^2,S_2>-g_1^2\right)$$

(12)

$$=<f_1^2,S_2-t_1+t_2>+t_1{h}_1^2-t_2{g}_1^2$$

so that we have

$$u_1^2=\underset{f_2^2\ge 0}{sup}\underset{t\ge 0}{inf}\mathcal{L}(f_1^2,t)$$

(13)

or

$$p:\left\{\begin{array}{c}{\displaystyle u_1^2=inf{t}_1{h}_1^2-t_2{g}_1^2}\\ {\displaystyle t_1-t_2\ge \underset{\omega \in \Omega }{sup}{S}_2\left(\omega \right)}\end{array}\right.$$

(14)

Solving the latter linear programing we will have:

$${\displaystyle u_1^2\left(B_{1,i}\right)=h_1^2\left(B_{1,i}\right)\underset{B_{1,i}}{max}{S}_2\left(B_{1,i}|S_1\left(B_{1,i}\right)\right)=\left\{\begin{array}{cc}0.9\left(4\right)=3.6& ifi=1,\\ 0.95\left(1\right)=0.95& ifi=2.\end{array}\right.}$$

(15)

Now consider the following diagram and maximization problem

$$\left\{\begin{array}{c}{\displaystyle u_0^2=max{\mathbf{E}}_0\left[f_1^2\left(S_1+u_1^2\right)\right]}\\ {\displaystyle g_0^1\le {\mathbf{E}}_0\left[f_1^2\right]\le h_0^1.}\end{array}\right.$$

(16)

Similar to example (1), this problem has the solution

$$u_0^2=h_0^1\left[\underset{\omega \in \Omega }{max}(S_1\left(\omega \right)+u_1^2\left(\omega \right))\right]=\left(0.95\right)\left(5.6\right)=3.42$$

(17)

Therefore 3.42 is the highest ask price for $(.,S_1,S_2$) offered at time $t=0$ to have the no-arbitrage condition satisfied. That means for any offered price bigger than 3.42 one should be able to build a portfolio creating an arbitrage.

In fact for an offered bid price of $b_0^2>3.42$, since the dual problem solutions are $t_1=0,t_2=5.6,t_1\left(B_{1,1}\right)=0,t_2\left(B_{1,}1\right)=4,t_1\left(B_{1,2}\right)=0,t_2\left(B_{1,2}\right)=1$, one can buy 5.6 unites of bond $1^{1,0}=(-0.95,1,0)$ at time $t=0$ for the price of 3.42 and receive 5.6 at time $t=1$ so that $S_1$ can be delivered and left with at least $3.6=max\left(u_1^2\right)\left(\omega \right)$ so that one is able to deliver $S_2$ at time $t=2$ and still making a profit of at least ${\displaystyle \frac{b_0^2-3.42}{\left(0.95\right)\left(h_1^2\right)}>0}$.

Similarly we can find a lowest bid price $l_0^2$ for which one can construct a portfolio providing an arbitrage if any ask price smaller than $l_0^2$ is available, where analogous steps to example (1) leads to

$$l_0^2=g_0^1\left[\underset{\omega \in \Omega }{min}(S_1\left(\omega \right)+l_1^2\left(\omega \right))\right]=\left(0.9\right)\left(0.725\right)=0.6525$$

(18)

Therefore 0.6525 is the lowest bid price (sub-hedging bound) for $(.,S_1,S_2)$ offered at time $t=0$ to have the no-arbitrage condition satisfied. That means for any offered ask smaller than 0.6525 one should be able to build a portfolio creating an arbitrage.

Next, we consider a problem involving options using a similar approach.

Example 3.

Let $\Omega =\left\{{\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4\right\}$ and consider a two-period model with the information structure ${\mathcal{F}}_0\subset {\mathcal{F}}_1\subset {\mathcal{F}}_2$ where for $k=0,1,2$, the σ-algebra ${\mathcal{F}}_k$ is generated by the set ${\mathcal{P}}_k$ which are defined as ${\mathcal{P}}_0=\left\{B_{0,1}\right\},{\mathcal{P}}_1=\{B_{1,1},B_{1,2}\},{\mathcal{P}}_2=\{B_{2,1},B_{2,2},B_{2,3},B_{2,4}\}$. The sets $B_{i,j}$ are all subsets of Ω and they are defined as in the following diagram

We define the risk-free bonds as

$$1^{1,0}=(-h_0^1,1,0){\tilde{1}}^{1,0}=(g_0^1,-1,0)$$

$$1^{2,0}=(-h_0^2,0,1){\tilde{1}}^{2,0}=(g_0^2,0,-1)$$

$$1^{2,1}=(0,-h_1^2,1){\tilde{1}}^{2,1}=(0,g_1^2,-1)$$

where $h_0^1=0.95,g_0^1=0.9,h_0^2=0.9,g_0^2=0.8$ and also $h_1^2\left(B_{1,1}\right)=0.9,h_1^2\left(B_{1,2}\right)=0.95,g_1^2\left(B_{1,1}\right)=0.85,g_1^2\left(B_{1,2}\right)=0.9$. Let $S^1=S$ be our only risky asset with the above price diagram with zero-cost cash flows

$$S^{i0}=(-a_0^2,S_1,S_2){\tilde{S}}^{i0}=(b_0^2,-S_1,-S_2)$$

$$S^{i1}=(0,-a_1^2,S_2){\tilde{S}}^{i1}=(0,b_1^2,-S_2)$$

and also according to our calculations in the previous example

$$0.6525=l_0^2\le b_0^2\le a_0^2\le u_0^2=3.42,$$

$$0.85=l_1^2\left(B_{1,1}\right)\le b_1^2\left(B_{1,1}\right)\le a_1^2\left(B_{1,1}\right)\le u_1^2\left(B_{1,1}\right)=3.6,$$

$$0.225=l_1^2\left(B_{1,2}\right)\le b_1^2\left(B_{1,2}\right)\le a_1^2\left(B_{1,2}\right)\le u_1^2\left(B_{1,2}\right)=0.95.$$

Now consider an option with the payoff of $c_t$ at times $t=1,2$ and $S^1$ as the underlying asset. Additionally, assume the strike price of $K=1$ at time $t=2$. Then the payoffs are $c_2\left(B_{2,1}\right)=3,c_2\left(B_{2,2}\right)=c_2\left(B_{2,3}\right)=c_2\left(B_{2,4}\right)=0$.

Consider the cash flow $(.,0,c_2)$. We would like to find the highest ask-price at time $t=0$ for this cash flow. Therefore we consider the following maximization problem

$$\left\{\begin{array}{c}{\displaystyle u_0^2=max{\mathbf{E}}_0\left[f_0^1{c}_1+f_0^2{c}_2\right]=max{\mathbf{E}}_0\left[f_0^1\left(c_1+{\mathbf{E}}_1\left[f_1^2{c}_2\right]\right)\right]}\\ {\displaystyle g_0^1\le {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1,}\\ {\displaystyle g_0^2\le {\mathbf{E}}_0\left[f_0^2\right]\le h_0^2,}\\ {\displaystyle b_0^2\le {\mathbf{E}}_0\left[f_0^1{S}_1+f_0^2{S}_2\right]\le a_0^2.}\end{array}\right.$$

(19)

On the other hand, we know that

$$\left\{\begin{array}{c}{\displaystyle u_1^2=max{\mathbf{E}}_1\left[f_1^2{c}_2\right]}\\ {\displaystyle g_1^2\le {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2,}\\ {\displaystyle b_1^2\le {\mathbf{E}}_1\left[f_1^2{S}_2\right]\le a_1^2.}\end{array}\right.$$

(20)

Therefore, similar to our previous example, first we find a super-hedging bound for $c_2$ (the random variable $u_1^2$), at time $t=1$. Since $u_1^2$ is a random variable taking value on $B_{1,1}$ and $B_{1,2}$, for $k=1,2$ which corresponds to the two sub-branches of the diagram at time $t=1$, we set up a linear programming maximization as

$${\displaystyle p_k:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,k}\right)=\underset{B_{2,j}\subset B_{1,k}}{max}\left[c_2^T{f}_1^2\right]\left(B_{1,k}\right)}\\ {\displaystyle g_1^2\left(B_{1,k}\right)\le {\left(f_1^2\right)}^T\left[\begin{array}{c}1\\ 1\end{array}\right]\le h_1^2\left(B_{1,k}\right),}\\ {\displaystyle b_1^2\left(B_{1,k}\right)\le S_2^T{f}_1^2\le a_1^2\left(B_{1,k}\right),}\end{array}\right.}$$

(21)

which has the values of $u_1^2\left(B_{1,1}\right)=2.7$ and $u_1^2\left(B_{1,2}\right)=0$.

Now that we have $u_1^2$ values determined and since $c_1=0$, we use the following problem to calculate $u_0^2$

$$\left\{\begin{array}{c}{\displaystyle u_0^2=max{\mathbf{E}}_0\left[f_0^1\left(c_1+u_1^2\right)\right]=max{\mathbf{E}}_0\left[f_0^1\left(u_1^2\right)\right]}\\ {\displaystyle g_0^1\le {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1,}\end{array}\right.$$

(22)

which has the maximum value of $u_0^2\left(c_2\right)=u_1^2\left(B_{1,1}\right)h_0^1=2.7\left(0.95\right)=2.565$.

Now if at time $t=0$ there is an available cash flow $(b_0,0,-c_2)$ with $b_0>2.565=u_0^2\left(c_2\right)$, then one can use the following zero-cost trading strategy to create an arbitrage. In fact the arbitrage strategy is to invest all of $b_0$ amount into $1^{10}=(-h_0^1,1,0)$ at time $t=0$ and then invest the revenue received at time $t=1$ into $S^{i1}=(0,-a_1^2,S_2)$, therefore at time $t=2$ one will have

$${\displaystyle \frac{b_0}{h_0^1}\frac{S_2}{a_1^2}>\frac{2.565}{0.95}\frac{S_2}{a_1^2}=2.7\left(\frac{S_2}{a_1^2}\right)=\left\{\begin{array}{c}{\displaystyle 2.7\left(\frac{S_2\left(B_{2,1}\right)}{a_1^2\left(B_{1,1}\right)}\right)=3}\\ {\displaystyle 2.7\left(\frac{S_2\left(B_{2,2}\right)}{a_1^2\left(B_{1,1}\right)}\right)>0}\\ {\displaystyle 2.7\left(\frac{S_2\left(B_{2,3}\right)}{a_1^2\left(B_{1,2}\right)}\right)>0}\\ {\displaystyle 2.7\left(\frac{S_2\left(B_{2,4}\right)}{a_1^2\left(B_{1,2}\right)}\right)>0}\end{array}\right.}$$

so that an arbitrage is available.

Again, we can find the lowest bid-price $l_0^2$ at time $t=0$ for the cash flow $(.,0,c_2)$ as

$$l_0^2=\left(g_0^1\right)\left(l_1^2\left(B_{1,1}\right)\right)=\left(0.9\right)\left(0.6375\right)=0.57375$$

and this is the lowest bid price possible under no-arbitrage condition. Now, if at time $t=0$ there is a cash flow $(-a_0,0,c_2)$ available where $a_0<0.57375$, then one should be able to have an arbitrage. In fact, by constructing the following zero-cost trading strategy, that is shorting $a_0$ units of ${\tilde{1}}^{10}$ at time $t=0$ and then shorting ${\displaystyle \frac{a_0}{g_0^1}}$ units of ${\tilde{S}}^{i1}=(0,b_1^2,-S_2)$ at time $t=1$ one would have a negative balance of

$$\frac{a_0}{g_0^1}\frac{S_2}{b_1^2}<c_2$$

smaller than $c_2$, thus an arbitrage.

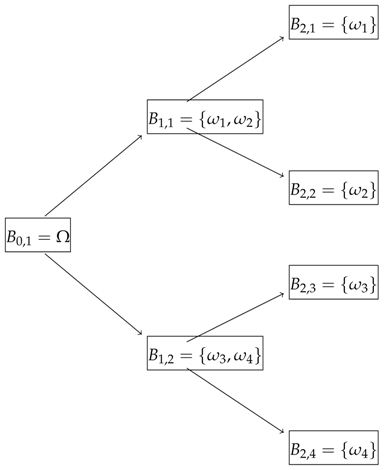
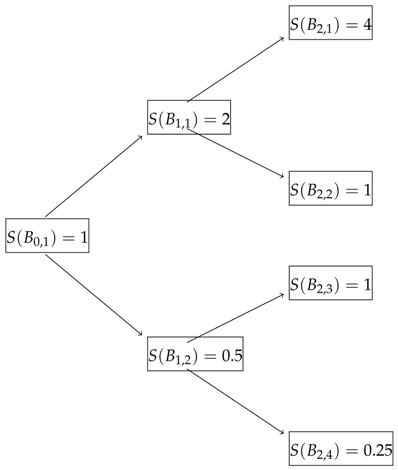
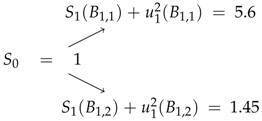
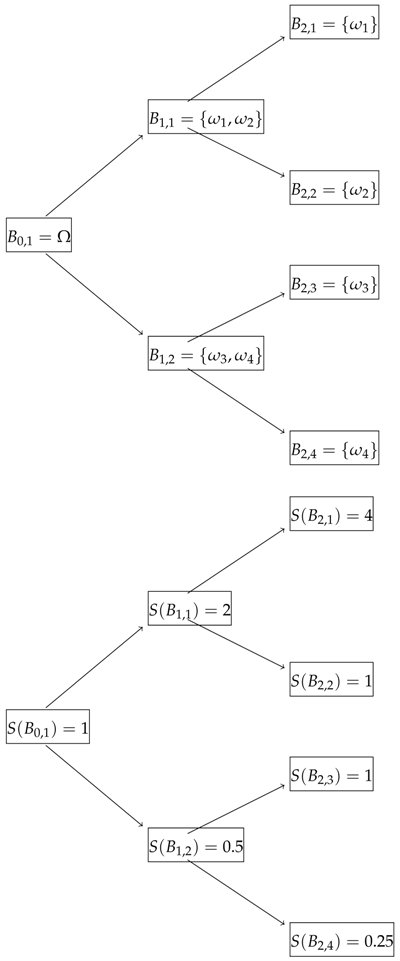
4.3.2. Involving 2-Period Bond

As we noticed above, the arbitrage trading strategy was involved with a bond on the first period and risky asset on second period. This was not coincidental since the cash flow $c_2$ was a very simplified case, also derived from the risky asset which itself was priced by the risk-free bond. In fact we had no need nor had to solve the dual problem. However. in a more general case we need to write the dual problem and solve it to find the solution and optimal value. Thus, let us consider the following maximization problem for the following diagram

that is

$${\displaystyle p_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,1}\right)=max\left[{\displaystyle r_1\left(B_{1,1}\right)c_2\left(B_{2,1}\right)+r_2\left(B_{1,1}\right)c_2\left(B_{2,2}\right)}\right]\left(B_{1,1}\right)}\\ {\displaystyle g_1^2\left(B_{1,1}\right)\le r_1\left(B_{1,1}\right)+r_2\left(B_{1,1}\right)\le h_1^2\left(B_{1,1}\right),}\\ {\displaystyle b_1^2\left(B_{1,1}\right)\le r_1\left(B_{1,1}\right)S_2\left(B_{2,1}\right)+r_2\left(B_{1,1}\right)S_2\left(B_{2,2}\right)\le a_1^2\left(B_{1,1}\right).}\end{array}\right.}$$

(23)

for which the constrains in all one-sided inequalities can be written as

$${\displaystyle p_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,1}\right)=max\left[{\displaystyle r_1\left(B_{1,1}\right)c_2\left(B_{2,1}\right)+r_2\left(B_{1,1}\right)c_2\left(B_{2,2}\right)}\right]\left(B_{1,1}\right)}\\ {\displaystyle r_1\left(B_{1,1}\right)+r_2\left(B_{1,1}\right)\le h_1^2\left(B_{1,1}\right),}\\ {\displaystyle -r_1\left(B_{1,1}\right)-r_2\left(B_{1,1}\right)\le -g_1^2\left(B_{1,1}\right),}\\ {\displaystyle r_1\left(B_{1,1}\right)S_2\left(B_{2,1}\right)+r_2\left(B_{1,1}\right)S_2\left(B_{2,2}\right)\le a_1^2\left(B_{1,1}\right),}\\ {\displaystyle -r_1\left(B_{1,1}\right)S_2\left(B_{2,1}\right)-r_2\left(B_{1,1}\right)S_2\left(B_{2,2}\right)\le -b_1^2\left(B_{1,1}\right),}\\ r_1,r_2\ge 0.\end{array}\right.}$$

(24)

and having the objective function and constrains in matrix form we have

$${\displaystyle p_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,1}\right)=max\left(\left[\begin{array}{cc}{c}_2\left(B_{2,1}\right)& c_2\left(B_{2,2}\right)\end{array}\right]\left[\begin{array}{c}{r}_1\left(B_{1,1}\right)\\ r_2\left(B_{1,1}\right)\end{array}\right]\right)}\\ \left[\begin{array}{cc}1& 1\\ -1& -1\\ S_2\left(B_{2,1}\right)& S_2\left(B_{2,2}\right)\\ -S_2\left(B_{2,1}\right)& -S_2\left(B_{2,2}\right)\end{array}\right]\left[\begin{array}{c}{r}_1\left(B_{1,1}\right)\\ r_2\left(B_{1,1}\right)\end{array}\right]\le \left[\begin{array}{c}{h}_1^2\left(B_{1,1}\right)\\ -g_1^2\left(B_{1,1}\right)\\ a_1^2\left(B_{1,1}\right)\\ -b_1^2\left(B_{1,1}\right)\end{array}\right],\\ r_1,r_2\ge 0.\end{array}\right.}$$

(25)

Now we write the dual to this linear programming problem which is

$${\displaystyle d_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,1}\right)=min\left(\left[\begin{array}{cccc}{h}_1^2\left(B_{1,1}\right)& -g_1^2\left(B_{1,1}\right)& a_1^2\left(B_{1,1}\right)& -b_1^2\left(B_{1,1}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\right)}\\ \left[\begin{array}{cccc}1& -1& S_2\left(B_{2,1}\right)& -S_2\left(B_{2,1}\right)\\ 1& -1& S_2\left(B_{2,2}\right)& -S_2\left(B_{2,2}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\ge \left[\begin{array}{c}{c}_2\left(B_{2,1}\right)\\ c_2\left(B_{2,2}\right)\end{array}\right],\\ t_1,t_2,t_3,t_4\ge 0.\end{array}\right.}$$

(26)

or equivalently

$${\displaystyle d_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,1}\right)=min\left(\left[\begin{array}{cccc}{h}_1^2\left(B_{1,1}\right)& -g_1^2\left(B_{1,1}\right)& a_1^2\left(B_{1,1}\right)& -b_1^2\left(B_{1,1}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\right)}\\ \left[\begin{array}{cccc}-1& 1& -S_2\left(B_{2,1}\right)& S_2\left(B_{2,1}\right)\\ -1& 1& -S_2\left(B_{2,2}\right)& S_2\left(B_{2,2}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\le \left[\begin{array}{c}-c_2\left(B_{2,1}\right)\\ -c_2\left(B_{2,2}\right)\end{array}\right],\\ t_1,t_2,t_3,t_4\ge 0.\end{array}\right.}$$

(27)

If we let, as an example, $a_1^2\left(B_{1,1}\right)=3$, $b_1^2\left(B_{1,1}\right)=2$, $c_2\left(B_{2,1}\right)=3$ and $c_2\left(B_{2,2}\right)=2$, then by solving Equation (27) using linear programming with complementary slackness conditions (we used MATLAB for our purpose) we have ${\displaystyle t_1=\frac{5}{3},t_3=\frac{1}{3},t_2=t_4=0}$ (which is the solution to the dual problem $d_1$ and indicates the portfolio strategy one needs to choose in the case of existence of any arbitrage opportunity) and $u_1^2\left(B_{1,1}\right)=2.5$.

Similarly by solving the dual problem for the other part of the diagram

that is

$${\displaystyle d_1:=\left\{\begin{array}{c}{\displaystyle u_1^2\left(B_{1,2}\right)=min\left(\left[\begin{array}{cccc}{h}_1^2\left(B_{1,2}\right)& -g_1^2\left(B_{1,2}\right)& a_1^2\left(B_{1,2}\right)& -b_1^2\left(B_{1,2}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\right)}\\ \left[\begin{array}{cccc}-1& 1& -S_2\left(B_{2,3}\right)& S_2\left(B_{2,3}\right)\\ -1& 1& -S_2\left(B_{2,4}\right)& S_2\left(B_{2,4}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\le \left[\begin{array}{c}-c_2\left(B_{2,3}\right)\\ -c_2\left(B_{2,4}\right)\end{array}\right].\\ t_1,t_2,t_3,t_4\ge 0.\end{array}\right.}$$

(28)

and if we let $a_1^2\left(B_{1,2}\right)=0.7$ and $b_1^2\left(B_{1,2}\right)=0.4$ also let $c_2\left(B_{2,3}\right)=1$ and $c_2\left(B_{2,2}\right)=0.5$, then the solution is ${\displaystyle t_1=\frac{1}{3},t_2=t_4=0,t_3=\frac{2}{3}}$ and ${\displaystyle u_1^2\left(B_{1,2}\right)=0.7833}$.

Now for the last part consider the following picture and its corresponding linear programming in dual form

with

$${\displaystyle d_1:=\left\{\begin{array}{c}{\displaystyle u_0^2\left(B_{0,1}\right)=min\left(\left[\begin{array}{cccc}{h}_0^1\left(B_{0,1}\right)& -g_0^1\left(B_{0,1}\right)& a_0^1\left(B_{0,1}\right)& -b_0^1\left(B_{0,1}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\right)}\\ \left[\begin{array}{cccc}-1& 1& -S_1\left(B_{1,1}\right)& S_1\left(B_{1,1}\right)\\ -1& 1& -S_1\left(B_{1,2}\right)& S_1\left(B_{1,2}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\le \left[\begin{array}{c}-u_1^2\left(B_{1,1}\right)\\ -u_1^2\left(B_{1,2}\right)\end{array}\right],\\ t_1,t_2,t_3,t_4\ge 0.\end{array}\right.}$$

(29)

for which when $a_0^1\left(B_{0,1}\right)=1.6,b_0^1\left(B_{0,1}\right)=1.5$ (here we simply assumed that $c_1=0$), the corresponding solution becomes ${\displaystyle t_1=\frac{19}{90},t_3=\frac{103}{90},t_2=t_4=0}$ and $u_0^2\left(B_{0,1}\right)=2.0317$. For any bid price offered at time $t=0$ larger than $2.0317$, there is an arbitrage and the trading strategy is as following:

buy ${\displaystyle \frac{19}{90}}$ units of $1^{10}$ and ${\displaystyle \frac{103}{90}}$ units of $S^{01}$ and at time $t=1$ in either case we are able cover the asked price of $c_2$ at time $t=2$. In fact in the case of $B_{1,1}$ possibility, we buy ${\displaystyle \frac{5}{3}}$ units of $1^{21}$ and ${\displaystyle \frac{1}{3}}$ units of $S^{12}$, and in the case of $B_{1,2}$ possibility, we buy ${\displaystyle \frac{1}{3}}$ units of $1^{21}$ and ${\displaystyle \frac{2}{3}}$ units of $S^{12}$, and in either case $c_2$ will be covered to deliver and the difference will be an arbitrage.

As we noted in the last diagram, at least ${\displaystyle \frac{1}{3}}$ of the risk-free bond $1^{21}$ is needed to be bought at time $t=1$. Now we consider a trading strategy which purchases $\frac{1}{3}$ of the bond $1^{20}$ bought at time $t=0$. Therefore the trading strategy can be replaced by

where $t_1,t_2,t_3,t_4$ are the solutions to the new linear programming problem below

$${\displaystyle \left\{\begin{array}{c}{\displaystyle min\left(\left[\begin{array}{cccc}{h}_0^1\left(B_{0,1}\right)& -g_0^1\left(B_{0,1}\right)& a_0^1\left(B_{0,1}\right)& -b_0^1\left(B_{0,1}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\right)}\\ \left[\begin{array}{cccc}-1& 1& -S_1\left(B_{1,1}\right)& S_1\left(B_{1,1}\right)\\ -1& 1& -S_1\left(B_{1,2}\right)& S_1\left(B_{1,2}\right)\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\\ t_4\end{array}\right]\le \left[\begin{array}{c}-{\tilde{u}}_1^2\left(B_{1,1}\right)\\ -{\tilde{u}}_1^2\left(B_{1,2}\right)\end{array}\right],\\ t_1,t_2,t_3,t_4\ge 0.\end{array}\right.}$$

(30)

and

$$\left\{\begin{array}{l}{\displaystyle {\tilde{u}}_1^2\left(B_{1,1}\right)=\frac{4}{3}{h}_1^2\left(B_{1,1}\right)+\frac{1}{3}{a}_1^2\left(B_{1,1}\right)=\frac{11}{5}}\\ {\displaystyle {\tilde{u}}_1^2\left(B_{1,2}\right)=\frac{2}{3}{a}_1^2\left(B_{1,2}\right)=\frac{7}{15}}\end{array}\right.$$

(31)

Solution to the linear programming above is ${\displaystyle t_2=t_4=0,t_1=\frac{1}{9},t_3=\frac{73}{72}}$ so that the largest ask price for $c_2$ in this case becomes

$$\frac{1}{3}{h}_0^2+\frac{1}{9}\left(h_0^1\right)+\frac{73}{72}{a}_0^1=2.02778$$

and as we see, this upper bound is smaller and much more accurate than the upper bound $u_0^2=2.0317$ which we found above without using the $1^{20}$ bond.

Now consider the cash flow $(.,c_1,c_2)$ and let $\alpha$ to be the portion of $1^{20}=(-h_0^2,0,1)$ that we carry in the trading strategy at time $t=0$. We would like to find the highest ask-price at time $t=0$ for this cash flow. Therefore we consider the following maximization problem and unlike the example above, we try to solve this problem in one step

$$\left\{\begin{array}{c}{\displaystyle u_0^2=max{\mathbf{E}}_0\left[f_0^1{c}_1+f_0^2{c}_2\right]=max{\mathbf{E}}_0\left[f_0^2\alpha +f_0^1\left(c_1+{\mathbf{E}}_1\left[f_0^2\left(c_2-\alpha \right)\right]\right)\right]}\\ {\displaystyle g_0^1\le {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1,}\\ {\displaystyle g_0^2\le {\mathbf{E}}_0\left[f_0^2\right]\le h_0^2,}\\ {\displaystyle b_0^2\le {\mathbf{E}}_0\left[f_0^1{S}_1+f_0^2{S}_2\right]\le a_0^2,}\end{array}\right.$$

(32)

and by the definition of expectation and letting ${\displaystyle r_{ij}=f_0^i\left(B_{i,j}\right)Q\left(B_{i,j}\right)}$ we have

$$u_0^2\left(\alpha \right)=max\{\alpha \left[s_{21}+s_{22}+s_{23}+s_{24}\right]+r_{11}\left[c_1\left(B_{11}\right)+r_{21}{c}_2\left(B_{21}\right)+r_{22}{c}_2\left(B_{22}\right)\right]$$

$$+r_{12}\left[c_1\left(B_{12}\right)+r_{23}{c}_2\left(B_{23}\right)+r_{24}{c}_2\left(B_{24}\right)\right]-\alpha \left[r_{11}(r_{21}+r_{22})+r_{12}(r_{23}+r_{24})\right]\}$$

where

$$\left\{\begin{array}{c}{r}_{11}+r_{12}\le h_0^1,\\ -r_{11}-r_{12}\le -g_0^1,\\ s_{21}+s_{22}+s_{23}+s_{24}\le h_0^2,\\ -s_{21}-s_{22}-s_{23}-s_{24}\le -g_0^2,\\ r_{11}\left[S_1\left(B_{11}\right)+r_{21}{S}_2\left(B_{21}\right)+r_{22}{S}_2\left(B_{22}\right)\right]+r_{12}\left[S_1\left(B_{12}\right)+r_{23}{S}_2\left(B_{23}\right)+r_{24}{S}_2\left(B_{24}\right)\right]\le a_0^2,\\ -r_{11}\left[S_1\left(B_{11}\right)+r_{21}{S}_2\left(B_{21}\right)+r_{22}{S}_2\left(B_{22}\right)\right]-r_{12}\left[S_1\left(B_{12}\right)+r_{23}{S}_2\left(B_{23}\right)+r_{24}{S}_2\left(B_{24}\right)\right]\le b_0^2.\end{array}\right.$$

(33)

As we can see, the above linear programming is a ten variable linear programming with one parameter $\alpha$ and this is only for a binary priced market where at each time there are only two possibilities for the stock and cash flow price. We are only considering one risky asset.

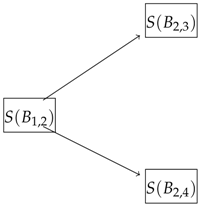
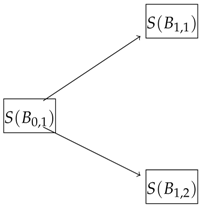
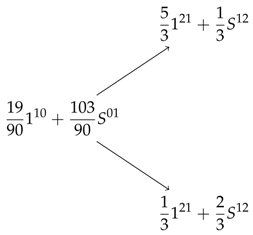
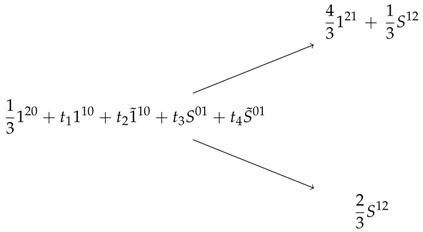
4.4. Complexity of Multi-Period Model

Consider a 2-period model and let $v_2$ be the number of variables in the linear programming associated with this model and $p_2$ be the number of parameters associated with 2-period bonds in this model. We already know that $v_1=2$ and $p_1=0$. We can see that adding a single 1-period bond into the model, adds 2 variables and one parameter to the linear programming problem.

On the other hand a 2-period model is equivalent to a composition of a 1-period model followed by two 1-period models as illustrated in following diagram

Since a 2-period model is the composition of a 1-period followed by two 1-period models, then $\left(\begin{array}{c}{v}_2\\ p_2\end{array}\right)$=$\left(\begin{array}{c}{v}_1\\ p_1\end{array}\right)$ + 2 $\left(\begin{array}{c}{v}_1\\ p_1\end{array}\right)$ + 2-period bond =$\left(\begin{array}{c}2\\ 0\end{array}\right)$+2$\left(\begin{array}{c}2\\ 0\end{array}\right)$+$\left(\begin{array}{c}4\\ 1\end{array}\right)$= $\left(\begin{array}{c}10\\ 1\end{array}\right)$ which coincides with what we found before. This is the case for a over simplified case, binary model with a two states at each time.

Now consider a T-period model and let $v_T$ be the number of variables in the linear programming associated with this model and $p_T$ be the number of parameters associated with multi-period bonds in this model. A T-period model is equivalent to a composition of a 1-period model followed by two $(T-1)$-period models as illustrated in following diagram

For example, a 3-period model is the composition of a 1-period followed by two 2-period models, so that

$\left(\begin{array}{c}{v}_3\\ p_3\end{array}\right)$=$\left(\begin{array}{c}{v}_1\\ p_1\end{array}\right)$ + 2 $\left(\begin{array}{c}{v}_2\\ p_2\end{array}\right)$ + 2-period bond + 3-period bond

  =$\left(\begin{array}{c}2\\ 0\end{array}\right)$+2$\left(\begin{array}{c}10\\ 1\end{array}\right)$+$\left(\begin{array}{c}4\\ 1\end{array}\right)$+$\left(\begin{array}{c}8\\ 1\end{array}\right)$= $\left(\begin{array}{c}34\\ 4\end{array}\right)$

Now for a T-period model we have

$\left(\begin{array}{c}{v}_T\\ p_T\end{array}\right)$=$\left(\begin{array}{c}{v}_1\\ p_1\end{array}\right)$ + 2 $\left(\begin{array}{c}{v}_{T-1}\\ p_{T-1}\end{array}\right)$ + 2-period bond + 3-period bond +⋯+ T-period bond =$\left(\begin{array}{c}2\\ 0\end{array}\right)$+2 $\left(\begin{array}{c}{v}_{T-1}\\ p_{T-1}\end{array}\right)$ + $\left(\begin{array}{c}4\\ 1\end{array}\right)$+$\left(\begin{array}{c}8\\ 1\end{array}\right)$ + ⋯ + $\left(\begin{array}{c}{2}^T\\ 1\end{array}\right)$=$\left(\begin{array}{c}2v_{T-1}+2+4+8+\dots +2^T\\ 2p_{T-1}+T-1\end{array}\right)$

or

$\left(\begin{array}{c}{v}_T\\ p_T\end{array}\right)$ = $\left(\begin{array}{c}2v_{T-1}+2^{T+1}-2\\ 2p_{T-1}+T-1\end{array}\right)$

As it can be seen, when the periods of the model increases, the number of variables and parameters increase at an exponential rate. Considering the fact that this calculation was only done for the simplest case of a model (binary prices and one risky asset) we notice that for a T-period model, the parametrized linear programming with $p_T$ parameters and $v_T$ variables make the problem very complicated to solve.

Lemma 1.

For a T-period model with $v_T$ as the number of variables in the linear programming associated with the model and $p_T$ as the number of parameters associated with multi-period bonds, we have

$$\left(\begin{array}{c}{v}_2\\ p_2\end{array}\right)=\left(\begin{array}{c}2\\ 0\end{array}\right)\mathrm{and}\left(\begin{array}{c}{v}_T\\ p_T\end{array}\right)=\left(\begin{array}{c}2v_{T-1}+2^{T+1}-2\\ 2p_{T-1}+T-1\end{array}\right)$$

(34)

As a result of the reason explained above, we suggest solving the problem one step at a time, which means (similar to the 2-period linear programming problem that we solved) starting form the end and solving multiple 1-period problems on each step and continuing this process backward until we reach the initial time on the problem.

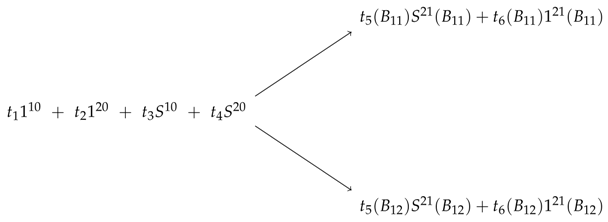
4.5. Estimate of Multi-Period Bounds (Breaking into One Periods)

Consider the following portfolio of zero-cost cash flows

$$(p_0,p_1,p_2)=t_1{1}^{10}+t_2{1}^{20}+t_3{S}^{10}+t_4{S}^{20}+t_5{S}^{21}+t_6{1}^{21}$$

$$=t_1\left(-h_0^1,1,0\right)+t_2\left(-h_0^2,0,1\right)+t_3\left(-a_0^1,S_1,0\right)+t_4(-a_0^2,0,S_2)$$

$$+t_5\left(0,-a_1^2,1\right)+t_6\left(0,-h_1^2,1\right)$$

(35)

where

$$p_0=-t_1{h}_0^1-t_2{h}_0^2-t_3{a}_0^1-t_4{a}_0^2$$

$$p_1=t_1+t_3{S}_1-t_5{a}_1^2-t_6{h}_1^2$$

$$p_2=t_2+t_4{S}_2+t_5{S}_2+t_6$$

(36)

also $t_1,t_2,t_3,t_4\in {\mathcal{F}}_0$ and $t_5,t_6\in {\mathcal{F}}_1$. In fact we have the following trading diagram corresponding to the above portfolio at time $t=0$ and $t=1$

Since we are assuming to deliver $c_2\in {\mathcal{F}}_2$ at $t=2$, indeed we have to solve the linear programing problem

$$\left\{\begin{array}{c}min(-p_0)\\ \mathrm{such}\mathrm{that};\\ p_1\ge 0\\ p_2-c_2\ge 0\\ t_1,\dots ,t_6\ge 0\end{array}\right.$$

(37)

We can define the corresponding Lagrangian as

$$\mathcal{L}(t_1,\dots ,t_6,{\lambda }_1,{\lambda }_2)=(-p_0)-{\lambda }_1{p}_1-{\lambda }_2(p_2-c_2)$$

(38)

where ${\lambda }_1\in {\mathcal{F}}_1$ and ${\lambda }_2\in {\mathcal{F}}_2$ are the random variable Lagrange multipliers. Therefore our minimization problem can be stated as

$$\underset{t\ge 0}{inf}\underset{\lambda \ge 0}{sup}\mathcal{L}(t_1,\dots ,t_6,{\lambda }_1,{\lambda }_2)$$

(39)

where

$$\begin{array}{cc}\hfill & \mathcal{L}(t_1,\dots ,t_6,{\lambda }_1\left(B_{11}\right),{\lambda }_1\left(B_{12}\right),{\lambda }_2\left(B_{21}\right),{\lambda }_2\left(B_{22}\right),{\lambda }_2\left(B_{24}\right),{\lambda }_2\left(B_{24}\right))=\hfill \\ \hfill & t_1{h}_0^1+t_2{h}_0^2+t_3{a}_0^1+t_4{a}_0^2\hfill \\ \hfill & -{\lambda }_1\left(B_{11}\right)\left[t_1+t_3{S}_1\left(B_{11}\right)-t_5\left(B_{11}\right)a_1^2\left(B_{11}\right)-t_6\left(B_{11}\right)h_1^2\left(B_{11}\right)\right]\hfill \\ \hfill & -{\lambda }_1\left(B_{12}\right)\left[t_1+t_3{S}_1\left(B_{12}\right)-t_5\left(B_{12}\right)a_1^2\left(B_{12}\right)-t_6\left(B_{12}\right)h_1^2\left(B_{12}\right)\right]\hfill \\ \hfill & -{\lambda }_2\left(B_{21}\right)\left[t_2+t_4{S}_2\left(B_{21}\right)+t_5\left(B_{11}\right)S_2\left(B_{21}\right)+t_6\left(B_{11}\right)-c_2\left(B_{21}\right)\right]\hfill \\ \hfill & -{\lambda }_2\left(B_{22}\right)\left[t_2+t_4{S}_2\left(B_{22}\right)+t_5\left(B_{11}\right)S_2\left(B_{22}\right)+t_6\left(B_{11}\right)-c_2\left(B_{22}\right)\right]\hfill \\ \hfill & -{\lambda }_2\left(B_{23}\right)\left[t_2+t_4{S}_2\left(B_{23}\right)+t_5\left(B_{12}\right)S_2\left(B_{23}\right)+t_6\left(B_{12}\right)-c_2\left(B_{23}\right)\right]\hfill \\ \hfill & -{\lambda }_2\left(B_{24}\right)\left[t_2+t_4{S}_2\left(B_{24}\right)+t_5\left(B_{12}\right)S_2\left(B_{24}\right)+t_6\left(B_{12}\right)-c_2\left(B_{24}\right)\right]\hfill \end{array}$$

(40)

Now by Linearity Constraint Qualification the problem is feasible so that by Lagrangian strong duality we have

$$\underset{t\ge 0}{inf}\underset{\lambda \ge 0}{sup}\mathcal{L}(t_1,\dots ,t_6,{\lambda }_1,{\lambda }_2)=\underset{\lambda \ge 0}{sup}\underset{t\ge 0}{inf}\mathcal{L}(t_1,\dots ,t_6,{\lambda }_1,{\lambda }_2)$$

(41)

hence $\mathcal{L}(t_1,\dots ,t_6,{\lambda }_1,{\lambda }_2)$ can be written as

$$\begin{array}{cc}\hfill & \mathcal{L}(t_1,\dots ,t_6,{\lambda }_1\left(B_{11}\right),{\lambda }_1\left(B_{12}\right),{\lambda }_2\left(B_{21}\right),{\lambda }_2\left(B_{22}\right),{\lambda }_2\left(B_{24}\right),{\lambda }_2\left(B_{24}\right))\hfill \\ \hfill & =t_1\left[h_0^1-\sum _{j=1}^2{\lambda }_1\left(B_{1j}\right)\right]+t_2\left[h_0^2-\sum _{k=1}^4{\lambda }_2\left(B_{2k}\right)\right]\hfill \\ \hfill & +t_3\left[a_0^1-\sum _{j=1}^2{\lambda }_1\left(B_{1j}\right)S_1\left(B_{1j}\right)\right]+t_4\left[a_0^2-\sum _{k=1}^4{\lambda }_2\left(B_{2k}\right)S_2\left(B_{2k}\right)\right]\hfill \\ \hfill & +t_5\left(B_{11}\right)\left[{\lambda }_1\left(B_{11}\right)a_1^2\left(B_{11}\right)-{\lambda }_2\left(B_{21}\right)S_2\left(B_{21}\right)-{\lambda }_2\left(B_{22}\right)S_2\left(B_{22}\right)\right]\hfill \\ \hfill & +t_5\left(B_{12}\right)\left[{\lambda }_1\left(B_{12}\right)a_1^2\left(B_{12}\right)-{\lambda }_2\left(B_{23}\right)S_2\left(B_{23}\right)-{\lambda }_2\left(B_{24}\right)S_2\left(B_{24}\right)\right]\hfill \\ \hfill & +t_6\left(B_{11}\right)\left[{\lambda }_1\left(B_{11}\right)h_1^2\left(B_{11}\right)-{\lambda }_2\left(B_{21}\right)-{\lambda }_2\left(B_{22}\right)\right]\hfill \\ \hfill & +t_6\left(B_{12}\right)\left[{\lambda }_1\left(B_{12}\right)h_1^2\left(B_{12}\right)-{\lambda }_2\left(B_{23}\right)-{\lambda }_2\left(B_{24}\right)\right]\hfill \\ \hfill & +\sum _{k=1}^4{\lambda }_2\left(B_{2k}\right)c_2\left(B_{2k}\right)\hfill \end{array}$$

(42)

We can see that the corresponding maximization problem to the Lagrangian above is

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & max\left(\sum _{k=1}^4{\lambda }_2\left(B_{2k}\right)c_2\left(B_{2k}\right)\right)\hfill \\ \hfill & \mathrm{such}\mathrm{that};\hfill \\ \hfill & {\lambda }_1\left(B_{11}\right)+{\lambda }_1\left(B_{12}\right)\le h_0^1\hfill \\ \hfill & {\lambda }_2\left(B_{21}\right)+{\lambda }_2\left(B_{22}\right)+{\lambda }_2\left(B_{23}\right)+{\lambda }_2\left(B_{24}\right)\le h_0^2\hfill \\ \hfill & {\lambda }_1\left(B_{11}\right)S_1\left(B_{11}\right)+{\lambda }_1\left(B_{12}\right)S_1\left(B_{12}\right)\le a_0^1\hfill \\ \hfill & {\lambda }_2\left(B_{21}\right)S_2\left(B_{21}\right)+{\lambda }_2\left(B_{22}\right)S_2\left(B_{22}\right)+{\lambda }_2\left(B_{23}\right)S_2\left(B_{23}\right)+{\lambda }_2\left(B_{24}\right)S_2\left(B_{24}\right)\le a_0^2\hfill \\ \hfill & {\displaystyle \frac{{\lambda }_2\left(B_{21}\right)}{{\lambda }_1\left(B_{11}\right)}{S}_2\left(B_{21}\right)+\frac{{\lambda }_2\left(B_{22}\right)}{{\lambda }_1\left(B_{11}\right)}{S}_2\left(B_{22}\right)\le a_1^2\left(B_{11}\right)}\hfill \\ \hfill & {\displaystyle \frac{{\lambda }_2\left(B_{23}\right)}{{\lambda }_1\left(B_{12}\right)}{S}_2\left(B_{23}\right)+\frac{{\lambda }_2\left(B_{24}\right)}{{\lambda }_1\left(B_{12}\right)}{S}_2\left(B_{24}\right)\le a_1^2\left(B_{12}\right)}\hfill \\ \hfill & {\displaystyle \frac{{\lambda }_2\left(B_{21}\right)}{{\lambda }_1\left(B_{11}\right)}+\frac{{\lambda }_2\left(B_{22}\right)}{{\lambda }_1\left(B_{11}\right)}\le h_1^2\left(B_{11}\right)}\hfill \\ \hfill & {\displaystyle \frac{{\lambda }_2\left(B_{23}\right)}{{\lambda }_1\left(B_{12}\right)}+\frac{{\lambda }_2\left(B_{24}\right)}{{\lambda }_1\left(B_{12}\right)}\le h_1^2\left(B_{12}\right)}\hfill \\ \hfill & {\lambda }_1,{\lambda }_2\ge 0\hfill \end{array}\end{array}\right.$$

(43)

Unsurprisingly, we observe that ${\lambda }_1,{\lambda }_2$ are the pricing factors in the expectation form. In fact, as we defined before, if we let

$$\begin{array}{cc}\hfill & {\displaystyle {\lambda }_1\left(B_{1j}\right)=f_0^1\left(B_{1j}\right)=r_{1j}j=1,2}\hfill \\ \hfill & {\displaystyle {\lambda }_2\left(B_{1k}\right)=f_0^2\left(B_{1k}\right)=u_{k}k=1,2,3,4}\hfill \\ \hfill & {\displaystyle {\lambda }_2\left(B_{1k}\right)=f_1^2\left(B_{2k}\right)=r_{2k}k=1,2,3,4}\hfill \end{array}$$

(44)

then the linear programming in Equation (43) becomes

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & max\left(u_1{c}_2\left(B_{21}\right)+u_2{c}_2\left(B_{22}\right)+u_3{c}_2\left(B_{23}\right)+u_4{c}_2\left(B_{24}\right)\right)\hfill \\ \hfill & \mathrm{such}\mathrm{that};\hfill \\ \hfill & r_{11}+r_{12}\le h_0^1\hfill \\ \hfill & u_1+u_2+u_3+u_4\le h_0^2\hfill \\ \hfill & r_{11}{S}_1\left(B_{11}\right)+r_{12}{S}_1\left(B_{12}\right)\le a_0^1\hfill \\ \hfill & u_1{S}_2\left(B_{21}\right)+u_2{S}_2\left(B_{22}\right)+u_3{S}_2\left(B_{23}\right)+u_4{S}_2\left(B_{24}\right)\le a_0^2\hfill \\ \hfill & {\displaystyle r_{21}{S}_2\left(B_{21}\right)+r_{22}{S}_2\left(B_{22}\right)\le a_1^2\left(B_{11}\right)}\hfill \\ \hfill & {\displaystyle r_{23}{S}_2\left(B_{23}\right)+r_{24}{S}_2\left(B_{24}\right)\le a_1^2\left(B_{12}\right)}\hfill \\ \hfill & {\displaystyle r_{21}+r_{22}\le h_1^2\left(B_{11}\right)}\hfill \\ \hfill & {\displaystyle r_{23}+r_{24}\le h_1^2\left(B_{12}\right)}\hfill \\ \hfill & r_{11},r_{12},r_{21},r_{22},r_{23},r_{24},u_1,u_2,u_3,u_4\ge 0\hfill \end{array}\end{array}\right.$$

(45)

which, as we can see, is the primal maximization problem (the dual of the dual in this case) corresponding to our initial portfolio. We can also observe that the problem in Equation (45) is indeed the expectation form of a super-hedging problem as

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & max{\mathbf{E}}_0\left[f_0^2{c}_2\right]\hfill \\ \hfill & \mathrm{such}\mathrm{that};\hfill \\ \hfill & {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1\hfill \\ \hfill & {\mathbf{E}}_0\left[f_0^2\right]\le h_0^2\hfill \\ \hfill & {\mathbf{E}}_0\left[f_0^1{S}_1\right]\le a_0^1\hfill \\ \hfill & {\mathbf{E}}_0\left[f_0^2{S}_2\right]\le a_0^2\hfill \\ \hfill & {\mathbf{E}}_1\left[f_1^2{S}_2\right]\le a_1^2\hfill \\ \hfill & {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2\hfill \end{array}\end{array}\right.$$

(46)

Solving the linear programming problem in Equation (45) we have the following solutions

$t_1$	1.3327	$t_5\left(B_{11}\right)$	0.1371
$t_2$	0.5256	$t_5\left(B_{12}\right)$	0.4847
$t_3$	0.2725	$t_6\left(B_{11}\right)$	1.5377
$t_4$	0.0969	$t_6\left(B_{12}\right)$	0.6964

with a super-hedging value of

$$u_0^2=2.5649$$

As we notice, there is slightly small decrease on the value of upper bound for the asked price comparing with the case where we calculated this upper bound one step at a time. This is completely justified because the minimization above has more constraints since we are using the two-period bond and asset to formulate our problem. As we stated before, for multi-period cases (that requires us to solve linear models with multiple variables and parameters with a very small adjustments) we will find the upper-bound and lower-bound by solving linear programming problems one at a time.

4.6. The General 2-Period Model

In this section we use the results from the examples in this section to summarize the two different cases on a 2-period model. First case is when one can use all possibilities of bonds and assets (both 1-period and 2-periods).

Theorem 5.

Let $T=2$, $t=0,1$, $c=(c_1,c_2)\in \mathcal{C}$ an acceptable cash flow and consider the following linear programing problem

$$\left\{\begin{array}{c}{\displaystyle u_0^2\left(II\right)=sup{\mathbf{E}}_0\left[f_0^1{c}_1+f_0^2{c}_2\right]}\\ subjectto\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1,{\mathbf{E}}_0\left[f_0^1\left(-1\right)\right]\le -g_0^1,}\\ {\displaystyle {\mathbf{E}}_0\left[f_0^2\right]\le h_0^2,{\mathbf{E}}_0\left[f_0^2\left(-1\right)\right]\le -g_0^2,}\\ {\displaystyle {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2,{\mathbf{E}}_1\left[f_1^2\left(-1\right)\right]\le -g_1^2,}\\ {\displaystyle {\mathbf{E}}_1\left[f_1^2{S}_2^i\right]\le a_1^i,{\mathbf{E}}_1\left[f_1^2\left(-S_2^i\right)\right]\le -b_1^i,}\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1{S}_1^i+f_0^2{S}_2^i\right]\le a_0^i,}\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1\left(-S_1^i\right)+f_0^2\left(-S_2^i\right)\right]\le -b_0^i.}\end{array}\right.$$

(47)

Then $u_0^2\left(II\right)$ is a super-hedging bound and the solution to dual problem is a portfolio by which one is able to construct an arbitrage opportunity if the market bid price of c exceeds $u_0^2\left(II\right)$.

Proof. 

In Appendix A.  □

In this version of the problem one is able to take advantage of the both 2-period bond and assets, however as we saw before there is some complexity in solving and finding the right strategy to construct the portfolio, where as the number of assets and their price possibilities increase, the complexity of finding the right portfolio strategy increases exponentially.

On the other hand, we can find a super-hedge value for a 2-period linear programming problem by solving two 1-period problems successively, in which case we have the following theorem.

Theorem 6.

Let $c=(c_1,c_2)\in \mathcal{C}$ be an acceptable cash flow and suppose

$$\left\{\begin{array}{c}{\displaystyle u_1^2=sup{\mathbf{E}}_1\left[f_1^2{c}_2\right]}\\ subjectto\\ {\displaystyle {\mathbf{E}}_1\left[f_1^2\right]\le h_1^2,{\mathbf{E}}_1\left[f_1^2\left(-1\right)\right]\le -g_1^2,}\\ {\displaystyle {\mathbf{E}}_1\left[f_1^2{S}_2^i\right]\le a_1^i,{\mathbf{E}}_1\left[f_1^2\left(-S_2^i\right)\right]\le -b_1^i.}\end{array}\right.$$

(48)

is a super-hedging bound for $c_2$ paid at time $t=1$ (the largest ask price for $c_2$ under no-arbitrage assumption). Now consider the following linear programming problem

$$\left\{\begin{array}{c}{\displaystyle u_0^2\left(I\right)=sup{\mathbf{E}}_0\left[f_0^1\left(c_1+u_1^2\right)\right]}\\ subjectto\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1\right]\le h_0^1,{\mathbf{E}}_0\left[f_0^1\left(-1\right)\right]\le -g_0^1,}\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1{S}_1^i\right]\le a_0^i,}\\ {\displaystyle {\mathbf{E}}_0\left[f_0^1\left(-S_1^i\right)\right]\le -b_0^i.}\end{array}\right.$$

(49)

then the solution to linear programming problems in Equations (48) and (49) and their duals gives us a trading strategy by which we can take advantage if any arbitrage opportunity is available.

Proof. 

In Appendix A.  □

As we saw above, we can find a super-hedging bound by two different approaches and because of that there is a slight difference in the values of $u_0^2\left(I\right)$ on these two approaches. The following theorem summarizes our above discussion on an upper bound for the difference between two values.

Theorem 7.

Let $u_0^2\left(II\right)$ and $u_0^2\left(I\right)$ be the two super-hedging values found in Theorem (5) and Theorem (6) respectively. Then

(1)

${\displaystyle u_0^2\left(II\right)\le u_0^2\left(I\right)}$

(2)

${\displaystyle u_0^2\left(I\right)-u_0^2\left(II\right)\le \left[\left(h_0^1\underset{\omega \in \Omega }{max}{h}_1^2\left(\omega \right)-h_0^2\right)+\sum _{i=1}^M\left(\frac{a_0^{i1}{max}_{\omega \in \Omega }{a}_1^{i2}\left(\omega \right)-a_0^{i2}}{{min}_{\omega \in \Omega }{S}_2^i\left(\omega \right)}\right)\right]\underset{\omega \in \Omega }{max}{c}_2\left(\omega \right)}$

Proof. 

In Appendix A.  □

Remark 4.

The upper bound we found above, is an over estimate, but it is small relative to the portfolio price.

5. Multi-Period Case Theorem

The discussion in Section 4 showed that deriving the most accurate super- and sub-hedging bounds is too complex to be practical. An iterative process dealing with one period (bonds and assets) at a time provides a good compromise between accuracy and tractability.

Theorem 8.

Let $0\le t\le T-1$ and consider the following linear programming problem

$$\left\{\begin{array}{c}{\displaystyle u_t^T=sup{\mathbf{E}}_t\left[f_t^{t+1}\left(c_{t+1}+{\mathbf{E}}_{t+1}\left[f_{t+1}^{t+2}\left(c_{t+2}+\dots +{\mathbf{E}}_{T-1}\left[f_{T-1}^T{c}_T\right]\right)\right]\right)\right]}\\ subjectto\hfill \\ {\displaystyle {\mathbf{E}}_s\left[f_s^{s+1}\right]\le h_s^{s+1},{\mathbf{E}}_s\left[f_s^{s+1}\left(-1\right)\right]\le -g_s^{s+1},s=t,\dots ,T-1}\\ {\displaystyle {\mathbf{E}}_s\left[f_s^{s+1}{S}_{s+1}^i\right]\le a_s^i,{\mathbf{E}}_s\left[f_s^{s+1}\left(-S_{s+1}^i\right)\right]\le -b_s^i,i=1,\dots ,M}\end{array}\right.$$

(50)

Then $u_t^T$ is a super-hedging bound and the solution to dual problem is a trading strategy by which one is able to construct an arbitrage opportunity if the market bid price of c exceeds $u_t^T$.

Proof. 

In Appendix A.  □

Remark 5.

Even though the value of $u_t^T$ we find in the Theorem above may not be the lowest super-hedging value for the ask price of the cash flow c, it is still a close estimate, as we discussed in Theorem 7 and an upper bound for the exact super-hedging value $u_t\left(c\right)$.

6. Conclusions

We used convex duality in a multi-period conic finance (two-price economy) to extend the refined version of FTAP. This helped us to provide a framework to drive non-arbitrage lower and upper price bounds and corresponding trading strategies which one can take advantage of when a preferable bid (ask) price exists. We also analyzed the computation complexity of implementation in two settings:

(a)

using only one-period bonds,

(b)

involving all available bonds.

and we showed that involving all available bonds makes the problem unrealistically complex. We provided estimates on the error between the prices for one period and all bonds, which we saw that it is small. Therefore we recommended method dealing only with one-period bonds in practice, where the problems becomes pricing one period at a time. Finding a better approximation for the price bounds and shrinking the non-arbitrage region and lowering the computation complexity are two problems that one could consider for further exploration.