Nonparametric Malliavin–Monte Carlo Computation of Hedging Greeks
Abstract
:1. Introduction
2. Greeks Computation via Malliavin Calculus and the Rescaled Variation
2.1. Two Examples
2.1.1. The Black–Scholes Model
2.1.2. The CEV Model
3. Simulation Study
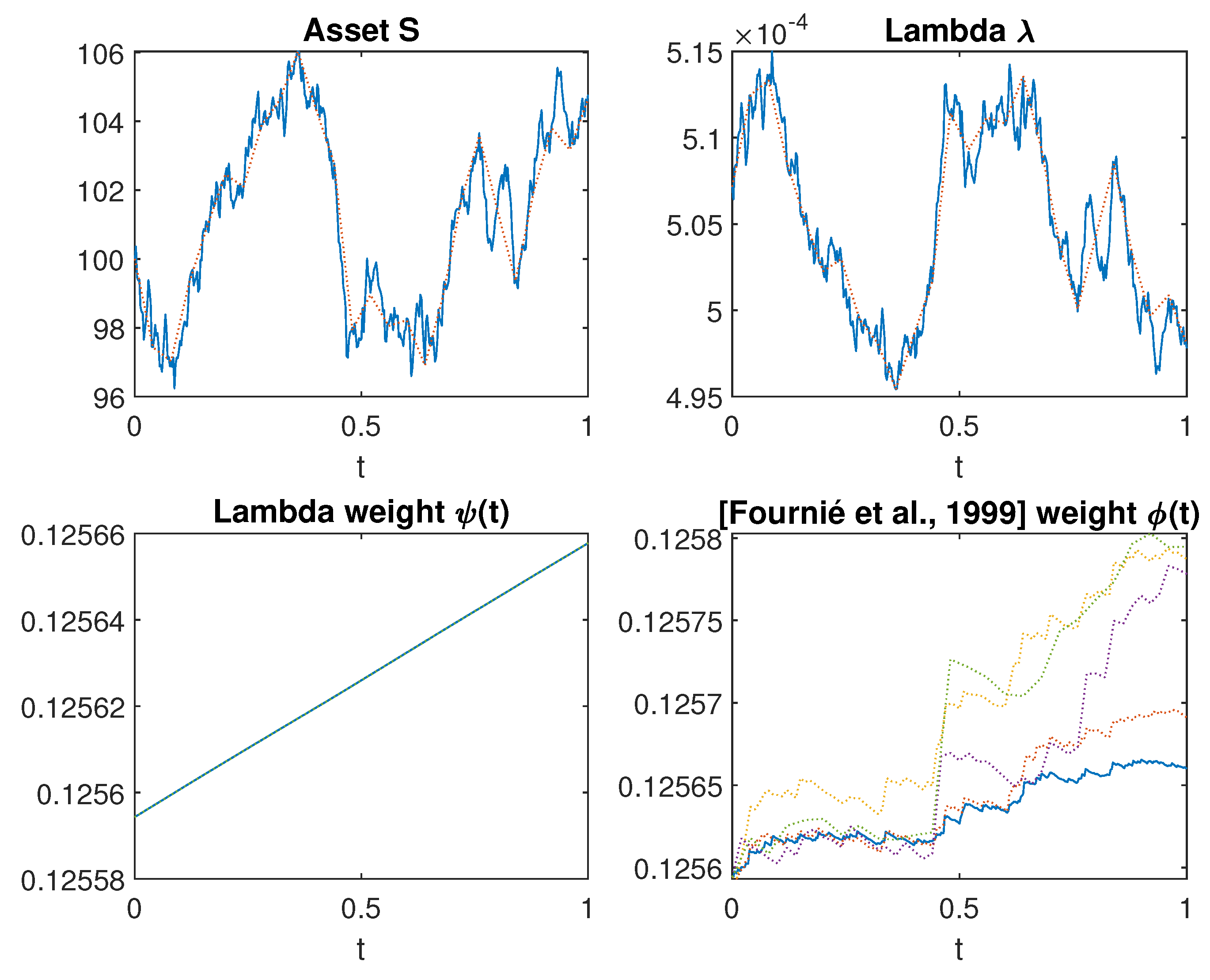
3.1. Computation of the Weight
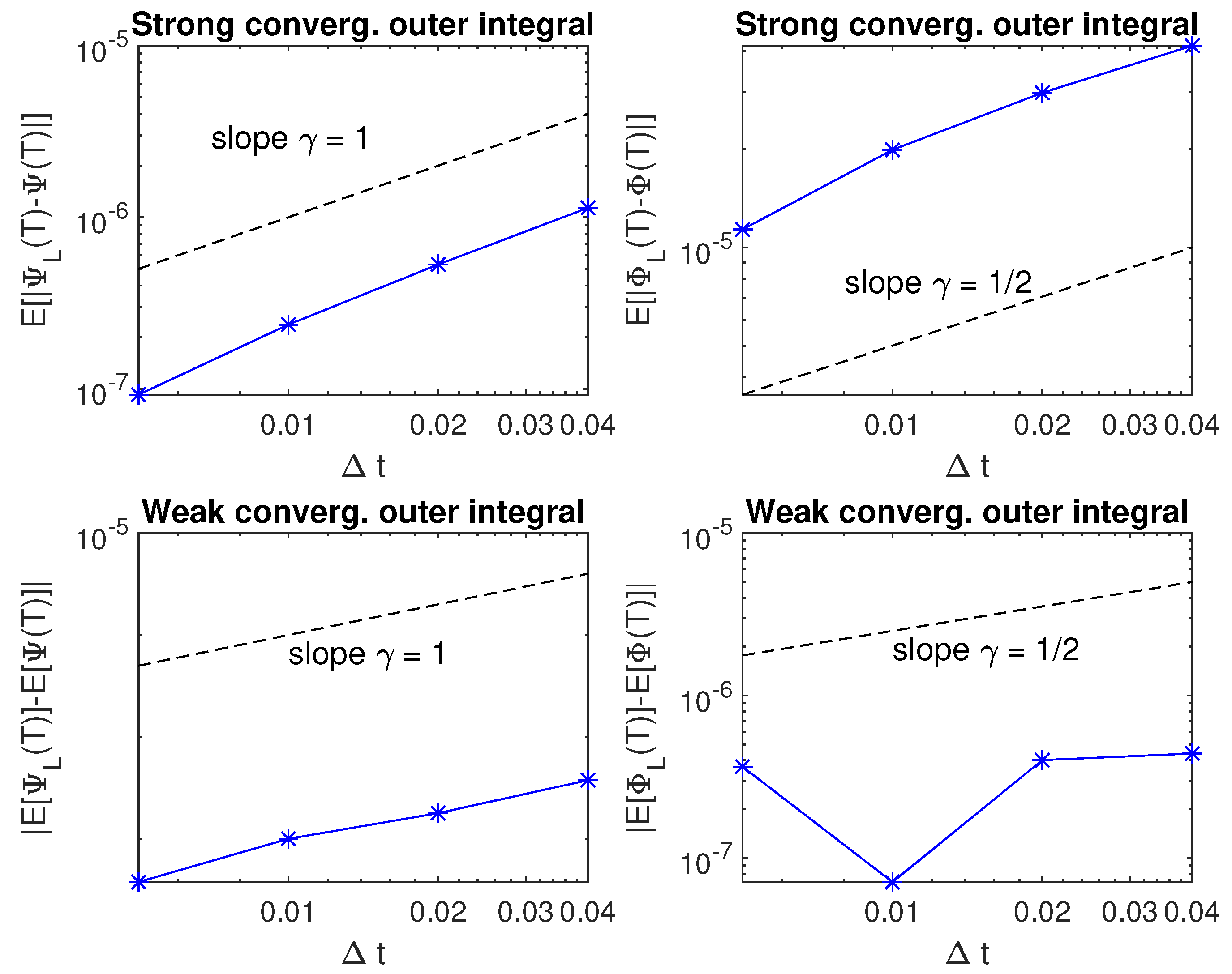
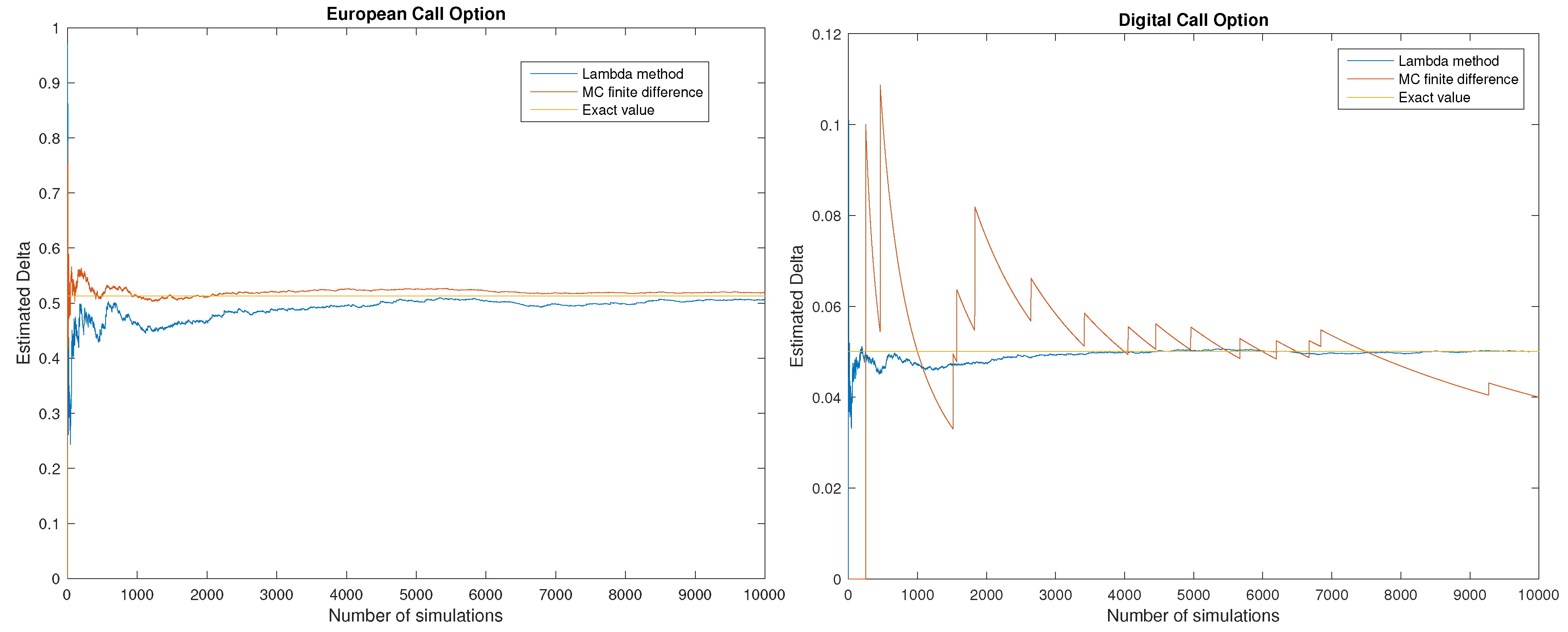
3.2. Efficiency of the Method
- European Call/Put option: , ;
- Digital Call/Put option: ,
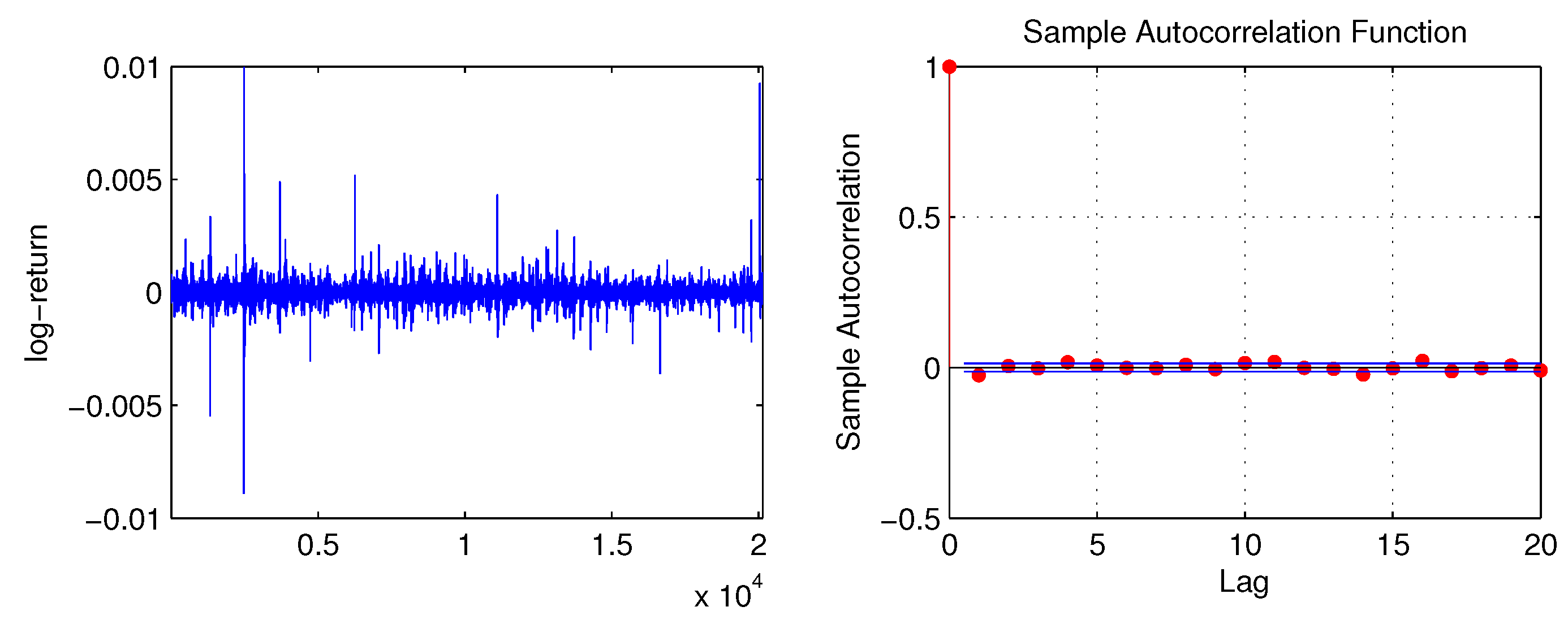
4. Greek Estimation from Observed Underlying Prices. An Empirical Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Aït-Sahalia, Yacine. 1996. Nonparametric Pricing of Interest Rate Derivative Securities. Econometrica 64: 527–60. [Google Scholar] [CrossRef] [Green Version]
- Barucci, Emilio, Paul Malliavin, Maria Elvira Mancino, Roberto Renò, and Anton Thalmaier. 2003. The price-volatility feedback rate: An implementable mathematical indicator of market stability. Mathematical Finance 13: 17–35. [Google Scholar] [CrossRef] [Green Version]
- Benhamou, Eric. 2003. Optimal Malliavin Weighting Function for the Computation of the Greeks. Mathematical Finance 13: 37–53. [Google Scholar] [CrossRef]
- Bouleau, Nicolas. 2003. Error calculus and path Sensitivity in Financial Models. Mathematical Finance 13: 115–34. [Google Scholar] [CrossRef] [Green Version]
- Cox, J., and S. Ross. 1976. The valuation of options for alternative stochastic processes. Journal of Financial Economics 3: 407–32. [Google Scholar] [CrossRef]
- Davydov, D., and V. Linetsky. 2001. Pricing and Hedging Path-Dependent Options Under the CEV Process. Management Science 47: 949–65. [Google Scholar] [CrossRef] [Green Version]
- Derman, E., and I. Kani. 1994. Riding on the Smile. RISK 7: 32–39. [Google Scholar]
- Dupire, B. 1994. Pricing with a smile. RISK 7: 18–20. [Google Scholar]
- Elie, R., J.-D. Fermian, and N. Touzi. 2007. Kernel estimation of Greek weights by parameter randomization. The Annals of Applied Probability 17: 1399–423. [Google Scholar] [CrossRef] [Green Version]
- Fournié, E., J.M. Lasry, J. Lebuchoux, P.L. Lions, and N. Touzi. 1999. Applications of Malliavin calculus to Monte Carlo methods in finance. Finance and Stochastics 3: 391–412. [Google Scholar] [CrossRef]
- Fournié, E., J.M. Lasry, J. Lebuchoux, and P.L. Lions. 2001. Applications of Malliavin calculus to Monte Carlo methods in finance. II. Finance and Stochastics 5: 201–36. [Google Scholar] [CrossRef]
- Hayashi, T., and P.A. Mykland. 2005. Evaluating hedging errors: An asymptotic approach. Mathematical Finance 15: 309–43. [Google Scholar] [CrossRef]
- Hobson, D., and L. Rigers. 1998. Complete models with stochastic volatility. Mathematical Finance 8: 27–48. [Google Scholar] [CrossRef]
- Hull, J.C. 2018. Options, Futures and Other Derivatives. London: Pearson. [Google Scholar]
- Kenmoe, R., and S. Sanfelici. 2014. An application of nonparametric volatility estimators to option pricing. Decisions in Economics and Finance 37: 393–412. [Google Scholar] [CrossRef]
- Kohatsu-Higa, A., and M. Monteiro. 2001. An Application of Malliavin Calculus to Finance. Available online: https://arxiv.org/pdf/cond-mat/0111563.pdf (accessed on 10 November 2020).
- Malliavin, P. 1997. Stochastic Analysis. A Series of Comprehensive Studies in Mathematics; Berlin/Heildelberg: Springer, vol. 313. [Google Scholar]
- Malliavin, P., and M.E. Mancino. 2002a. Fourier Series method for measurement of Multivariate Volatilities. Finance and Stochastics 6: 49–61. [Google Scholar] [CrossRef]
- Malliavin, P., and M.E. Mancino. 2002b. Instantaneous liquidity rate, its econometric measurement by volatility feedback. Comptes Rendus Mathematique 334: 505–8. [Google Scholar] [CrossRef]
- Malliavin, P., and M.E. Mancino. 2009. A Fourier transform method for nonparametric estimation of volatility. The Annals of Statistics 37: 1983–2010. [Google Scholar] [CrossRef] [Green Version]
- Malliavin, P., and A. Thalmaier. 2006. Stochastic Calculus of Variations in Mathematical Finance. Berlin/Heidelberg: Springer. [Google Scholar]
- Mancino, M.E., M.C. Recchioni, and S. Sanfelici. 2017. Fourier-Malliavin Volatility Estimation: Theory and Practice. Springer Briefs in Quantitative Finance Series; Berlin/Heidelberg: Springer, ISBN 978-3-319-50969-3. [Google Scholar]
- Mancino, M.E., and S. Sanfelici. 2008. Robustness of the Fourier Estimator of Integrated Volatility in Presence of Microstructure Noise. Computational Statistics and Data Analysis 52: 2966–89. [Google Scholar] [CrossRef]
- Mancino, M.E., and S. Sanfelici. 2020. Identifying financial instability conditions using high frequency data. Journal of Economic Interaction and Coordination 15: 221–42. [Google Scholar] [CrossRef]
- Tavella, D., and C. Randall. 1998. Pricing Financial Instruments. The Finite Difference Method. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
| 1. | We emphasize the dependence on the Brownian path, using the subindex W. |
| 2. | The prime stands here for the first derivative with respect to the level . |
| 3. | It should be noticed that the last integral in (7) is a Skohorod integral, for the duality formula with the Malliavin derivative operator . However, if the integrand is adapted to the filtration, then the Skohorod integral and the Itô integral coincide. |
| 4. | In particular, as discussed in Mancino and Sanfelici (2008), the cutting frequencies for the functions and can be taken as and , respectively. Finally, the feedback rate function can be estimated at distinct points in the interval by taking in the Fourier expansion for . Being , this procedure allows for a reconstruction of the feedback rate function at 125 nodes in the interval . |


| Option | N | n | λ-Method | Fournié et al. (1999) | MC Fin. Diff. | Analytic |
|---|---|---|---|---|---|---|
| EC | 1000 | 200 | 0.620603 | 0.584784 | 0.620490 | 0.636831 |
| EP | 1000 | 200 | −0.382432 | −0.409168 | −0.378079 | −0.363169 |
| DC | 1000 | 200 | 0.018054 | 0.017937 | 0.190246 | 0.018762 |
| DP | 1000 | 200 | −0.019501 | −0.020261 | −0.190246 | −0.018762 |
| Option | N | n | λ-Method | Fournié et al. (1999) | MC Fin. Diff. | Analytic |
|---|---|---|---|---|---|---|
| EC | 5000 | 200 | 0.641900 | 0.646569 | 0.633642 | 0.636831 |
| EP | 5000 | 200 | −0.355614 | −0.368940 | −0.364584 | −0.363169 |
| DC | 5000 | 200 | 0.018898 | 0.018950 | 0.019025 | 0.018762 |
| DP | 5000 | 200 | −0.018348 | −0.018951 | −0.019025 | −0.018762 |
| Option | N | n | λ-Method | Fournié et al. (1999) | MC Fin. Diff. | Analytic |
|---|---|---|---|---|---|---|
| EC | 10,000 | 200 | 0.642683 | 0.634604 | 0.633323 | 0.636831 |
| EP | 10,000 | 200 | −0.351281 | −0.359368 | −0.364866 | −0.363169 |
| DC | 10,000 | 200 | 0.018758 | 0.018717 | 0.019025 | 0.018762 |
| DP | 10,000 | 200 | −0.018252 | −0.018755 | −0.019025 | −0.018762 |
| Option | λ-Method | Fournié et al. (1999) | MC Fin. Diff. | Analytic |
|---|---|---|---|---|
| EC | 0.0.506340 | 0.506337 | 0.519070 | 0.512955 |
| EP | −0.468663 | −0.468662 | −0.481571 | −0.487045 |
| DC | 0.050183 | 0.050182 | 0.040000 | 0.050090 |
| DP | −0.048846 | −0.048846 | −0.040000 | −0.050090 |
| Variable | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|
| EUR/USD exchange rate | 1.124517 | 0.015473 | 1.082280 | 1.161020 |
| 5-min log-return (%) | 2.028925 × 10−4 | 3.302504 × 10−2 | −8.892366 × 10−1 | 9.972291 × 10−1 |
| Underlying asset value S | 0.9500 | 1.0500 | 1.1000 | 1.1500 | 1.2500 |
| Option delta | |||||
| Lambda method | −0.9892 | −0.9740 | −0.5319 | −0.0938 | 0 |
| Standard deviation | (0.2749) | (0.2021) | (0.0932) | (0.0419) | (0) |
| Monte Carlo finite difference | −0.9899 | −0.7651 | −0.4547 | −0.1590 | −0.0103 |
| Standard deviation | (0.0045) | (0.0045) | (0.0033) | (0.0009) | (0.0004) |
| Finite Difference Method | −0.9974 | −0.8109 | −0.5225 | −0.1774 | −0.0023 |
| Black–Scholes formula | −0.9988 | −0.7957 | −0.4900 | −0.1502 | −0.0021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancino, M.E.; Sanfelici, S. Nonparametric Malliavin–Monte Carlo Computation of Hedging Greeks. Risks 2020, 8, 120. https://doi.org/10.3390/risks8040120
Mancino ME, Sanfelici S. Nonparametric Malliavin–Monte Carlo Computation of Hedging Greeks. Risks. 2020; 8(4):120. https://doi.org/10.3390/risks8040120
Chicago/Turabian StyleMancino, Maria Elvira, and Simona Sanfelici. 2020. "Nonparametric Malliavin–Monte Carlo Computation of Hedging Greeks" Risks 8, no. 4: 120. https://doi.org/10.3390/risks8040120
APA StyleMancino, M. E., & Sanfelici, S. (2020). Nonparametric Malliavin–Monte Carlo Computation of Hedging Greeks. Risks, 8(4), 120. https://doi.org/10.3390/risks8040120






