Use of Neural Networks to Accommodate Seasonal Fluctuations When Equalizing Time Series for the CZK/RMB Exchange Rate
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
- The self-sufficient variable was time and the dependent variable was defined as the CZK/RMB exchange rate.
- Time was an independent variable. The seasonal variable was characterized by a categorical variable represented by year, month, day of month, and day of week, in which the value was measured for each variable independently. The purpose was to work with the potential daily, monthly, and annual seasonal fluctuations in time series. The dependent variable was the CZK/RMB exchange rate.
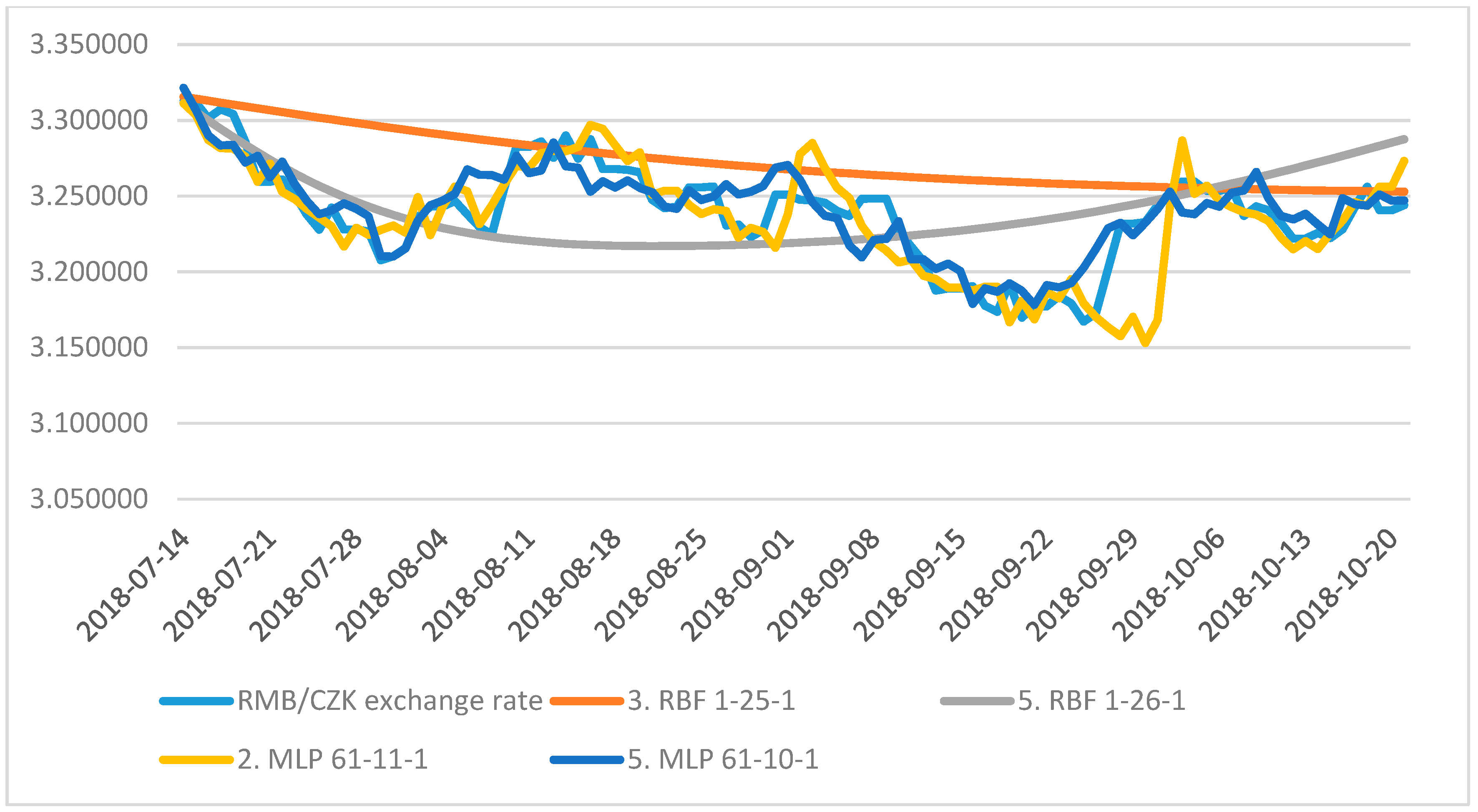
4. Results
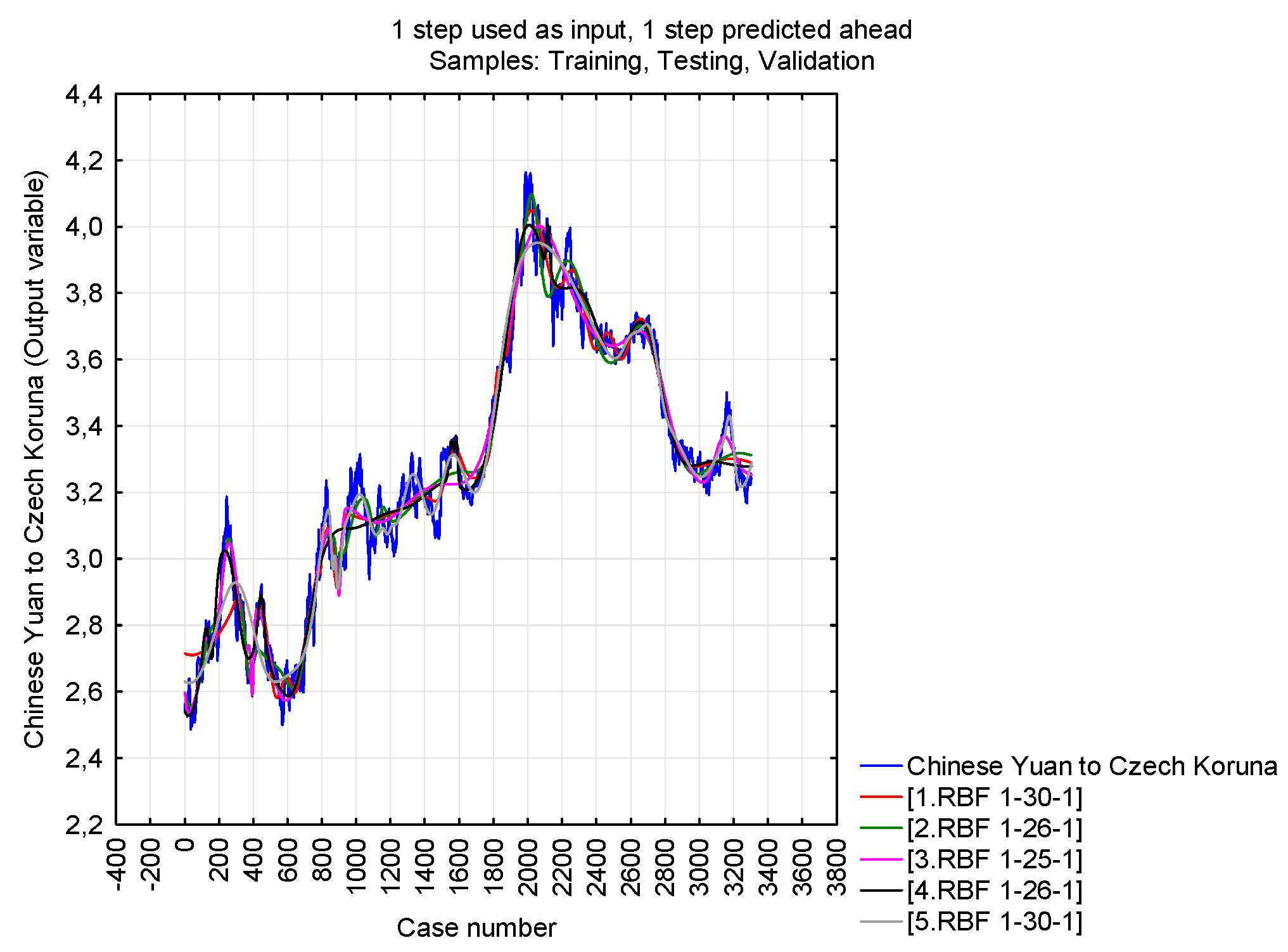
4.1. Neural Structure A
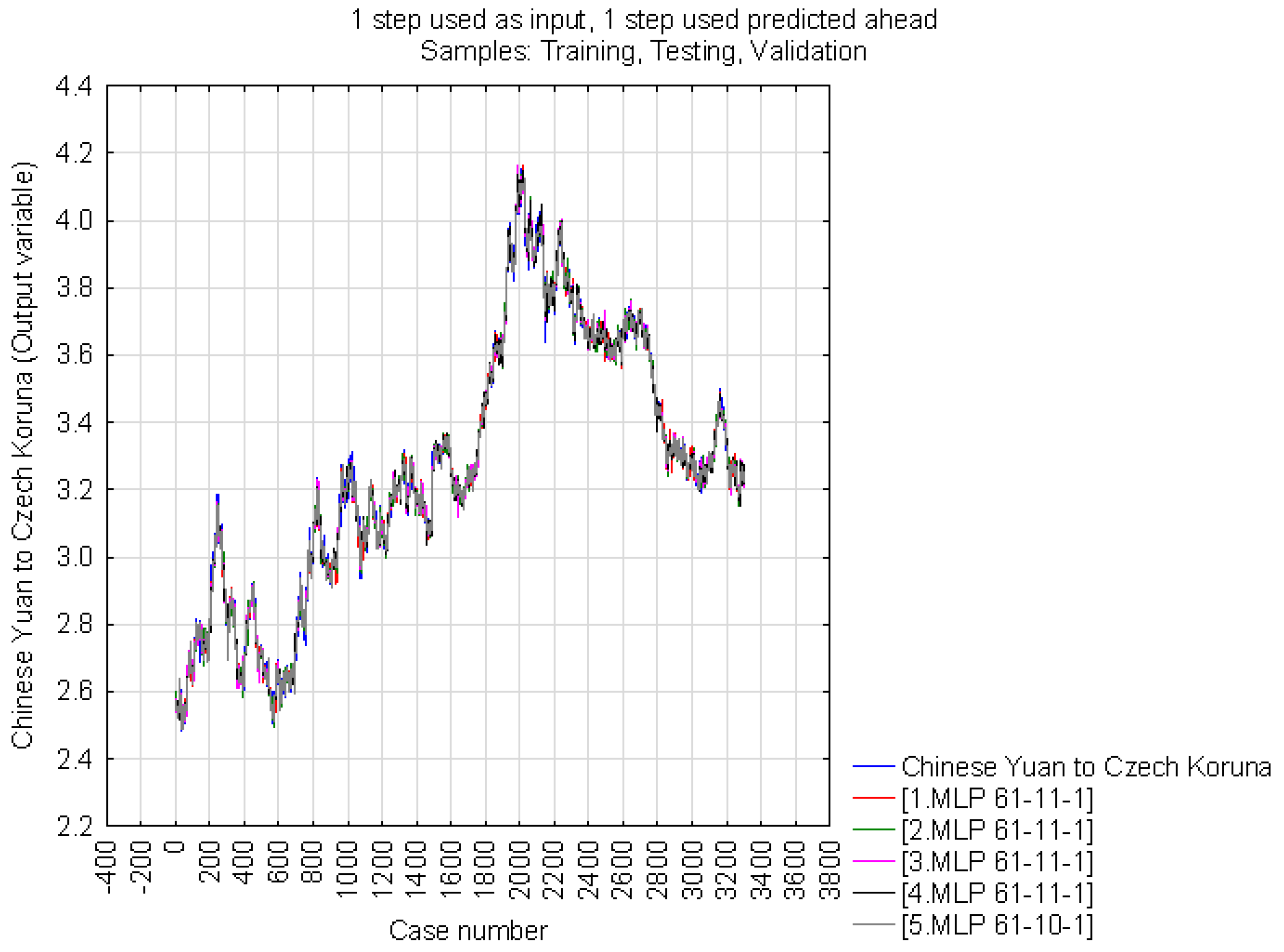
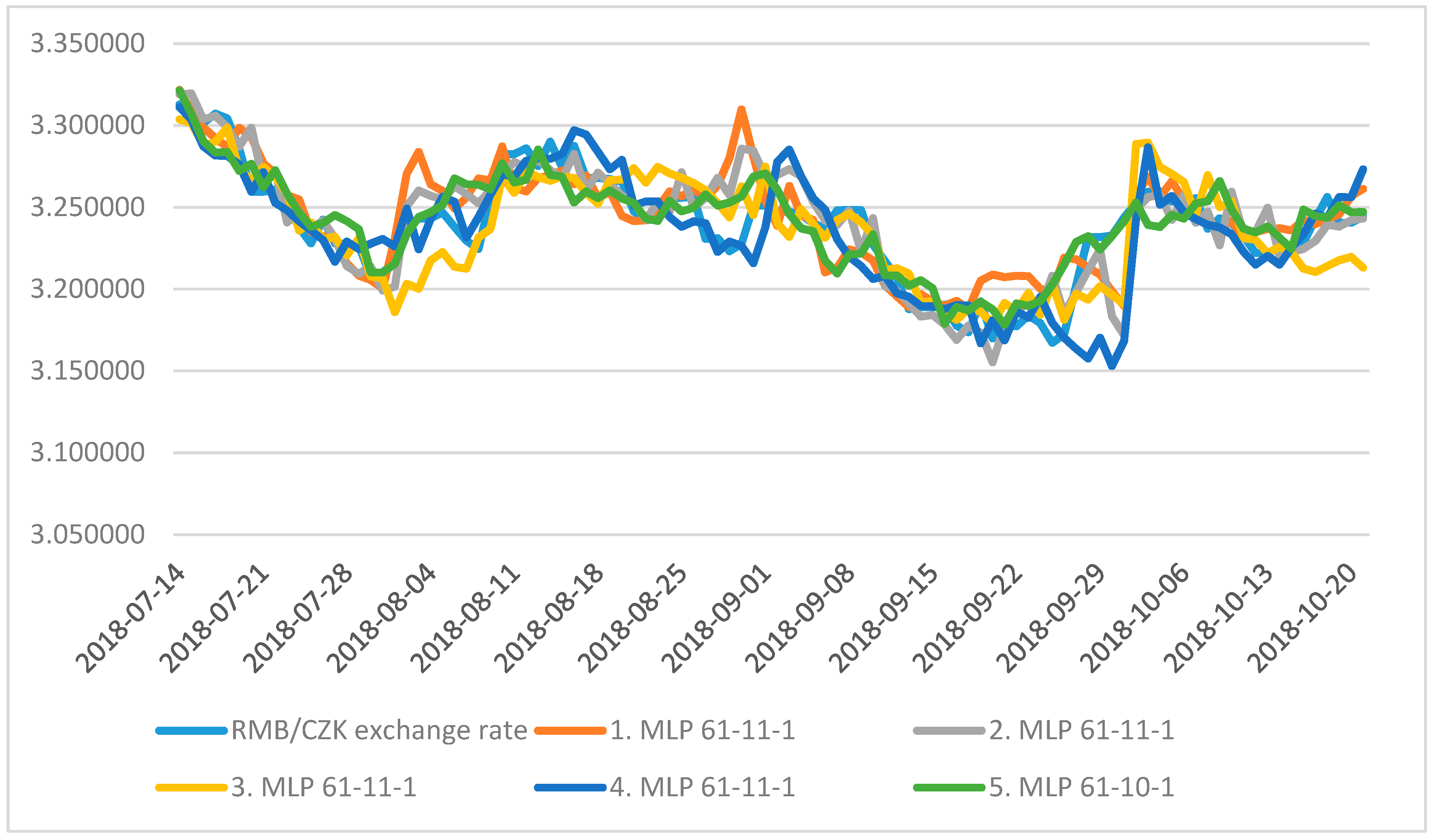
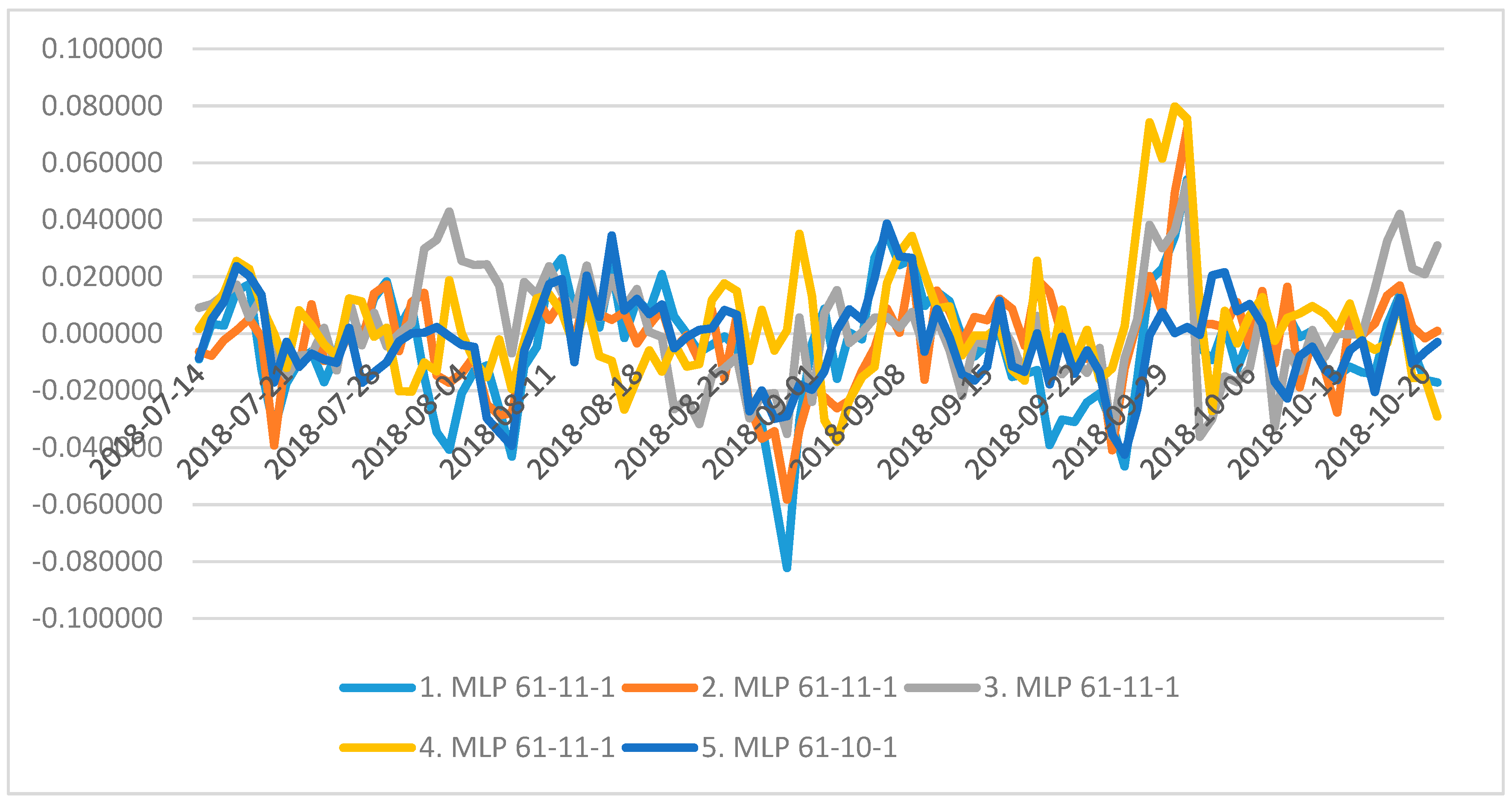
4.2. Neural Structure B
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abdullah, Lazim. 2013. Performance of exchange rate forecast using distance-based fuzzy time series. International Journal of Engineering and Technology 5: 452–59. [Google Scholar]
- Accominotti, Olivier, Jason Cen, David Chambers, and Ian W. Marsh. 2019. Currency regimes and the carry trade. Journal of Financial and Quantitative Analysis 54: 2233–60. [Google Scholar] [CrossRef] [Green Version]
- Aizenman, Joshua, Yin-Wong Cheung, and Xiangwang Qian. 2020. The currency composition of international reserves, demand for international reserves, and global safe assets. Journal of International Money and Finance 102. [Google Scholar] [CrossRef]
- Alonso-Monsalve, Saúl, Andrés L. Suarez-Cetrulo, Alejandro Cervantes, and David Quintana. 2020. Convolution on neural networks for high-frequency trend prediction of cryptocurrency exchange rates using technical indicators. Expert Systems with Applications 149. [Google Scholar] [CrossRef]
- Amo Baffour, Alexander, Jingchun Feng, and Evans Kwesi Taylor. 2019. A hybrid artificial neural network-GJR modeling approach to forecasting currency exchange rate volatility. Neurocomputing 365: 285–301. [Google Scholar] [CrossRef]
- Arneric, Josip, Tea Poklepovic, and Zdravka Aljinovic. 2014. GARCH based artificial neural networks in forecasting conditional variance of stock returns. Croatian Operational Research Review 5: 329–43. [Google Scholar] [CrossRef] [Green Version]
- Augustin, Patrick, Mikhail Chernov, and Dongho Song. 2020. Sovereign credit risk and exchange rates: Evidence from CDS quanto spreads. Journal of Financial Economics 137: 129–51. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Scott W. Hegerty. 2007. Exchange rate volatility and trade flows: A review article. Journal of Economic Studies 34: 211–55. [Google Scholar] [CrossRef]
- Bernard, Andrew B. 2004. Exporting and productivity in the USA. Oxford Review of Economic Policy 20: 343–57. [Google Scholar] [CrossRef]
- Bielecki, Anrzej, Pawel Hajto, and Robert Schaefer. 2008. Hybrid neural systems in exchange rate prediction. Studies in Computational Intelligence: Natural Computing in Computational Finance 100: 211–30. [Google Scholar] [CrossRef]
- Bodart, Vincent, and Jean-Francois Carpantier. 2020. Currency collapses and output dynamics in commodity dependent countries. Emerging Markets Review 42. [Google Scholar] [CrossRef]
- Bonadio, Barthélémy, Andreas Fischer, and Philip Sauré. 2020. The speed of exchange rate pass-through. Journal of the European Economic Association 18: 506–38. [Google Scholar] [CrossRef]
- Budikova, Marie, Maria Kralova, and Bohumil Maros. 2010. Průvodce Základními Statistickými Metodami [Guide to Basic Statistical Methods]. Prague: Grada. [Google Scholar]
- Bulut, Levent. 2018. Google Trends and the forecasting performance of exchange rate models. Journal of Forecasting 37: 303–15. [Google Scholar] [CrossRef]
- Cai, Zongwu, Linna Chen, and Ying Fang. 2012. A new forecasting model for USD/CNY exchange rate. Studies on Nonlinear Dynamics and Econometrics 16. [Google Scholar] [CrossRef] [Green Version]
- Chari, V.V., Alessandro Dovis, and Patrick J. Kehoe. 2020. Rethinking optimal currency areas. Journal of Monetary Economics 111: 80–94. [Google Scholar] [CrossRef] [Green Version]
- Cheong, Calvin W.H., Jothee Sinnakkannu, and Sockalingam Ramasamy. 2017. On the predictability of carry trade returns: The case of the Chinese Yuan. Research in International Business and Finance 39: 358–76. [Google Scholar] [CrossRef]
- Cheong, Chongcheul, Tesfa Mehari, and Leighton Vaughan Williams. 2006. Dynamic links between unexpected exchange rate variation, prices, and international trade. Open Economies Review 17: 221–33. [Google Scholar] [CrossRef]
- Chernov, Mikhail, Jeremy Graveline, and Irina Zviadadze. 2018. Crash risk in currency returns. Journal of Financial and Quantitative Analysis 53: 137–70. [Google Scholar] [CrossRef] [Green Version]
- Cheung, Yin-Wong, Cho-Hoi Hui, and Andrew Tsang. 2018. Renminbi central parity: An empirical investigation. Pacific Economic Review 23: 164–83. [Google Scholar] [CrossRef] [Green Version]
- Cheung, Yin-Wong, Menzie D. Chinn, Antonio Garcia Pascual, and Yi Zhang. 2019. Exchange rate prediction redux: New models, new data, new currencies. Journal of International Money and Finance 95: 332–62. [Google Scholar] [CrossRef] [Green Version]
- Chiappini, Raphael, and Delphine Lahet. 2020. Exchange rate movements in emerging economies—Global vs regional factors in Asia. China Economic Review 60. [Google Scholar] [CrossRef]
- Cho, Jae-Beom, Hong-Ghi Min, and Judith Ann McDonald. 2020. Volatility and dynamic currency hedging. Journal of International Financial Markets, Institutions and Money 64. [Google Scholar] [CrossRef]
- Choi, Yoonho, and E. Kwan Choi. 2018. Unemployment and optimal exchange rate in an open economy. Economic Modelling 69: 82–90. [Google Scholar] [CrossRef]
- Colacito, Ric, Mariano M. Croce, Federico Gavazzoni, and Robert Ready. 2018. Currency risk factors in a recursive multicountry economy. The Journal of Finance 73: 2719–56. [Google Scholar] [CrossRef]
- Dahlquist, Magnus, and Henrik Hasseltoft. 2020. Economic momentum and currency returns. Journal of Financial Economics 136: 152–67. [Google Scholar] [CrossRef] [Green Version]
- De Baets, Shari, and Nigel Harvey. 2018. Forecasting from time series subject to sporadic perturbations: Effectiveness of different types of forecasting support. International Journal of Forecasting 34: 163–80. [Google Scholar] [CrossRef]
- De Boer, Jantke, Kim J. Bövers, and Steffen Meyer. 2020. Business cycle variations in exchange rate correlations: Revisiting global currency hedging. Finance Research Letters 33. [Google Scholar] [CrossRef]
- Dhamija, Ajay K., and V. K. Bhalla. 2011. Exchange rate forecasting: comparison of various architectures of neural networks. Neural Computing and Applications 20: 355–63. [Google Scholar] [CrossRef]
- Ding, Haoyuan, Yuying Jin, Cong Qin, and Jiezhou Ying. 2020. Tail causality between crude oil price and RMB exchange rate. China & World Economy 28: 116–34. [Google Scholar] [CrossRef]
- Dogru, Tarik, Cem Isik, and Ercan Sirakaya-Turk. 2019. The balance of trade and exchange rates: Theory and contemporary evidence from tourism. Tourism Management 74: 12–23. [Google Scholar] [CrossRef]
- Dunis, Christian L., Jason Laws, and Georgios Sermpinis. 2011. Higher order and recurrent neural architectures for trading the EUR/USD exchange rate. Quantitative Finance 11: 615–29. [Google Scholar] [CrossRef]
- Faris, Hossam, Ibrahim Aljarah, and Seyedali Mirjalili. 2017. Evolving Radial Basis Function networks using Moth-Flame optimizer. Handbook of Neural Computation, 537–50. [Google Scholar] [CrossRef]
- Forbes, Kristin, Ida Hjortsoe, and Tsvetelina Nenova. 2018. The shocks matter: Improving our estimates of exchange rate pass-through. Journal of International Economics 114: 255–75. [Google Scholar] [CrossRef] [Green Version]
- Foreign Direct Investment. 2018–2019. Obecný metodický popis a komentář k vývoji přímých zahraničních investic [General methodological description and commentary on the development of foreign direct investment]. In Www.cnb.cz. Prague: Czech National Bank. [Google Scholar]
- Gopinath, Gita, Emine Boz, Camila Casas, Federico J. Díez, Pierre-Olivier Gourinchas, and Mikkel Plagborg-Møller. 2020. Dominant currency paradigm. American Economic Review 110: 677–719. [Google Scholar] [CrossRef] [Green Version]
- Grabowski, Wojciech, and Aleksander Welfe. 2020. The Tobit cointegrated vector autoregressive model: An application to the currency market. Economic Modelling 89: 88–100. [Google Scholar] [CrossRef]
- Groll, Dominik, and Tommaso Monacelli. 2020. The inherent benefit of monetary unions. Journal of Monetary Economics 111: 63–79. [Google Scholar] [CrossRef] [Green Version]
- Guresen, Erkam, Gulgun Kayakutlu, and Tugrul U. Daim. 2011. Using artificial neural network models in stock market index prediction. Expert systems with Applications 38: 10389–97. [Google Scholar] [CrossRef]
- Ha, Jongrim, M. Marc Stocker, and Hakan Yilmazkuday. 2020. Inflation and exchange rate pass-through. Journal of International Money and Finance 105. [Google Scholar] [CrossRef] [Green Version]
- Han, Liyan, Li Wan, and Yang Xu. 2020. Can the Baltic Dry Index predict foreign exchange rates? Finance Research Letters 32. [Google Scholar] [CrossRef]
- Henriquez, Jonatan, and Werner Kristjanpoller. 2019. A combined independent component analysis-neural network model for forecasting exchange rate variation. Applied Soft Computing 83. [Google Scholar] [CrossRef]
- Hnat, Pavel, and Martin Tlapa. 2014. China-V4 Investment regime–a Czech perspective. Paper presented at Trends and Perspectives in Development of China-V4 Trade and Investment, Bratislava, Slovakia, March 12–14; pp. 82–95. [Google Scholar]
- Ho, Chi Ming. 2020. Does virtual currency development harm financial stocks’ value? Comparing Taiwan and China markets. Economic Research-Ekonomska Istraživanja 33: 361–78. [Google Scholar] [CrossRef]
- Ho, S. F., and Norzitah Abdul Karim. 2012. Exchange rate, macroeconomic fundamentals and international trade. 2012 IEEE Colloquium on Humanities, Science and Engineering Research, 534–38. [Google Scholar] [CrossRef]
- Horak, Jakub, and Veronika Machova. 2019. Comparison of neural networks and regression time series on forecasting development of US imports from the PRC. Littera Scripta 12: 22–36. [Google Scholar]
- Horak, Jakub. 2019. Using artificial intelligence to analyse businesses in agriculture industry. Paper presented at SHS Web of Conferences–Innovative Economic Symposium 2018 Innovative Economic Symposium 2018: Milestones and Trend of World Economy, Beijing, China, November 8–9; vol. 61. [Google Scholar] [CrossRef]
- Huang, Shupei, Haizhong An, and Brian Lucey. 2020. How do dynamic responses of exchange rates to oil price shocks co-move? From a time-varying perspective. Energy Economics 86. [Google Scholar] [CrossRef]
- Ilzetzki, Ethan, Carmen M. Reinhart, and Kenneth S. Rogoff. 2019. Exchange arrangements entering the twenty-first century: Which anchor will hold? The Quarterly Journal of Economics 134: 599–646. [Google Scholar] [CrossRef] [Green Version]
- Ismail, Munira, Nurul Zafirah Jubley, and Zalina Mohd Ali. 2018. Forecasting Malaysian Foreign exchange rate using artificial neural network and ARIMA time series. Paper presented at International Conference on Mathematics, Engineering and Industrial Applications, Kuala Lumpur, Malaysia, July 24–26; vol. 2013. [Google Scholar] [CrossRef]
- Jiang, Chuanjin, and Fugen Song. 2010. Forecasting chaotic time series of exchange rate based on nonlinear autoregressive model. Paper presented at 2nd IEEE International Conference on Advanced Computer Control, ICACC, Shenyang, China, March 27–29; vol. 5, pp. 238–41. [Google Scholar] [CrossRef]
- Khademalomoom, Siroos, and Paresh Kumar Narayan. 2020. Intraday-of-the-week effects: What do the exchange rate data tell us? Emerging Markets Review 43. [Google Scholar] [CrossRef]
- Khalafi, Farshad Faghihi H., and Seyed Mohammad Mirvakili. 2011. A literature survey of neutronics and thermal-hydraulics codes for investigating reactor core parameters; artificial neural networks as the VVER-1000 core predictor. Nuclear Power–System Simulations and Operation, 103–22. [Google Scholar] [CrossRef] [Green Version]
- Kharrat, Sabrine, Yacine Hammami, and Ibrahim Fatnassi. 2020. On the cross-sectional relation between exchange rates and future fundamentals. Economic Modelling 89: 484–501. [Google Scholar] [CrossRef]
- Kriwoluzky, Alexander, Gernot J. Müller, and Martin Wolf. 2019. Exit expectations and debt crises in currency unions. Journal of International Economics 121. [Google Scholar] [CrossRef] [Green Version]
- Kunze, F. 2019. Predicting exchange rates in Asia: New insights on the accuracy of survey forecasts. Journal of Forecasting 39: 313–33. [Google Scholar] [CrossRef] [Green Version]
- Laily, Vania Orva Nur, Budi Warsito, and Di Asih I. Maruddani. 2018. Comparison of ARCH/GARCH model and Elman Recurrent Neural Network on data return of closing price stock. Paper presented at 7th International Seminar on New Paradigm and Innovation on Natural Science and its Application, Semarang, Indonesia, October 17. [Google Scholar]
- León-Alvarez, Alba Luz, Jorge Iván Betancur-Gomez, Fabián Jaimes-Barragan, and Hugo Grisales-Romero. 2016. Ronda clínica y epidemiológica. Series de tiempo. IATREIA 29: 373–81. [Google Scholar] [CrossRef] [Green Version]
- Li, Nan, Liepeng Sun, Xiao Luo, Rong Kang, and Mingde Jia. 2019. Foreign trade structure, opening degree and economic growth in Western China. Economies 7: 56. [Google Scholar] [CrossRef] [Green Version]
- Liu, Li, Siming Tan, and Yudong Wang. 2020. Can commodity prices forecast exchange rates? Energy Economics 87. [Google Scholar] [CrossRef]
- Liu, Tao, and Wing Thye Woo. 2018. Understanding the U.S.-China trade war. China Economic Journal 11: 319–40. [Google Scholar] [CrossRef]
- Liu, Zhao Cheng, Xi Yu Liu, and Zi Ran Zheng. 2011. Modeling and prediction of the CNY exchange rates using RBF neural networks versus GARCH models. Quantum, Nano, Micro and Information Technologies 36: 375–82. [Google Scholar] [CrossRef]
- Lu, Xunfa, Danfeng Que, and Guangxi Cao. 2016. Volatility forecast based on the hybrid artificial neural network and GARCH-type models. Paper presented at Promoting Business Analytics and Quantitative Management of Technology: 4th International Conference on Information Technology and Quantitative Management, Asan, Korea, August 16–18; pp. 1044–49. [Google Scholar] [CrossRef] [Green Version]
- Ma, Guonan, and Robert N. Mccauley. 2011. The implications of Renminbi basket management for Asian currency stability. Frontiers of Economics and Globalization: Evolving Role of Asia in Global Finance 9: 97–121. [Google Scholar] [CrossRef]
- Machova, Veronika, and Jan Marecek. 2019. Estimation of the development of Czech Koruna to Chinese Yuan exchange rate using artificial neural networks. Paper presented at SHS Web of Conferences–Innovative Economic Symposium 2018: Milestones and Trend of World Economy, Beijing, China, November 8–9; vol. 61. [Google Scholar] [CrossRef]
- Maggiori, Matteo, Brent Neiman, and Jesse Schreger. 2020. International currencies and capital allocation. Journal of Political Economy 128: 2019–66. [Google Scholar] [CrossRef]
- Mai, Yong, Huan Chen, Jun-Zhong Zou, and Sai-Ping Li. 2018. Currency co-movement and network correlation structure of foreign exchange market. Physica A: Statistical Mechanics and Its Applications 492: 65–74. [Google Scholar] [CrossRef]
- Maurer, Thomas A., Thuy-Duong Tô, and Ngoc-Khanh Tran. 2019. Pricing risks across currency denominations. Management Science 65: 5308–36. [Google Scholar] [CrossRef]
- Min, Yujuana, and Oh Suk Yang. 2019. The impact of exchange volatility exposure on firms’ foreign-denominated debts. Management Decision 57: 3035–60. [Google Scholar] [CrossRef]
- Mohamed, Rania Ahmed Hamed. 2013. A comparison between the models ARIMA/GARCH and artificial neural networks in modelling financial returns to the Arab Republic of Egypt market securities. Advances and Applications in Statistics 36: 131–50. [Google Scholar]
- Narayan, Paresh Kumar, Susan Sunila Sharma, Ding Hoang Bach Phan, and Guangqiang Liu. 2020. Predicting exchange rate returns. Emerging Markets Review 42. [Google Scholar] [CrossRef]
- Nguyen, Thi-Ngoc Anh, and Kiyotaka Sato. 2020. Invoice currency choice, nonlinearities and exchange rate pass-through. Applied Economics 52: 1048–69. [Google Scholar] [CrossRef]
- Opie, Wei, and Steven J. Riddiough. 2020. Global currency hedging with common risk factors. Journal of Financial Economics 136: 780–805. [Google Scholar] [CrossRef]
- Ornelas, José Renato Haas, and Roberto Baltieri Mauad. 2019. Implied volatility term structure and exchange rate predictability. International Journal of Forecasting 35: 1800–13. [Google Scholar] [CrossRef]
- Ortiz Arango, Francisco. 2017. Prognosis of oil prices: A comparison between GARCH models and differential neural networks. Investigacion Economica 73: 105–26. [Google Scholar] [CrossRef]
- Parot, Alejandro, Kevin Michell, and Werner D. Kristjanpoller. 2019. Using artificial neural networks to forecast exchange rate, including VAR-VECM residual analysis and prediction linear combination. Intelligent Systems in Accounting Finance & Management 26: 3–15. [Google Scholar] [CrossRef] [Green Version]
- Petrica, Andreea Cristina, and Stelian Stancu. 2017. Empirical results of modelling EUR/RON exchange rate using ARCH, GARCH, EGARCH, TARCH and PARCH models. Romanian Statistical Review, 57–72. [Google Scholar]
- Ponomareva, Natalia, Jeffrey Sheen, and Ben Zhe Wang. 2019. Forecasting exchange rates using principal components. Journal of International Financial Markets, Institutions and Money 63. [Google Scholar] [CrossRef]
- Quaicoe, Michael Techie, Frank B. K. Twenefour, Emmanuel M. Baah, and Ezekiel N. N. Nortey. 2015. Modeling variations in the cedi/dollar exchange rate in Ghana: An autoregressive conditional geteroscedastic (ARCH) models. Springerplus 4. [Google Scholar] [CrossRef] [Green Version]
- Rajković, Milos, Predrag Bjelić, Danijela Jaćimović, and Miroslav Verbič. 2020. The impact of the exchange rate on the foreign trade imbalance during the economic crisis in the new EU member states and the Western Balkan countries. Economic Research-Ekonomska Istraživanja 33: 182–203. [Google Scholar] [CrossRef]
- Ramchoun, Hassan, Mohammed Amine Janati Idrissi, Youssef Ghanou, and Mohamed Ettaouil. 2017. New modeling of multilayer perceptron architecture optimization with regularization: An application to pattern classification. IAENG International Journal of Computer Science 44: 261–69. [Google Scholar]
- Ribeiro, Rafael S. M., John S. L. Mccombie, and Gilberto Tadeu Lima. 2020. Does real exchange rate undervaluation really promote economic growth? Structural Change and Economic Dynamics 52: 408–17. [Google Scholar] [CrossRef]
- Salkind, Neil J. 2010. Encyclopedia of Research Design. Thousand Oaks: SAGE Publications. [Google Scholar] [CrossRef]
- Sheikhan, Mansour, Najmeh Mohammadi, and Robert Schaefer. 2013. Time series prediction using PSO-optimized neural network and hybrid feature selection algorithm for IEEE load data. Neural Computing and Applications 23: 1185–94. [Google Scholar] [CrossRef]
- Sindelarova, Irena. 2012. Exchange rate prediction: A wavelet-neural approach. Paper presented at 30th International Conference Mathematical Methods in Economics, Karvina, Czech Republic, September 11–13; pp. 875–78. [Google Scholar]
- Smallwood, Aaron D. 2019. Analyzing exchange rate uncertainty and bilateral export growth in China: A multivariate GARCH-based approach. Economic Modelling 82: 332–44. [Google Scholar] [CrossRef]
- Tian, Gary Gang, and Shiguang Ma. 2010. The relationship between stock returns and the foreign exchange rate: The ARDL approach. Journal of the Asia Pacific Economy 15: 490–508. [Google Scholar] [CrossRef]
- Turkington, David, and Alireza Yazdani. 2020. The equity differential factor in currency markets. Financial Analysts Journal 76: 70–81. [Google Scholar] [CrossRef] [Green Version]
- Vochozka, Marek, and Jaromir Vrbka. 2019. Estimation of the development of the Euro to Chinese Yuan exchange rate using artificial neural networks. Paper presented at SHS Web of Conferences–Innovative Economic Symposium 2018: Milestones and Trend of World Economy, Beijing, China, November 8–9; vol. 61. [Google Scholar]
- Vochozka, Marek, Jakub Horak, and Petr Suler. 2019. Equalizing seasonal time series using artificial neural networks in predicting the Euro-Yuan exchange rate. Journal of Risk and Financial Management 12: 76. [Google Scholar] [CrossRef] [Green Version]
- Vochozka, Marek, Zuzana Rowland, Petr Suler, and Josef Marousek. 2020. The influence of the international price of oil on the value of the EUR/USD exchange rate. Journal of Competitiveness 19: 167–90. [Google Scholar] [CrossRef]
- Vrbka, Jaromir, Petr Suler, Veronika Machova, and Jakub Horak. 2019. Considering seasonal fluctuations in equalizing time series by means of artificial neural networks for predicting development of USA and People’s Republic of China trade balance. Littera Scripta 12: 178–93. [Google Scholar] [CrossRef]
- Wen, Tiange, and Gang-Jin Wang. 2020. Volatility connectedness in global foreign exchange markets. Journal of Multinational Financial Management 54. [Google Scholar] [CrossRef]
- World Bank. 2020. Official Exchange Rate. Available online: https://data.worldbank.org/indicator/PA.NUS.FCRF (accessed on 20 April 2020).
- Xing, Yuqing. 2018. Rising wages, yuan’s appreciation and China’s processing exports. China Economic Review 48: 114–22. [Google Scholar] [CrossRef]
- Yin, Dian, and Wanyi Chen. 2016. The forecast of USD/CNY exchange rate based on the Elman neural network with volatility updating. Paper presented at 35th Chinese Control Conference, Chengdu, China, July 27–29; pp. 9562–66. [Google Scholar] [CrossRef]
- You, Yu, and Xiaochun Liu. 2020. Forecasting short-run exchange rate volatility with monetary fundamentals: A GARCH-MIDAS approach. Journal of Banking & Finance 116. [Google Scholar] [CrossRef]
- Zhang, Gioqinang, and Michael Y. Hu. 1998. Neural network forecasting of the British Pound/US Dollar exchange rate: comparison of various architectures of neural networks. Omega 26: 495–506. [Google Scholar] [CrossRef]
- Zhang, Zhaoyong, and Kiyotaka Sato. 2012. Should Chinese Renminbi be blamed for its trade surplus? A structural VAR approach. The World Economy 35: 632–50. [Google Scholar] [CrossRef]




| Statistics | Date–Input Variable | RMB to CZK–Output (Aim) |
|---|---|---|
| Minimum (training) | 40,092.00 | 2.485800 |
| Maximum (training) | 43,394.00 | 4.163000 |
| Diameter (training) | 41,734.79 | 3.265645 |
| Standard deviation (training) | 939.26 | 0.392383 |
| Minimum (testing) | 40,102.00 | 2.496100 |
| Maximum (testing) | 43,393.00 | 4.155700 |
| Diameter (testing) | 41,755.71 | 3.272882 |
| Standard deviation (testing) | 957.97 | 0.394309 |
| Minimum (validation) | 40,111.00 | 2.498900 |
| Maximum (validation) | 43,388.00 | 4.152900 |
| Diameter (validation) | 41,768.68 | 3.246446 |
| Standard deviation (validation) | 1,438.25 | 0.499822 |
| Minimum (overall) | 40,092.00 | 2.485800 |
| Maximum (overall) | 43,394.00 | 4.163000 |
| Diameter (overall) | 41,743.00 | 3.263852 |
| Standard deviation (overall) | 953.64 | 0.392668 |
| Network | Training Perform. | Testing Perform. | Validation Perform. | Training Error | Testing Error | Validation Error | Training Algorithm | Error Function | Activ. of Hidden Layer | Output Activ. Function | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | RBF 1-30-1 | 0.983490 | 0.983020 | 0.984843 | 0.002516 | 0.002616 | 0.002319 | RBFT | Sum.quar. | Gauss | Identity |
| 2 | RBF 1-26-1 | 0.984841 | 0.985412 | 0.984883 | 0.002312 | 0.002255 | 0.002309 | RBFT | Sum.quar. | Gauss | Identity |
| 3 | RBF 1-25-1 | 0.986071 | 0.986443 | 0.985769 | 0.002126 | 0.002109 | 0.002179 | RBFT | Sum.quar. | Gauss | Identity |
| 4 | RBF 1-26-1 | 0.985491 | 0.985337 | 0.984503 | 0.002213 | 0.002262 | 0.002367 | RBFT | Sum.quar. | Gauss | Identity |
| 5 | RBF 1-30-1 | 0.984297 | 0.983784 | 0.984732 | 0.002394 | 0.002499 | 0.002339 | RBFT | Sum.quar. | Gauss | Identity |
| Statistics | 1.RBF 1-30-1 | 2.RBF 1-26-1 | 3.RBF 1-25-1 | 4.RBF 1-26-1 | 5.RBF 1-30-1 |
|---|---|---|---|---|---|
| Minimal prediction (training) | 2.58183 | 2.55340 | 2.52919 | 2.52734 | 2.62556 |
| Maximal prediction (training) | 4.04950 | 4.09743 | 4.00225 | 4.00540 | 3.95151 |
| Minimal prediction (testing) | 2.58355 | 2.55342 | 2.52917 | 2.52741 | 2.62557 |
| Maximal prediction (testing) | 4.04944 | 4.09741 | 4.00223 | 4.00544 | 3.95152 |
| Minimal prediction (validation) | 2.58184 | 2.55531 | 2.53062 | 2.52749 | 2.62600 |
| Maximal prediction (validation) | 4.04951 | 4.09682 | 4.00226 | 4.00505 | 3.95129 |
| Minimal residuals (training) | −0.22414 | −0.21614 | −0.30694 | −0.24314 | −0.28141 |
| Maximal residuals (training) | 0.37317 | 0.23107 | 0.22900 | 0.21521 | 0.29266 |
| Minimal residuals (testing) | −0.21388 | −0.18746 | −0.28546 | −0.22842 | −0.26051 |
| Maximal residuals (testing) | 0.37307 | 0.23378 | 0.22341 | 0.20519 | 0.29323 |
| Minimal residuals (validation) | −0.21094 | −0.17494 | −0.17479 | −0.20650 | −0.23232 |
| Maximal residuals (validation) | 0.26023 | 0.22773 | 0.18504 | 0.21784 | 0.21065 |
| Minimal standard residuals (training) | −4.46833 | −4.49505 | −6.65757 | −5.16815 | −5.75120 |
| Maximal standard residuals (training) | 7.43936 | 4.80567 | 4.96689 | 4.57450 | 5.98108 |
| Minimal standard residuals (testing) | −4.18178 | −3.94719 | −6.21611 | −4.80292 | −5.21090 |
| Maximal standard residuals (testing) | 7.29438 | 4.92251 | 4.86501 | 4.31438 | 5.86540 |
| Minimal standard residuals (validation) | −4.38041 | −3.64037 | −3.74445 | −4.24472 | −4.80316 |
| Maximal standard residuals (validation) | 5.40392 | 4.73891 | 3.96396 | 4.47779 | 4.35511 |
| Characteristics | 1.RBF 1-24-1 | 2.RBF 1-29-1 | 3.RBF 1-30-1 | 4.RBF 1-28-1 | 5.RBF 1-26-1 |
|---|---|---|---|---|---|
| Aggregate of residuals | 0.150758 | −1.025922566 | −3.350398611 | −1.785245346 | −3.244516106 |
| Network | Training Perform. | Testing Perform. | Validation Perform. | Training Error | Testing Error | Validation Error | Training Algorithm | Error Function | Activ. of Hidden Layer | Output Activ. Function | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | MLP 61-11-1 | 0.998718 | 0.996990 | 0.997563 | 0.000197 | 0.000468 | 0.000374 | BFGS (Quasi-Newton) 392 | Sum quart. | Tanh | Identity |
| 2 | MLP 61-11-1 | 0.998927 | 0.997313 | 0.997517 | 0.000165 | 0.000417 | 0.000382 | BFGS (Quasi-Newton) 461 | Sum quart. | Logistic | Identity |
| 3 | MLP 61-11-1 | 0.998919 | 0.997606 | 0.997632 | 0.000166 | 0.000377 | 0.000364 | BFGS (Quasi-Newton) 569 | Sum quart. | Tanh | Identity |
| 4 | MLP 61-11-1 | 0.998791 | 0.997572 | 0.997594 | 0.000186 | 0.000377 | 0.000372 | BFGS (Quasi-Newton) 558 | Sum quart. | Tanh | Exponential |
| 5 | MLP 61-10-1 | 0.998640 | 0.997059 | 0.997641 | 0.000209 | 0.000457 | 0.000363 | BFGS (Quasi-Newton) 436 | Sum quart. | Tanh | Tanh |
| Statistics | 1.MLP 61-11-1 | 2.MLP 61-11-1 | 3.MLP 61-11-1 | 4.MLP 61-11-1 | 5.MLP 61-10-1 |
|---|---|---|---|---|---|
| Minimal prediction (training) | 5.99845 | 6.00641 | 5.99154 | 5.99371 | 6.00098 |
| Maximal prediction (training) | 9.84882 | 9.89527 | 9.87232 | 9.83699 | 9.88105 |
| Minimal prediction (testing) | 6.45895 | 6.46012 | 6.45663 | 6.45980 | 6.46002 |
| Maximal prediction (testing) | 9.95255 | 9.99209 | 9.96231 | 9.95287 | 9.99096 |
| Minimal prediction (validation) | 6.38529 | 6.39955 | 6.38028 | 6.38217 | 6.39652 |
| Maximal prediction (validation) | 9.83693 | 9.84308 | 9.83457 | 9.83696 | 9.84264 |
| Minimal residuals (training) | −0.17159 | −0.19452 | −0.16813 | −0.17882 | −0.19039 |
| Maximal residuals (training) | 0.40824 | 0.50655 | 0.50247 | 0.55336 | 0.55220 |
| Minimal residuals (testing) | −0.26528 | −0.23472 | −0.19660 | −0.24778 | −0.19037 |
| Maximal residuals (testing) | 0.20029 | 0.23874 | 0.22354 | 0.19344 | 0.21280 |
| Minimal residuals (validation) | −0.18526 | −0.18002 | −0.17583 | −0.17599 | −0.17991 |
| Maximal residuals (validation) | 0.49820 | 0.48575 | 0.49862 | 0.49338 | 0.48770 |
| Minimal standard residuals (training) | −5.65878 | −5.87540 | −5.56482 | −5.12649 | −5.87337 |
| Maximal standard residuals (training) | 14.23498 | 15.85302 | 15.20208 | 14.18194 | 15.03849 |
| Minimal standard residuals (testing) | −5.02283 | −5.74512 | −6.00274 | −6.12485 | −5.34937 |
| Maximal standard residuals (testing) | 5.20498 | 4.99831 | 5.48930 | 5.40087 | 4.35498 |
| Minimal standard residuals (validation) | −4.94651 | −3.99879 | −4.84632 | −4.57713 | −3.96781 |
| Maximal standard residuals (validation) | 11.59751 | 11.00974 | 11.75020 | 11.34307 | 11.01994 |
| Characteristics | 1.MLP 61-11-1 | 2.MLP 61-11-1 | 3.MLP 61-11-1 | 4.MLP 61-11-1 | 5.MLP 61-10-1 |
|---|---|---|---|---|---|
| Aggregate of residuals | 0.632230639 | 0.120515671 | −0.437742553 | 0.738084025 | 0.803606299 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rowland, Z.; Lazaroiu, G.; Podhorská, I. Use of Neural Networks to Accommodate Seasonal Fluctuations When Equalizing Time Series for the CZK/RMB Exchange Rate. Risks 2021, 9, 1. https://doi.org/10.3390/risks9010001
Rowland Z, Lazaroiu G, Podhorská I. Use of Neural Networks to Accommodate Seasonal Fluctuations When Equalizing Time Series for the CZK/RMB Exchange Rate. Risks. 2021; 9(1):1. https://doi.org/10.3390/risks9010001
Chicago/Turabian StyleRowland, Zuzana, George Lazaroiu, and Ivana Podhorská. 2021. "Use of Neural Networks to Accommodate Seasonal Fluctuations When Equalizing Time Series for the CZK/RMB Exchange Rate" Risks 9, no. 1: 1. https://doi.org/10.3390/risks9010001
APA StyleRowland, Z., Lazaroiu, G., & Podhorská, I. (2021). Use of Neural Networks to Accommodate Seasonal Fluctuations When Equalizing Time Series for the CZK/RMB Exchange Rate. Risks, 9(1), 1. https://doi.org/10.3390/risks9010001




