Reassessment of Thin-Layer Drying Models for Foods: A Critical Short Communication
Abstract
1. Introduction
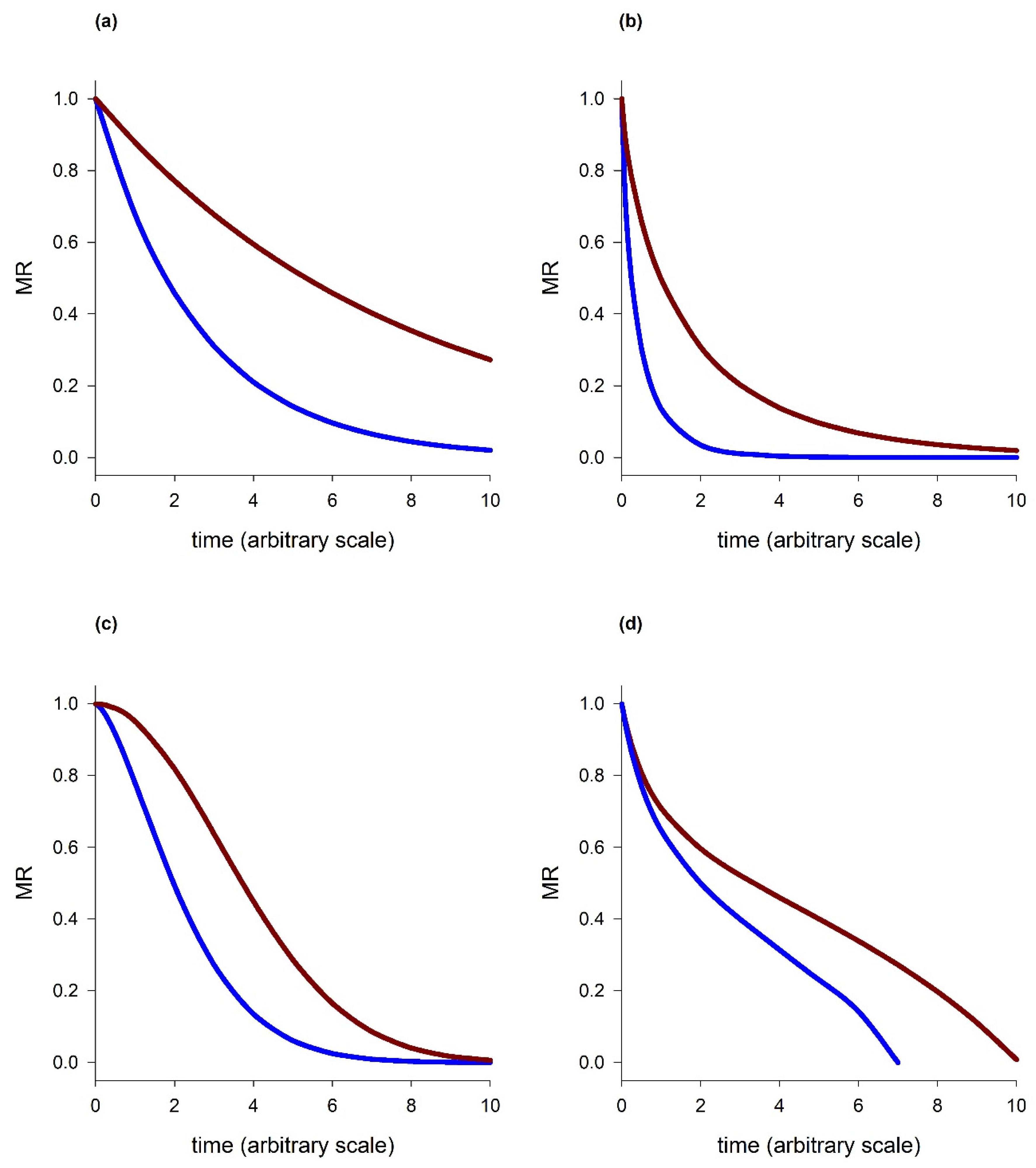
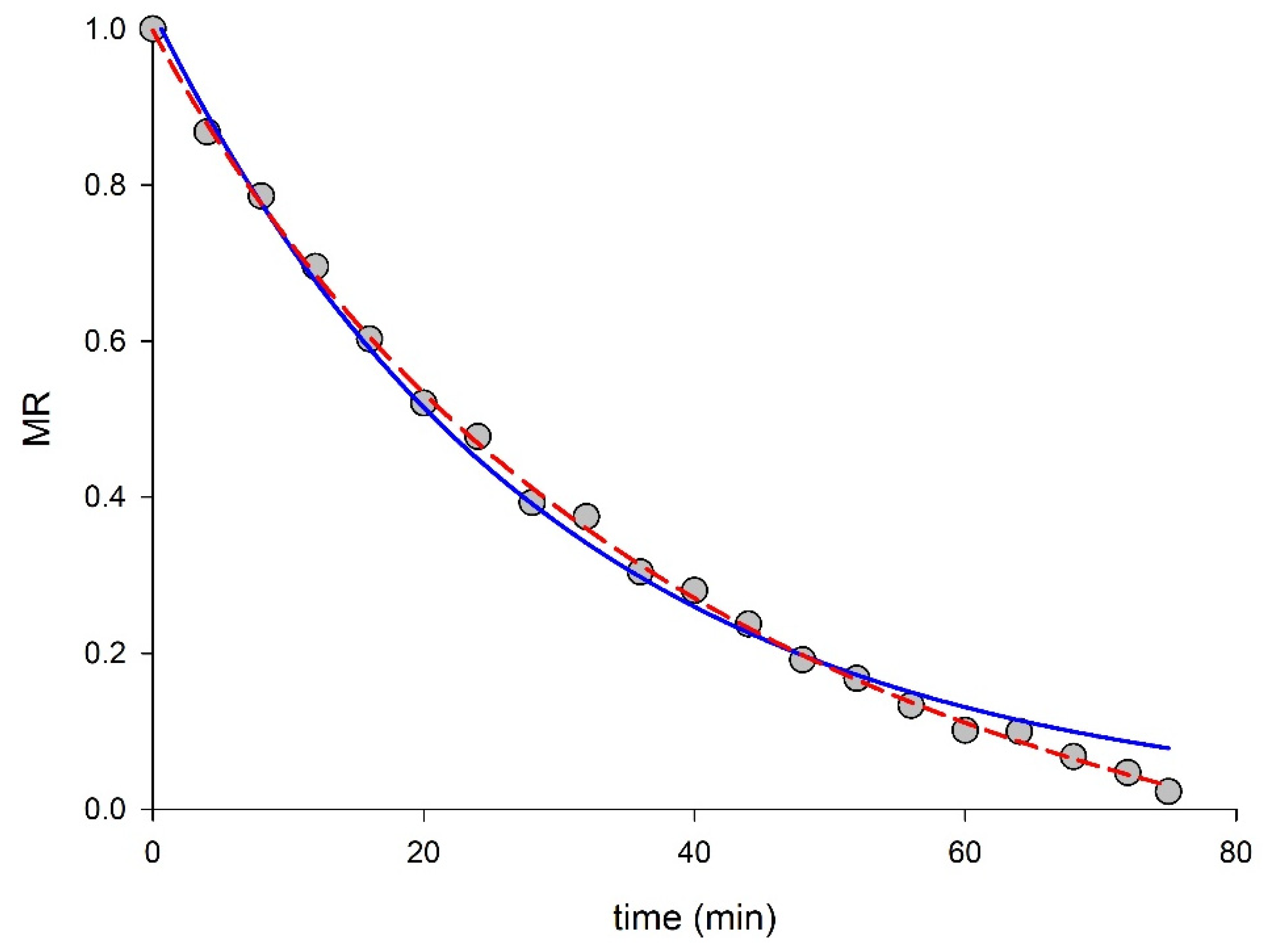
2. Types of Drying Curves
3. Modification of the Models
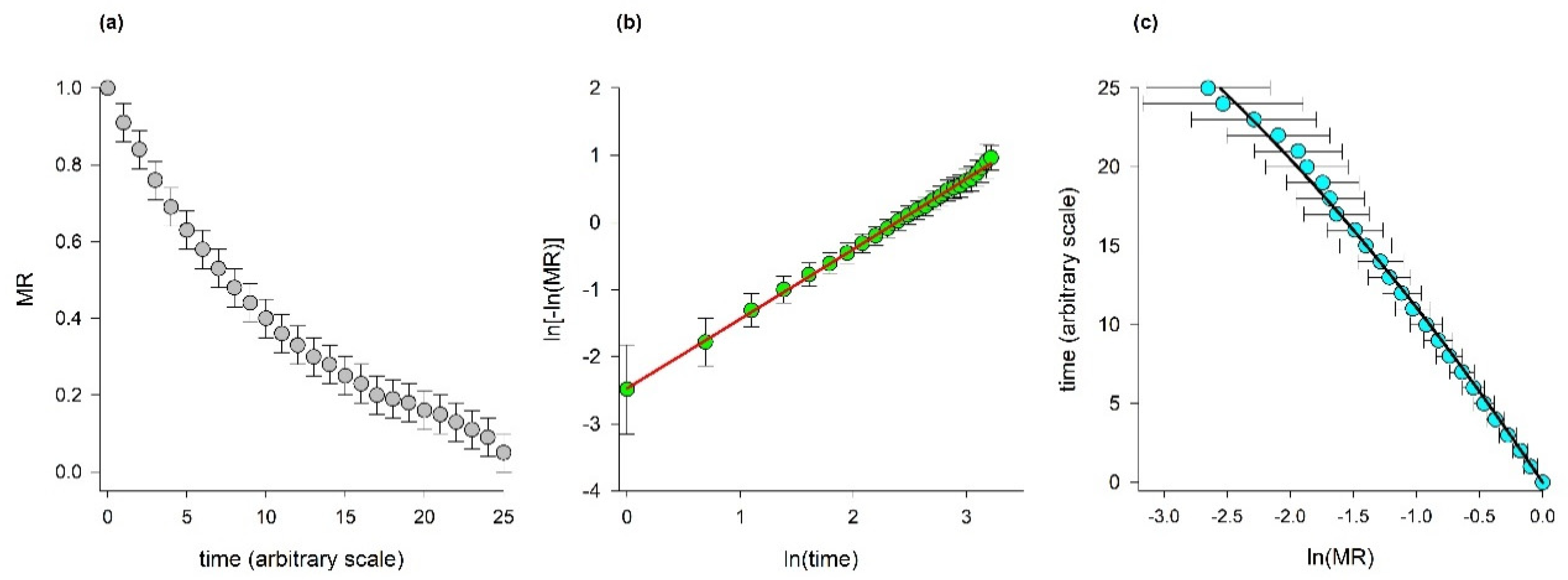
4. Models That Require Transformation
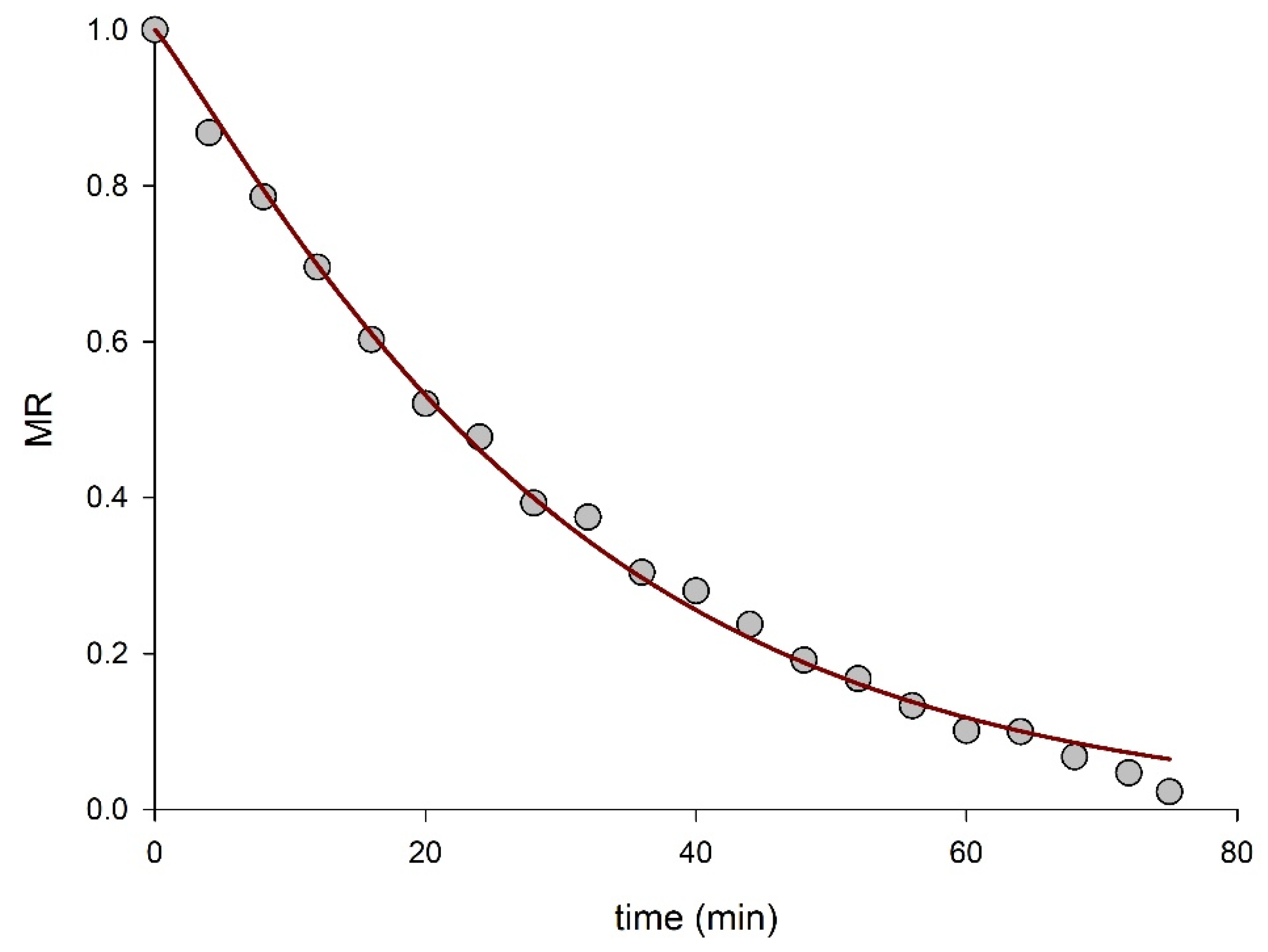
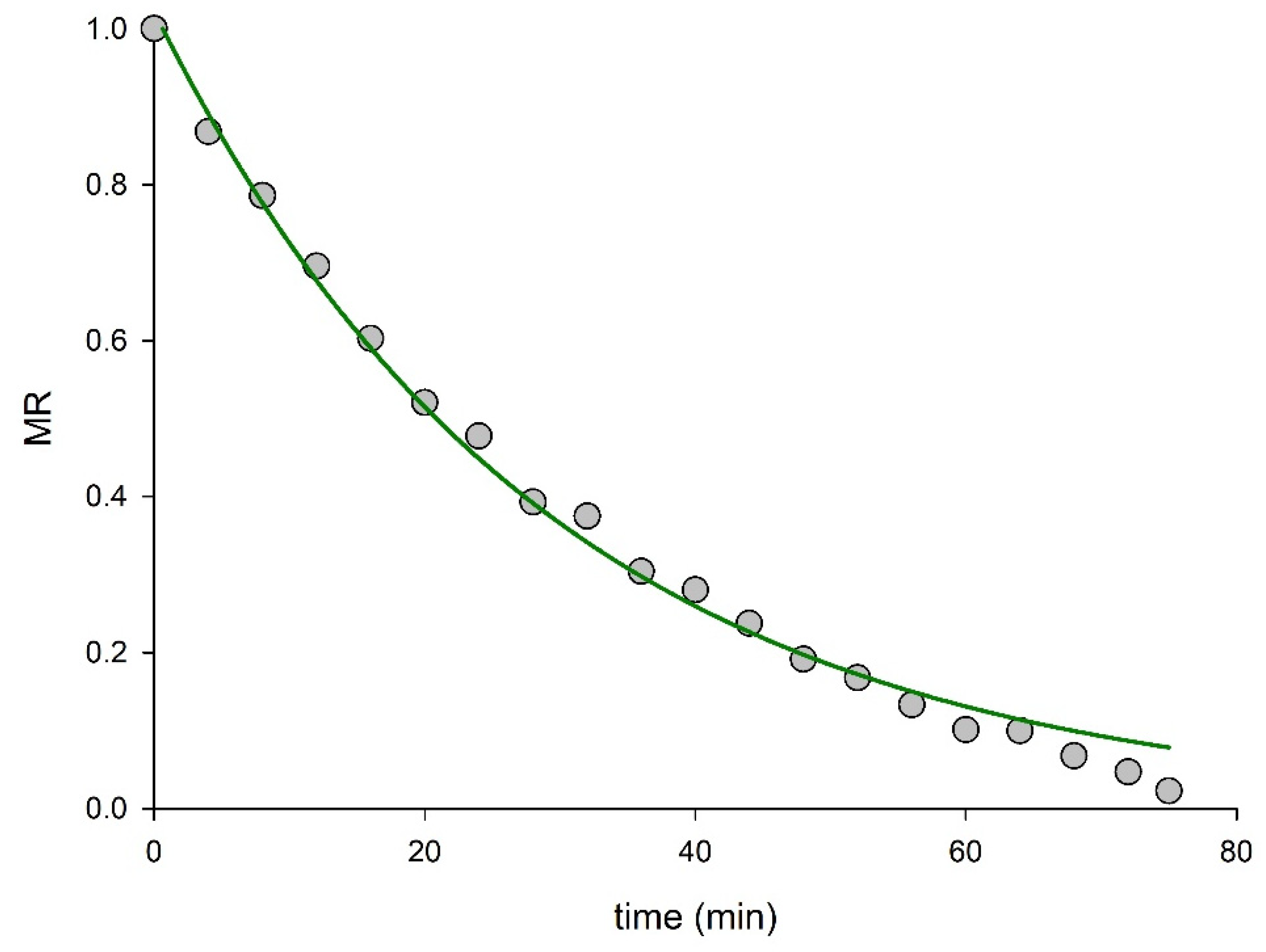
5. Use of Complex Models for Drying Data
6. Models Proposed for Drying of Foods
- (i)
- Models that require transformed data;
- (ii)
- Complex models or models that have more than three parameters;
- (iii)
- Models that have the same fit with another model but have more parameters.
7. Conclusions
- –
- The arbitrary use of thin-layer drying models should be avoided;
- –
- Complex models, most of the time, result in insignificant parameters;
- –
- Models with two adjustable parameters work well for drying data;
- –
- Logarithmic transformation generates heteroscedastic data and should not be used.
- The simplest possible model that can describe the data should be considered as the best model (known as Ockham’s razor or rule of parsimony). Most drying data can be described with the two-parameter models. Therefore, it is best to try them first. More complex models should only be used if the simple model is not adequate to describe the data;
- Two different forms of the same models (having the same number of parameters) should not be used together because they are not rival models but the same models with different mathematical structures. The one that has less uncertainty on parameters and also a correlation between the parameters could be preferred;
- Parameters should also be listed together with their standard errors or confidence intervals, since uncertainties could also give information on the parameters’ significance;
- The meaning of the parameters and the effect of their values on the curve’s shape should be well known, even if the model used is an empirical one;
- The R2 alone is not adequate to compare the models, and the RMSE and residuals should also be used to compare the models with the same number of parameters. A comparison of the models that have a different number of parameters (i.e., comparing a three-parameter model with a two-parameter model) may require different analyses, such as the F-test.
Funding
Data Availability Statement
Conflicts of Interest
References
- Babalis, S.J.; Papanicolaou, E.; Kyriakis, N.; Belessiotis, V.G. Evaluation of thin-layer drying models for describing drying kinetics of figs (Ficus carica). J. Food Eng. 2006, 75, 205–214. [Google Scholar] [CrossRef]
- Kamal, M.M.; Ali, M.R.; Shishir, M.R.I.; Mondal, S.C. Thin-layer drying kinetics of yam slices, physicochemical, and functional attributes of yam flour. J. Food Process Eng. 2020, 43, e13448. [Google Scholar] [CrossRef]
- Shishir, M.R.I.; Karim, N.; Bao, T.; Gowd, V.; Ding, T.; Sun, C.; Chen, W. Cold plasma pretreatment—A novel approach to improve the hot air drying characteristics, kinetic parameters, and nutritional attributes of shiitake mushroom. Dry. Technol. 2020, 38, 2134–2150. [Google Scholar] [CrossRef]
- İlter, I.; Akyıl, S.; Devseren, E.; Okut, D.; Koç, M.; Kaymak Ertekin, F. Microwave and hot air drying of garlic puree: Drying kinetics and quality characteristics. Heat Mass Transf. 2018, 54, 2101–2112. [Google Scholar] [CrossRef]
- Sadeghi, E.; Movagharnejad, K.; Asl, A.H. Mathematical modeling of infrared radiation thin-layer drying of pumpkin samples under natural and forced convection. J. Food Process. Preserv. 2019, 43, e14229. [Google Scholar] [CrossRef]
- Keey, R.B. Drying Principles and Practice; Pergamon Press: Oxford, UK, 1972; pp. 1–18. [Google Scholar]
- Klemes, J.; Smith, R.; Kim, J.K. Handbook of Water and Energy Management in Food Processing; Woodhead Publishing: Cambridge, UK; CRC Press: Boca Raton, FL, USA, 2008; pp. 449–629. [Google Scholar]
- Onwude, D.I.; Hashim, N.; Janius, R.B.; Nawi, N.M.; Abdan, K. Modeling the thin-layer drying of fruits and vegetables: A review. Compr. Rev. Food Sci. Food Saf. 2016, 15, 599–618. [Google Scholar] [CrossRef] [PubMed]
- Giri, S.K.; Prasad, S. Drying kinetics and rehydration characteristics of microwave vacuum and convective-hot air-dried mushrooms. J. Food Eng. 2007, 78, 512–521. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F. A review of thin layer drying of foods: Theory, modeling, and experimental results. Crit. Rev. Food Sci. Nutr. 2009, 50, 441–464. [Google Scholar] [CrossRef] [PubMed]
- Sopade, P.A.; Xun, P.Y.; Halley, P.J.; Hardin, M. Equivalence of the Peleg, Pilosof and SinghKulshrestha models for water absorption in food. J. Food Eng. 2007, 78, 730–734. [Google Scholar] [CrossRef]
- Bryś, A.; Kaleta, A.; Górnicki, K.; Głowacki, S.; Tulej, W.; Bryś, J.; Wichowski, P. Some Aspects of the Modelling of Thin-Layer Drying of Sawdust. Energies 2021, 14, 726. [Google Scholar] [CrossRef]
- Kaleta, A.; Górnicki, K. Some remarks on evaluation of drying models of red beet particles. Energy Convers. Manag. 2010, 51, 2967–2978. [Google Scholar] [CrossRef]
- Ashtiani, S.-H.M.; Salarikia, A.; Golzarian, M.R. Analyzing drying characteristics and modeling of thin layers of peppermint leaves under hot-air and infrared treatments. Inf. Process. Agric. 2017, 4, 128–139. [Google Scholar]
- Górnicki, K.; Kaleta, A.; Choińska, A. Suitable model for thin-layer drying of root vegetables and onion. Int. Agrophys. 2020, 34, 79–86. [Google Scholar] [CrossRef]
- Ertekin, C.; Firat, M.Z. A comprehensive review of thin-layer drying models used in agricultural products. Crit. Rev. Food Sci. Nutr. 2017, 57, 701–717. [Google Scholar] [CrossRef] [PubMed]
- Van Boekel, M.A.J.S. Statistical aspects of kinetic modeling for food science problems. J. Food Sci. 1996, 61, 477–485, 489. [Google Scholar] [CrossRef]
- Jayas, D.S.; Cenkowski, S.; Pabis, S.; Muir, W.E. Review of thin-layer drying and wetting equations. Dry. Technol. 1991, 9, 551–588. [Google Scholar] [CrossRef]
- Zhu, A.; Shen, X. The model and mass transfer characteristics of convection drying of peach slices. Int. J. Heat Mass Transf. 2014, 72, 345–351. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rate of Air Drying Shelled Corn in Thin-Layers. Master’s Thesis, Purdue University, West Lafayette, Indiana, 1949. [Google Scholar]
- Overhults, D.G.; White, G.M.; Hamilton, H.E.; Ross, I.J. Drying soybeans with heated air. Trans. ASAE 1973, 16, 112–113. [Google Scholar] [CrossRef]
- Karacabey, E.; Buzrul, S. Modeling and predicting the drying kinetics of apple and pear: Application of the Weibull model. Chem. Eng. Commun. 2017, 204, 573–579. [Google Scholar] [CrossRef]
- Toğrul, İ.T.; Pehlivan, D. Modelling of drying kinetics of single apricot. J. Food Eng. 2003, 58, 23–32. [Google Scholar] [CrossRef]
- Kingsly, R.P.; Goyal, R.K.; Manikantan, M.R.; Ilyas, S.M. Effects of pretreatments and drying air temperature on drying behaviour of peach slice. Int. J. Food Sci. Technol. 2007, 42, 65–69. [Google Scholar] [CrossRef]
- Diamante, L.M.; Munro, P.A. Mathematical modelling of the thin layer solar drying of sweet potato slices. Sol. Energy 1993, 51, 271–276. [Google Scholar] [CrossRef]
- Van Boekel, M.A.J.S. Kinetic Modeling of Reactions in Foods; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Lutovska, M.; Mitrevski, V.; Pavkov, I.; Mijakovski, V.; Radojčin, M. Mathematical modelling of thin layer drying of pear. Chem. Ind. Chem. Eng. Q. 2016, 22, 191–199. [Google Scholar] [CrossRef]
- Turan, O.Y.; Fıratlıgil, F.E. Modelling and characteristics of thin layer convective air-drying of thyme (Thymus vulgaris) leaves. Czech J. Food Sci. 2019, 37, 128–134. [Google Scholar] [CrossRef]
- Diamante, L.M.; Ihns, R.; Savage, G.P.; Vanhanen, L. A new mathematical model for thin layer drying of fruits. Int. J. Food Sci. Technol. 2010, 45, 1956–1962. [Google Scholar] [CrossRef]
- Thompson, T.L.; Peart, R.M.; Foster, G.H. Mathematical simulation of corn drying—A new model. Trans. ASAE 1968, 11, 582–586. [Google Scholar] [CrossRef]
- Schaffner, D.W. Predictive food microbiology Gedanken experiment: Why do microbial growth data require a transformation? Food Microbiol. 1998, 15, 185–189. [Google Scholar] [CrossRef]
- Karathanos, V.T. Determination ofwater content of dried fruits by drying kinetics. J. Food Eng. 1999, 39, 337–344. [Google Scholar] [CrossRef]
- Buzrul, S. Letter to the Editor: Models with Insignificant Parameters. Appl. Environ. Microbiol. 2008, 74, 6481–6482. [Google Scholar] [CrossRef][Green Version]
- Henderson, S.M.; Pabis, S. Grain drying theory I: Temperature effect on drying coefficient. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Buzrul, S.; Alpas, H. Modeling the synergistic effect of high pressure and heat on the inactivation kinetics of Listeria innocua: A preliminary study. FEMS Microbiol. Lett. 2004, 238, 29–36. [Google Scholar] [PubMed]
- Midilli, A.; Kucuk, H.; Yapar, Z. A new model for single-layer drying. Dry. Technol. 2002, 20, 1503–1513. [Google Scholar] [CrossRef]
- Motulsky, H.J.; Christopoulos, A. Fitting models to biological data using linear and nonlinear regression. In A Practical Guide to Curve Fitting; GraphPad Software Inc.: San Diego, CA, USA, 2003. [Google Scholar]
- Motulsky, H.J.; Ransnas, L.A. Fitting curves to data using nonlinear regression: A practical and nonmathematical review. FASEB J. 1987, 1, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Lewis, W.K. The rate of drying of solid materials. IEC-Symp. Dry. 1921, 3, 427–432. [Google Scholar] [CrossRef]
- Henderson, S.M. Progress in developing the thin layer drying equation. Trans. ASAE 1974, 17, 1167–1172. [Google Scholar] [CrossRef]
- Yagcioglu, A.; Degirmencioglu, A.; Cagatay, F. Drying characteristics of laurel leaves under different drying conditions. In Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, Adana, Turkey, 26–27 May 1999; pp. 426–431. [Google Scholar]
- Ghazanfari, A.; Emami, S.; Tabil, L.G.; Panigrahi, S. Thin-layer drying of flax fiber: Modeling drying process using semi-theoretical and empirical models. Dry. Technol. 2006, 24, 1637–1642. [Google Scholar] [CrossRef]
- Demir, V.; Gunhan, T.; Yagcioglu, A.K. Mathematical modelling of convection drying of green table olives. Biosys. Eng. 2007, 98, 47–53. [Google Scholar] [CrossRef]
- Sharaf-Eldeen, Y.I.; Blaisdell, J.L.; Hamdy, M.Y. A model for ear corn drying. Trans. ASAE 1980, 23, 1261–1271. [Google Scholar] [CrossRef]
- Verma, L.R.; Bucklin, R.A.; Ednan, J.B.; Wratten, F.T. Effects of drying air parameters on rice drying models. Trans. ASAE 1985, 28, 296–301. [Google Scholar] [CrossRef]
- Wang, C.Y.; Singh, R.P. A Single Layer Drying Equation for Rough Rice; ASAE Paper No. 3001; ASAE: St. Joseph, MI, USA, 1978. [Google Scholar]
- Aghbashlo, M.; Kianmehr, M.H.; Khani, S.; Ghasemi, M. Mathematical modeling of thin-layer drying of carrot. Intl. Agrophys. 2009, 23, 313–317. [Google Scholar]
- Baltacıoğlu, C.; Okur, İ.; Buzrul, S. Model based comparison of drying of asparagus (Asparagus officinalis L.) with traditional method and microwave. J. Food 2020, 45, 572–580. [Google Scholar]
- Corzo, O.; Bracho, N.; Pereira, A.; Vasquez, A. Weibull distribution for modeling air drying of coroba slices. LWT—Food Sci. Technol. 2008, 41, 2023–2028. [Google Scholar] [CrossRef]
- Hutchinson, D.; Otten, L. Thin-layer air drying of soybeans and white beans. J. Food Technol. 1983, 18, 507–522. [Google Scholar] [CrossRef]
- Van Boekel, M.A.J.S. To pool or not to pool: That is the question in microbial kinetics. Int. J. Food Microbiol. 2021, 354, 109283. [Google Scholar] [CrossRef] [PubMed]

| Sample | T (°C) | Air Velocity (m/s) | Thickness (mm) | Page | Modified Page | R2 | RMSE | Reference |
|---|---|---|---|---|---|---|---|---|
| Apple | 50 | 1.3 | 5.0 | k = 0.0023 ± 0.0003 n = 1.3182 ± 0.0295 | K = 0.0098 ± 0.0001 n = 1.3182 ± 0.0295 | 0.9988 | 0.0142 | [22] |
| Apricot | 70 | 0.5 | Whole fruit | k = 0.0018 ± 0.0002 n = 1.1445 ± 0.0226 | K = 0.0039 ± 5.3 × 10−5 n = 1.1445 ± 0.0226 | 0.9963 | 0.0216 | [23] |
| Peach | 65 | 0.8 | 3.5 | k = 0.0083 ± 0.0019 n = 1.1237 ± 0.0519 | K = 0.0141 ± 0.0004 n = 1.1237 ± 0.0519 | 0.9973 | 0.0196 | [24] |
| Peach | 60 | 0.946 | 3.0 | k = 0.0227 ± 0.0023 n = 1.1102 ± 0.0288 | K = 0.0331 ± 0.0005 n = 1.1102 ± 0.0288 | 0.9960 | 0.0192 | [19] |
| Pear | 80 | 1.3 | 5.0 | k = 0.0042 ± 0.0007 n = 1.3205 ± 0.0395 | K = 0.0158 ± 0.0003 n = 1.3182 ± 0.0295 | 0.9984 | 0.0175 | [22] |
| Parameter | Estimate | Standard Error | p Value |
|---|---|---|---|
| a | 0.3369 | 0.0406 | <0.0001 |
| k | 0.0343 | 0.0869 | 0.6994 |
| b | 0.3486 | 0.0580 | <0.0001 |
| g | 0.0343 | 0.3713 | 0.9278 |
| c | 0.3364 | 0.0580 | <0.0001 |
| h | 0.0343 | 0.3583 | 0.9251 |
| Parameter | Estimate | Standard Error | p Value |
|---|---|---|---|
| a | 0.5134 | 0.0380 | <0.0001 |
| k | 0.0343 | 0.1004 | 0.7372 |
| b | 0.5085 | 0.0542 | <0.0001 |
| g | 0.0343 | 0.5067 | 0.9469 |
| Parameter | Estimate | Standard Error | p Value |
|---|---|---|---|
| a | 0.9984 | 0.0098 | <0.0001 |
| k | 0.0319 | 0.0036 | <0.0001 |
| n | 0.9688 | 0.0361 | <0.0001 |
| b | −0.0012 | 0.0002 | <0.0001 |
| Model No. | Model Name | Model Equation | Reason | Reference |
|---|---|---|---|---|
| 1 | Henderson–Pabis | Initial condition | [40] | |
| 2 | Modified Henderson–Pabis | Initial condition Insignificant parameters | [32] | |
| 3 | Modified Page II | Simpler version with the same fit but fewer parameters is available | [25] | |
| 4 | Logarithmic (Asymptotic) | Initial condition Final condition | [41] | |
| 5 | Midilli | Initial condition Final condition Insignificant parameters | [36] | |
| 6 | Modified Midilli I | Final condition Insignificant parameters | [42] | |
| 7 | Modified Midilli II | Initial condition Final condition Insignificant parameters | [43] | |
| 8 | Two-term | Initial condition Insignificant parameters | [34] | |
| 9 | Modified two-term I | Insignificant parameters | [44] | |
| 10 | Modified two-term II | Insignificant parameters | [45] | |
| 11 | Diamante | Transformation Heteroscedastic data | [29] | |
| 12 | Thompson | Transformation Heteroscedastic data | [30] | |
| 13 | Wang–Singh | Final condition | [46] | |
| 14 | Aghbashlo | Final condition | [47] |
| Model No. | Model Name | Model Equation | Comment | Reference |
|---|---|---|---|---|
| 1 | Lewis (Newton) | Simplest model, but not flexible enough to describe many drying data | [39] | |
| 2 | Page * | Simple, and can be used to describe drying data of many foods. Strong correlation between the parameters. | [20] | |
| 3 | Modified Page I * | Same fit with the Page model; however, it has fewer errors on the rate parameter (K), and also correlation between the parameters are low. | [21] | |
| 4 | Weibull * | Same fit with the Page model, low parameter correlation (same as Modified Page I). | [49] | |
| 5 | Weibull I * | Same fit with the Page model, mild parameter correlation. Interpretable time parameter (δ) that can be roughly estimated by visual inspection of the data. | [22] | |
| 6 | Modified two-term III | Mild to strong parameter correlation | [50] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buzrul, S. Reassessment of Thin-Layer Drying Models for Foods: A Critical Short Communication. Processes 2022, 10, 118. https://doi.org/10.3390/pr10010118
Buzrul S. Reassessment of Thin-Layer Drying Models for Foods: A Critical Short Communication. Processes. 2022; 10(1):118. https://doi.org/10.3390/pr10010118
Chicago/Turabian StyleBuzrul, Sencer. 2022. "Reassessment of Thin-Layer Drying Models for Foods: A Critical Short Communication" Processes 10, no. 1: 118. https://doi.org/10.3390/pr10010118
APA StyleBuzrul, S. (2022). Reassessment of Thin-Layer Drying Models for Foods: A Critical Short Communication. Processes, 10(1), 118. https://doi.org/10.3390/pr10010118






