Optimal Design Method for Static Precision of Heavy-Duty Vertical Machining Center Based on Gravity Deformation Error Modelling
Abstract
:1. Introduction
2. Precision Design Method of Heavy-Duty Machine Tool Based on Gravity Deformation Error Modelling
3. Modelling of Machine Tool Static Error Based on Multibody System
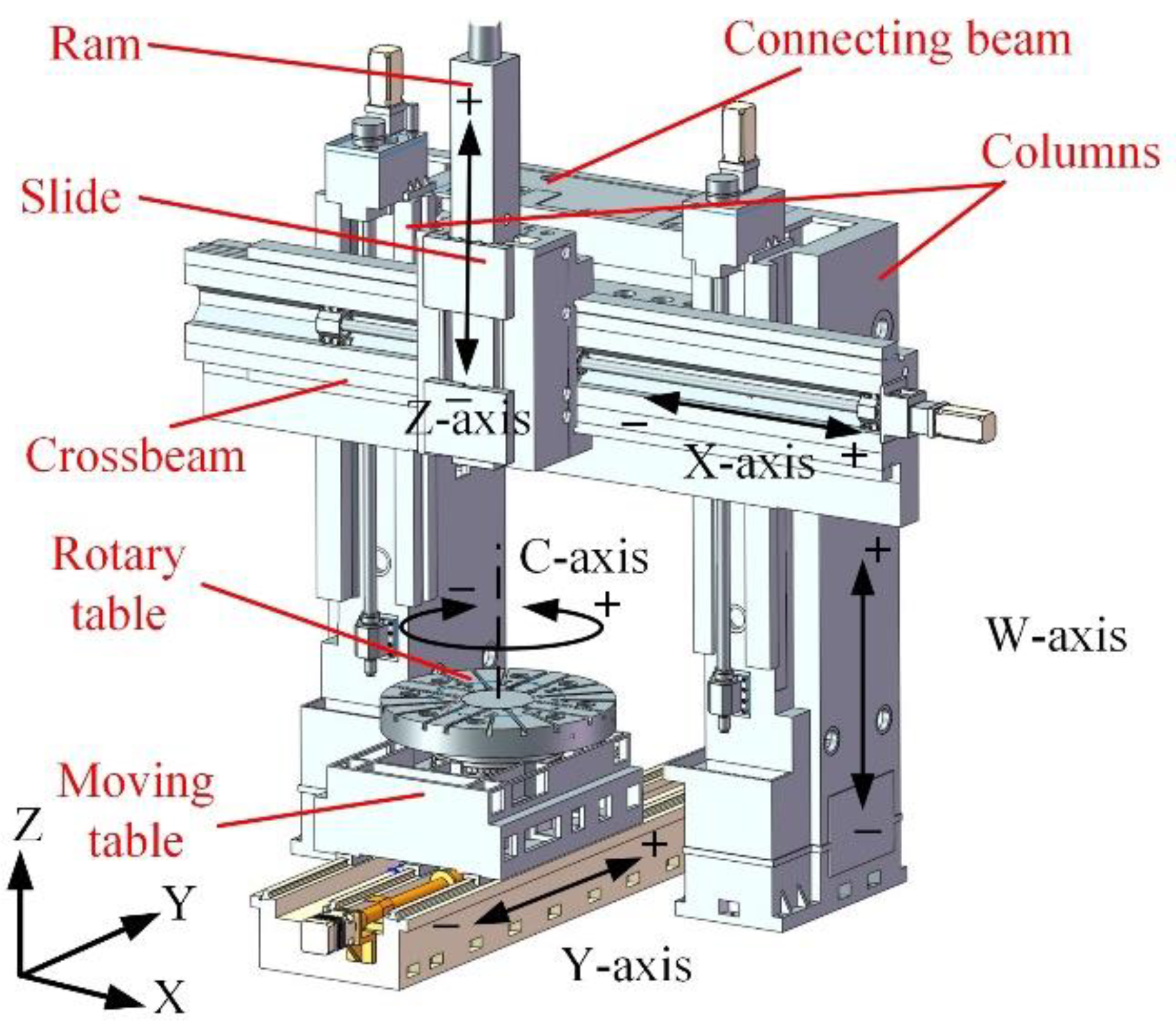
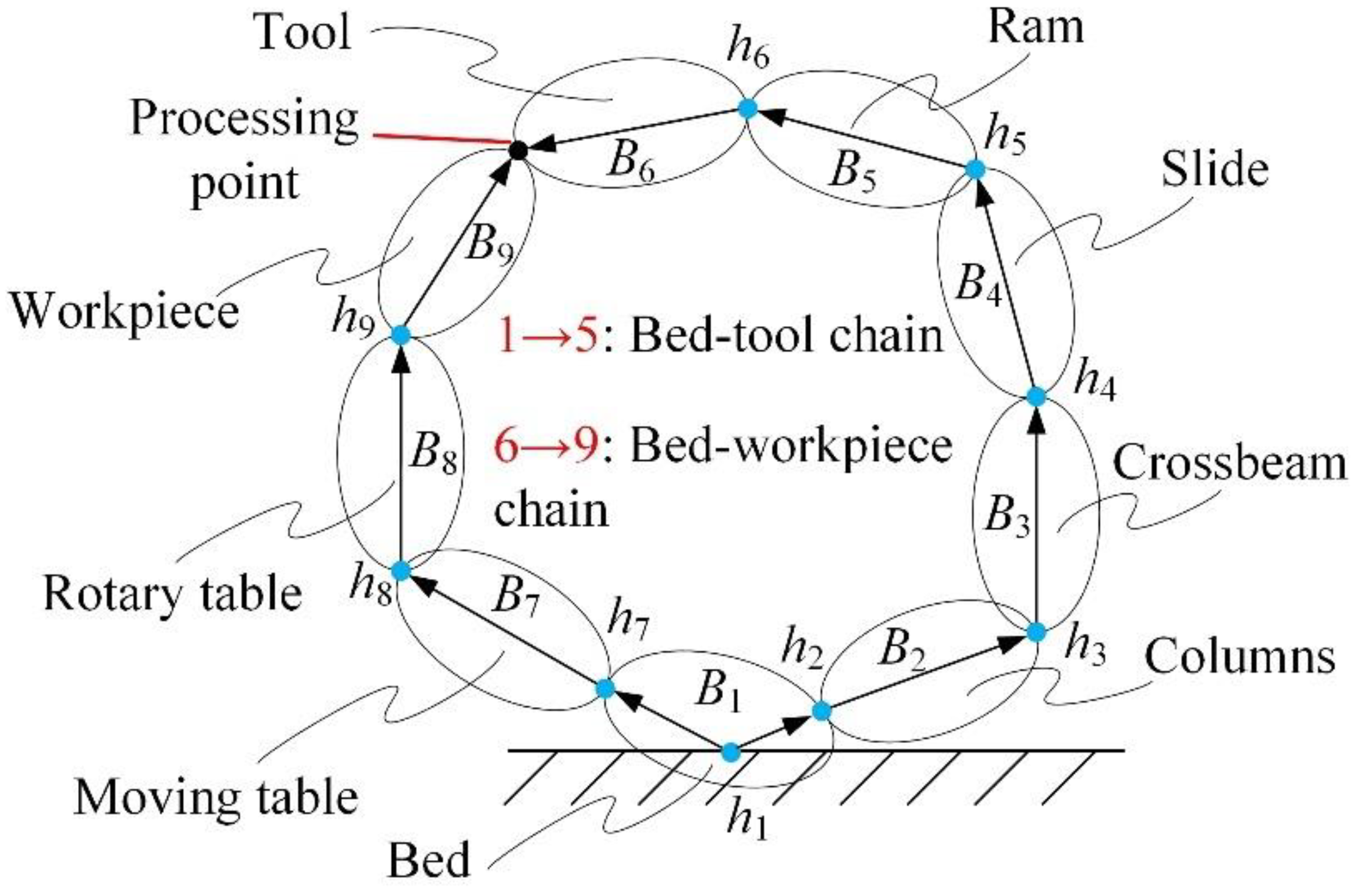
3.1. Machine Tool Topology and Coordinate System
3.2. Static Error Analysis of Heavy-Duty Vertical Machining Center
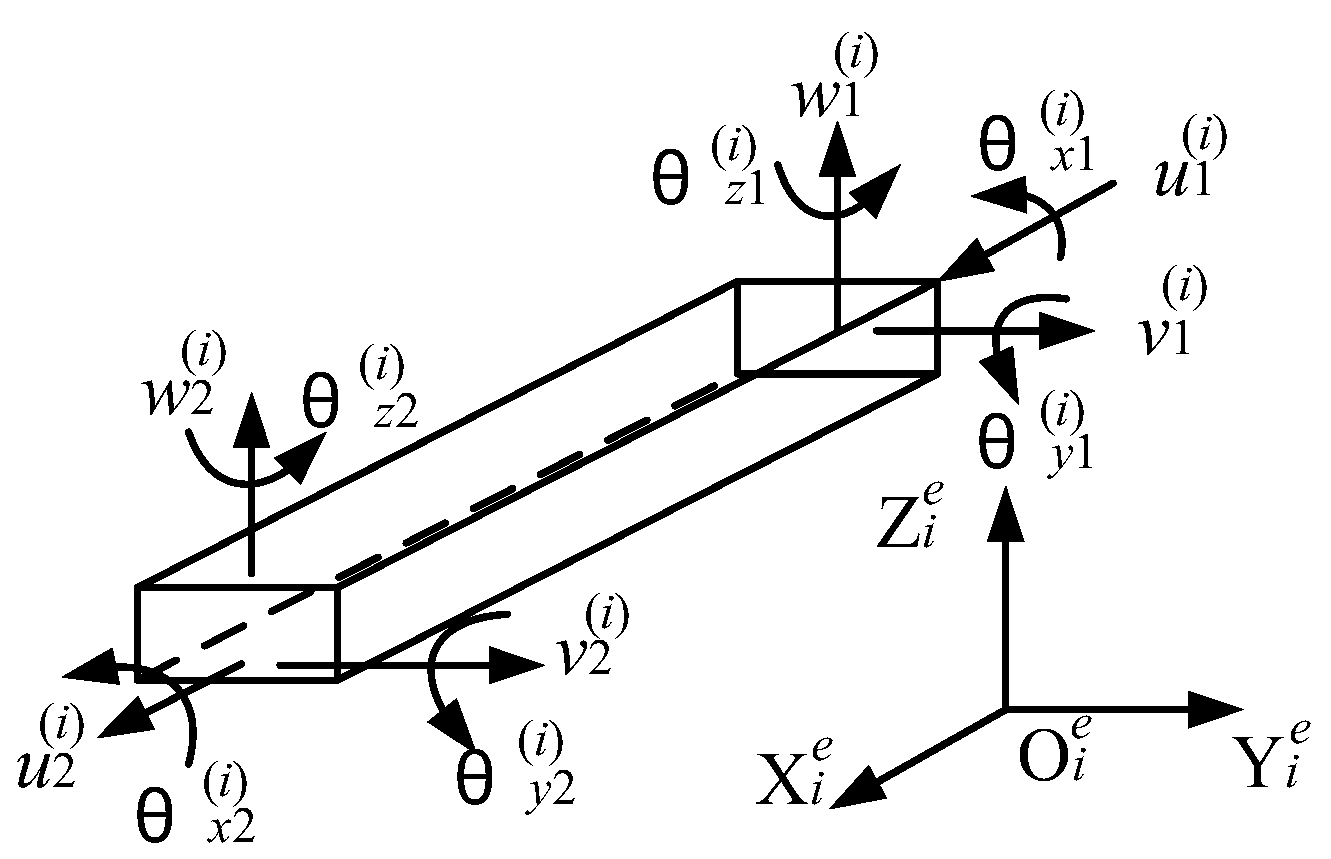
3.3. Static Error Modelling of Heavy-Duty Vertical Machining Center
4. Structural Stiffness Model of Machine Tool Based on Spatial Beam Element
4.1. Spatial Beam Element Model
4.2. Equivalent Nodal Load of Gravity
5. Design Optimization of Geometric Parameters and Structural Parameters
5.1. Design Variables
5.2. Constraints
5.3. Objective Function
5.4. Optimization Results
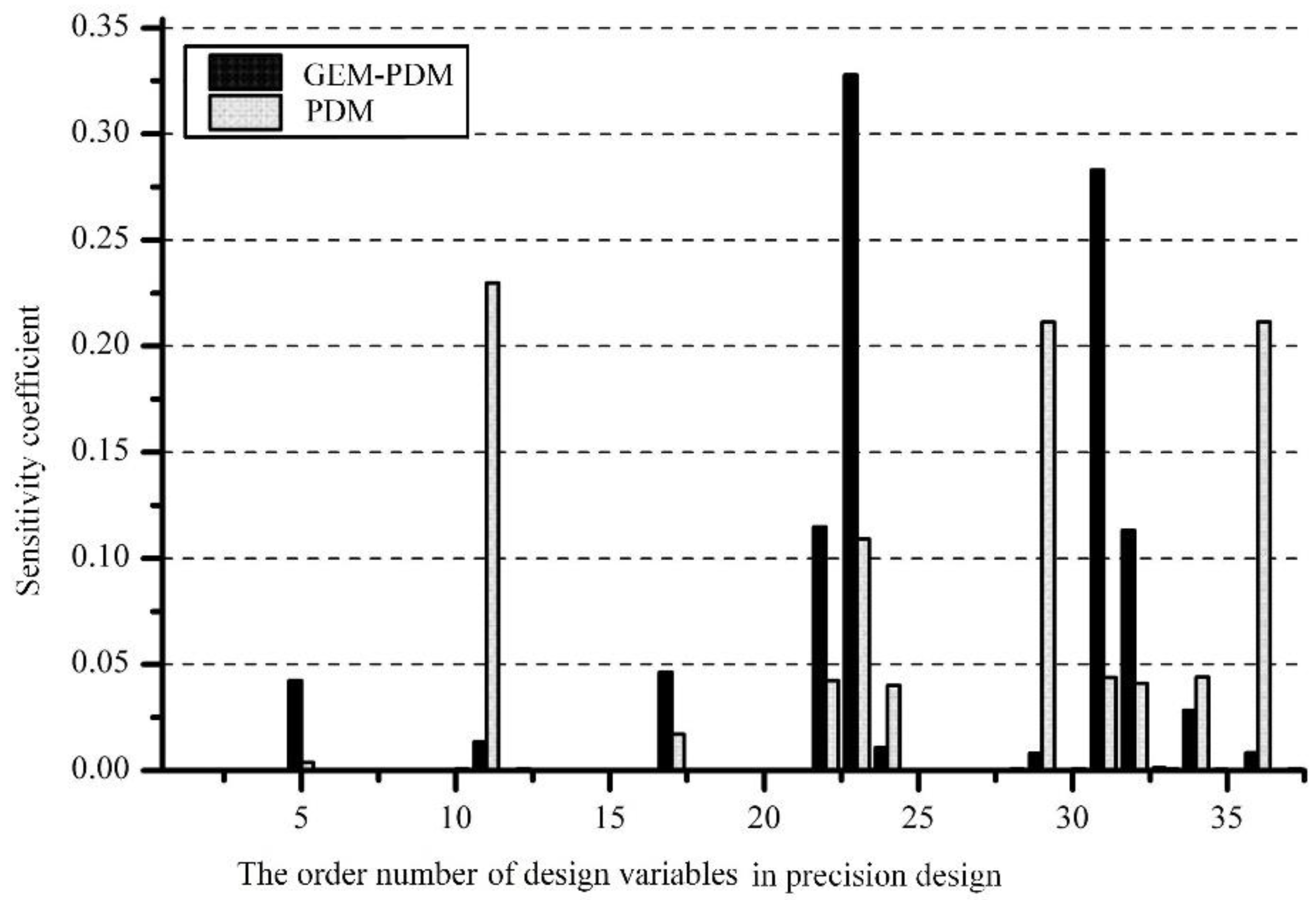
6. Comparative Analysis of Optimization Results and Existing Designs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | The cross-sectional area of the spatial beam element. |
| B | The body in the multibody system. |
| C | The structural compliance. |
| E | The elastic modulus. |
| Ev | The volumetric error of the theoretical forming point of the actual machine tool. |
| Evx | The component of the volumetric error in the X-direction (mm). |
| Evy | The component of the volumetric error in the Y-direction (mm). |
| Evz | The component of the volumetric error in the Z-direction (mm). |
| F | The external load vector. |
| Fzi | The external force along the Z-axis direction received by the ith node in the global coordinate system |
| fg1 | The relative cost function. |
| fg2 | The equalization objective function. |
| fg3 | The robust optimization objective function. |
| fd1 | The compliance objective function. |
| fd2 | The stiffness loss function. |
| g | The acceleration of gravity. |
| h | The hinge in the multibody system. |
| Iy | The moment of inertia of the cross section around the neutral axis parallel to the y-axis. |
| I′y | The moment of inertia of the cross-section of the optimized spatial beam element. |
| Iz | The moment of inertia of the cross section around the neutral axis parallel to the z-axis. |
| I′z | The torsional moment of inertia of the cross section of the optimized spatial beam element. |
| J | The torsional moment of inertia of the cross section. |
| J′ | The torsional moment of inertia of the cross section of the optimized spatial beam element. |
| K | The overall stiffness matrix of the structure. |
| Ke | The stiffness matrix of the spatial beam element in the local coordinate system. |
| kji (j = x, y, z) | The stiffness coefficient of the spatial beam element. |
| LEj (j = 1~5, 8~11) | The element length of the machine tool component represented by the jth element. |
| l | The element length. |
| Mj(i) (j = x, y, z) | The nodal moment of each node around the X-, Y-, Z-axes. |
| Myi | The external moment of the ith node around the Y-axis in the global coordinate system. |
| mE | The mass of the machine tool component represented by the element. |
| m′E | The mass of machine tool components represented by the optimized element. |
| n | The number of elements. |
| P | The overall nodal load vector. |
| Pactual | The actual position coordinate of the TCP. |
| Pe | The nodal load vector in the local coordinate system of the element. |
| Pideal | The actual position coordinate of the TCP. |
| Pi(i) (I = u, v, w) | The nodal force of each node along the X-, Y-, Z-directions. |
| Pt | The position coordinate vector Pt of the TCP in the tool coordinate system. |
| ptx, pty, ptz | The position coordinates of the TCP in the X-, Y-, Z-directions of the tool coordinate system. |
| q | The displacement vector of the structural node. |
| qe | The nodal displacement vector in the local coordinate system of the element. |
| R | The support reaction force vector. |
| Sxy, Sxz, Syz, Syz, Syz, Syz, Syz | The squareness error components between the axes denoted in the corresponding subscript. |
| Te | The transformation matrix of the element from the local coordinate system to the global coordinate system. |
| Tij | The ideal HTMs of position and orientation of Bj with respect to Bi. |
| Tijs | The ideal HTMs of position and orientation that come from static state. |
| Tijp | The ideal HTMs of position and orientation that come from motion state. |
| T′ij | The actual HTMs of position and orientation of Bj with respect to Bi under error conditions. |
| ΔTij | The HTMs with parameters of static error components. |
| U | The nodal displacement vector of the entire structure. |
| vfi | The optimized volume fraction of the ith element. |
| xi (i = 1, 2, …, 37) | The design variables in the precision design. |
| xiF | The part of the structural gravity deformation error in the static error design variable xi. |
| xiG | The geometric error caused by the manufacturing process in the static error design variable xi. |
| xsi | The normalized relative value of the design variable xi. |
| δx(x), δy(x), δz(x) | The linear error components of the X-axis along the X-, Y- and Z-directions. |
| δx(y), δy(y), δz(y) | The linear error components of the Y-axis along the X-, Y- and Z-directions. |
| δx(z), δy(z), δz(z) | The linear error components of the Z-axis along the X-, Y- and Z-directions. |
| δx(w), δy(w), δz(w) | The linear error components of the W-axis along the X-, Y- and Z-directions. |
| δx(γ), δy(γ), δz(γ) | The linear error components of the C-axis along the X-, Y- and Z-directions. |
| δz(x)M | The geometric error caused by manufacturing. |
| δz(x)F | The structural gravity deformation error. |
| εx(x), εy(x), εz(x) | The angular error components of the X-axis around the X-, Y- and Z-directions. |
| εx(y), εy(y), εz(y) | The angular error components of the Y-axis around the X-, Y- and Z-directions. |
| εx(z), εy(z), εz(z) | The angular error components of the Z-axis around the X-, Y- and Z-directions. |
| εx(w), εy(w), εz(w) | The angular error components of the W-axis around the X-, Y- and Z-z directions. |
| εx(γ), εy(γ), εz(γ) | The angular error components of the C-axis around the X-, Y- and Z-directions. |
| ω1, ω2 and ω3 | The weights of the objective functions. |
References
- Shen, H.; Fu, J.; He, Y.; Yao, X. On-line Asynchronous Compensation Methods for Static/Quasi-Static Error Implemented on CNC Machine Tools. Int. J. Mach. Tools Manuf. 2012, 60, 14–26. [Google Scholar] [CrossRef]
- Slocum, H. Precision Machine Design; Society of Manufacturing Engineers: Southfield, MI, USA, 1992. [Google Scholar]
- Kiridena, V.S.B.; Ferreira, P.M. Kinematic Modeling of Quasistatic Errors of Three-axis Machining Centers. Int. J. Mach. Tools Manuf. 1994, 34, 85–100. [Google Scholar] [CrossRef]
- Rahman, M.; Heikkala, J.; Lappalainen, K. Modeling, Measurement and Error Compensation of Multi-axis Machine Tools. Part I: Theory. Int. J. Mach. Tools Manuf. 2000, 40, 1535–1546. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, J.; Zhang, Y.; Shen, J.; Wang, C. Measurement and Compensation for Volumetric Positioning Errors of CNC Machine Tools Considering Thermal Effect. Int. J. Adv. Manuf. Technol. 2011, 55, 275–283. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Ji, S.J.; Wang, X. A New Error Compensation Method for a Four-Axis Horizontal Machine Tool. Key Eng. Mater. 2016, 679, 1–5. [Google Scholar] [CrossRef]
- Fu, G.; Fu, J.; Shen, H.; Yao, X.; Chen, Z. NC Codes Optimization for Geometric Error Compensation of Five-axis Machine Tools with One Novel Mathematical Model. Int. J. Adv. Manuf. Technol. 2015, 80, 1879–1894. [Google Scholar] [CrossRef]
- Fu, G.; Gong, H.; Fu, J.; Gao, H.; Deng, X. Geometric Error Contribution Modeling and Sensitivity Evaluating for Each Axis of Five-axis Machine Tools Based on POE Theory and Transforming Differential Changes Between Coordinate Frames. Int. J. Mach. Tools Manuf. 2019, 147, 103455. [Google Scholar] [CrossRef]
- Wu, C.; Fan, J.; Wang, Q.; Chen, D. Machining Accuracy Improvement of Non-orthogonal Five-axis Machine Tools by A New Iterative Compensation Methodology Based on the Relative Motion. Int. J. Mach. Tools Manuf. 2018, 124, 80–98. [Google Scholar] [CrossRef]
- Breitzke, A.; Wolfgang, H. Workshop-Suited Geometric Errors Identification of Three-Axis Machine Tools Using On-Machine Measurement for Long Term Precision Assurance. Precis. Eng. 2022, 75, 235–247. [Google Scholar] [CrossRef]
- Gu, J.; Agapiou, J. Assessment and Implementation of Global Offset Compensation Method. J. Manuf. Syst. 2018, 48, 38–44. [Google Scholar]
- Inigo, B.; Colinas-Armijo, N.; de Lacalle, L.N.L.; Aguirre, G. Digital Twin-Based Analysis of Volumetric Error Mapping Procedures. Precis. Eng. 2021, 72, 823–836. [Google Scholar] [CrossRef]
- Chen, G.; Sun, Y.; Lu, L.; Chen, W. A New Static Accuracy Design Method for Ultra-Precision Machine Tool Based on Global Optimisation and Error Sensitivity Analysis. Int. J. Nanomanufacturing 2016, 12, 167–180. [Google Scholar] [CrossRef]
- Chen, G.D.; Sun, Y.Z.; Zhang, F.H.; Lu, L.H.; Chen, W.Q.; Yu, N. Dynamic Accuracy Design Method of Ultra-precision Machine Tool. Chin. J. Mech. Eng. 2018, 31, 8. [Google Scholar] [CrossRef]
- Fan, J.; Tao, H.; Wu, C.; Pan, R.; Tang, Y.; Li, Z. Kinematic Errors Prediction for Multi-axis Machine Tools’ Guideways Based on Tolerance. Int. J. Adv. Manuf. Technol. 2018, 98, 1131–1144. [Google Scholar] [CrossRef]
- Wu, C.; Wang, Q.; Fan, J.; Pan, R. A Novel Prediction Method of Machining Accuracy for Machine Tools Based on Tolerance. Int. J. Adv. Manuf. Technol. 2020, 110, 629–653. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Wang, S.; Du, H.; Chai, B.; Hu, S.J. Active Precision Design for Complex Machine Tools: Methodology and Case Study. Int. J. Adv. Manuf. Technol. 2015, 80, 581–590. [Google Scholar] [CrossRef]
- Li, J.; Xie, F.; Liu, X.J. Geometric Error Modeling and Sensitivity Analysis of a Five-axis Machine Tool. Int. J. Adv. Manuf. Technol. 2016, 82, 2037–2051. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Mou, W.; Hao, X.; Li, Z.; Jin, Y. Sculptured Surface-oriented Machining Error Synthesis Modeling for Five-axis Machine Tool Accuracy Design Optimization. Int. J. Adv. Manuf. Technol. 2016, 89, 3285–3298. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Z.; Cheng, Q.; Qi, Y.; Cai, L. An Approach of Comprehensive Error Modeling and Accuracy Allocation for the Improvement of Reliability and Optimization of Cost of a Multi-axis NC Machine Tool. Int. J. Adv. Manuf. Technol. 2017, 89, 561–579. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Rout, A.K.; Das, D.K. Response Surface and Artificial Neural Network Prediction Model and Optimization for Surface Roughness in Machining. Int. J. Ind. Eng. Comput. 2015, 6, 229–240. [Google Scholar] [CrossRef]
- Peng, F.; Yan, R.; Chen, W.; Yang, J.; Li, B. Anisotropic Force Ellipsoid Based Multi-axis Motion Optimization of Machine Tools. Chin. J. Mech. Eng. 2012, 25, 960–967. [Google Scholar] [CrossRef]
- Portman, V.T.; Shneor, Y.; Chapsky, V.S.; Shapiro, A. Form-shaping function theory expansion: Stiffness model of multi-axis machines. Int. J. Adv. Manuf. Technol. 2014, 76, 1063–1078. [Google Scholar] [CrossRef]
- Ma, J.; Lu, D.; Zhao, W. Assembly Errors Analysis of Linear Axis of CNC Machine Tool Considering Component Deformation. Int. J. Adv. Manuf. Technol. 2015, 86, 281–289. [Google Scholar] [CrossRef]
- Shi, X.; Liu, H.; Li, H.; Liu, C.; Tan, G. Comprehensive Error Measurement and Compensation Method for Equivalent Cutting Forces. Int. J. Adv. Manuf. Technol. 2016, 85, 149–156. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, X.; Zhang, H.; Nie, Y.; Zhang, D. A New Top-Down Design Method for The Stiffness of Precision Machine Tools. Int. J. Adv. Manuf. Technol. 2016, 83, 1887–1904. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Sun, Y.; Chen, W.; Wang, B. Volumetric Error Modeling and Sensitivity Analysis for Designing a Five-Axis Ultra-Precision Machine Tool. Int. J. Adv. Manuf. Technol. 2013, 68, 2525–2534. [Google Scholar] [CrossRef]




| Axis | Errors |
|---|---|
| X | δx(x), δy(x), δz(x), εx(x), εy(x), εz(x) |
| Y | δx(y), δy(y), δz(y), εx(y), εy(y), εz(y) |
| Z | δx(z), δy(z), δz(z), εx(z), εy(z), εz(z) |
| W | δx(w), δy(w), δz(w), εx(w), εy(w), εz(w) |
| C | δx(γ), δy(γ), δz(γ), εx(γ), εy(γ), εz(γ) |
| Design Variable | Value Range | Design Variable | Value Range | Design Variable | Value Range |
|---|---|---|---|---|---|
| δx(x), (x1) | [0.006, 0.025] mm | δy(x), (x2) | [0.006, 0.03] mm | δz(x), (x3) | [0.006, 0.03] mm |
| εx(x), (x4) | [0.01, 0.04] mrad | εy(x), (x5) | [0.01, 0.04] mrad | εz(x), (x6) | [0.01, 0.04] mrad |
| δx(y), (x7) | [0.006, 0.03] mm | δy(y), (x8) | [0.006, 0.025] mm | δz(y), (x9) | [0.006, 0.03] mm |
| εx(y), (x10) | [0.01, 0.04] mrad | εy(y), (x11) | [0.01, 0.04] mrad | εz(y), (x12) | [0.01, 0.04] mrad |
| δx(z), (x13) | [0.006, 0.03] mm | δy(z), (x14) | [0.006, 0.03] mm | δz(z), (x15) | [0.006, 0.025] mm |
| εx(z), (x16) | [0.01, 0.04] mrad | εy(z), (x17) | [0.01, 0.04] mrad | εz(z), (x18) | [0.01, 0.04] mrad |
| δx(w), (x19) | [0.01, 0.03] mm | δy(w), (x20) | [0.01, 0.03] mm | δz(w), (x21) | [0.01, 0.025] mm |
| εx(w), (x22) | [0.01, 0.04] mrad | εy(w), (x23) | [0.01, 0.04] mrad | εz(w), (x24) | [0.01, 0.04] mrad |
| δx(γ), (x25) | [0.003, 0.01] mm | δy(γ), (x26) | [0.003, 0.01] mm | δz(γ), (x27) | [0.003, 0.01] mm |
| εx(γ), (x28) | [0.01, 0.04] mrad | εy(γ), (x29) | [0.01, 0.04] mrad | εz(γ), (x30) | [0.01, 0.04] mrad |
| Sxw, (x31) | [0.01, 0.04] mrad | Syw, (x32) | [0.01, 0.04] mrad | Sxy, (x33) | [0.01, 0.03] mrad |
| Sxz, (x34) | [0.01, 0.06] mrad | Syz, (x35) | [0.01, 0.06] mrad | Sxc, (x36) | [0.01, 0.02] mrad |
| Syc, (x37) | [0.01, 0.02] mrad |
| Design Variable | Variable Meaning | Value Range | Design Variable | Variable Meaning | Value Range |
|---|---|---|---|---|---|
| x38 | Section width of connecting beam | [0.7, 1] m | x47 | X-directional stiffness coefficient of column | [0.2, 1] |
| x39 | Section height of connecting beam | [0.9, 1.2] m | x48 | Y-directional stiffness coefficient of column | [0.2, 1] |
| x40 | Volume factor of connecting beam | [0.25, 1] | x49 | Z-directional stiffness coefficient of column | [0.2, 1] |
| x41 | Z-directional stiffness coefficient of connecting beam | [0.2, 1] | x50 | Section width of crossbeam | [0.67, 0.8] m |
| x42 | Y-directional stiffness coefficient of connecting beam | [0.2, 1] | x51 | Section height of crossbeam | [1, 1.2] m |
| x43 | X-directional stiffness coefficient of connecting beam | [0.2, 1] | x52 | Volume factor of crossbeam | [0.45, 1] |
| x44 | Section width of column | [0.6, 0.8] m | x53 | X-directional stiffness coefficient of crossbeam | [0.2, 1] |
| x45 | Section height of column | [1, 1.25] m | x54 | Y-directional stiffness coefficient of crossbeam | [0.2, 1] |
| x46 | Volume factor of column | [0.25, 1] | x55 | Z-directional stiffness coefficient of crossbeam | [0.2, 1] |
| Design Variable | Optimized Value | Design Variable | Optimized Value | Design Variable | Optimized Value |
|---|---|---|---|---|---|
| δx(x), (x1) | 0.017 mm | δy(x), (x2) | 0.009 mm | δz(x), (x3) | 0.011 mm |
| εx(x), (x4) | 0.028 mrad | εy(x), (x5) | 0.022 mrad | εz(x), (x6) | 0.016 mrad |
| δx(y), (x7) | 0.013 mm | δy(y), (x8) | 0.018 mm | δz(y), (x9) | 0.027 mm |
| εx(y), (x10) | 0.022 mrad | εy(y), (x11) | 0.012 mrad | εz(y), (x12) | 0.04 mrad |
| δx(z), (x13) | 0.014 mm | δy(z), (x14) | 0.027 mm | δz(z), (x15) | 0.009 mm |
| εx(z), (x16) | 0.038 mrad | εy(z), (x17) | 0.011 mrad | εz(z), (x18) | 0.04 mrad |
| δx(w), (x19) | 0.029 mm | δy(w), (x20) | 0.03 mm | δz(w), (x21) | 0.014 mm |
| εx(w), (x22) | 0.04 mrad | εy(w), (x23) | 0.027 mrad | εz(w), (x24) | 0.035 mrad |
| δx(γ), (x25) | 0.013 mm | δy(γ), (x26) | 0.008 mm | δz(γ), (x27) | 0.017 mm |
| εx(γ), (x28) | 0.017 mrad | εy(γ), (x29) | 0.017 mrad | εz(γ), (x30) | 0.024 mrad |
| Sxw, (x31) | 0.026 mrad | Syw, (x32) | 0.039 mrad | Sxy, (x33) | 0.021 mrad |
| Sxz, (x34) | 0.017 mrad | Syz, (x35) | 0.054 mrad | Sxc, (x36) | 0.012 mrad |
| Syc, (x37) | 0.02 mrad |
| Design Variable | Optimized Value | Design Variable | Optimized Value |
|---|---|---|---|
| x38 | 0.75 m | x47 | 0.32 |
| x39 | 0.91 m | x48 | 0.62 |
| x40 | 0.26 | x49 | 0.2 |
| x41 | 0.2 | x50 | 0.7 m |
| x42 | 0.2 | x51 | 1.2 m |
| x43 | 0.21 | x52 | 0.46 |
| x44 | 0.78 m | x53 | 0.57 |
| x45 | 1.24 m | x54 | 0.21 |
| x46 | 0.27 | x55 | 0.37 |
| Item | GEM-PDM | PDM |
|---|---|---|
| Evx (mm) | −0.0054 | −0.0337 |
| Evx (mm) | −0.0020 | −0.0157 |
| Evx (mm) | 0.0396 | 0.040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, T.; Sun, X.; Mynors, D.; Wu, T. Optimal Design Method for Static Precision of Heavy-Duty Vertical Machining Center Based on Gravity Deformation Error Modelling. Processes 2022, 10, 1930. https://doi.org/10.3390/pr10101930
Wang H, Li T, Sun X, Mynors D, Wu T. Optimal Design Method for Static Precision of Heavy-Duty Vertical Machining Center Based on Gravity Deformation Error Modelling. Processes. 2022; 10(10):1930. https://doi.org/10.3390/pr10101930
Chicago/Turabian StyleWang, Han, Tianjian Li, Xizhi Sun, Diane Mynors, and Tao Wu. 2022. "Optimal Design Method for Static Precision of Heavy-Duty Vertical Machining Center Based on Gravity Deformation Error Modelling" Processes 10, no. 10: 1930. https://doi.org/10.3390/pr10101930





