WSN-Based SHM Optimisation Algorithm for Civil Engineering Structures
Abstract
:1. Introduction
2. Related Work
3. Methodology
3.1. VMD-GRU Optimisation Algorithm
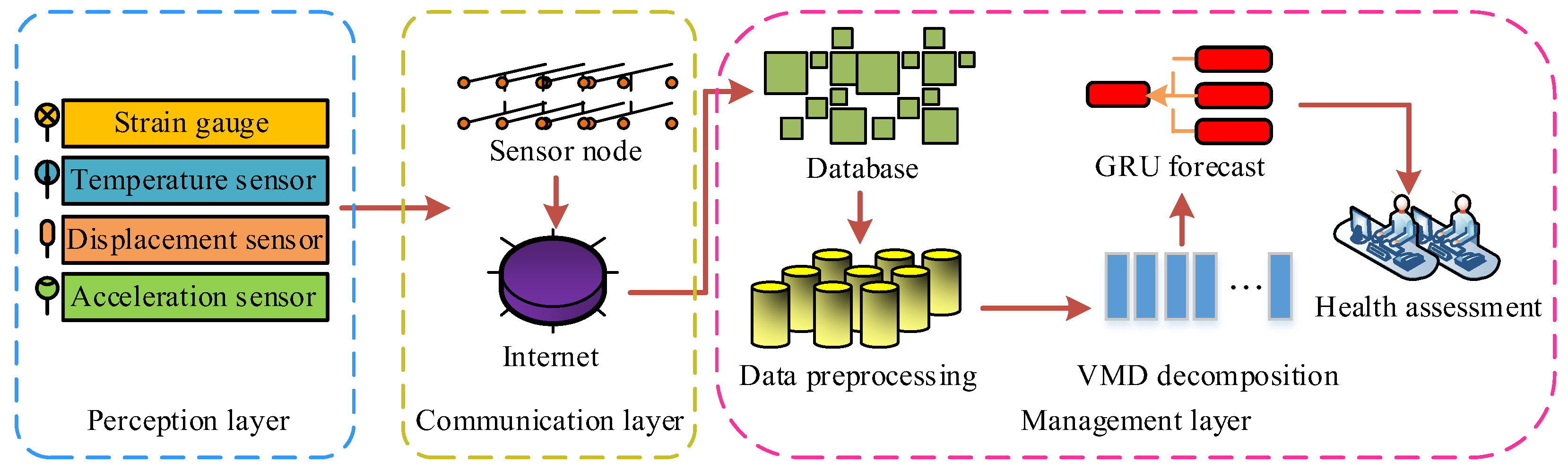
3.2. WSN Civil Structural SHM Model Incorporating VMD-GRU
4. Application of WSN Civil and SHM Models Incorporating VMD-GRU
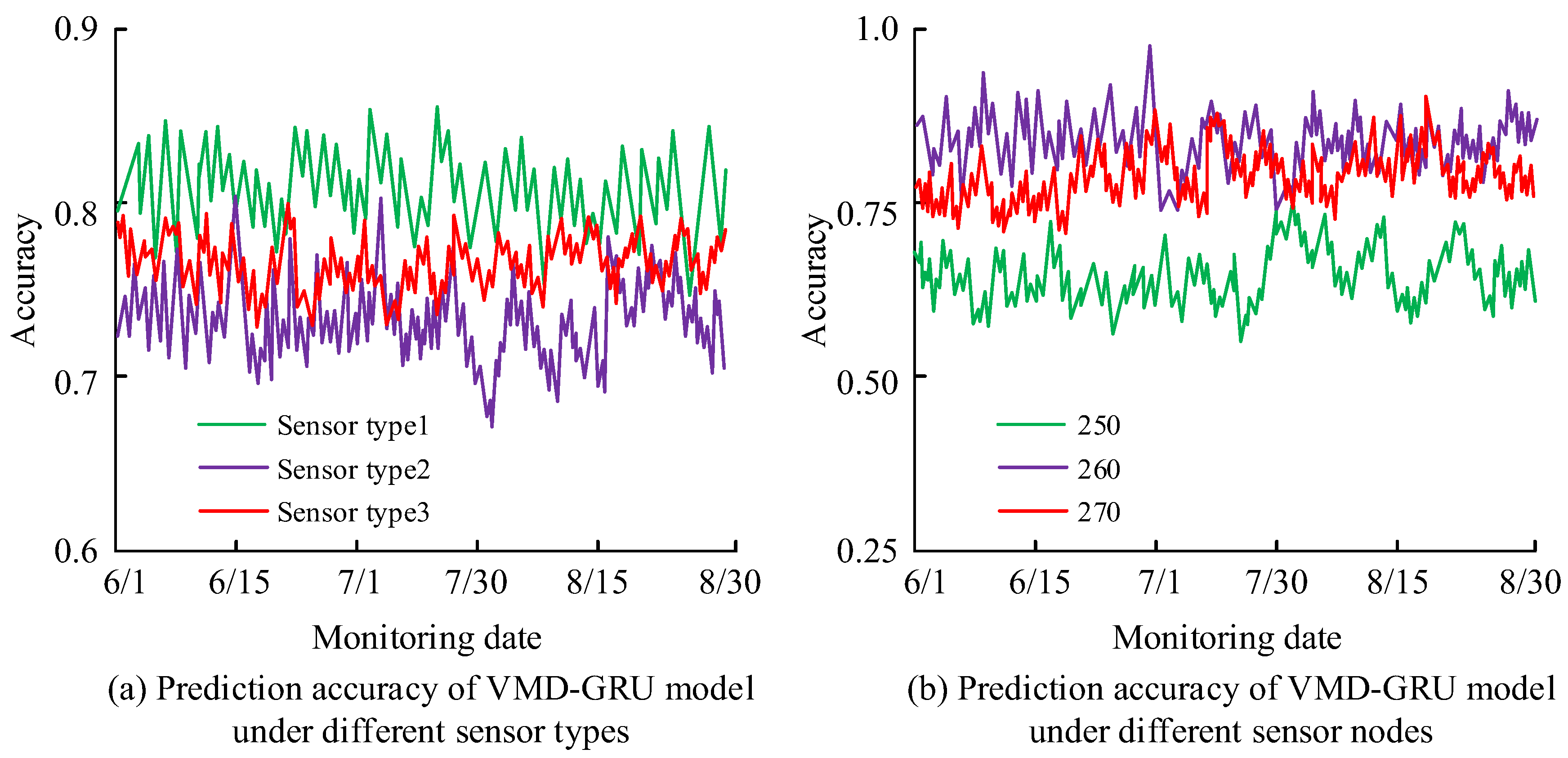
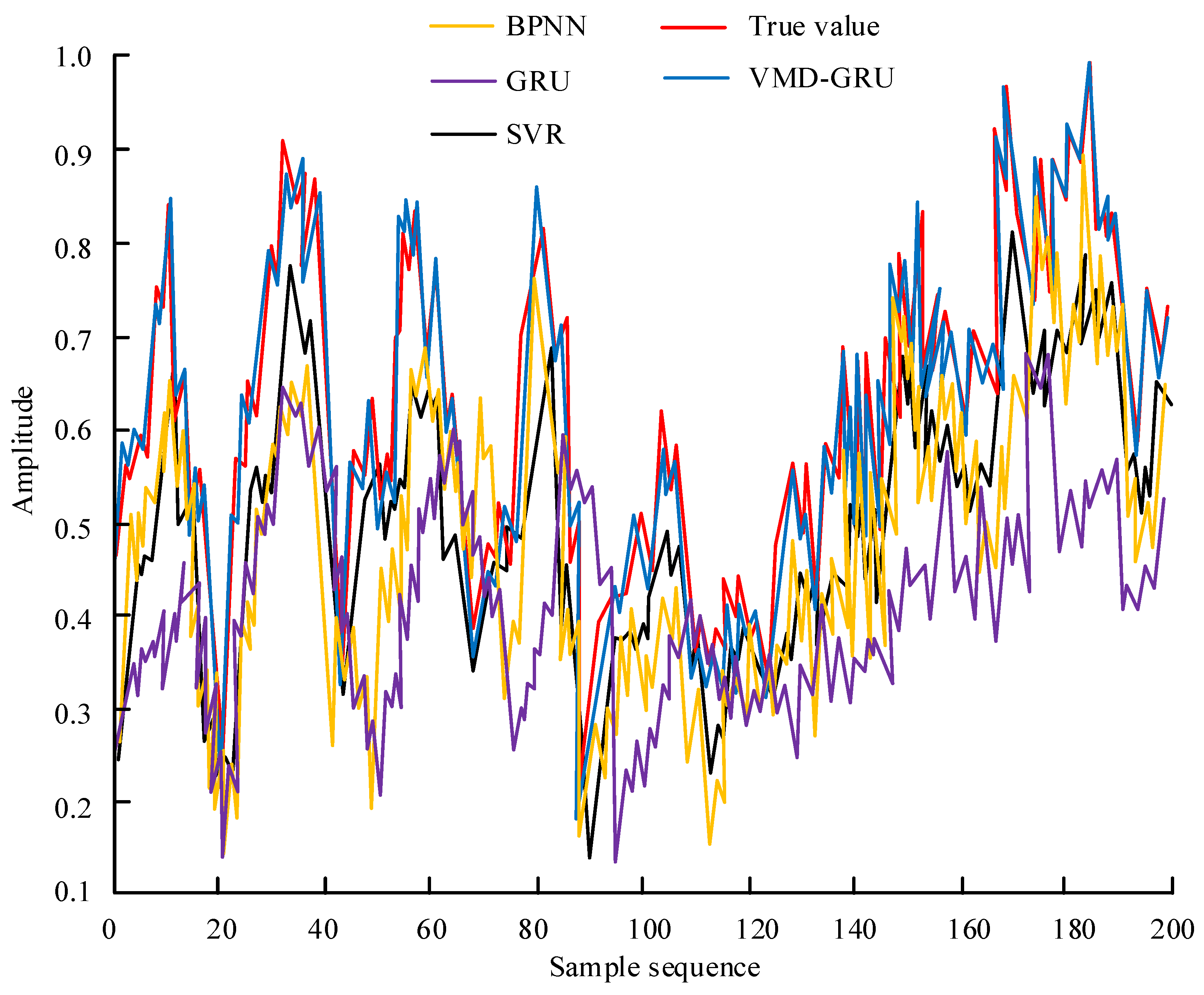
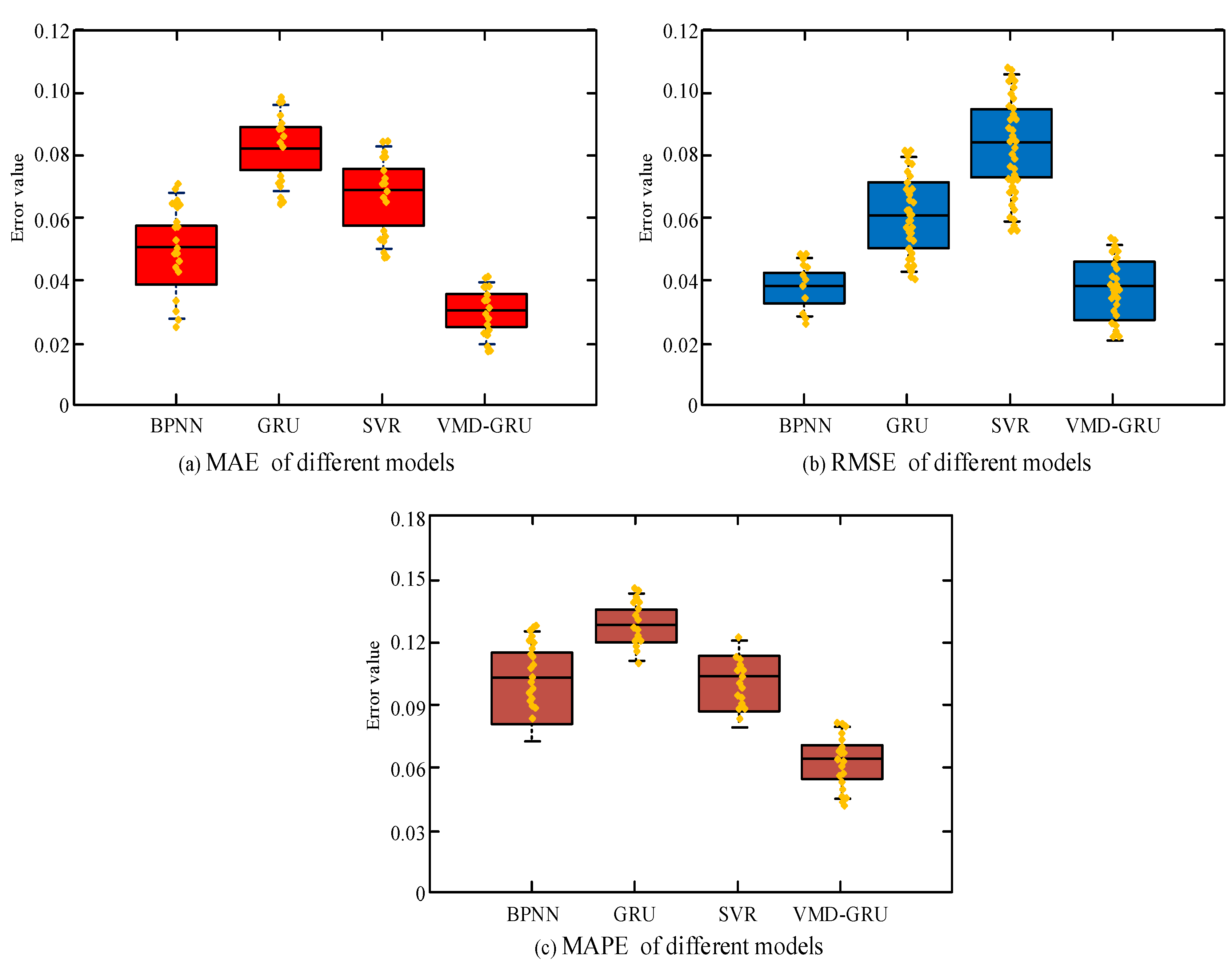
4.1. Performance Analysis of the VMD-GRU Algorithm
4.2. Analysis of SHM Results for Civil Structures
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nichols, J.M.; Tomor, A.K.; Benedetti, A. Development of a time-dependent structural reliability model for civil engineering structures. Mason. Int. 2019, 32, 72–79. [Google Scholar]
- Xiao, X.; Mu, B.; Cao, G.; Yang, Y.; Wang, M. Flexible battery-free wireless electronic system for food monitoring. J. Sci. Adv. Mater. Devices 2022, 7, 100430. [Google Scholar] [CrossRef]
- Wu, H.; Jin, S.; Yue, W. Pricing policy for a dynamic spectrum allocation scheme with batch requests and impatient packets in cognitive radio networks. J. Syst. Sci. Syst. Eng. 2022, 31, 133–149. [Google Scholar] [CrossRef]
- Zheng, H.; Jin, S. A multi–source fluid queue based stochastic model of the probabilistic offloading strategy in a MEC system with multiple mobile devices and a single MEC server. Int. J. Appl. Math. Comput. Sci. 2022, 32, 125–138. [Google Scholar]
- Zonzini, F.; Aguzzi, C.; Gigli, L.; Sciullo, L.; Testoni, N.; De Marchi, L.; Di Felice, M.; Cinotti, T.S.; Mennuti, C.; Marzani, A. Structural health monitoring and prognostic of industrial plants and civil structures: A sensor to cloud architecture. IEEE Instrum. Meas. Mag. 2020, 23, 21–27. [Google Scholar] [CrossRef]
- Sui, T.; Marelli, D.; Sun, X.; Fu, M. Multi-sensor state estimation over Lossy channels using coded measurements. Automatica 2020, 111, 108561. [Google Scholar] [CrossRef]
- Wang, Y.; Han, X.; Jin, S. MAP based modeling method and performance study of a task offloading scheme with time-correlated traffic and VM repair in MEC systems. Wirel. Netw. 2022. [Google Scholar] [CrossRef]
- Sun, W.; Lv, X.; Qiu, M. Distributed estimation for stochastic Hamiltonian systems with fading wireless channels. IEEE Trans. Cybern. 2022, 52, 4897–4906. [Google Scholar] [CrossRef]
- Pal, P.; Sharma, R.P.; Tripathi, S.; Kumar, C.; Ramesh, D. 2.4 GHz RF received signal strength based node separation in WSN monitoring infrastructure for millet and rice vegetation. IEEE Sens. J. 2021, 21, 18298–18306. [Google Scholar] [CrossRef]
- Liu, Z.; He, Q.; Li, Z.; Peng, Z.; Zhang, W. Vision-based moving mass detection by time-varying structure vibration monitoring. IEEE Sens. J. 2020, 20, 11566–11577. [Google Scholar] [CrossRef]
- Zhou, X.; Bai, Y.; Nardi, D.C.; Wang, Y.; Wang, Y.; Liu, Z.; Picón, R.A.; Flórez-López, J. Damage evolution modeling for steel structures subjected to combined high cycle fatigue and high-intensity dynamic loadings. Int. J. Struct. Stab. Dyn. 2022, 22, 2240012. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Processing 2022, 177, 109175. [Google Scholar] [CrossRef]
- Xi, Y.; Jiang, W.; Wei, K.; Hong, T.; Cheng, T.; Gong, S. Wideband RCS reduction of Microstrip antenna array using coding Metasurface with low Q resonators and fast optimization method. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 656–660. [Google Scholar] [CrossRef]
- Wang, Z.; Cha, Y.J. Unsupervised deep learning approach using a deep auto-encoder with an one-class support vector machine to detect structural damage. Struct. Health Monit. 2020, 20, 406–425. [Google Scholar] [CrossRef]
- Guo, L.; Li, R.; Jiang, B. A cascade broad neural network for concrete structural crack damage automated classification. IEEE Trans. Ind. Inform. 2020, 17, 2737–2742. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Zhang, C.; Xiao, X. Structural health monitoring and performance analysis of a 12-story recycled aggregate concrete structure. Eng. Struct. 2020, 205, 110102. [Google Scholar] [CrossRef]
- Carratu, M.; Espirito-Santo, A.; Monte, G.; Paciello, V. Earthquake early detection as an IEEE1451 transducer network trigger for urban infrastructure monitoring and protection. IEEE Instrum. Meas. Mag. 2020, 23, 43–49. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, L.; Ma, S.; Cao, S.; Xia, Q.; Liu, Y.; Zhang, H. Adaptive sparse reconstruction of damage localization via Lamb waves for structure health monitoring. Computing 2019, 101, 679–692. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, X.; Chen, B.; Li, Q.; Luo, P.; Pronk, A. Design, construction and monitoring of an ice composite shell structure. Autom. Constr. 2019, 106, 102862. [Google Scholar] [CrossRef]
- Peckens, C.; Cook, I.; Fogg, C. Bio-inspired sensing and actuating architectures for feedback control of civil structures. Bioinspiration Biomim. 2019, 14, 1748–3190. [Google Scholar] [CrossRef]
- Shen, W.; Niyitangamahoro, A.; Feng, Z.; Zhu, H. Tuned inerter dampers for civil structures subjected to earthquake ground motions: Optimum design and seismic performance. Eng. Struct. 2019, 198, 109470. [Google Scholar] [CrossRef]
- Li, Z.; Fu, J.; Liang, Q.; Mao, H.; He, Y. Modal identification of civil structures via covariance-driven stochastic subspace method. Math. Biosci. Eng. 2019, 16, 5709–5728. [Google Scholar] [CrossRef] [PubMed]
- Raffaele, L.; Bruno, L. Windblown sand action on civil structures: Definition and probabilistic modelling. Eng. Struct. 2019, 178, 88–101. [Google Scholar] [CrossRef]
- De-La-Colina, J.; Arias-Lara, D.; Valdés-González, J. Effect of noise on the assessment of displacements computed from accelerations recorded at linear and nonlinear civil engineering structures. Measurement 2019, 136, 724–734. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gao, Z.; Shu, X.; Zhang, K.; Xie, L.; Zhang, Z. A new dam structural response estimation paradigm powered by deep learning and transfer learning techniques. Struct. Health Monit. 2021, 21, 770–787. [Google Scholar] [CrossRef]
- Tibaduiza, D. Temperature prediction using multivariate time series deep learning in the lining of an electric arc furnace for ferronickel production. Sensors 2021, 21, 6894. [Google Scholar]
- Zhang, P.; Cui, Z.; Wang, Y.; Ding, S. Application of BPNN optimized by chaotic adaptive gravity search and particle swarm optimization algorithms for fault diagnosis of electrical machine drive system. Electr. Eng. 2021, 104, 819–831. [Google Scholar] [CrossRef]
- Shu, W.; Cai, K.; Xiong, N.N. A short-term traffic flow prediction model based on an improved gate recurrent unit neural network. IEEE Trans. Intell. Transp. Syst. 2021, 23, 16654–16665. [Google Scholar] [CrossRef]
- Leibold, C. Neural kernels for recursive support vector regression as a model for episodic memory. Biol. Cybern. 2022, 116, 377–386. [Google Scholar] [CrossRef]
- Gao, D.; Hu, B.; Qin, F.; Chang, L.; Lyu, X. A real time gravity compensation method for INS based on BPNN. IEEE Sens. J. 2021, 21, 13584–13593. [Google Scholar] [CrossRef]
- Fu, B.; Yuan, W.; Cui, X.; Yu, T.; Zhao, X.; Li, C. Correlation analysis and augmentation of samples for a bidirectional gate recurrent unit network for the remaining useful life prediction of bearings. IEEE Sens. J. 2021, 21, 7989–8001. [Google Scholar] [CrossRef]
- Jassim, M.S.; Coskuner, G.; Zontul, M. Comparative performance analysis of support vector regression and artificial neural network for prediction of municipal solid waste generation. Waste Manag. Res. 2022, 40, 195–204. [Google Scholar] [CrossRef] [PubMed]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y. WSN-Based SHM Optimisation Algorithm for Civil Engineering Structures. Processes 2022, 10, 2113. https://doi.org/10.3390/pr10102113
Liu Y. WSN-Based SHM Optimisation Algorithm for Civil Engineering Structures. Processes. 2022; 10(10):2113. https://doi.org/10.3390/pr10102113
Chicago/Turabian StyleLiu, Ying. 2022. "WSN-Based SHM Optimisation Algorithm for Civil Engineering Structures" Processes 10, no. 10: 2113. https://doi.org/10.3390/pr10102113
APA StyleLiu, Y. (2022). WSN-Based SHM Optimisation Algorithm for Civil Engineering Structures. Processes, 10(10), 2113. https://doi.org/10.3390/pr10102113





