An Analysis of Energy and Internal Flow Characteristics of Open Inlet Channel Axial Flow Pumping Devices
Abstract
:1. Introduction
2. Numerical Computing Module, Meshing, and Calculation Approach
2.1. Numerical Computational Modules
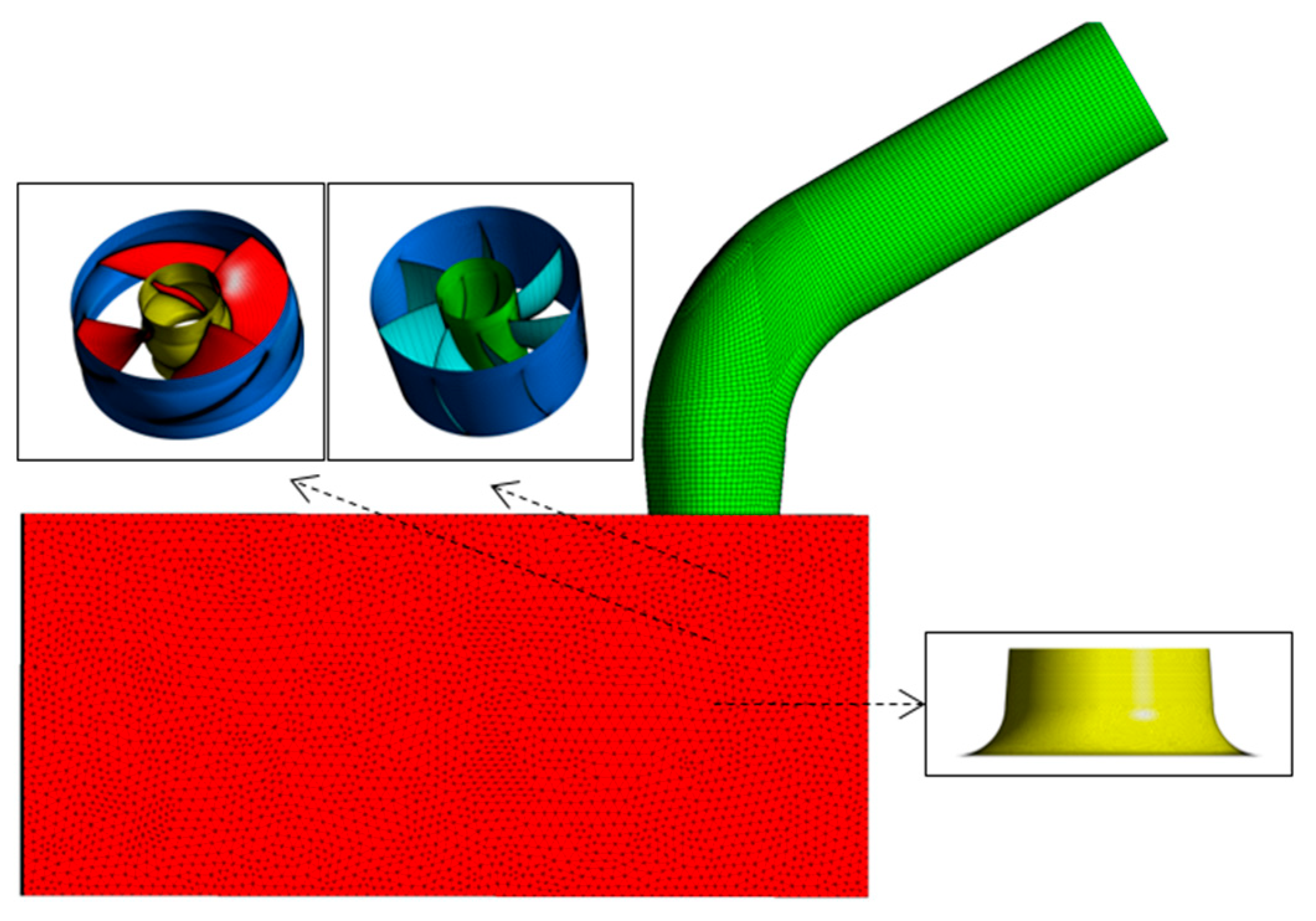
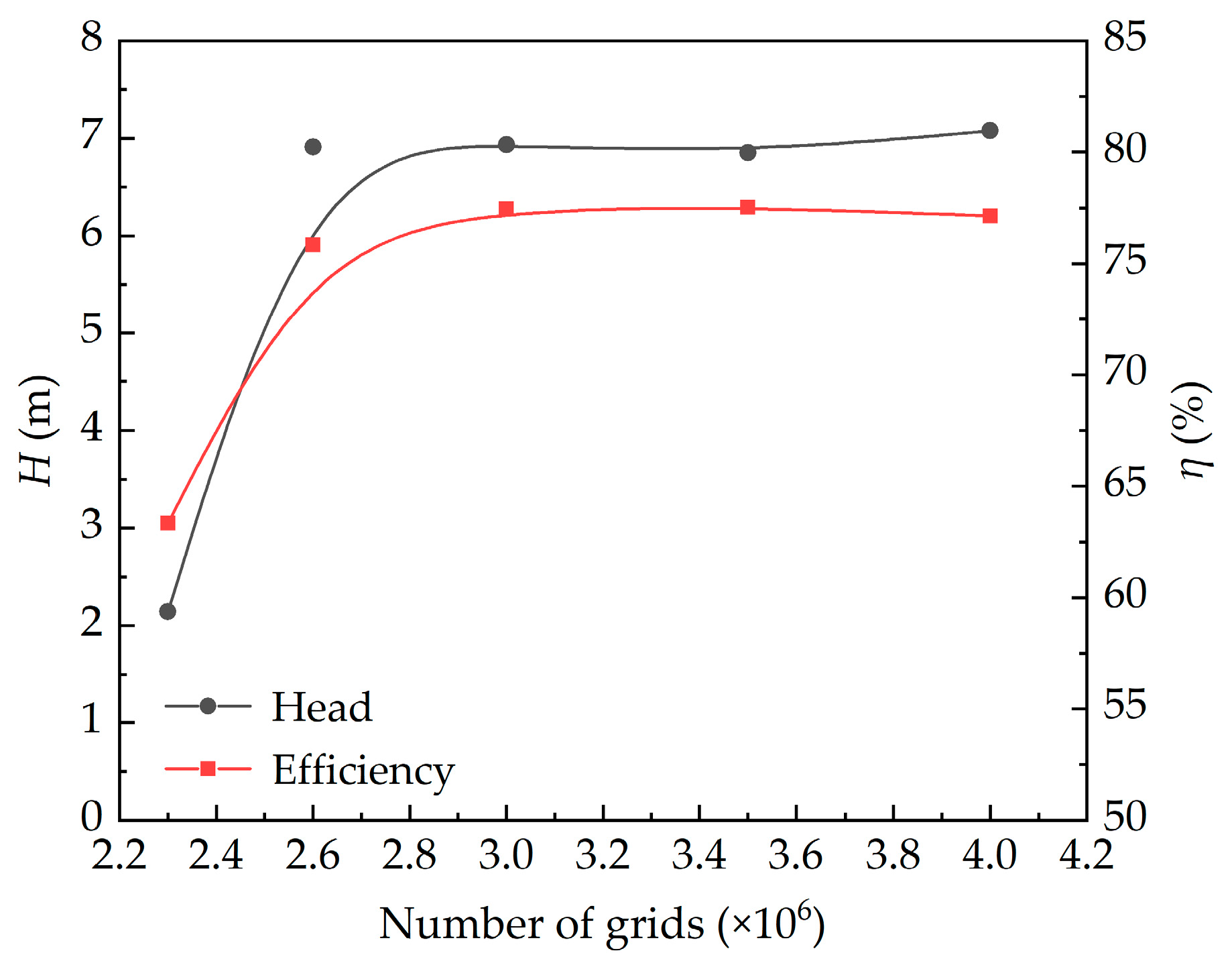
2.2. Mesh Division
2.3. Control Equations and Boundary Conditions
2.4. Calculation Method
3. Test Rig and Test Approach
3.1. Test Rig
3.2. Experimental Test Approach
4. Pump Unit Energy and Internal Flow Characteristic Analysis
4.1. Pump Unit Energy Characteristic Analysis
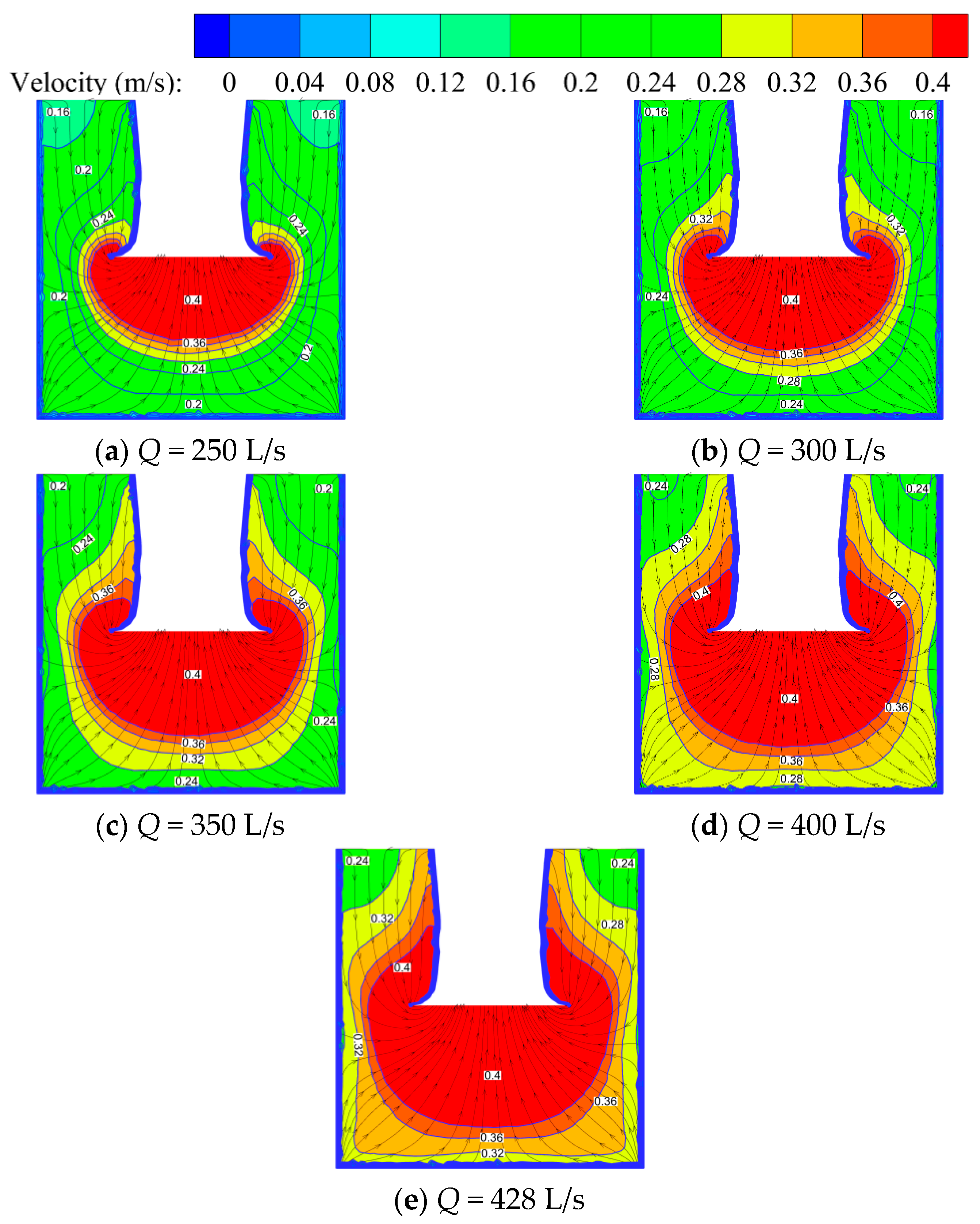
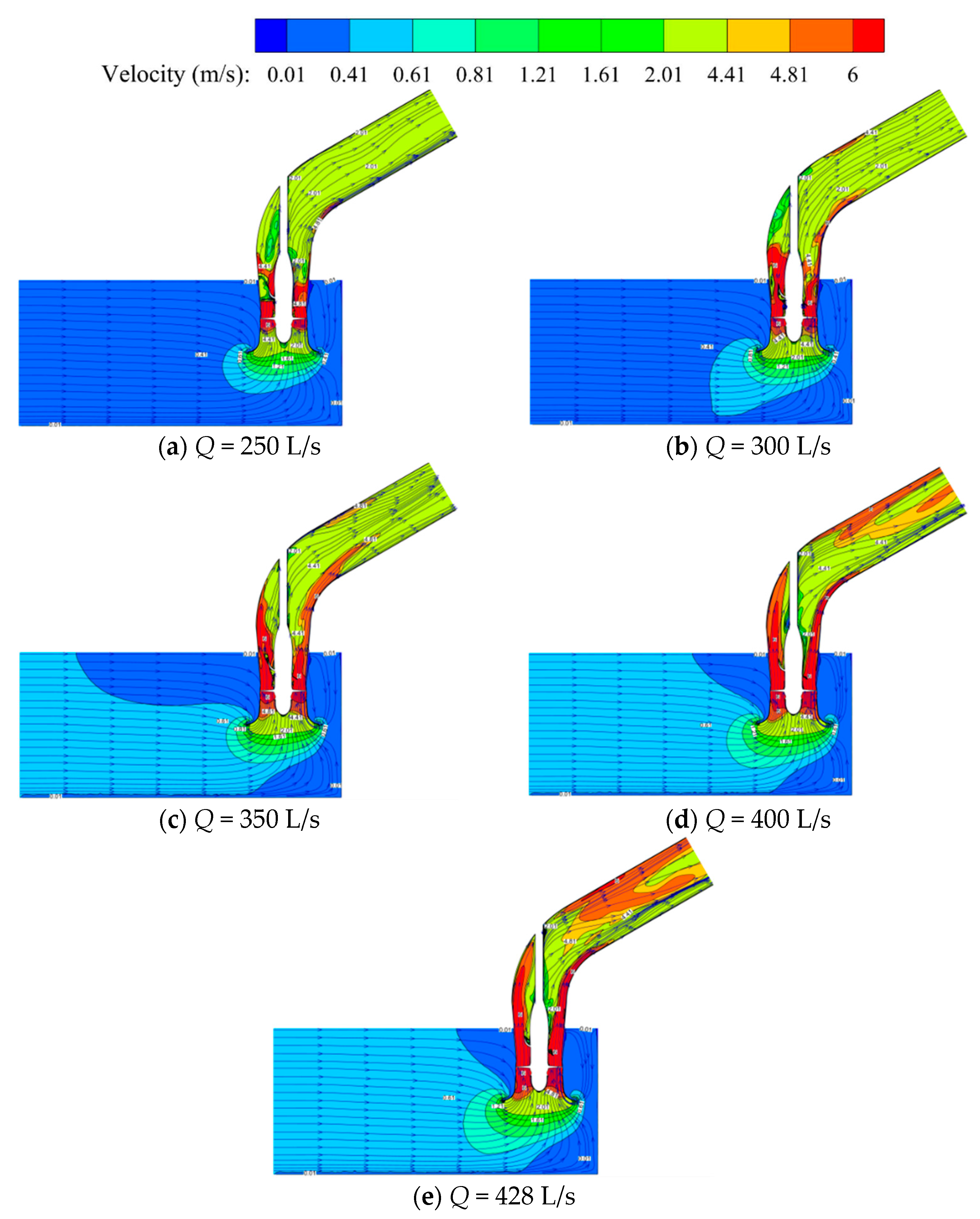
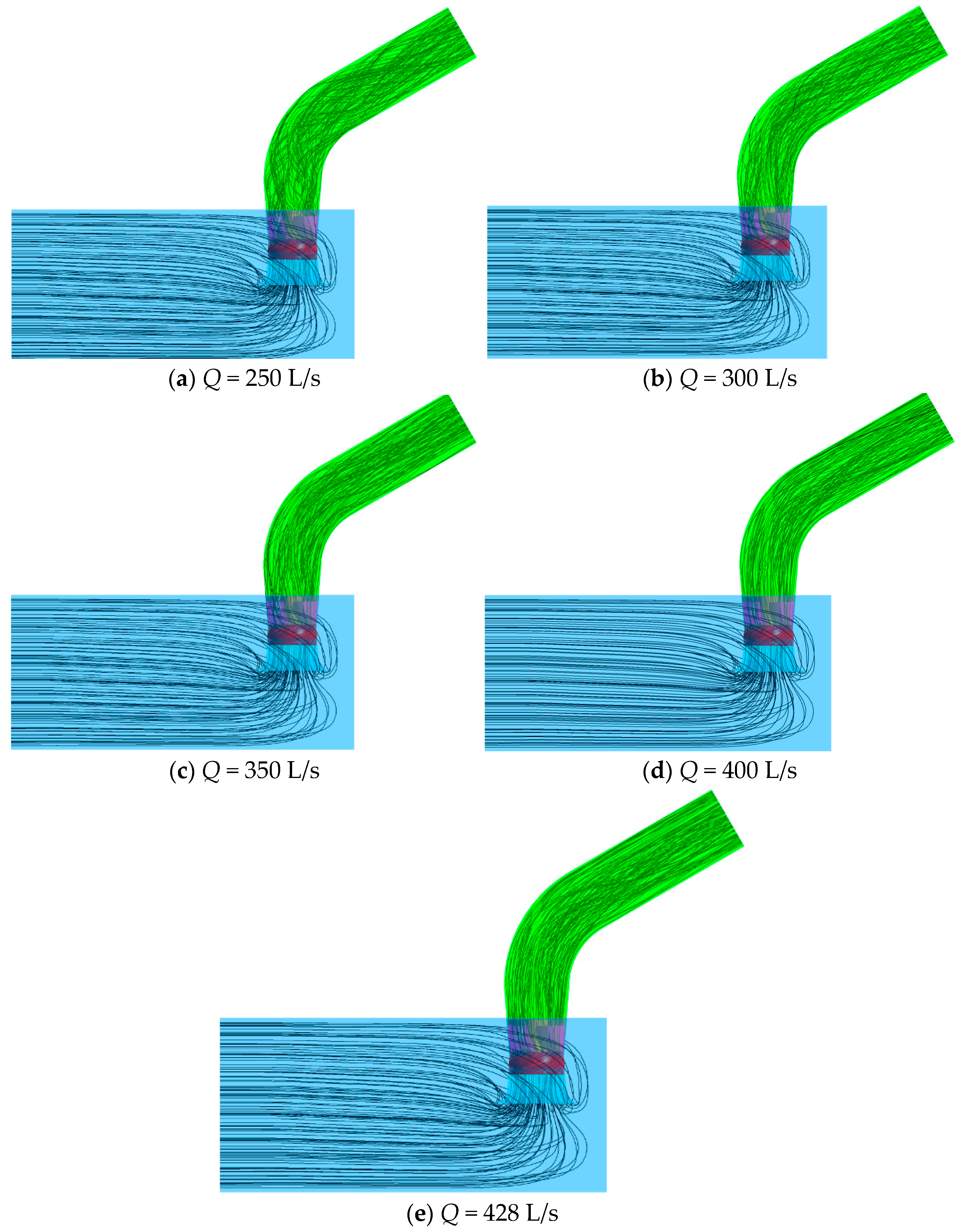
4.2. Analysis of the Internal Flow Characteristics of the Pump Unit
5. Conclusions
- (1)
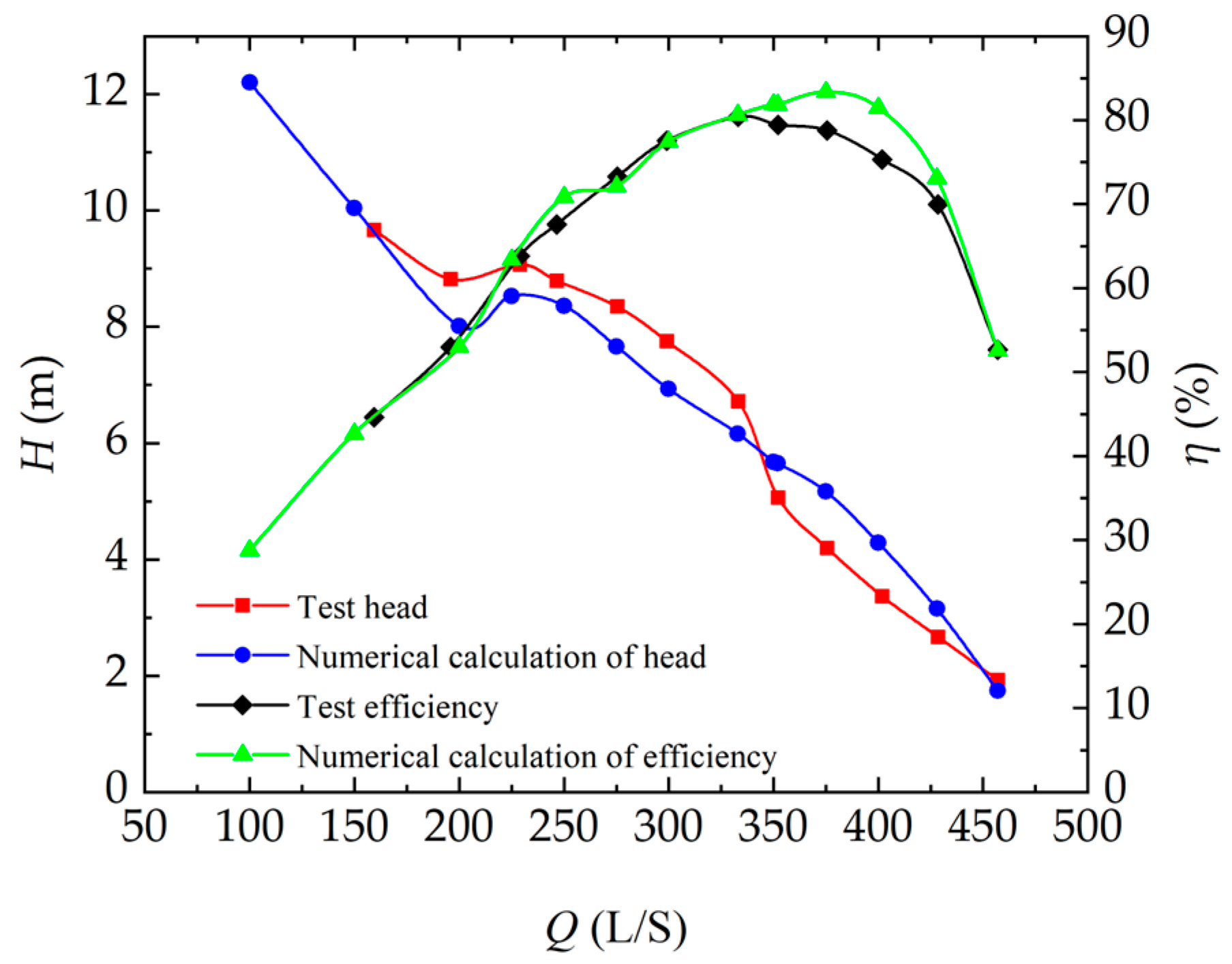
- The test results suggest that the highest efficiency working conditions of the pump rig are Q1 = 333.27 L/s, head H1 = 6.718 m, efficiency η1 = 80.38%, the design working conditions are Q2 = 350 L/s, head H2 = 5.065 m, efficiency η2 = 79.56%, and the highest working head is H4 = 9.027 m (which is about 1.78 times that of the design head). Further, the pump rig can be said to have a wide range of operating conditions and the design conditions are within the designated high-efficiency operating conditions, therefore meeting the design requirements. The numerical calculation and test comparison error margins are within 5.0%, the numerical calculation and test measurement errors are small, and the numerical calculation results are credible.
- (2)
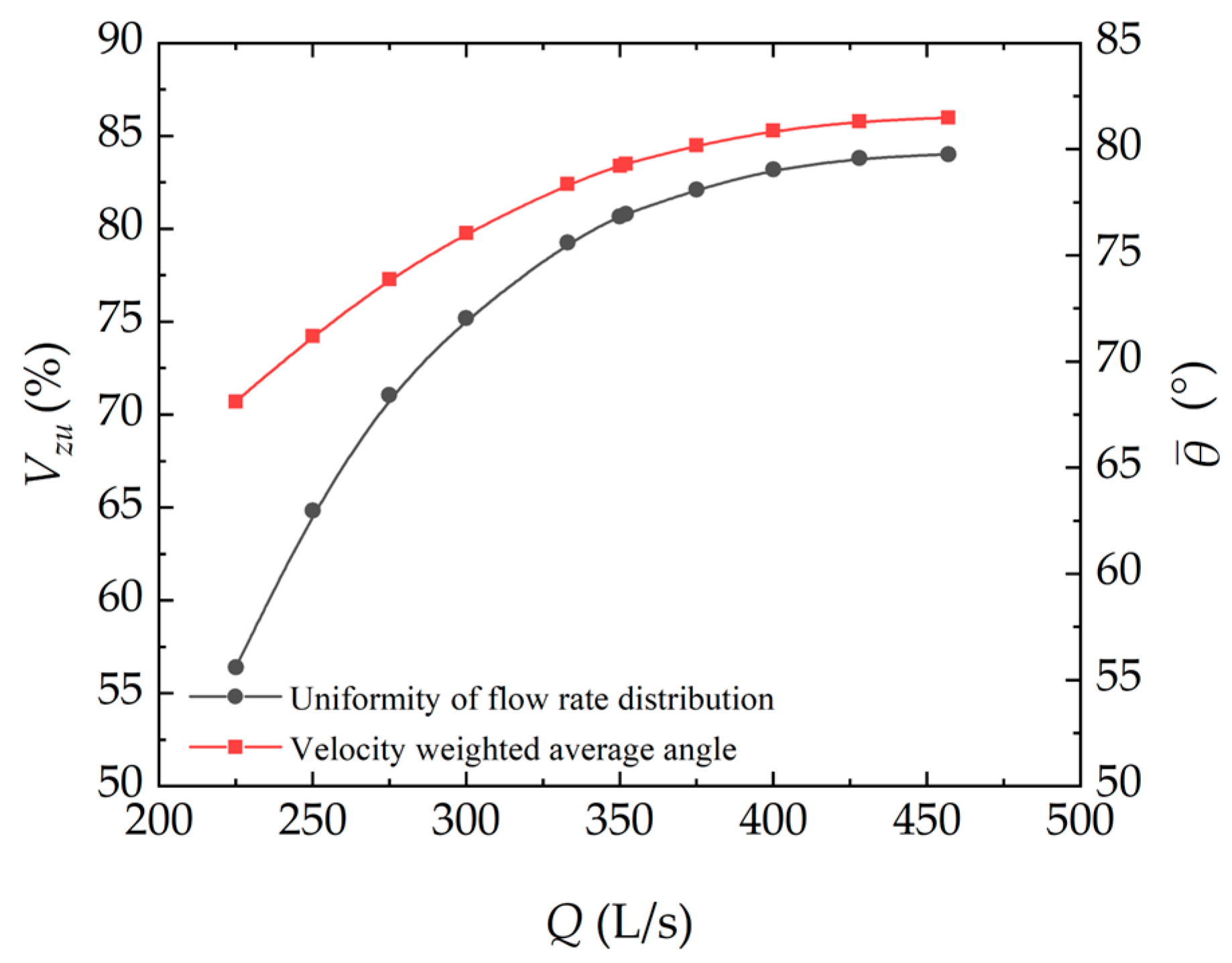
- The numerical calculation results demonstrate that the hydraulic loss of the inlet channel meets the relation hf = 0.5517Q2. Additionally, the hydraulic loss of the outlet bend meets the relation hf = 29.439Q2 − 22.27Q + 4.4992. Further, 80.675% of the inlet flow velocity uniformity of the pump unit’s impeller is in its design working condition (Q = 350 L/s), and 79.223% is in the weighted average angle of the flow velocity. As the flow increased, both the flow uniformity and the flow speed weighted average angle increased.
- (3)
- Through a comprehensive analysis of the flow patterns in the inlet channel, impeller, guide leaf, and outlet channel at different flow rates, it was found that the internal flow of the pump units is the most stable under the design condition Q = 350 L/s and, as a result, there are fewer bad flow patterns. The flow patterns of the inlet channel and outlet channel become worse when the flow rate decreases, and the flow pattern of the inlet channel is improved when the flow rate increases. However, compared with the design condition, the improvement is limited, and the flow pattern of the outlet channel is significantly worse.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, Y.; Yan, D.; Liu, C.; Cao, Z.; Jin, H. Experimental study on open inlet channels of pumping stations. J. Jiangsu Agric. Coll. 1989, 2, 47–52. [Google Scholar]
- Lu, L.; Xu, L.; Liang, J.; Liu, J.; Huang, J. Numerical calculation of three-dimensional flow and hydraulic loss in the inlet channel of pumping station. Drain. Irrig. Mach. 2008, 5, 55–58. [Google Scholar]
- Cheng, L.; Liu, C. Study on the objective function of optimal design of inlet and outlet water channels of pump stations. Water Pump Technol. 2007, 3, 39–42. [Google Scholar]
- Ye, P. Numerical Simulation and Experiments of Flow in Horn Pipe Inlet Channel of Axial Flow Pump. Master’s Thesis, Yangzhou University, Yangzhou, China, 2018. [Google Scholar]
- Qiu, C.; Zhang, Y. Simulation and analysis of the influence of the back wall distance of pumping station inlet basin on the water inlet conditions of pumps. Jiangsu Water Resour. 2012, 12, 17–18. [Google Scholar]
- Fu, J.; Li, N. Numerical optimization of pump station forebay and open intake channel. Jiangxi Sci. 2022, 40, 165–170. [Google Scholar]
- Sui, H. Study on the Hydraulic Optimization Design of Open Type Low Head Large Pumping Unit; Yangzhou University: Yangzhou, China, 2015. [Google Scholar]
- Zhang, W.; Shi, L.; Tang, F.; Duan, X.; Liu, H.; Sun, Z. Analysis of inlet flow passage conditions and their influence on the performance of an axial-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 733–746. [Google Scholar] [CrossRef]
- Widodo, E.; Pradhana, R.Y. Analysis of pipe diameter variation in axial pumps for reducing head loss. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 403. [Google Scholar]
- Yang, F.; Jiang, D.; Yuan, Y.; Lv, Y.; Jian, H.; Gao, H. Influence of Rotation Speed on Flow Field and Hydraulic Noise in the Conduit of a Vertical Axial-Flow Pump under Low Flow Rate Condition. Machines 2022, 10, 691. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Yuan, Y.; Liu, C.; Zhang, Y.; Jin, Y. Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions. Energies 2021, 14, 5245. [Google Scholar] [CrossRef]
- Liu, X.; Xu, F.; Cheng, L.; Pan, W.; Jiao, W. Stress Characteristics Analysis of Vertical Bi-Directional Flow Channel Axial Pump Blades Based on Fluid–Structure Coupling. Machines 2022, 10, 368. [Google Scholar] [CrossRef]
- Pan, Q.; Zhao, R.; Wang, X.; Shi, W.; Zhang, D. LES study of transient behaviour and turbulent characteristics of free-surface and floor-attached vortices in pump sump. J. Hydraul. Res. 2019, 57, 733–743. [Google Scholar] [CrossRef]
- Park, I.; Kim, H.J.; Seong, H.; Rhee, D.S. Experimental Studies on Surface Vortex Mitigation Using the Floating Anti-Vortex Device in Sump Pumps. Water 2018, 10, 441. [Google Scholar] [CrossRef] [Green Version]
- Václav, U.; Pavel, P.; Milan, S.; Martin, K.; Daniel, D. Experimental and Numerical Study on Vortical Structures and Their Dynamics in a Pump Sump. Water 2022, 14, 2039. [Google Scholar]
- Shinichiro, Y. Numerical Study of the Vortical Structures in the Pump Sump. Proc. Fluids Eng. Conf. 2018, 2018, os15-11. [Google Scholar]
- Jiao, W.; Chen, H.; Cheng, L.; Zhang, B.; Yang, Y.; Luo, C. Experimental study on flow evolution and pressure fluctuation characteristics of the underwater suction vortex of water jet propulsion pump unit in shallow water. Ocean. Eng. 2022, 266, 112569. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Liu, Q. Numerical Study of Roll Wave Characteristics Based on Navier-Stokes Equations: A Two-Dimensional Simulation. J. Eng. Mech. 2021, 147, 04020149. [Google Scholar] [CrossRef]
- Alessandro, T.; Alberto, B.; Michele, C.; Gaetano, G.; Giorgio, M.; Francesca, S. Cfd simulations of early- to fully-turbulent conditions in unbaffled and baffled vessels stirred by a rushton turbine. Chem. Eng. Res. Des. 2021, 171, 36–47. [Google Scholar]
- Xie, C.; Zhang, C.; Fu, T.; Zhang, T.; Feng, A.; Jin, Y. Numerical Analysis and Model Test Verification of Energy and Cavitation Characteristics of Axial Flow Pumps. Water 2022, 14, 2853. [Google Scholar] [CrossRef]
- Madhu, B.P.; Mahendramani, G.; Bhaskar, K. Numerical analysis on flow properties in convergent—Divergent nozzle for different divergence angle. Mater. Today Proc. 2021, 45, 207–215. [Google Scholar] [CrossRef]
- Xie, C.; Feng, A.; Fu, T.; Zhang, C.; Zhang, T.; Yang, F. Analysis of Energy Characteristics and Internal Flow Field of “S” Shaped Airfoil Bidirectional Axial Flow Pump. Water 2022, 14, 2839. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Meng, F.; Osman, M.K. The Effect of Root Clearance on Mechanical Energy Dissipation for Axial Flow Pump Device Based on Entropy Production. Processes 2020, 8, 1506. [Google Scholar] [CrossRef]
- Stuparu, A.; Baya, A.; Bosioc, A.; Anton, L.; Mos, D. Experimental investigation of a pumping station from CET power plant Timisoara. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 240. [Google Scholar]
- Xie, C.; Tang, F.; Yang, F.; Zhang, W.; Zhou, J.; Liu, H. Numerical simulation optimization of axial flow pump device for elbow inlet channel. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 240. [Google Scholar]
- Sun, Z.; Yu, J.; Tang, F. The Influence of Bulb Position on Hydraulic Performance of Submersible Tubular Pump Device. J. Mar. Sci. Eng. 2021, 9, 831. [Google Scholar] [CrossRef]
- Ji, D.; Lu, W.; Lu, L.; Xu, L.; Liu, J.; Shi, W.; Huang, G. Study on the Comparison of the Hydraulic Performance and Pressure Pulsation Characteristics of a Shaft Front-Positioned and a Shaft Rear-Positioned Tubular Pump Devices. J. Mar. Sci. Eng. 2021, 10, 8. [Google Scholar] [CrossRef]
- Xie, C.; Xuan, W.; Feng, A.; Sun, F. Analysis of Hydraulic Performance and Flow Characteristics of Inlet and Outlet Channels of Integrated Pump Gate. Water 2022, 14, 2747. [Google Scholar] [CrossRef]
- Ahmed, N.; Yang, F.; Zhang, Y.; Wang, T.; Mahmoud, H. Analysis of the Flow Pattern and Flow Rectification Measures of the Side-Intake Forebay in a Multi-Unit Pumping Station. Water 2021, 13, 2025. [Google Scholar]
- Xie, C.; Fu, T.; Xuan, W.; Bai, C.; Wu, L. Optimization and Internal Flow Analysis of Inlet and Outlet Horn of Integrated Pump Gate. Processes 2022, 10, 1753. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Chen, H.; Zheng, Y.; Zhou, D.; Maxima, B. Study on a horizontal axial flow pump during runaway process with bidirectional operating conditions. Sci. Rep. 2021, 11, 21834. [Google Scholar] [CrossRef]
- Xie, C.; Yuan, Z.; Feng, A.; Wang, Z.; Wu, L. Energy Characteristics and Internal Flow Field Analysis of Centrifugal Prefabricated Pumping Station with Two Pumps in Operation. Water 2022, 14, 2705. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, F.; Shi, L.; Hu, Q.; Zhou, Y. Effects of an Inlet Vortex on the Performance of an Axial-Flow Pump. Energies 2020, 13, 2854. [Google Scholar] [CrossRef]
- Yang, F.; Zhao, H.; Liu, C. Improvement of the Efficiency of the Axial-Flow Pump at Part Loads due to Installing Outlet Guide Vanes Mechanism. Math. Probl. Eng. 2016, 2016 Pt 2, 6375314. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, T.; Yuan, Z.; Feng, A.; Wu, L. Optimization Design and Internal Flow Analysis of Prefabricated Barrel in Centrifugal Prefabricated Pumping Station with Double Pumps. Processes 2022, 10, 1877. [Google Scholar] [CrossRef]



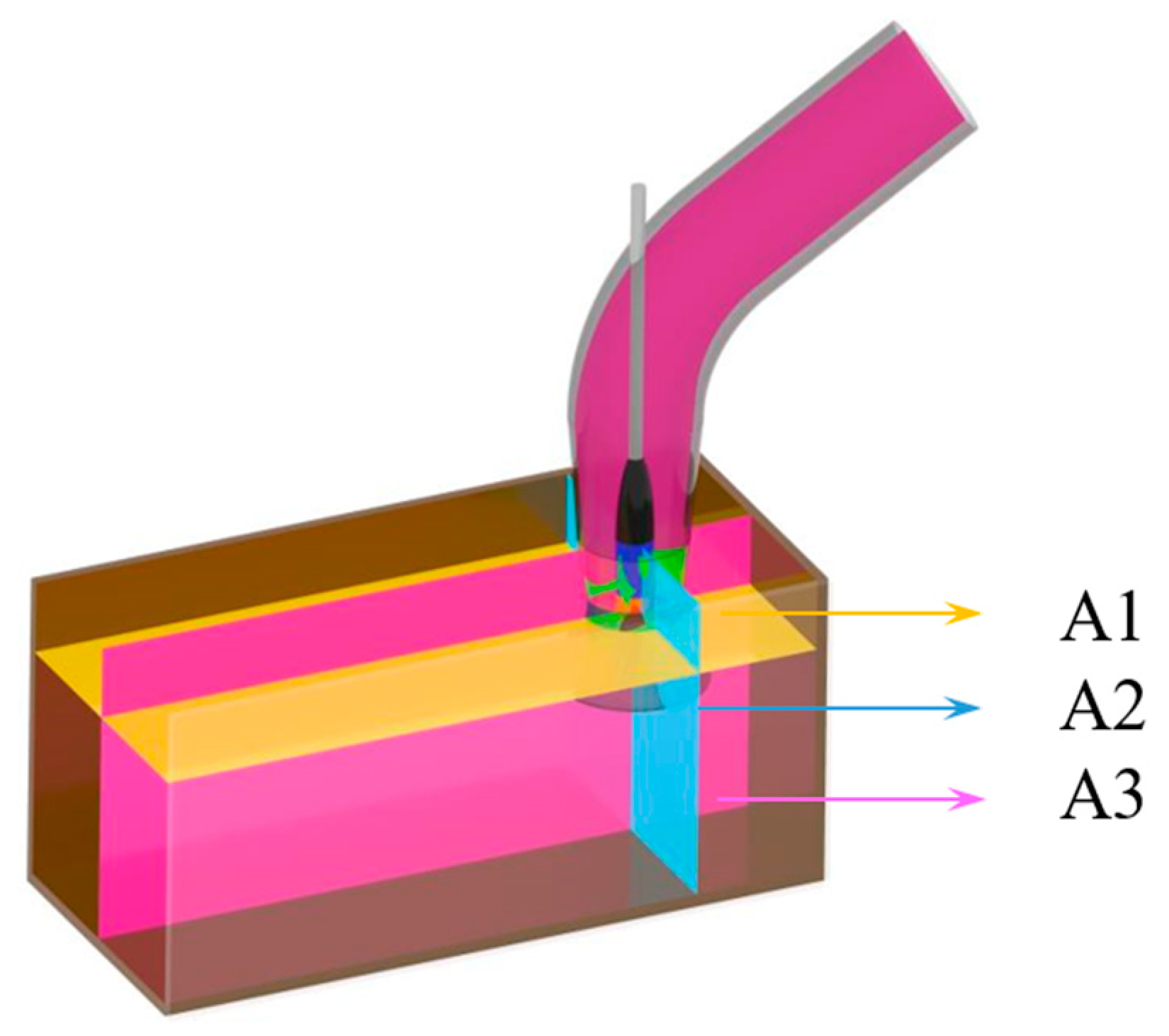

| Data | Numerical Values |
|---|---|
| Impeller diameter, D | (300–0.2) mm |
| Impeller rotation rate, n | 1450 r/min |
| Design flow, Q | 350 L/s |
| Design head, H | 5.0 m |
| Design efficiency, η | 80.0% |
| Parameters | Numerical Value | Remarks |
|---|---|---|
| Diving depth | 475 mm (1.58D) | Distance between the inlet surface of the flare and the bottom surface of the channel |
| Posterior wall distance | 375 mm (1.25D) | Distance between the center of the impeller and the back wall of the channel |
| Side wall distance | 450 mm (1.5D) | Distance between the impeller center and channel sidewall |
| Sump length | 2071 mm (6.9D) | / |
| Sump width | 900 mm (3D) | / |
| Settings | Parameters |
|---|---|
| Rotational speed, n | 1450 r/min |
| Inlet section | Mass flow rate |
| Outlet section | Average static pressure (1.0 atm) |
| No mobile solid wall surface | Static |
| Free liquid surface | Symmetry |
| Close-to-the-wall zone | Standard wall functions |
| Moving and standing interfaces | Frozen rotor, GGI grid stitching technology |
| Numerical Calculations | Test | ||||
|---|---|---|---|---|---|
| Flow Rate Q (L/s) | Head H (m) | Efficiency η (%) | Flow Rate Q (L/s) | Head H (m) | Efficiency η (%) |
| 100 (0.286 Qd) | 12.205 | 28.79 | 159.49 (0.456 Qd) | 9.664 | 44.60 |
| 150 (0.429 Qd) | 10.040 | 42.67 | 195.96 (0.560 Qd) | 8.821 | 52.97 |
| 200 (0.571 Qd) | 8.018 | 53.01 | 228.98 (0.654 Qd) | 9.072 | 63.78 |
| 225 (0.643 Qd) | 8.531 | 63.39 | 246.65 (0.705 Qd) | 8.791 | 67.58 |
| 250 (0.714 Qd) | 8.361 | 70.87 | 275.46 (0.787 Qd) | 8.346 | 73.25 |
| 275 (0.786 Qd) | 7.663 | 72.13 | 299.18 (0.855 Qd) | 7.754 | 77.53 |
| 300 (0.857 Qd) | 6.932 | 77.46 | 300.00 (0.857 Qd) | 7.729 | 77.60 |
| 333 (0.951 Qd) | 6.164 | 80.65 | 333.27 (0.952 Qd) | 6.718 | 80.38 |
| 350 (1.0 Qd) | 5.674 | 81.89 | 352.35 (1.007 Qd) | 5.061 | 79.45 |
| 352 (1.005 Qd) | 5.653 | 81.84 | 375.73 (1.074 Qd) | 4.194 | 78.76 |
| 375 (1.071 Qd) | 5.173 | 83.35 | 401.98 (1.149 Qd) | 3.367 | 75.31 |
| 400 (1.143 Qd) | 4.290 | 81.48 | 428.49 (1.224 Qd) | 2.669 | 69.94 |
| 428 (1.223 Qd) | 3.153 | 73.08 | 457.03 (1.306 Qd) | 1.926 | 52.64 |
| 457 (1.306 Qd) | 1.745 | 52.56 | / | / | / |
| Flow Rate Q (L/s) | Uniformity of Flow Rate Distribution VZU (%) | Velocity Weighted Average Angle θ (°) |
|---|---|---|
| 225 (0.643 Qd) | 56.400 | 68.119 |
| 250 (0.714 Qd) | 64.831 | 71.193 |
| 275 (0.786 Qd) | 71.063 | 73.879 |
| 300 (0.857 Qd) | 75.183 | 76.055 |
| 333 (0.951 Qd) | 79.265 | 78.357 |
| 350 (1.000 Qd) | 80.675 | 79.223 |
| 352 (1.005 Qd) | 80.796 | 79.308 |
| 375 (1.071 Qd) | 82.123 | 80.183 |
| 400 (1.143 Qd) | 83.198 | 80.872 |
| 428 (1.223 Qd) | 83.798 | 81.317 |
| 457 (1.306 Qd) | 84.014 | 81.491 |
| Flow Rate Q (L/s) | Hydraulic Loss of Inlet Channel hf (m) | Hydraulic Loss of Outlet Bend hf (m) |
|---|---|---|
| 225 (0.643 Qd) | 0.0244 | 0.8958 |
| 250 (0.714 Qd) | 0.0307 | 0.8508 |
| 275 (0.786 Qd) | 0.0396 | 0.6443 |
| 300 (0.857 Qd) | 0.0489 | 0.4767 |
| 333 (0.951 Qd) | 0.0609 | 0.3187 |
| 350 (1.000 Qd) | 0.0676 | 0.3183 |
| 375 (1.071 Qd) | 0.0781 | 0.2785 |
| 400 (1.143 Qd) | 0.0891 | 0.2688 |
| 428 (1.223 Qd) | 0.1022 | 0.3320 |
| 457 (1.306 Qd) | 0.1165 | 0.5150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, C.; Zhang, C.; Fu, T.; Feng, A.; Zhang, T.; Yang, F. An Analysis of Energy and Internal Flow Characteristics of Open Inlet Channel Axial Flow Pumping Devices. Processes 2022, 10, 2284. https://doi.org/10.3390/pr10112284
Xie C, Zhang C, Fu T, Feng A, Zhang T, Yang F. An Analysis of Energy and Internal Flow Characteristics of Open Inlet Channel Axial Flow Pumping Devices. Processes. 2022; 10(11):2284. https://doi.org/10.3390/pr10112284
Chicago/Turabian StyleXie, Chuanliu, Cheng Zhang, Tenglong Fu, Andong Feng, Tao Zhang, and Fan Yang. 2022. "An Analysis of Energy and Internal Flow Characteristics of Open Inlet Channel Axial Flow Pumping Devices" Processes 10, no. 11: 2284. https://doi.org/10.3390/pr10112284
APA StyleXie, C., Zhang, C., Fu, T., Feng, A., Zhang, T., & Yang, F. (2022). An Analysis of Energy and Internal Flow Characteristics of Open Inlet Channel Axial Flow Pumping Devices. Processes, 10(11), 2284. https://doi.org/10.3390/pr10112284










