Abstract
Differential Evolution (DE) has been extensively adopted for multi-objective optimization due to its efficient and straightforward framework. In DE, the mutation operator influences the evolution of the population. In this paper, an adaptive Grid-based Multi-Objective Differential Evolution is proposed to address multi-objective optimization (ad-GrMODE). In ad-GrMODE, an adaptive grid environment is employed to perform a mutation strategy in conjunction with performance indicators. The grid reflects the convergence and diversity performance together but is associated with the user-specified parameter “div”. To solve this problem, we adaptively tune the parameter “div”. Among the DE mutation strategies, “DE/current-to-best/1” is applied extensively in single-objective optimization. This paper extends the application of “DE/current-to-best/1” to multi-objective optimization. In addition, a two-stage environmental selection is adopted in ad-GrMODE, where in the first stage, one-to-one selection between the parent and its corresponding offspring solution is performed. In addition, to preserve elitism, a stochastic selection is adopted with respect to performance metrics. We conducted experiments on 16 benchmark problems, including the DTLZ and WFG, to validate the performance of the proposed ad-GrMODE algorithm. Besides the benchmark problem, we evaluated the performance of the proposed method on real-world problems. Results of the experiments show that the proposed algorithm outperforms the eight state-of-the-art algorithms.
1. Introduction
Multi-objective Optimization Problems (MOPs) are optimization problems involving multiple conflicting objectives [1]. Due to the conflicting behavior of objectives in MOPs, a set of nondominated solutions is determined, known as the Pareto optimal Set (PS), which represents the Pareto Front (PF) in the objective space [1,2]. Recently, population search-based metaheuristic genetic algorithms [3,4,5], Particle Swarm Optimization (PSO) [6], and DE [7,8] have been able to obtain Pareto-optimal solutions in a single run. Evolutionary Algorithms (EAs) have been proven efficient in tackling MOPs. Due to their population-based search mechanism, EAs can obtain pareto-optimal solutions a one-time run. In general, when solving MOPs, the algorithms aim to achieve two main goals: convergence (find solutions as close to the PF as possible) and diversity (identifying solutions that are well distributed) [1,2]. DE is one of the simplest and most powerful EAs to be used in continuous optimization and has now emerged as one of the state-of-the-art EAs for global optimization issues and MOPs [9,10]. In the past few decades, after the initial extension of DE for MOPs [11], research has focused on implementing various multi-objective DE algorithms that have also produced promising results [10].
In the evolution of DE, three significant operators exist, mutation, crossover, and selection, to guide the algorithm towards the PF [12,13]. Using the mutation operator, individuals are exposed to an abrupt change or perturbation, allowing them to discover the search space. Following the mutation operation is the crossover operation that increases the population’s diversity. The selection operator selects the best population from a parent and its offspring for the next generation, which makes sure that the population never deteriorates. DE has proven to solve Single-objective Optimization Problems (SOPs) efficiently. Recent advances of DE in handling SOPs can be categorized as (a) designing new mutation operators [14,15]; (b) developing new parameter control techniques [9,16]; (c) developing crossover operators [17,18]; and (d) combining different mutation strategies [19]. However, extending DE to deal with MOPs is not straightforward. Based on the review of the literature, the existing multi-objective DE approaches focus on designing adaptive strategies for mutation operators and control parameters [20,21]. Despite this, few studies have examined how to design efficient selection operators for maintaining population diversity [22,23,24]. Moreover, designing efficient mutation operators in Multi-Objective Differential Evolutions (MODEs) to handle MOPs is a crucial but under-explored area of research. Because some mutation strategies are extensively applied in single-objective problems. Unlike single-objective problems, MOPs cannot have just one optimal solution. Therefore, it is challenging to modify it to cope with MOPs.
Taking advantage of these observations, in this study, we introduce a grid-based mutation operator for DE to deal with MOPs. The proposed mutation operator employs the “DE/current-to-best/1” mutation strategy based on grid settings. The “DE/current-to-best/1” mutation strategy is widely adopted in SOPs but extending it to deal with MOPs is challenging. In single-objective problems, one optimal solution can be considered as best, but in MOPs, no single solution can be considered as best. Consequently, a set of promising solutions are required to have good convergence and diversity properties. On the other hand, the grid reflects convergence as well as diversity as one of its inherent characteristics. In the grid, all solutions have a deterministic location. The convergence of a solution can be assessed by comparing the grid location of the solution with other solutions, while diversity can be estimated by determining the number of solutions that have grid locations that are identical to or similar to the solutions. Additionally, as opposed to the Pareto dominance criterion, a grid-based criterion provides both quantitative information and qualitative information on the differences between the various solutions [25]. Hence, grid settings are employed to facilitate the implementation of the “DE/current-to-best/1” mutation strategy.
In the literature, grid settings are adopted in GrEA [25], PESA-II [26], Grid-IGD [27], etc. However, these approaches are sensitive to the parameter settings in the grid. In grid settings, the parameter “div” challenges the performance of the algorithm. Furthermore, choosing an inappropriate value of “div” would degrade the performance of the algorithm severely. However, adapting the parameter “div” can serve as a solution for the aforementioned issue. Hence, in this paper, we propose an adaptive strategy for grid settings that fine tunes the parameter “div” and enhances the performance of the algorithm. Next, the grid setting divides the objective space into different grids, and with the help of performance indicators and ISDE, the mutation operation is performed. In the environmental selection, first, one-to-one selection between the parent and its corresponding offspring solution is performed based on dominance. Then, the stochastic ranking based on and ISDE is adopted to select better solutions as parents for the next generations. We highlight the main contributions of this work as follows:
(1) This paper proposes an adaptive grid-based mutation strategy for differential evolution to solve MOPs. (2) In ad-GrMODE, a novel and efficient mutation strategy based on a grid environment is developed. (3) Based on the grid, convergence and diversity are reflected simultaneously. (4) As “DE/current-to-best/1” has been extensively applied to single-objective optimization, this paper extends its application to multi-objective optimization. (5) To facilitate the implementation of the “DE/current-to-best/1” mutation strategy, grid settings are used. (6) To identify the best solution, within each grid, two performance indicators and ISDE are employed in ad-GrMODE. (7) In addition, a two-level environmental selection approach employs one-to-one selection along with a stochastic selection with respect to the indicators. (8) ad-GrMODE employs an adaptive grid environment for mutation strategies in DE.
Following are the remaining sections of the paper. Section 2 discusses the background of MOP, grid structure, and related work. In Section 3, the new algorithm ad-GrMODE is described in detail. The experimental setup is presented in Section 4. Section 5 describes the experimental results and Section 6 concludes the paper.
2. Background
The following sections provide a brief overview of multi-objective optimization in addition to the definitions of the grid structure and related work.
2.1. Multi-Objective Optimization Problem (MOP)
Multi-objective optimization problems (MOPs) can be defined as problems that have multiple objectives that are in conflict and must be optimized at the same time [1]. In MOPs, unlike SOPs, a set of optimal solutions known as PS in decision space and PF in objective space must be found. A mathematical formulation for MOP is shown below:
where f(x) represents the vector of simultaneous objective functions. The number of objective functions and the decision vectors are denoted as m and x, respectively. Rn denotes the decision space.
Definition 1 (Pareto dominance).
Suppose there are two different solutions of A and B ∈ S, then A dominates B if and only if:
Definition 2 (Pareto-optimal solution).
When no solution dominates a solution x*, it can be Pareto-optimal. (non-dominated solution).
Definition 3 (Pareto-optimal set).
In decision variable space, a set of non-dominated solutions (Pareto-optimal solutions) are nominated as a PS.
Definition 4 (Pareto front).
The PF is a set of optimal solutions in the space of objective functions in MOPs. The Pareto front signifies a set of solutions that are not superior to each other. However, they are superior to other solutions in space.
2.2. Definition of a Grid Structure
There is a general tendency for a grid to reflect the distribution of solutions in the evolutionary process using its grid position (i.e., grid coordinates). The difference in grid coordinates among solutions illustrates the distance between them and, subsequently, reveals the density of solutions [25].
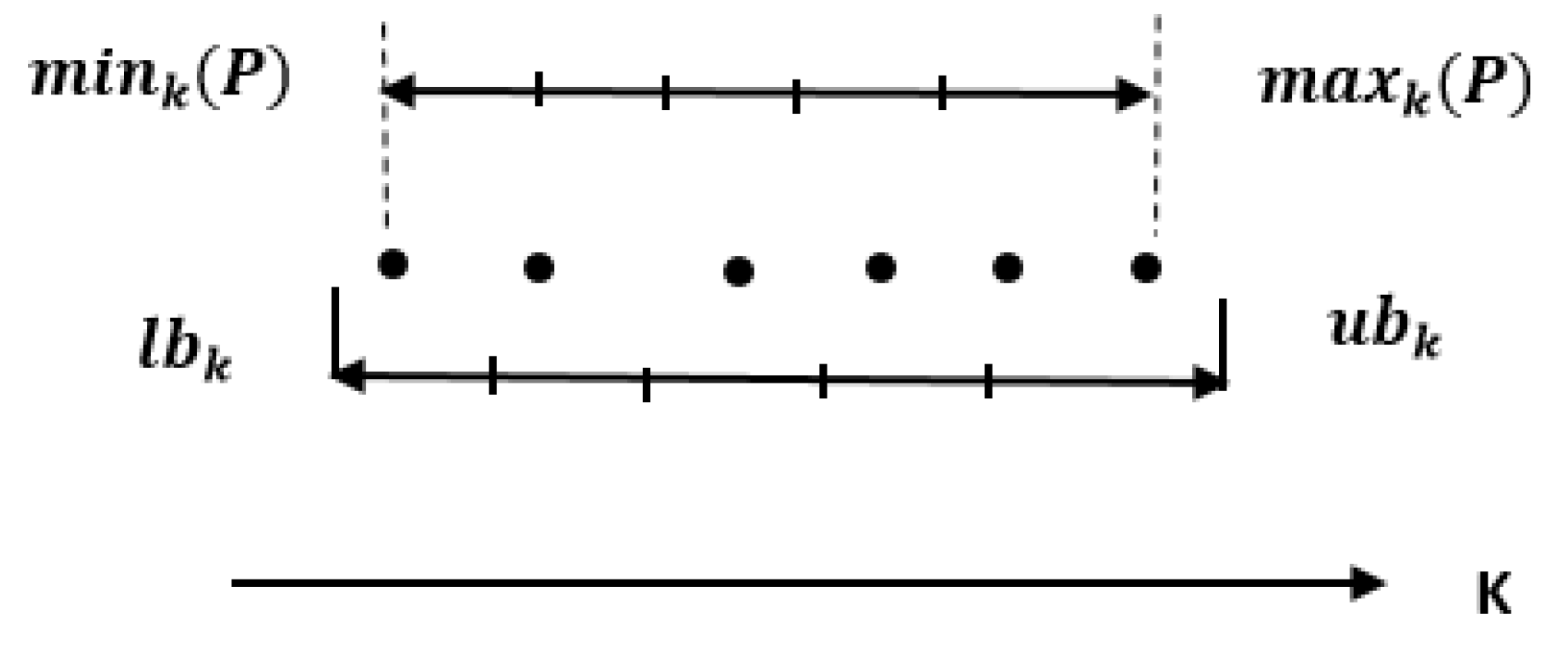
In terms of convergence, a grid can also serve as a reliable indicator of how solutions are evolving. As well as comparing whether one solution is better than another, the grid coordinates also consider the differences in objective values. Therefore, the grid can identify the solutions tied in the sense of Pareto dominance, which results in more significant selection pressure during the evolution of many-objective optimization. In [25], a Grid-based Evolutionary Algorithm (GrEA) is proposed to solve many-objective optimization problems. In GrEA, grid bounds can be changed after each iteration. In Figure 1, the grid setting for the kth objective is indicated. As a first step, the mink(P) and maxk(P) values of the kth objective are identified based on the individuals of a population P. In every iteration, the lower and upper grid bounds must be computed to build the grid structure. The following equation is used for the calculation:
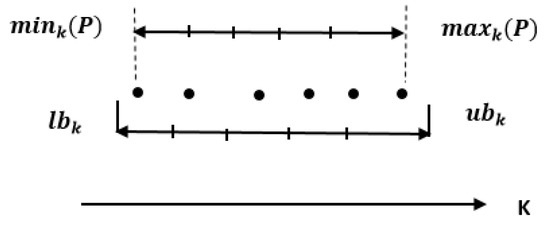
Figure 1.
Grid setting for the kth objective [25].
A lower boundary is marked by lbk whereas an upper boundary is marked by ubk. The minimum and maximum values are identified by mink(P) and maxk(P) div is the number of subdivisions of the objective zone per dimension (e.g., in Figure 1, div = 5). Therefore, the initial M-dimensional objective space is subdivided into divM hyperboxes. The width dk of each hyperbox can be determined as:
By using lbk and dk, it is possible to determine the grid location of an individual within the kth objective:
where ⌊.⌋ refers to the floor function, and Gk (x) and Fk (x) define the grid coordinates and objective function value, respectively.
Gk (x) = ⌊Fk (x) − lbk/dk⌋
2.3. Related Work
In this section, we provide the details of the proposed works of DE and grid-based approaches. According to a literature review by the authors in [10], numerous types of MODEs have produced positive results for a variety of MOPs. A Generalized DE (GDE3) is introduced in [28] that can consider any number of objectives and constraints. The Pareto DE (PDE) algorithm is described in [11]. The algorithm starts by producing a mutation operation, in which mutations are randomly generated based on a Gaussian distribution. Then, it eliminates the solution with the lowest neighbor distance until a certain threshold is reached for non-dominated solutions. In [29], an expanded PDE algorithm based on self-adaptive crossovers and mutations is introduced. Additionally, [30] proposes a method known as the PDE Algorithm (PDEA) based on non-dominated sorting as well as the ranking selection described in [31]. PDEA has been proved to be suitable for solving MOPs. A new method that substitutes the crossover and mutation in NSGA-II with a simple DE method is introduced in [32]. The results show that their approach outperforms NSGA-II when applied to rotated MOPs. An algorithm for parallel MOPs based on DE multi-populations is presented in [33] and a new algorithm called Multi-Objective DE (MODE) was introduced in [34], which uses Pareto-based ranking and crowding distance [31]. The Pareto-optimal solutions of MOPs are determined in [35] using a penal function and weighting factor approach. A DEMO was designed in [36], which follows the ranking and sorting technique of NSGAII [3] for convergence and diversity. Rather than a single population in MODE, different subpopulations are used in [37] and [38] to increase the diversity of the solutions. The authors in [20] design a self-adaptive MODE (MOSaDE) using the mutation strategy described in [10] for use in MOPs. In an approach presented in [39], with a secondary population, the e-dominance principle is adopted to increase the variety of the solutions. In [40], an optimal mutation method composed of five mutation strategies is proposed to improve the DE algorithm through a wavelet basis function capable of improving search quality, accelerating convergence, and preventing stagnation. The paper [8] presented an effective solution to the MOED problem based on the MOED framework, problem-specific mutation, and crossover operators.
A self-adaptive MODE is proposed in [41], which uses the valuable information extracted from the archived inferior solutions to the superior ones to enhance search performance. In [42], the adaptive MODE is presented and how crowding entropy is used to estimate diversity is described. The authors in [43] present a new variation of DE, known as MCDEmv, which uses a mixed-variable co-evolutionary procedure that optimizes continuous as well as discrete variables at the same time. In [44], a Multi Objective Evolutionary Algorithm (MOEA) was designed to use a set of impossible solutions to guide the individuals, resulting in a new strategy to handle constraints. A Grid-based Bidirectional Local Search algorithm (GrBLS) is presented in [45] to obtain sets of solutions that achieve improved convergence to the real Pareto optimal front and are more distributed. In the GrBLS, the best individual is selected based on the grid-based method. A grid-based adaptive multi-objective differential evolution algorithm is developed in [24]. Here, by using feedback information throughout evolution, the proposed algorithm can appropriately adjust the convergence and diversity. The MOEA algorithm employing constrained decomposition with grids (CCDG-K) is developed to cluster and estimate the optimal value of k (the number of clusters) [46]. In CCDG-K, a grid-based decomposition procedure is adopted. The grid-based weighted sum approach is described in [47] that is applied to the Pareto local search for combinatorial MOPs. This approach was obtained by applying both the Pareto dominance and weighted sum in a grid system. The Grid Search-based Multi-population Particle Swarm Optimization algorithm (GSMPSO-MM) is proposed in [48] to solve multimodal MOPs, providing high-quality solutions in decision space using a grid in GSMPSO-MM. The authors in [49] introduce a novel optimization algorithm that was inspired by nature and is referred to as MOWOA, which uses a new global grid ranking technique based on the grid to optimize performance. By integrating grid system concepts, ref. [5] introduced an adaptive multi-objective evolutionary algorithm that an adaptive selection procedure dynamically allocates evolutionary opportunities by analyzing the quality and dominance relationship between subspaces. In addition, an evolutionary scheme and an external archive technique are discussed to enhance evolutionary effectiveness. In [50], the multi-objective bat algorithm and multi-objective bat algorithm with the grid are compared based in the performance of the drum. In the multi-objective bat algorithm with the grid, a pareto dominance process is applied to analyze the relationships between solutions and continuously modify the PS. In this paper, ref. [51], a grid-based multi-objective Cauchy differential evolution is developed to solve stochastic dynamic economic emission dispatch with uncertainty due to wind power. A Cauchy mutation is used to improve differential evolution, while an adaptive grid is constructed to retain the Pareto fronts diversity distribution.
3. Proposed Method
This section presents a comprehensive description of the general framework for the ad-GrMODE. Here, we propose an algorithm that belongs to the class of DE for MOPs. Based on the literature, it is apparent that grid-based approaches improve algorithm convergence and diversity. Consequently, the proposed method takes advantage of grid-based methods and integrates them into the mutation process of DE.
3.1. General Framework of ad-GrMODE
In Algorithm 1, the general framework for ad-GrMODE is described. The proposed ad-GrMODE randomly starts with the initialization of the parent population (P) of size “N”. Then, the [52] and ISDE [53] indicators for the parent population are determined. Next, the adaptive grid-based mutation strategy is employed to produce the mutant parents, followed by a crossover operation to generate the offspring population. The indicator values for the offspring population are calculated and a two-level environmental selection technique is adapted to preserve the ‘N’ elite solutions. This process continues until the termination condition is satisfied.
| Algorithm 1: General framework of ad-GrMODE |
 |
3.2. Grid-Based Mutation Strategy
The grid-based mutation strategy essentially involves three steps. In the first step, the objective space of the parent population is segregated into different grids using the adaptive grid settings. As mentioned earlier, the “div” parameter influences the performance of grid-based approaches, and obtaining the appropriation “div” parameter is challenging. Hence, in this paper, we adopt the “div” parameter linearly as follows:
where gt and gmax are the current number of generations and the maximum number of generations, respectively. Ns is an integer. In the experimental section, we analyze the performance of the proposed algorithm with different Ns values.
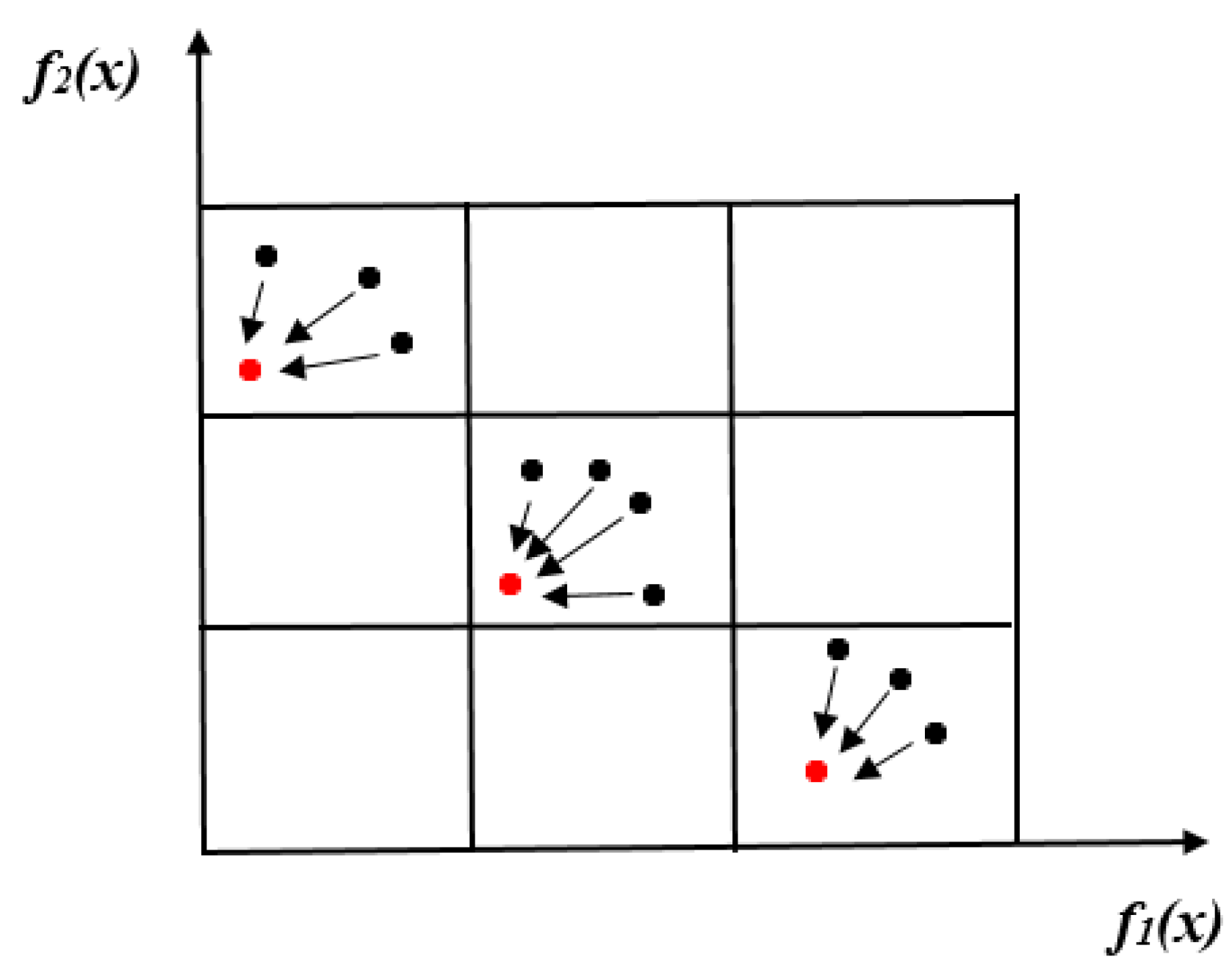
After the grid settings, the best solution for adopting the mutation strategy “DE/current-to-best/1” [54] is obtained in the second step. In single-objective approaches, determining the best solution is straightforward because the solution with the best objective value can be considered as the best one. The main issue in employing the “DE/current-to-best/1” [54] mutation strategy for MOPs is that a single solution cannot be considered the best due to the conflicting nature of objectives. Hence, the various solutions can represent the best solution in MOPs. In this paper, we adopt grid settings, and within each grid, the solution with a better value of and ISDE is chosen as the best solution. A schematic of how the best solution is obtained is presented in Figure 2.
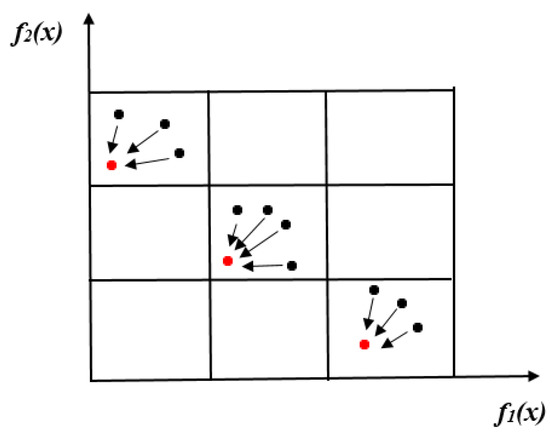
Figure 2.
Adaptive grid-based mutation strategy.
In Figure 2, f1(x) and f2(x) are two minimization objectives. The red color denotes the best solution, whereas the black color shows the remaining solutions in each grid.
From Figure 2, we can observe that the individuals in the parent population are segregated into different grid locations. Then, within each grid, the best solution is obtained. Next, all the solutions try to converge towards the best solution. Selecting the best solution from each grid improves the diversity along with the convergence. To identify the best solution in each grid, a stochastic selection method is employed. If rand < 0.5, ISDE is chosen, otherwise is chosen. For instance, let us assume the best solution is chosen with respect to the ISDE indicator. As suggested in [53], the ISDE indicator improves both convergence and diversity. The solution with a better ISDE value within each grid reflects better convergence and diversity performance than the remaining solutions. Thus, the solution will guide the search towards the PF. Similarly, the indicator also improves the convergence and distribution of the solutions. Hence, in the proposed ad-GrMODE, the advantages of both [52] and ISDE [53] are combined to improve convergence and diversity.
Finally, the mutation strategy is performed within each grid as:
where Xcur and Ocur are the current parent and its corresponding offspring solution, respectively, F is the scaling factor, and Xr1 and Xr2 represent random solutions. The description of grid-based mutation is presented in Algorithm 2.
Ocur = Xcur + F (Pbest − Xcur) + F (Xr1 − Xr2)
| Algorithm 2: Grid-based mutation |
 |
3.3. Crossover
In DE, the binomial crossover [40,55] is the most common crossover type. Hence, we apply binomial crossover to produce the offspring in the proposed algorithm. Implementing the binomial crossover is described as follows:
The βi,j,n can be expressed as real random numbers uniformly distributed in the range between 0 and 1, whereas CR ∈ [0, 1] represents the crossover rate.
The offspring oi,n is expected to be entirely distinct from either parent. EAs are frequently based on this principle. If the offspring reproduces vi,n, then a randomly selected parameter from xi,n, xi,j,n, replaces the associated parameter of the offspring oi,n, oi,j,n. In contrast, if oi,n inherits none of the properties from vi,n, therefore no evolution occurs, a parameter randomly selected by the offspring oi,n, oi,j,n will be substituted with the mutant parameter vi,n, vi,j,n. Furthermore, the polynomial mutation [56] is employed to enable better exploration of the solution space surrounding the good solution.
3.4. Environmental Selection
A process of environmental selection preserves the elite solutions as the parent population for the next generations. The environmental selection in ad-GrMODE is a two-level selection process where in the first level, a one-to-one comparison between a parent and its corresponding offspring is performed based on dominance. In other words, the generated offspring population is checked for dominance with respect to the parent population. Let ‘p’ be a parent solution and ‘q’ be its corresponding offspring solution. If individual ‘p’ Pareto dominates individual ‘q’, therefore ‘q’ is eliminated. If individual ‘q’ Pareto dominates individual ‘p’, that means ‘p’ is replaced by ‘q’ in the parent population. If both the individuals ‘p’ and ‘q’ are non-dominated with respect to each other, then both the individuals are preserved for the second level of environmental selection.
In the second level of environmental selection, the ‘N’ elite individuals are selected from the preserved pool. A stochastic selection ranking [57] is employed based on [52] and ISDE [53] to preserve the elite individuals. The individuals are stochastically ranked according to and ISDE, and the best ‘N’ individuals are preferred. The description of environmental selection is presented in Algorithm 3.
| Algorithm 3: Environmental selection |
 |
4. Experimental Setup
The following sections explain the algorithms, overall parameter settings, benchmark problems, and evaluation criteria in detail. The experiments are intended to provide the following:
- (a)
- An analysis of the performance of the proposed algorithm with different grid settings;
- (b)
- A comparison of the performance of the proposed algorithm with state-of-art algorithms.
In this study, the simulations were conducted on a PC with an Intel Core i5-10400 CPU processor running at 2.90 GHz and a 64-bit version of Windows 10 with MATLAB 2021b. As part of this section, eight common MOEAs such as NSGA-III [58], SPEA-R [59], VaEA [60], SRA [57], MODE [34], EMyO-C [61], MyODEMR [62], and GAMODE [24] are used for comparison to evaluate the performance of the proposed ad-GrMODE. Experiments were conducted on 16 test problems from two benchmark test suites, DTLZ [63] and WFG [64]. In the DTLZ and WFG benchmark problems, 3, 5, 8, and 10 objectives were taken into account. Depending on the objective, the population size varies. In other words, the population sizes for 3, 5, 8, and 10 objectives were maintained as 120, 126, 156, and 275, respectively. During the simulation process, for NSGAIII, SPEA-R, VaEA, and SRA algorithms, the simulated binary crossover [65] and polynomial mutation [56] were used as variation operators. The crossover distribution index and probability were chosen as nc = 20 and pc = 1.0, respectively. The mutation index and probability were set as nm = 20 and pm = 1/D, where D denotes the number of decision variables. For the MODE algorithm, the “DE/rand/1” mutation strategy and binomial crossover were adopted with the scaling factor F as 0.5 and crossover rate CR as 0.2 as mentioned in [34]. For EMyO-C and MyODEMR, the restricted polynomial mutation was applied with the mutation index and probability set to 20 and 1/D, respectively, as described in [61,62]. A binomial crossover with a 0.15 crossover rate was implemented in EMyO-C and MyODEMR according to [61,62]. In GAMODE, “DE/current-to-best/1” mutation and binomial crossover were conducted with scaling factor F of 0.1 and crossover rate CR of 0.1 [24]. In the proposed ad-GrMODE scaling factor F and crossover rate CR were set as 0.5 and 0.15.
4.1. Description of Benchmark Problems
There are seven tests in the DTLZ (DTLZ1-DTLZ7) suite [63], while the WFG (WFG1-WFG9) suite includes nine tests [64]. The DTLZ problem sets are composed of several features and evaluate several MOEA capabilities. DTLZ1, DTLZ3, and DTLZ6 are typically multimodal and evaluate the convergence of MOEAs through multiple local Pareto-optimal fronts. MOEAs have problems converging to the Pareto optimal front owing to the existence of local Pareto fronts. There are still other test problems, including DTLZ2 and DTLZ4-DTLZ7, which examine the MOEAs’ ability to solve problems of various forms. The WFG benchmark problems are based on Pareto-optimal fronts with properties such as convex, concave, linear, multimodal, degenerated, biased, and disconnected geometries; hence, they illustrate the range of MOEA abilities. Table 1 shows the parameters and settings for each problem and their iteration numbers.

Table 1.
Parameters and settings of the DTLZ and WFG problem suite.
4.2. Performance Metric
In the present study, we used the hypervolume indicator (HV) [66], which measures the algorithms’ efficiency. An algorithm’s convergence and diversity can be assessed using the hypervolume indicator. A hypervolume metric [66] has the following definition:
where Vol(.) refers to the Lebesgue measure, indicates the reference point on the Pareto-optimal front dominated by all objectives, and S denotes the approximate solution set. To evaluate the hypervolume metric, a reference point for M-dimensional is required. From the reference point, a hypercube is constructed and an HV metric evaluates the volume of the hypercube dominated by the approximated solution set. First, the objective values of the approximated solution set obtained by each algorithm are normalized for the lower and upper bounds of the true PF. Then, a set of reference points is set as 1.1 times the upper bounds of the true PF. To evaluate the HV indicator, the Monte Carlo approach is employed with 1,000,000 sampling points. The algorithms with higher HV values are considered the best-performing algorithms.
According to mathematics, the inverted generational distance (IGD) [67] is defined as follows:
where P* refers to uniform distribution sampling points in PF, and S denotes the approximate solution set obtained by the algorithm. d(x,P*) indicates the minimum Euclidean distance from x to P*. During simulation, a uniform set is composed of around 500, 2000, 4000, and 10,000 points for 3-, 5-, 8-, and 10-objective instances, respectively. The small IGD value indicates a better-quality approximated set of solutions.
5. Experimental Results
In this section, we provide a detailed analysis of the experimental results. The analysis is conducted in the following order:
- (a)
- First, the performance of the proposed algorithm is analyzed with different grid settings. The important parameter in the grid is “div”, which controls the search space. Hence, we evaluate our algorithm with different values of “div”. Our approach proposes an adaptive grid setting.
- (b)
- Second, the performance of the proposed method with the adaptive grid settings is compared with state-of-the-art algorithms.
5.1. Analysis of Grid Setting in the Proposed Method
In this section, we analyze the performance of the proposed method with different grid settings. Table 2 presents the description of the grid settings employed in the experiments. The mean values of the hypervolume indicator obtained for the grid settings are presented in Appendix A Table A1 and Table A2. Table 2 shows that for ad-GrMODE1*, the “div” value linearly increases from the minimum value of ‘2’ to ‘Ns’. We analyzed the performance of the ad-GrMODE approach by varying ‘Ns’ from 3 to 20.

Table 2.
Description of grid settings for the proposed algorithm.
Table 3 presents the Friedman test ranking [68] results corresponding to each grid setting. The results presented in Table 3 show that the adaptation of the “div” parameter exhibits better performance than the fixed value of “div”. In the fixed “div” grid settings, the performance deteriorates as the value of “div” increases. A similar phenomenon can also be observed in the adaption of the “div” setting. In other words, in the adaptation, as the ‘Ns’ value increase, the performance significantly degrades. With the adaptation of “div” settings, the ‘Ns’ values with 3 and 5 perform better compared with the other approaches. Hence, we compared the performance of ad-GrMODE1* and ad-GrMODE2* with state-of-the-art algorithms.

Table 3.
Friedman test ranking results of different grid settings on DTLZ and WFG problems.
The main factors contributing to the better performance of the grid setting with the ‘Ns’ value ranging between 3 and 5 are listed as follows:
- (a)
- The number of grids into which the objective space can be partitioned is evaluated as divM, where M is the number of objectives. For instance, if “div = 20” and “M = 10” then the objective space is divided into 2010 grids. As arbitrarily large population size cannot be used for the evolutionary process, dividing the controlled population size into 2010 grids results in an inadequate number of solutions in each grid. In other words, each grid is associated with hardly one or two solutions, and the proposed grid-based mutation does not work with insufficient solutions within each grid because selection pressure is lost. Thus, the grid setting with minimum “div”, value performs better than and the performance degrades as the “div” value increases.
- (b)
- Second, fixed grid settings do not work for all types of problems. Instead, different grid settings are helpful in exploring the search space at every stage of evolution. The adaptive approach provides different grid settings at each evolution stage and helps achieve better convergence and diversity.
- (c)
- The main principle behind our grid-based mutation is that a few grids are used initially to achieve convergence. Gradually, the number of grids increases, which improves the diversity by providing a proper distribution of solutions.
Based on these observations, the approaches ad-GrMODE1* and ad-GrMODE2* with ‘Ns’ values 3 and 5, respectively, perform better than the rest of the grid settings. Because further increasing the number of grids is not advisable, ‘Ns’ with values ranging from 3 to 5 have a better performance. In the next section, we compare the performance of ad-GrMODE1* and ad-GrMODE2* with state-of-the-art algorithms.
5.2. Comparing the Proposed Method and State-of-the-Art Algorithms Using the DTLZ Problems Based on the HV Metric
Appendix ATable A3, compares the mean and standard deviation of the HV indicators for the DTLZ problems to evaluate each algorithm. The proposed algorithm was compared with the algorithms under consideration by means of symbols ((+/=/-) and (†/≡/↓)), and significance tests were carried out for each algorithm. The symbols ‘+’ and ‘†’ indicate that the proposed ad-GrMODE is superior to the related algorithms, the symbols ‘=’ and ‘≡’ indicate that the ad-GrMODE is similar to the related algorithms, and the symbols ‘-’ and ‘↓’ indicate that the ad-GrMODE performs poorly compared with the related algorithms.
As exhibited in Appendix A Table A3, ad-GrMODE1* achieved 16, 22, 23, 15, 20, 12, 25, and 26 best results out of 28 test instances for the DTLZ test problems compared with NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, respectively. In contrast, ad-GrMODE1* demonstrated an inferior performance compared with NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 9, 4, 2, 8, 5, 11, 1, and 1 out of 28 test instances, respectively. ad-GrMODE1* demonstrated a similar performance to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on three, two, three, five, three, five, two, and one out of 28 test instances, respectively. Appendix A Table A3 illustrates that our proposed ad-GrMODE1* is superior to SPEA-R, VaEA, MODE, MyODEMR, and GAMODE for DTLZ problems. Compared with NSGAIII and SRA, the ad-GrMODE1* algorithm also achieves better performance. It is worth noting that the number of tests in which ad-GrMODE1* outperforms EMyO-C is almost identical to the number of tests in which ad-GrMODE1* performs poorly compared with EMyO-C (12 versus 11). Therefore, according to the results presented in Appendix A Table A3, ad-GrMODE1* is highly competitive with EMyO-C.
Next, we analyzed the ad-GrMODE2* results based on the DTLZ problem as shown in Appendix A Table A3. The test results show that ad-GrMODE2* outperforms NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 16, 22, 21, 13, 20, 13, 25 and 26 out of 28 test instances, respectively. ad-GrMODE2* performs poorly compared with NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 10, 5, 4, 12, 6, 12, 2 and 1 out of 28 test instances, respectively. ad-GrMODE2* performed similarly to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on two, one, three, three, two, three, one and one out of 28 test instances, respectively. In Appendix A Table A3, ad-GrMODE2* demonstrates to be superior to SPEA-R, VaEA, MODE, MyODEMR, and GAMODE for the DTLZ problems. In addition, results indicate that the ad-GrMODE2* algorithm outperforms NSGAIII and can maintain competitive performance compared with EMyO-C and SRA.
5.3. Comparing the Proposed Method and State-of-the-Art Algorithms Using the WFG Problems Based on the HV Metric
In this section, we experimentally compare the performance of the ad-GrMODE1* and ad-GrMODE2* algorithms with state-of-art algorithms using the WFG problems. In Appendix A Table A4, the results of the HV indicator are expressed as mean values and standard deviations. In Appendix A Table A4, it can be observed that the performance of ad-GrMODE is better when compared with NSGAIII, SPEA-R and EMyO-C and it is superior to the MODE, MyODEMR, and GAMODE competitive when compared with VaEA and SRA. According to Appendix A Table A4, ad-GrMODE1* achieved 16, 19, 15, 16, 28, 20, 28, and 22 best results out of 36 test instances for the WFG problem compared with NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, respectively. ad-GrMODE1* performed similarly to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 14, 10, 9, 8, 8, 12, 5, and 11 out of 36 test instances, respectively. Hence, based on the comparison of the number of best and similar test results, Ad-GrMODE1* demonstrates the best performance.
Next, we assessed the ad-GrMODE2* performance on the WFG test problems as shown in Appendix A Table A4. According to the results, ad-GrMODE2* performs similarly to ad-GrMODE1* (the proportion of test instances are the same) when compared with SPEA-R, VaEA, SRA, MODE, and EMyO-C. As also shown in Appendix A Table A4, ad-GrMODE2* produces better results on 15 test cases, is competitive on 14 test cases, and performed poorly on 7 out of 36 WFG test problems compared with NSGAIII. The ad-GrMODE2* exhibits consistently impressive results on the WFG6, WFG7, and WFG8 test problems, but performs poorly on the WFG4 and WFG9. Compared to the MyODEMR, the ad-GrMODE2* algorithm achieved better results in 28 cases, similar results in four cases, and poor results in four cases. As compared to GAMODE, the ad-GrMODE2* generated better results in 22 cases, equivalent results in 10 cases, and poor outcomes in three cases. Additionally, the ad-GrMODE2* is significantly more effective on WFG1, WFG2, WFG5, WFG6, WFG7, WFG8, and WFG9 test problems and is less successful on the WFG4.
5.4. Comparing the Proposed Method and State-of-the-Art Algorithms Using the DTLZ Problems Based on the IGD Metric
Here, we evaluate the performance of the ad-GrMODE1* and ad-GrMODE2* algorithms with state-of-art algorithms for the DTLZ problems based on the IGD indicator. Appendix A Table A5 shows the mean and standard deviation of the IGD indicators. Based on Appendix A Table A5, ad-GrMODE1* performed best for 23, 23, 23, 23, 23, 20, 24, and 26 out of 28 tests compared to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE. ad-GrMODE1* showed similar results to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on one, two, one, one, zero, one, zero, and one out of 28 test instances, respectively. Despite this, ad-GrMODE1* performed weaker than NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on four, three, four, four, five, seven, four, and one out of 28 test instances, respectively. As shown in Appendix A Table A5, the proposed ad-GrMODE1* is superior to NSGA-III, SPEA-R, VaEA, SRA, MODE, MyODEMR, and GAMODE in terms of DTLZ problems.
Then, we examined the ad-GrMODE2* outcomes using DTLZ based on IGD, which is shown in Appendix A Table A5. A comparison of the test results shows that ad-GrMODE2* performs better than NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 22, 23, 23, 19, 23, 20, 24, and 27 out of 28 test instances, respectively. ad-GrMODE2* was comparable to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on one, zero, one, three, zero, one, zero, and zero out of 28 tests instances, respectively. ad-GrMODE2* is inferior to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on five, five, four, six, five, seven, four, and one out of 28 tests instances, respectively. According to Appendix A Table A5, the proposed ad-GrMODE2* is superior to NSGA-III, SPEA-R, VaEA, MODE, MyODEMR, and GAMODE on DTLZs. Furthermore, the outcomes show that the ad-GrMODE2* algorithm outperforms SRA and EMyO-C.
5.5. Comparing the Proposed Method and State-of-the-Art Algorithms Using the WFG Problems Based on the IGD Metric
The IGD indicator results for the WFG problems are compared in Appendix A Table A6 to evaluate each algorithm. From Appendix A Table A6, it is evident that the performance of ad-GrMODE1* is significantly better than NSGA-III, SPEA-R, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, and it is better than the VaEA. In Appendix A Table A6, ad-GrMODE1* obtained 23, 25, 21, 24, 31, 25, 33, and 24 best results out of 36 test cases for the WFG problem in comparison to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, respectively. ad-GrMODE1* showed similar performance to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on six, five, five, five, four, five, five, and one out of 36 tests cases, respectively. ad-GrMODE1* showed poor performance on NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 7, 6, 10, 7, 1, 6, 2, and 8 out of 36 tests cases, respectively.
Next, we evaluated the ad-GrMODE2* performance for WFG tests, summarized in Appendix A Table A6. In Appendix A Table A6, ad-GrMODE2* achieved 22, 24, 21, 23, 31, 24, 33, and 23 best outcomes out of 36 test cases on WFG, compared with NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, respectively. ad-GrMODE2* showed similar performance to NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on five, eight, four, five, five, four, one, and three out of 36 tests cases, respectively. ad-GrMODE2* displayed poor results on NSGA-III, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE on 9, 4, 11, 8, 0, 8, 2, and 10 out of 36 tests cases, respectively. As can be seen in Appendix A Table A6, the result of ad-GrMODE2* is superior to NSGA-III, SPEA-R, SRA, MODE, EMyO-C, MyODEMR, and GAMODE, and it is better than the VaEA.
5.6. Overall Performance Comparison of ad-GrMODE with State-of-the-Art Algorithms for the DTLZ and WFG Problems
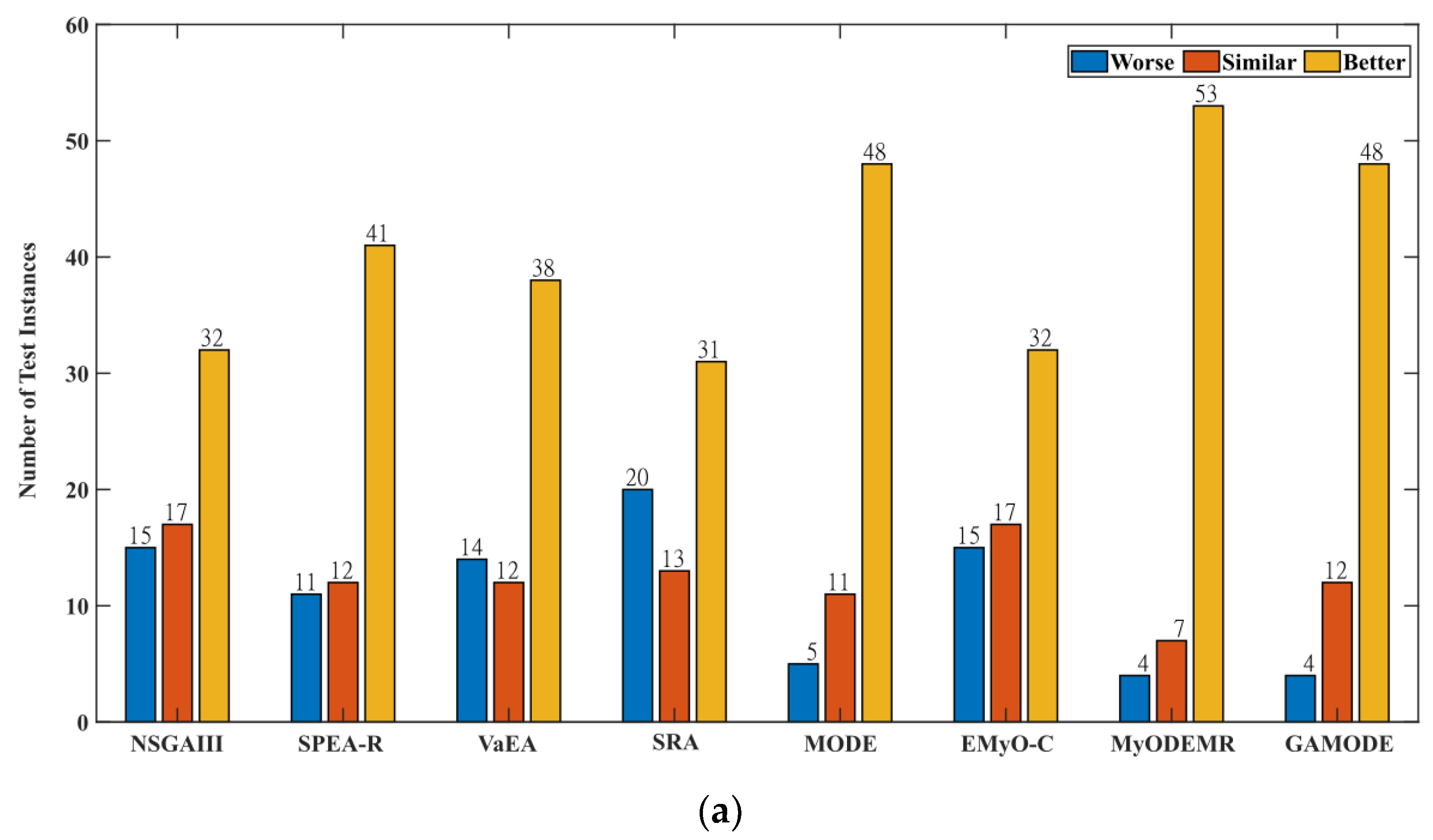
This section presents the overall comparison of the ad-GrMODE1* and ad-GrMODE2* algorithms against state-of-the-art algorithms for both the DTLZ and WFG tests based on HV and IGD indicators. Additionally, the Wilcoxon signed-rank tests at the 5% significance level for the HV and the parallel coordinates of the Pareto front solutions determined using the various algorithms are presented. Based on HV results shown in Table 4, it can be observed that out of 64 tests, the ad-GrMODE1* algorithm is more effective in 32 cases, is similar in 17 cases, and worse in 15 cases compared with the NSGAIII algorithm. Based on the comparisons between SPEA-R and ad-GrMODE1*, ad-GrMODE1* perform better in 41 instances, similarly in 12 cases, and poorly in 11 instances. Compared with the VaEA and SRA algorithms, the ad-GrMODE1* algorithm demonstrates superior performance in 38 and 31 instances, equivalent performance in 12 and 13 instances, and worse performance in 14 and 20 instances, respectively. ad-GrMODE1* performs better than MODE and EMyOC in 48 and 32 instances, similar in 11 and 17 instances, and worse in 5 and 15 instances respectively. A comparison of the ad-GrMODE1* algorithm with the MyODEMR algorithm highlights that it performs better in 53 instances, similarly in seven instances, and worse in four instances. Comparing ad-GrMODE1* with the GAMODE indicates that it has a better performance in 48 instances, similar performance in 12 instances, and poor performance in four.

Table 4.
Overall performance comparison of the proposed algorithm with state-of-the-art algorithms based on HV and IGD for DTLZ and WFG test problems.
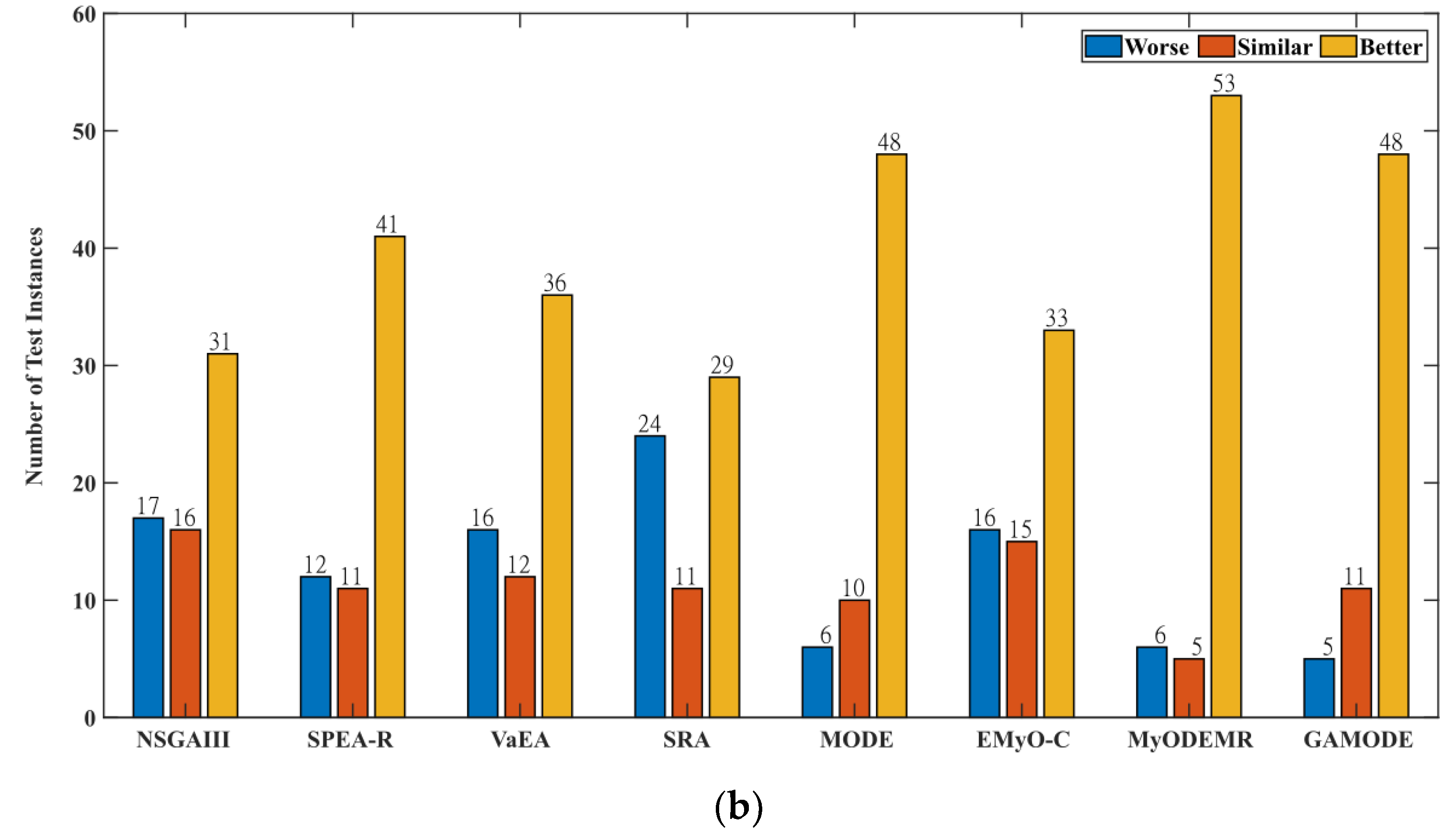
Likewise for ad-GrMODE2*, the HV results in Table 4 show that out of the 64 test instances, ad-GrMODE2* performed better than NSGAIII in 31 tests, similarly in 16 tests, and worse in 17 tests. Comparing the ad-GrMODE2* approach with the SPEA-R and VaEA algorithms, the results show that ad-GrMODE2* performs better in 41 and 36 tests, similarly in 11 and 12 tests, and worse in 12 and 16 tests, respectively. In comparison with the SRA algorithm, the proposed algorithm performed better in 29 cases, similarly in 11 cases, and worse in 24 cases. Compared to MODE and EMyOC, ad-GrMODE2* outperforms on 48 and 33 tests, is similar on 10 and 15 tests, and is worse on 6 and 16 tests, respectively. Comparing the ad-GrMODE2* with the MyODEMR and GAMODE algorithms shows that ad-GrMODE2* performs better in 53 and 48 instances, similarly in 5 and 11 instances, and worse in six and five instances. The signs ‘+’, ‘=’, and ‘-’ depicts the instances, ad-GrMODE1* performs better, similar and worse with respect to state-of-the-art algorithms. The signs ‘†’, ‘≡’, and ‘↓’ depicts the instances, ad-GrMODE2* performs better, similar and worse with respect to state-of-the-art algorithms.
In accordance with the IGD results shown in Table 4, from the analysis of 64 tests, the ad-GrMODE1* algorithm showed better results in 46, 48, 44, 47, 54, 45, 57, and 50 cases, showed similar results in 7, 7, 6, 6, 4, 6, 1, and 5 cases, and showed worse results in 11, 9, 14, 11, 6, 13, 6, and 9 cases compared with the NSGAIII, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE algorithms, respectively. The ad-GrMODE2* algorithm produced better outcomes in 44, 47, 44, 42, 54, 44, 57, and 50 cases, exhibited similar outcomes in 6, 8, 5, 8, 5, 5, 1, and three cases, and produced poorer outcomes in 14, 9, 15, 14, 5, 15, 6, and 11 cases compared with the NSGAIII, SPEA-R, VaEA, SRA, MODE, EMyO-C, MyODEMR, and GAMODE algorithms, respectively.
To further compare the proposed algorithm with state-of-the-art algorithms and evaluate its effectiveness, we applied the Wilcoxon signed-rank tests at a 5% significance level with respect to the HV metrics on the DTLZ and WFG problems as shown in Figure 3. The symbols in Figure 3 indicate the number of tests in which the proposed ad-GrMODE1* and ad-GrMODE2* perform worse, similar, and better than the state-of-the-art algorithms. Figure 3a illustrates that ad-GrMODE1* outperforms the state-of-the-art algorithms for the DTLZ and WFG problems. Additionally, it can be observed that the difference is significant with respect to the number of instances where ad-GrMODE1* performs more efficiently and worse than the state-of-the-art algorithms. Figure 3b shows that the ad-GrMODE2* algorithm performs better than the NSGAIII, SPEA-R, VaEA, MODE, EMyO-C, MyODEMR, and GAMODE algorithms for the overall test instances (DTLZ and WFG). The SRA algorithm; however, shows a competitive performance when compared with the ad-GrMODE2* method. Furthermore, similar to ad-GrMODE1*, there is a large difference in the number of instances where ad-GrMODE2* is better and worse than state-of-the-art algorithms.
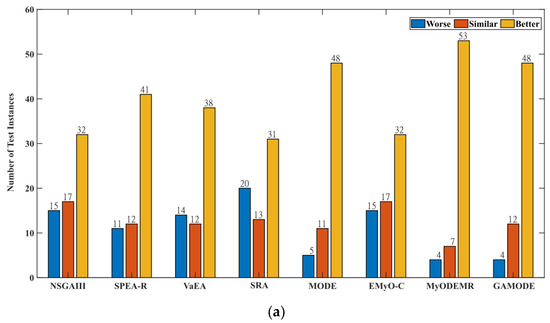
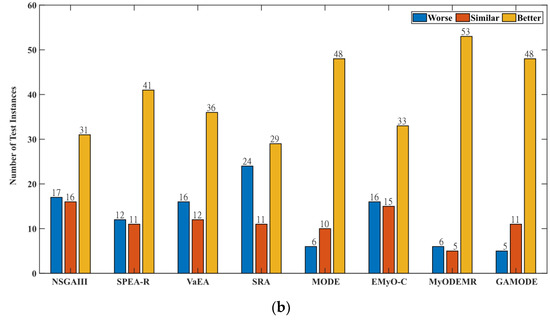
Figure 3.
Wilcoxon signed-rank tests at a 5% significance level with respect to the HV for the DTLZ and WFG problems using ad-GrMODE and state-of-the-art algorithms: (a) ad-GrMODE1* compared with state-of-the-art algorithms; (b) ad-GrMODE2* compared with state-of-the-art algorithms.
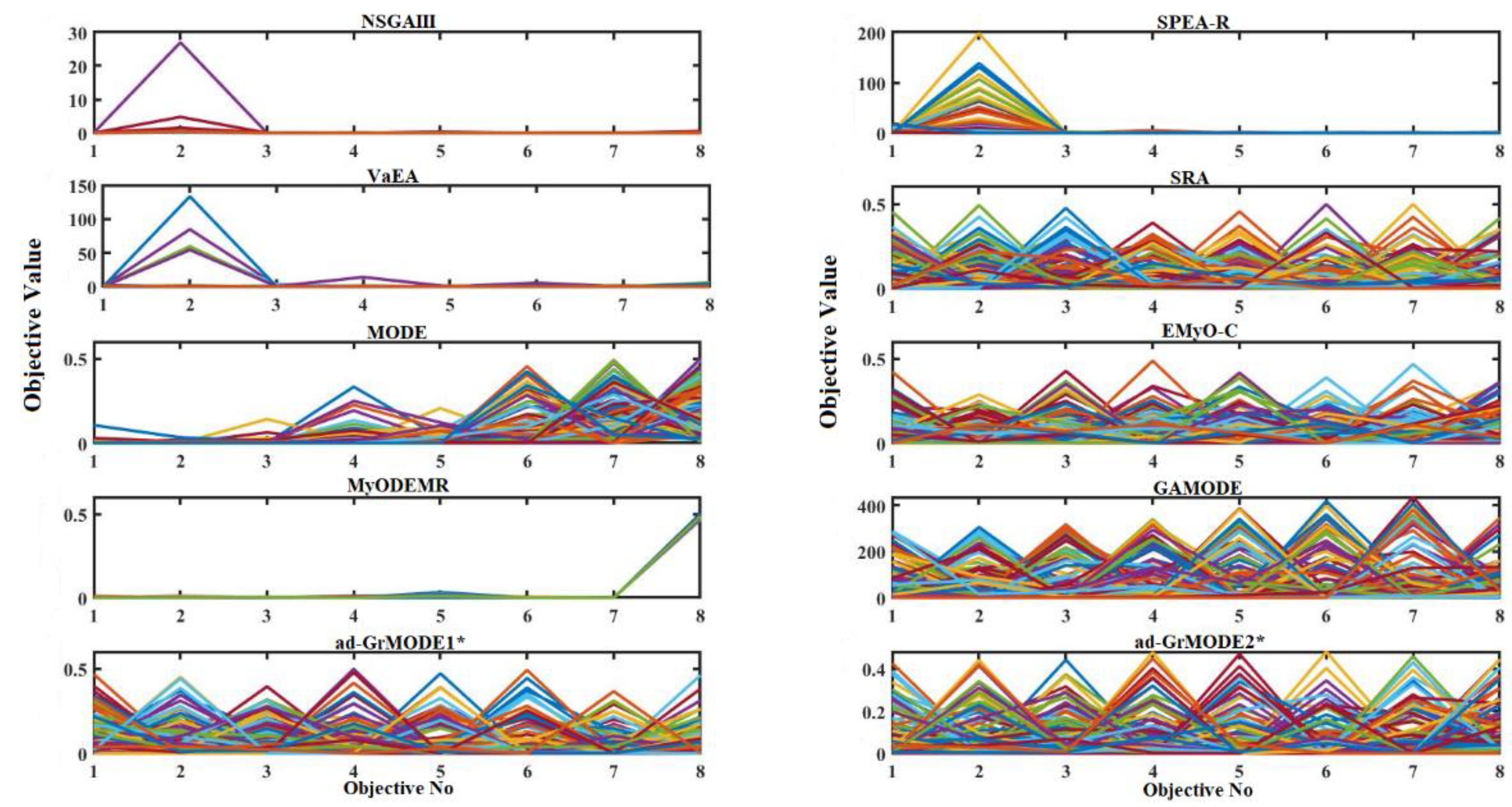
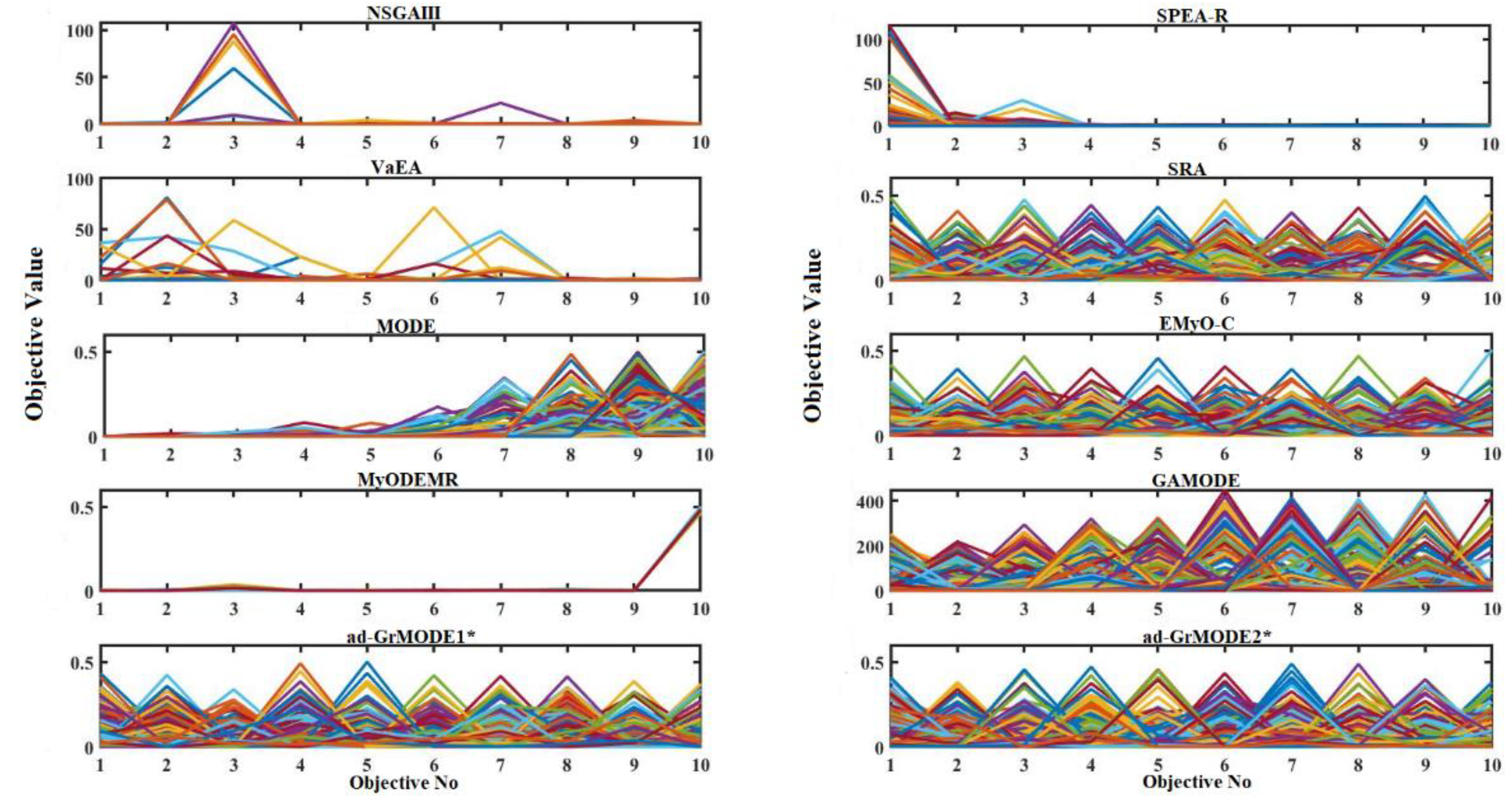
A parallel set of coordinates that represent the Pareto front solutions based on the different algorithms was also determined. Figure 4 and Figure 5 illustrate the parallel coordinates in the objective space for the 8- and 10-objective DTLZ1 problems. As can be observed from Figure 4, for the eight-objective DTLZ1 problem, all the algorithms except the NSGAIII, SPEA-R, VaEA, MODE, and MyODEMR algorithms show better convergence capabilities as well as good distributions. Figure 5, showing plots of the 10-objective DTLZ1 problem, demonstrates that the proposed method achieves better convergence and diversity when compared with the other algorithms. Instead, NSGAIII, SPEA-R, VaEA, MODE, and MyODEMR result in poor convergence and diversity.
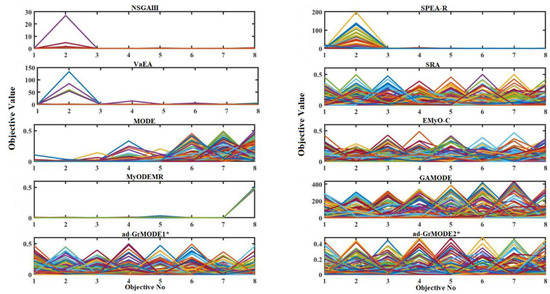
Figure 4.
A parallel set of coordinates corresponding to the different Pareto front algorithms on the eight-objective DTLZ1 problem.
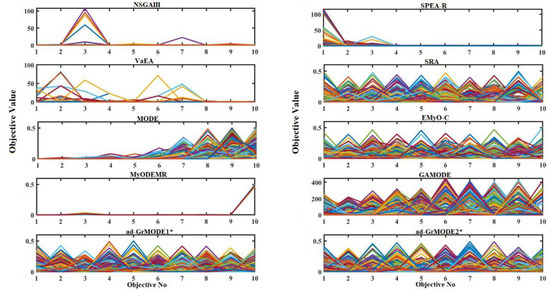
Figure 5.
A parallel set of coordinates corresponding to the different Pareto front algorithms on the 10-objective DTLZ1 problem.
5.7. Runtime Evaluation of ad-GrMODE Compared with State-of-the-Art Algorithms
The runtime performance evaluation of the ad-GrMODE algorithm against state-of-art algorithms for 3-, 5-, 8-, and 10-objective problems is presented in this section. To compare time, all simulations were performed on a PC running a 2.90 GHz Intel Core i5-10400 CPU and Windows 10, 64-bit with MATLAB 2021b installed. Considering the results shown in Table 5, it is apparent that ad-GrMODE takes less computational time compared with the other algorithms except NSGAIII, SPEA-R, and VaEA for all of the objectives in the DTLZ1 problem. Despite the longer computation time of the proposed algorithm when compared with the NSGAIII, SPEA-R, and VaEA algorithms, it outperforms these algorithms in terms of HV results. MODE requires less computation time than the proposed method for the 3- and 10-objective problems. For the five- and eight-objective problems, ad-GrMODE has a faster execution time compared with MODE.

Table 5.
Runtime evaluation of the proposed algorithm compared with state-of-the-art algorithms for the DTLZ1 problem.
5.8. Overall Performance Comparison of ad-GrMODE with State-of-the-Art Algorithms on Real-World Problem
Here, we evaluate the performance of the proposed ad-GrMODE algorithm with state-of-the-art algorithms on real-world problems. In this study, we examined three real-world problems: the Reinforced concrete beam design (RCBD) problem [69], the Pressure vessel design (PVD) problem [69], and the Gear train design (GTD) problem [69]. The Reinforced concrete beam design problem described in [69] consists of two-objective functions with three decision variables. The pressure vessel design problem [69] is a two-objective problem involving four variables. The gear train design problem [69] problem is composed of three objective functions and four decision variables. The real-world problems considered in this paper have PFs associated with mixed, concave, and disconnected characteristics in nature. The population sizes are maintained as 100, 100, and 120 for RCBD [69], PVD [69], and GTD [69] problems, respectively. The number of iterations is set as 250 for all the problems. We have presented the HV results for real-world problems in order to analyze the performance comparison of the proposed algorithm with the state-of-the-art algorithms. In Table 6, the mean and standard deviation of the HV indicator values are shown. To measure the HV indicator value, a similar process that is used to measure the HV value for DTLZ and WFG problems was applied. The results shown in Table 6 reveal that the proposed algorithm outperforms the state-of-the-art algorithm on all three real-world problems.

Table 6.
Mean and standard deviation values of HV results of proposed algorithm with state of art algorithms on real-world problems.
6. Conclusions and Future Work
DE has become a popular approach used to solve single-objective problems and has been extended to solve multi-objective problems due to its efficient and straightforward structure. In DE, mutation and crossover operators play a prominent role in influencing the evolution of the population. This article presents an ad-GrMODE algorithm for multi-objective optimization. With ad-GrMODE, a novel and efficient mutation strategy based on a grid environment is proposed. The mutation strategy “DE/current-to-best/1”, popularly adopted for single-objective optimization, is extended for multi-objective optimization using the adaptive grid environment. Furthermore, the performance indicators and ISDE are employed to find the best solution to perform the “DE/current-to-best/1” mutation strategy. A two-level environmental selection is performed to preserve ‘N’ elite individuals for the next generation. In the experimental design, we evaluated the performance of the proposed approach with different grid settings. Then, the methods with better grid settings compete against existing algorithms. The experimental results show that the proposed approach exhibits better performance than the existing algorithms. As discussed above, the proposed ad-GrMODE algorithm has proven to exhibit good performance when solving MOPs.
Consequently, future research could explore how this algorithm can be applied to constrained multi-objective problems.
Author Contributions
Conceptualization, S.G. and S.H.; methodology, S.G. and S.H.; software, S.G.; validation, S.G.; formal analysis, S.G. and Y.J.; investigation, S.G. and Y.J.; resources, S.G.; data curation, S.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G.; visualization, S.G. and Y.J.; supervision, S.H.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea No. 20202010600010).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable, the study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DE | Differential Evolution |
| ad-GrMODE | adaptive Grid-based multi-objective differential evolution |
| MOP | Multi-objective Optimization Problem |
| PS | Pareto optimal Set |
| PF | Pareto Front |
| PSO | Particle Swarm Optimization |
| EA | Evolutionary Algorithm |
| SOP | Single-objective Optimization Problem |
| MODE | Multi-Objective Differential Evolution |
| GrEA | Grid-based evolutionary algorithm |
| PESA-II | Pareto envelope-based selection algorithm II |
| Grid-IGD | Grid-based Inverted Generational Distance |
| GDE3 | Generalized Differential Evolution |
| PDE | Pareto Differential Evolution |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| PDEA | Pareto Differential Evolution Algorithm |
| DEMO | Differential Evolution for Multi-objective Optimization |
| MOED | Multi-objective Energy Disaggregation |
| MOSaDE | Multi-objective Optimization based on Self-adaptive Differential Evolution |
| GrBLS | Grid-based Bidirectional Local Search |
| MOEA | Multi objective Evolutionary Algorithm |
| CCDG-K | Multi objective evolutionary algorithm base on Constrained Decomposition with Grids |
| GSMPSO-MM | Grid Search-based Multi-population Particle Swarm Optimization |
| MOWOA | opposition-based Multi-Objective Whale Optimization Algorithm with global grid ranking |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
| SPEA-R | Strength Pareto Evolutionary Algorithm based on Reference direction |
| VaEA | Vector angle-based Evolutionary Algorithm |
| SRA | Stochastic Ranking Algorithm |
| EMyO-C | Clustering-based selection for Evolutionary Many-objective Optimization |
| MyODEMR | Many-Objective Differential Evolution with Mutation Restriction |
| GAMODE | Grid-based Adaptive Multi-Objective Differential Evolution |
| HV | Hypervolume |
| IGD | Inverted Generational Distance |
| RCBD | Reinforced Concrete Beam Design |
| PVD | Pressure Vessel Design |
| GTD | Gear Train Design |
Appendix A

Table A1.
The mean values of the HV indicator for different grid settings of the proposed algorithm on DTLZ.
Table A1.
The mean values of the HV indicator for different grid settings of the proposed algorithm on DTLZ.
| # | M | ad-GrMODE1 | ad-GrMODE2 | ad-GrMODE3 | ad-GrMODE4 | ad-GrMODE2 | ad-GrMODE1* | ad-GrMODE2* | ad-GrMODE3* | ad-GrMODE4* | ad-GrMODE5* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 0.8397 | 0.8365 | 0.8128 | 0.7322 | 0.6750 | 0.8392 | 0.8392 | 0.8385 | 0.8374 | 0.8364 |
| 5 | 0.9677 | 0.9515 | 0.1453 | 0.0043 | 0.0023 | 0.9692 | 0.9674 | 0.9671 | 0.9651 | 0.9641 | |
| 8 | 0.9879 | 0.6445 | 0.0302 | 0.0000 | 0.0000 | 0.9927 | 0.9930 | 0.9913 | 0.9894 | 0.9904 | |
| 10 | 0.9974 | 0.9604 | 0.1336 | 0.0063 | 0.0000 | 0.9989 | 0.9987 | 0.9987 | 0.9981 | 0.9785 | |
| DTLZ2 | 3 | 0.5653 | 0.5639 | 0.5631 | 0.5619 | 0.5612 | 0.5659 | 0.5651 | 0.5653 | 0.5644 | 0.5648 |
| 5 | 0.7899 | 0.7688 | 0.7503 | 0.7454 | 0.7461 | 0.7976 | 0.7964 | 0.7941 | 0.7920 | 0.7905 | |
| 8 | 0.8469 | 0.7730 | 0.7492 | 0.7473 | 0.7418 | 0.8889 | 0.8762 | 0.8645 | 0.8563 | 0.8560 | |
| 10 | 0.8980 | 0.8182 | 0.7929 | 0.7833 | 0.7788 | 0.9273 | 0.9215 | 0.9110 | 0.9044 | 0.9007 | |
| DTLZ3 | 3 | 0.5115 | 0.2798 | 0.0609 | 0.0000 | 0.0014 | 0.5546 | 0.5248 | 0.4865 | 0.3856 | 0.3112 |
| 5 | 0.6572 | 0.0417 | 0.0000 | 0.0000 | 0.0000 | 0.7606 | 0.6724 | 0.4271 | 0.2507 | 0.1664 | |
| 8 | 0.5135 | 0.0400 | 0.0000 | 0.0000 | 0.0000 | 0.7730 | 0.7109 | 0.6526 | 0.3768 | 0.2751 | |
| 10 | 0.8629 | 0.2162 | 0.0000 | 0.0000 | 0.0000 | 0.9334 | 0.8773 | 0.8474 | 0.7967 | 0.7024 | |
| DTLZ4 | 3 | 0.5308 | 0.5184 | 0.5224 | 0.5052 | 0.5122 | 0.5442 | 0.5364 | 0.5581 | 0.5454 | 0.5467 |
| 5 | 0.7656 | 0.7438 | 0.7244 | 0.7223 | 0.7251 | 0.7857 | 0.7760 | 0.7815 | 0.7724 | 0.7673 | |
| 8 | 0.8998 | 0.8875 | 0.8832 | 0.8788 | 0.8708 | 0.9144 | 0.9109 | 0.9049 | 0.9056 | 0.9019 | |
| 10 | 0.9606 | 0.9559 | 0.9511 | 0.9442 | 0.9454 | 0.9609 | 0.9668 | 0.9655 | 0.9643 | 0.9654 | |
| DTLZ5 | 3 | 0.1996 | 0.1998 | 0.1996 | 0.1997 | 0.1995 | 0.1998 | 0.1998 | 0.1998 | 0.1997 | 0.1997 |
| 5 | 0.1244 | 0.1247 | 0.1239 | 0.1227 | 0.1234 | 0.1246 | 0.1246 | 0.1245 | 0.1246 | 0.1241 | |
| 8 | 0.1012 | 0.1007 | 0.0984 | 0.0972 | 0.0966 | 0.1003 | 0.1003 | 0.0994 | 0.1004 | 0.1003 | |
| 10 | 0.0955 | 0.0963 | 0.0939 | 0.0920 | 0.0904 | 0.0952 | 0.0952 | 0.0955 | 0.0948 | 0.0944 | |
| DTLZ6 | 3 | 0.1996 | 0.1437 | 0.0000 | 0.0000 | 0.0000 | 0.1999 | 0.1999 | 0.2001 | 0.1907 | 0.1930 |
| 5 | 0.0375 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1165 | 0.1152 | 0.0688 | 0.0381 | 0.0226 | |
| 8 | 0.0010 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0507 | 0.0361 | 0.0222 | 0.0097 | 0.0009 | |
| 10 | 0.0090 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0759 | 0.0543 | 0.0537 | 0.0171 | 0.0185 | |
| DTLZ7 | 3 | 0.3894 | 0.3896 | 0.3908 | 0.3983 | 0.3810 | 0.3844 | 0.3882 | 0.3972 | 0.3717 | 0.4000 |
| 5 | 0.3225 | 0.2932 | 0.2128 | 0.2077 | 0.2074 | 0.3239 | 0.3251 | 0.3283 | 0.3205 | 0.3208 | |
| 8 | 0.1358 | 0.0096 | 0.0102 | 0.0099 | 0.0102 | 0.2227 | 0.2110 | 0.2208 | 0.1950 | 0.1748 | |
| 10 | 0.0301 | 0.0009 | 0.0007 | 0.0006 | 0.0009 | 0.1862 | 0.1736 | 0.1233 | 0.0843 | 0.0901 |

Table A2.
The mean values of the HV indicator for different grid settings of the proposed algorithm on WFG.
Table A2.
The mean values of the HV indicator for different grid settings of the proposed algorithm on WFG.
| # | M | ad-GrMODE1 | ad-GrMODE2 | ad-GrMODE3 | ad-GrMODE4 | ad-GrMODE2 | ad-GrMODE1* | ad-GrMODE2* | ad-GrMODE3* | ad-GrMODE4* | ad-GrMODE5* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WFG1 | 3 | 0.2852 | 0.2811 | 0.2805 | 0.2793 | 0.2793 | 0.2855 | 0.2827 | 0.2817 | 0.2811 | 0.2810 |
| 5 | 0.2800 | 0.2794 | 0.2789 | 0.2752 | 0.2494 | 0.2801 | 0.2797 | 0.2798 | 0.2795 | 0.2795 | |
| 8 | 0.2294 | 0.2295 | 0.2295 | 0.2268 | 0.2060 | 0.2294 | 0.2294 | 0.2293 | 0.2294 | 0.2294 | |
| 10 | 0.2071 | 0.2070 | 0.2073 | 0.2073 | 0.2054 | 0.2071 | 0.2071 | 0.2072 | 0.2072 | 0.2073 | |
| WFG2 | 3 | 0.2352 | 0.2351 | 0.2347 | 0.2345 | 0.2342 | 0.2352 | 0.2352 | 0.2351 | 0.2352 | 0.2351 |
| 5 | 0.2115 | 0.2113 | 0.2106 | 0.2101 | 0.2100 | 0.2115 | 0.2115 | 0.2114 | 0.2116 | 0.2116 | |
| 8 | 0.1854 | 0.1851 | 0.1840 | 0.1838 | 0.1836 | 0.1855 | 0.1855 | 0.1854 | 0.1853 | 0.1854 | |
| 10 | 0.1729 | 0.1729 | 0.1723 | 0.1720 | 0.1716 | 0.1730 | 0.1730 | 0.1729 | 0.1730 | 0.1730 | |
| WFG3 | 3 | 0.0923 | 0.0919 | 0.0908 | 0.0905 | 0.0902 | 0.0925 | 0.0920 | 0.0922 | 0.0923 | 0.0920 |
| 5 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 8 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| WFG4 | 3 | 0.1951 | 0.1926 | 0.1834 | 0.1756 | 0.1731 | 0.1964 | 0.1964 | 0.1948 | 0.1938 | 0.1932 |
| 5 | 0.2159 | 0.1969 | 0.1928 | 0.1918 | 0.1932 | 0.2257 | 0.2237 | 0.2203 | 0.2174 | 0.2133 | |
| 8 | 0.1639 | 0.1620 | 0.1605 | 0.1636 | 0.1617 | 0.1685 | 0.1692 | 0.1674 | 0.1704 | 0.1695 | |
| 10 | 0.1599 | 0.1616 | 0.1596 | 0.1615 | 0.1618 | 0.1598 | 0.1624 | 0.1640 | 0.1657 | 0.1638 | |
| WFG5 | 3 | 0.4585 | 0.4562 | 0.4495 | 0.4432 | 0.4414 | 0.4584 | 0.4584 | 0.4584 | 0.4583 | 0.4573 |
| 5 | 0.4622 | 0.4478 | 0.4385 | 0.4366 | 0.4361 | 0.4671 | 0.4652 | 0.4640 | 0.4622 | 0.4611 | |
| 8 | 0.4587 | 0.4431 | 0.4368 | 0.4391 | 0.4380 | 0.4656 | 0.4640 | 0.4611 | 0.4582 | 0.4588 | |
| 10 | 0.4727 | 0.4586 | 0.4533 | 0.4534 | 0.4518 | 0.4770 | 0.4763 | 0.4735 | 0.4724 | 0.4702 | |
| WFG6 | 3 | 0.1914 | 0.1910 | 0.1906 | 0.1905 | 0.1899 | 0.1915 | 0.1915 | 0.1916 | 0.1914 | 0.1913 |
| 5 | 0.1919 | 0.1915 | 0.1903 | 0.1901 | 0.1898 | 0.1920 | 0.1920 | 0.1920 | 0.1919 | 0.1919 | |
| 8 | 0.1893 | 0.1889 | 0.1874 | 0.1869 | 0.1871 | 0.1893 | 0.1893 | 0.1892 | 0.1890 | 0.1890 | |
| 10 | 0.1880 | 0.1878 | 0.1868 | 0.1862 | 0.1863 | 0.1881 | 0.1881 | 0.1881 | 0.1881 | 0.1881 | |
| WFG7 | 3 | 0.0924 | 0.0886 | 0.0823 | 0.0801 | 0.0764 | 0.0931 | 0.0925 | 0.0921 | 0.0920 | 0.0909 |
| 5 | 0.1380 | 0.1260 | 0.0955 | 0.0768 | 0.0725 | 0.1448 | 0.1448 | 0.1411 | 0.1386 | 0.1373 | |
| 8 | 0.1456 | 0.1286 | 0.0639 | 0.0525 | 0.0505 | 0.1540 | 0.1512 | 0.1494 | 0.1467 | 0.1442 | |
| 10 | 0.1515 | 0.1360 | 0.0602 | 0.0489 | 0.0490 | 0.1544 | 0.1544 | 0.1512 | 0.1500 | 0.1488 | |
| WFG8 | 3 | 0.2312 | 0.2313 | 0.2303 | 0.2299 | 0.2292 | 0.2314 | 0.2314 | 0.2316 | 0.2315 | 0.2317 |
| 5 | 0.2379 | 0.2354 | 0.2299 | 0.2278 | 0.2271 | 0.2386 | 0.2382 | 0.2380 | 0.2371 | 0.2374 | |
| 8 | 0.2397 | 0.2355 | 0.2246 | 0.2225 | 0.2228 | 0.2408 | 0.2403 | 0.2397 | 0.2389 | 0.2387 | |
| 10 | 0.2420 | 0.2394 | 0.2268 | 0.2228 | 0.2216 | 0.2426 | 0.2424 | 0.2419 | 0.2412 | 0.2409 | |
| WFG9 | 3 | 0.3753 | 0.3716 | 0.3614 | 0.3565 | 0.3536 | 0.3763 | 0.3757 | 0.3761 | 0.3744 | 0.3759 |
| 5 | 0.4675 | 0.4310 | 0.4143 | 0.4024 | 0.4059 | 0.4995 | 0.4932 | 0.4770 | 0.4733 | 0.4733 | |
| 8 | 0.4339 | 0.3800 | 0.3712 | 0.3704 | 0.3739 | 0.4675 | 0.4597 | 0.4485 | 0.4423 | 0.4322 | |
| 10 | 0.4521 | 0.4103 | 0.3979 | 0.3939 | 0.3989 | 0.4957 | 0.4848 | 0.4697 | 0.4659 | 0.4626 |

Table A3.
Mean and standard deviation values of HV results of proposed method with state of art algorithms on DTLZ problems.
Table A3.
Mean and standard deviation values of HV results of proposed method with state of art algorithms on DTLZ problems.
| # | M | NSGAIII | SPEA-R | VaEA | SRA | MODE | EMyO-C | MyODEMR | GAMODE | adGrMOEA1* | adGrMOEA2* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 8.435 × 10−1 (7.81 × 10−4)-(↓) | 8.392 × 10−1 (1.04 × 10−2)=(≡) | 8.144 × 10−1 (4.84 × 10−2)+(†) | 8.332 × 10−1 (2.73 × 10−3)+(†) | 8.136 × 10−1 (4.66 × 10−3)+(†) | 8.390 × 10−1 (1.41 × 10−3)+(†) | 7.012 × 10−1 (1.89 × 10−1)+(†) | 0.7128 × 10−1 (2.03 × 10−1)+(†) | 8.392 × 10−1 (1.04 × 10−3) | 8.392 × 10−1 (1.14 × 10−3) |
| 5 | 9.743 × 10−1 (8.87 × 10−4)-(↓) | 9.282 × 10−1 (6.09 × 10−2)+(†) | 8.785 × 10−1 (4.52 × 10−2)+(†) | 9.692 × 10−1 (1.83 × 10−3)=(↓) | 9.0144. × 10−1 (1.18 × 10−2)+(†) | 9.667 × 10−1 (1.92 × 10−3)+(†) | 8.241 × 10−1 (6.74 × 10−2)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.692 × 10−1 (1.21 × 10−3) | 9.674 × 10−1 (1.57 × 10−3) | |
| 8 | 9.799 × 10−1 (6.89 × 10−2)+(†) | 7.815 × 10−1 (3.00 × 10−1)+(†) | 8.119 × 10−1 (2.28 × 10−1)+(†) | 9.949 × 10−1 (9.25 × 10−4)-(↓) | 9.161 × 10−1 (1.24 × 10−2)+(†) | 9.927 × 10−1 (7.03 × 10−4)=(†) | 4.673 × 10−1 (1.80 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.927 × 10−1 (1.67 × 10−3) | 9.930 × 10−1 (1.39 × 10−3) | |
| 10 | 9.151 × 10−1 (1.63 × 10−1)+(†) | 7.083 × 10−1 (2.67 × 10−1)+(†) | 8.870 × 10−1 (1.78 × 10−1)+(†) | 9.989 × 10−1 (1.21 × 10−4)=(≡) | 9.313 × 10−1 (8.05 × 10−3)+(†) | 9.989 × 10−1 (2.04 × 10−4)=(≡) | 5.374 × 10−1 (1.85 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.989 × 10−1 (2.43 × 10−4) | 9.989 × 10−1 (3.79 × 10−4) | |
| DTLZ2 | 3 | 5.621 × 10−1 (5.01 × 10−4)+(†) | 5.593 × 10−1 (1.66 × 10−3)+(†) | 5.651 × 10−1 (1.11 × 10−3)+(≡) | 5.578 × 10−1 (2.22 × 10−3)+(†) | 5.386 × 10−1 (6.89 × 10−3)+(†) | 5.582 × 10−1 (1.35 × 10−3)+(†) | 5.435 × 10−1 (4.04 × 10−3)+(†) | 5.2890 × 10−1 (4.80 × 10−3)+(†) | 5.659 × 10−1 (1.21 × 10−3) | 5.651 × 10−1 (1.08 × 10−3) |
| 5 | 7.921 × 10−1 (6.97 × 10−4)+(†) | 7.878 × 10−1 (2.39 × 10−3)+(†) | 7.717 × 10−1 (3.04 × 10−3)+(†) | 7.807 × 10−1 (3.33 × 10−3)+(†) | 6.582 × 10−1 (1.96 × 10−2)+(†) | 7.831 × 10−1 (2.91 × 10−3)+(†) | 7.508 × 10−1 (8.13 × 10−3)+(†) | 0.2011 × 10−1 (2.25 × 10−2)+(†) | 7.976 × 10−1 (1.65 × 10−3) | 7.964 × 10−1 (2.12 × 10−3) | |
| 8 | 9.065 × 10−1 (3.91 × 10−2)-(↓) | 9.059 × 10−1 (3.16 × 10−3)-(↓) | 8.889 × 10−1 (5.62 × 10−3)=(↓) | 8.960 × 10−1 (4.84 × 10−3)-(↓) | 6.764 × 10−1 (2.05 × 10−2)+(†) | 9.162 × 10−1 (2.49 × 10−3)-(↓) | 8.889 × 10−1 (8.71 × 10−3)=(↓) | 0.000 × 100 (0.00 × 100)+(†) | 8.889 × 10−1 (1.05 × 10−2) | 8.762 × 10−1 (1.52 × 10−2) | |
| 10 | 9.612 × 10−1 (2.06 × 10−2)-(↓) | 9.500 × 10−1 (3.37 × 10−3)-(↓) | 9.106 × 10−1 (1.49 × 10−2)+(†) | 9.493 × 10−1 (1.67 × 10−3)-(↓) | 6.979 × 10−1 (1.53 × 10−2)+(†) | 9.646 × 10−1 (1.09 × 10−3)-(↓) | 9.502 × 10−1 (4.24 × 10−3)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 9.273 × 10−1 (8.23 × 10−3) | 9.215 × 10−1 (1.14 × 10−2) | |
| DTLZ3 | 3 | 5.546 × 10−1 (5.19 × 10−3)=(↓) | 4.060 × 10−1 (7.83 × 10−2)+(†) | 5.471 × 10−1 (9.45 × 10−3)+(↓) | 5.437 × 10−1 (9.50 × 10−3)+(↓) | 5.036 × 10−1 (1.08 × 10−2)+(†) | 5.148 × 10−1 (1.01 × 10−1)+(†) | 4.663 × 10−1 (1.11 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 5.546 × 10−1 (2.61 × 10−2) | 5.248 × 10−1 (8.89 × 10−3) |
| 5 | 7.766 × 10−1 (3.23 × 10−2)-(↓) | 1.274 × 10−1 (1.61 × 10−1)+(†) | 4.929 × 10−1 (2.10 × 10−1)+(†) | 7.606 × 10−1 (1.10 × 10−2)=(↓) | 1.221 × 10−3 (6.57 × 10−3)+(†) | 7.756 × 10−1 (7.05 × 10−3)-(↓) | 3.779 × 10−1 (1.95 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 7.606 × 10−1 (6.16 × 10−2) | 6.724 × 10−1 (2.07 × 10−1) | |
| 8 | 6.727 × 10−1 (2.16 × 10−1)+(†) | 0.000 × 100 (0.00 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 8.890 × 10−1 (9.47 × 10−3)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 9.015 × 10−1 (8.05 × 10−3)-(↓) | 1.670 × 10−1 (9.99 × 10−2)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 7.730 × 10−1 (2.07 × 10−1) | 7.109 × 10−1 (2.26 × 10−1) | |
| 10 | 8.311 × 10−1 (1.48 × 10−1)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.484 × 10−1 (2.84 × 10−3)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 9.566 × 10−1 (6.92 × 10−3)-(↓) | 1.392 × 10−1 (6.86 × 10−2)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.334 × 10−1 (7.34 × 10−3) | 8.773 × 10−1 (1.17 × 10−1) | |
| DTLZ4 | 3 | 3.615 × 10−1 (1.53 × 10−1)+(†) | 5.583 × 10−1 (1.55 × 10−3)-(↓) | 5.570 × 10−1 (1.57 × 10−3)-(↓) | 5.298 × 10−1 (7.38 × 10−2)+(†) | 2.688 × 10−1 (6.04 × 10−2)+(†) | 5.571 × 10−1 (1.65 × 10−3)-(↓) | 5.364 × 10−1 (5.65 × 10−3)+(≡) | 4.8446 × 10−1 (6.01 × 10−2)+(†) | 5.442 × 10−1 (6.69 × 10−2) | 5.364 × 10−1 (7.57 × 10−2) |
| 5 | 7.059 × 10−1 (8.25 × 10−2)+(†) | 7.857 × 10−1 (2.54 × 10−3)=(↓) | 7.700 × 10−1 (3.25 × 10−3)+(†) | 7.857 × 10−1 (1.55 × 10−2)=(↓) | 3.766 × 10−1 (5.43 × 10−2)+(†) | 7.857 × 10−1 (2.81 × 10−3)=(↓) | 7.603 × 10−1 (3.85 × 10−3)+(†) | 2.9786 × 10−1 (5.66 × 10−2)+(†) | 7.857 × 10−1 (3.27 × 10−2) | 7.760 × 10−1 (4.59 × 10−2) | |
| 8 | 8.837 × 10−1 (5.07 × 10−2)+(†) | 9.006 × 10−1 (5.49 × 10−3)+(†) | 8.772 × 10−1 (9.07 × 10−3)+(†) | 9.109 × 10−1 (3.59 × 10−3)+(≡) | 4.998 × 10−1 (5.74 × 10−2)+(†) | 9.243 × 10−1 (2.37 × 10−3)-(↓) | 9.040 × 10−1 (4.47 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.144 × 10−1 (1.25× 10−2) | 9.109 × 10−1 (1.36 × 10−2) | |
| 10 | 9.429 × 10−1 (3.52 × 10−2)+(†) | 9.380 × 10−1 (6.35 × 10−3)+(†) | 8.996 × 10−1 (1.46 × 10−2)+(†) | 9.609 × 10−1 (1.52 × 10−3)=(†) | 6.318 × 10−1 (3.65 × 10−2)+(†) | 9.702 × 10−1 (1.08 × 10−3)-(↓) | 9.583 × 10−1 (2.20 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 9.609 × 10−1 (3.56 × 10−3) | 9.668 × 10−1 (3.66 × 10−3) | |
| DTLZ5 | 3 | 1.938 × 10−1 (1.93 × 10−3)+(†) | 1.860 × 10−1 (1.76 × 10−3)+(†) | 1.998 × 10−1 (3.01 × 10−4)=(≡) | 1.982 × 10−1 (6.43 × 10−4)+(†) | 1.998 × 10−1 (1.99 × 10−3)=(≡) | 1.998 × 10−1 (4.45 × 10−4)=(≡) | 1.928 × 10−1 (4.11 × 10−3)+(†) | 1.998 × 10−1 (6.01 × 10−4)=(≡) | 1.998 × 10−1 (4.50 × 10−4) | 1.998 × 10−1 (5.60 × 10−4) |
| 5 | 1.246 × 10−1 (1.58 × 10−3)=(≡) | 2.536 × 10−2 (2.30 × 10−2)+(†) | 9.292 × 10−2 (5.92 × 10−3)+(†) | 1.064 × 10−1 (4.15 × 10−3)+(†) | 1.246 × 10−1 (2.91 × 10−3)=(≡) | 1.145 × 10−1 (2.65 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 0.8839 × 10−1 (8.31 × 10−3)+(†) | 1.246 × 10−1 (1.40 × 10−3) | 1.246 × 10−1 (1.14 × 10−3) | |
| 8 | 9.847 × 10−2 (1.90 × 10−3)+(†) | 3.295 × 10−3 (1.14 × 10−2)+(†) | 8.150 × 10−2 (5.84 × 10−3)+(†) | 4.805 × 10−2 (1.56 × 10−2)+(†) | 7.354 × 10−2 (9.58 × 10−3)+(†) | 8.947 × 10−2 (5.40 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 0.4154 × 10−1 (2.01 × 10−2)+(†) | 1.003 × 10−1 (2.23 × 10−3) | 1.003 × 10−1 (3.97 × 10−3) | |
| 10 | 9.526 × 10−2 (1.17 × 10−3)=(≡) | 1.470 × 10−3 (7.63 × 10−3)+(†) | 7.226 × 10−2 (9.91 × 10−3)+(†) | 3.393 × 10−2 (1.99 × 10−2)+(†) | 5.544 × 10−2 (1.23 × 10−2)+(†) | 8.530 × 10−2 (6.39 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 4.0901 × 10−2 (1.63 × 10−2)+(†) | 9.526 × 10−2 (2.17 × 10−3) | 9.526 × 10−2 (2.81 × 10−3) | |
| DTLZ6 | 3 | 1.879 × 10−1 (5.33 × 10−3)+(†) | 1.837 × 10−1 (2.18 × 10−3)+(†) | 1.999 × 10−1 (4.60 × 10−4)=(≡) | 1.989 × 10−1 (1.67 × 10−3)+(†) | 1.961 × 10−1 (1.35 × 10−3)+(†) | 1.999 × 10−1 (4.54 × 10−4)=(≡) | 1.879 × 10−1 (6.77 × 10−3)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 1.999 × 10−1 (4.83 × 10−4) | 1.999 × 10−1 (9.30 × 10−4) |
| 5 | 1.047 × 10−1 (9.41 × 10−3)+(†) | 3.482 × 10−3 (8.66 × 10−3)+(†) | 3.271 × 10−2 (4.08 × 10−2)+(†) | 1.095 × 10−1 (4.70 × 10−3)+(†) | 1.242 × 10−1 (2.69 × 10−3)-(↓) | 1.150 × 10−1 (3.68 × 10−3)+(†) | 4.538 × 10−2 (4.62 × 10−2)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 1.165 × 10−1 (3.42 × 10−3) | 1.152 × 10−1 (2.29 × 10−2) | |
| 8 | 7.919 × 10−2 (3.16 × 10−2)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 7.075 × 10−2 (2.14 × 10−2)-(↓) | 9.317 × 10−2 (9.28 × 10−3)-(↓) | 9.434 × 10−2 (7.31 × 10−3)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 5.073 × 10−2 (4.24 × 10−2) | 3.618 × 10−2 (3.55 × 10−2) | |
| 10 | 8.399 × 10−2 (1.57 × 10−2)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 5.632 × 10−2 (2.91 × 10−2)+(↓) | 7.596 × 10−2 (1.42 × 10−2)=(↓) | 8.682 × 10−2 (1.18 × 10−2)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 7.596 × 10−2 (2.79 × 10−2) | 5.437 × 10−2 (3.99 × 10−2) | |
| DTLZ7 | 3 | 4.160 × 10−1 (1.60 × 10−2)-(↓) | 4.119 × 10−1 (2.41 × 10−3)-(↓) | 4.178 × 10−1 (1.63 × 10−2)-(↓) | 4.118 × 10−1 (2.40 × 10−2)-(↓) | 3.995 × 10−1 (6.24 × 10−3)-(↓) | 4.195 × 10−1 (1.59 × 10−2)-(↓) | 3.844 × 10−1 (2.42 × 10−2)=(†) | 3.9261 × 10−1 (2.83 × 10−2)-(↓) | 3.844 × 10−1 (3.70 × 10−2) | 3.882 × 10−1 (3.93 × 10−2) |
| 5 | 3.113 × 10−1 (4.83 × 10−3)+(†) | 3.008 × 10−1 (3.31 × 10−3)+(†) | 3.036 × 10−1 (5.11 × 10−3)+(†) | 3.251 × 10−1 (3.57 × 10−3)-(≡) | 3.171 × 10−1 (5.86 × 10−3)+(†) | 3.010 × 10−1 (1.18 × 10−2)+(†) | 2.583 × 10−1 (2.13 × 10−2)+(†) | 1.1457 × 10−1 (2.52 × 10−2)+(†) | 3.239 × 10−1 (1.80 × 10−2) | 3.251 × 10−1 (1.45 × 10−2) | |
| 8 | 2.067 × 10−1 (7.55 × 10−3)+(†) | 1.801 × 10−1 (1.84 × 10−2)+(†) | 1.877 × 10−1 (8.11 × 10−3)+(†) | 9.480 × 10−2 (1.37 × 10−2)+(†) | 2.550 × 10−1 (4.17 × 10−3)-(↓) | 5.193 × 10−2 (1.96 × 10−2)+(†) | 1.508 × 10−1 (1.36 × 10−2)+(†) | 3.33 × 10−8 (0.00 × 100)+(†) | 2.227 × 10−1 (3.73 × 10−2) | 2.110 × 10−1 (3.09 × 10−2) | |
| 10 | 1.909 × 10−1 (7.00 × 10−3)-(↓) | 1.590 × 10−1 (1.25 × 10−2)+(†) | 1.394 × 10−1 (1.30 × 10−2)+(†) | 1.054 × 10−1 (2.60 × 10−2)+(†) | 2.403 × 10−1 (2.93 × 10−3)-(↓) | 8.381 × 10−3 (3.76 × 10−3)+(†) | 1.321 × 10−1 (1.16 × 10−2)+(†) | 0.000 × 100 (0.00 × 100)+(†) | 0.1862 (3.79 × 10−2) | 1.736 × 10−1 (4.27 × 10−2) | |
| Ad-GrMODE1* (+/=/-) | 16/3/9 | 22/2/4 | 23/3/2 | 15/5/8 | 20/3/5 | 12/5/11 | 25/2/1 | 26/1/1 | |||
| Ad-GrMODE2* (†/≡/↓) | 16/2/10 | 22/1/5 | 21/3/4 | 13/3/12 | 20/2/6 | 13/3/12 | 25/1/2 | 26/1/1 | |||
The signs ‘+’, ‘=’, and ‘-’ depicts the instances, ad-GrMODE1* performs better, similar and worse with respect to state-of-the-art algorithms. The signs ‘†’, ‘≡’, and ‘↓’ depicts the in-stances, ad-GrMODE2* performs better, similar and worse with respect to state-of-the-art algorithms.

Table A4.
Mean and standard deviation values of HV results of proposed method with state of art algorithms on WFG problems.
Table A4.
Mean and standard deviation values of HV results of proposed method with state of art algorithms on WFG problems.
| # | M | NSGAIII | SPEA-R | VaEA | SRA | MODE | EMyO-C | MyODEMR | GAMODE | adGrMOEA1* | adGrMOEA2* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WFG1 | 3 | 2.800 × 10−1 (3.73 × 10−2)+(†) | 3.087 × 10−1 (3.56 × 10−4)-(↓) | 3.049 × 10−1 (1.17 × 10−3)-(↓) | 3.021 × 10−1 (1.92 × 10−3)-(↓) | 0.000 × 100 (0.00 × 100)+(†) | 1.414 × 10−1 (1.48 × 10−2)+(†) | 1.625 × 10−1 (2.68 × 10−2)+(†) | 1.71 × 10−1 (2.15 × 10−2)+(†) | 2.855 × 10−1 (2.77 × 10−3) | 2.827 × 10−1 (3.13 × 10−3) |
| 5 | 2.597 × 10−1 (4.04 × 10−2)+(†) | 2.431 × 10−1 (4.29 × 10−2)+(†) | 2.843 × 10−1 (4.47 × 10−4)-(↓) | 2.657 × 10−1 (8.09 × 10−4)+(†) | 8.122 × 10−3 (1.17 × 10−2)+(†) | 2.660 × 10−1 (2.57 × 10−3)+(†) | 2.306 × 10−1 (1.44 × 10−2)+(†) | 1.78 × 10−1 (1.54 × 10−2)+(†) | 2.801 × 10−1 (9.09 × 10−4) | 2.797 × 10−1 (9.22 × 10−4) | |
| 8 | 2.294 × 10−1 (2.84 × 10−3)=(≡) | 2.138 × 10−1 (1.70 × 10−2)+(†) | 2.311 × 10−1 (4.71 × 10−4)-(↓) | 2.198 × 10−1 (6.64 × 10−4)+(†) | 7.802 × 10−2 (9.71 × 10−3)+(†) | 2.294 × 10−1 (3.72 × 10−4)=(≡) | 1.966 × 10−1 (1.38 × 10−2)+(†) | 1.87 × 10−1 (1.26 × 10−2)+(†) | 2.294 × 10−1 (6.10 × 10−4) | 2.294 × 10−1 (5.30 × 10−4) | |
| 10 | 2.071 × 10−1 (3.94 × 10−4)=(≡) | 2.071 × 10−1 (3.38 × 10−4)=(≡) | 2.031 × 10−1 (4.76 × 10−4)+(†) | 2.071 × 10−1 (4.07 × 10−4)=(≡) | 1.065 × 10−1 (6.96 × 10−3)+(†) | 2.071 × 10−1 (3.83 × 10−4)=(≡) | 1.816 × 10−1 (9.85 × 10−3)+(†) | 1.93 × 10−1 (7.18 × 10−3)+(†) | 2.071 × 10−1 (5.19 × 10−4) | 2.071 × 10−1 (4.70 × 10−4) | |
| WFG2 | 3 | 2.352 × 10−1 (4.84 × 10−4)=(≡) | 2.352 × 10−1 (4.56 × 10−4)=(≡) | 2.352 × 10−1 (5.03 × 10−4)=(≡) | 2.352 × 10−1 (5.54 × 10−4)=(≡) | 2.352 × 10−1 (5.49 × 10−4)=(≡) | 2.352 × 10−1 (5.14 × 10−4)=(≡) | 2.267 × 10−1 (3.50 × 10−3)+(†) | 2.35 × 10−1 (2.83 × 10−4)=(≡) | 2.352 × 10−1 (5.35 × 10−4) | 2.352 × 10−1 (4.91 × 10−4) |
| 5 | 2.115 × 10−1 (4.90 × 10−4)=(≡) | 2.115 × 10−1 (4.13 × 10−4)=(≡) | 2.115 × 10−1 (5.11 × 10−4)=(≡) | 2.115 × 10−1 (4.79 × 10−4)=(≡) | 2.115 × 10−1 (6.47 × 10−4)=(≡) | 2.115 × 10−1 (4.10 × 10−4)=(≡) | 1.416 × 10−1 (4.46 × 10−2)+(†) | 2.11 × 10−1 (4.19 × 10−4)=(≡) | 2.115 × 10−1 (4.77 × 10−4) | 2.115 × 10−1 (3.26 × 10−4) | |
| 8 | 1.855 × 10−1 (3.02 × 10−4)=(≡) | 1.855 × 10−1 (4.29 × 10−4)=(≡) | 1.855 × 10−1 (4.40 × 10−4)=(≡) | 1.855 × 10−1 (4.73 × 10−4)=(≡) | 1.855 × 10−1 (3.75 × 10−4)=(≡) | 1.855 × 10−1 (4.01 × 10−4)=(≡) | 9.438 × 10−2 (1.78 × 10−2)+(†) | 1.85 × 10−1 (3.58 × 10−4)=(≡) | 1.855 × 10−1 (4.80 × 10−4) | 1.855 × 10−1 (3.67 × 10−4) | |
| 10 | 1.730 × 10−1 (3.92× 10−4)=(≡) | 1.730 × 10−1 (3.65 × 10−4)=(≡) | 1.730 × 10−1 (3.25 × 10−4)=(≡) | 1.730 × 10−1 (3.92 × 10−4)=(≡) | 1.730 × 10−1 (3.66 × 10−4)=(≡) | 1.730 × 10−1 (3.12 × 10−4)=(≡) | 9.701 × 10−2 (2.36 × 10−2)+(†) | 1.73 × 10−1 (3.10 × 10−4)=(≡) | 1.730 × 10−1 (3.11 × 10−4) | 1.730 × 10−1 (3.56 × 10−4) | |
| WFG3 | 3 | 8.360 × 10−2 (5.18 × 10−4)+(†) | 8.033 × 10−2 (5.34 × 10−4)+(†) | 8.533 × 10−2 (3.69 × 10−4)+(†) | 8.448 × 10−2 (5.13 × 10−4)+(†) | 8.458 × 10−2 (3.41 × 10−4)+(†) | 8.362 × 10−2 (4.84 × 10−4)+(†) | 3.364 × 10−2 (1.20 × 10−2)+(†) | 9.10 × 10−2 (3.81 × 10−4)+(†) | 9.250 × 10−2 (6.91 × 10−4) | 9.209 × 10−2 (4.94 × 10−4) |
| 5 | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.00 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100) | 0.000 × 100 (0.00 × 100) | |
| 8 | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.00 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100) | 0.000 × 100 (0.00 × 100) | |
| 10 | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100)=(≡) | 0.00 × 100 (0.00 × 100)=(≡) | 0.000 × 100 (0.00 × 100) | 0.000 × 100 (0.00 × 100) | |
| WFG4 | 3 | 1.964 × 10−1 (1.12 × 10−3)=(≡) | 1.956 × 10−1 (6.19 × 10−4)+(†) | 1.933 × 10−1 (1.73 × 10−3)+(†) | 1.946 × 10−1 (1.67 × 10−3)+(†) | 1.596 × 10−1 (6.36 × 10−3)+(†) | 1.728 × 10−1 (3.79 × 10−3)+(†) | 1.836 × 10−1 (4.02 × 10−3)+(†) | 1.70 × 10−1 (7.22 × 10−3)+(†) | 1.964 × 10−1 (1.70 × 10−3) | 1.964 × 10−1 (1.66 × 10−3) |
| 5 | 2.535 × 10−1 (2.46 × 10−3)-(↓) | 2.475 × 10−1 (1.71 × 10−3)-(↓) | 2.429 × 10−1 (2.44 × 10−3)-(↓) | 2.355 × 10−1 (4.35 × 10−3)-(↓) | 1.603 × 10−1 (7.29 × 10−3)+(†) | 1.199 × 10−1 (1.70 × 10−2)+(†) | 2.341 × 10−1 (3.47 × 10−3)-(↓) | 2.09 × 10−1 (1.13 × 10−2)+(†) | 2.257 × 10−1 (5.15 × 10−3) | 2.237 × 10−1 (6.17 × 10−3) | |
| 8 | 2.127 × 10−1 (1.63 × 10−2)-(↓) | 2.227 × 10−1 (4.46 × 10−3)-(↓) | 2.241 × 10−1 (2.62 × 10−3)-(↓) | 1.949 × 10−1 (9.35 × 10−3)-(↓) | 1.331 × 10−1 (4.34 × 10−3)+(†) | 1.674 × 10−2 (1.14 × 10−2)+(†) | 2.053 × 10−1 (5.61 × 10−3)-(↓) | 1.89 × 10−1 (4.74 × 10−3)-(↓) | 1.685 × 10−1 (1.10 × 10−2) | 1.692 × 10−1 (9.86 × 10−3) | |
| 10 | 2.150 × 10−1 (9.07 × 10−3)-(↓) | 2.178 × 10−1 (2.47 × 10−3)-(↓) | 2.110 × 10−1 (3.63 × 10−3)-(↓) | 2.011 × 10−1 (6.87 × 10−3)-(↓) | 1.281 × 10−1 (3.51 × 10−3)+(†) | 6.537 × 10−3 (5.84 × 10−3)+(†) | 1.950 × 10−1 (3.18 × 10−3)-(↓) | 1.83 × 10−1 (3.66 × 10−3)-(↓) | 1.598 × 10−1 (1.05 × 10−2) | 1.624 × 10−1 (6.79 × 10−3) | |
| WFG5 | 3 | 4.584 × 10−1 (1.49 × 10−3)=(≡) | 4.584 × 10−1 (1.47 × 10−3)=(≡) | 4.608 × 10−1 (8.70 × 10−4)-(↓) | 4.525 × 10−1 (1.83 × 10−3)+(†) | 4.301 × 10−1 (3.83 × 10−3)+(†) | 4.486 × 10−1 (2.76 × 10−3)+(†) | 4.346 × 10−1 (5.11 × 10−3)+(†) | 4.56 × 10−1 (1.19 × 10−3)+(†) | 4.584 × 10−1 (1.55 × 10−3) | 4.584 × 10−1 (1.75 × 10−3) |
| 5 | 4.652 × 10−1 (2.70 × 10−3)+(≡) | 4.458 × 10−1 (2.88 × 10−3)+(†) | 4.708 × 10−1 (2.17 × 10−3)-(↓) | 4.597 × 10−1 (5.14 × 10−3)+(†) | 4.305 × 10−1 (5.20 × 10−3)+(†) | 4.606 × 10−1 (5.10 × 10−3)+(†) | 4.459 × 10−1 (5.07 × 10−3)+(†) | 4.68 × 10−1 (3.08 × 10−3)-(↓) | 4.671 × 10−1 (3.59 × 10−3) | 4.652 × 10−1 (3.65 × 10−3) | |
| 8 | 4.612 × 10−1 (3.15 × 10−3)+(†) | 4.368 × 10−1 (4.12 × 10−3)+(†) | 4.536 × 10−1 (2.81 × 10−3)+(†) | 4.533 × 10−1 (3.81 × 10−3)+(†) | 4.347 × 10−1 (4.10 × 10−3)+(†) | 4.557 × 10−1 (4.70 × 10−3)+(†) | 4.357 × 10−1 (7.30 × 10−3)+(†) | 4.65 × 10−1 (1.36 × 10−3)=(↓) | 4.656 × 10−1 (3.69 × 10−3) | 4.640 × 10−1 (3.76 × 10−3) | |
| 10 | 4.682 × 10−1 (2.88 × 10−3)+(†) | 4.426 × 10−1 (3.73 × 10−3)+(†) | 4.636 × 10−1 (1.93 × 10−3)+(†) | 4.608 × 10−1 (2.38 × 10−3)+(†) | 4.499 × 10−1 (2.63 × 10−3)+(†) | 4.886 × 10−1 (3.26 × 10−3)-(↓) | 4.356 × 10−1 (6.70 × 10−2)+(†) | 4.70 × 10−1 (1.31 × 10−3)+(†) | 4.770 × 10−1 (3.02 × 10−3) | 4.763 × 10−1 (2.78 × 10−3) | |
| WFG6 | 3 | 1.878 × 10−1 (2.09 × 10−3)+(†) | 1.887 × 10−1 (6.67 × 10−4)+(†) | 1.894 × 10−1 (6.80 × 10−4)+(†) | 1.897 × 10−1 (7.73 × 10−4)+(†) | 1.858 × 10−1 (1.35 × 10−3)+(†) | 1.915 × 10−1 (5.98 × 10−4)=(≡) | 1.864 × 10−1 (3.84 × 10−3)+(†) | 1.89 × 10−1 (9.51 × 10−4)+(†) | 1.915 × 10−1 (5.18 × 10−4) | 1.915 × 10−1 (4.54 × 10−4) |
| 5 | 1.908 × 10−1 (9.12 × 10−4)+(†) | 1.887 × 10−1 (1.34 × 10−3)+(†) | 1.908 × 10−1 (8.89 × 10−4)+(†) | 1.905 × 10−1 (8.90 × 10−4)+(†) | 1.879 × 10−1 (1.33 × 10−3)+(†) | 1.920 × 10−1 (9.28 × 10−4)=(≡) | 1.843 × 10−1 (4.19 × 10−3)+(†) | 1.92 × 10−1 (6.58 × 10−4)=(≡) | 1.920 × 10−1 (4.44 × 10−4) | 1.920 × 10−1 (4.38 × 10−4) | |
| 8 | 1.893 × 10−1 (1.10 × 10−3)=(≡) | 1.838 × 10−1 (2.80 × 10−3)+(†) | 1.893 × 10−1 (7.27 × 10−4)=(≡) | 1.874 × 10−1 (1.34 × 10−3)+(†) | 1.862 × 10−1 (7.79 × 10−4)+(†) | 1.882 × 10−1 (6.69 × 10−4)+(†) | 1.810 × 10−1 (4.44 × 10−3)+(†) | 1.89 × 10−1 (5.84 × 10−4)=(≡) | 1.893 × 10−1 (5.00 × 10−4) | 1.893 × 10−1 (6.27 × 10−4) | |
| 10 | 1.812 × 10−1 (9.56 × 10−4)+(†) | 1.723 × 10−1 (4.14 × 10−3)+(†) | 1.780 × 10−1 (5.21 × 10−4)+(†) | 1.867 × 10−1 (6.13 × 10−4)+(†) | 1.855 × 10−1 (9.59 × 10−4)+(†) | 1.881 × 10−1 (3.36 × 10−4)=(≡) | 1.815 × 10−1 (2.95 × 10−3)+(†) | 1.88 × 10−1 (5.15 × 10−4)=(≡) | 1.881 × 10−1 (3.57 × 10−4) | 1.881 × 10−1 (3.56 × 10−4) | |
| WFG7 | 3 | 8.092 × 10−2 (1.54 × 10−2)+(†) | 8.430 × 10−2 (2.24 × 10−3)+(†) | 9.021 × 10−2 (1.06 × 10−3)+(†) | 9.506 × 10−2 (9.43 × 10−4)-(↓) | 4.362 × 10−3 (4.36 × 10−3)+(†) | 5.366 × 10−2 (1.02 × 10−2)+(†) | 8.373 × 10−2 (2.03 × 10−3)+(†) | 7.65 × 10−2 (2.14 × 10−3)+(†) | 9.312 × 10−2 (1.39 × 10−3) | 9.251 × 10−2 (1.58 × 10−3) |
| 5 | 7.877 × 10−2 (5.86 × 10−2)+(†) | 1.421 × 10−1 (1.65 × 10−3)+(†) | 1.490 × 10−1 (1.21 × 10−3)-(↓) | 1.521 × 10−1 (1.58 × 10−3)-(↓) | 8.289 × 10- (5.32 × 10−3)+(†) | 8.907 × 10−2 (1.24 × 10−2)+(†) | 1.448 × 10−1 (3.76 × 10−3)=(≡) | 1.18 × 10−1 (9.11 × 10−3)+(†) | 1.448 × 10−1 (4.29 × 10−3) | 1.448 × 10−1 (3.25 × 10−3) | |
| 8 | 1.175 × 10−1 (4.62 × 10−2)+(†) | 1.502 × 10−1 (7.26 × 10−3)+(†) | 1.490 × 10−1 (1.40 × 10−3)+(†) | 1.641 × 10−1 (2.13 × 10−3)-(↓) | 1.058 × 10−2 (2.54 × 10−3)+(†) | 1.274 × 10−1 (7.73 × 10−3)+(†) | 1.371 × 10−1 (4.09 × 10−3)+(†) | 9.86 × 10−2 (1.37 × 10−2)+(†) | 1.540 × 10−1 (2.68 × 10−3) | 1.512 × 10−1 (3.85 × 10−3) | |
| 10 | 1.544 × 10−1 (5.14 × 10−3)=(≡) | 1.544 × 10−1 (3.41 × 10−3)=(≡) | 1.544 × 10−1 (1.41 × 10−3)=(≡) | 1.618 × 10−1 (2.06 × 10−3)-(↓) | 1.201 × 10−2 (1.77 × 10−3)+(†) | 1.430 × 10−1 (4.65 × 10−3)+(†) | 1.409 × 10−1 (3.19 × 10−3)+(†) | 8.59 × 10−2 (7.42 × 10−3)+(†) | 1.544 × 10−1 (1.94 × 10−3) | 1.544 × 10−1 (2.23 × 10−3) | |
| WFG8 | 3 | 2.257 × 10−1 (1.14 × 10−3)+(†) | 2.281 × 10−1 (1.00 × 10−3)+(†) | 2.236 × 10−1 (1.24 × 10−3)+(†) | 2.277 × 10−1 (1.08 × 10−3)+(†) | 2.314 × 10−1 (2.40 × 10−3)=(≡) | 2.277 × 10−1 (7.22 × 10−4)+(†) | 2.243 × 10−1 (2.88 × 10−3)+(†) | 2.24 × 10−1 (9.67 × 10−4)+(†) | 2.314 × 10−1 (7.68 × 10−4) | 2.314 × 10−1 (8.87 × 10−4) |
| 5 | 2.325 × 10−1 (1.21 × 10−3)+(†) | 2.334 × 10−1 (1.65 × 10−3)+(†) | 2.317 × 10−1 (8.80 × 10−4)+(†) | 2.311 × 10−1 (1.28 × 10−3)+(†) | 2.293 × 10−1 (1.94 × 10−3)+(†) | 2.333 × 10−1 (6.80 × 10−4)+(†) | 1.674 × 10−1 (2.49 × 10−2)+(†) | 2.32 × 10−1 (7.55 × 10−4)+(†) | 2.386 × 10−1 (6.68 × 10−4) | 2.382 × 10−1 (6.27 × 10−4) | |
| 8 | 2.299 × 10−1 (1.58 × 10−3)+(†) | 2.180 × 10−1 (6.92 × 10−3)+(†) | 2.355 × 10−1 (7.91 × 10−4)+(†) | 2.334 × 10−1 (1.32 × 10−3)+(†) | 2.325 × 10−1 (1.64 × 10−3)+(†) | 2.345 × 10−1 (9.49 × 10−4)+(†) | 1.428 × 10−1 (1.38 × 10−2)+(†) | 2.35 × 10−1 (8.82 × 10−4)+(†) | 2.408 × 10−1 (7.60 × 10−4) | 2.403 × 10−1 (6.83 × 10−4) | |
| 10 | 2.334 × 10−1 (2.07 × 10−3)+(†) | 2.217 × 10−1 (4.81 × 10−3)+(†) | 2.385 × 10−1 (5.64 × 10−4)+(†) | 2.374 × 10−1 (6.99 × 10−4) +(†) | 2.342 × 10−1 (9.34 × 10−4)+(†) | 2.360 × 10−1 (9.87 × 10−4)+(†) | 1.451 × 10−1 (6.89 × 10−3)+(†) | 2.37 × 10−1 (6.63 × 10−4)+(†) | 2.426 × 10−1 (5.27 × 10−4) | 2.424 × 10−1 (5.30 × 10−4) | |
| WFG9 | 3 | 3.763 × 10−1 (5.81 × 10−3)=(↓) | 3.720 × 10−1 (4.90 × 10−3)+(†) | 3.682 × 10−1 (6.89 × 10−3)+(†) | 3.828 × 10−1 (5.06 × 10−3)-(↓) | 2.053 × 10−1 (1.20 × 10−2)+(†) | 3.658 × 10−1 (3.88 × 10−3)+(†) | 3.600 × 10−1 (5.93 × 10−3)+(†) | 3.40 × 10−1 (6.05 × 10−3)+(†) | 3.763 × 10−1 (4.30 × 10−3) | 3.757 × 10−1 (3.68 × 10−3) |
| 5 | 5.388 × 10−1 (1.43 × 10−2)-(↓) | 5.447 × 10−1 (9.97 × 10−3)-(↓) | 5.258 × 10−1 (9.08 × 10−3)-(↓) | 5.209 × 10−1 (6.09 × 10−3)-(↓) | 1.816 × 10−1 (1.16 × 10−2)+(†) | 5.046 × 10−1 (7.77 × 10−3)-(↓) | 4.995 × 10−1 (1.03 × 10−2)=(↓) | 4.40 × 10−1 (2.19 × 10−2)+(†) | 4.995 × 10−1 (1.20 × 10−2) | 4.932 × 10−1 (1.57 × 10−2) | |
| 8 | 5.861 × 10−1 (2.19 × 10−2)-(↓) | 6.050 × 10−1 (1.54 × 10−2)-(↓) | 5.903 × 10−1 (1.29 × 10−2)-(↓) | 5.657 × 10−1 (1.81 × 10−2)-(↓) | 1.684 × 10−1 (1.07 × 10−2)+(†) | 5.131 × 10−1 (1.29 × 10−2)-(↓) | 3.683 × 10−1 (8.25 × 10−2)+(†) | 3.82 × 10−1 (1.31 × 10−2)+(†) | 4.675 × 10−1 (1.89 × 10−2) | 4.597 × 10−1 (1.99 × 10−2) | |
| 10 | 6.254 × 10−1 (1.56 × 10−2)-(↓) | 6.290 × 10−1 (1.34 × 10−2)-(↓) | 5.938 × 10−1 (9.68 × 10−3)-(↓) | 5.875 × 10−1 (1.31 × 10−2)-(↓) | 1.706 × 10−1 (9.90 × 10−3)+(†) | 5.407 × 10−1 (9.80 × 10−3)-(↓) | 4.069 × 10−1 (6.41 × 10−2)+(†) | 3.98 × 10−1 (1.17 × 10−2)+(†) | 4.957 × 10−1 (1.30 × 10−2) | 4.848 × 10−1 (1.30 × 10−2) | |
| Ad-GrMODE1* (+/=/-) | 16/14/6 | 19/10/7 | 15/9/12 | 16/8/12 | 28/8/0 | 20/12/4 | 28/5/3 | 22/11/3 | |||
| Ad-GrMODE2* (†/≡/↓) | 15/14/7 | 19/10/7 | 15/9/12 | 16/8/12 | 28/8/0 | 20/12/4 | 28/4/4 | 22/10/4 | |||
The signs ‘+’, ‘=’, and ‘-’ depicts the instances, ad-GrMODE1* performs better, similar and worse with respect to state-of-the-art algorithms. The signs ‘†’, ‘≡’, and ‘↓’ depicts the in-stances, ad-GrMODE2* performs better, similar and worse with respect to state-of-the-art algorithms.

Table A5.
Mean and standard deviation values of IGD results of proposed method with state of art algorithms on DTLZ problems.
Table A5.
Mean and standard deviation values of IGD results of proposed method with state of art algorithms on DTLZ problems.
| # | M | NSGAIII | SPEA-R | VaEA | SRA | MODE | EMyO-C | MyODEMR | GAMODE | adGrMOEA1* | adGrMOEA2* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 1.79 × 10−2 (9.67 × 10−2)-(↓) | 1.98 × 10−2 (2.68 × 10−3)=(↓) | 3.46 × 10−2 (2.53 × 10−2)+(†) | 2.19 × 10−2 (1.94 × 10−3)+(†) | 3.04 × 10−2 (2.50 × 10−3)+(†) | 2.05 × 10−2 (4.32 × 10−4)+(†) | 8.95 × 10−2 (1.10 × 10−1)+(†) | 1.36 × 100 (1.07 × 100)+(†) | 1.98 × 10−2 (7.92 × 10−4) | 2.01 × 10−2 (7.91 × 10−4) |
| 5 | 6.26 × 10−2 (1.45 × 10−3)+(†) | 9.67 × 10−2 (2.66 × 10−2)+(†) | 1.21 × 10−1 (2.73 × 10−2)+(†) | 6.46 × 10−2 (2.10 × 10−3)+(†) | 9.14 × 10−2 (6.98 × 10−3)+(†) | 6.15 × 10−2 (6.74 × 10−4)+(†) | 1.18 × 10−1 (3.45 × 10−2)+(†) | 1.15 × 10+1 (6.69 × 100)+(†) | 5.48 × 10−2 (1.19 × 10−3) | 5.61 × 10−2 (8.45 × 10−4) | |
| 8 | 1.17 × 10−1 (2.88 × 10−2)+(†) | 2.00 × 10−1 (1.09 × 10−1)+(†) | 2.31 × 10−1 (6.87 × 10−2)+(†) | 1.02 × 10−1 (2.24 × 10−3)=(≡) | 1.71 × 10−1 (1.06 × 10−2)+(†) | 9.95 × 10−2 (6.62 × 10−4)-(↓) | 3.26 × 10−1 (7.21 × 10−2)+(†) | 4.20 × 10−1 (5.49 × 10−1)+(†) | 1.02 × 10−1 (1.72 × 10−3) | 1.02 × 10−1 (1.96 × 10−3) | |
| 10 | 1.57 × 10−1 (8.06 × 10−2)+(†) | 2.46 × 10−1 (9.31 × 10−2)+(†) | 2.27 × 10−1 (7.67 × 10−2)+(†) | 1.07 × 10−1 (1.99 × 10−3)+(≡) | 1.86 × 10−1 (9.50 × 10−3)+(†) | 1.02 × 10−1 (7.09 × 10−4)-(↓) | 3.05 × 10−1 (7.48 × 10−2)+(†) | 1.49 × 10+2 (1.97 × 10+1)+(†) | 1.05 × 10−1 (1.07 × 10−3) | 1.07 × 10−1 (2.44 × 10−3) | |
| DTLZ2 | 3 | 5.50 × 10−2 (1.94 × 10−4)-(↓) | 5.78 × 10−2 (1.31 × 10−3)-(↓) | 5.33 × 10−2 (7.52 × 10−4)-(↓) | 7.75 × 10−2 (6.61 × 10−3)+(↓) | 7.49 × 10−2 (3.89 × 10−3)-(↓) | 5.73 × 10−2 (1.52 × 10−3)-(↓) | 6.84 × 10−2 (2.77 × 10−3)-(↓) | 7.09 × 10−2 (2.62 × 10−3)-(↓) | 7.58 × 10−2 (5.70 × 10−3) | 7.85 × 10−2 (3.76 × 10−3) |
| 5 | 1.85 × 10−1 (5.10 × 10−4)-(↓) | 1.90 × 10−1 (2.87 × 10−3)-(↓) | 1.93 × 10−1 (1.18 × 10−3)-(↓) | 2.07 × 10−1 (2.94 × 10−3)-(↓) | 2.62 × 10−1 (1.34 × 10−2)+(†) | 1.92 × 10−1 (1.65 × 10−3)-(↓) | 2.08 × 10−1 (3.83 × 10−3)-(↓) | 6.72 × 10−1 (4.28 × 10−2)+(†) | 2.20 × 10−1 (3.66 × 10−3) | 2.19 × 10−1 (3.77 × 10−3) | |
| 8 | 3.77 × 10−1 (6.88 × 10−2)+(†) | 3.43 × 10−1 (2.19 × 10−3)+(†) | 3.72 × 10−1 (2.59 × 10−3)+(†) | 3.59 × 10−1 (2.61 × 10−3)+(†) | 5.18 × 10−1 (1.77 × 10−2)+(†) | 3.55 × 10−1 (1.87 × 10−3)+(†) | 3.74 × 10−1 (4.65 × 10−3)+(†) | 1.81 × 100 (3.05 × 10−1)+(†) | 2.76 × 10−1 (1.22 × 10−2) | 2.85 × 10−1 (2.44 × 10−2) | |
| 10 | 4.56 × 10−1 (3.87 × 10−2)+(†) | 4.32 × 10−1 (3.72 × 10−3)=(↓) | 4.39 × 10−1 (8.31 × 10−3)+(†) | 4.09 × 10−1 (1.97 × 10−3)-(↓) | 6.03 × 10−1 (1.88 × 10−2)+(†) | 4.08 × 10−1 (1.49 × 10−3)-(↓) | 4.22 × 10−1 (5.87 × 10−3)-(↓) | 1.45 × 100 (6.20 × 10−2)+(†) | 4.32 × 10−1 (1.58 × 10−2) | 4.37 × 10−1 (1.94 × 10−2) | |
| DTLZ3 | 3 | 5.64 × 10−2 (2.61 × 10−3)-(↓) | 2.3 × 10−1 (1.10 × 10−1)+(†) | 5.57 × 10−2 (4.74 × 10−3)-(↓) | 7.96 × 10−2 (5.58 × 10−3)+(↓) | 1.72 × 10−1 (1.95 × 10−2)+(†) | 8.96 × 10−2 (1.73 × 10−3)+(†) | 1.59 × 10−1 (1.68 × 10−1)+(†) | 6.89 × 10−1 (1.63 × 10−1)+(†) | 7.70 × 10−2 (1.04 × 10−2) | 8.06 × 10−2 (7.97 × 10−2) |
| 5 | 1.93 × 10−1 (2.54 × 10−2)+(†) | 1.28 × 100 (9.29 × 10−1)+(†) | 4.85 × 10−1 (3.92 × 10−1)+(†) | 2.12 × 10−1 (5.38 × 10−3)+(†) | 1.41 × 100 (4.20 × 10−1)+(†) | 1.89 × 10−1 (2.32 × 10−3)+(†) | 6.32 × 10−1 (2.48 × 10−1)+(†) | 1.91 × 10+2 (5.27 × 10+1)+(†) | 1.79 × 10−1 (3.76 × 10−2) | 1.77 × 10−1 (1.73 × 10−1) | |
| 8 | 5.44 × 10−1 (1.61 × 10−1)+(†) | 1.17 × 10−1 (5.50 × 100)+(†) | 5.32 × 100 (2.97 × 100)+(†) | 3.64 × 10−1 (3.54 × 10−3)+(†) | 9.79 × 100 (1.26 × 100)+(†) | 3.49 × 10−1 (2.86 × 10−3)+(†) | 1.15 × 100 (1.75 × 10−1)+(†) | 7.79 × 10+2 (2.13 × 10+2)+(†) | 3.22 × 10−1 (1.24 × 10−1) | 3.41 × 10−1 (2.60 × 10−1) | |
| 10 | 5.55 × 10−1 (1.11 × 10−1)+(†) | 2.57 × 10+1 (1.52 × 10+1)+(†) | 1.09 × 10+1 (4.06 × 100)+(†) | 4.10 × 10−1 (2.45 × 10−3)+(†) | 1.74 × 10+1 (2.76 × 100)+(†) | 4.02 × 10−1 (4.57 × 10−3)+(†) | 1.19 × 100 (4.81 × 10−2)+(†) | 9.29 × 10+2 (1.05 × 10+2)+(†) | 3.40 × 10−1 (1.20 × 10−2) | 3.75 × 10−1 (6.40 × 10−2) | |
| DTLZ4 | 3 | 4.65 × 10−1 (2.93 × 10−1)+(†) | 5.83 × 10−2 (1.67 × 10−3)-(↓) | 5.33 × 10−2 (1.01 × 10−3)-(↓) | 1.40 × 10−1 (1.68 × 10−1)+(≡) | 4.88 × 10−1 (1.18 × 10−1)+(†) | 5.76 × 10−2 (1.41 × 10−3)-(↓) | 7.25 × 10−2 (3.01 × 10−3)-(↓) | 2.09 × 10−1 (1.66 × 10−1)+(†) | 1.23 × 10−1 (1.44 × 10−1) | 1.40 × 10−1 (1.70 × 10−1) |
| 5 | 3.42 × 10−1 (1.46 × 10−1)+(†) | 1.90 × 10−1 (2.68 × 10−3)+(†) | 1.95 × 10−1 (1.45 × 10−3)+(†) | 2.17 × 10−1 (4.08 × 10−2)+(†) | 6.60 × 10−1 (7.93 × 10−2)+(†) | 1.98 × 10−1 (2.46 × 10−3)+(†) | 2.25 × 10−1 (5.47 × 10−3)+(†) | 4.91 × 10−1 (3.07 × 10−2)+(†) | 1.67 × 10−1 (7.58 × 10−2) | 1.80 × 10−1 (8.60 × 10−2) | |
| 8 | 4.29 × 10−1 (8.58 × 10−2)+(†) | 3.75 × 10−1 (4.82 × 10−3)+(†) | 3.75 × 10−1 (4.43 × 10−3)+(†) | 3.65 × 10−1 (2.48 × 10−3)+(†) | 7.29 × 10−1 (4.92 × 10−2)+(†) | 3.71 × 10−1 (2.47 × 10−3)+(†) | 4.10 × 10−1 (6.69 × 10−3)+(†) | 1.59 × 100 (1.91 × 10−1)+(†) | 3.29 × 10−1 (2.59 × 10−2) | 3.38 × 10−1 (3.22 × 10−2) | |
| 10 | 5.07 × 10−1 (6.52 × 10−2)+(†) | 4.83 × 10−1 (6.29 × 10−3)+(†) | 4.51 × 10−1 (1.02 × 10−2)+(†) | 4.11 × 10−1 (2.88 × 10−3)-(↓) | 7.45 × 10−1 (2.54 × 10−2)+(†) | 4.38 × 10−1 (1.78 × 10−3)=(†) | 4.79 × 10−1 (5.64 × 10−3)+(†) | 1.56 × 100 (1.94 × 10−1)+(†) | 4.38 × 10−1 (1.37 × 10−2) | 4.12 × 10−1 (1.21 × 10−2) | |
| DTLZ5 | 3 | 1.58 × 10−2 (4.30 × 10−3)+(†) | 2.96 × 10−2 (3.53 × 10−3)+(†) | 4.45 × 10−3 (1.76 × 10−4)+(†) | 5.18 × 10−3 (7.31 × 10−4)+(†) | 7.71 × 10−3 (1.20 × 10−3)+(†) | 4.78 × 10−3 (2.44 × 10−4)+(†) | 1.04 × 10−2 (1.76 × 10−3)+(†) | 4.18 × 10−3 (1.41 × 10−4)=(†) | 4.18 × 10−3 (4.05 × 10−4) | 4.09 × 10−3 (3.50 × 10−4) |
| 5 | 6.27 × 10−2 (1.51 × 10−2)+(†) | 2.41 × 10−1 (6.50 × 10−2)+(†) | 1.55 × 10−1 (4.47 × 10−2)+(†) | 4.11 × 10−2 (7.24 × 10−3)+(†) | 1.22 × 10−2 (2.57 × 10−3)-(↓) | 4.08 × 10−2 (5.06 × 10−3)+(†) | 7.34 × 10−1 (5.05 × 10−2)+(†) | 1.22 × 10−1 (2.56 × 10−2)+(†) | 1.91 × 10−2 (4.04 × 10−3) | 1.65 × 10−2 (3.16 × 10−3) | |
| 8 | 9.24 × 10−2 (2.28 × 10−2)+(†) | 3.71 × 10−1 (8.17 × 10−2)+(†) | 3.45 × 10−1 (6.47 × 10−2)+(†) | 1.01 × 10−1 (1.83 × 10−2)+(†) | 4.17 × 10−2 (6.11 × 10−3)+(†) | 6.75 × 10−2 (1.25 × 10−2)+(†) | 1.35 × 100 (9.23 × 10−2)+(†) | 2.17 × 10−1 (3.27 × 10−2)+(†) | 2.27 × 10−2 (5.41 × 10−3) | 2.11 × 10−2 (5.47 × 10−3) | |
| 10 | 8.20 × 10−2 (2.15 × 10−2)+(†) | 4.72 × 10−1 (1.61 × 10−1)+(†) | 4.05 × 10−1 (8.55 × 10−2)+(†) | 1.17 × 10−1 (1.69 × 10−2)+(†) | 5.59 × 10−2 (8.06 × 10−3)+(†) | 6.50 × 10−2 (1.47 × 10−2)+(†) | 1.37 × 100 (1.43 × 10−1)+(†) | 1.77 × 10−1 (3.73 × 10−2)+(†) | 2.27 × 10−2 (6.19 × 10−3) | 1.95 × 10−2 (5.94 × 10−3) | |
| DTLZ6 | 3 | 3.71 × 10−2 (2.01 × 10−2)+(†) | 3.44 × 10−2 (4.42 × 10−3)+(†) | 4.31 × 10−3 (2.63 × 10−4)+(≡) | 5.59 × 10−3 (2.93 × 10−3)+(†) | 8.70 × 10−3 (1.30 × 10−3)+(†) | 4.91 × 10−3 (1.87 × 10−4)+(†) | 1.83 × 10−2 (2.13 × 10−2)+(†) | 4.43 × 100 (2.22 × 10−1)+(†) | 4.24 × 10−3 (4.25 × 10−4) | 4.31 × 10−3 (7.13 × 10−4) |
| 5 | 1.41 × 10−1 (6.70 × 10−2)+(†) | 7.20 × 10−1 (3.76 × 10−1)+(†) | 4.33 × 10−1 (2.03 × 10−1)+(†) | 6.46 × 10−2 (1.59 × 10−2)+(†) | 1.05 × 10−2 (1.52 × 10−3)-(↓) | 5.41 × 10−2 (1.40 × 10−2)+(†) | 7.02 × 10−1 (1.11 × 10−1)+(†) | 9.44 × 100 (6.58 × 10−1)+(†) | 4.34 × 10−2 (8.72 × 10−3) | 4.94 × 10−2 (3.11 × 10−2) | |
| 8 | 2.56 × 10−1 (2.57 × 10−1)+(↓) | 2.11 × 100 (7.06 × 10−1)+(†) | 3.11 × 100 (9.10 × 10−1)+(†) | 1.68 × 10−1 (3.13 × 10−2)-(↓) | 2.29 × 10−2 (5.43 × 10−3)-(↓) | 8.22 × 10−2 (2.23 × 10−2)-(↓) | 1.04 × 100 (1.15 × 10−1)+(†) | 9.90 × 100 (4.57 × 10−2)+(†) | 2.27 × 10−1 (3.55 × 10−1) | 3.26 × 10−1 (4. × 10 × 10−1) | |
| 10 | 2.32 × 10−1 (5.65 × 10−2)+(†) | 3.43 × 100 (7.72 × 10−1)+(†) | 3.07 × 100 (6.55 × 10−1)+(†) | 2.03 × 10−1 (5.65 × 10−2)+(†) | 4.47 × 10−2 (2.30 × 10−2)-(↓) | 9.96 × 10−2 (3.81 × 10−2)+(†) | 1.00 × 100 (1.02 × 10−1)+(†) | 9.82 × 100 (2.17 × 10−1)+(†) | 8.81 × 10−2 (1.36 × 10−1) | 8.98 × 10−2 (3.31 × 10−1) | |
| DTLZ7 | 3 | 9.03 × 10−2 (9.14 × 10−2)+(†) | 8.71 × 10−2 (2.94 × 10−3)+(†) | 8.54 × 10−2 (9.16 × 10−2)+(†) | 1.28 × 10−1 (1.39 × 10−1)+(†) | 1.71 × 10−1 (6.14 × 10−2)+(†) | 8.21 × 10−2 (9.40 × 10−2)+(†) | 3.88 × 10−1 (1.06 × 10−1)+(†) | 1.50 × 10−1 (2.04 × 10−1)+(†) | 3.61 × 10−2 (2.09 × 10−1) | 3.12 × 10−2 (2.42 × 10−1) |
| 5 | 3.09 × 10−1 (1.01 × 10−2)+(†) | 3.65 × 10−1 (7.01 × 10−3)+(†) | 3.20 × 10−1 (9.75 × 10−3)+(†) | 2.95 × 10−1 (2.96 × 10−2)+(†) | 5.03 × 10−1 (5.79 × 10−2)+(†) | 2.91 × 10−1 (1.01 × 10−2)+(≡) | 8.14 × 10−1 (1.11 × 10−1)+(†) | 5.18 × 10−1 (3.60 × 10−2)+(†) | 2.13 × 10−1 (2.39 × 10−1) | 2.91 × 10−1 (2.15 × 10−1) | |
| 8 | 6.99 × 10−1 (2.30 × 10−2)+(†) | 9.27 × 10−1 (3.42 × 10−2)+(†) | 6.74 × 10−1 (1.93 × 10−2)=(†) | 7.76 × 10−1 (2.32 × 10−2)+(†) | 1.16 × 100 (1.15 × 10−1)+(†) | 8.03 × 10−1 (4.76 × 10−2)+(†) | 3.30 × 100 (4.94 × 10−1)+(†) | 2.86 × 100 (8.59 × 10−1)+(†) | 6.74 × 10−1 (1.66 × 10−1) | 6.42 × 10−1 (1.20 × 10−1) | |
| 10 | 7.48 × 10−1 (3.52 × 10−2)=(≡) | 1.60 × 100 (4.42 × 10−2)+(†) | 9.40 × 10−1 (2.95 × 10−2)+(†) | 8.34 × 10−1 (1.01 × 10−2)+(†) | 1.45 × 100 (1.63 × 10−1)+(†) | 1.04 × 100 (5.04 × 10−2)+(†) | 4.55 × 100 (5.21 × 10−1)+(†) | 3.96 × 100 (1.34 × 100)+(†) | 7.48 × 10−1 (1.75 × 10−1) | 7.48 × 10−1 (6.33 × 10−2) | |
| Ad-GrMODE1* (+/=/-) | 23/1/4 | 23/2/3 | 23/1/4 | 23/1/4 | 23/0/5 | 20/1/7 | 24/0/4 | 26/1/1 | |||
| Ad-GrMODE2* (†/≡/↓) | 22/1/5 | 23/0/5 | 23/1/4 | 19/3/6 | 23/0/5 | 20/1/7 | 24/0/4 | 27/0/1 | |||
The signs ‘+’, ‘=’, and ‘-’ depicts the instances, ad-GrMODE1* performs better, similar and worse with respect to state-of-the-art algorithms. The signs ‘†’, ‘≡’, and ‘↓’ depicts the in-stances, ad-GrMODE2* performs better, similar and worse with respect to state-of-the-art algorithms.

Table A6.
Mean and standard deviation values of IGD results of proposed method with state of art algorithms on WFG problems.
Table A6.
Mean and standard deviation values of IGD results of proposed method with state of art algorithms on WFG problems.
| # | M | NSGAIII | SPEA-R | VaEA | SRA | MODE | EMyO-C | MyODEMR | GAMODE | adGrMOEA1* | adGrMOEA2* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WFG1 | 3 | 1.58 × 100 (9.52 × 10−2)+(†) | 1.53 × 100 (7.83 × 10−4)+(†) | 1.53 × 100 (2.09 × 10−3)+(†) | 1.53 × 100 (3.97 × 10−3)+(†) | 2.38 × 100 (5.74 × 10−2)+(†) | 1.83 × 100 (2.05 × 10−2)+(†) | 1.89 × 100 (6.79 × 10−2)+(†) | 1.68 × 100 (5.81 × 10−2)+(†) | 1.46 × 100 (4.75 × 10−3) | 1.46 × 100 (6.31 × 10−3) |
| 5 | 2.14 × 100 (1.33 × 10−1)+(†) | 2.39 × 100 (3.06 × 10−1)+(†) | 2.21 × 100 (5.80 × 10−3)+(†) | 1.99 × 100 (6.43 × 10−3)-(↓) | 2.58 × 100 (3.63 × 10−2)+(†) | 2.10 × 100 (1.11 × 10−2)+(†) | 2.66 × 100 (4.07 × 10−1)+(†) | 2.08 × 100 (3.08 × 10−2)+(†) | 2.04 × 100 (1.61 × 10−2) | 2.05 × 100 (1.70 × 10−2) | |
| 8 | 2.72 × 100 (7.44 × 10−2)+(†) | 2.78 × 100 (1.91 × 10−1)+(†) | 2.66 × 100 (1.53 × 10−2)-(↓) | 2.63 × 100 (2.25 × 10−2)-(↓) | 2.96 × 100 (2.20 × 10−2)+(†) | 2.70 × 100 (8.69 × 10−3)=(≡) | 3.89 × 100 (6.35 × 10−1)+(†) | 2.65 × 100 (2.35 × 10−2)-(↓) | 2.70 × 100 (1.75 × 10−2) | 2.70 × 100 (1.94 × 10−2) | |
| 10 | 3.01 × 100 (5.28 × 10−2)-(↓) | 3.02 × 100 (3.70 × 10−2)-(↓) | 3.02 × 100 (1.90 × 10−2)-(↓) | 3.19 × 100 (2.06 × 10−2)+(†) | 3.19 × 100 (9.09 × 10−3)+(†) | 3.03 × 100 (9.74 × 10−3)-(↓) | 4.59 × 100 (8.47 × 10−1)+(†) | 2.99 × 100 (1.57 × 10−2)-(↓) | 3.05 × 100 (2.25 × 10−2) | 3.06 × 100 (2.51 × 10−2) | |
| WFG2 | 3 | 3.04 × 100 (3.90 × 10−3)-(↓) | 3.04 × 100 (2.37 × 10−3)-(↓) | 3.04 × 100 (2.27 × 10−3)-(↓) | 3.05 × 100 (2.96 × 10−3)=(≡) | 3.05 × 100 (5.13 × 10−3)=(≡) | 3.04 × 100 (4.62 × 10−3)-(↓) | 3.12 × 100 (2.94 × 10−2)+(†) | 3.04 × 100 (1.11 × 10−3)-(↓) | 3.05 × 100 (3.13 × 10−3) | 3.05 × 100 (4.04 × 10−3) |
| 5 | 5.69 × 100 (4.83 × 10−3)+(†) | 5.69 × 100 (2.95 × 10−3)+(†) | 5.69 × 100 (2.55 × 10−3)+(†) | 5.69 × 100 (1.20 × 10−3)+(†) | 5.71 × 100 (1.18 × 10−2)+(†) | 5.69 × 100 (3.04 × 10−3)+(†) | 7.12 × 100 (9.66 × 10−1)+(†) | 5.69 × 100 (1.26 × 10−3)+(†) | 4.66 × 100 (2.01 × 10−3) | 4.67 × 100 (1.56 × 10−3) | |
| 8 | 9.41 × 100 (1.26 × 10−2)=(≡) | 9.41 × 100 (9.11 × 10−4)=(≡) | 9.41 × 100 (1.44 × 10−3)=(≡) | 9.41 × 100 (1.11 × 10−3)=(≡) | 9.45 × 100 (2.70 × 10−2)+(†) | 9.41 × 100 (3.40 × 10−3)=(≡) | 1.29 × 10+1 (7.06 × 10−1)+(†) | 9.41 × 100 (1.42 × 10−3)=(≡) | 9.41 × 100 (1.51 × 10−3) | 9.41 × 100 (1.40 × 10−3) | |
| 10 | 1.20 × 10+1 (4.55 × 10−3)=(≡) | 1.20 × 10+1 (1.41 × 10−3)=(≡) | 1.20 × 10+1 (1.54 × 10−3)=(≡) | 1.20 × 10+1 (1.11 × 10−3)=(≡) | 1.20 × 10+1 (2.44 × 10−2)=(≡) | 1.20 × 10+1 (4.57 × 10−3)=(≡) | 1.60 × 10+1 (1.27 × 100)+(†) | 1.20 × 10+1 (1.39 × 10−3)=(≡) | 1.20 × 10+1 (1.03 × 10−3) | 1.20 × 10+1 (8.86 × 10−4) | |
| WFG3 | 3 | 1.39 × 100 (4.46 × 10−3)+(†) | 1.39 × 100 (1.02 × 10−3)+(†) | 1.38 × 100 (1.82 × 10−3)+(†) | 1.38 × 100 (7.19 × 10−4)+(†) | 1.39 × 100 (6.16 × 10−3)+(†) | 1.38 × 100 (5.49 × 10−4)+(†) | 2.74 × 100 (2.31 × 10−1)+(†) | 1.44 × 100 (2.08 × 10−3)+(†) | 1.23 × 100 (4.63 × 10−4) | 1.13 × 100 (2.39 × 10−4) |
| 5 | 2.33 × 100 (8.13 × 10−2)+(†) | 2.28 × 100 (5.09 × 10−3)+(†) | 2.25 × 100 (1.68 × 10−3)+(†) | 2.25 × 100 (1.52 × 10−3)+(†) | 2.27 × 100 (1.41 × 10−2)+(†) | 2.24 × 100 (1.77 × 10−3)+(†) | 5.84 × 100 (3.18 × 10−2)+(†) | 2.32 × 100 (3.04 × 10−3)+(†) | 1.61 × 100 (1.14 × 10−3) | 1.31 × 100 (2.06 × 10−3) | |
| 8 | 3.72 × 100 (4.15 × 10−2)=(†) | 6.28 × 100 (8.42 × 10−1)+(†) | 3.67 × 100 (3.84 × 10−3)-(↓) | 3.67 × 100 (5.33 × 10−3)-(↓) | 3.71 × 100 (1.95 × 10−2)-(≡) | 3.66 × 100 (3.58 × 10−3)-(↓) | 1.04 × 10+1 (9.96 × 10−2)+(†) | 3.74 × 100 (4.92 × 10−3)+(†) | 3.72 × 100 (5.00 × 10−3) | 3.71 × 100 (5.44 × 10−3) | |
| 10 | 3.47 × 100 (1.70 × 10−2)+(†) | 4.88 × 100 (8.23 × 10−1)+(†) | 3.41 × 100 (2.19 × 10−3)+(†) | 3.41 × 100 (4.35 × 10−3)+(†) | 3.44 × 100 (2.11 × 10−2)+(†) | 3.40 × 100 (2.74 × 10−3)+(†) | 9.94 × 100 (1.05 × 10−1)+(†) | 3.53 × 100 (2.55 × 10−3)+(†) | 3.21 × 100 (1.74 × 10−3) | 3.12 × 100 (2.33 × 10−3) | |
| WFG4 | 3 | 7.95 × 100 (2.20 × 10−3)+(†) | 7.93 × 10−1 (1.22 × 10−3)+(†) | 8.06 × 10−1 (4.13 × 10−3)+(†) | 8.47 × 10−1 (9.26 × 10−3)+(†) | 1.06 × 100 (6.75 × 10−2)+(†) | 8.24 × 10−1 (7.07 × 10−3)+(†) | 8.20 × 10−1 (6.89 × 10−3)+(†) | 8.61 × 10−1 (2.14 × 10−2)+(†) | 6.48 × 10−1 (1.01 × 10−2) | 6.48 × 10−1 (7.88 × 10−3) |
| 5 | 1.62 × 100 (8.33 × 10−3)+(†) | 1.65 × 100 (3.48 × 10−3)+(†) | 1.64 × 100 (9.27 × 10−3)+(†) | 1.78 × 100 (2.31 × 10−2)+(†) | 2.95 × 100 (2.61 × 10−1)+(†) | 2.10 × 100 (1.13 × 10−1)+(†) | 1.71 × 100 (2.18 × 10−2)+(†) | 1.75 × 100 (3.61 × 10−2)+(†) | 1.42 × 100 (3.74 × 10−2) | 1.49 × 100 (4.77 × 10−2) | |
| 8 | 3.71 × 100 (1.55 × 10−1)-(↓) | 3.57 × 100 (2.96 × 10−2)-(↓) | 3.36 × 100 (1.85 × 10−2)-(↓) | 3.94 × 100 (1.68 × 10−1)-(↓) | 6.73 × 100 (4.36 × 10−1)+(†) | 4.93 × 100 (1.84 × 10−1)+(†) | 3.73 × 100 (8.90 × 10−2)-(↓) | 3.76 × 100 (5.93 × 10−2)-(↓) | 4.23 × 100 (2.10 × 10−1) | 4.22 × 100 (2.00 × 10−1) | |
| 10 | 4.82 × 100 (1.59 × 10−1)-(↓) | 4.87 × 100 (1.72 × 10−2)-(↓) | 4.32 × 100 (2.24 × 10−2)-(↓) | 5.67 × 100 (3.55 × 10−1)-(↓) | 8.68 × 100 (5.27 × 10−1)+(†) | 6.54 × 100 (2.26 × 10−1)+(†) | 4.93 × 100 (9.02 × 10−2)-(↓) | 4.98 × 100 (9.08 × 10−2)-(↓) | 5.86 × 100 (3.09 × 10−1) | 5.77 × 100 (4.54 × 10−1) | |
| WFG5 | 3 | 3.39 × 10−1 (7.17 × 10−3)+(↓) | 3.49 × 10−1 (1.01 × 10−3)+(↓) | 3.17 × 10−1 (3.06 × 10−3)-(↓) | 3.72 × 10−1 (1.17 × 10−2)+(†) | 3.83 × 10−1 (9.54 × 10−3)+(†) | 3.23 × 10−1 (3.63 × 10−3)+(↓) | 3.68 × 10−1 (1.02 × 10−2)+(≡) | 3.29 × 10−1 (2.52 × 10−3)+(↓) | 3.20 × 10−1 (1.33 × 10−2) | 3.68 × 10−1 (1.09 × 10−2) |
| 5 | 2.31 × 100 (2.43 × 10−2)-(≡) | 2.50 × 100 (2.41 × 10−2) +(†) | 2.23 × 100 (7.90 × 10−3)-(↓) | 2.29 × 100 (1.71 × 10−2)-(↓) | 2.51 × 100 (5.59 × 10−2)+(†) | 2.20 × 100 (9.98 × 10−3)-(↓) | 2.34 × 100 (4.35 × 10−2)=(†) | 2.25 × 100 (1.06 × 10−2)-(↓) | 2.34 × 100 (2.07 × 10−2) | 2.31 × 100 (1.89 × 10−2) | |
| 8 | 6.76 × 100 (2.51 × 10−2)+(†) | 6.83 × 100 (2.64 × 10−2)+(†) | 6.68 × 100 (1.16 × 10−2)+(†) | 6.80 × 100 (2.60 × 10−2)+(†) | 7.23E × 100 (8.51 × 10−2)+(†) | 6.64 × 100 (8.54 × 10−3)+(†) | 7.21 × 100 (1.27 × 10−1)+(†) | 6.74 × 100 (1.84 × 10−2)+(†) | 6.02 × 100 (8.29 × 10−2) | 6.00 × 100 (6.95 × 10−2) | |
| 10 | 9.82 × 100 (2.31 × 10−2)-(↓) | 9.92 × 100 (2.27 × 10−2)-(↓) | 9.76 × 100 (1.29 × 10−2)-(↓) | 9.94 × 100 (3.74 × 10−2)-(↓) | 1.04 × 10+1 (7.00 × 10−2)+(†) | 9.72 × 100 (1.07 × 10−2)-(↓) | 1.07 × 10+1 (1.50 × 100)+(†) | 9.85 × 100 (1.25 × 10−2)-(↓) | 1.01 × 10+1 (9.71 × 10−2) | 1.01 × 10+1 (8.99 × 10−2) | |
| WFG6 | 3 | 2.20 × 100 (3.96 × 10−2)+(†) | 2.18 × 100 (3.01 × 10−3)+(†) | 2.17 × 100 (4.27 × 10−3)+(†) | 2.17 × 100 (3.79 × 10−3)+(†) | 2.22 × 100 (1.57 × 10−2)+(†) | 2.17 × 100 (6.04 × 10−3)+(†) | 2.25 × 100 (3.90 × 10−2)+(†) | 2.18 × 100 (3.00 × 10−3)+(†) | 2.13 × 100 (2.53 × 10−3) | 2.11 × 100 (2.46 × 10−3) |
| 5 | 5.78 × 100 (6.65 × 10−3)=(↓) | 5.78 × 100 (7.77 × 10−3)=(↓) | 5.78 × 100 (5.21 × 10−3)=(↓) | 5.81 × 100 (8.17 × 10−3)+(↓) | 5.87 × 100 (3.39 × 10−2)+(†) | 5.78 × 100 (1.16 × 10−2)=(↓) | 6.08 × 100 (7.74 × 10−2)+(†) | 5.78 × 100 (3.60 × 10−3)=(↓) | 5.78 × 100 (6.74 × 10−3) | 5.82 × 100 (9.97 × 10−3) | |
| 8 | 1.17 × 10+1 (1.30 × 10−2)+(†) | 1.17 × 10+1 (2.65 × 10−2)+(†) | 1.17 × 10+1 (3.99 × 10−3)+(†) | 1.17 × 10+1 (1.92 × 10−2)+(†) | 1.18 × 10+1 (3.86 × 10−2)+(†) | 1.17 × 10+1 (1.62 × 10−2)+(†) | 1.23 × 10+1 (7.11 × 10−2)+(†) | 1.17 × 10+1 (4.49 × 10−3)+(†) | 1.07 × 10+1 (1.33 × 10−2) | 1.07 × 10+1 (1.08 × 10−2) | |
| 10 | 1.56 × 10+1 (4.64 × 10−2)=(≡) | 1.56 × 10+1 (3.33 × 10−2)=(≡) | 1.56 × 10+1 (2.20 × 10−3)=(≡) | 1.56 × 10+1 (3.95 × 10−2)=(≡) | 1.56 × 10+1 (3.34 × 10−2)=(≡) | 1.55 × 10+1 (1.55 × 10−2)-(↓) | 1.63 × 10+1 (5.04 × 10−2)+(†) | 1.54 × 10+1 (3.90 × 10−3)-(↓) | 1.56 × 10+1 (1.03 × 10−2) | 1.56 × 10+1 (1.00 × 10−2) | |
| WFG7 | 3 | 1.34 × 100 (2.46 × 10−1)+(†) | 1.30 × 100 (7.80 × 10−3)+(†) | 1.29 × 100 (4.36 × 10−3)+(†) | 1.30 × 100 (7.11 × 10−3)+(†) | 1.68 × 100 (6.05 × 10−2)+(†) | 1.32 × 100 (1.00 × 10−2)+(†) | 1.34 × 100 (1.44 × 10−2)+(†) | 1.33 × 100 (9.56 × 10−3)+(†) | 1.21 × 100 (6.55 × 10−3) | 1.11 × 100 (8.02 × 10−3) |
| 5 | 2.78 × 100 (7.06 × 10−1)+(†) | 2.21 × 100 (6.47 × 10−3)+(†) | 2.30 × 100 (1.04 × 10−2)+(†) | 2.39 × 100 (2.74 × 10−2)+(†) | 3.16 × 100 (6.71 × 10−2)+(†) | 2.37 × 100 (3.92 × 10−2)+(†) | 2.47 × 100 (4.19 × 10−2)+(†) | 2.42 × 100 (2.69 × 10−2)+(†) | 2.11 × 100 (3.14 × 10−2) | 2.15 × 100 (3.29 × 10−2) | |
| 8 | 4.59 × 100 (7.77 × 10−1)+(†) | 4.29 × 100 (8.99 × 10−2)+(†) | 4.51 × 100 (3.46 × 10−2)+(†) | 4.56 × 100 (5.53 × 10−2)+(†) | 5.76 × 100 (8.00 × 10−2)+(†) | 4.45 × 100 (5.71 × 10−2)+(†) | 4.68 × 100 (6.66 × 10−2)+(†) | 4.58 × 100 (3.98 × 10−2)+(†) | 3.63 × 100 (6.23 × 10−2) | 3.64 × 100 (4.62 × 10−2) | |
| 10 | 5.33 × 100 (5.34 × 10−2)+(†) | 5.51 × 100 (3.60 × 10−2)+(†) | 5.65 × 100 (3.19 × 10−2)+(†) | 5.61 × 100 (5.15 × 10−2)+(†) | 6.99 × 100 (6.45 × 10−2)+(†) | 5.47 × 100 (4.98 × 10−2)+(†) | 5.83 × 100 (4.02 × 10−2)+(†) | 5.80 × 100 (3.95 × 10−2)+(†) | 4.76 × 100 (8.51 × 10−2) | 4.77 × 100 (7.68 × 10−2) | |
| WFG8 | 3 | 2.17 × 100 (2.83 × 10−2)+(†) | 2.09 × 100 (2.54 × 10−3)+(†) | 2.11 × 100 (2.34 × 10−2)+(†) | 2.15 × 100 (2.72 × 10−2)+(†) | 2.14 × 100 (1.71 × 10−2)+(†) | 2.08 × 100 (3.12 × 10−3)+(†) | 2.17 × 100 (3.74 × 10−2)+(†) | 2.10 × 100 (2.43 × 10−3)+(†) | 2.03 × 100 (3.20 × 10−2) | 2.04 × 100 (2.25 × 10−2) |
| 5 | 5.77 × 100 (1.57 × 10−2)+(†) | 5.71 × 100 (3.38 × 10−3)+(†) | 5.72 × 100 (6.52 × 10−3)+(†) | 5.74 × 100 (1.55 × 10−2)+(†) | 5.80 × 100 (2.80 × 10−2)+(†) | 5.70 × 100 (1.07 × 10−2)+(†) | 6.34 × 100 (1.36 × 10−1)+(†) | 5.70 × 100 (4.83 × 10−3)+(†) | 5.59 × 100 (9.66 × 10−3) | 5.52 × 100 (1.12 × 10−2) | |
| 8 | 1.17 × 10+1 (2.68 × 10−2)+(†) | 1.17 × 10+1 (2.64 × 10−2)+(†) | 1.16 × 10+1 (1.04 × 10−2)+(†) | 1.17 × 10+1 (1.58 × 10−2)+(†) | 1.17 × 10+1 (5.16 × 10−2)+(†) | 1.16 × 10+1 (1.29 × 10−2)+(†) | 1.28 × 10+1 (2.00 × 10−1)+(†) | 1.16 × 10+1 (4.33 × 10−3)+(†) | 1.13 × 10+1 (1.23 × 10−2) | 1.12 × 10+1 (1.85 × 10−2) | |
| 10 | 1.55 × 10+1 (2.09 × 10−2)=(≡) | 1.55 × 10+1 (2.22 × 10−2)=(≡) | 1.55 × 10+1 (7.43 × 10−3)=(≡) | 1.55 × 10+1 (1.17 × 10−2)=(≡) | 1.55 × 10+1 (4.88 × 10−2)=(≡) | 1.55 × 10+1 (1.71 × 10−2)=(≡) | 1.67 × 10+1 (2.53 × 10−1)+(†) | 1.55 × 10+1 (4.99 × 10−3)=(≡) | 1.55 × 10+1 (2.09 × 10−2) | 1.55 × 10+1 (3.08 × 10−2) | |
| WFG9 | 3 | 4.00 × 10−1 (9.52 × 10−3)-(↓) | 4.14 × 10−1 (7.36 × 10−3)+(†) | 4.15 × 10−1 (1.17 × 10−2)+(†) | 4.53 × 10−1 (1.60 × 10−2)+(†) | 1.27 × 100 (1.57 × 10−1)+(†) | 4.07 × 10−1 (6.94 × 10−3)+(†) | 4.35 × 10−1 (8.79 × 10−3)+(†) | 4.80 × 10−1 (8.67 × 10−3)+(†) | 4.05 × 10−1 (1.35 × 10−2) | 4.01 × 10−1 (1.35 × 10−2) |
| 5 | 1.13 × 100 (4.00 × 10−2)+(↓) | 1.11 × 100 (8.65 × 10−3)=(↓) | 1.18 × 100 (1.16 × 10−2)+(†) | 1.28 × 100 (1.89 × 10−2)+(†) | 4.57 × 100 (4.04 × 10−1)+(†) | 1.27 × 100 (3.00 × 10−2)+(†) | 1.35 × 100 (4.03 × 10−2)+(†) | 1.51 × 100 (1.62 × 10−1)+(†) | 1.11 × 100 (2.87 × 10−2) | 1.15 × 100 (6.58 × 10−2) | |
| 8 | 3.45 × 100 (1.69 × 10−1)+(†) | 3.22 × 100 (1.16 × 10−1)+(†) | 3.09 × 100 (3.57 × 10−2)+(†) | 3.29 × 100 (1.38 × 10−1)+(†) | 1.01 × 10+1 (4.22 × 10−1)+(†) | 3.80 × 100 (1.94 × 10−1)+(†) | 6.64 × 100 (1.91 × 100)+(†) | 5.59 × 100 (3.66 × 10−1)+(†) | 2.46 × 100 (3.40 × 10−1) | 2.47 × 100 (3.96 × 10−1) | |
| 10 | 4.65 × 100 (2.94 × 10−1)+(†) | 4.66 × 100 (9.98 × 10−2)+(†) | 4.25 × 100 (8.17 × 10−2)-(↓) | 4.54 × 100 (2.39 × 10−1)+(†) | 1.34 × 10+1 (4.62 × 10−1)+(†) | 5.70 × 100 (2.17 × 10−1)+(†) | 8.90 × 100 (1.65 × 100)+(†) | 8.16 × 100 (4.16 × 10−1)+(†) | 4.51 × 100 (4.74 × 10−1) | 4.52 × 100 (3.85 × 10−1) | |
| Ad-GrMODE1* (+/=/-) | 23/6/7 | 25/5/6 | 21/5/10 | 24/5/7 | 31/4/1 | 25/5/6 | 33/1/2 | 24/4/8 | |||
| Ad-GrMODE2* (†/≡/↓) | 22/5/9 | 24/8/4 | 21/4/11 | 23/5/8 | 31/5/0 | 24/4/8 | 33/1/2 | 23/3/10 | |||
The signs ‘+’, ‘=’, and ‘-’ depicts the instances, ad-GrMODE1* performs better, similar and worse with respect to state-of-the-art algorithms. The signs ‘†’, ‘≡’, and ‘↓’ depicts the instances, ad-GrMODE2* performs better, similar and worse with respect to state-of-the-art algorithms.
References
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. CSUR 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Palakonda, V.; Ghorbanpour, S.; Mallipeddi, R. Pareto dominance-based MOEA with multiple ranking methods for many-objective optimization. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018. [Google Scholar]
- Chen, J.; Ding, J.; Tan, K.C.; Chen, Q. A decomposition-based evolutionary algorithm for scalable multi/many-objective optimization. Memetic Comput. 2021, 13, 413–432. [Google Scholar] [CrossRef]
- Li, L.; Wang, X. An adaptive multiobjective evolutionary algorithm based on grid subspaces. Memetic Comput. 2021, 13, 249–269. [Google Scholar] [CrossRef]
- Rashno, A.; Shafipour, M.; Fadaei, S. Particle ranking: An Efficient Method for Multi-Objective Particle Swarm Optimization Feature Selection. Knowl.-Based Syst. 2022, 245, 108640. [Google Scholar] [CrossRef]
- Pan, J.-S.; Liu, N.; Chu, S.-C. A competitive mechanism based multi-objective differential evolution algorithm and its application in feature selection. Knowl.-Based Syst. 2022, 245, 108582. [Google Scholar] [CrossRef]
- Ghorbanpour, S.; Pamulapati, T.; Mallipeddi, R.; Lee, M. Energy disaggregation considering least square error and temporal sparsity: A multi-objective evolutionary approach. Swarm Evol. Comput. 2021, 64, 100909. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, G. Multi-objective differential evolution: A recent survey. Soft. Comput. Appl. 2013, 1, 1–9. [Google Scholar]
- Abbass, H.A.; Sarker, R.; Newton, C. PDE: A Pareto-frontier differential evolution approach for multi-objective optimization problems. In Proceedings of the 2001 congress on evolutionary computation (IEEE Cat. No. 01TH8546), Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Neri, F.; Tirronen, V. Recent advances in differential evolution: A survey and experimental analysis. Artif. Intell. Rev. 2010, 33, 61–106. [Google Scholar] [CrossRef]
- Ghosh, S.; Das, S.; Vasilakos, A.V.; Suresh, K. On convergence of differential evolution over a class of continuous functions with unique global optimum. IEEE Trans. Syst. Man Cybern. Part B 2011, 42, 107–124. [Google Scholar] [CrossRef]
- Tang, L.; Dong, Y.; Liu, J. Differential evolution with an individual-dependent mechanism. IEEE Trans. Evol. Comput. 2014, 19, 560–574. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009, 13, 526–553. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Islam, S.M.; Das, S.; Ghosh, S.; Roy, S.; Suganthan, P.N. An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization. IEEE Trans. Syst. Man Cybern. Part B 2011, 42, 482–500. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Enhancing the search ability of differential evolution through orthogonal crossover. Inf. Sci. 2012, 185, 153–177. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Huang, V.L.; Qin, A.K.; Suganthan, P.N.; Tasgetiren, M.F. Multi-objective optimization based on self-adaptive differential evolution algorithm. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Huang, V.L.; Zhao, S.Z.; Mallipeddi, R.; Suganthan, P.N. Multi-objective optimization using self-adaptive differential evolution algorithm. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009. [Google Scholar]
- Wang, X.; Dong, Z.; Tang, L. Multiobjective differential evolution with personal archive and biased self-adaptive mutation selection. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5338–5350. [Google Scholar] [CrossRef]
- Tang, L.; Wang, X.; Dong, Z. Adaptive multiobjective differential evolution with reference axis vicinity mechanism. IEEE Trans. Cybern. 2018, 49, 3571–3585. [Google Scholar] [CrossRef]
- Cheng, J.; Yen, G.G.; Zhang, G. A grid-based adaptive multi-objective differential evolution algorithm. Inf. Sci. 2016, 367, 890–908. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Corne, D.W.; Jerram, N.R.; Knowles, J.D.; Oates, M.J. PESA-II: Region-based selection in evolutionary multiobjective optimization. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–11 July 2001. [Google Scholar]
- Cai, X.; Xiao, Y.; Li, M.; Hu, H.; Ishibuchi, H.; Li, X. A grid-based inverted generational distance for multi/many-objective optimization. IEEE Trans. Evol. Comput. 2020, 25, 21–34. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. GDE3: The third evolution step of generalized differential evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005. [Google Scholar]
- Abbass, H.A. The self-adaptive pareto differential evolution algorithm. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Madavan, N.K. Multiobjective optimization using a Pareto differential evolution approach. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Iorio, A.W.; Li, X. Solving rotated multi-objective optimization problems using differential evolution. In Australasian Joint Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Parsopoulos, K.E.; Tasoulis, D.K.; Pavlidis, N.G.; Plagianakos, V.P.; Vrahatis, M.N. Vector evaluated differential evolution for multiobjective optimization. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753), Portland, OR, USA, 19–23 June 2004. [Google Scholar]
- Xue, F.; Sanderson, A.C.; Graves, R.J. Pareto-based multi-objective differential evolution. In Proceedings of the 2003 Congress on Evolutionary Computation, 2003. CEC’03, Canberra, ACT, Australia, 8–12 December 2003. [Google Scholar]
- Babu, B.; Jehan, M.M.L. Differential evolution for multi-objective optimization. In Proceedings of the 2003 Congress on Evolutionary Computation, CEC’03, Canberra, ACT, Australia, 8–12 December 2003. [Google Scholar]
- Tušar, T.; Filipič, B. DEMO (Differential Evolution for Multiobjective Optimization); Institut “Jožef Stefan”: Ljubljana, Slovenia, 2009. [Google Scholar]
- Yu, W.-J.; Zhang, J. Multi-population differential evolution with adaptive parameter control for global optimization. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011. [Google Scholar]
- Wang, X.; Tang, L. Multi-objective optimization using a hybrid differential evolution algorithm. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, 10–15 June 2012. [Google Scholar]
- Santana-Quintero, L.V.; Coello, C.A.C. An algorithm based on differential evolution for multi-objective problems. Int. J. Comput. Intell. Res. 2005, 1, 151–169. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Song, Y.; Zhao, H. Differential evolution algorithm with wavelet basis function and optimal mutation strategy for complex optimization problem. Appl. Soft Comput. 2021, 100, 106724. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. Self-adaptive multi-objective differential evolution with direction information provided by archived inferior solutions. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008. [Google Scholar]
- Wang, Y.-N.; Wu, L.-H.; Yuan, X.-F. Multi-objective self-adaptive differential evolution with elitist archive and crowding entropy-based diversity measure. Soft Comput. 2010, 14, 193–209. [Google Scholar] [CrossRef]
- Peng, H.; Han, Y.; Deng, C.; Wang, J.; Wu, Z. Multi-strategy co-evolutionary differential evolution for mixed-variable optimization. Knowl.-Based Syst. 2021, 229, 107366. [Google Scholar] [CrossRef]
- Liang, J.J.; Zheng, B.; Xu, F.Y.; Qu, B.Y.; Song, H. Multi-objective differential evolution algorithm based on fast sorting and a novel constraints handling technique. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014. [Google Scholar]
- Jin, Q.B.; Li, Y.T.; Cai, W. A novel grid-based bidirectional local search algorithm for many-objective optimization. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018. [Google Scholar]
- Wang, L.; Cui, G.; Zhou, Q.; Li, K. A multi-clustering method based on evolutionary multiobjective optimization with grid decomposition. Swarm Evol. Comput. 2020, 55, 100691. [Google Scholar] [CrossRef]
- Cai, X.; Sun, H.; Zhang, Q.; Huang, Y. A grid weighted sum Pareto local search for combinatorial multi and many-objective optimization. IEEE Trans. Cybern. 2018, 49, 3586–3598. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Zhang, W.; Wang, Z.; Tu, H.; You, W. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization. Swarm Evol. Comput. 2021, 62, 100843. [Google Scholar] [CrossRef]
- Wang, W.L.; Li, W.K.; Wang, Z.; Li, L. Opposition-based multi-objective whale optimization algorithm with global grid ranking. Neurocomputing 2019, 341, 41–59. [Google Scholar] [CrossRef]
- Duan, M.; Huang, Q.; Xu, R.; Wang, C.; Xu, J. Optimization of Shearer Drum Based on Multi-Objective Bat Algorithm with Grid (MOBA/G). Machines 2022, 10, 733. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, X.; Wang, C.; Yue, N.; Xie, X. Adaptive grid based multi-objective Cauchy differential evolution for stochastic dynamic economic emission dispatch with wind power uncertainty. PLoS ONE 2017, 12, e0185454. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Li, M.; Yang, S.; Liu, X. Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 2013, 18, 348–365. [Google Scholar] [CrossRef]
- Leon, M.; Xiong, N. Differential evolution enhanced with eager random search for solving real-parameter optimization problems. Int. J. Adv. Res. Artif. Intell. 2015 IJARAI-15 2015, 4, 49–57. [Google Scholar] [CrossRef]
- Lin, C.; Qing, A.; Feng, Q. A comparative study of crossover in differential evolution. J. Heuristics 2011, 17, 675–703. [Google Scholar] [CrossRef]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Li, B.; Tang, K.; Li, J.; Yao, X. Stochastic ranking algorithm for many-objective optimization based on multiple indicators. IEEE Trans. Evol. Comput. 2016, 20, 924–938. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 329–346. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans. Evol. Comput. 2016, 21, 131–152. [Google Scholar] [CrossRef]
- Denysiuk, R.; Costa, L.; Santo, I.E. Clustering-based selection for evolutionary many-objective optimization. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Denysiuk, R.; Costa, L.; Santo, I.E. Many-objective optimization using differential evolution with variable-wise mutation restriction. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 6–10 June 2013. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable test problems for evolutionary multiobjective optimization. In Evolutionary Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 105–145. [Google Scholar]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex. Syst. 1995, 9, 115–148. [Google Scholar]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.; da Fonseca, V. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Tanabe, R.; Ishibuchi, H. An easy-to-use real-world multi-objective optimization problem suite. Appl. Soft Comput. 2020, 89, 106078. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).