Research on Green Reentrant Hybrid Flow Shop Scheduling Problem Based on Improved Moth-Flame Optimization Algorithm
Abstract
:1. Introduction
- (1)
- By combining the LCA with reentrant flow shop production, an environmental impact assessment model for a reentrant flow shop was constructed and weighted with standardized environmental impact types. Thus, we obtained the lifecycle environmental emission inventory of the reentrant flow shop.
- (2)
- We constructed a GRHFSP model based on the LCA.
- (3)
- We developed an improved moth-flame optimization (MFO) algorithm to solve the GRHFSP.
- (4)
- For ten benchmark problems, the proposed algorithm was compared with four classical multi-objective optimization algorithms, and the effectiveness and superiority of the proposed algorithm were proved.
2. Literature Review
2.1. GRHFSP
2.2. LCA
2.3. Algorithms
3. Problem Description and Mathematical Modeling
3.1. Problem Description
3.1.1. GRHFSP
- (1)
- The machine is available at time zero, and all workpieces can be machined at time zero.
- (2)
- Special circumstances, such as machine failures, are not considered.
- (3)
- A workpiece can be processed at most on a single machine at any time. The workpieces do not affect each other.
- (4)
- The number of reentrant layers per workpiece, processing time of the sequence, and specific energy consumption of the machine are known and constant.
- (5)
- The buffer zone of each station is infinite.
- (6)
- The processing time and path of the workpiece are deterministic.
3.1.2. LCA for Environmental Impact
3.2. Mathematical Model
3.2.1. Variable Definitions
- (1) Indices and collection
- I: Station serial number,
- j: Workpiece serial number,
- q: Machine code,
- a: Machine serial number at station i,
- k: Process number of workpiece j,
- Ojk: kth process of workpiece j
- Ui: Set of all operations processed at station i
- Lj: Ljth-layer operation of workpiece j
- (2) Parameters
- S: Total number of workstations
- N: Total number of workpieces
- M: Total number of machines
- mi: Number of parallel machines in station i, mi = 1, 2, 3, …….
- Nj: Total number of operations of workpiece j
- L: Number of reentrant layers
- We: Theoretical weight of workpiece j
- Pjk: Processing time of operation Ojk
- Tjq(Lj): Machining time of the Ljth-layer operation of workpiece j on machine q
- Wqj: Machining power of machine q for processing workpiece j
- Wp: Startup energy consumption of machine q
- Ws: Idling power of machine q
- tsj: Idling time after machine q completes the processing of workpiece j
- EIe: Resources and environmental impact of electricity generation (unit: (KWh)−1)
- EIr: Resources and environmental impact of raw materials (unit: (kg)−1)
- EIp: Resources and environmental impact of thermal processing (unit: (kg)−1)
- A: Sufficiently large positive number
- (3) Decision variables
- Yqt: If machine q is in the processing state at processing time t, it is 1; otherwise, it is 0.
- rijka: If operation Ojk is processed on the ath machine at station i, it is 1; otherwise, it is 0.
- Hjkj’k’: If Ojk is processed before Oj’k’, it is 1; otherwise, it is 0.
- Sjk: Processing start time of operation Ojk
- Ejk: Machining end time of operation Ojk
- Cj: Completion time of workpiece j
- Cmax: Completion time
- EIL: Comprehensive resource and environmental impact
3.2.2. Model Building
- (1)
- Minimizing the makespan: The time at which the last workpiece is processed is referred to as the maximum completion time of the entire process.
- (2)
- Minimizing the comprehensive resource and environmental impacts: These include the impacts of raw material lifecycle emissions, the environmental impacts of electricity consumption, and the environmental impacts of resources in the production process. The minimization of the comprehensive resource and environmental impacts is a measure of the impact of resource consumption during the entire production process and pollutant discharge on environmental resources and can be expressed as
4. Algorithm Design
4.1. Principle of MFO Algorithm
4.2. Design of IMFO Algorithm
4.2.1. Encoding and Decoding
4.2.2. Population Initialization
4.2.3. Moth Location Update Strategy
4.2.4. Flame Number Update
4.2.5. IMFO Algorithm Flowchart
5. Experiments and Discussion
5.1. Parameter Settings
- (1)
- Convergence index: The approximation degree between the obtained Pareto front and the optimal Pareto front is evaluated. A smaller value indicates better convergence of the algorithm and better diversity of noninferior solutions.
- (2)
- Diffusion of nondominant solutions, SNS: When quantifying the diversity of nondominant solutions, a larger SNS value corresponds to richer diversity of nondominant solutions and better quality of the solutions.
- (3)
- The dominance rate POD quantifies the ability of an algorithm to dominate other algorithms. A higher POD value corresponds to better performance of the algorithm.
5.2. Discussion
6. Conclusions and Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Graves, S.C.; Meal, H.C.; Stefek, D.; Zeghmi, A.H. Scheduling of re-entrant flow shops. J. Oper. Manag. 1983, 3, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, Z.; Ahmed, T.; Antunes, A. Environmental Life Cycle Assessment of Leather Processing Industry: A Case Study of Bangladesh. J. Soc. Leather Technol. Chem. 2018, 102, 18–26. [Google Scholar]
- Dugardin, F.; Yalaoui, F.; Amodeo, L. New multi-objective method to solve reentrant hybrid flow shop scheduling problem. Eur. J. Oper. Res. 2010, 203, 22–31. [Google Scholar] [CrossRef]
- Ying, K.; Lin, S.; Wan, S. Bi-objective reentrant hybrid flowshop scheduling: An iterated Pareto greedy algorithm. Int. J. Prod. Res. 2014, 52, 5735–5747. [Google Scholar] [CrossRef]
- Geng, K.F.; Ye, C.M.; Cao, L.; Liu, L. Multi-Objective Reentrant Hybrid Flowshop Scheduling with Machines Turning on and off Control Strategy Using Improved Multi-Verse Optimizer Algorithm. Math. Probl. Eng. 2019, 2019, 2573873. [Google Scholar] [CrossRef]
- Rifai, A.P.; Nguyen, H.T.; Dawal, S. Multi-objective adaptive large neighborhood search for distributed reentrant permutation flow shop scheduling. Appl. Soft Comput. 2016, 40, 42–57. [Google Scholar] [CrossRef]
- Chamnanlor, C.; Sethanan, K.; Gen, M.; Chien, C.-F. Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints. J. Intell. Manuf. 2017, 28, 1915–1931. [Google Scholar] [CrossRef]
- Luo, H.; Du, B.; Huang, G.Q.; Chen, H.; Li, X. Hybrid flow shop scheduling considering machine electricity consumption cost. Int. J. Prod. Econ. 2013, 146, 423–439. [Google Scholar] [CrossRef]
- Li, M.; Wang, G. A review of green shop scheduling problem. Inf. Sci. 2022, 589, 478–496. [Google Scholar] [CrossRef]
- Guo, J.; Wang, L.; Kong, L.; Lv, X. Energy-efficient flow-shop scheduling with the strategy of switching the power statuses of machines. Sustain. Energy Technol. Assess. 2022, 53, 102649. [Google Scholar] [CrossRef]
- Dong, J.; Ye, C. Green scheduling of distributed two-stage reentrant hybrid flow shop considering distributed energy resources and energy storage system. Comput. Ind. Eng. 2022, 169, 108146. [Google Scholar] [CrossRef]
- Ghorbani Saber, R.; Ranjbar, M. Minimizing the total tardiness and the total carbon emissions in the permutation flow shop scheduling problem. Comput. Oper. Res. 2022, 138, 105604. [Google Scholar] [CrossRef]
- Xiuli, W.; Xianli, S.; Qi, C. Multi-Objective Flexible Flow Shop Scheduling Problem Considering Variable Processing Time due to Renewable Energy. Sustainability 2018, 10, 841. [Google Scholar]
- Lu, C.; Huang, Y.; Meng, L.; Gao, L.; Zhang, B.; Zhou, J. A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robot. Comput.-Integr. Manuf. 2022, 74, 102277. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Aktas, E.; Besikci, U. Green scheduling of a two-machine flowshop: Trade-off between makespan and energy consumption. Eur. J. Oper. Res. 2016, 248, 772–788. [Google Scholar] [CrossRef] [Green Version]
- Tang, D.; Dai, M.; Salido, M.A.; Giret, A. Energy-efficient dynamic scheduling for a flexible flow shop using an improved particle swarm optimization. Comput. Ind. 2016, 81, 82–95. [Google Scholar] [CrossRef]
- Masmoudi, O.; Yalaoui, A.; Ouazene, Y.; Chehade, H. Multi-item capacitated lot-sizing problem in a flow-shop system with energy consideration. IFAC-Pap. 2016, 49, 301–306. [Google Scholar] [CrossRef]
- Giglio, D.; Paolucci, M.; Roshani, A. Integrated lot sizing and energy-efficient job shop scheduling problem in manufacturing/remanufacturing systems. J. Clean. Prod. 2017, 148, 624–641. [Google Scholar] [CrossRef]
- Nilakantan, M.J.; Ponnambalam, S.G.; Jawahar, N. Design of energy efficient RAL system using evolutionary algorithms. Eng. Comput. 2016, 33. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Q.; Zhang, L. Minimizing energy consumption and cycle time in two-sided robotic assembly line systems using restarted simulated annealing algorithm. J. Clean. Prod. 2016, 135, 508–522. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. A novel mathematical model and multi-objective method for the low-carbon flexible job shop scheduling problem. Sustain. Comput. Inform. Syst. 2017, 13, 15–30. [Google Scholar] [CrossRef]
- Roy, P.; Nei, D.; Orikasa, T.; Xu, Q.; Okadome, H.; Nakamura, N.; Shiina, T. A review of life cycle assessment (LCA) on some food products. J. Food Eng. 2009, 90, 1–10. [Google Scholar] [CrossRef]
- Zheng, G.; Jing, Y.; Huang, H.; Zhang, X.; Gao, Y. Application of Life Cycle Assessment (LCA) and extenics theory for building energy conservation assessment. Energy 2009, 34, 1870–1879. [Google Scholar] [CrossRef]
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Basbagill, J.; Flager, F.; Lepech, M.; Fischer, M. Application of life-cycle assessment to early stage building design for reduced embodied environmental impacts. Build. Environ. 2013, 60, 81–92. [Google Scholar] [CrossRef]
- Loiseau, E.; Saikku, L.; Antikainen, R.; Droste, N.; Hansjürgens, B.; Pitkänen, K.; Leskinen, P.; Kuikman, P.; Thomsen, M. Green economy and related concepts: An overview. J. Clean. Prod. 2016, 139, 361–371. [Google Scholar] [CrossRef]
- Chen, C.; Ji, Z.C.; Wang, Y. NSGA-II applied to dynamic flexible job shop scheduling problems with machine breakdown. Mod. Phys. Lett. B 2018, 32, 18401115. [Google Scholar] [CrossRef]
- Komaki, G.M.; Kayvanfar, V. Grey Wolf Optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time. J. Comput. Sci. 2015, 8, 109–120. [Google Scholar] [CrossRef]
- Li, J.Q.; Song, M.X.; Wang, L.; Duan, P.Y.; Han, Y.Y.; Sang, H.Y.; Pan, Q.K. Hybrid Artificial Bee Colony Algorithm for a Parallel Batching Distributed Flow-Shop Problem with Deteriorating Jobs. IEEE Trans. Cybern. 2020, 50, 2425–2439. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.H.; Yuan, Y.B. A Hybrid Intelligent Approach for Co-Scheduling of Cascaded Locks With Multiple Chambers. IEEE Trans. Cybern. 2019, 49, 1236–1248. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Niar, S.; Ammari, A.C. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem. J. Intell. Manuf. 2018, 29, 603–615. [Google Scholar] [CrossRef]
- Yazdani, M.; Aleti, A.; Khalili, S.M.; Jolai, F. Optimizing the sum of maximum earliness and tardiness of the job shop scheduling problem. Comput. Ind. Eng. 2017, 107, 12–24. [Google Scholar] [CrossRef]
- Yazdani, M.; Khalili, S.M.; Babagolzadeh, M.; Jolai, F. A single-machine scheduling problem with multiple unavailability constraints: A mathematical model and an enhanced variable neighborhood search approach. J. Comput. Des. Eng. 2017, 4, 46–59. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Becherif, M.; Abdelaziz, A.Y. Dynamic performance enhancement for wind energy conversion system using Moth-Flame Optimization based blade pitch controller. Sustain. Energy Technol. Assess. 2018, 27, 206–212. [Google Scholar] [CrossRef]
- Elsakaan, A.A.; El-Sehiemy, R.A.; Kaddah, S.S.; Elsaid, M.I. An enhanced moth-flame optimizer for solving non-smooth economic dispatch problems with emissions. Energy 2018, 157, 1063–1078. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Gaber, T.; Mokhtar, U.; Hefny, H. An improved moth flame optimization algorithm based on rough sets for tomato diseases detection. Comput. Electron. Agric. 2017, 136, 86–96. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Yang, B.; Zhao, X.; Hu, L.; Cai, Z.; Huang, H.; Tong, C. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing 2017, 267, 69–84. [Google Scholar] [CrossRef]
- Shen, J.N.; Wang, L.; Deng, J. A Pareto-Based Discrete Harmony Search Algorithm for Bi-objective Reentrant Hybrid Flowshop Scheduling Problem. Harmon. Search Algorithm 2016, 382, 435–445. [Google Scholar]
- Cho, H.M.; Bae, S.J.; Kim, J.; Jeong, I.J. Bi-objective scheduling for reentrant hybrid flow shop using Pareto genetic algorithm. Comput. Ind. Eng 2011, 61, 529–541. [Google Scholar] [CrossRef]
- Bektaş, Y.; Karaca, H. Red deer algorithm based selective harmonic elimination for renewable energy application with unequal DC sources. Energy Rep. 2022, 8, 588–596. [Google Scholar] [CrossRef]
- Yazdani, M.; Jolai, F. Lion Optimization Algorithm (LOA): A nature-inspired metaheuristic algorithm. J. Comput. Des. Eng. 2016, 3, 24–36. [Google Scholar] [CrossRef]







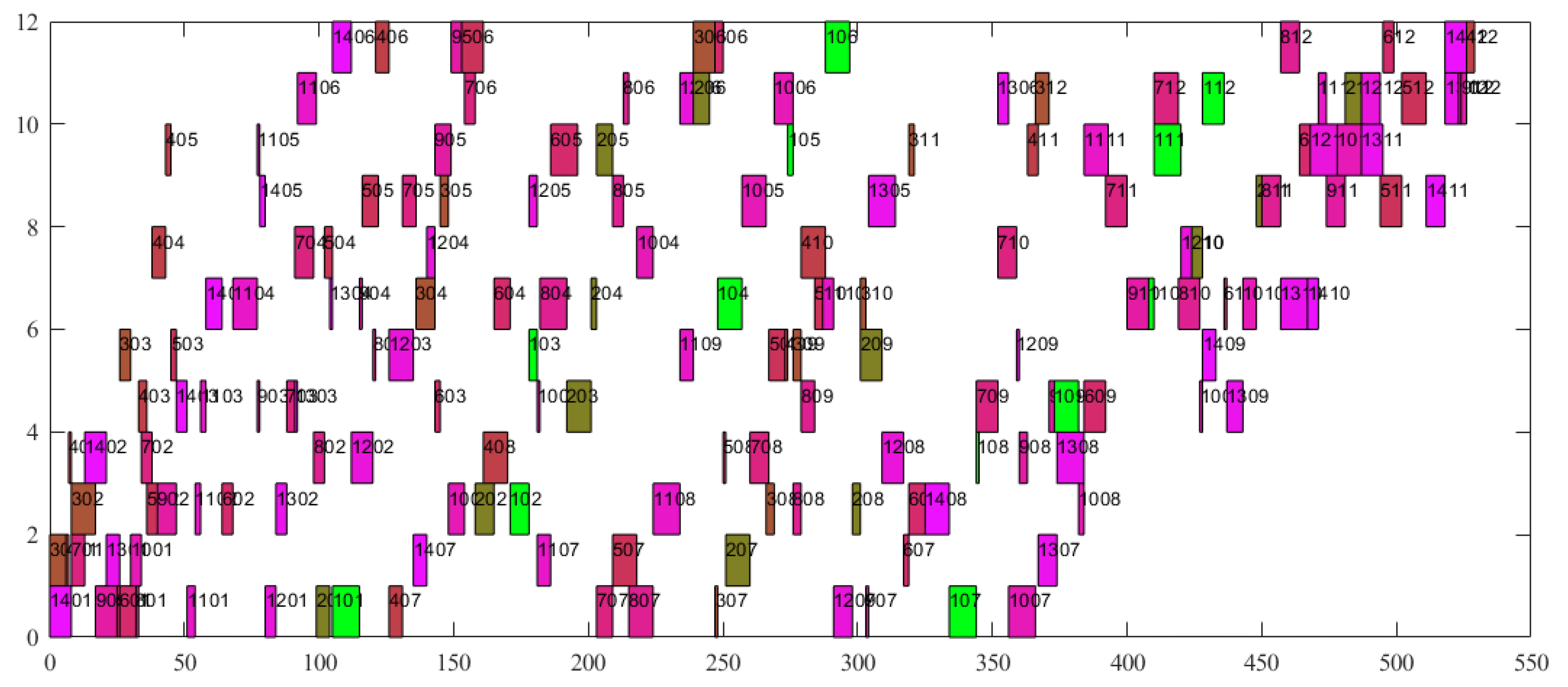
| Example Name | Number of Reentrant Layers | Location Number | Number of Jobs | Number of Machines | Processing Time |
|---|---|---|---|---|---|
| L2i10j20-2 | 2 | 10 | 20 | 2 | [1, 10] |
| L2i6j14-2 | 2 | 6 | 14 | 2 | [1, 10] |
| L2i8j12-2 | 2 | 8 | 12 | 2 | [1, 10] |
| L2i6j16-2 | 2 | 6 | 16 | 2 | [1, 10] |
| L2i8j16-2 | 2 | 8 | 16 | 2 | [1, 10] |
| L6i6j30-4 | 6 | 6 | 30 | 4 | [1, 10] |
| L6i6j40-4 | 6 | 6 | 40 | 4 | [1, 10] |
| L6i14j44-4 | 6 | 14 | 44 | 4 | [1, 10] |
| L6i13j25-4 | 6 | 13 | 25 | 4 | [1, 10] |
| L6i14j29-4 | 6 | 14 | 29 | 4 | [1, 10] |
| Numerical Example | IMFO | IGWO | DABC | NSGA-II | MOPSO | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| γ | SNS | POD | γ | SNS | POD | γ | SNS | POD | γ | SNS | POD | γ | SNS | POD | |
| L2i10j20-2 | 60.87 | 67.47 | 52.09 | 66.48 | 34.76 | 45.54 | 181.87 | 46.46 | 54.38 | 90.94 | 35.17 | 45.54 | 149.24 | 40.30 | 47.56 |
| L2i6j14-2 | 44.29 | 72.36 | 35.4 | 67.79 | 68.86 | 28.61 | 82.15 | 14.80 | 27.77 | 76.92 | 18.37 | 30.57 | 148.84 | 13.26 | 17.97 |
| L2i8j12-2 | 25.72 | 58.06 | 68.77 | 96.34 | 48.44 | 67.25 | 82.28 | 64.97 | 29.06 | 61.36 | 57.11 | 40.83 | 53.90 | 53.31 | 57.51 |
| L2i6j16-2 | 86.26 | 68.27 | 83.18 | 99.35 | 48.95 | 40.83 | 209.22 | 51.63 | 24.73 | 157.96 | 77.31 | 40.11 | 187.81 | 67.94 | 43.45 |
| L2i8j16-2 | 83.28 | 51.79 | 52.00 | 55.23 | 26.28 | 34.64 | 163.00 | 45.83 | 15.60 | 146.22 | 35.87 | 48.58 | 116.38 | 39.31 | 51.91 |
| L6i6j30-4 | 71.81 | 60.85 | 78.47 | 51.50 | 25.92 | 74.07 | 225.54 | 48.36 | 61.09 | 125.36 | 53.61 | 74.12 | 204.51 | 44.31 | 27.57 |
| L6i6j40-4 | 47.87 | 72.75 | 66.26 | 115.26 | 55.29 | 47.45 | 135.54 | 48.07 | 48.95 | 97.09 | 70.36 | 47.45 | 83.25 | 58.08 | 42.39 |
| L6i14j44-4 | 104.90 | 80.78 | 83.73 | 126.74 | 52.76 | 57.00 | 263.16 | 45.01 | 63.05 | 178.42 | 79.97 | 69.43 | 195.56 | 64.66 | 23.89 |
| L6i13j25-4 | 122.47 | 82.15 | 74.84 | 162.12 | 28.12 | 67.72 | 282.19 | 72.05 | 30.43 | 225.13 | 63.05 | 57.00 | 148.10 | 62.13 | 37.47 |
| L6i14j29-4 | 91.52 | 83.36 | 86.77 | 89.25 | 77.99 | 61.69 | 386.25 | 77.07 | 44.31 | 273.81 | 67.19 | 67.72 | 289.01 | 73.35 | 31.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Tang, H.; Xun, Q.; Lan, H.; Liu, X.; Xing, W.; Zhu, T.; Wang, L.; Pang, S. Research on Green Reentrant Hybrid Flow Shop Scheduling Problem Based on Improved Moth-Flame Optimization Algorithm. Processes 2022, 10, 2475. https://doi.org/10.3390/pr10122475
Xu F, Tang H, Xun Q, Lan H, Liu X, Xing W, Zhu T, Wang L, Pang S. Research on Green Reentrant Hybrid Flow Shop Scheduling Problem Based on Improved Moth-Flame Optimization Algorithm. Processes. 2022; 10(12):2475. https://doi.org/10.3390/pr10122475
Chicago/Turabian StyleXu, Feng, Hongtao Tang, Qining Xun, Hongyi Lan, Xia Liu, Wenfang Xing, Tianyi Zhu, Lei Wang, and Shibao Pang. 2022. "Research on Green Reentrant Hybrid Flow Shop Scheduling Problem Based on Improved Moth-Flame Optimization Algorithm" Processes 10, no. 12: 2475. https://doi.org/10.3390/pr10122475
APA StyleXu, F., Tang, H., Xun, Q., Lan, H., Liu, X., Xing, W., Zhu, T., Wang, L., & Pang, S. (2022). Research on Green Reentrant Hybrid Flow Shop Scheduling Problem Based on Improved Moth-Flame Optimization Algorithm. Processes, 10(12), 2475. https://doi.org/10.3390/pr10122475







