Reinforcement Learning Control with Deep Deterministic Policy Gradient Algorithm for Multivariable pH Process
Abstract
:1. Introduction
- Develop the RL control using the multi-DDPG agents to handle the multivariable pH process with highly nonlinear dynamics and use the grid search—hyperparameter tuning technique—to optimize the RL control performance.
- Study the control performance of the pH and level control by comparing the RL controller with multi-DDPG agents and the multi-single-input and single-output controllers.
2. Preliminary
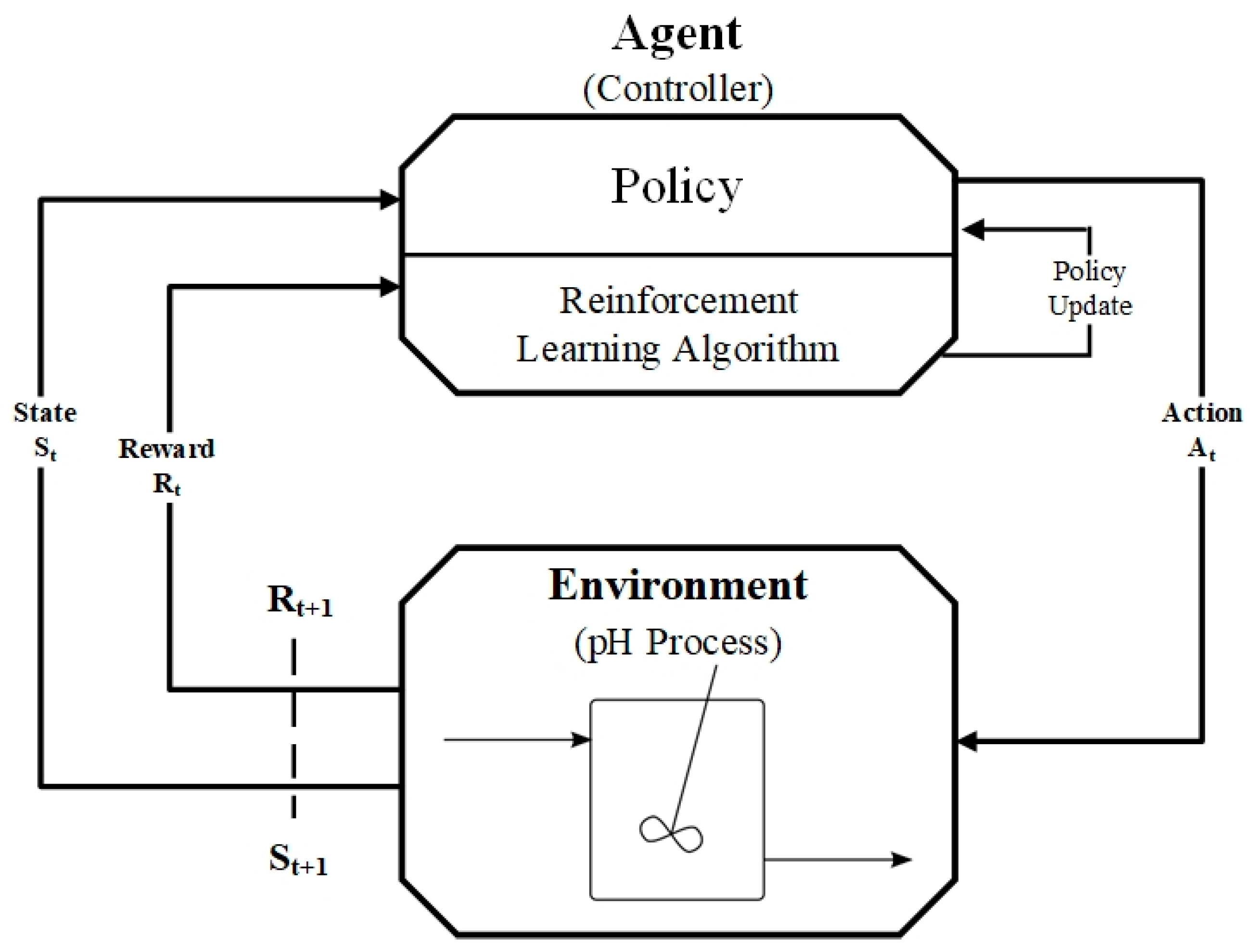
2.1. Reinforcement Learning Control
2.2. Deep Deterministic Policy Gradient Algorithm
2.3. Gated Recurrent Unit Network
2.4. Hyperparameter Tuning Technique
3. Development of RL for pH Process
3.1. Process Description and Modeling
3.2. Design RL Network Structures
3.3. Design RL Policies
3.4. Training Algorithm Setup
4. Results and Discussion
4.1. Liquid Level Control
4.1.1. Hyperparameter Tuning Results
4.1.2. Setpoint Tracking Performance of the RL Level Control
4.2. pH Control
4.2.1. Hyperparameter Tuning Results
4.2.2. Setpoint Tracking Performance of the RL pH Control
4.3. Implementation of Coupled pH and Level RL Control System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shan, Y.; Zhang, L.; Ma, X.; Hu, X.; Hu, Z.; Li, H.; Du, C.; Meng, Z. Application of the Modified Fuzzy-PID-Smith Predictive Compensation Algorithm in a PH-Controlled Liquid Fertilizer System. Processes 2021, 9, 1506. [Google Scholar] [CrossRef]
- Palacio-Morales, J.; Tobón, A.; Herrera, J. Optimization Based on Pattern Search Algorithm Applied to pH Non-Linear Control: Application to Alkalinization Process of Sugar Juice. Processes 2021, 9, 2283. [Google Scholar] [CrossRef]
- Chi, Q.; Fei, Z.; Liu, K.; Liang, J. Latent-Variable Nonlinear Model Predictive Control Strategy for a pH Neutralization Process: Q. Chi et al.: Latent-Variable NMPC Strategy for a pH Process. Asian J. Control 2015, 17, 2427–2434. [Google Scholar] [CrossRef]
- Estofanero, L.; Edwin, R.; Claudio, G. Predictive Controller Applied to a pH Neutralization Process. IFAC-Pap. 2019, 52, 202–206. [Google Scholar] [CrossRef]
- Mahmoodi, S.; Poshtan, J.; Jahed-Motlagh, M.R.; Montazeri, A. Nonlinear Model Predictive Control of a pH Neutralization Process Based on Wiener–Laguerre Model. Chem. Eng. J. 2009, 146, 328–337. [Google Scholar] [CrossRef]
- Salehi, S.; Shahrokhi, M.; Nejati, A. Adaptive Nonlinear Control of pH Neutralization Processes Using Fuzzy Approximators. Control Eng. Pract. 2009, 17, 1329–1337. [Google Scholar] [CrossRef]
- Dressler, O.J.; Howes, P.D.; Choo, J.; deMello, A.J. Reinforcement Learning for Dynamic Microfluidic Control. ACS Omega 2018, 3, 10084–10091. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2014; pp. 387–395. [Google Scholar]
- Fujii, F.; Kaneishi, A.; Nii, T.; Maenishi, R.; Tanaka, S. Self-Tuning Two Degree-of-Freedom Proportional–Integral Control System Based on Reinforcement Learning for a Multiple-Input Multiple-Output Industrial Process That Suffers from Spatial Input Coupling. Processes 2021, 9, 487. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2019, arXiv:1509.02971. [Google Scholar]
- Yoo, H.; Kim, B.; Kim, J.W.; Lee, J.H. Reinforcement Learning Based Optimal Control of Batch Processes Using Monte-Carlo Deep Deterministic Policy Gradient with Phase Segmentation. Comput. Chem. Eng. 2021, 144, 107133. [Google Scholar] [CrossRef]
- Syafiie, S.; Tadeo, F.; Martinez, E. Model-Free Learning Control of Neutralization Processes Using Reinforcement Learning. Eng. Appl. Artif. Intell. 2007, 20, 767–782. [Google Scholar] [CrossRef]
- Shah, H.; Gopal, M. Model-Free Predictive Control of Nonlinear Processes Based on Reinforcement Learning. IFAC-Pap. 2016, 49, 89–94. [Google Scholar] [CrossRef]
- Alves Goulart, D.; Dutra Pereira, R. Autonomous pH Control by Reinforcement Learning for Electroplating Industry Wastewater. Comput. Chem. Eng. 2020, 140, 106909. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Rezazadeh, A. Adaptive PID Controller Based on Reinforcement Learning for Wind Turbine Control. Int. Sch. Sci. Res. Innov. 2008, 2, 124–129. [Google Scholar]
- Gao, Y.; Matsunami, Y.; Miyata, S.; Akashi, Y. Operational Optimization for Off-Grid Renewable Building Energy System Using Deep Reinforcement Learning. Appl. Energy 2022, 325, 119783. [Google Scholar] [CrossRef]
- Options for DDPG Agent—MATLAB. Available online: https://www.mathworks.com/help/reinforcement-learning/ref/rlddpgagentoptions.html (accessed on 9 November 2022).
- Schepers, J.; Eyckerman, R.; Elmaz, F.; Casteels, W.; Latré, S.; Hellinckx, P. Autonomous Building Control Using Offline Reinforcement Learning. In Proceedings of the Advances on P2P, Parallel, Grid, Cloud and Internet Computing; Barolli, L., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 246–255. [Google Scholar]













| Parameter | Value | Unit |
|---|---|---|
| A | 0.0284 | m2 |
| 1000 | kg/m3 | |
| 1010.71 | kg/m3 | |
| 0.3159 | mol/L | |
| 0–6 | L/s | |
| 0–0.02 | L/s |
| Case Number | Episode Number | Reward Function of Policy | Number of Nodes in Hidden Layer | Average Cumulative Reward | Performance Indexes | ||
|---|---|---|---|---|---|---|---|
| ITAE | ISE | IAE | |||||
| 1 | 300 | 1 | 10 | 79.95 | 87.105 | 0.042 | 0.247 |
| 2 | 20 | 97 | 37.097 | 0.034 | 0.118 | ||
| 3 | 30 | 108.55 | 94.323 | 0.039 | 0.262 | ||
| 4 | 2 | 10 | 17.88 | 110.568 | 0.070 | 0.355 | |
| 5 | 20 | −99.05 | 96.154 | 0.062 | 0.348 | ||
| 6 | 30 | −99.05 | 96.154 | 0.062 | 0.348 | ||
| 7 | 500 | 1 | 10 | 265 | 33.465 | 0.028 | 0.112 |
| 8 | 20 | 29.30 | 66.683 | 0.038 | 0.196 | ||
| 9 | 30 | −94.40 | 40.642 | 0.029 | 0.124 | ||
| 10 | 2 | 10 | 174.30 | 46.696 | 0.028 | 0.134 | |
| 11 | 20 | 11.45 | 20.227 | 0.026 | 0.066 | ||
| 12 | 30 | −252.75 | 109.028 | 0.066 | 0.418 | ||
| 13 | 700 | 1 | 10 | 194.35 | 30.654 | 0.028 | 0.097 |
| 14 | 20 | 15.60 | 48.080 | 0.030 | 0.140 | ||
| 15 | 30 | −210.40 | 27.686 | 0.028 | 0.089 | ||
| 16 | 2 | 10 | 241.10 | 54.849 | 0.038 | 0.165 | |
| 17 | 20 | 51.21 | 78.877 | 0.044 | 0.216 | ||
| 18 | 30 | −297.12 | 59.814 | 0.034 | 0.197 | ||
| Height Level Change | Controller | Settling Time (s) | Performance Index | ||
|---|---|---|---|---|---|
| ITAE | ISE | IAE | |||
| From 10 to 80 cm | Proposed | 20 | 20.227 | 0.026 | 0.066 |
| PI | 35 | 29.804 | 0.029 | 0.096 | |
| Case Number | Episode Number | Reward Function of Policy | Number of Nodes in Hidden Layer | Average Cumulative Reward | Performance Indexes | ||
|---|---|---|---|---|---|---|---|
| ITAE | ISE | IAE | |||||
| 1 | 300 | 1 | 40 | −400 | 6664 | 151.775 | 26.947 |
| 2 | 60 | −224.25 | 6664 | 151.775 | 26.947 | ||
| 3 | 80 | −298.75 | 6664 | 151.775 | 26.947 | ||
| 4 | 2 | 40 | −67.45 | 6664 | 151.775 | 26.947 | |
| 5 | 60 | −137.30 | 6664 | 151.775 | 26.947 | ||
| 6 | 80 | −197.25 | 4060 | 40.453 | 19.788 | ||
| 7 | 500 | 1 | 40 | −321.14 | 6664 | 151.775 | 26.947 |
| 8 | 60 | −299.33 | 6372 | 141.819 | 26.082 | ||
| 9 | 80 | −309.03 | 6664 | 151.775 | 26.947 | ||
| 10 | 2 | 40 | 2.95 | 6664 | 151.775 | 26.947 | |
| 11 | 60 | −93.30 | 3423 | 39.220 | 19.415 | ||
| 12 | 80 | −90 | 2647 | 34.956 | 11.049 | ||
| 13 | 700 | 1 | 40 | −222 | 6658 | 155.371 | 26.926 |
| 14 | 60 | −400 | 6660 | 151.638 | 26.935 | ||
| 15 | 80 | −182.75 | 6283 | 133.827 | 25.285 | ||
| 16 | 2 | 40 | −21.80 | 6664 | 151.775 | 26.947 | |
| 17 | 60 | 1901 | 2818 | 38.976 | 17.186 | ||
| 18 | 80 | −200 | 2953 | 42.803 | 22.064 | ||
| pH Change | Controller | Settling Time (s) | Performance Index | ||
|---|---|---|---|---|---|
| ITAE | ISE | IAE | |||
| From pH 8.4 to 9.1 | Proposed | 16 | 2647 | 34.956 | 11.049 |
| PI | 38 | 5047 | 128.800 | 23.620 | |
| Control | Step Change | Controller | Settling Time (s) | Performance Index | ||
|---|---|---|---|---|---|---|
| ITAE | ISE | IAE | ||||
| Liquid Level | From 0.2 to 0.1 | Proposed | 227 | 1.393 | 1.982 × 10−4 | 0.005 |
| PI | - | 6.687 | 8.662 × 10−4 | 0.021 | ||
| pH | pH = 9 | Proposed | 883 | 1390 | 6.360 | 5.338 |
| PI | - | 1490 | 6.448 | 6.717 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panjapornpon, C.; Chinchalongporn, P.; Bardeeniz, S.; Makkayatorn, R.; Wongpunnawat, W. Reinforcement Learning Control with Deep Deterministic Policy Gradient Algorithm for Multivariable pH Process. Processes 2022, 10, 2514. https://doi.org/10.3390/pr10122514
Panjapornpon C, Chinchalongporn P, Bardeeniz S, Makkayatorn R, Wongpunnawat W. Reinforcement Learning Control with Deep Deterministic Policy Gradient Algorithm for Multivariable pH Process. Processes. 2022; 10(12):2514. https://doi.org/10.3390/pr10122514
Chicago/Turabian StylePanjapornpon, Chanin, Patcharapol Chinchalongporn, Santi Bardeeniz, Ratthanita Makkayatorn, and Witchaya Wongpunnawat. 2022. "Reinforcement Learning Control with Deep Deterministic Policy Gradient Algorithm for Multivariable pH Process" Processes 10, no. 12: 2514. https://doi.org/10.3390/pr10122514
APA StylePanjapornpon, C., Chinchalongporn, P., Bardeeniz, S., Makkayatorn, R., & Wongpunnawat, W. (2022). Reinforcement Learning Control with Deep Deterministic Policy Gradient Algorithm for Multivariable pH Process. Processes, 10(12), 2514. https://doi.org/10.3390/pr10122514








