Numerical Investigation of the Use of Boron Nitride/Water and Conventional Nanofluids in a Microchannel Heat Sink
Abstract
1. Introduction
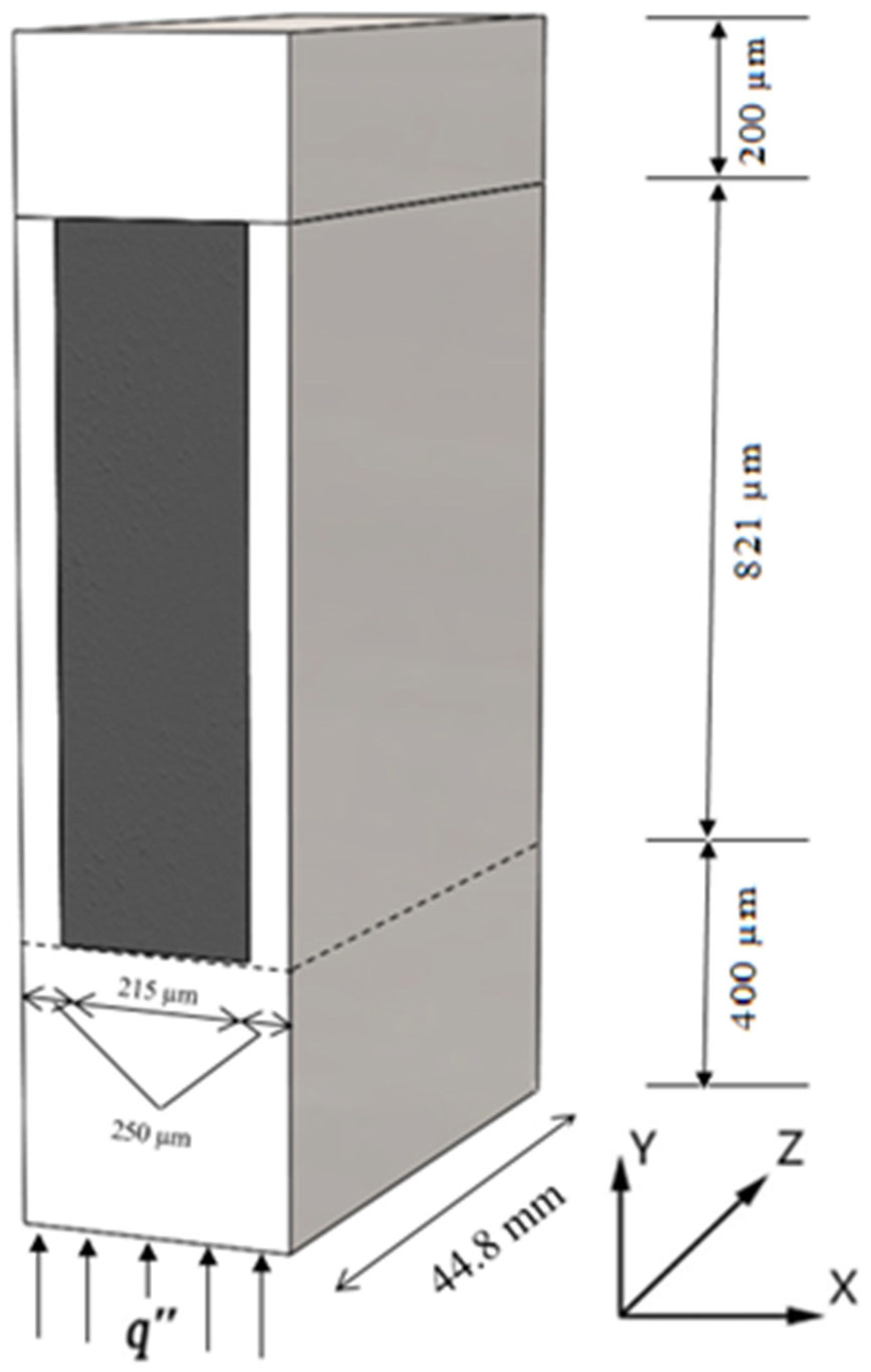
2. Materials and Methods
2.1. Governing and Additional Equations
2.2. Numerical Procedure
2.3. Nanofluid Properties
3. Results and Discussion
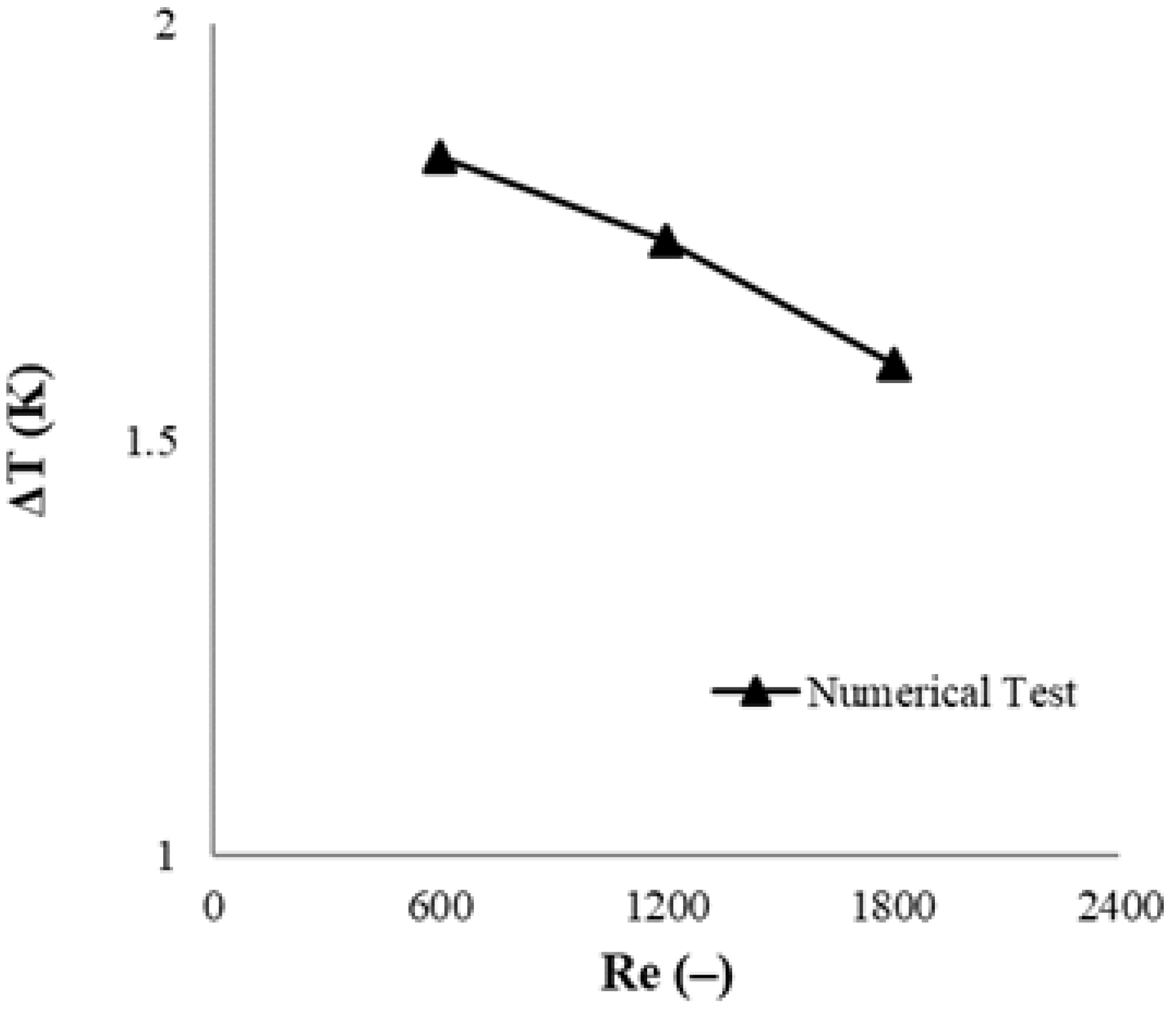
3.1. Numerical Validation
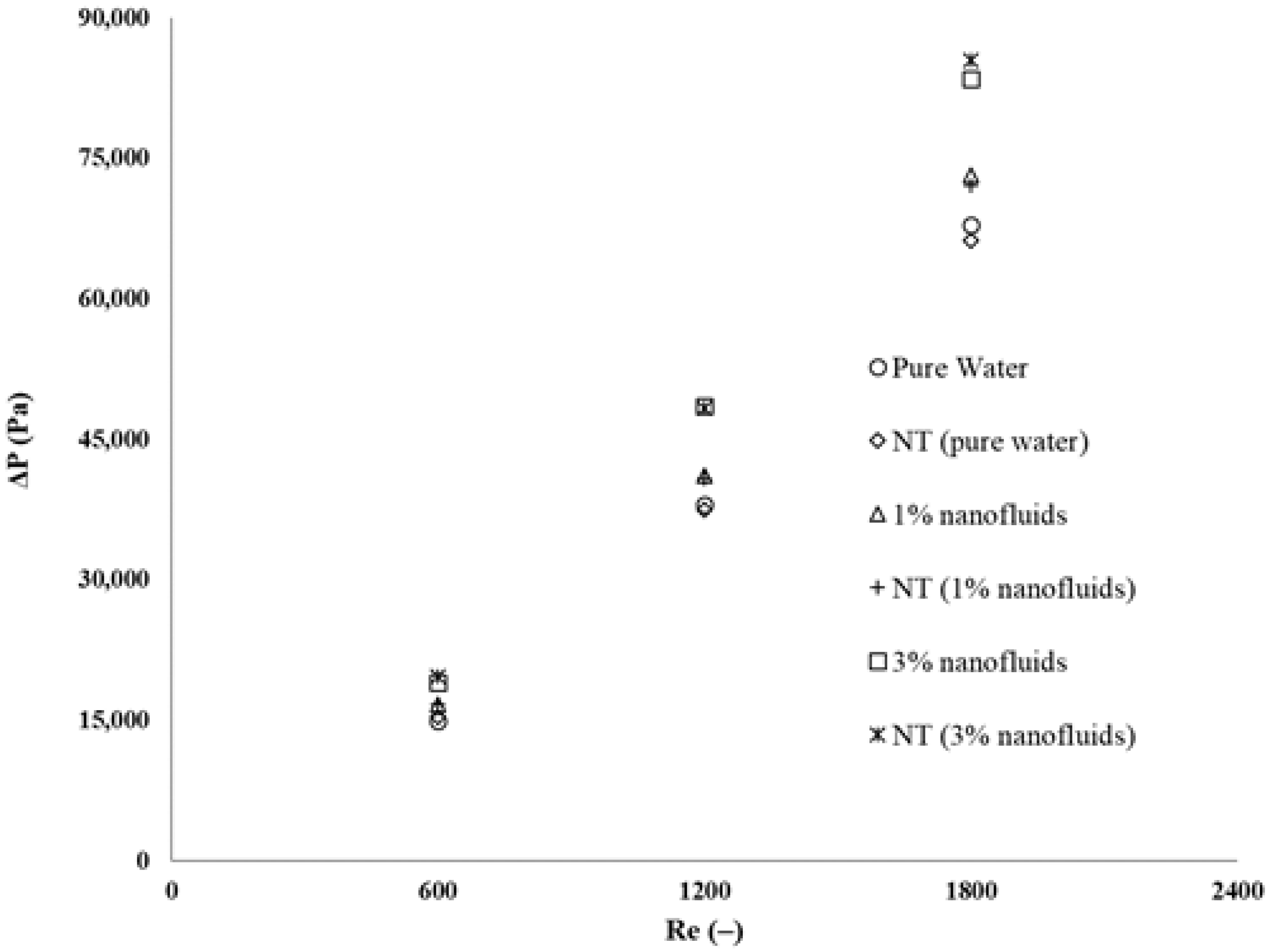
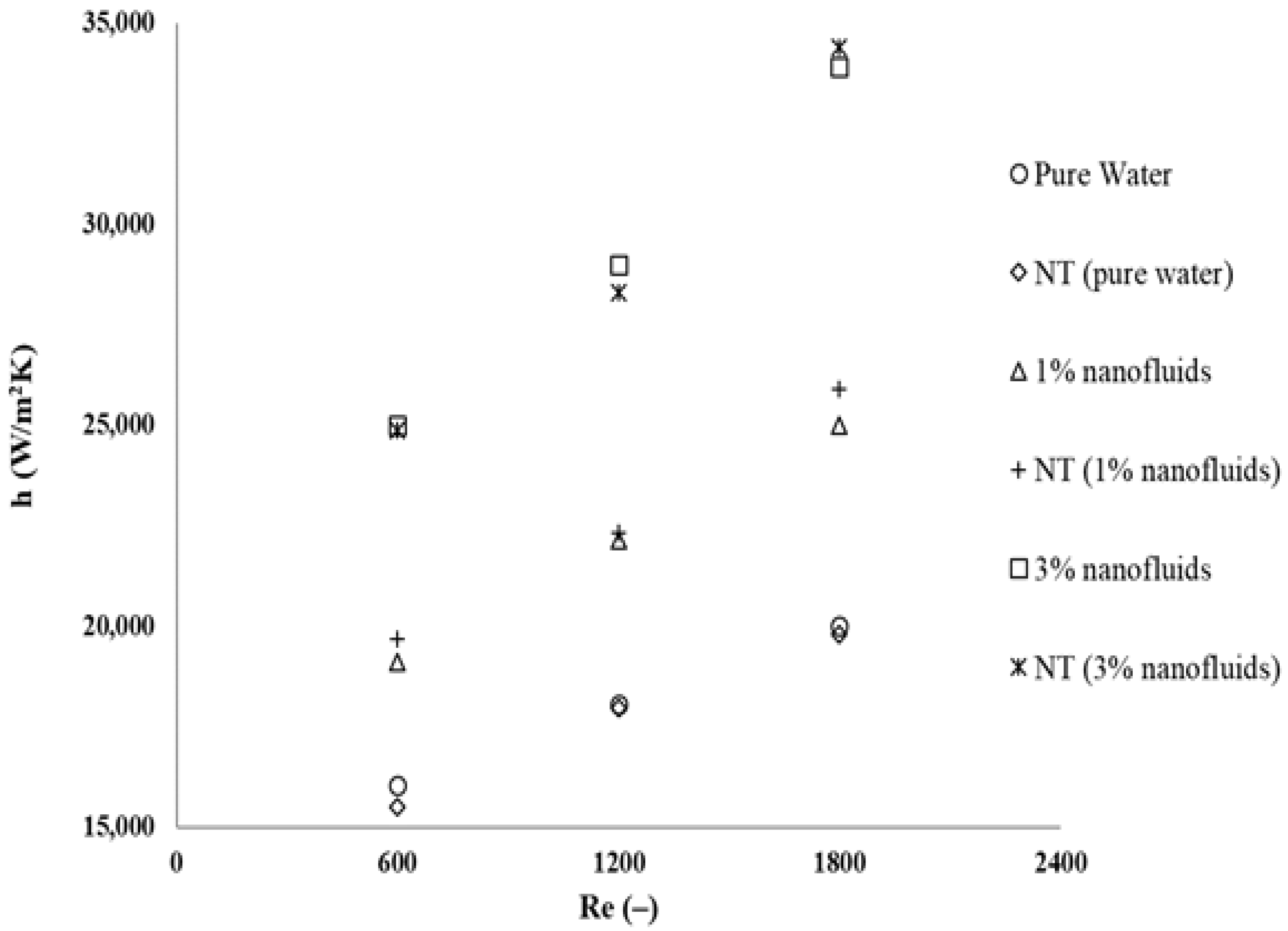
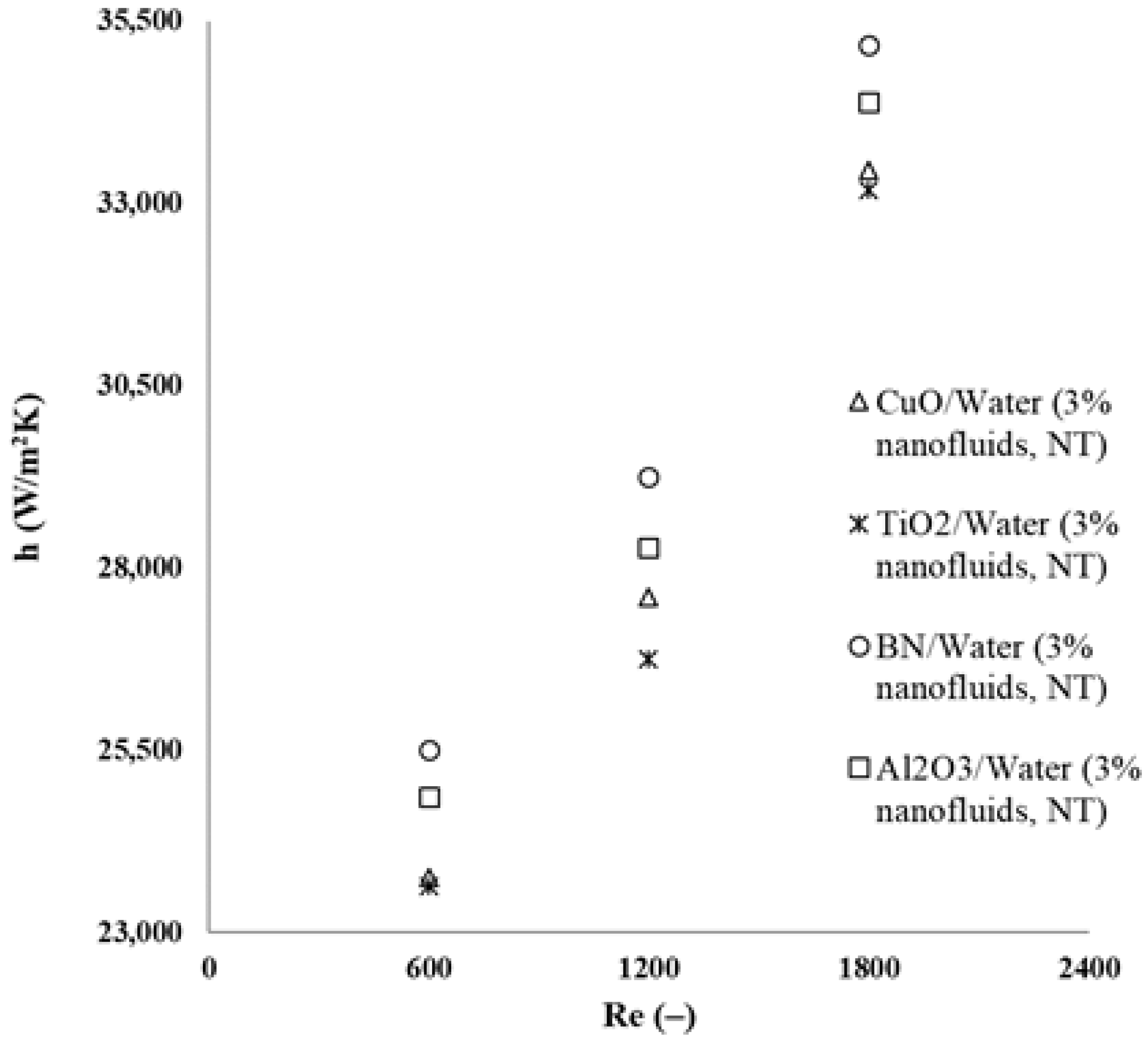
3.2. Analysis of Performance Characteristics of Nanofluids
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Naqiuddin, N.H.; Saw, L.H.; Yew, M.C.; Yusof, F.; Ng, T.C.; Yew, M.K. Overview of micro-channel design for high heat flux application. Renew. Sustain. Energy Rev. 2018, 82, 901–914. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, X.; Zhang, N.; Yuan, Y.; Zhao, X.; Hardy, D. Micro-channel heat sink: A review. J. Therm. Sci. 2020, 29, 1431–1462. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Grande, W.J. Evolution of Microchannel Flow Passages–Thermohydraulic Performance and Fabrication Technology. Heat Transf. Eng. 2003, 24, 3–17. [Google Scholar] [CrossRef]
- Shao, N.; Gavriilidis, A.; Angeli, P. Flow Regimes for Adiabatic Gas–Liquid Flow in Microchannels. Chem. Eng. Sci. 2009, 64, 2749–2761. [Google Scholar] [CrossRef]
- Bermejo, P.; Revellin, R.; Charnay, R.; Garbrecht, O.; Hugon, J.; Bonjour, J. Modeling of a Microchannel Evaporator for Space Electronics Cooling:Entropy Generation Minimization Approach. Heat Transf. Eng. 2013, 34, 303–312. [Google Scholar] [CrossRef]
- Gong, L.; Zhao, J.; Huang, S. Numerical Study on Layout of Micro-Channel Heat Sink for Thermal Management of Electronic Devices. Appl. Therm. Eng. 2015, 88, 480–490. [Google Scholar] [CrossRef]
- Kaya, F. Numerical Investigation of Effects of Ramification Length and Angle on Pressure Drop and Heat Transfer in a Ramified Microchannel. J. Appl. Fluid Mech. 2016, 9, 767–772. [Google Scholar] [CrossRef]
- Saenen, T.; Baelmans, M. Numerical Model of a Two-Phase Microchannel Heat Sink Electronics Cooling System. Int. J. Therm. Sci. 2012, 59, 214–223. [Google Scholar] [CrossRef]
- Sharma, C.S.; Tiwari, M.K.; Michel, B.; Poulikakos, D. Thermofluidics and Energetics of a Manifold Microchannel Heat Sink for Electronics with Recovered Hot Water as Working fluid. Int. J. Heat Mass Transf. 2013, 58, 135–151. [Google Scholar] [CrossRef]
- Zunaid, M.; Jindal, A.; Gakhar, D.; Sinha, A. Numerical Study of Pressure Drop and Heat Transfer in a Straight Rectangular and Semi Cylindrical Projections Microchannel Heat Sink. J. Therm. Eng. 2017, 3, 1453–1465. [Google Scholar] [CrossRef]
- Prasad, A.R.; Singh, S.; Nagar, H. A Review on Nanofluids: Properties and Applications. Int. J. Adv. Res. Innov. Ideas Educ. 2017, 3, 3185–3209. [Google Scholar]
- Das, S. Nanofluids for Heat Transfer: An Analysis of Thermophysical Properties. IOSR J. Appl. Phys. 2015, 7, 34–40. [Google Scholar]
- Abdollahi, A.; Mohammed, H.A.; Vanaki, S.M.; Osia, A.; Haghighi, M.R.G. Fluid Flow and Heat Transfer of Nanofluids in Microchannel Heat Sink with V-Type Inlet/Outlet Arrangement. Alex. Eng. J. 2017, 56, 161–170. [Google Scholar] [CrossRef]
- Coskun, T.; Cetkin, E. Heat Transfer Enhancement in a Microchannel Heat Sink: Nanofluids and/or Micro Pin Fins. Heat Transf. Eng. 2020, 41, 1818–1828. [Google Scholar] [CrossRef]
- Sabaghan, A.; Edalatpour, M.; Moghadam, M.C.; Roohi, E.; Niazmand, H. Nanofluid Flow and Heat Transfer in a Microchannel with Longitudinal Vortex Generators: Two-Phase Numerical Simulation. Appl. Therm. Eng. 2016, 100, 179–189. [Google Scholar] [CrossRef]
- Belhadj, A.; Bouchenafa, R.; Saim, R. Numerical Investigation of Forced Convection of Nanofluid in Microchannels Heat Sinks. J. Therm. Eng. 2018, 4, 2263–2273. [Google Scholar] [CrossRef]
- Shi, X.; Li, S.; Wei, Y.; Gao, J. Numerical Investigation of Laminar Convective Heat Transfer and Pressure Drop of Water-Based Al2O3 Nanofluids in a Microchannel. Int. Commun. Heat Mass Transf. 2018, 90, 111–120. [Google Scholar] [CrossRef]
- Kahani, M. Simulation of Nanofluid Flow Through Rectangular Microchannel by Modified Thermal Dispersion Model. Heat Transf. Eng. 2020, 41, 377–392. [Google Scholar] [CrossRef]
- Gonçalves, I.M.; Rocha, C.; Souza, R.R.; Coutinho, G.; Pereira, J.E.; Moita, A.S.; Moreira, A.L.N.; Lima, R.; Miranda, J.M. Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment. Appl. Sci. 2021, 11, 2440. [Google Scholar] [CrossRef]
- Zainon, S.N.M.; Azmi, W.H.; Hamisa, A.H. Thermo-physical Properties of TiO2-SiO2 Hybrid Nanofluids Dispersion with Water/Bio-glycol Mixture. J. Phys. Conf. Ser. 2021, 2000, 012003. [Google Scholar] [CrossRef]
- Saba, F.; Noor, S.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T.; Bano, Z.; Sherif, E.-S.M.; Khan, I. Heat Transfer Enhancement by Coupling of Carbon Nanotubes and SiO2 Nanofluids: A Numerical Approach. Processes 2019, 7, 937. [Google Scholar] [CrossRef]
- Rashid, U.; Baleanu, D.; Liang, H.; Abbas, M.; Iqbal, A.; ul Rahman, J. Marangoni Boundary Layer Flow and Heat Transfer of Graphene–Water Nanofluid with Particle Shape Effects. Processes 2020, 8, 1120. [Google Scholar] [CrossRef]
- Han, W.; Wang, L.; Zhang, R.; Ge, C.; Ma, Z.; Yang, Y.; Zhang, X. Water-Dispersible Boron Nitride Nanospheres with High Thermal Conductivity for Heat-Transfer Nanofluids. Eur. J. Inorg. Chem. 2017, 46, 5466–5474. [Google Scholar] [CrossRef]
- Hou, X.; Wang, M.; Fu, L.; Chen, Y.; Jiang, N.; Lin, C.T.; Wang, Z.; Yu, Z. Boron Nitride Nanosheet Nanofluids for Enhanced Thermal Conductivity. Nanoscale 2018, 10, 13004–13010. [Google Scholar] [CrossRef]
- Velmurugan, V.; Bharathithasan, I.; Grace, A.N. Synthesis and Physiothermal Analysis of Boron Nitride Based Nanofluid. Indian J. Sci. Technol. 2016, 9, 39. [Google Scholar] [CrossRef][Green Version]
- Kumar, S.; Tiwari, A.K. Performance evaluation of evacuated tube solar collector using boron nitride nanofluid. Sustain. Energy Technol. Assess. 2022, 53, 102466. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Yang, R.; Wen, J.; Li, X. Photothermal conversion characteristics and exergy analysis of TiN@h-BN composite nanofluids. J. Mater. Sci. 2022, 57, 19799–19816. [Google Scholar] [CrossRef]
- Mat, M.N.H.; Mohd-Ghazali, N.; Shamsuddin, H.S.; Estellé, P. Thermofuid behaviour of boron nitride nanotube nanofuid in a microchannel under optimized conditions. J. Therm. Anal. Calorim. 2022. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Xu, Z. Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication. Fluids 2016, 1, 16. [Google Scholar] [CrossRef]
- Bianco, V.; Chiacchio, F.; Manca, O.; Nardini, S. Numerical investigation of nanofluids forced convection in circular tubes. Appl. Therm. Eng. 2009, 29, 3632–3642. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Assessment of the effectiveness of nanofluids for single-phase and two-phase heat transfer in micro-channels. Int. Jounal Heat Mass Transf. 2007, 50, 452–463. [Google Scholar] [CrossRef]
- Bello, O.T.; Meyer, J.P.; Ighalo, F.U. Combined Numerical Optimization and Constructal Theory for the Design of Microchannel Heat Sinks. Numer. Heat Transf. A 2010, 58, 882–899. [Google Scholar] [CrossRef]

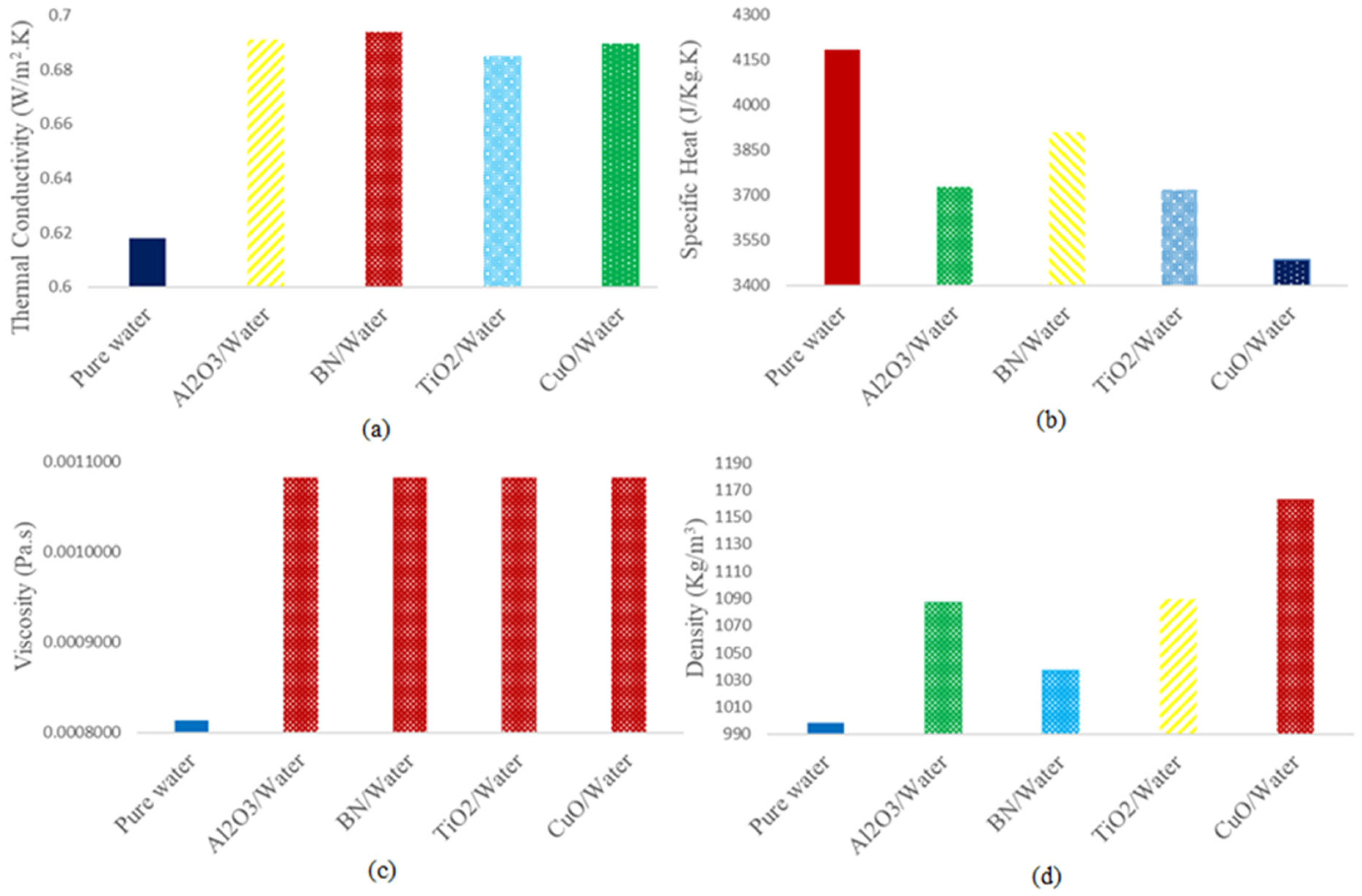


| Property | Water | Al2O3 | TiO2 | CuO | BN |
|---|---|---|---|---|---|
| Density (kg/m3) | 998.2 | 3970 | 4050 | 6500 | 2300 |
| Specific heat (J/kg.K) | 4182 | 765 | 697 | 536 | 1150 |
| Thermal conductivity (W/m.K) | −0.93314 + 0.00853 · T −0.000011259 · T2 [17] | 25 | 11.8 | 20 | 52 |
| Viscosity (kg/m.s) | 0.01723−9.25951e−5·T+ 1.2681e−7·T2 [17] | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, F. Numerical Investigation of the Use of Boron Nitride/Water and Conventional Nanofluids in a Microchannel Heat Sink. Processes 2022, 10, 2639. https://doi.org/10.3390/pr10122639
Kaya F. Numerical Investigation of the Use of Boron Nitride/Water and Conventional Nanofluids in a Microchannel Heat Sink. Processes. 2022; 10(12):2639. https://doi.org/10.3390/pr10122639
Chicago/Turabian StyleKaya, Fuat. 2022. "Numerical Investigation of the Use of Boron Nitride/Water and Conventional Nanofluids in a Microchannel Heat Sink" Processes 10, no. 12: 2639. https://doi.org/10.3390/pr10122639
APA StyleKaya, F. (2022). Numerical Investigation of the Use of Boron Nitride/Water and Conventional Nanofluids in a Microchannel Heat Sink. Processes, 10(12), 2639. https://doi.org/10.3390/pr10122639







