Physical and Chemical Macroscopic Processes in Wooden Construction Materials of Buildings during WUI Fires: Recent and Advanced Developments

Abstract

Forest fires are one of the strongest natural phenomena, occurring both for natural and man-made reasons. Forest fires entail not only economic losses, but also affect the ecological, biological and demographic picture of the region of its origin and far beyond its borders. Around the world, work is underway to develop effective methods for predicting the impact of a forest fire on the environment, the speed and direction of propagation and impact on various infrastructure facilities near the wildland–urban interface (WUI). The purpose of the work is to review recent and significant research works on the physical and chemical processes in wooden construction materials during WUI fires. As a result of the analysis of literary sources, works devoted to the modeling and experimental study of various physical and chemical processes, namely, the impact of forest fires on residential and industrial facilities, heat and mass transfer in structural materials, drying processes, pyrolysis, and ignition of structural materials, are highlighted. The results of the analysis of literature sources and promising directions are presented in the Discussion section. The formulated conclusions are presented in the Conclusion section. The main conclusion is that the existing experimental and theoretical work can be integrated into the developed deterministic–probabilistic approach for predicting the impact of a forest fire on buildings.

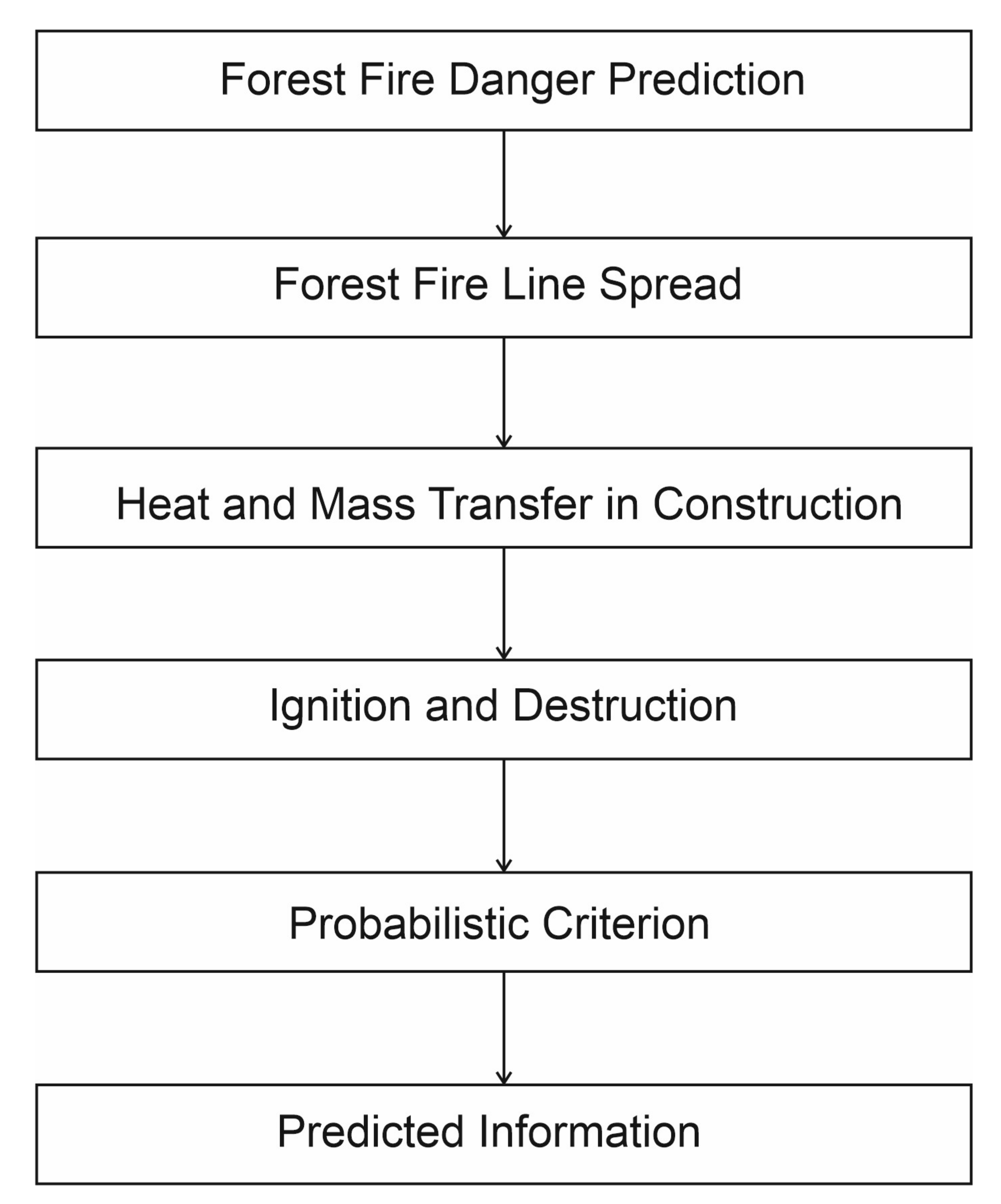
1. Introduction

Since 2018, there has been a significant growth in settlements near WUI zones [1]. The problem of the occurrence of forest fires inside the WUI is becoming more and more significant [2,3,4]. Due to the sharp growth in settlements near the WUI zones, the number of potential sources of ignition has increased, which has increased the likely destructive impact [5,6].

The problem of fires inside the WUI is complex. The fire danger of the WUI is influenced by many factors. Depending on the scale of consideration, three areas of research can be distinguished [7]:

(1)

Landscape scale—in this case, the main threat is WUI forestry.

(2)

The scale of the settlement.

(3)

The scale of a single structure.

Consideration of the problem on each individual scale allows us to develop a set of preventive measures to ensure the fire safety of WUI zones. Currently, the developed recommendations [8], aimed at reducing the fire danger of buildings, are based on simple fire models based on the effect of radiation heating and a flat wall surface, which does not provide completeness of data on the impact of a forest fire [2]. Thus, there is a need to refine the methods for analyzing the fire danger of structures in buildings in the WUI zones.

For a qualitative analysis of the fire safety of a wooden structure, a comprehensive consideration of all processes occurring on the surface and in the depth of the structure under the influence of a forest fire is necessary. These processes include the following:

(1)

Predicting the impact of a forest fire front;

(2)

Processes of heat transfer in the building enclosures;

(3)

Drying of elements of the building enclosures;

(4)

Ignition of a wooden structure;

(5)

Wood combustion processes.

To assess the course of each process in a wooden structure, it is necessary to study the influence of many factors on its course. For example, the influence of the shape of the structure, material, influence of neighboring buildings, wood moisture, vertical speed, etc. Deterministic mathematical models are excellent for this task, but experiments are required to further verify the model and simulation results in the future.

The purpose of the work is to review recent and significant research works of physical and chemical processes in wooden construction materials during WUI fires.

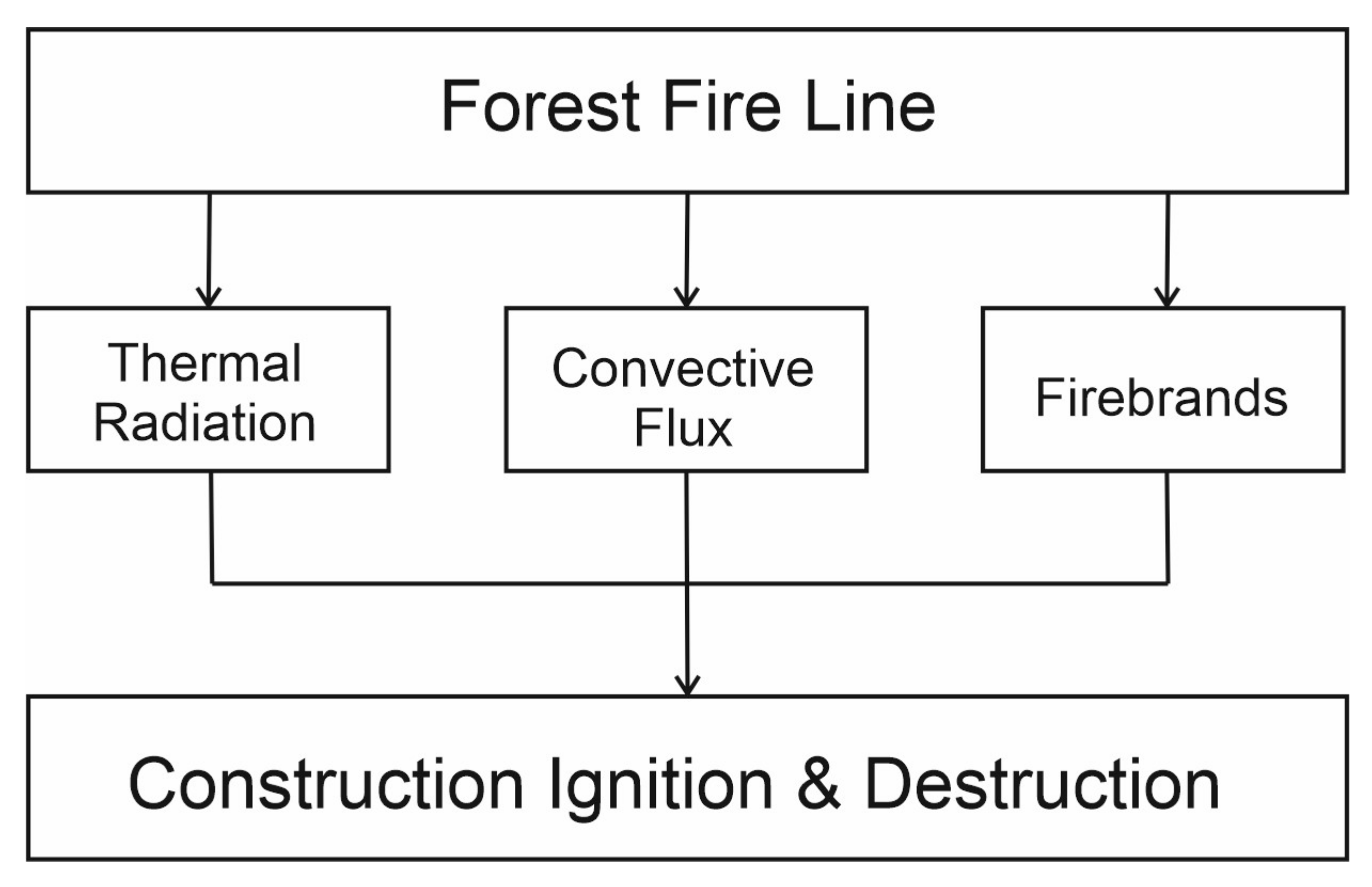
The rest of the article is organized in the following structure: 2. Summary, 3. Prediction of Forest Fire Impact, 4. Heat Transfer in Enclosure Construction, 5. Drying of Enclosure Construction Element, 6. Ignition and Combustion of Enclosure Construction, 7. Wooden Materials Properties, 8. Discussion, and 9. Conclusion. The gap in the published research and the main idea of the review is presented in Section 2. Current published results on forest fire impact are described in Section 3. Heat transfer studies are described in Section 4. The drying of enclosure elements is described in Section 5. Processes of enclosure pyrolysis and combustion are presented in Section 6. Density, conductivity, heat capacity, rate of charring and other material properties are considered in Section 7. Key findings accompanied with some considerations and discussions are presented in Section 8. A summary of review and further developments are described in the Conclusion section.

2. Summary

For more than 10 years, the Tomsk Polytechnic University has been intensively developing a deterministic–probabilistic approach to predicting forest fire danger [9]. The main advantage of this approach is the combined use of probabilistic criteria [10,11] and deterministic mathematical models of forest fuel ignition by various natural and anthropogenic sources [12,13,14,15]. This makes it possible to take into account both the stochastic and deterministic nature of the forest fire danger. The same approach is proposed to be used in predicting the impact of a forest fire on residential and industrial facilities in the WUI territories. Earlier, a probabilistic criterion for the impact of a forest fire on an industrial facility was developed [16]. Therefore, the main purpose of this review is to study the literature in the context of the possible application of various deterministic models of heat and mass transfer in structural materials under the influence of a forest fire. In this context of deterministic–probabilistic predicting of the impact of a forest fire on buildings, there is a significant gap in the scientific periodicals.

A multifaceted analysis of the problem to consider the impact of forest fires on structural materials shows that there are many disparate studies in the literature on individual structural materials, individual thermophysical and physicochemical processes, and individual materials properties. When it comes to a narrow study of someone’s material, this is a normal situation. If the complex problem of fire safety of any object or residential building is considered, then systematization and summation of the results of various studies is necessary. To date, there are virtually no research or review publications, especially when this task is considered in the context of developing a deterministic-probabilistic approach for predicting the fire safety of a building. The considered experimental results for various wooden structural materials can be used to formulate mathematical models and their subsequent verification. On the other hand, these experimental data can serve as criteria for the fulfillment of certain conditions in the framework of assessing the fire safety of a building. For example, the values of heat flux and surface temperature, together with the values of the ignition delay, can be used as criteria for the ignition of structural materials within the framework of simplified thermophysical models. In turn, mathematical models of various thermophysical and physicochemical processes can be integrated with probabilistic criteria to calculate the ignition probability of a building under conditions of a forest fire. It should be emphasized once again that such complex and interconnected descriptions of the results are not available in the scientific periodicals. This work is intended to fill this gap in the scientific literature, as well as to identify further ways of developing this area of research.

Figure 1 shows a diagram of a deterministic–probabilistic prediction of the forest fire impact on residential and industrial facilities. Figure 2 shows the physical mechanism of heat transfer from the forest fire front to the structural materials of the building.

In the framework of this review, Scopus and Web of Science databases were used. Information sources were initially searched by keywords with a total amount of about 3000 references. Mainly, articles, reviews and conference papers were used for initial selection. There are no selections on project or non-project articles. Then the source filtering procedure was carried out using a multi-stage algorithm: by title, additional keywords, abstract and skim reading of articles. Then, an analysis and close reading of the sources was carried out in order to identify specific information relevant to the subject of the review in the context of deterministic–probabilistic predicting of the impact of a forest fire on residential and industrial facilities in the WUI territories. Then, the sources were grouped according to separate physicochemical processes. At the last stage, the results were prepared for writing the discussion and conclusion sections. Promising areas of research were identified, and conclusions were drawn.

3. Prediction of Forest Fire Impact

To carry out mathematical modeling of the front impact on building structures, it is necessary to solve two main problems [17]:

(1)

Determine the speed and direction of the forest fire front.

(2)

Determine the thermal effect of flames from a forest fire front.

Solving these problems allows us to define safety zones for buildings and people. The tasks associated with determining the direction of flame propagation are well solved using deep learning of neural networks [18,19]. They are also suitable for assessing the risks associated with the occurrence of forest fires depending on climatic conditions [20,21,22]. Additionally, machine learning models are applicable to systems for the early detection of an ignition [22,23]. However, to determine the values of heat fluxes from the forest fire flame front, more accurate, deterministic models are required, which have been verified by experimental studies.

So, in [17], a study was carried out to determine the safety zones during the movement of the flame front. To determine the heat flux from the forest fire front, a continuous flame model was used, where the visible flame can be represented as a geometric body, the radiation of which is uniform for each point on the surface. The heat flux can be found by the formula

$$Q=E_p\tau F,$$

(1)

where $E_P$ is the heat flux density from the flame surface, flame emissivity. This value depends on the brightness of the flame and can be obtained using semi-empirical expressions. τ is the transmission coefficient of the atmosphere, depends on many factors, the concentration of carbon dioxide, air humidity and the distance from the border of the flame to the object of influence. F is the visibility factor.

$$E_p=E_b\epsilon ,$$

(2)

where $\epsilon$ is the flame emissivity, and E_b is the blackbody radiation.

$$E_b=\sigma T_f^4,$$

(3)

where $T_f^4$ is the flame surface temperature, K, and σ is the Stefan–Boltzmann constant, $\frac{W}{m^2{K}^4}$.

The calculations were performed under the condition that ε = 1. The data obtained in [17] showed that with a decrease in the distance between the forest fire front and the sensor, a slow increase in the value of the heat flux is observed. Then, upon reaching a distance of 5–30 m for flame heights of 5–40 m, a rapid increase in heat flux is observed, respectively, and reaches maximum values from 55 to 118 kW/m². In this case, the increase in the heat flux in this range is tens of times. The model was tested on test data and the results showed good agreement with the results obtained in [24]. This model was used to identify safe areas during a forest fire.

At present, CFD (computational fluids dynamics) models show themselves well for calculating heat fluxes from the forest front. In [25], the values of heat fluxes were obtained depending on the distance.

For numerical modeling, a multiphase setting was used to include vegetation in the three-dimensional CFD area [26]. In each location, six sensors were installed; due to the integral nature of the measurement, the responses of the sensors coincide with a correction for different viewing angles [27]. The simulation results showed a lower rate of increase in the heat flux with decreasing distance. Due to the occurrence of the local behavior of the crown forest fire, the heat fluxes turned out to be significantly higher. A rapid increase in the heat flux was observed at a distance of less than 5 m. The maximum values of heat fluxes were 60 kW/m² [25]. In this case, the significance of the experimental data and the simulation data are consistent.

The work [27] described the measurements of temperature, velocity and heat flux, which were obtained experimentally. The areas of surface and crown forest fire flames are compared. The maximum heat fluxes are 40 and 50 kW/m² for the surface and crown fires, respectively. For surface fire, a significant increase is seen at distances less than 6 m. For crown fire, the distance at which a significant increase in heat flux is observed is less than 18 m.

In [28], experimental studies of thermal radiation from a forest fire were carried out. The dependences obtained in this work make it possible to quite simply find the values of heat fluxes depending on the flame height and the distance between the forest fire flame front and the building structure. These dependencies can be used for further numerical study of the influence of the heat flux from the forest fire front on the enclosing structures of various kinds of infrastructure facilities near the WUI.

The value of the heat flux depending on the distance d can be found by the formula [28]

$$q_{fd}=16.638·d+29.772,\frac{kW}{m^2}$$

(4)

The value of the heat flux, depending on the height of the flame front h, can be determined by the formula [28]

$$q_{fh}=326.37·\mathrm{EXP}\left(-0.2791·h\right), kW/m^2$$

(5)

In [29], formulas were proposed that combine the effect of height and distance on the heat flux from the forest fire front.

In the event of a surface forest fire [29],

$$q_{ff}=\left(q_{fd}+\frac{xf}{50d}{q}_{fh}\right)/2, kW/m^2$$

(6)

In the event of a crown forest fire [29],

$$q_{ff}=\left(q_{fd}+\frac{t_{exp}xf}{10d}{q}_{fh}\right)/2, kW/m^2,$$

(7)

where xf is the distance at the moment in time t_exp, m; t_exp is the exposure time, s; d is the initial distance from forest fire front to building, m; fd is the fire distance; fh is the fire height; and ff is the total flux of forest fire.

Detailed characteristics can be found in

Table 1. Fire impact modeling.

N	Approach	Parameters	Reference
1	Numerical study	Radiant Heat Flux (RHF)	[17]
2	Neural network	MAE (mean absolute error), SMSE (Standard mean square error), MAPE (mean absolute percentage error), Bias	[18]
3	Neural network	Relative Operating Characteristic (ROC)	[19]
4	Neural network	Hf, αf	[20]
5	Neural network	Generalized fire risk (F)	[21]
6	Neural network	Detection speed (FPS)	[22]
7	Neural network	Detection rate (DTR)	[23]
8	Experimental study	RHF	[24,28]
9	Experimental, numerical study	RHF	[25]
10	Experimental study	RHF, temperature	[27]
11	Numerical study	RHF, temperature	[29]

.

The terminology used in Table 1 should be clarified. The term mathematical modeling refers to the use of deterministic mathematical models based on ordinary differential equations or partial differential equations with appropriate initial and boundary conditions. Neural networks are related to artificial intelligence technologies. Until recently, this interpretation of these types of modeling was mainly used in scientific periodicals. Recently, modern terminology has been used, which refers both types of research to modeling. However, deterministic mathematical models are hard modeling, while neural networks are soft modeling.

4. Heat Transfer in Enclosure Construction

To predict the fire safety of a building surrounded by a forest fire, it is simple to do a little numerical modeling of heat transfer in the building enclosures. These studies make it possible to determine the temperatures of the near-surface layers of enclosing structures, which provides information on the release of combustible gases by the structure, the likely thermal decomposition of wood, and the deformation of steel structures. In recent years, the understanding of the fire resistance of building structures has greatly improved; this is due to a large number of studies of the behavior of structural elements during a fire [30,31,32,33,34,35,36,37,38].

Currently, there are works aimed at modeling heat transfer in a structure using a neural network approach [39,40]. Additionally, in modeling heat transfer, not only can an individual structural element, but also an entire building be considered an idealized object [41].

During the ignition of a building, the decisive factor in its fire safety is the correct calculation of the escape routes. Currently, the spread of a fire inside a building can be calculated even at the design stage. BIM (building information model or modeling) helps in solving this problem [42,43,44,45,46]. BIM is an approach in construction, which involves the collection and processing of the design process of all architectural and design documentation, technological parts, and other information about the building with all its relationships and dependencies. In BIM, a three-dimensional model of an object is linked to a database, in which each element is assigned the necessary attributes. In BIM, a building and everything related to it is treated as a single object. BIM carries a full set of characteristics of individual building elements and their interrelationships, which allows the use of external software tools to simulate the behavior of a fire, the center of which can be located both inside the building and outside.

Validation of numerical simulation data requires test data sets that must be obtained experimentally. In addition, the fire safety standards for the design of building structures have always been based on experimental data [47]. As a result of experimental studies of the impact, it was noted that the destruction of structures during a fire is associated with thermal deformations of structural elements [48,49]. The characteristics of a structure associated with its stability during a fire comprise several stages [50]:

(1)

Determination of possible scenarios of fire;

(2)

Determination of the boundary conditions and subsequent study of heat transfer from the flame to the structural element;

(3)

Calculation of the reaction of structural elements to thermal and mechanical stress.

The experimental values of the surface temperatures at known values of the heat flux were obtained in [51]. The heat flux from the radiating surface with dimensions of 200 mm × 400 mm heated the test specimen. To ensure the repeatability of the experimental conditions, the emitting elements were calibrated. Approximate values of heat flux ranged from 5 kW/m² at a distance of 850 mm between the sample and the heater to 130 kW/m² at a distance of 100 mm. This test technique allows testing samples for fire resistance under any boundary conditions and scenarios of the effect of a heat flux on the sample.

As a result, temperatures were obtained at different depths of the surface of the concrete specimen. The results obtained were compared with the data in [52] and showed good agreement. At an exposure time of 15 min, the temperature at a depth of 10 mm reached 300 ℃; at a depth of 20 mm, 200 ℃; and 100 ℃ at a sample depth of 45 mm.

The convective component of heat transfer will not have an effect in cases where the distance between the heat flux source and the object under study is large enough [53]; however, in tight spaces and in cases when the release of combustible gases from wood is large, the effect of convective heat transfer cannot be ruled out [54]. At high heat fluxes, the heating rate can be extremely high. As shown by the study [54], the surface of a cylindrical particle of softwood with a diameter of 1 mm can reach 1600 K at a heat flux of 300 kW/m².

Heat transfer studies based on deterministic models were carried out in [29,55,56]. The development of deterministic models is in full swing, various physical properties and characteristics of the environment are added to the model. Such models are easily scalable, which allows them to be used on huge computational grids. The study of heat transfer by radiation using the P1 model is also in full swing [57,58,59,60].

However, the operation of deterministic models on large computational grids is a rather time-consuming procedure; at the same time, reducing the size of the computational grids can affect the simulation accuracy. So, for example, the difference method for approximating the heat equation proposed in [61,62] with a small number of points can give a significant error, a comparison of the simulation results for different numbers of nodes is demonstrated in [29]. At present, the problem of the speed of calculations associated with modeling heat transfer processes is solved by introducing algorithms with parallel implementation [63,64,65]. Detailed characteristics can be found in

Table 2. Heat transfer in construction element.

N	Study	Element	Parameters	Reference
1	Numerical study	Structure	Temperature	[30]
2	Numerical study	Concrete section	Euler buckling force (NB)	[31]
3	Numerical study	Axially loaded members	Buckling coefficient	[32]
4	Experimental study	Scoria aggregate concrete (SAC)	Stress–strain parameters	[33]
5	Numerical study	Steel bulk construction	Temperature, displacement	[34]
6	Numerical study	Steel tubular T-joints	Temperature, joint rotation	[35]
7	Numerical study	Stainless steel composite beam	Mid-span vertical deformation, temperature	[36]
8	Numerical study	Concrete	Stress–strain parameters	[37]
9	Experimental study	Concrete tunnel slabs	Temperature, displacement	[38]
10	Neural network	Wall section	Temperature	[39,40]
11	Numerical study	Idealized object	Temperature	[41]
12	Numerical study	Composite steel framed structure	Temperature, Axial Force	[48,49]
13	Experimental study	Concrete specimen	Temperature	[51]
14	Experimental study	High-strength concrete slabs	Temperature	[52]
15	Numerical study	Softwood cylindrical particle	Heat flux, temperature	[54]
16	Numerical study	Passenger carriage	Heat flux, temperature	[55]
17	Numerical study	Wall	Heat flux, temperature	[56]
18	Numerical study	Specimen	Temperature	[57,58]
19	Numerical study		RHF	[59,60]

.

5. Drying of Enclosure Construction Elements

The enclosing structures of a wooden building, before becoming part of the structure, undergo processing; one of the processing stages is drying the wood. This procedure prevents the processes of decay of the supporting structures of the building. However, during operation, the wood is again saturated with moisture [66]. Moisture in wood under thermal action will play the role of a heat sink, since energy will be spent on the evaporation of incoherent moisture, increasing the thermal inertia of the material.

Modeling of processes associated with drying is one of the important processes in the study of fire safety of a wooden structure due to the growth of internal stresses and shrinkage of the material during the drying process, which can cause premature destruction of load-bearing units, which, against the background of thermal destruction, is not the main destructive force. Often in models reflecting heat and mass transfer in wood, two approaches are considered based on the classical concepts of diffusion [67,68,69,70,71] and based on the phenomenological multiphase transfer inside wood [72,73,74,75].

There are many drying mechanisms, often divided into categories such as the following:

(1)

Air drying [76].

(2)

Drying at atmospheric pressure [77].

(3)

Drying after steaming [78].

(4)

Microwave drying [79].

(5)

Drying under the sun [80].

(6)

Vacuum drying [81].

In forest fire conditions, forest fire drying mechanisms can be divided into two types:

(1)

Low temperature convective drying at atmospheric pressure.

(2)

High temperature drying at atmospheric pressure.

The processes of material deformation during drying are described by the relations [82]

$${\epsilon }^{sh}=H\left(\overrightarrow{x}\right)\left[\begin{array}{ccc}A& 0& 0\\ 0& B& 0\\ 0& 0& C\end{array}\right]$$

(8)

$$H\left(\overrightarrow{x}\right)=\left\{\begin{array}{cc}0\hfill & if X\left(\overrightarrow{x}\right)\ge X_{fsp}\hfill \\ X\left(\overrightarrow{x}\right)-X_{fsp}\hfill & if X\left(\overrightarrow{x}\right)\le X_{fsp}\hfill \end{array}\right.$$

(9)

$${\epsilon }^{mec}={\epsilon }^{elas}+{\epsilon }^{mem}$$

(10)

$$\left\{\begin{array}{c}{\epsilon }_{ij}^{tot}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right) over \mathsf{\Omega }\\ {\sigma }_{ij,j}+\rho f_i=0 over \mathsf{\Omega }\\ {\sigma }_{ij}=a_{ijkl}\left({\epsilon }_{ij}^{tot}-{\epsilon }_{kl}^0\right) over \mathsf{\Omega } with {\epsilon }^0={\epsilon }^{sh}+{\epsilon }^{mem} and \forall i, {\mathsf{Г}}_{D_i}\oplus {\mathsf{Г}}_{T_i}=\mathsf{Г}\\ {\sigma }_{ij}{n}_j=T_i on {\mathsf{Г}}_{T_i}\\ u_i=D_i=0\hspace{1em}on\hspace{1em}{\mathsf{Г}}_{D_i}\end{array}\right.$$

(11)

where ${\epsilon }^{sh}$ is the deformation field, ${\epsilon }^{mec}$ is the strain tensor, ${\epsilon }^{elas}$ is the elastic strain, ${\epsilon }^{mem}$ is the memory strain, ${\epsilon }^{tot}$ is the total strain field, $X\left(\overrightarrow{x}\right)$ is the moisture content of wood within a vector $\overrightarrow{x}$, $X_{fsp}$ is the minimum moisture content in equilibrium with a saturated atmosphere, $\mathsf{Г}$ is the surface surrounding the domain $\mathsf{\Omega }$, ${\mathsf{Г}}_{D_i}$ is the subdomain of G where the i component of the displacement is known, ${\mathsf{Г}}_{T_i}$ is the subdomain of G where the i component of the traction force is known, $T_i$ is the temperature, $\rho$ is the density, and ${\sigma }_{ij}$ is the surface tension.

The moisture content of wood varies throughout the year and depends on the region [83]. The values of moisture content in wood, depending on the species, are presented in [84] and range from 0.1875 to 0.0180 (kg·kg⁻¹).

6. Ignition and Combustion of Enclosure Construction

When modeling the behavior of the enclosing structures of a wooden building under fire conditions, the key factor is whether the wood ignites or does not ignite. Under fire conditions, the ignition of wood is caused by the effect of a radiant heat flux from the flame and at small distances by direct contact between the flame and the structure [85]. The fact of ignition of a structure during modeling can be detected by comparing experimental data on the ignition temperature, the duration of action and the magnitude of the heat flux, the thermal thickness of the wood, and the moisture content. The risk of ignition of a structure is associated with the quality indicators of the material, the type of thermal radiation source and the distance to it [86,87].

Wooden elements can be divided by thickness into two types: thermally thin (a few millimeters thick) and thermally thick bodies. Thermally thin bodies are those bodies that, when heated or cooled, will have a small temperature difference in the cross section. For such bodies, the values of Bi < 0.25.

The Biot number (Bi) is a criterion for the similarity of stationary heat exchange between a body and the environment and determines the similarity of temperature fields for geometrically similar bodies. Bi characterizes the ratio of the thermal resistance of the wall to the thermal resistance of heat transfer on the surface.

Bi = αl/λ

(12)

where α is the coefficient of heat transfer from the surface of the body to the environment, W/(m²·K), λ is the coefficient of thermal conductivity of the body material, W/(m·K), and l is the characteristic size of the body.

Thermally thin bodies will have the same surface temperature on all their planes, which leads to the release of combustible gases over the entire area of the element. Thermally thin bodies include building sheathing, such as sheets of plywood or drywall. Thermally thick bodies, when heated or cooled, will have a significant temperature difference across the cross section. For such bodies, the values of Bi >0.5. Thermally thick bodies (usually more than 10 mm) will have a high temperature at the interface with the heating source, but at the second boundary they will have an ambient temperature. Such materials include timber.

The ignition delay is due to the fact that in order to ignite the gases escaping from the wood, the concentration of these gases must be sufficient for ignition. The dependence of the ignition delay on the material properties can be described by equations [88].

In the case of a thermally thin body [88],

$$t_{ign}=\rho c{L}_0\frac{\left(T_{ig}-T_0\right)}{q_{net}^{″}},$$

(13)

where $\rho$ is the density, $c$ is the thermal conductivity of the material, $L_0$ is the sample thickness, $T_{ig}$ is the ignition temperature, $T_0$ is the ambient temperature, and $q_{net}^{″}$ is the net heat flux to the sample surface.

In the case of a thermally thick body [88],

$$t_{ign}=\frac{\pi }{4}\rho ck\frac{{\left(T_{ig}-T_0\right)}^2}{q_{net}^{″}},$$

(14)

where $\rho$ is the density, $k$ is the specific heat, $T_{ig}$ is the ignition temperature, $T_0$ is the ambient temperature, and $q_{net}^{″}$ is the net heat flux to the sample surface.

The ignition temperatures of various wood species under the influence of heat flux have been well studied experimentally [89,90]. The values of the ignition delays for thermally thin bodies were obtained experimentally [91]. In [92], a large array of data was collected on ignition temperatures for autoignition and piloted ignition under the action of various heat fluxes. Ignition can be conditionally divided into two mechanisms: (1) Piloted ignition is the ignition when in contact with a hot particle or flame. (2) Autoignition is the ignition from a hot surface [93]. Detailed characteristics on ignition can be found in

Table 3. Values of ignition delay times and surface temperature depending on heat flux [89,90,93,94,95,96].

Species	q, kW/m2	Time to Autoignition, s	Time to Piloted Ignition, s	Tign, K	Reference
Beech	20	865	624		[93]
	30	194	64		[93]
	50	46	29 39	370.6	[93] [93]
	75		18	378.9	[93]
Oak	20	621	451		[93]
	30	240	81		[93]
	50	40	36 57	488.6	[93] [94]
	75		23	398.6	[94]
Pine	20	509	302		[93]
	30	59	50		[93]
	50	20	25 27	433.1	[93] [94]
	75		12	314.0	[94]
	438	Less 2		848$\pm$17	[89]
	745	Less 2		861 $\pm 15$	[89]
	1420	Less 2		894 $\pm 103$	[89]
Birch	438	Less 2		811 $\pm 11$	[89]
	745	Less 2		848 $\pm 39$	[89]
	1420	Less 2		872 $\pm 43$	[89]
OSB	44	142		287	[90]
	46	70		358	[90]
	48	64		252	[90]
	50	58		319	[90]
Plywood	37.5	23±6			[95]
Chipboard	37.5	24±2.1			[95]
Cardboard	10 30 60	118 20 10			[96] [96] [96]

.

Ignition of the structure will mean that the structural element not only absorbs energy, but is itself a source of radiation, which, during the simulation process, can be reflected at significantly lower temperatures for longer exposure times.

Wood pyrolysis is one of the most important areas of woodworking. When in the process of pyrolysis, flammable gases and liquids of various chemical compositions are released. One of the methods for producing methanol, which is later used in the gas industry, in the production of technical fluids, etc. The simulation of pyrolysis processes will also help to improve the accuracy of predicting the fire danger of buildings in the vicinity of the WUI.

There are many works related to the modeling of pyrolysis processes. These works are aimed at establishing the influence of various parameters of a material or medium on pyrolysis processes. In [94], a multiscale model of wood pyrolysis and oxidation is presented. The kinetic model of pyrolysis is presented in [97], where it was noted that the models of one reaction are superior to the models of parallel reactions when simulating small-scale kinetic experiments and are more applicable for modeling heat release from a fire. In [98], a numerical simulation of pyrolysis of a large piece of wood was carried out using the single reaction model and the parallel reaction model. The model reflected the processes of wood drying during pyrolysis. The simulation of pyrolysis made it possible to establish the influence of particle size, humidity, oven temperature, etc., on pyrolysis processes. However, the authors themselves argued that experimental studies are required to determine the activation energy, gas permeability, thermal conductivity, etc. In Refs. [99,100], the moisture content of the sample was singled out as a key parameter. This is due to the fact that, upon evaporation, water can gasify the outer layer of the sample.

In [101], experimental studies were carried out on the thermal decomposition of double-walled corrugated board in a fire propagation apparatus (FPA). The tests were carried out with heat flow levels of 20, 60 and 100 kW/m². It was found that the rate of heat release is comparatively inferior to the falling heat flux. The study [102] considered an approach to the development of a one-dimensional pyrolysis model based on experimental studies carried out in laboratory conditions. The tests were carried out using a conical calorimeter in the heat flux range from 20 to 80 kW/m². The generalized pyrolysis model presented in [103] can be used to simulate the processes of gasification of solid combustible substances arising during fires, which has good agreement with experimental data.

Additionally, pyrolysis modeling processes can take place in two stages [104,105]. First, an experimental study of material pyrolysis is carried out. These can be studies using a flame spreading device or a cone calorimeter. Then, using an optimization algorithm, the pyrolysis model is fitted to the experimental data [105].

7. Wooden Materials Properties

High temperature affects the thermophysical characteristics of wood materials. As the study [106,107] shows, the heat capacity of wood decreases up to 250 °C, after which it increases. When the temperature in wood reaches more than 250 °C, a sharp decrease in the density of the material occurs with an increase in temperature [106,108,109,110]. At the same time, in the presence of heating and high pressure on the sample, the density can increase [111]. The thermal conductivity of wood increases with temperature, but a significant increase is observed at temperatures above 600 °C [106,107]. The depth of wood charring during a fire is the main indicator of wood wear during a fire [112]. As shown in [113,114,115,116,117], the rate of charring depends on the density of the wood. In [113], an experimental study was carried out to determine the thickness of the charring layer and to determine the zones of wood pyrolysis, after which the bending strength of the material was assessed. The rate of wood charring increases with an increase in the temperature of the material or with an increase in the incident heat flux [118,119,120]. In [120], the characteristics of such species as Redwood, Southern pine, Red oak, and Basswood were studied. The studies were carried out in the range of heat flows from 18 to 58 kW/m². The charring rate for different types of wood increased at different rates, and it turned out to be the maximum for Basswood (1.2 mm/min at a heat flux of 58 kW/m²). In [120], samples from Oak, Larch, and Red cedar were studied in the range of heat fluxes from 20 to 50 kW/m²; the maximum charging rates were obtained for Red cedar (more than 1.2 mm/min).

Detailed characteristics on wooden materials properties can be found in

Table 4. Wooden materials properties.

Material	Process	Parameter	Reference
Plasterboard	Combustion	Density, Heat capacity	[106]
Wood	Combustion	Density, Conductivity, Heat capacity	[107]
Pinewood	Combustion	Density	[109]
Hardwood	Combustion	Density	[110]
Pinewood	Drying	Density	[111]
Jati putin, Bajur, Rajumas	Combustion	Pyrolysis zone, Depth of Char and Pyrolysis	[113]
Paulownia, Toon, Elm	Combustion	Rate of Charring	[114]
China fir, Japanese cedar, Douglas fir, Southern pine	Combustion	Rate of Charring	[115]
Softwood, hardwood	Combustion	Rate of Charring	[116,117]
Western hemlock, Western red cedar, Podo, Douglas fir, Larch, Abura, Ash and other	Combustion	Rate of Charring	[118]
Redwood, Southern pine, Red oak, Basswood	Combustion	Rate of Charring	[119]
Oak, Larch, Red cedar	Combustion	Rate of Charring	[120]

.

8. Discussion

The analysis of the topic under consideration shows that the overwhelming majority of publications in the world periodicals are devoted to individual issues of the impact of a forest fire on the structural materials of the enclosing structure of a residential or industrial building. The following sub-topics were highlighted: predicting the impact of a forest fire on buildings; heat transfer in the building enclosures; drying of the elements of the enclosing structure; and the ignition and combustion of structural materials of the enclosing structure, including pyrolysis of wood or wood-glued material.

Concerning the prediction of the impact of a forest fire, there are mainly various mathematical models that consider the advancement of a forest fire front, taking into account the physicochemical processes in the forest fire front. This allows theoretical estimates of the heat flux from the forest fire line and the temperature in the forest fire front. However, there are works devoted to parametric modeling of the propagation of a forest fire front on the basis of experimental data. Parametric formulas were developed to estimate the magnitude of the heat flux from the front of surface and crown forest fires. Applying these formulas can reduce the computational load and memory requirements when predicting the impact of a forest fire on a building. It was established that even the use of the parametric approach may require the use of multiprocessor computing systems for calculations on large computational domains. Therefore, the development of simple methods for modeling the impact of a forest fire on a building is a very urgent task at the present time.

As for the heat transfer in the enclosing structure, traditionally for these purposes, systems of partial differential equations of parabolic type, describing conductive heat transfer, with the corresponding initial and boundary conditions were used. It is clear that both commercial packages, such as Matlab, Comsol, Ansys, and Fluent, and high-level programming languages, such as Delphi, C, and Python, can be used to simulate heat conduction processes. When using commercial packages, built-in solvers and procedures are used. As a rule, in this case, there is no full-fledged computer program, since many processes are set parametrically in the corresponding blocks of the menu of commercial packages. However, if it is necessary to develop a separate independent information and computational system for predicting the state of the enclosing structures of a building or a whole complex of buildings when exposed to a forest fire, then the best option is to use your own program code. This makes it possible to embed the developed program into any information and computing system. In this case, the customer does not need to buy an expensive commercial package for its operation.

In mathematical modeling of heat transfer in building envelopes, only conductive heat transfer in the layered structure of the building enclosure is usually taken into account. It is also necessary to take into account the convective and radiation heat transfer in the pores of the used wood-glued materials or wood.

Separately, it should be noted that most works do not take into account the presence of paint and varnish or fire-retardant coatings on the surface of structural materials of the building enclosure. This issue should be worked out in more detail in future works, given the variety of paint and varnish and fire retardant coatings.

A number of works are devoted to the drying of elements of the building enclosures. As a rule, scenarios are considered with a given value of the initial moisture content of wood or wood-glued materials. However, from the standpoint of fire safety, research is needed to take into account the periodic moistening of the surface of structural materials. This corresponds to the humidification of the building walls in the presence of an active fire source next to the building. This technique is often used by firefighters in order to prevent a nearby building from catching fire when another adjacent building burns. Known approaches, as a rule, are based on mathematical modeling of conductive heat transfer in the enclosing structure, taking into account evaporation at the outer boundary of the wall or inside the near-surface layers of the structural material. It would probably be more adequate to develop mathematical models that take into account the advance of the evaporation front into the depth of the structural material.

A sufficient number of works are devoted to pyrolysis, ignition and combustion of wood. It should be noted that the overwhelming majority of these works are experimental. On the one hand, this allows the use of extensive experimental data for the verification of mathematical models. On the other hand, the range of materials under consideration is rather narrow. Mostly pure wood of various species is considered. However, there are currently a sufficient number of different cladding materials that should also be considered in the context of the impact of forest fires on the cladding structures. The biggest disadvantage of the prior art in this area is that it is usually considered a sample of a typical wood-glued material or wood. It is necessary to develop complex mathematical models that simultaneously take into account both the materials of the enclosing structure and the presence of door and window openings in this enclosing structure.

Analysis of the results of various studies shows that the most optimal approach is the development of analytical or parametric approaches to modeling the propagation of a forest fire front and assessing the parameters of the thermal effect of damaging factors of a forest fire on structural materials. This will allow avoiding the development of resource-intensive programs based on mathematical models that take into account a wide range of physicochemical processes. All presented works are interesting from the point of view of their integration with a deterministic–probabilistic approach to predicting the impact of a forest fire on residential or industrial facilities. Experimental studies can be used to verify new deterministic mathematical models of heat and mass transfer, pyrolysis, ignition and destruction of structural materials of building enclosures. In addition, critical values of temperature or heat flux can be used as criteria for the ignition of structural materials when exposed to a forest fire. Deterministic mathematical models can be used for integration with the developed probabilistic criterion for assessing the impact of a forest fire. In addition, the results of theoretical and experimental studies can be used to train neural networks, which are already being used to simulate thermal effects on structural materials. It should be noted that in recent years, a new direction for the creation of BIM models was developed. These technologies can be used as the basis for the creation of new information and computing systems for fire safety in rural settlements or industrial facilities.

9. Conclusions

The study of the impact of forest fires on structural wooden materials is an important aspect of the development of new information and computing systems for predicting fire safety in rural settlements and industrial facilities. Such systems can be developed on the basis of a deterministic–probabilistic approach that combines probabilistic criteria and deterministic mathematical models. The practical use of this review is due to the following provisions:

• To simulate the impact of a forest fire, it is promising to develop analytical or parametric approaches to assessing the parameters of propagation and heat release from the forest fire front to wooden materials.
• The results of experimental studies of drying, pyrolysis and ignition of structural wooden materials can be used to verify new mathematical models of heat and mass transfer in building enclosures when exposed to a forest fire.
• Mathematical models of heat and mass transfer in structural wooden materials under the influence of a forest fire can be associated with a probabilistic criterion within the framework of the deterministic-probabilistic approach.
• Theoretical and experimental results can be used to train neural network models in assessing the thermal effect of a forest fire on structural wooden materials.
• The critical values of temperature and heat flux can be used as criteria for the ignition of wooden structural materials.
• BIM models can become the basis for the development of new information and computing systems for predicting fire safety in rural settlements and industrial facilities.

The main contribution to the scientific community of this review is the systematization and detailed comparative analysis of various studies regarding the drying, pyrolysis and ignition of a certain set of wooden structural materials when exposed to a forest fire. Further development of a deterministic–probabilistic approach to fire safety predicting is impossible without this stage of analysis and systematization concerning the published results in scientific periodicals.

An analysis of literary sources shows that further research should be focused on expanding the range of building and finishing wooden materials in the study of their fire hazardous properties. In addition, it is important to study layered structures from various building and finishing materials, taking into account climatic and weather conditions in various geographical zones. Moreover, it is necessary to continue developing a deterministic–probabilistic approach to assessing and predicting the fire safety of residential and industrial buildings made of wooden materials. For these purposes, the concept of BIM models and information and computing systems based on them should also be involved.