A Population Balance Methodology Incorporating Semi-Mechanistic Residence Time Metrics for Twin Screw Granulation
Abstract
:1. Introduction
1.1. Twin Screw Granulation Population Balance Development
1.2. Objectives
2. Materials and Methods
3. Theory and Calculations
3.1. Particle Grid Configuration
3.2. PBE Configuration
3.3. Aggregation and Breakage Rates
3.4. PBE Compartmentalization
3.5. Axial Velocities and Dispersion Coefficients
3.6. Numerical Techniques
3.7. Output Metrics
3.8. Parameter Estimation
4. Results and Discussion
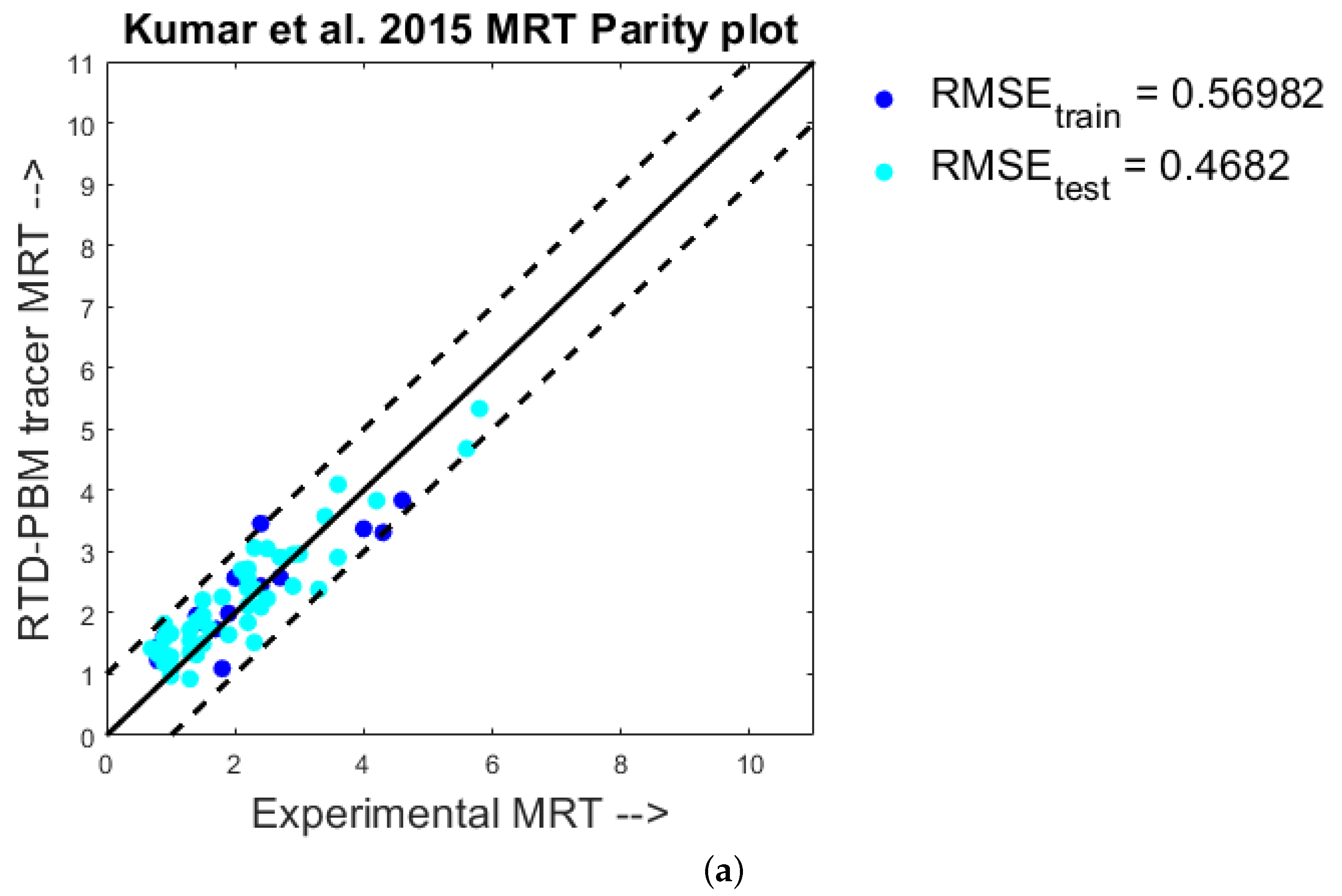
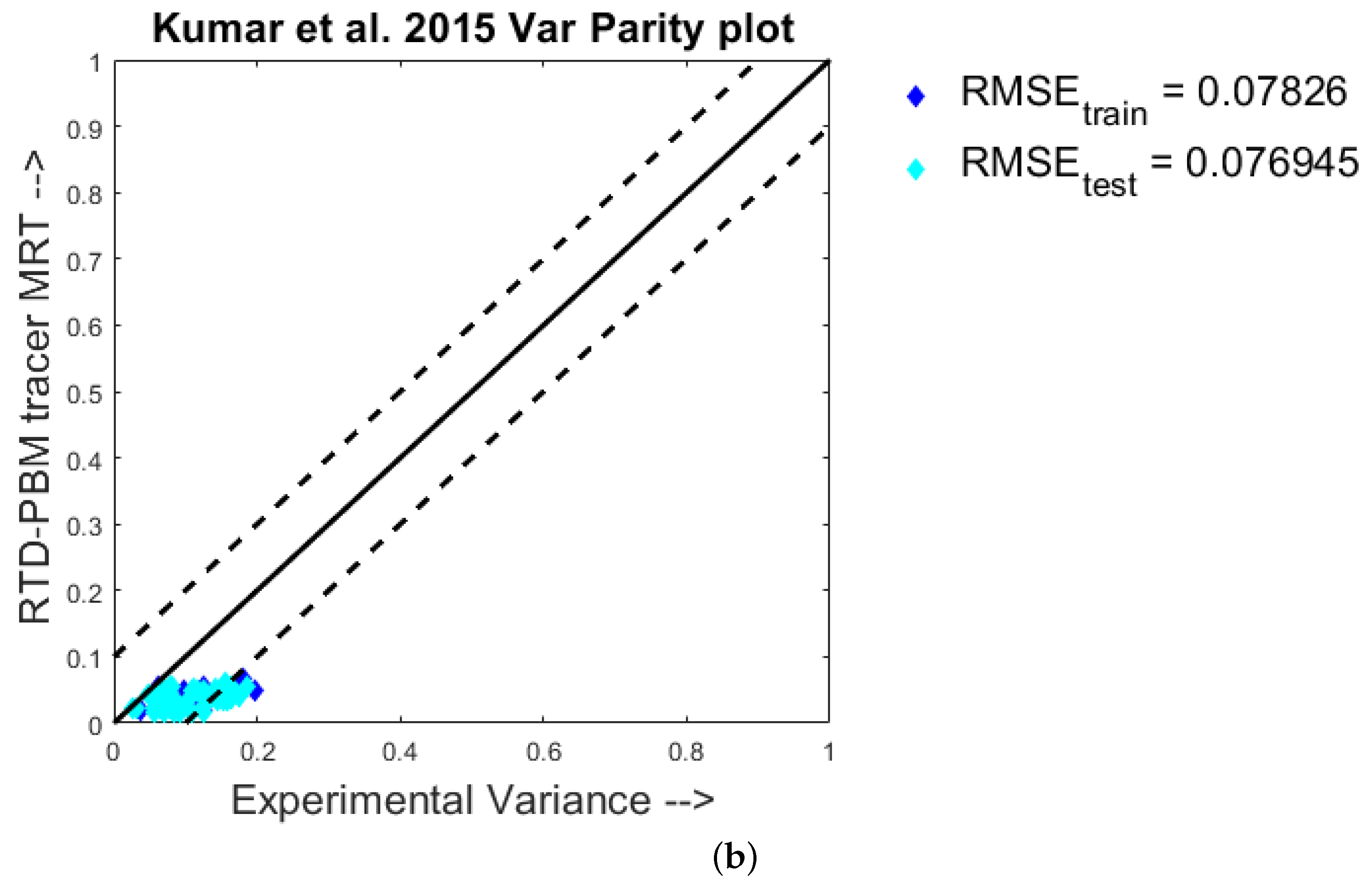
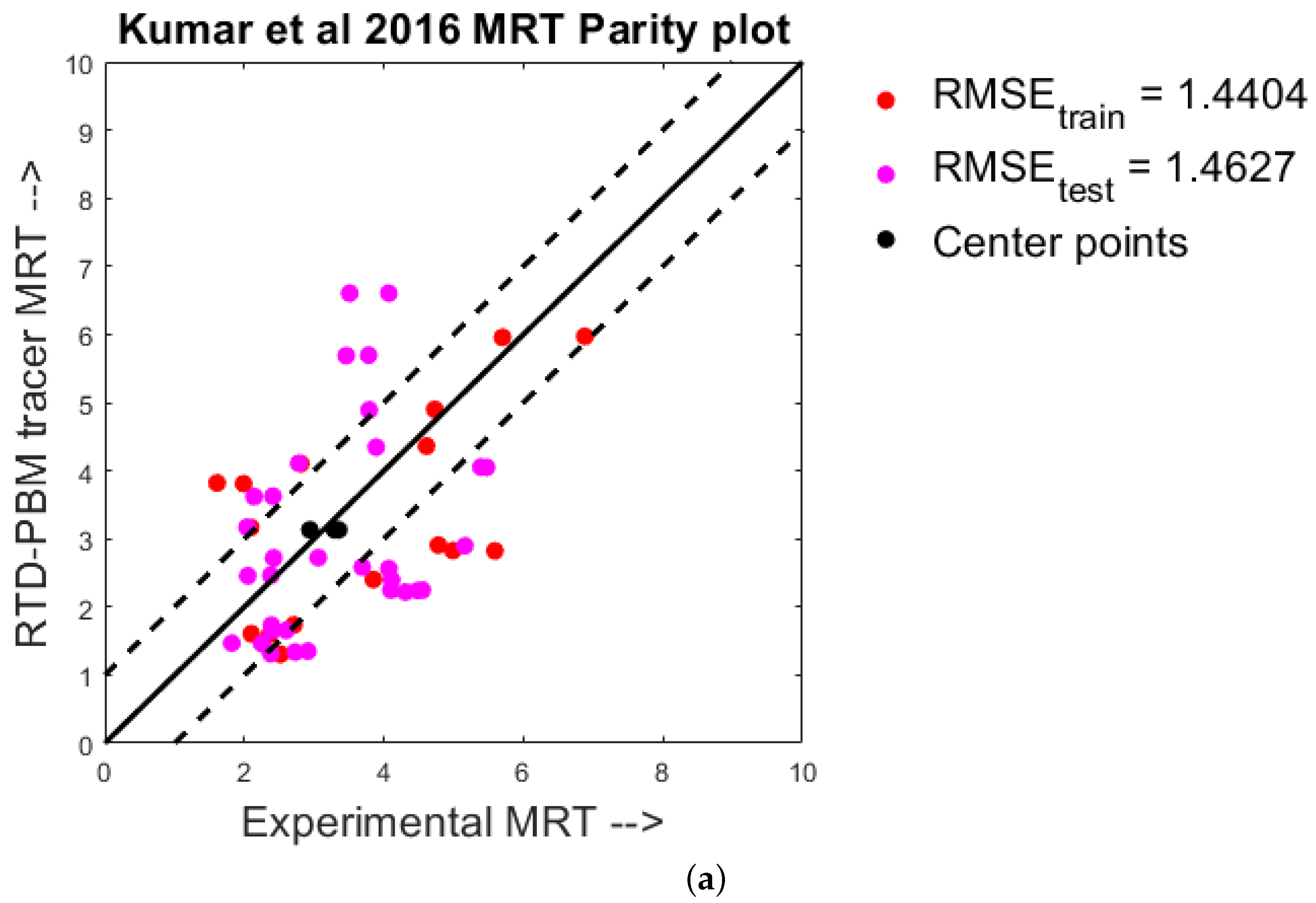
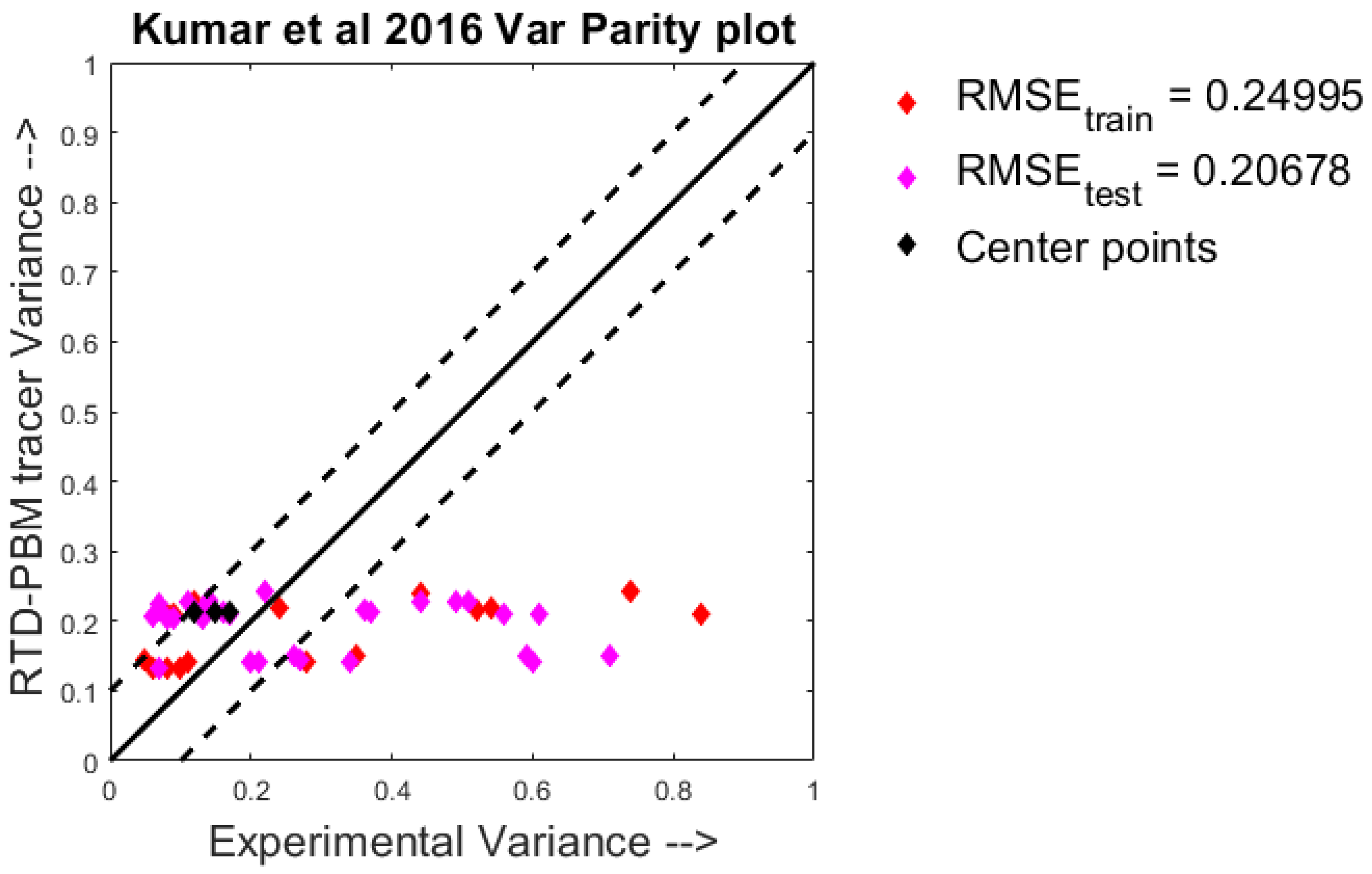
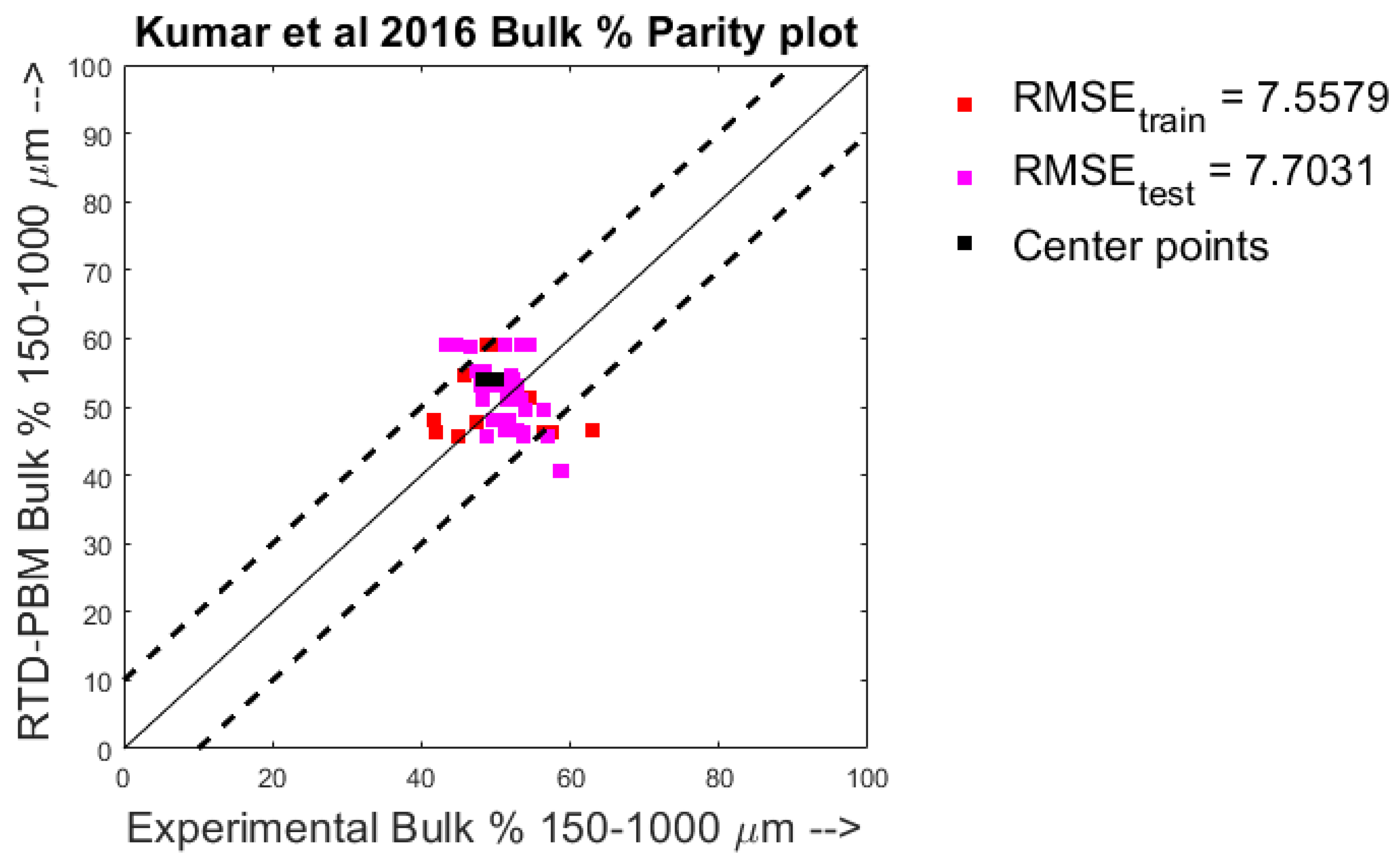
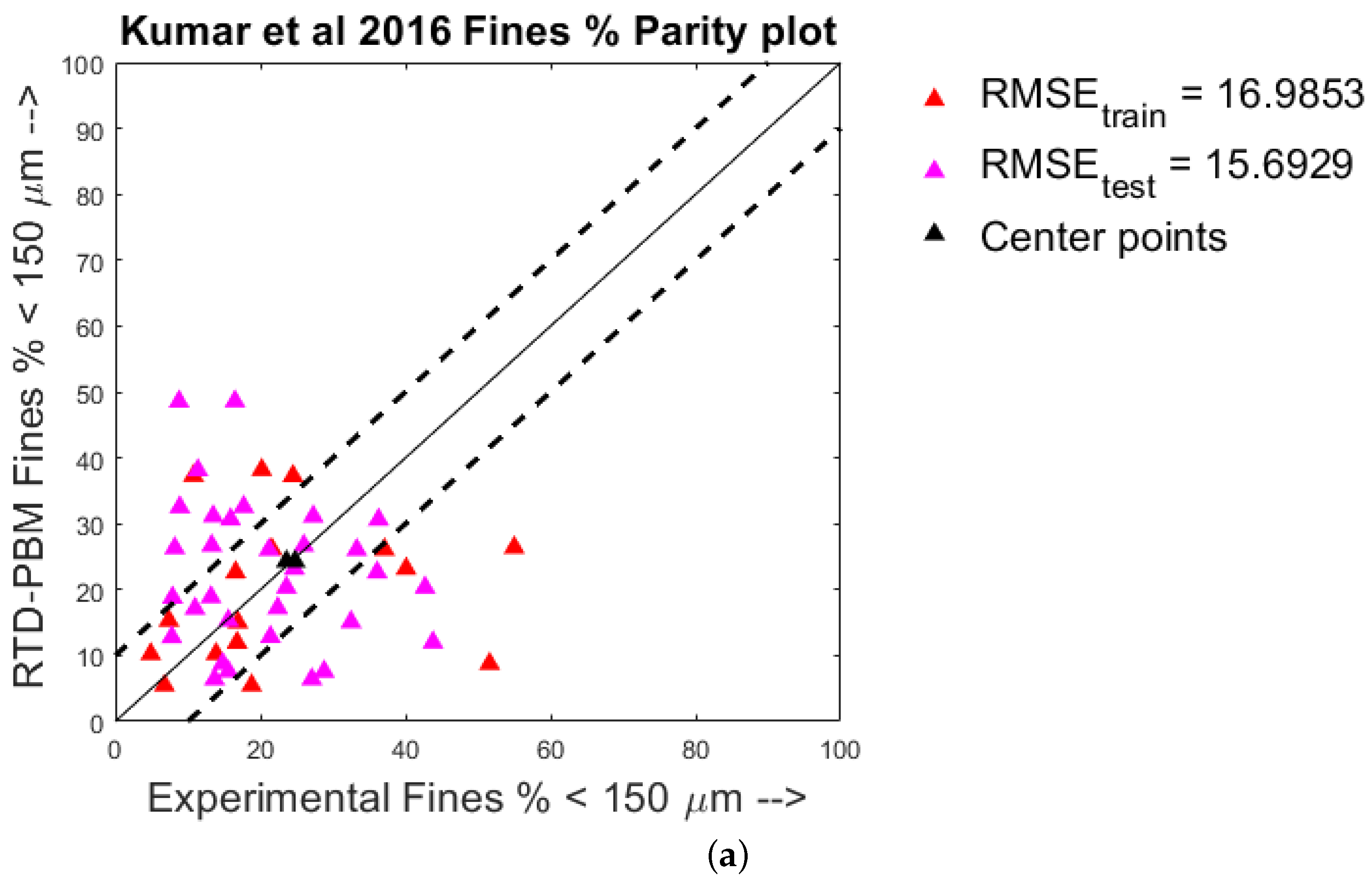
4.1. Quantitative Analysis—Parity Plots
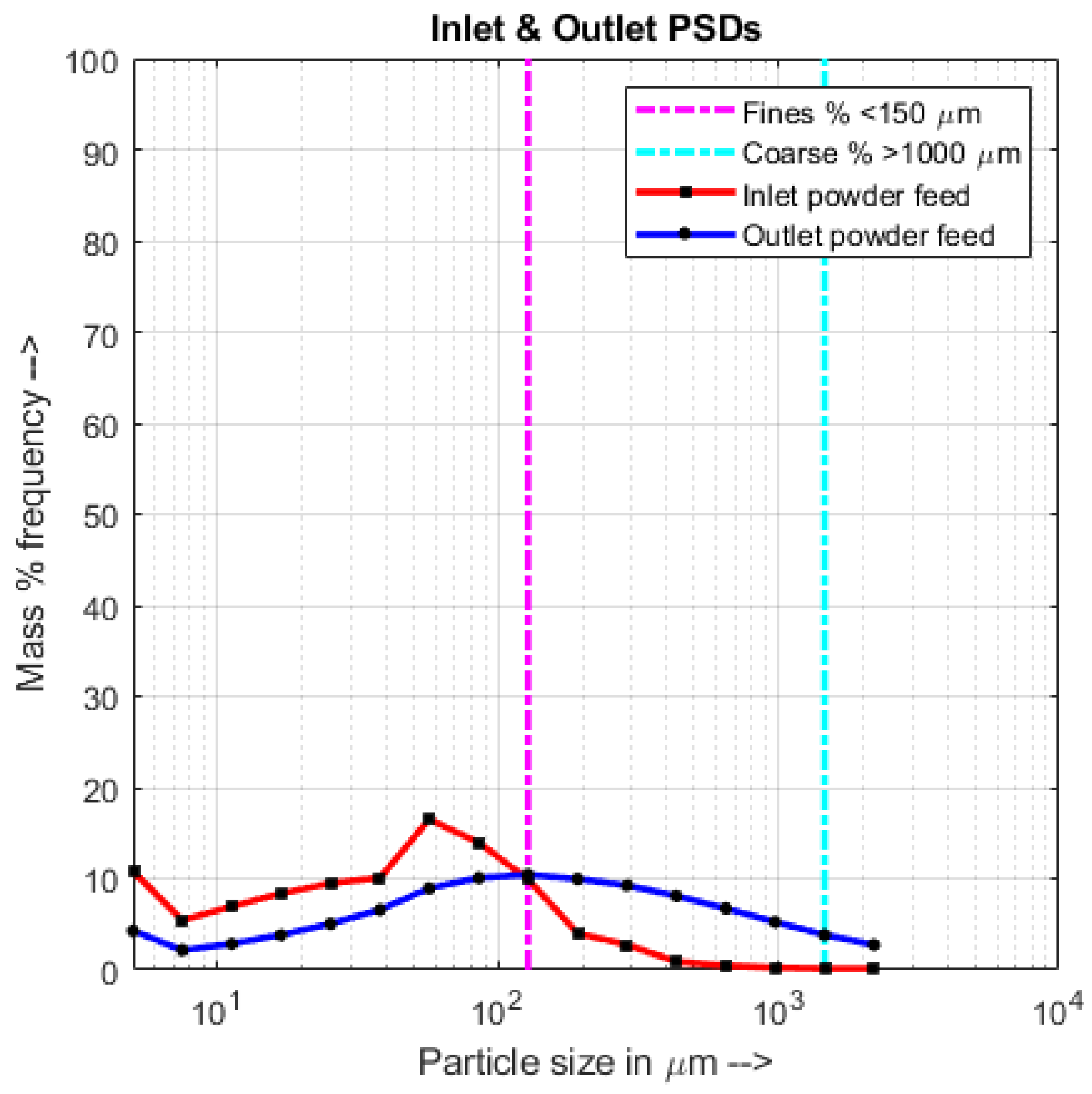
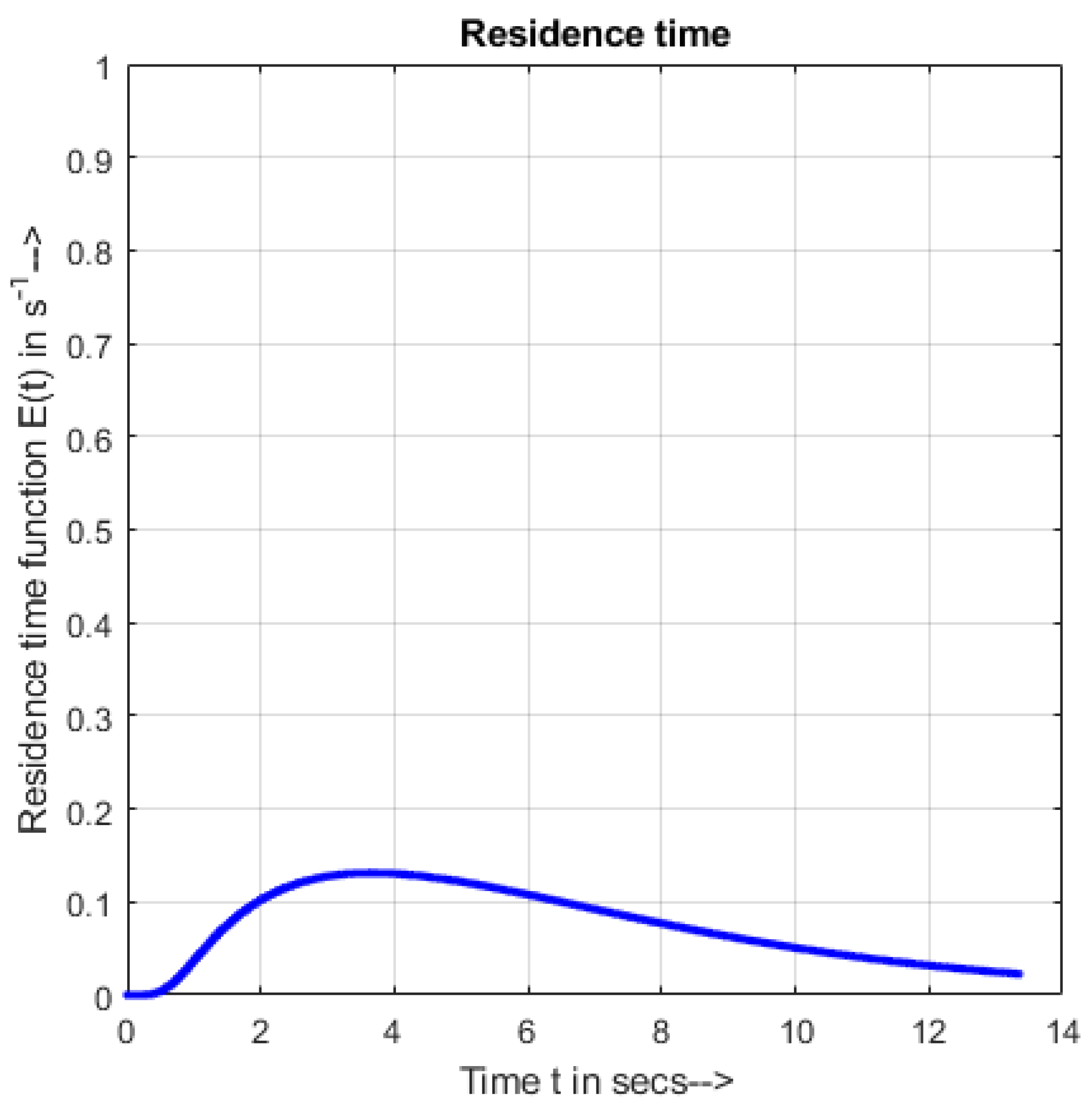
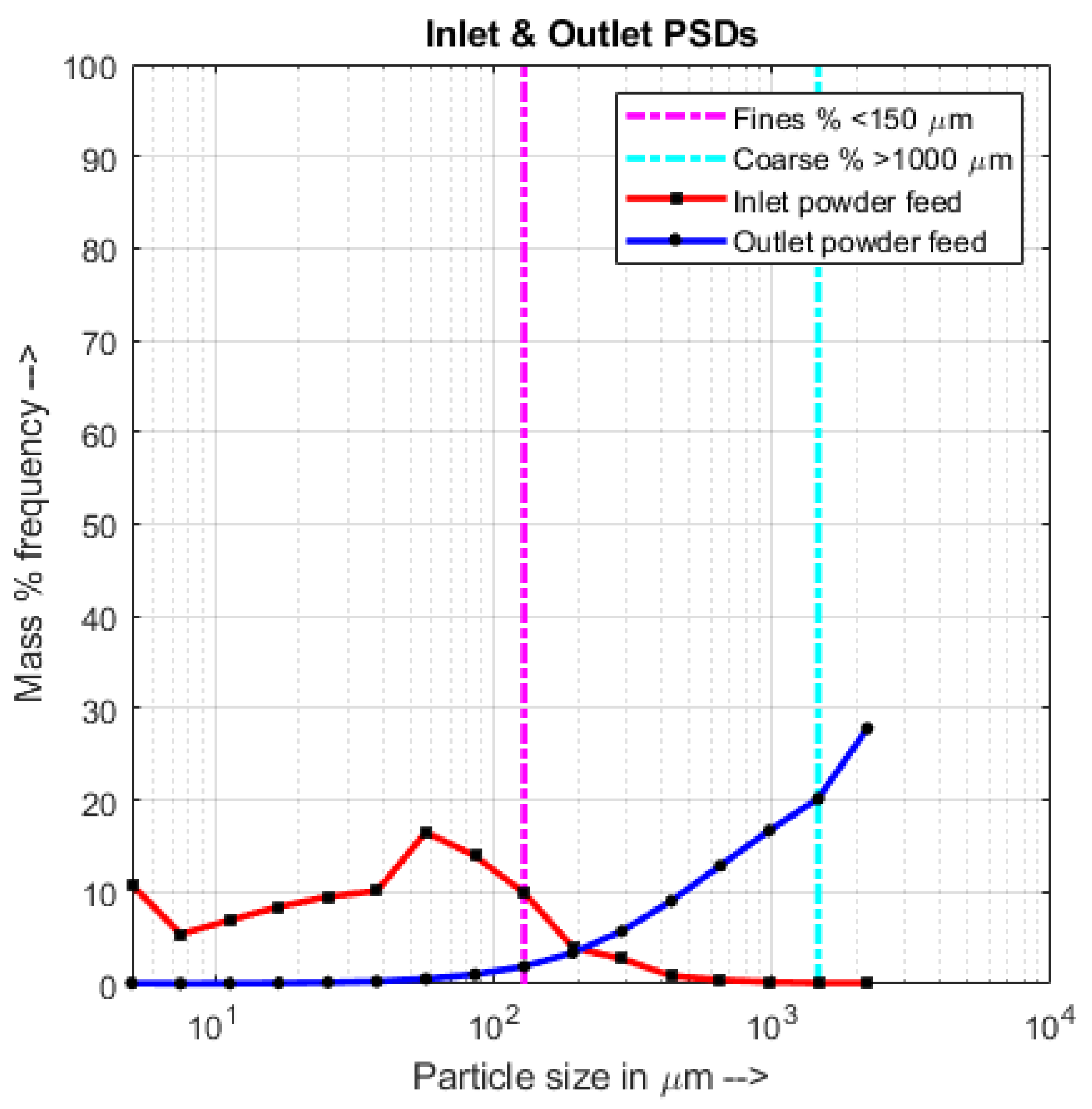
4.2. Qualitative Analysis—Correlation between RTD and PSD
4.3. Qualitative Analysis—Compartmental Holdup
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of Acronyms | |
| CFL condition | Courant–Freidrichs–Lewis condition |
| DEM | discrete element method |
| DOE | design of experiments |
| FR | powder feed rate |
| LS | liquid-to-solid ratio |
| MRT | mean residence time |
| NK | number of kneading elements |
| PBE | population balance equation |
| PEPT | positron emission particle tracking |
| PSD | particle size distribution |
| RMSE | root mean square error |
| RPM | rotations per minute |
| RTD | residence time distribution |
| SA | stagger angle |
| SSE | sum of square of errors |
| TSG | twin screw granulation or twin screw granulator |
| List of Symbols Used | ||
| Symbol | Unit | Quantity |
| z | unitless | external coordinate (spatial location) |
| s | volume | internal coordinate (particle solid volume) |
| t | time | time co-ordinate |
| unitless, number | number of bulk particles | |
| unitless, number | number of tracer particles | |
| number/time | net aggregation rate of particles | |
| number/time | net breakage rate of particles | |
| number/time | rate of bulk particles coming into the | |
| compartment | ||
| number/time | rate of bulk particles going out of the | |
| compartment | ||
| number/time | rate of tracer particles coming into the | |
| compartment | ||
| number/time | rate of tracer particles going out of the | |
| compartment | ||
| length/time | axial velocity of bulk particles | |
| leaving the compartment | ||
| length/time | axial velocity of tracer particles | |
| leaving the compartment | ||
| length/time | axial dispersion coefficient of bulk | |
| particles leaving the compartment | ||
| length/time | axial dispersion coefficient of tracer | |
| particles leaving the compartment | ||
| volume | liquid volume associated with bulk particle | |
| having coordinates | ||
| volume | liquid volume associated with tracer particle | |
| having coordinates | ||
| number/time | net formation rate of particles from aggregation | |
| number/time | net depletion rate of particles due to aggregation | |
| numbertime | specific aggregation rate between two chosen | |
| size classes of particles | ||
| number/time | net formation rate of particles from breakage | |
| number/time | net depletion rate of particles due to breakage | |
| unitless | probability of a larger number particle of size class | |
| breaking into 2 smaller particles | ||
| number/time | specific breakage rate of a particle | |
| time | aggregation rate pre-constant | |
| unitless | aggregation liquid depndency | |
| enhancing parameter | ||
| unitless | aggregation liquid dependency | |
| diminishing parameter | ||
| volume | total volume of the particle | |
| time | shear rate imparted due to screw rotation | |
| unitless | breakage rate pre-constant | |
| unitless | breakage liquid dependency | |
| L | length | length of compartment of interest |
| time | mean residence time | |
| volume/time | total volumetric flow rate | |
| of material into the system | ||
| volume | available vloume for particles to fill up | |
| inside the equipment | ||
| volme/time | volumetric dispense rate | |
| of materials per turn of screws | ||
| time | scaling factor for the MRT | |
| unitless | effect of material throughput on Holdup factor | |
| unitless | effect of material throughput on Flow factor | |
| unitless | effect of volumetric dispense rate on flow factor | |
| unitless | Péclet number | |
| unitless | stagger angle between kneading elements in degrees | |
| unitless | number of neakding elements in kneading block of concern | |
| unitless | scaling factor for the Péclet number | |
| unitless | effect of volumetric dispense rate on mixing factor | |
| unitless | scaling constant indicating ratio of MRT of tracer | |
| relative to MRT of bulk material | ||
| unitless | scaling constant indicating ratio of Pe of tracer | |
| relative to Pe of bulk material | ||
| SSE | unitless | sum of square of errors |
| RMSE | unitless | root mean square of the errors |
References
- Chaudhury, A.; Kapadia, A.; Prakash, A.V.; Barrasso, D.; Ramachandran, R. An extended cell-average technique for a multi-dimensional population balance of granulation describing aggregation and breakage. Adv. Powder Technol. 2013, 24, 962–971. [Google Scholar] [CrossRef]
- Chaudhury, A.; Ramachandran, R. Integrated population balance model development and validation of a granulation process. Part. Sci. Technol. 2013, 31, 407–418. [Google Scholar] [CrossRef]
- Ramachandran, R.; Chaudhury, A. Model-based design and control of a continuous drum granulation process. Chem. Eng. Res. Des. 2012, 90, 1063–1073. [Google Scholar] [CrossRef]
- Barrasso, D.; Walia, S.; Ramachandran, R. Multi-component population balance modeling of continuous granulation processes: A parametric study and comparison with experimental trends. Powder Technol. 2013, 241, 85–97. [Google Scholar] [CrossRef]
- Barrasso, D.; El Hagrasy, A.; Litster, J.D.; Ramachandran, R. Multi-dimensional population balance model development and validation for a twin screw granulation process. Powder Technol. 2015, 270, 612–621. [Google Scholar] [CrossRef]
- Kumar, A.; Vercruysse, J.; Mortier, S.T.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; Nopens, I. Model-based analysis of a twin-screw wet granulation system for continuous solid dosage manufacturing. Comput. Chem. Eng. 2016, 89, 62–70. [Google Scholar] [CrossRef]
- Shirazian, S.; Darwish, S.; Kuhs, M.; Croker, D.M.; Walker, G.M. Regime-separated approach for population balance modeling of continuous wet granulation of pharmaceutical formulations. Powder Technol. 2018, 325, 420–428. [Google Scholar] [CrossRef]
- McGuire, A.D.; Mosbach, S.; Lee, K.F.; Reynolds, G.; Kraft, M. A high-dimensional, stochastic model for twin-screw granulation—Part 1: Model description. Chem. Eng. Sci. 2018, 188, 221–237. [Google Scholar] [CrossRef] [Green Version]
- McGuire, A.D.; Mosbach, S.; Lee, K.F.; Reynolds, G.; Kraft, M. A high-dimensional, stochastic model for twin-screw granulation Part 2: Numerical methodology. Chem. Eng. Sci. 2018, 188, 18–33. [Google Scholar] [CrossRef] [Green Version]
- Van Hauwermeiren, D.; Verstraeten, M.; Doshi, P.; am Ende, M.T.; Turnbull, N.; Lee, K.; De Beer, T.; Nopens, I. On the modeling of granule size distributions in twin-screw wet granulation: Calibration of a novel compartmental population balance model. Powder Technol. 2019, 341, 116–125. [Google Scholar] [CrossRef]
- Wang, L.G.; Pradhan, S.U.; Wassgren, C.; Barrasso, D.; Slade, D.; Litster, J.D. A breakage kernel for use in population balance modeling of twin screw granulation. Powder Technol. 2020, 363, 525–540. [Google Scholar] [CrossRef]
- Lee, K.T.; Ingram, A.; Rowson, N.A. Twin screw wet granulation: The study of a continuous twin screw granulator using Positron Emission Particle Tracking (PEPT) technique. Eur. J. Pharm. Biopharm. 2012, 81, 666–673. [Google Scholar] [CrossRef]
- Zheng, C.; Zhang, L.; Govender, N.; Wu, C.Y. DEM analysis of residence time distribution during twin screw granulation. Powder Technol. 2020, 377, 924–938. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Pearson International Edition; Chapter Models for Nonideal Reactors; Prentice Hall: Hoboken, NJ, USA, 2006; p. 38. [Google Scholar]
- Barrasso, D.; Ramachandran, R. Qualitative assessment of a multi-scale, compartmental PBM-DEM model of a continuous twin-screw wet granulation process. J. Pharm. Innov. 2016, 11, 231–249. [Google Scholar] [CrossRef]
- Ge Wang, L.; Morrissey, J.P.; Barrasso, D.; Slade, D.; Clifford, S.; Reynolds, G.; Ooi, J.Y.; Litster, J.D. Model Driven Design for Twin Screw Granulation using Mechanistic-based Population Balance Model. Int. J. Pharm. 2021, 607, 120939. [Google Scholar] [CrossRef]
- Muddu, S.V.; Kotamarthy, L.; Ramachandran, R. A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation. Pharmaceutics 2021, 13, 393. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Vercruysse, J.; Vanhoorne, V.; Toiviainen, M.; Panouillot, P.E.; Juuti, M.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; et al. Conceptual framework for model-based analysis of residence time distribution in twin-screw granulation. Eur. J. Pharm. Sci. 2015, 71, 25–34. [Google Scholar] [CrossRef]
- Kumar, A.; Alakarjula, M.; Vanhoorne, V.; Toiviainen, M.; De Leersnyder, F.; Vercruysse, J.; Juuti, M.; Ketolainen, J.; Vervaet, C.; Remon, J.P.; et al. Linking granulation performance with residence time and granulation liquid distributions in twin-screw granulation: An experimental investigation. Eur. J. Pharm. Sci. 2016, 90, 25–37. [Google Scholar] [CrossRef]
- Madec, L.; Falk, L.; Plasari, E. modeling of the agglomeration in suspension process with multidimensional kernels. Powder Technol. 2003, 130, 147–153. [Google Scholar] [CrossRef]
- Pandya, J.; Spielman, L. Floc breakage in agitated suspensions: Effect of agitation rate. Chem. Eng. Sci. 1983, 38, 1983–1992. [Google Scholar] [CrossRef]
- Portillo, P.M.; Muzzio, F.J.; Ierapetritou, M.G. Using compartment modeling to investigate mixing behavior of a continuous mixer. J. Pharm. Innov. 2008, 3, 161–174. [Google Scholar] [CrossRef]
- Sen, M.; Singh, R.; Vanarase, A.; John, J.; Ramachandran, R. Multi-dimensional population balance modeling and experimental validation of continuous powder mixing processes. Chem. Eng. Sci. 2012, 80, 349–360. [Google Scholar] [CrossRef]






| Data Source | Equipment Name | Process Material | Varied Parameters | Number of Data Points |
|---|---|---|---|---|
| Kumar et al., 2015 [18] | ConsiGma-25 | -Lactose MH | FR, RPM, NK & SA | 66 |
| Kumar et al., 2016 [19] | ConsiGma-25 | -Lactose MH | FR, RPM, LS, NK & SA | 51 |
| Total: 117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muddu, S.V.; Ramachandran, R. A Population Balance Methodology Incorporating Semi-Mechanistic Residence Time Metrics for Twin Screw Granulation. Processes 2022, 10, 292. https://doi.org/10.3390/pr10020292
Muddu SV, Ramachandran R. A Population Balance Methodology Incorporating Semi-Mechanistic Residence Time Metrics for Twin Screw Granulation. Processes. 2022; 10(2):292. https://doi.org/10.3390/pr10020292
Chicago/Turabian StyleMuddu, Shashank Venkat, and Rohit Ramachandran. 2022. "A Population Balance Methodology Incorporating Semi-Mechanistic Residence Time Metrics for Twin Screw Granulation" Processes 10, no. 2: 292. https://doi.org/10.3390/pr10020292
APA StyleMuddu, S. V., & Ramachandran, R. (2022). A Population Balance Methodology Incorporating Semi-Mechanistic Residence Time Metrics for Twin Screw Granulation. Processes, 10(2), 292. https://doi.org/10.3390/pr10020292





