The Oxygen Gradient in Hypoxic Conditions Enhances and Guides Dictyostelium discoideum Migration
Abstract
:1. Introduction
2. Methods
2.1. Microfluidic Device
2.2. Cellular Experiments
2.3. Motility Analysis
3. Results
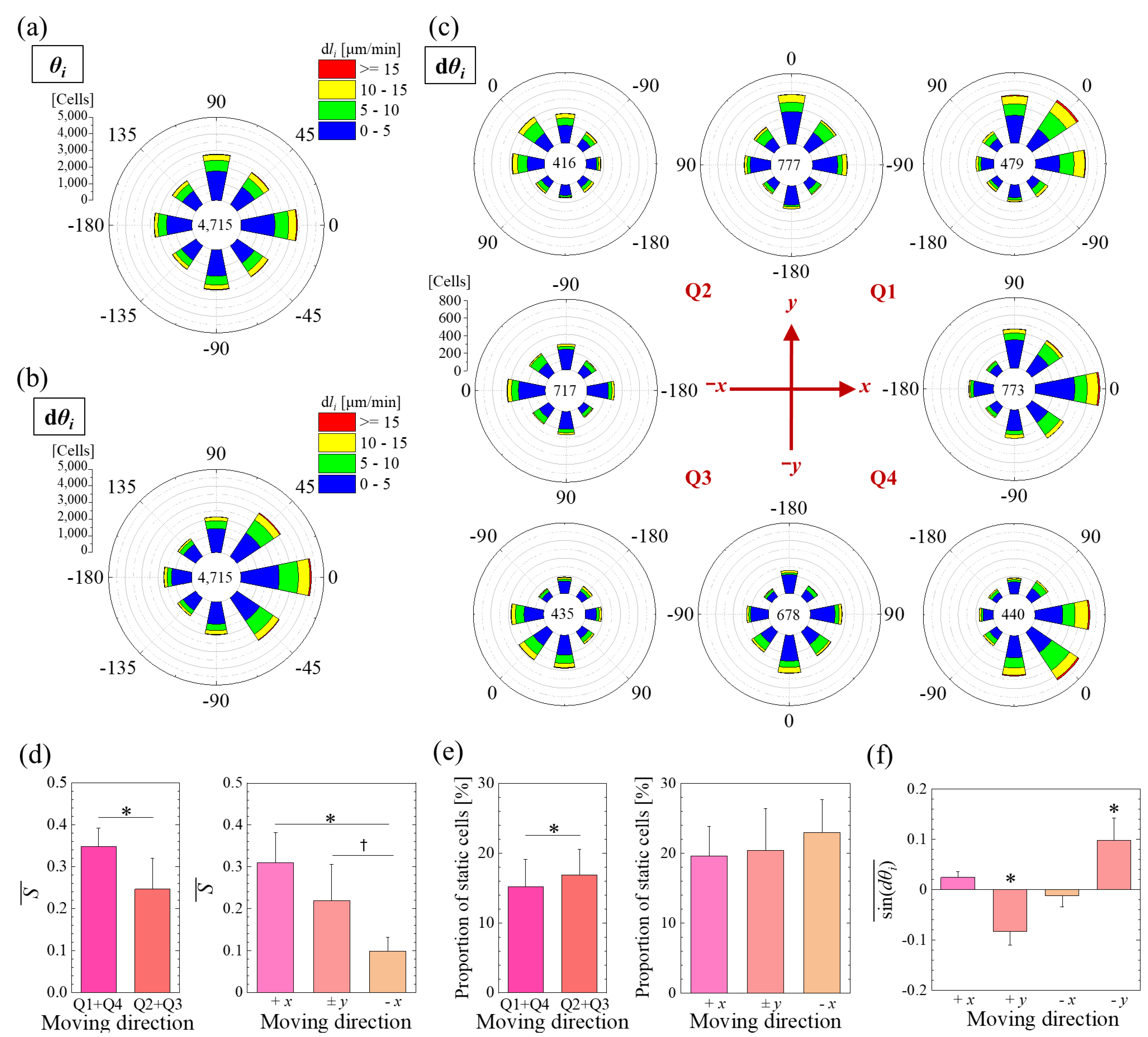
3.1. Migration Velocity under an Oxygen Concentration Gradient
3.2. Directionality of Migration under an Oxygen Concentration Gradient
3.3. Migration under a Uniform Oxygen Environment (Aerokinesis)
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hsia, C.C.; Schmitz, A.; Lambertz, M.; Perry, S.F.; Maina, J.N. Evolution of air breathing: Oxygen homeostasis and the transitions from water to land and sky. Compr. Physiol. 2013, 3, 849–915. [Google Scholar]
- Vaupel, P.; Schlenger, K.; Knoop, C.; Höckel, M. Oxygenation of human tumors: Evaluation of tissue oxygen distribution in breast cancers by computerized O2 tension measurements. Cancer Res. 1991, 51, 3316–3322. [Google Scholar] [PubMed]
- Semenza, G.L. HIF-1 and human disease: One highly involved factor. Genes Dev. 2000, 14, 1983–1991. [Google Scholar] [CrossRef] [PubMed]
- Eltzschig, H.K.; Carmeliet, P. Hypoxia and inflammation. New Engl. J. Med. 2011, 364, 656–665. [Google Scholar] [CrossRef] [Green Version]
- Krock, B.L.; Skuli, N.; Simon, M.C. Hypoxia-induced angiogenesis: Good and evil. Genes Cancer 2011, 2, 1117–1133. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, C.; Muthana, M.; Lewis, C.E. Hypoxia regulates macrophage functions in inflammation. J. Immunol. 2005, 175, 6257–6263. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, S.; Te Boekhorst, V.; Odenthal, J.; Bianchi, R.; van Helvert, S.; Ikenberg, K.; Ilina, O.; Stoma, S.; Xandry, J.; Jiang, L. Hypoxia induces a HIF-1-dependent transition from collective-to-amoeboid dissemination in epithelial cancer cells. Curr. Biol. 2017, 27, 392–400. [Google Scholar] [CrossRef] [Green Version]
- Muz, B.; de la Puente, P.; Azab, F.; Azab, A.K. The role of hypoxia in cancer progression, angiogenesis, metastasis, and resistance to therapy. Hypoxia 2015, 3, 83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deygas, M.; Gadet, R.; Gillet, G.; Rimokh, R.; Gonzalo, P.; Mikaelian, I. Redox regulation of EGFR steers migration of hypoxic mammary cells towards oxygen. Nat. Commun. 2018, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Taylor, B.L.; Zhulin, I.B.; Johnson, M.S. Aerotaxis and other energy-sensing behavior in bacteria. Annu. Rev. Microbiol. 1999, 53, 103–128. [Google Scholar] [CrossRef]
- Eichinger, L.; Pachebat, J.; Glöckner, G.; Rajandream, M.-A.; Sucgang, R.; Berriman, M.; Song, J.; Olsen, R.; Szafranski, K.; Xu, Q. The genome of the social amoeba Dictyostelium discoideum. Nature 2005, 435, 43–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Annesley, S.J.; Fisher, P.R. Dictyostelium discoideum—A model for many reasons. Mol. Cell. Biochem. 2009, 329, 73–91. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.S.; Boeckeler, K.; Gräf, R.; Müller-Taubenberger, A.; Li, Z.; Isberg, R.R.; Wessels, D.; Soll, D.R.; Alexander, H.; Alexander, S. Towards a molecular understanding of human diseases using Dictyostelium discoideum. Trends Mol. Med. 2006, 12, 415–424. [Google Scholar] [CrossRef] [PubMed]
- Poff, K.L.; Skokut, M. Thermotaxis by pseudoplasmodia of Dictyostelium discoideum. Proc. Natl. Acad. Sci. USA 1977, 74, 2007–2010. [Google Scholar] [CrossRef] [Green Version]
- Fisher, P.R. Genetics of phototaxis in a model eukaryote, Dictyostelium discoideum. Bioessays 1997, 19, 397–407. [Google Scholar] [CrossRef] [PubMed]
- Marée, A.F.M.; Panfilov, A.V.; Hogeweg, P. Phototaxis during the slug stage of Dictyostelium discoideum: A model study. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1999, 266, 1351–1360. [Google Scholar] [CrossRef]
- Zhao, M.; Jin, T.; McCaig, C.D.; Forrester, J.V.; Devreotes, P.N. Genetic analysis of the role of G protein–coupled receptor signaling in electrotaxis. J. Cell Biol. 2002, 157, 921–928. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konijn, T.M.; Chang, Y.-Y.; Bonner, J.T. Synthesis of cyclic AMP in Dictyostelium discoideum and Polysphondylium pallidum. Nature 1969, 224, 1211–1212. [Google Scholar] [CrossRef] [PubMed]
- Devreotes, P.N.; Zigmond, S.H. Chemotaxis in eukaryotic cells: A focus on leukocytes and Dictyostelium. Annu. Rev. Cell Biol. 1988, 4, 649–686. [Google Scholar] [CrossRef]
- Van Haastert, P.J.; Devreotes, P.N. Chemotaxis: Signalling the way forward. Nature reviews Mol. Cell Biol. 2004, 5, 626–634. [Google Scholar] [CrossRef]
- Pepper, I.L.; Brusseau, M.L. Physical-Chemical Characteristics of Soils and the Subsurface. In Environmental and Pollution Science, 3rd ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Xu, Y.; Wang, Z.A.; Green, R.S.; West, C.M. Role of the Skp1 prolyl-hydroxylation/glycosylation pathway in oxygen dependent submerged development of Dictyostelium. BMC Dev. Biol. 2012, 12, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Cardelli, J.A.; Dimond, R.L. Regulation of protein synthesis in Dictyostelium discoideum: Effects of starvation and anoxia on initiation. Biochemistry 1981, 20, 7391–7398. [Google Scholar] [CrossRef]
- Cotter, D.A.; Raper, K.B. Properties of germinating spores of Dictyostelium discoideum. J. Bacteriol. 1968, 96, 1680–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- West, C.M.; van der Wel, H.; Wang, Z.A. Prolyl 4-hydroxylase-1 mediates O2 signaling during development of Dictyostelium. Development 2007, 134, 3349–3358. [Google Scholar] [CrossRef] [Green Version]
- West, C.M.; Wang, Z.A.; van der Wel, H. A cytoplasmic prolyl hydroxylation and glycosylation pathway modifies Skp1 and regulates O2-dependent development in Dictyostelium. Biochim. Biophys. Acta 2010, 1800, 160–171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Semenza, G.L. Hypoxia-inducible factor 1 (HIF-1) pathway. Sci. STKE 2007, 2007, cm8. [Google Scholar] [CrossRef]
- Cochet-Escartin, O.; Demircigil, M.; Hirose, S.; Allais, B.; Gonzalo, P.; Mikaelian, I.; Funamoto, K.; Anjard, C.; Calvez, V.; Rieu, J.-P. Hypoxia triggers collective aerotactic migration in Dictyostelium discoideum. eLife 2021, 10, e64731. [Google Scholar] [CrossRef] [PubMed]
- Biondo, M.; Panuzzo, C.; Ali, S.M.; Osella, M.; Bozzaro, S.; Bracco, E.; Pergolizzi, B. The dynamics of aerotaxis in a simple eukaryotic model. Front. Cell Dev. Biol. 2021, 9, 720623. [Google Scholar] [CrossRef] [PubMed]
- Rieu, J.-P.; Cochet-Escartin, O.; Anjard, C.; Calvez, V.; Demircigil, M. Commentary: The Dynamics of Aerotaxis in a Simple Eukaryotic Model. Front. Cell Dev. Biol. 2022, in press. [Google Scholar]
- Halldorsson, S.; Lucumi, E.; Gómez-Sjöberg, R.; Fleming, R.M. Advantages and challenges of microfluidic cell culture in polydimethylsiloxane devices. Biosens. Bioelectron. 2015, 63, 218–231. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.-J.; Saadi, W.; Lin, F.; Nguyen, C.M.-C.; Jeon, N.L. Differential effects of EGF gradient profiles on MDA-MB-231 breast cancer cell chemotaxis. Exp. Cell Res. 2004, 300, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Butcher, E.C. T cell chemotaxis in a simple microfluidic device. Lab Chip 2006, 6, 1462–1469. [Google Scholar] [CrossRef] [PubMed]
- Diao, J.; Young, L.; Kim, S.; Fogarty, E.A.; Heilman, S.M.; Zhou, P.; Shuler, M.L.; Wu, M.; DeLisa, M.P. A three-channel microfluidic device for generating static linear gradients and its application to the quantitative analysis of bacterial chemotaxis. Lab Chip 2006, 6, 381–388. [Google Scholar] [CrossRef]
- Wang, L.; Liu, W.; Wang, Y.; Wang, J.-c.; Tu, Q.; Liu, R.; Wang, J. Construction of oxygen and chemical concentration gradients in a single microfluidic device for studying tumor cell–drug interactions in a dynamic hypoxia microenvironment. Lab Chip 2013, 13, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Lam, S.F.; Shirure, V.S.; Chu, Y.E.; Soetikno, A.G.; George, S.C. Microfluidic device to attain high spatial and temporal control of oxygen. PLoS ONE 2018, 13, e0209574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grist, S.M.; Schmok, J.C.; Liu, M.-C.A.; Chrostowski, L.; Cheung, K.C. Designing a microfluidic device with integrated ratiometric oxygen sensors for the long-term control and monitoring of chronic and cyclic hypoxia. Sensors 2015, 15, 20030–20052. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Chen, Q.; Liu, W.; Zhang, J.; Wang, S.; Lin, Z.; Lin, J.-M. Oxygen-induced cell migration and on-line monitoring biomarkers modulation of cervical cancers on a microfluidic system. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Funamoto, K.; Zervantonakis, I.K.; Liu, Y.; Ochs, C.J.; Kim, C.; Kamm, R.D. A novel microfluidic platform for high-resolution imaging of a three-dimensional cell culture under a controlled hypoxic environment. Lab Chip 2012, 12, 4855–4863. [Google Scholar] [CrossRef] [Green Version]
- Koens, R.; Tabata, Y.; Serrano, J.C.; Aratake, S.; Yoshino, D.; Kamm, R.D.; Funamoto, K. Microfluidic platform for three-dimensional cell culture under spatiotemporal heterogeneity of oxygen tension. Appl. Bioeng. 2020, 4, 11. [Google Scholar] [CrossRef]
- Hirose, S.; Tabata, Y.; Sone, K.; Takahashi, N.; Yoshino, D.; Funamoto, K. P21-activated kinase regulates oxygen-dependent migration of vascular endothelial cells in monolayers. Cell Adhes. Migr. 2021, 15, 272–284. [Google Scholar] [CrossRef]
- Hirose, S.; Rieu, J.-P.; Anjard, C.; Cochet-Escartin, O.; Kikuchi, H.; Funamoto, K. Aerotaxis and aerokinesis of Dictyostelium discoideum under hypoxic microenvironments. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2021, 2021, 1187–1190. [Google Scholar] [PubMed]
- Kim, M.-C.; Lam, R.H.; Thorsen, T.; Asada, H.H. Mathematical analysis of oxygen transfer through polydimethylsiloxane membrane between double layers of cell culture channel and gas chamber in microfluidic oxygenator. Microfluid. Nanofluidics 2013, 15, 285–296. [Google Scholar] [CrossRef] [Green Version]
- Merkel, T.; Bondar, V.; Nagai, K.; Freeman, B.; Pinnau, I. Gas sorption, diffusion, and permeation in poly (dimethylsiloxane). J. Polym. Sci. Part B Polym. Phys. 2000, 38, 415–434. [Google Scholar] [CrossRef]
- Blair, D.; Dufresne, E. The Matlab Particle Tracking Code Repository. Available online: https://site.physics.georgetown.edu/matlab/ (accessed on 20 January 2022).
- Amselem, G.; Theves, M.; Bae, A.; Bodenschatz, E.; Beta, C. A stochastic description of Dictyostelium chemotaxis. PLoS ONE 2012, 7, e37213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macnab, R.M.; Koshland, D.E. The gradient-sensing mechanism in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 1972, 69, 2509–2512. [Google Scholar] [CrossRef] [Green Version]
- Willard, S.S.; Devreotes, P.N. Signaling pathways mediating chemotaxis in the social amoeba, Dictyostelium discoideum. Eur. J. Cell Biol. 2006, 85, 897–904. [Google Scholar] [CrossRef]
- Song, L.; Nadkarni, S.M.; Bödeker, H.U.; Beta, C.; Bae, A.; Franck, C.; Rappel, W.-J.; Loomis, W.F.; Bodenschatz, E. Dictyostelium discoideum chemotaxis: Threshold for directed motion. Eur. J. Cell Biol. 2006, 85, 981–989. [Google Scholar] [CrossRef]
- Parent, C.A.; Devreotes, P.N. A cell’s sense of direction. Science 1999, 284, 765–770. [Google Scholar] [CrossRef] [Green Version]
- Takagi, H.; Sato, M.J.; Yanagida, T.; Ueda, M. Functional analysis of spontaneous cell movement under different physiological conditions. PLoS ONE 2008, 3, e2648. [Google Scholar] [CrossRef] [Green Version]
- Golé, L.; Rivière, C.; Hayakawa, Y.; Rieu, J.-P. A quorum-sensing factor in vegetative Dictyostelium discoideum cells revealed by quantitative migration analysis. PLoS ONE 2011, 6, e26901. [Google Scholar] [CrossRef] [Green Version]
- D’Alessandro, J.; Mas, L.; Aubry, L.; Rieu, J.-P.; Rivière, C.; Anjard, C. Collective regulation of cell motility using an accurate density-sensing system. J. R. Soc. Interface 2018, 15, 20180006. [Google Scholar] [CrossRef] [PubMed]
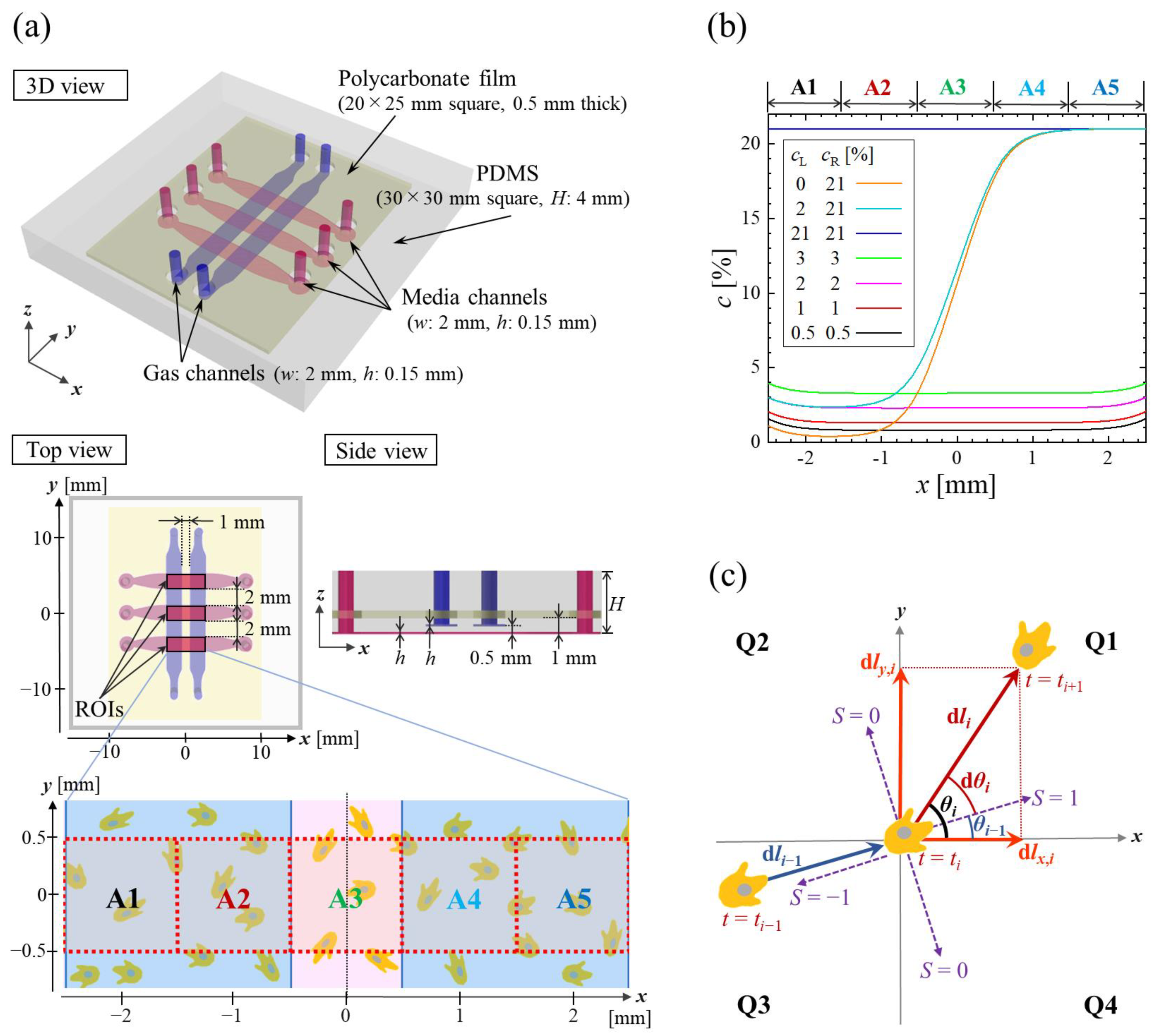




| Material | Medium | Gas | PDMS | PC film |
|---|---|---|---|---|
| Density, ρ [kg/m3] | 1.0 × 103 | 1 | ||
| Viscosity, μ [Pa s] | 1.0 × 10−3 | 1.0 × 10−5 | ||
| Diffusivity of oxygen, D [m2/s] | 2.0 × 10−9 | 2.0 × 10−5 | 4.0 × 10−9 | 2.0 × 10−12 |
| Concentration of oxygen in the material near the air interface (at 21% O2), CS [mM] | 0.218 | 1.25 | 1.25 | |
| Flow volume, Q [mL/min] | 0 | 30 | ||
| Oxygen tension, c [%] | 21 | 0–21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirose, S.; Rieu, J.-P.; Cochet-Escartin, O.; Anjard, C.; Funamoto, K. The Oxygen Gradient in Hypoxic Conditions Enhances and Guides Dictyostelium discoideum Migration. Processes 2022, 10, 318. https://doi.org/10.3390/pr10020318
Hirose S, Rieu J-P, Cochet-Escartin O, Anjard C, Funamoto K. The Oxygen Gradient in Hypoxic Conditions Enhances and Guides Dictyostelium discoideum Migration. Processes. 2022; 10(2):318. https://doi.org/10.3390/pr10020318
Chicago/Turabian StyleHirose, Satomi, Jean-Paul Rieu, Olivier Cochet-Escartin, Christophe Anjard, and Kenichi Funamoto. 2022. "The Oxygen Gradient in Hypoxic Conditions Enhances and Guides Dictyostelium discoideum Migration" Processes 10, no. 2: 318. https://doi.org/10.3390/pr10020318
APA StyleHirose, S., Rieu, J.-P., Cochet-Escartin, O., Anjard, C., & Funamoto, K. (2022). The Oxygen Gradient in Hypoxic Conditions Enhances and Guides Dictyostelium discoideum Migration. Processes, 10(2), 318. https://doi.org/10.3390/pr10020318







