Comparative Study between Flatness-Based and Field-Oriented Control Methods of a Grid-Connected Wind Energy Conversion System
Abstract
:1. Introduction
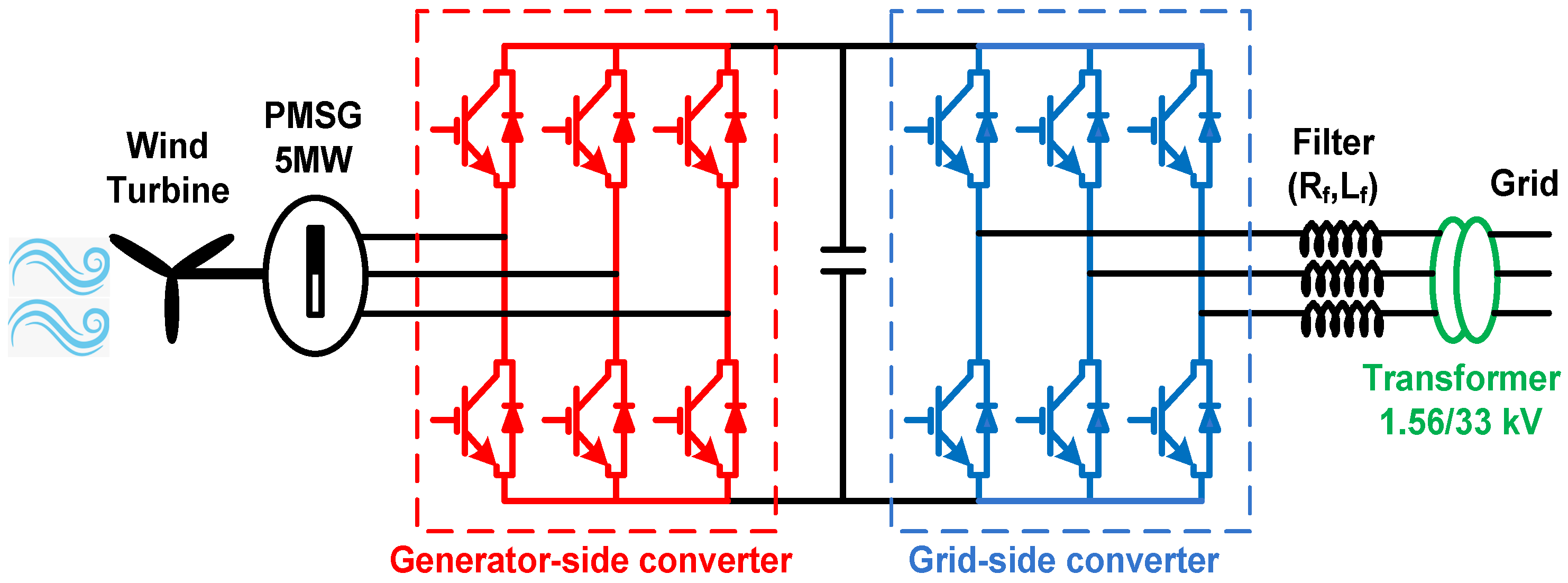
2. Model of the Wind Energy Conversion System
2.1. Wind Turbine Model
2.2. Model of Permanent Magnet Synchronous Generator (PMSG)
2.3. Voltage Source Converter (VSC)
2.4. Model of the Electrical Grid
3. Field-Oriented Control Method
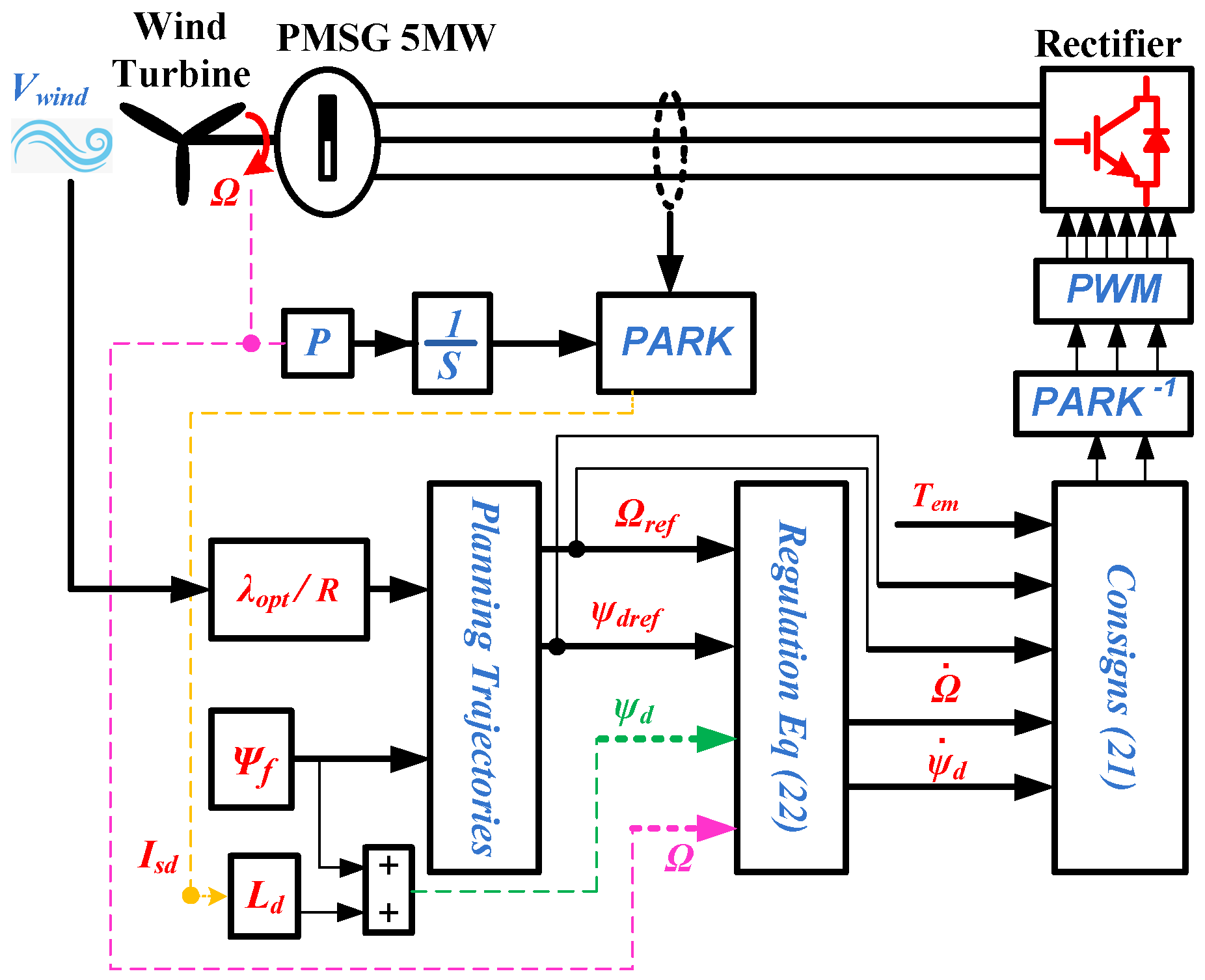
3.1. Wind Generator Control Method
3.1.1. Rotation Speed Control
3.1.2. Stator’s Current Control
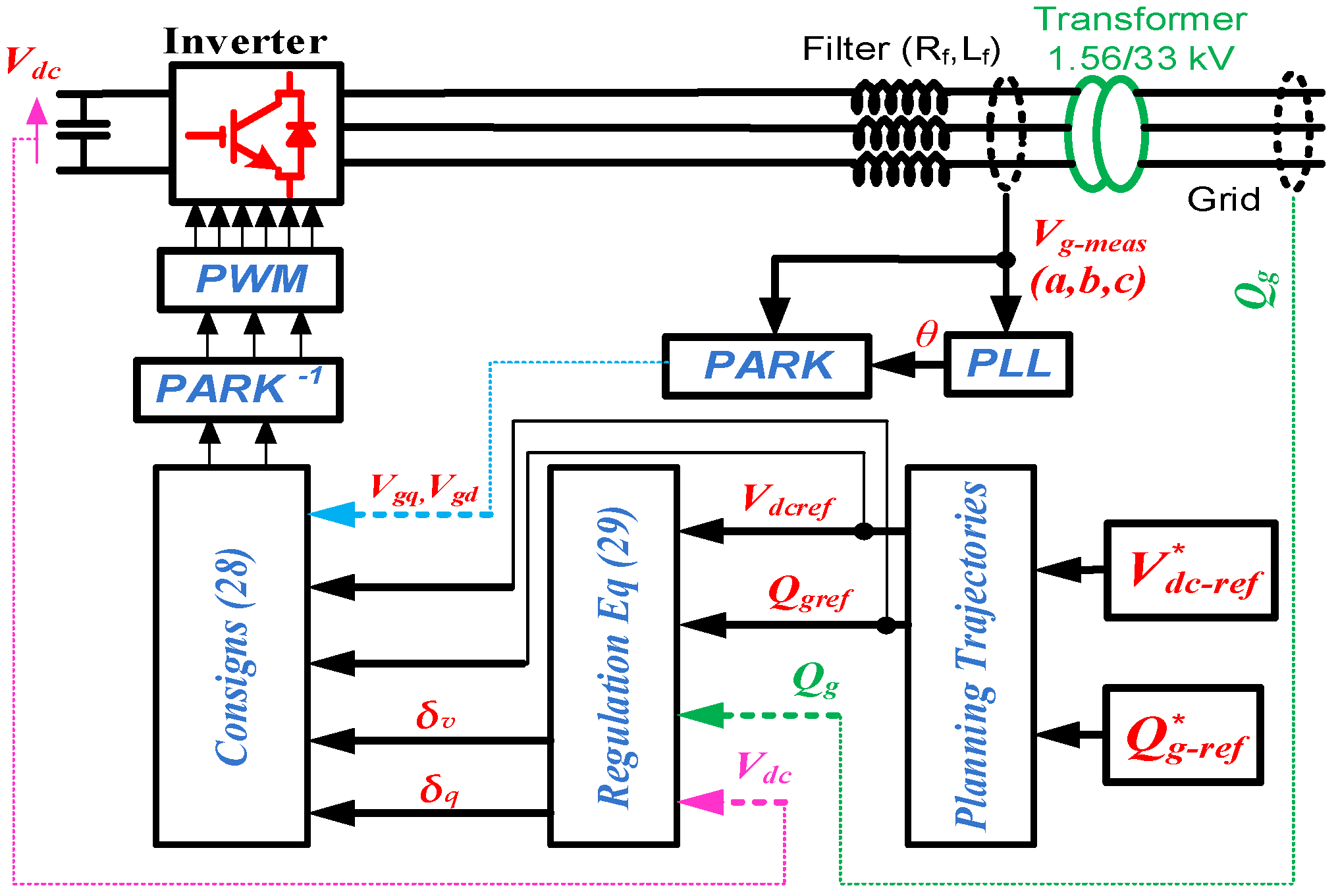
3.2. Energy Management between the PMSG and the Grid
3.2.1. DC-Bus Voltage and Reactive Power Control
3.2.2. Grid’s Currents Control
4. Flatness-Based Control
4.1. Wind Generator Control Method
4.2. Energy Management between the PMSG and the Grid
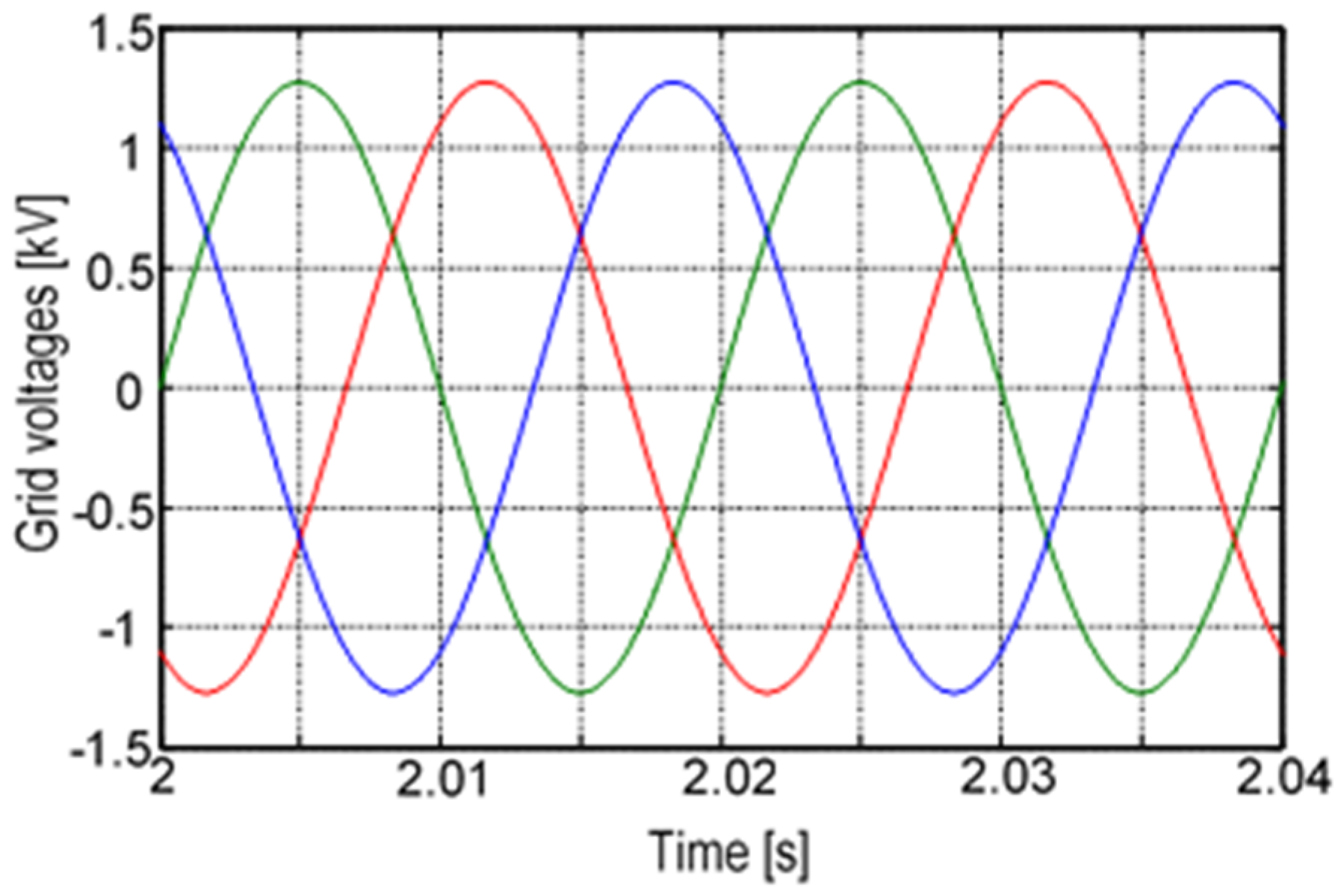
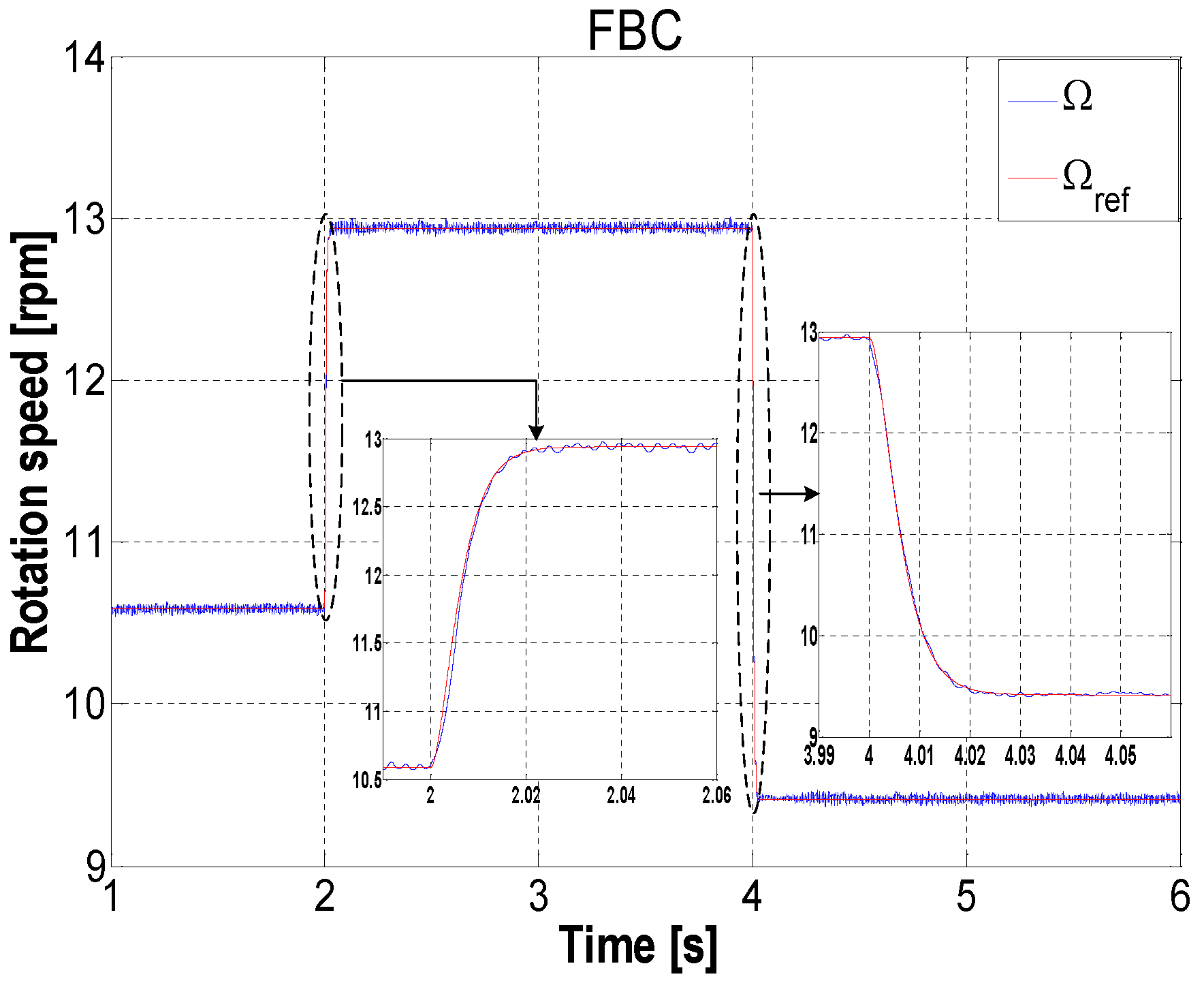
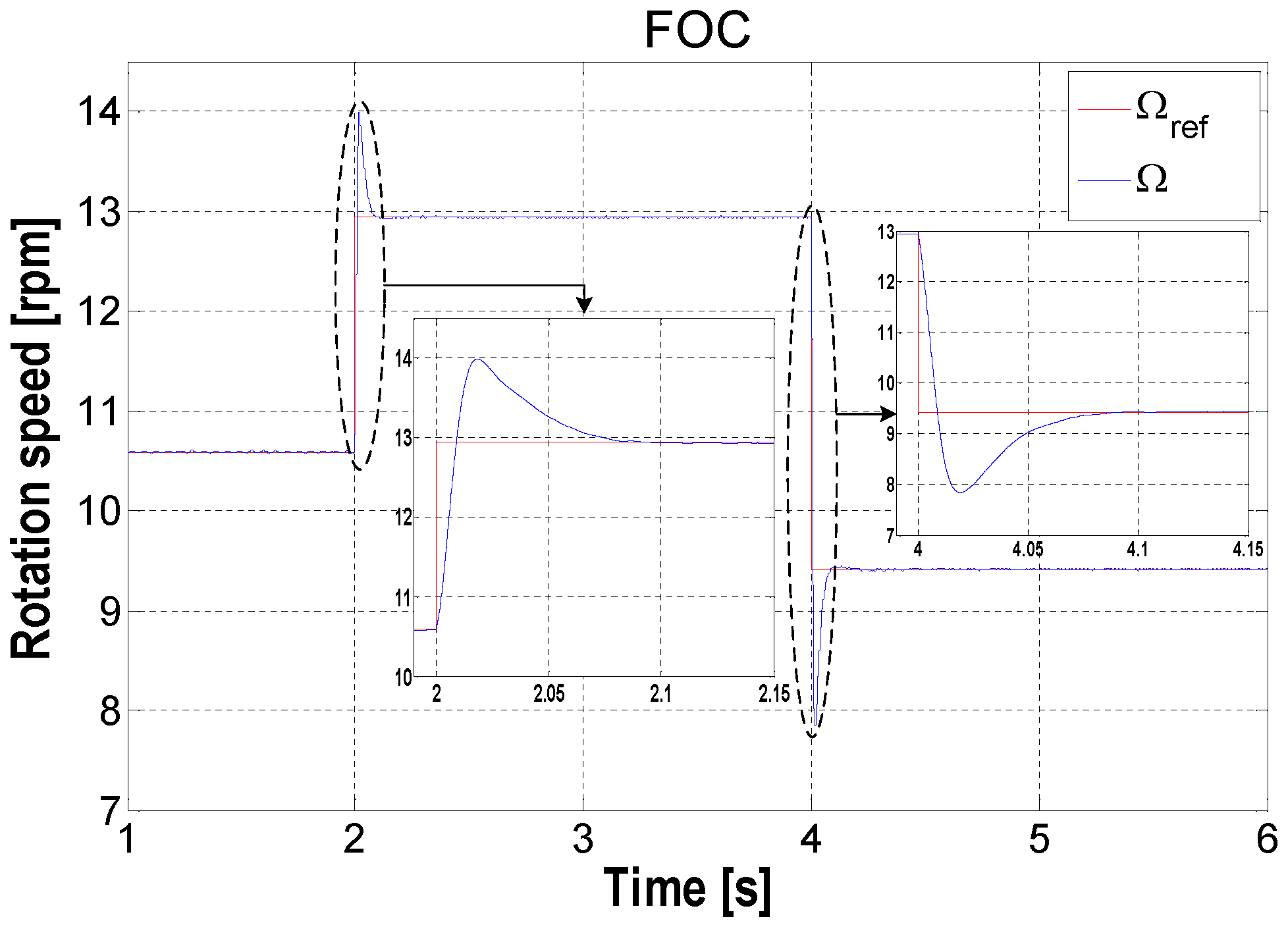
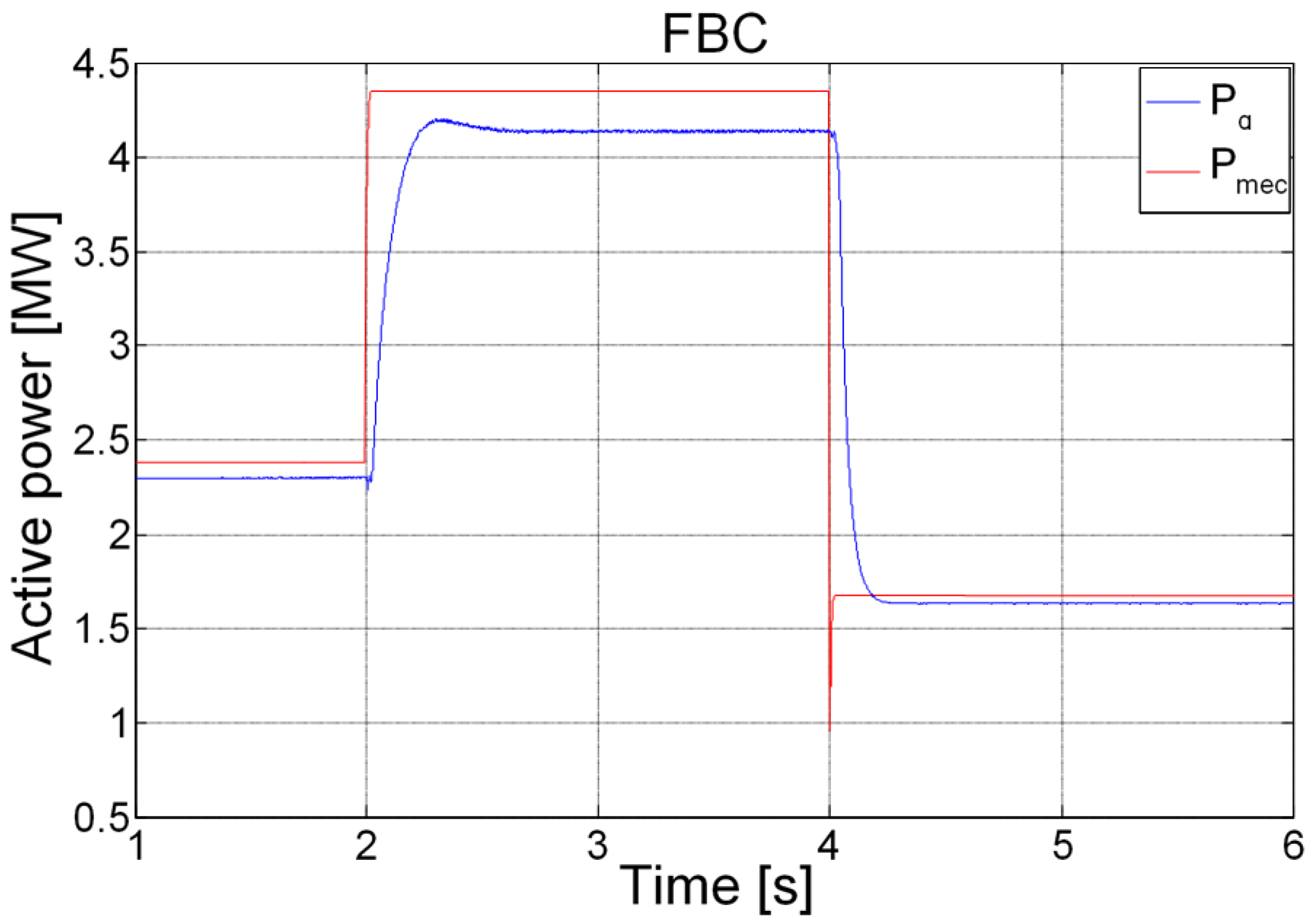
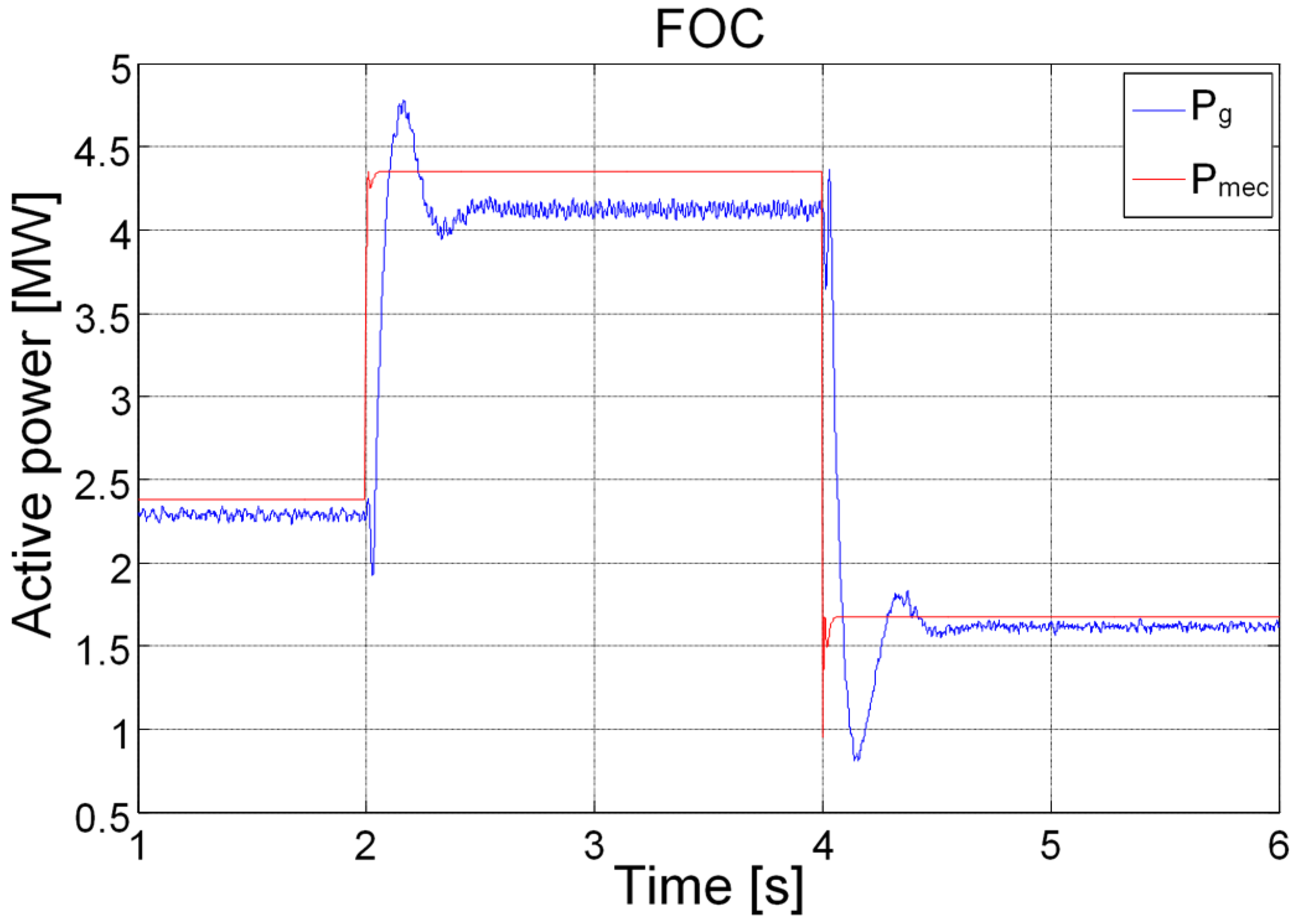
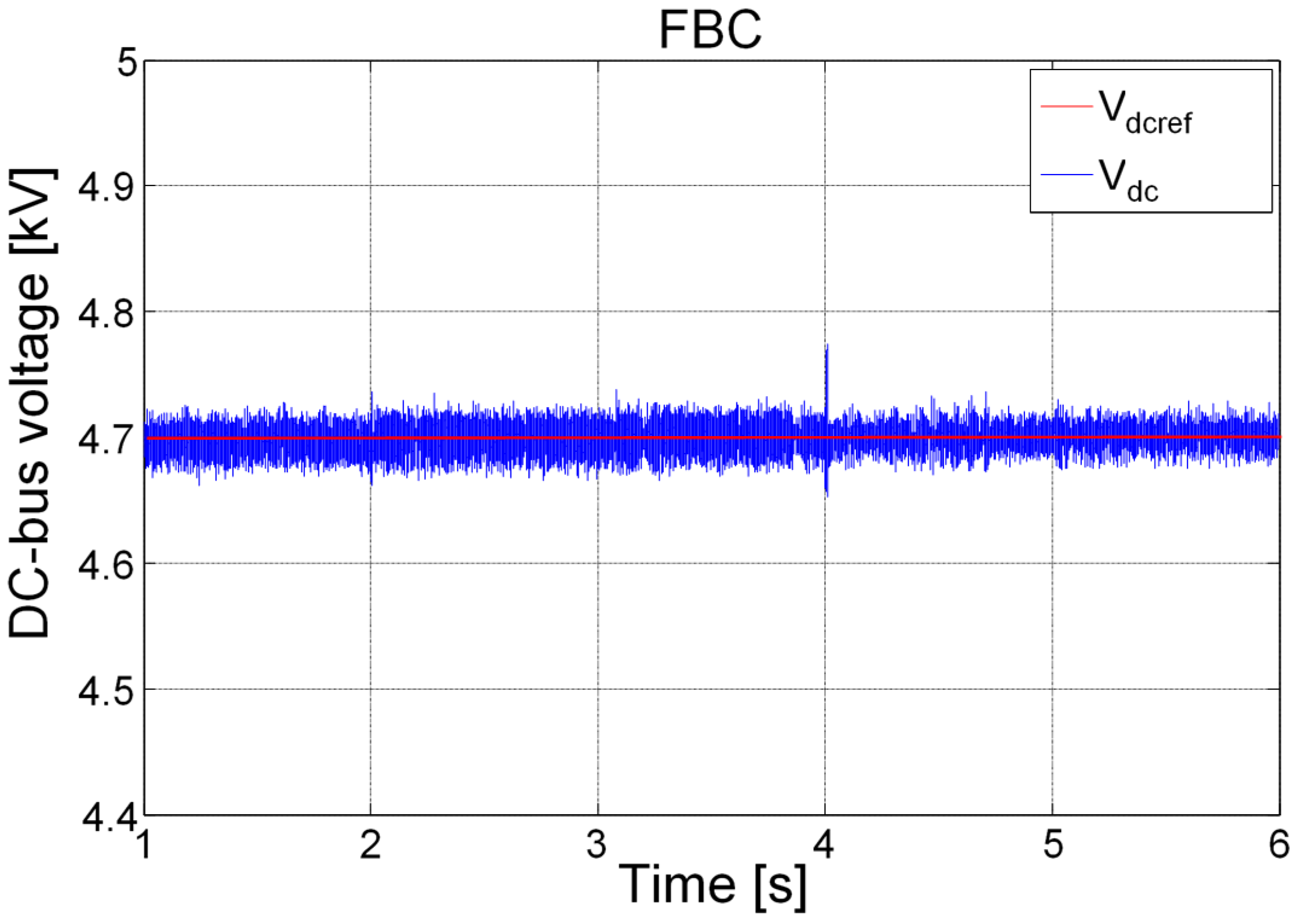
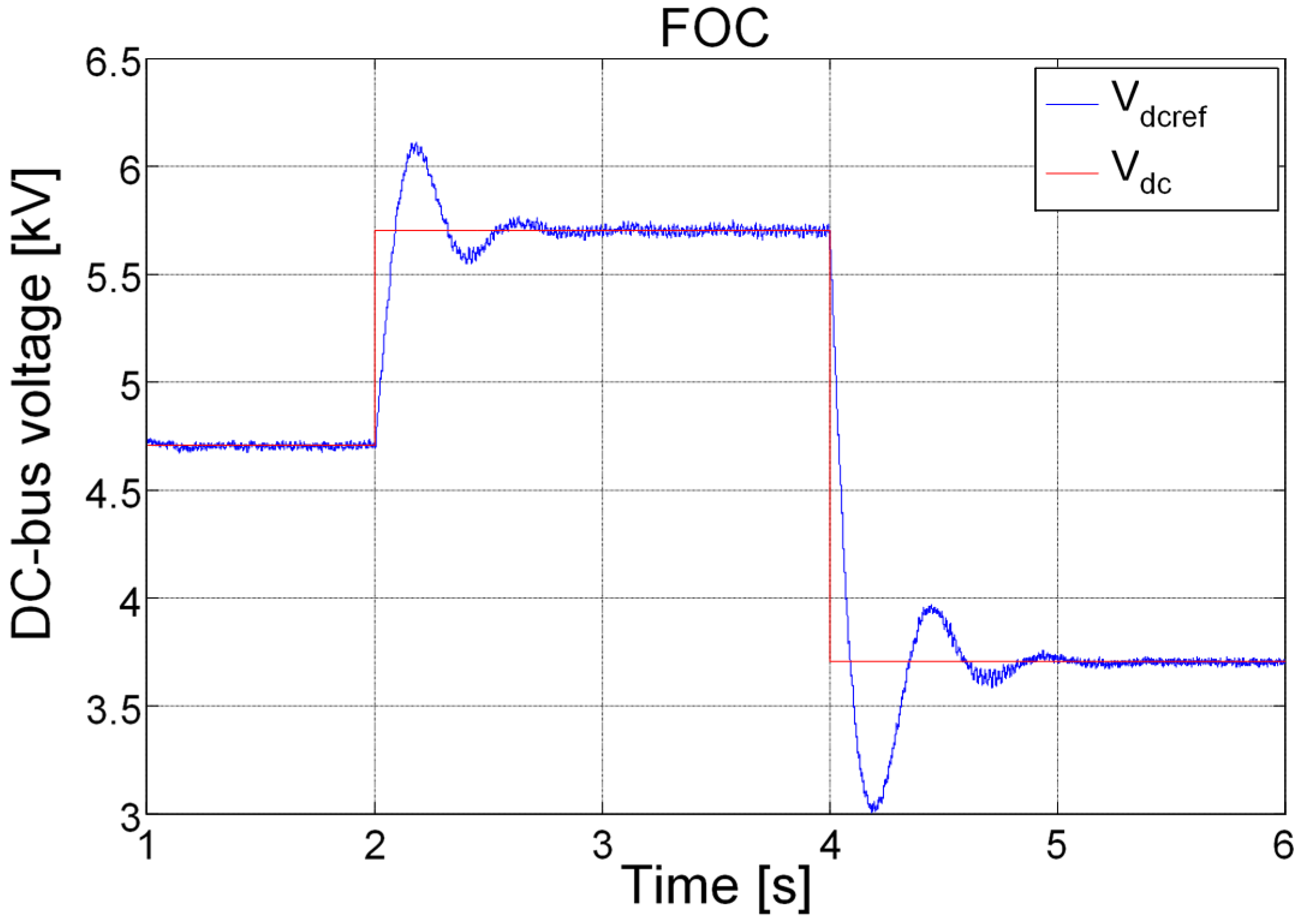
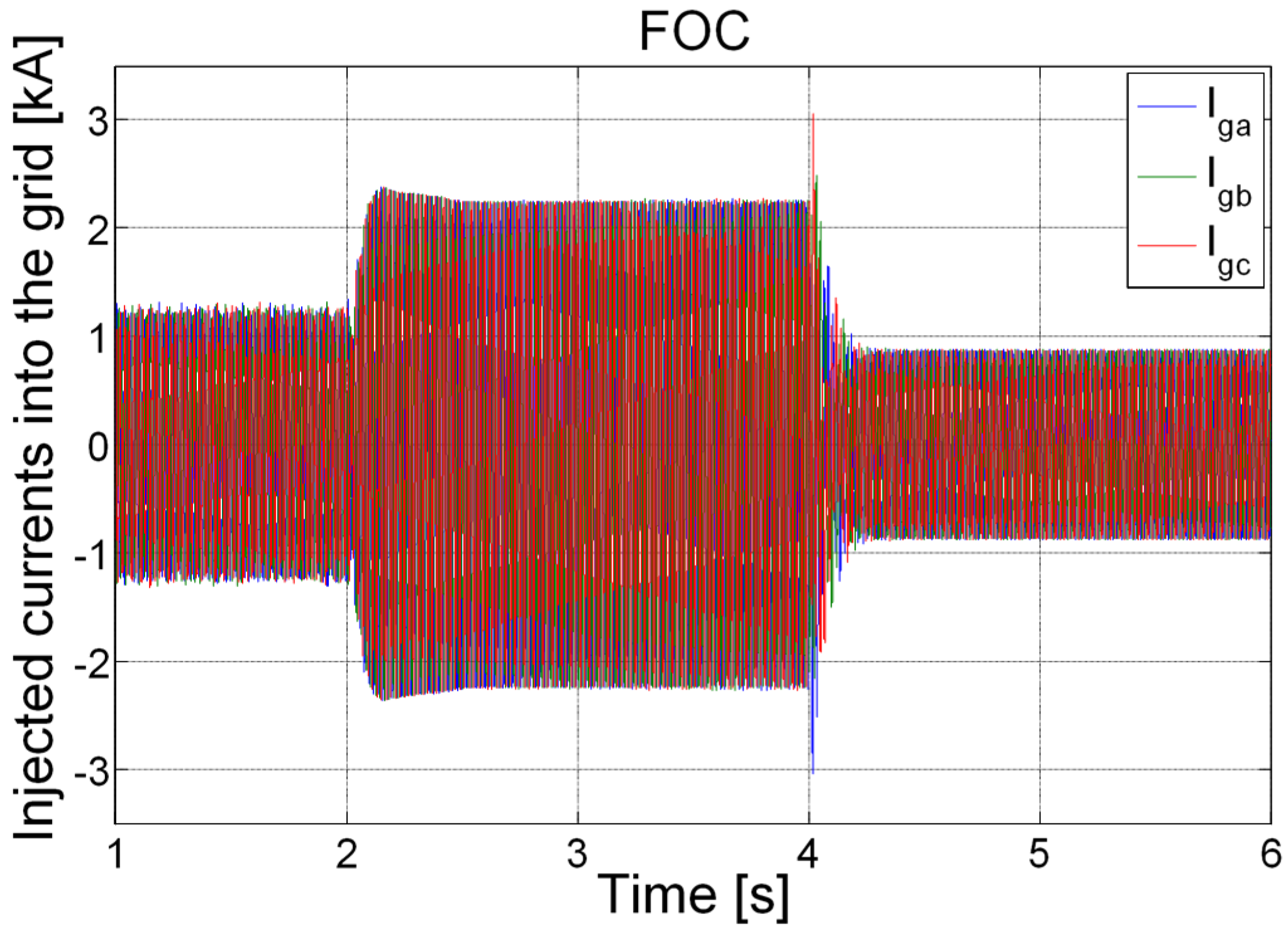
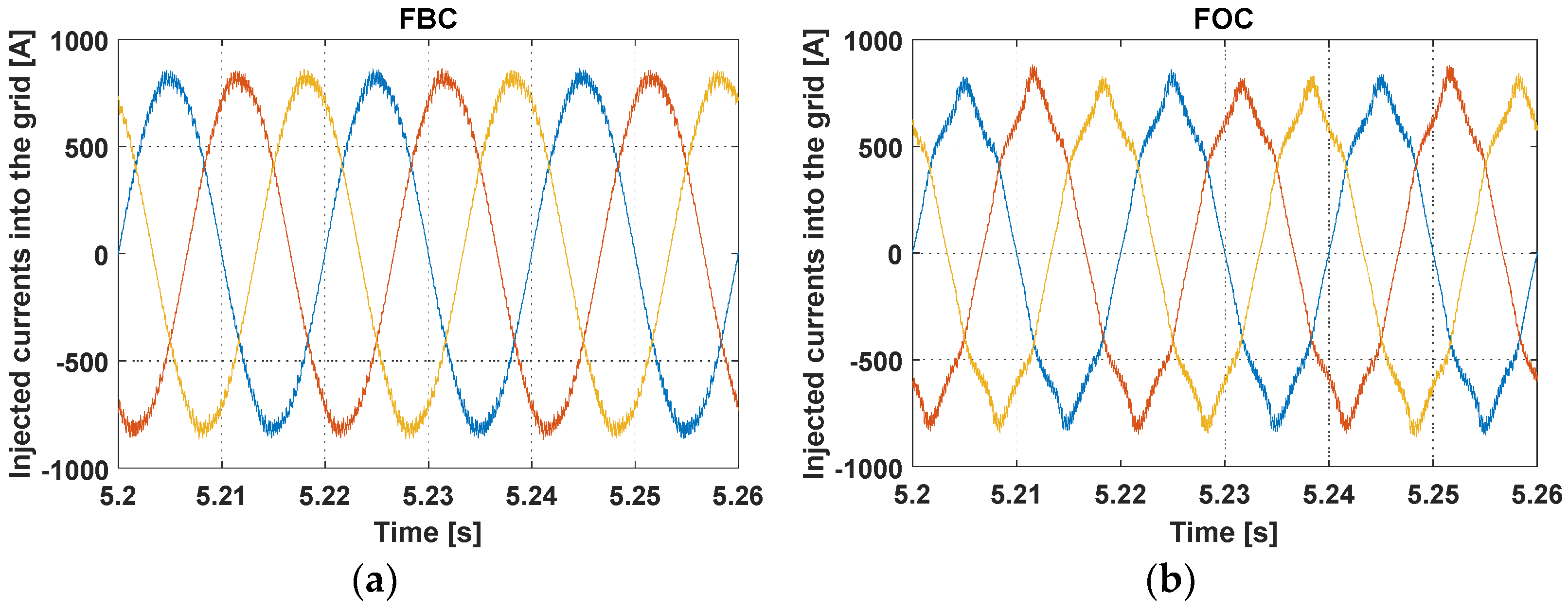
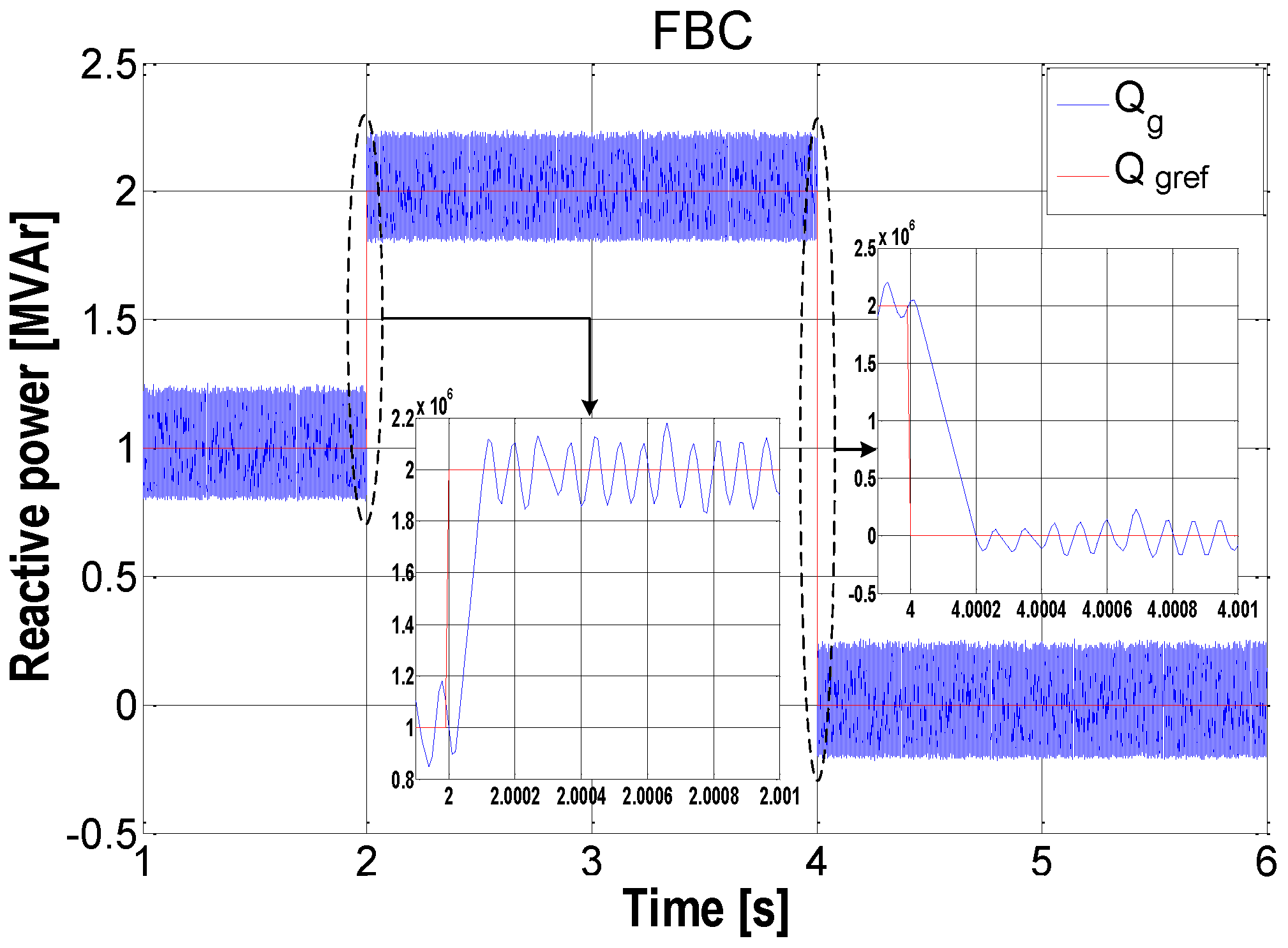
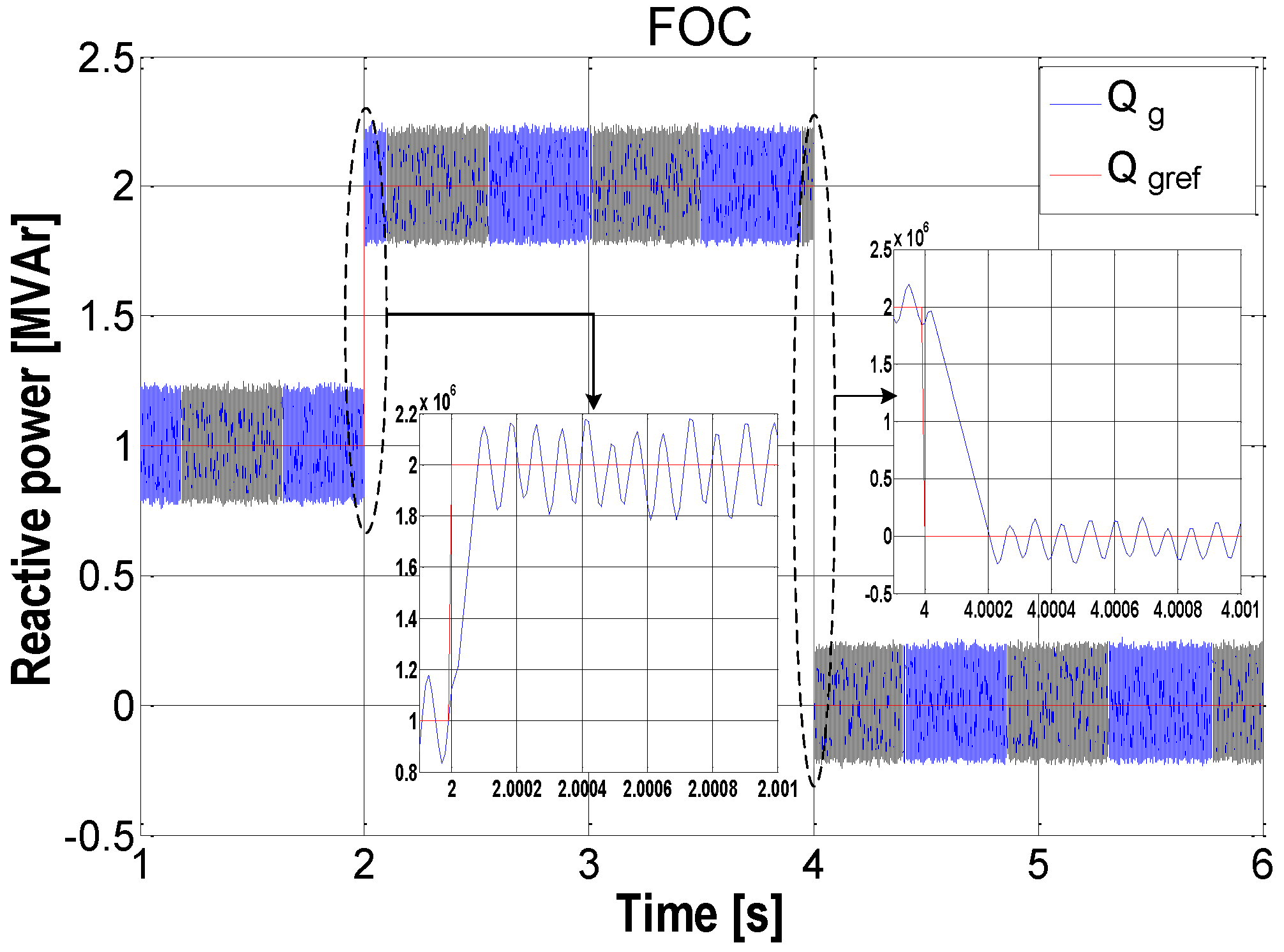
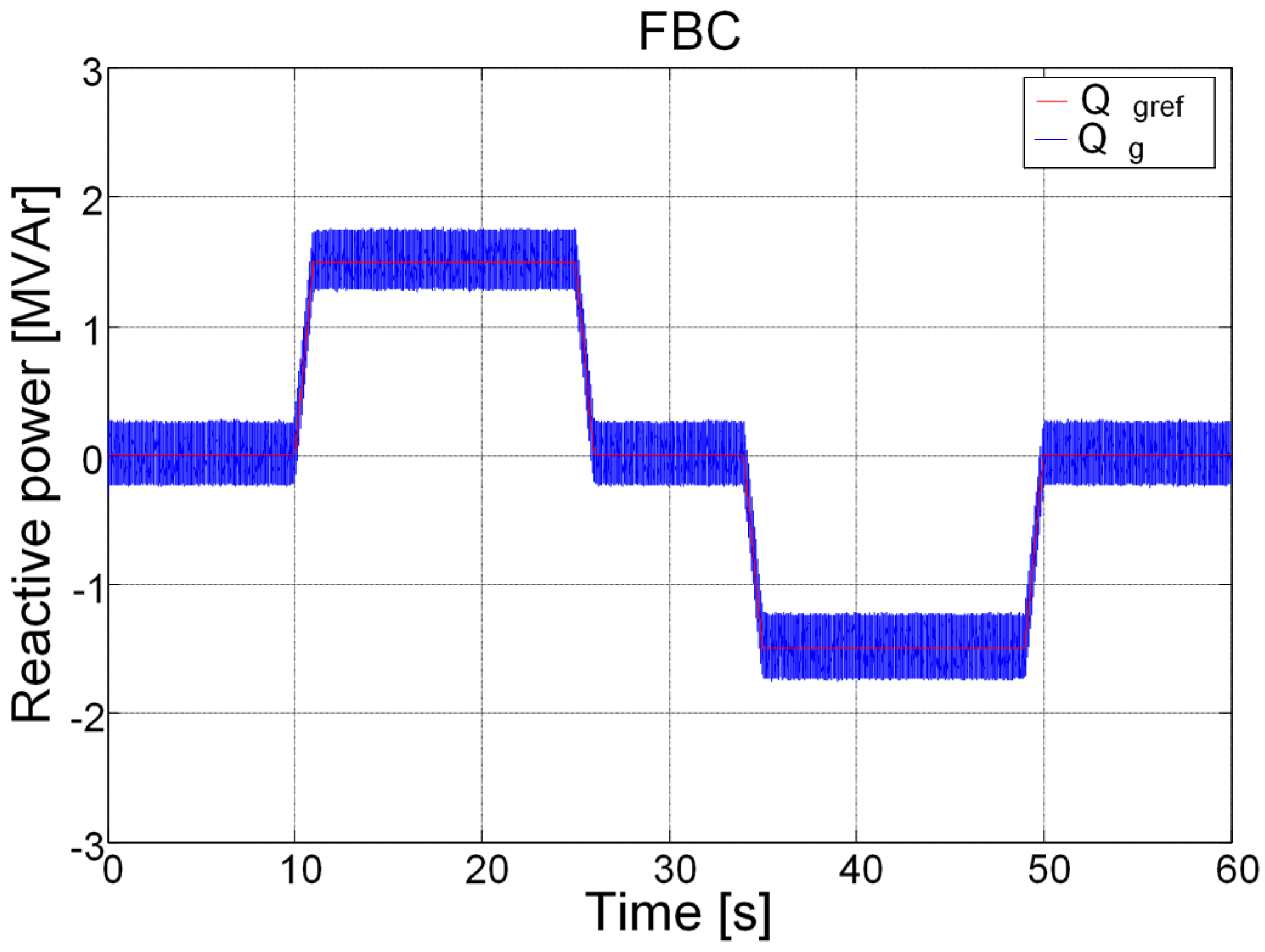
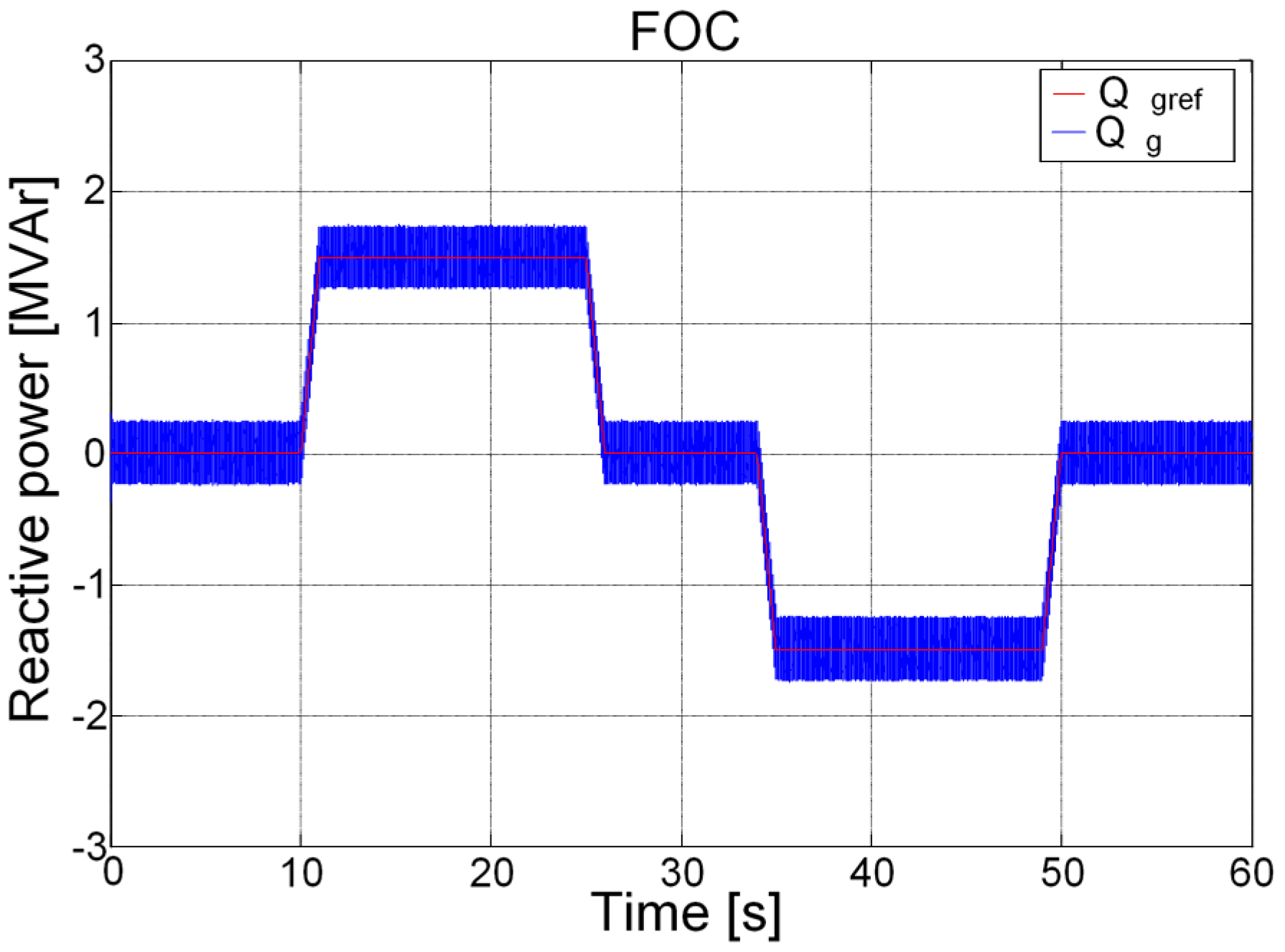
5. Simulation Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PWT | aerodynamic power (W) |
| ρ | air density (kg/m3) |
| Cp | power coefficient |
| R | radius of the rotor blade (m) |
| Vwi | wind speed (m/s) |
| λ | tip speed ratio |
| β | blade pitch angle in (deg) |
| Ωgen | angular speed of the wind turbine shaft (rad/s) |
| Rs | stator phase resistance (Ω) |
| ψf | permanent magnetic flux (Wb) |
| Ld-Lq | d-q axis inductances (H) |
| Vds-Vqs | d-q axis stator voltage (V) |
| Ids-Iqs | d-q axis stator current (I) |
| Tem | electromagnetic torque (Nm) |
| Pg, Qg | active and reactive power delivered to the grid (W) and (VAr) |
| I2 | input current of the grid-side converter (A) |
| Vdc | DC-bus voltage (V) |
| Lg, Rg | filter inductance and resistance (H) and (Ω) |
| Vgd-Vgq | d-q axis grid voltage (V) |
| Igd-Igq | d-q axis grid current (I) |
| ωg | fundamental frequency (rad/s) |
| Isd-ref, Isq-ref | references of d-q axis current |
| Vdcref | references of DC-bus voltage |
| J | inertia moment of turbine (kg·m2) |
| f | friction coefficient (Nm/(rad/s)) |
| Kpd-Kid | controller parameters of the d-axis stator current |
| Kpq-Kiq | controller parameters of the q-axis stator current |
| KpDC-KiDC | controller parameters of the DC-bus voltage |
| Kpq-Kiq | controller parameters of the reactive power |
| Kpdg-Kidg | controller parameters of the d-axis grid current |
| Kpqg-Kiqg | controller parameters of the q-axis grid current |
| εΩ | rotation speed error |
| εψd | flux linkage error |
| KΩ1, KΩ2, KΩ3 | parameters of rotation speed controller |
| Kψ1, Kψ2 | parameters of flux linkage controller |
| ξΩ, ωΩ | damping ratio and cut-off pulsation of rotation speed loop |
| ξψd, ωψd | damping ratio and cut-off pulsation of flux loop |
| kd1, kd2, kd3 | controller parameters of the DC-bus voltage used in the FBC method |
| kq1, kq2 | controller parameters of the reactive power used in the FBC method |
References
- Cordeiro-Costas, M.; Villanueva, D.; Feijóo-Lorenzo, A.; Martínez-Torres, J. Simulation of Wind Speeds with Spatio-Temporal Correlation. Appl. Sci. 2021, 11, 3355. [Google Scholar] [CrossRef]
- Chavero-Navarrete, E.; Trejo-Perea, M.; Jáuregui-Correa, J.C.; Carrillo-Serrano, R.V.; Ronquillo-Lomeli, G.; Ríos-Moreno, J.G. Pitch Angle Optimization for Small Wind Turbines Based on a Hierarchical Fuzzy-PID Controller and Anticipated Wind Speed Measurement. Appl. Sci. 2021, 11, 1683. [Google Scholar] [CrossRef]
- Lee, J.; Zhao, F. Global Wind Report 2019; GWEC Global Wind Energy Council: Brussels, Belgium, 2020. [Google Scholar]
- Sun, M.; Min, Y.; Chen, L.; Hou, K.; Xia, D.; Mao, H. Optimal auxiliary frequency control of wind turbine generators and coordination with synchronous generators. CSEE J. Power Energy Syst. 2021, 7, 78–85. [Google Scholar]
- Mansour, M.; Mansouri, M.; Mmimouni, M. Study and Control of a Variable-Speed Wind-Energy System Connected to the Grid. Int. J. Renew. Energy Res. 2011, 1, 96–104. [Google Scholar]
- Guo, Y.; Gao, H.; Wu, Q.; Zhao, H.; Østergaard, J.; Shahidehpour, M. Enhanced Voltage Control of VSC-HVDC-Connected Offshore Wind Farms Based on Model Predictive Control. IEEE Trans. Sustain. Energy 2018, 9, 474–487. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, Z.; Kazmierkowski, M.; Rodríguez, J.; Kennel, R. Robust Predictive Control of Three-Level NPC Back-to-Back Power Converter PMSG Wind Turbine Systems With Revised Predictions. IEEE Trans. Power Electron. 2018, 33, 9588–9598. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Guo, Q.; Sun, H.; Xue, Y. Distributed Model Predictive Control of a Wind Farm for Optimal Active Power ControlPart II: Implementation With Clustering-Based Piece-Wise Affine Wind Turbine Model. IEEE Trans. Sustain. Energy 2015, 6, 840–849. [Google Scholar] [CrossRef] [Green Version]
- Shariatpanah, H.; Fadaeinedjad, R.; Rashidinejad, M. A New Model for PMSG-Based Wind Turbine with Yaw Control. IEEE Trans. Energy Convers. 2013, 28, 929–937. [Google Scholar] [CrossRef]
- Ahmed, A.; Ran, L.; Bumby, J.R. New Constant Electrical Power Soft-Stalling Control for Small-Scale VAWT. IEEE Trans. Energy Convers. 2010, 25, 1152–1161. [Google Scholar] [CrossRef]
- Soliman, M.; Hasanien, H.; Azazi, H.; El-Kholy, E.; Mahmoud, S. An Adaptive Fuzzy Logic Control Strategy for Performance Enhancement of a Grid-Connected PMSG-Based Wind Turbine. IEEE Trans. Ind. Inform. 2019, 15, 3163–3173. [Google Scholar] [CrossRef]
- Yin, Y.; Liao, M.; Lyu, P. The dynamic stability analysis of wind turbines under different control strategies. In Proceedings of the 2015 IEEE 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015. [Google Scholar]
- Ikni, D.; Camara, M.B.; Payman, A.; Dakyo, B. Dynamic Control of Wind Energy Conversion System. In Proceedings of the 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Monaco, France, 27–30 March 2013. [Google Scholar]
- González-Longatt, F.M.; Wall, P.; Terzija, V. A Simplified Model for Dynamic Behavior of Permanent Magnet Synchronous Generator for Direct Drive Wind Turbines. In Proceedings of the IEEE PES Trondheim PowerTech, Trondheim, Norway, 19–23 January 2011. [Google Scholar]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of Permanent-Magnet Generators Applied to Variable-Speed Wind-Energy Systems Connected to the Grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Mahersi, E. The Wind energy Conversion System Using PMSG Controlled by Vector Control and SMC Strategies. Int. J. Renew. Energy Res. 2013, 3, 41–50. [Google Scholar]
- Thakur, D.; Jiang, J. Control of a PMSG Wind-Turbine under Asymmetrical Voltage Sags Using Sliding Mode Approach. IEEE Power Energy Technol. Syst. J. 2018, 5, 47–55. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X. Sliding mode control for maximum wind energy capture of DFIG-based wind turbine. In Proceedings of the 2015 IEEE 27th Chinese Control and Decision Conference (CCDC), Qingdao, China, 23–25 May 2015. [Google Scholar]
- Uehara, A.; Pratap, A.; Goya, T.; Senjyu, T.; Yona, A.; Urasaki, N.; Funabashi, T. A Coordinated Control Method to Smooth Wind Power Fluctuations of a PMSG-Based WECS. IEEE Trans. Energy Convers. 2011, 26, 550–558. [Google Scholar] [CrossRef]
- Lyu, X.; Zhao, J.; Jia, Y.; Xu, Z.; Wong, K. Coordinated Control Strategies of PMSG-Based Wind Turbine for Smoothing Power Fluctuations. IEEE Trans. Power Syst. 2019, 34, 391–401. [Google Scholar] [CrossRef]
- Luo, H.; Hu, Z.; Zhang, H.; Chen, H. Coordinated Active Power Control Strategy for Deloaded Wind Turbines to Improve Regulation Performance in AGC. IEEE Trans. Power Syst. 2019, 34, 98–108. [Google Scholar] [CrossRef]
- Palejiya, D.; Chen, D. Performance Improvements of Switching Control for Wind Turbines. IEEE Trans. Sustain. Energy 2016, 7, 526–534. [Google Scholar] [CrossRef]
- Payman, A.; Pierfederici, S.; Meibody-Tabar, F.; Davat, B. An Adapted Control Strategy to Minimize DC-Bus Capacitors of a Parallel Fuel Cell/Ultracapacitor Hybrid System. IEEE Trans. Power Electron. 2011, 26, 3843–3852. [Google Scholar] [CrossRef]
- Battiston1, A.; Martin, J.; Miliani, E.; Nahid-Mobarakeh, B.; Pierfederici, S.; Meibody-Tabar, F. Control of a PMSM Fed by a Quasi Z-Source Inverter Based on Flatness Properties and Saturation Schemes. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 3–5 September 2013; pp. 1–10. [Google Scholar]
- Delaleau, E.; Stankovic, A.M. Flatness-based hierarchical control of the PM synchronous motor. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Margaris, I.D.; Papathanassiou, S.; Hatziargyriou, N.; Hansen, A.; Sørensen, P. Frequency Control in Autonomous Power Systems With High Wind Power Penetration. IEEE Trans Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Zhao, X.; Meng, L.; Dragicevic, T.; Savaghebi, M.; Guerrero, J.M.; Vasquez, J.C.; Wu, X. Distributed low voltage ride-through operation of power converters in grid-connected microgrids under voltage sags. In Proceedings of the Industrial Electronics Society, IECON 2015—41st Annual Conference of the IEEE, Yokohama, Japan, 9–12 November 2015; pp. 1909–1914. [Google Scholar]
- Ghasemi, S.; Tabesh, A.; Askari-Marnani, J. Application of Fractional Calculus Theory to Robust Controller Design for Wind Turbine Generators. IEEE Trans. Energy Convers. 2014, 29, 780–787. [Google Scholar] [CrossRef]
- Chavero-Navarrete, E.; Trejo-Perea, M.; Jáuregui-Correa, J.C.; Carrillo-Serrano, R.V.; Ronquillo-Lomeli, G.; Ríos-Moreno, J.G. Pitch Angle Optimization by Intelligent Adjusting the Gains of a PI Controller for Small Wind Turbines in Areas with Drastic Wind Speed Changes. Sustainability 2019, 11, 6670. [Google Scholar] [CrossRef] [Green Version]
- Eisa, S.A. Modeling dynamics and control of type-3 DFIG wind turbines: Stability, Q Droop function, control limits and extreme scenarios simulation. Electr. Power Syst. Res. 2019, 166, 29–42. [Google Scholar] [CrossRef]
- Dekali1, Z.; Baghli1, L.; Boumediene, A.; Djemai, M. Control of a Grid Connected DFIG Based Wind Turbine Emulator. In Proceedings of the 2018 IEEE 5th International Symposium on Environment-Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018. [Google Scholar]
- Llano, D.; McMahon, R.; Tatlow, M. Control algorithms for permanent magnet generators evaluated on a wind turbine emulator test-rig. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014. [Google Scholar]
- Yin, M.; Xu, Y.; Shen, C.; Liu, J.; Dong, Z.Y.; Zou, Y. Turbine Stability-Constrained Available Wind Power of Variable Speed Wind Turbines for Active Power Control. IEEE Trans. Power Syst. 2017, 32, 2487–2488. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Meng, K. Optimal Power Sharing Control of Wind Turbines. IEEE Trans. Power Syst. 2017, 32, 824–825. [Google Scholar] [CrossRef]
- Sierra-García, J.; Santos, M. Improving Wind Turbine Pitch Control by Effective Wind Neuro-Estimators. IEEE Access 2021, 9, 10413–10425. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Z.; Lu, H.; Wang, X.; Meng, Y.; Li, S. Independent Pitch Control Strategy and Simulation for Reducing Unbalanced Load of Wind Turbine. In Proceedings of the 2020 IEEE 32th Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Furmanik, M.; Gorel, L.; Konvicný, D.; Rafajdus, P. Comparative Study and Overview of Field-Oriented Control Techniques for Six-Phase PMSMs. Appl. Sci. 2021, 11, 7841. [Google Scholar] [CrossRef]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef] [Green Version]
- Veeser, F.; Braun, T.; Kiltz, L.; Reuter, J. Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines. Energies 2021, 14, 1590. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Pn | 5 MW |
| R | 56 M |
| Rs | 6.25 mΩ |
| J | 104 kg·m2 |
| Vdcref | 4700 V |
| Number of blades | 3 |
| Ls | 4.23 mH |
| 11.15 Nm/A | |
| Cdc | 0.04 mF |
| Lf | 0.5 mH |
| Variable | Response Time (ms) | |
|---|---|---|
| FBC Method | FOC Method | |
| Rotation speed (Ω) | 15 | 60 |
| DC-bus voltage ) | 70 | 450 |
| Active power ) | 180 | 250 |
| Reactive power ) | 0.1 | 0.1 |
| Variable | Overshoot (%) | |
|---|---|---|
| FBC Method | FOC Method | |
| Rotation speed (Ω) | 0 | 40 |
| DC-bus voltage ) | 0 | 25 |
| Active power ) | 5 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aimene, M.; Payman, A.; Dakyo, B. Comparative Study between Flatness-Based and Field-Oriented Control Methods of a Grid-Connected Wind Energy Conversion System. Processes 2022, 10, 378. https://doi.org/10.3390/pr10020378
Aimene M, Payman A, Dakyo B. Comparative Study between Flatness-Based and Field-Oriented Control Methods of a Grid-Connected Wind Energy Conversion System. Processes. 2022; 10(2):378. https://doi.org/10.3390/pr10020378
Chicago/Turabian StyleAimene, Merzak, Alireza Payman, and Brayima Dakyo. 2022. "Comparative Study between Flatness-Based and Field-Oriented Control Methods of a Grid-Connected Wind Energy Conversion System" Processes 10, no. 2: 378. https://doi.org/10.3390/pr10020378
APA StyleAimene, M., Payman, A., & Dakyo, B. (2022). Comparative Study between Flatness-Based and Field-Oriented Control Methods of a Grid-Connected Wind Energy Conversion System. Processes, 10(2), 378. https://doi.org/10.3390/pr10020378







