The Influence of a Pumping Chamber on Hydraulic Losses in a Mixed-Flow Pump
Abstract
:1. Introduction
2. Numerical Simulation Method
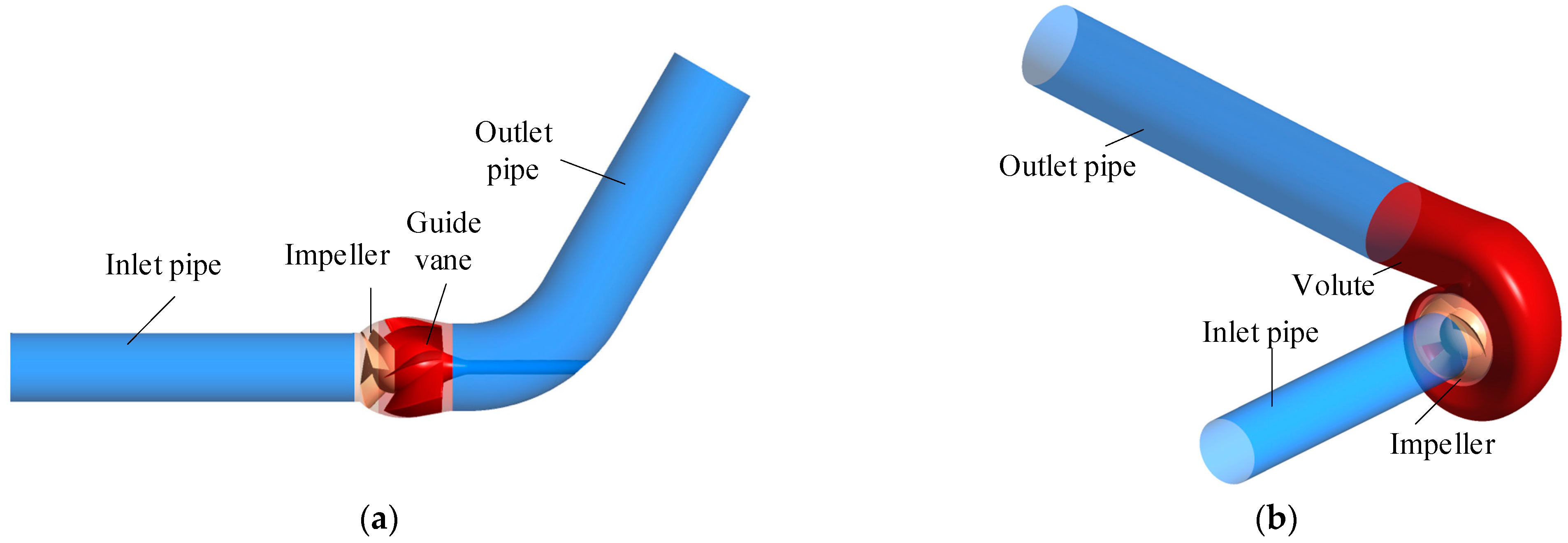
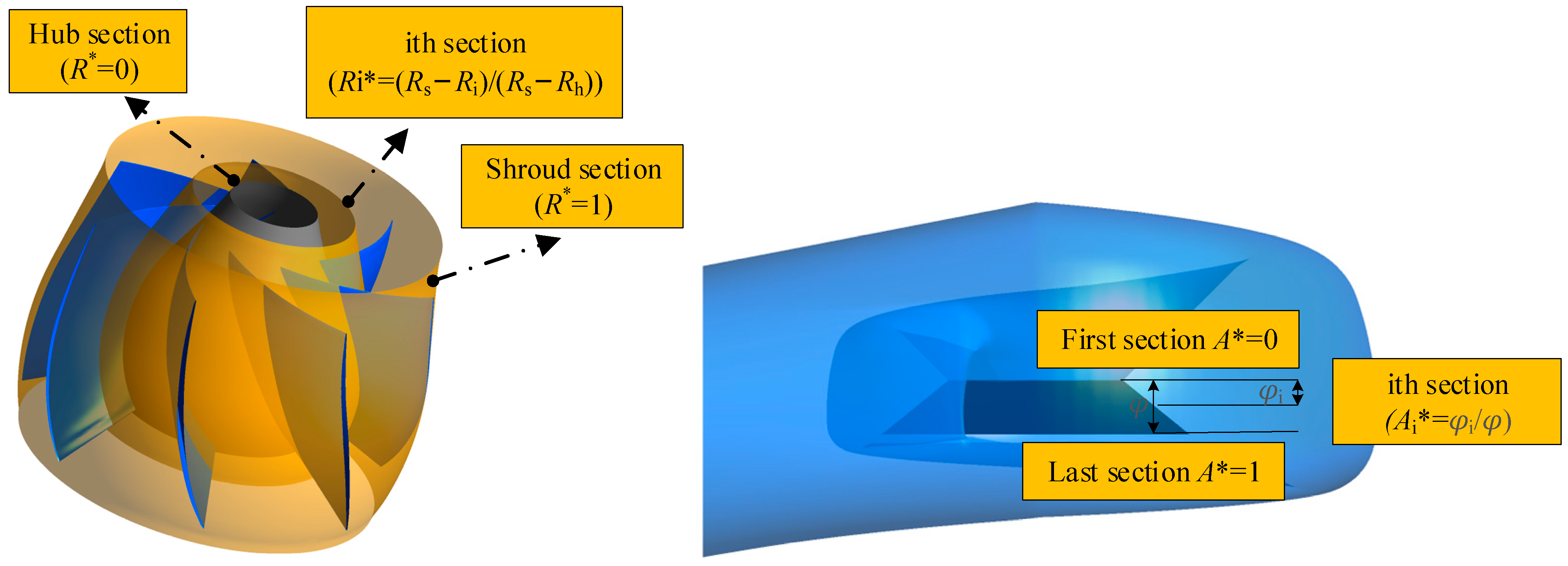
2.1. Three-Dimensional Geometry Model
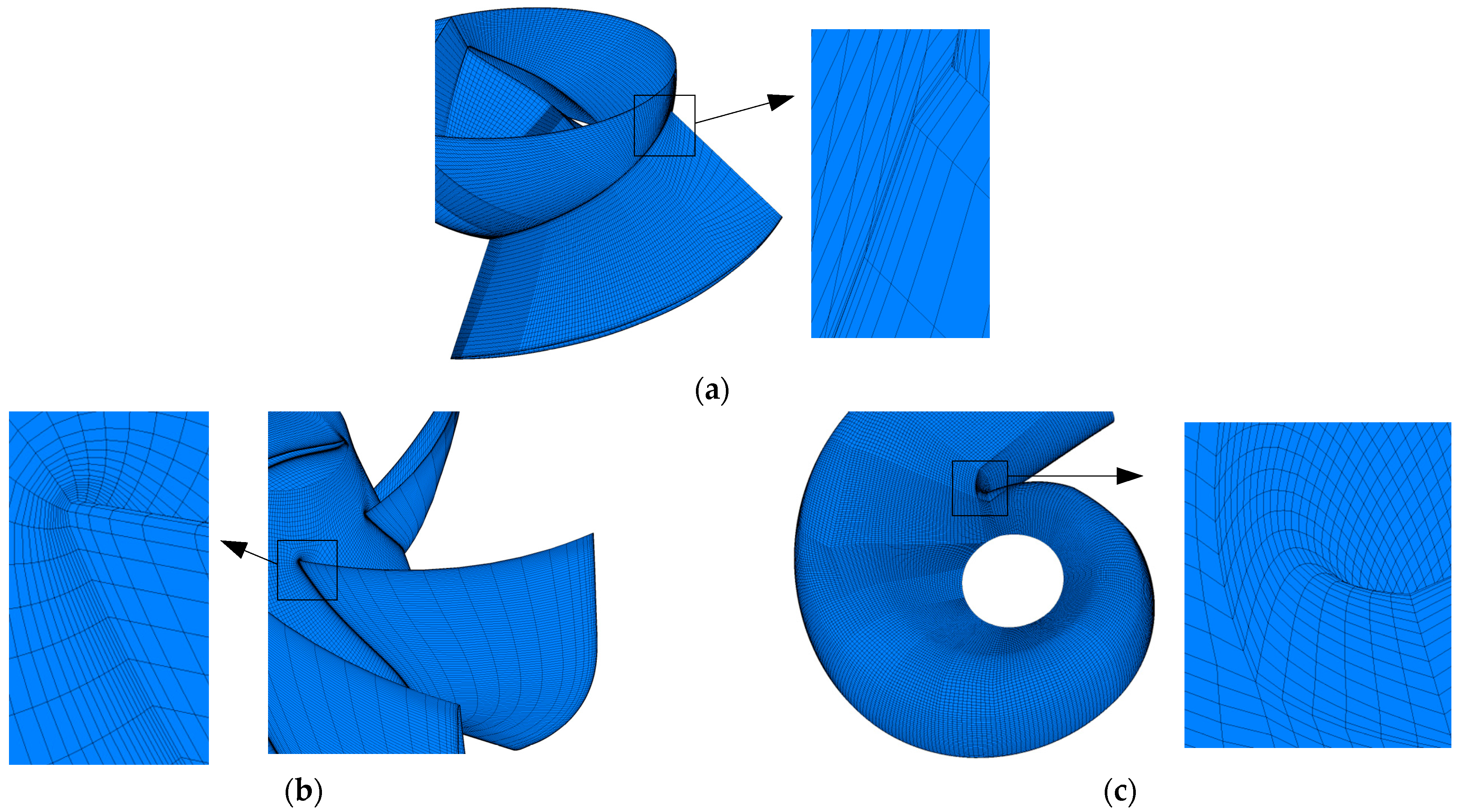
2.2. Mesh Generation
2.3. Conservation Equations and Boundary Conditions
2.4. Entropy Production Theory
2.5. Validation of Numerical Simulation
3. Analysis of Calculation Results
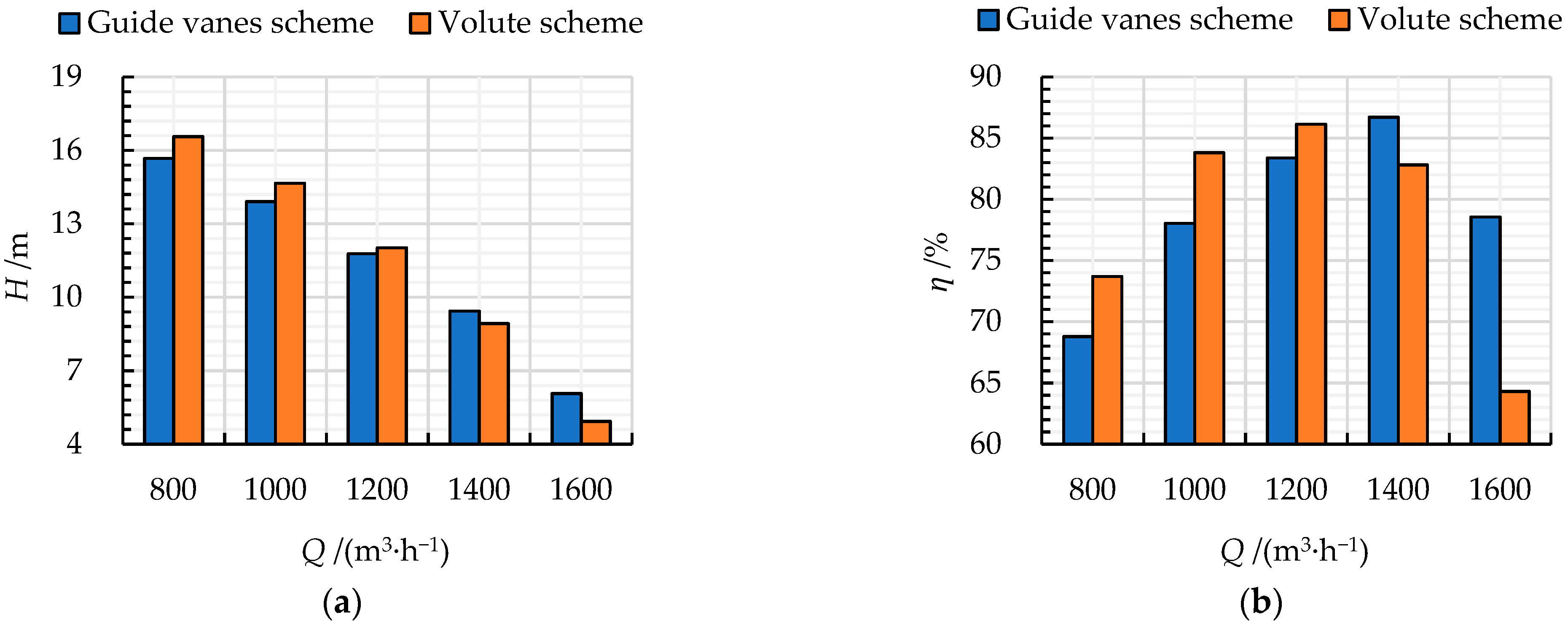
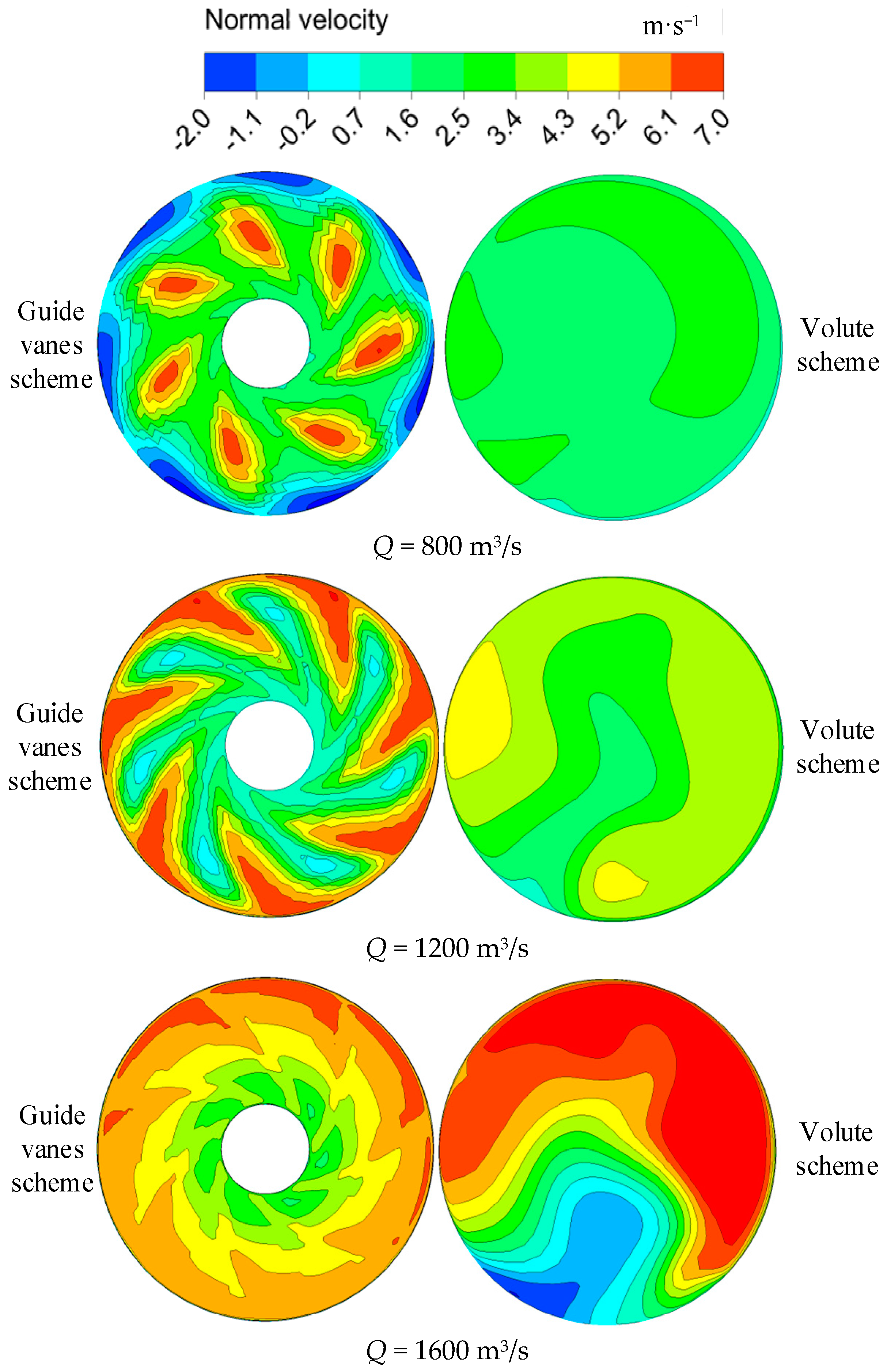
3.1. Comparison of Pump Performance
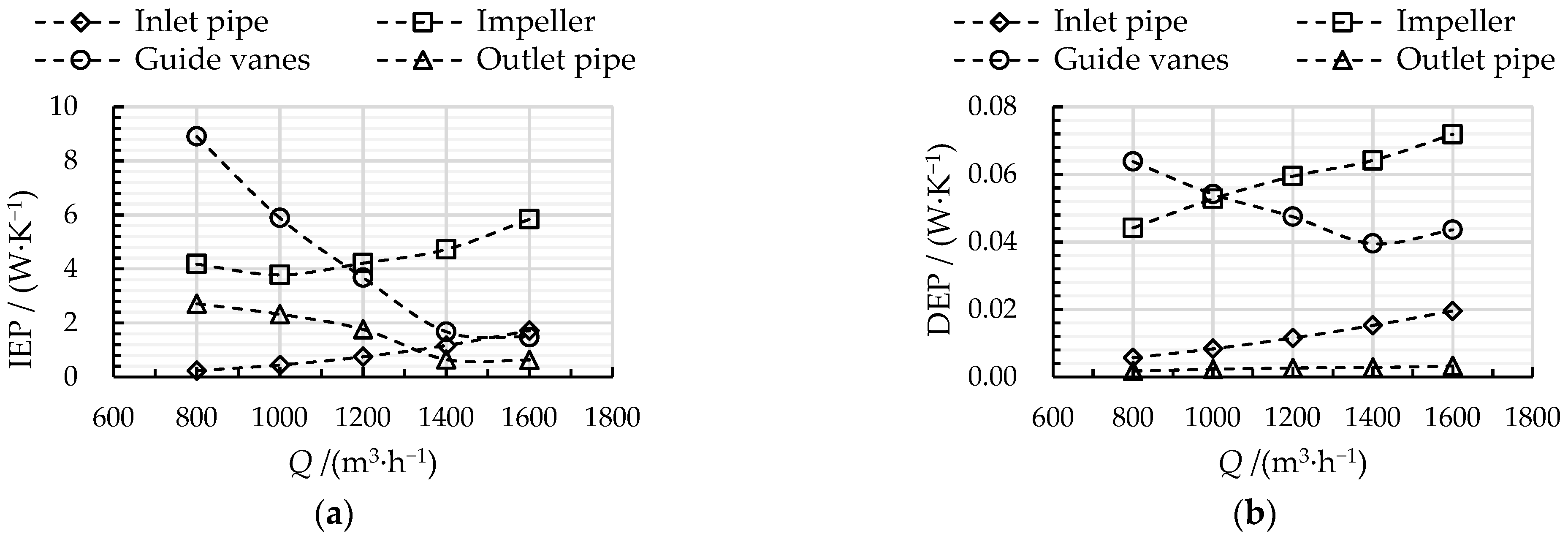
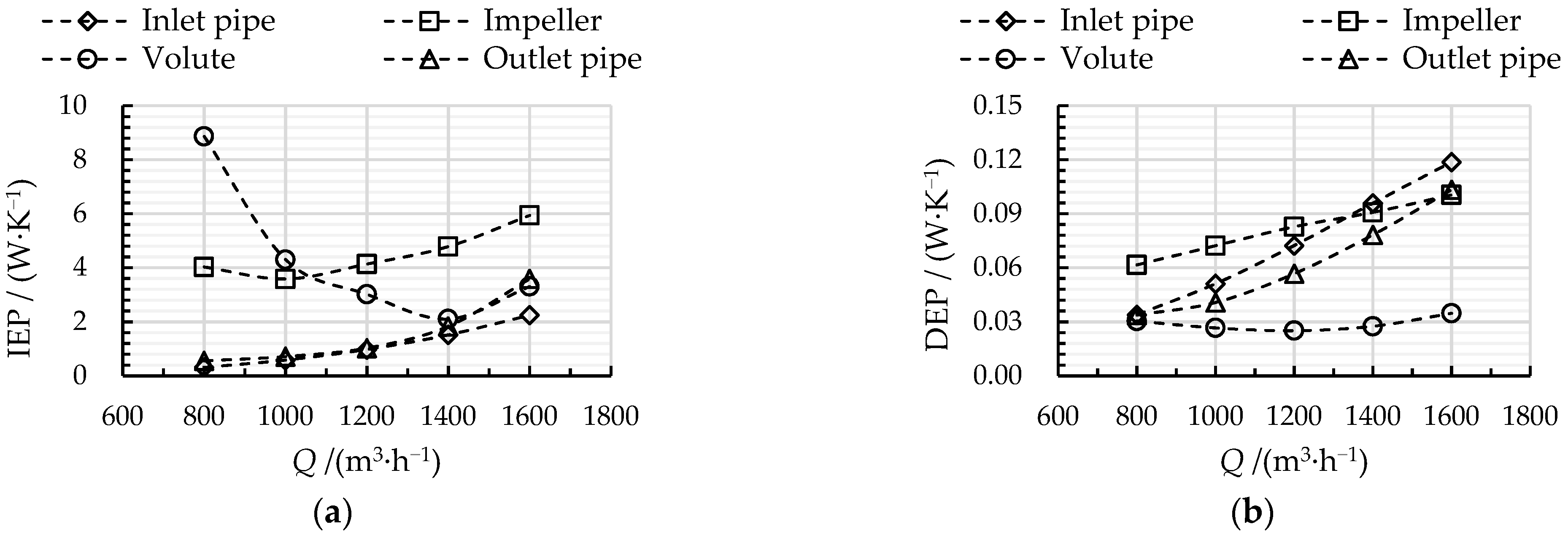
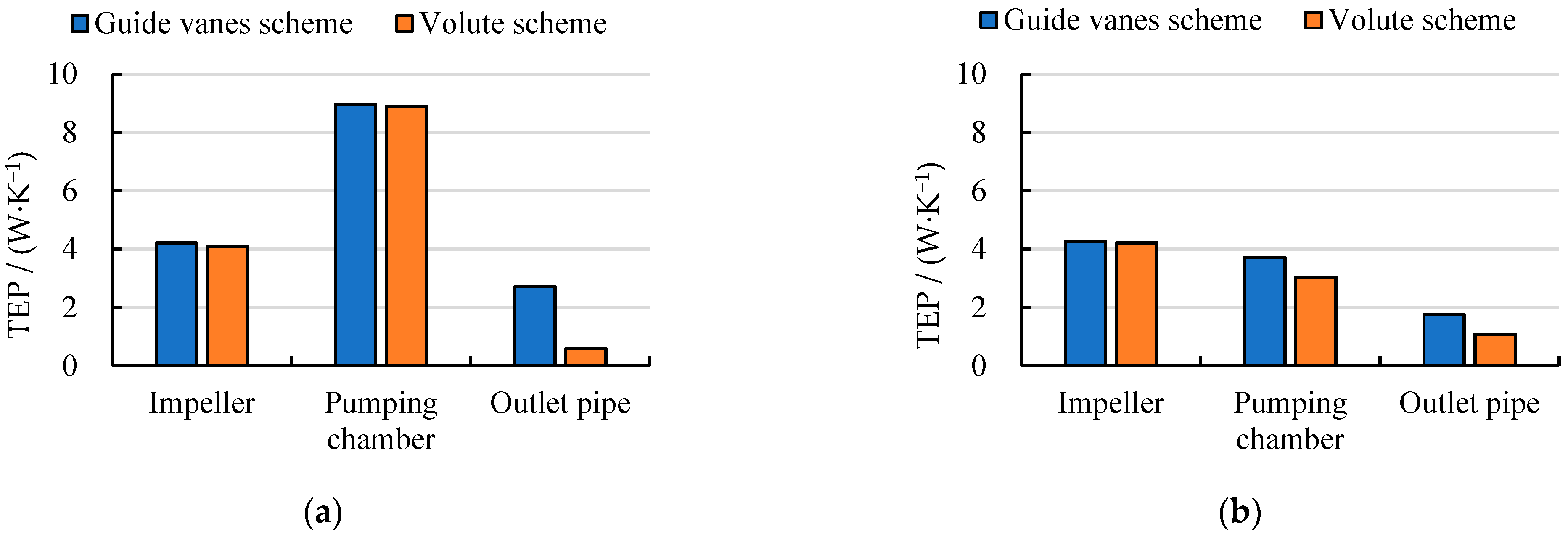
3.2. TEP Disstribution in Different Pump Components
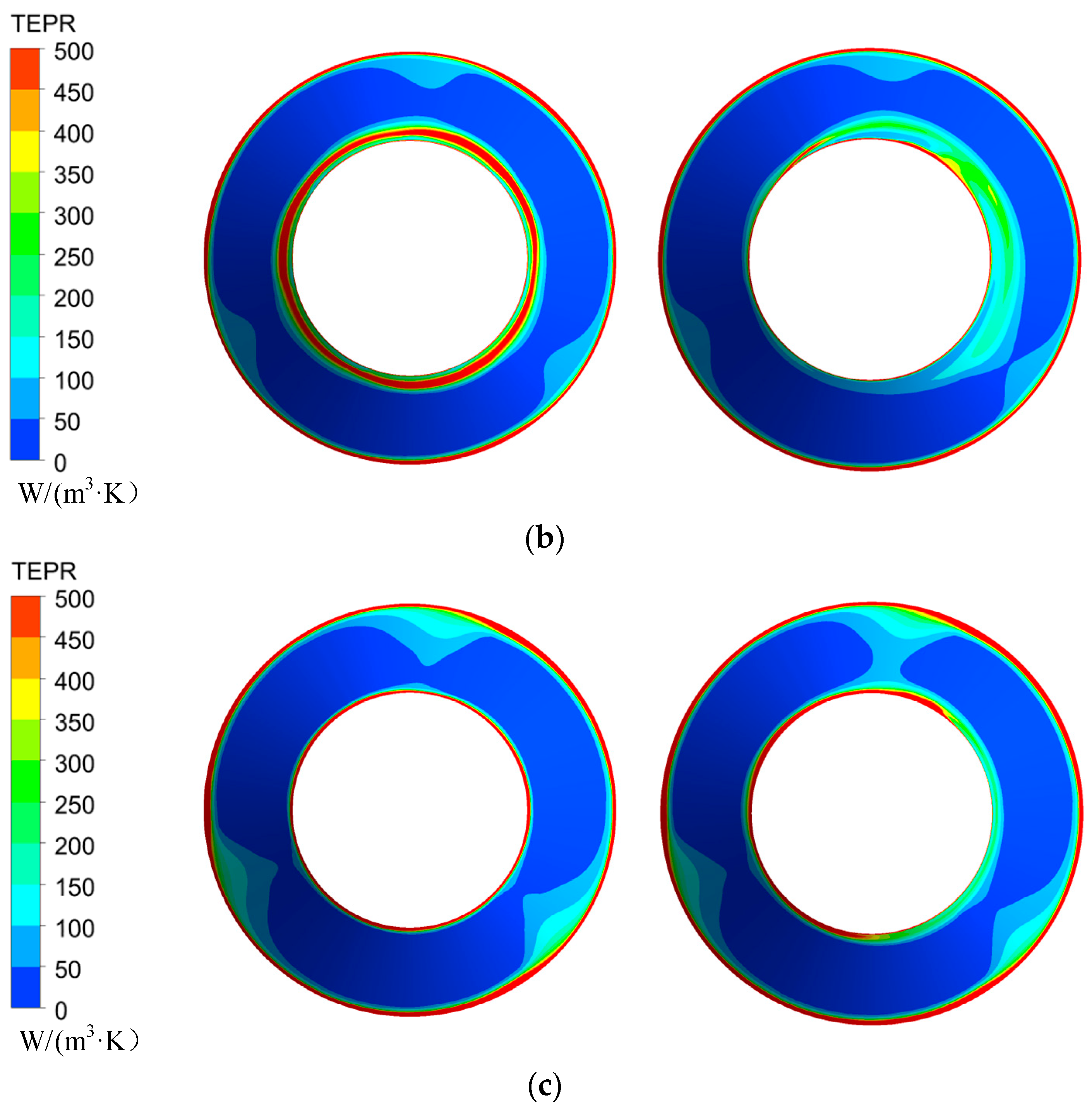
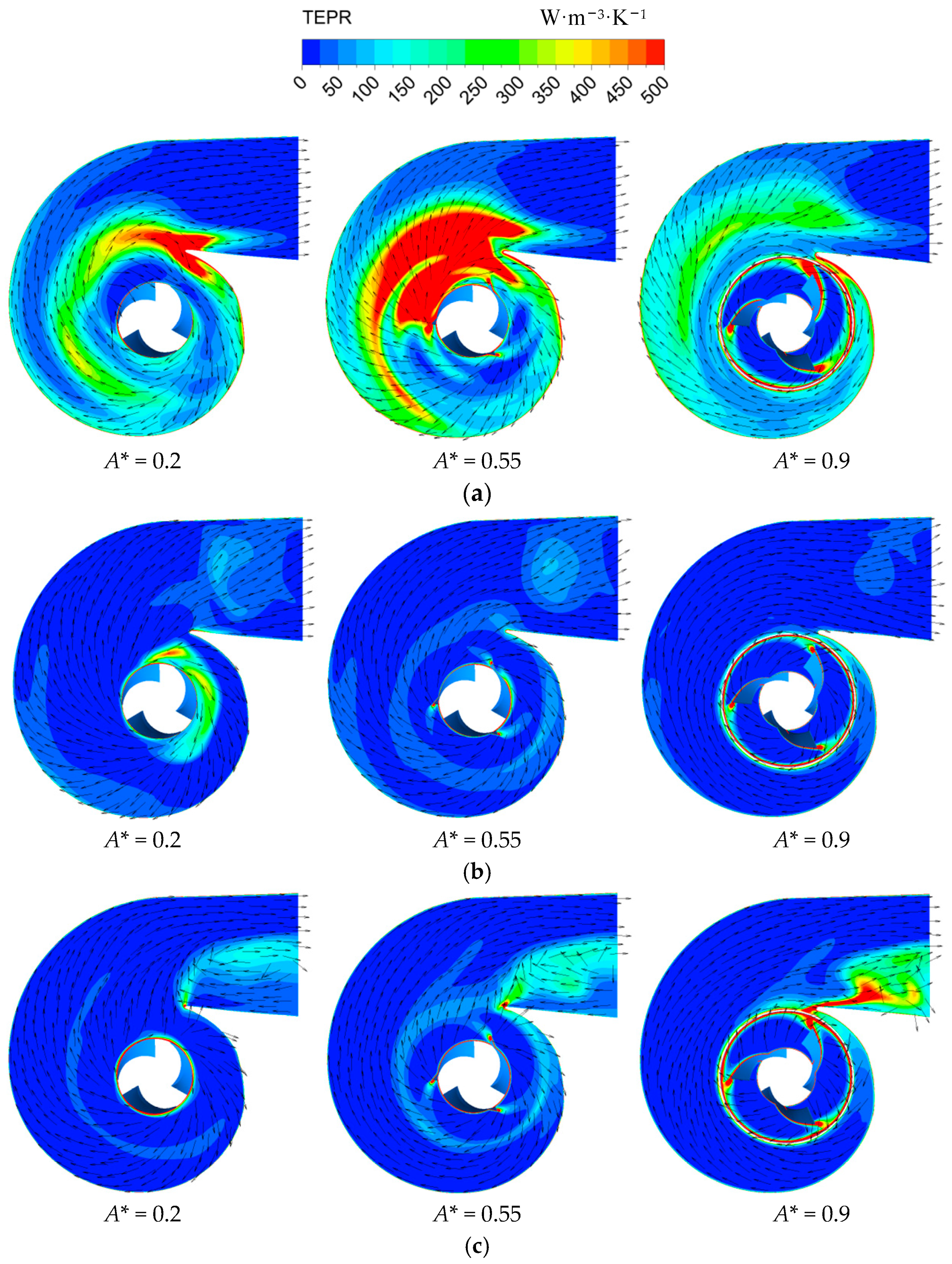
3.3. TEP Rate Distribution of Impeller-Pumping Chamber Interface
3.4. TEP Rate Distribution of Pumping Chamber
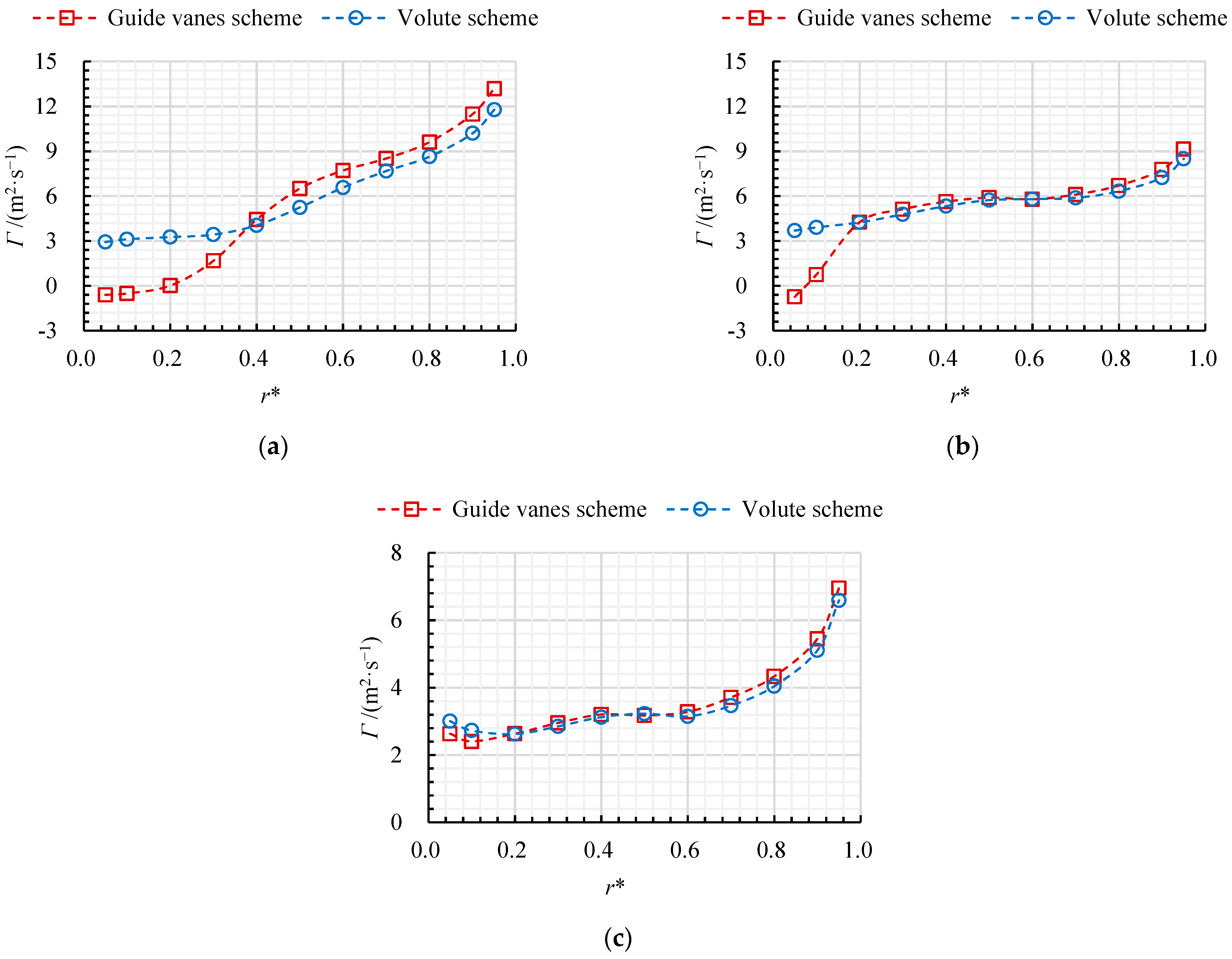
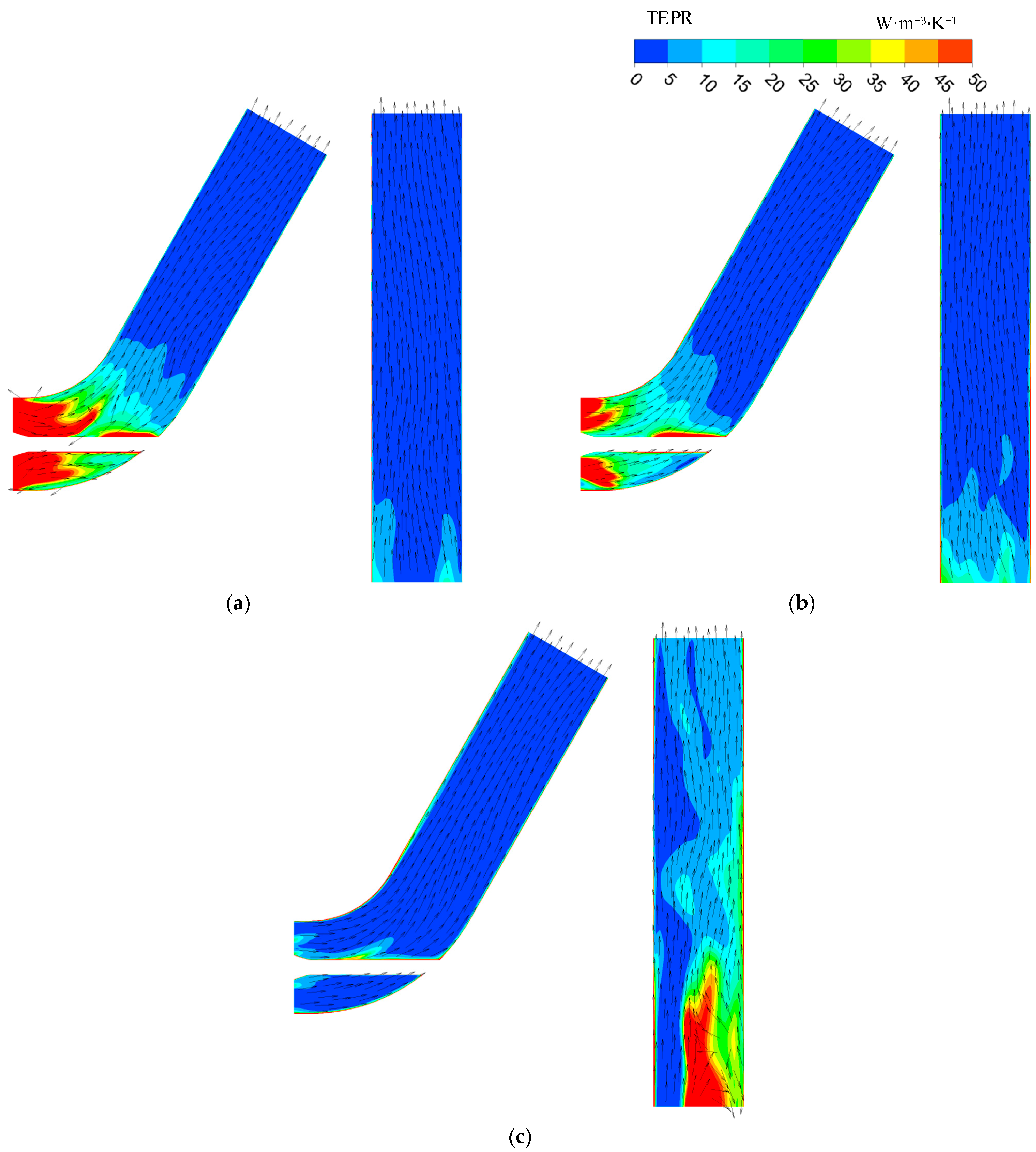
3.5. TEP Rate Distribution of Outlet Conduit
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| (m) | Pump head |
| (%) | Pump efficiency |
| (kg/m3) | Water density |
| (m/s2) | Gravitational acceleration |
| (Pa) | Total pressure of inlet |
| (Pa) | Total pressure of outlet |
| (W) | Shaft power |
| (m3/h) | Volume flow rate |
| (m3/h) | Best efficiency point |
| Pump head under best efficiency point | |
| (m/s) | Velocity component in the x direction of Cartesian coordinates |
| (m/s) | Velocity component in the y direction of Cartesian coordinates |
| (m/s) | Velocity component in the z direction of Cartesian coordinates |
| [W/(K·m3)] | Reversible heat transfer term |
| [W/K·m3)] | Entropy production due to dissipation increase |
| [W/(K·m3)] | Entropy production caused by the heat transfer |
| [J/(K·kg)] | Specific entropy |
| (W/m3) | Indirect dissipation rate |
| (W/m3) | Direct dissipation rate |
| (w/m3) | Total dissipation rate |
| (W/K) | Indirect entropy production |
| (W/K) | Direct entropy production |
| (W/K) | Total entropy production |
| (K) | Temperature |
| (W/kg) | Dissipation rate of turbulent kinetic energy |
| Measurement uncertainty of flow rate | |
| Measurement uncertainty of shaft power | |
| Measurement uncertainty of head | |
| Measurement uncertainty of test bench | |
| (m2/s) | Velocity circulation |
| L (m) | Length of calculated ring |
| (m/s) | Absolute circumferential velocity |
| (m) | Calculated radius |
| (m) | Hub radius |
| (m) | Rim radius |
| Radial coefficient | |
| (m/s) | Average axial velocity |
| (m/s) | Average circumferential velocity |
Abbreviation
| CFD | Computational fluid dynamics |
| IEP | Indirect entropy production |
| DEP | Direct entropy production |
| TEP | Total entropy production |
| TEPR | Total entropy production rate |
| AKP | Axial kinetic pressure |
| CKP | Circumferential kinetic pressure |
| SP | Static pressure |
References
- Xingfan, G. Modern Pump Theory and Design; China Aerospace Publishing House: Beijing, China, 2011. [Google Scholar]
- Lianyuan, W.; Baoguo, L. Application of 500HW-7 typed volute mixed flow pump in sea salt production. J. Salt Sci. Chem. Ind. 2018, 47, 36–37. [Google Scholar]
- Zhu, H.; Bo, G.; Zhou, Y.; Rentian, Z.; Jilin, C. Performance prediction of pump and pumping system based on combination of numerical simulation and non-full passage model test. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, H.; Noorollahi, Y.; Tahani, M.; Roshanak, F.; Salman, S. Numerical simulation for obtaining optimal impeller’s blade parameters of a centrifugal pump for high-viscosity fluid pumping. Sustain. Energy Technol. Assess. 2019, 34, 16–26. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, L.; Tang, F.; Xiaohui, D.; Haiyu, L.; Zhuangzhuang, S. Analysis of inlet flow passage conditions and their influence on the performance of an axial-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 733–746. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Han, Y.; Tan, L. Influence of rotating speed on tip leakage vortex in a mixed flow pump as turbine at pump mode. Renew. Energy 2020, 162, 144–150. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Shi, W.; Dazhuan, W. Numerical simulation of transient flow field in a mixed-flow pump during starting period. Int. J. Numer. Methods Heat Fluid Flow 2018, 29, 1319–1322. [Google Scholar] [CrossRef]
- Xu, Y.; Tan, L.; Liu, Y.; Shuliang, C. Pressure fluctuation and flow pattern of a mixed-flow pump under design and off-design conditions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2430–2440. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Fei, T.; Shuo, L.; Ramesh, A. Influence of different blade numbers on the performance of “saddle zone” in a mixed flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 15, 09576509211046074. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.I.; Kim, J.H.; Choi, Y.-S. Design optimization for mixed-flow pump impeller by improved suction performance and efficiency with variables of specific speeds. J. Mech. Sci. Technol. 2020, 34, 2377–2389. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.I.; Kim, J.H.; Young-Seok, C. Three-objective optimization of a mixed-flow pump impeller for improved suction performance and efficiency. Adv. Mech. Eng. 2019, 11, 1687814019898969. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Spurk, J.H. Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Herwig, H.; Kock, F. Local entropy production in turbulent shear flows: A tool for evaluating heat transfer performance. J. Therm. Sci. 2006, 15, 159–167. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in cfd codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Zhou, X.; Haiseng, H. Optimal hydraulic design of an ultra-low specific speed centrifugal pump based on the local entropy production theory. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 715–726. [Google Scholar] [CrossRef]
- Guan, H.; Jiang, W.; Yang, J.; Yuchuan, W.; Xinghai, Z.; Junxue, W. Energy loss analysis of the double-suction centrifugal pump under different flow rates based on entropy production theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4009–4023. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Hu, W.; Chao, L.; Dongjin, J.; Dongsheng, L.; Ahmed, N. Analysis of flow loss characteristics of slanted axial-flow pump device based on entropy production theory. R. Soc. Open Sci. 2022, 9, 211208. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Meng, F.; Cao, L.; Li, Y.; Wang, X. The Influence of a Pumping Chamber on Hydraulic Losses in a Mixed-Flow Pump. Processes 2022, 10, 407. https://doi.org/10.3390/pr10020407
Zhang H, Meng F, Cao L, Li Y, Wang X. The Influence of a Pumping Chamber on Hydraulic Losses in a Mixed-Flow Pump. Processes. 2022; 10(2):407. https://doi.org/10.3390/pr10020407
Chicago/Turabian StyleZhang, Huiyan, Fan Meng, Lei Cao, Yanjun Li, and Xinkun Wang. 2022. "The Influence of a Pumping Chamber on Hydraulic Losses in a Mixed-Flow Pump" Processes 10, no. 2: 407. https://doi.org/10.3390/pr10020407
APA StyleZhang, H., Meng, F., Cao, L., Li, Y., & Wang, X. (2022). The Influence of a Pumping Chamber on Hydraulic Losses in a Mixed-Flow Pump. Processes, 10(2), 407. https://doi.org/10.3390/pr10020407




