Vienna Rectifier-Based Control of a PMSG Wind Turbine Generator
Abstract
:1. Introduction
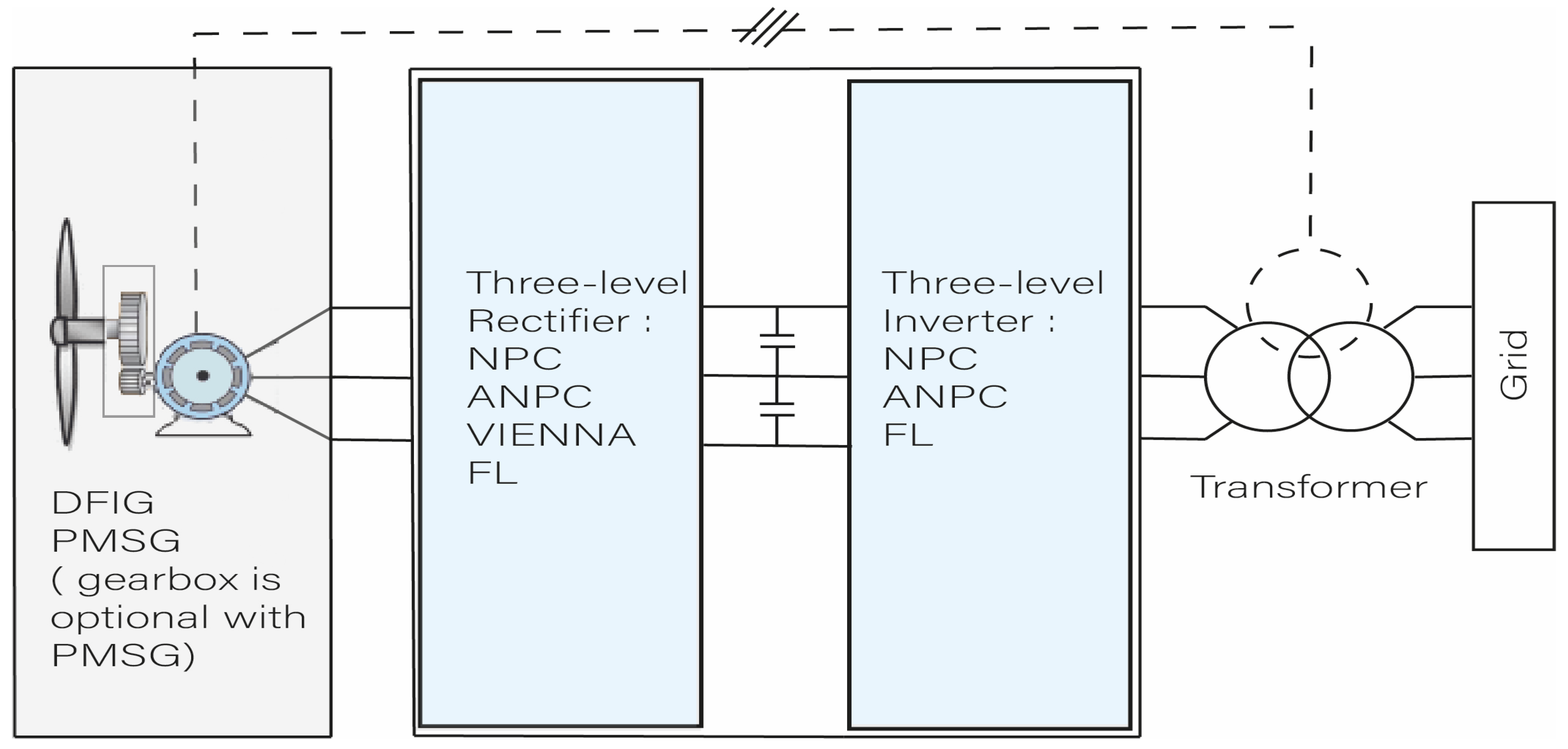
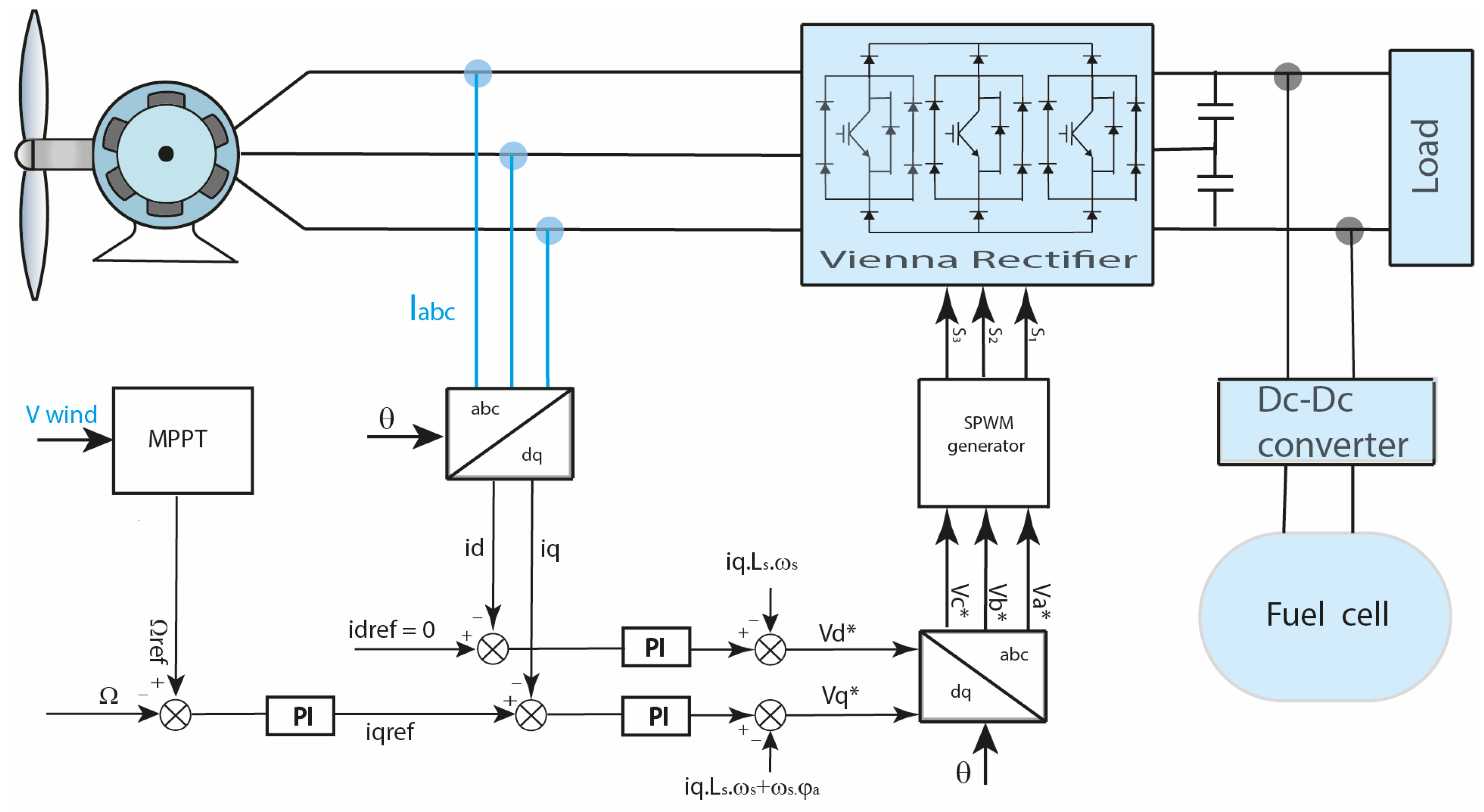
2. PMSG and Vienna Rectifier Models and MPPT Control Strategy
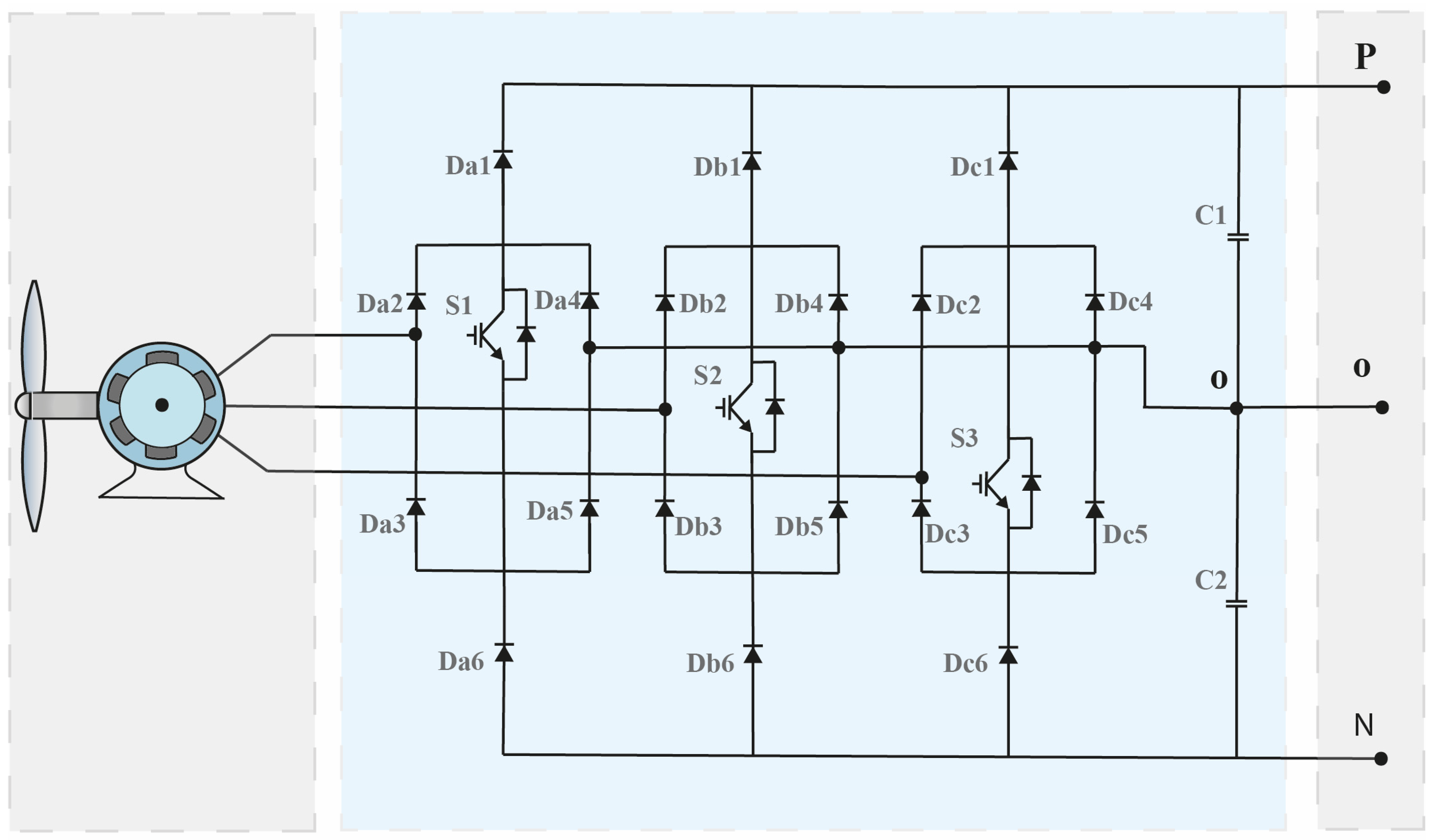
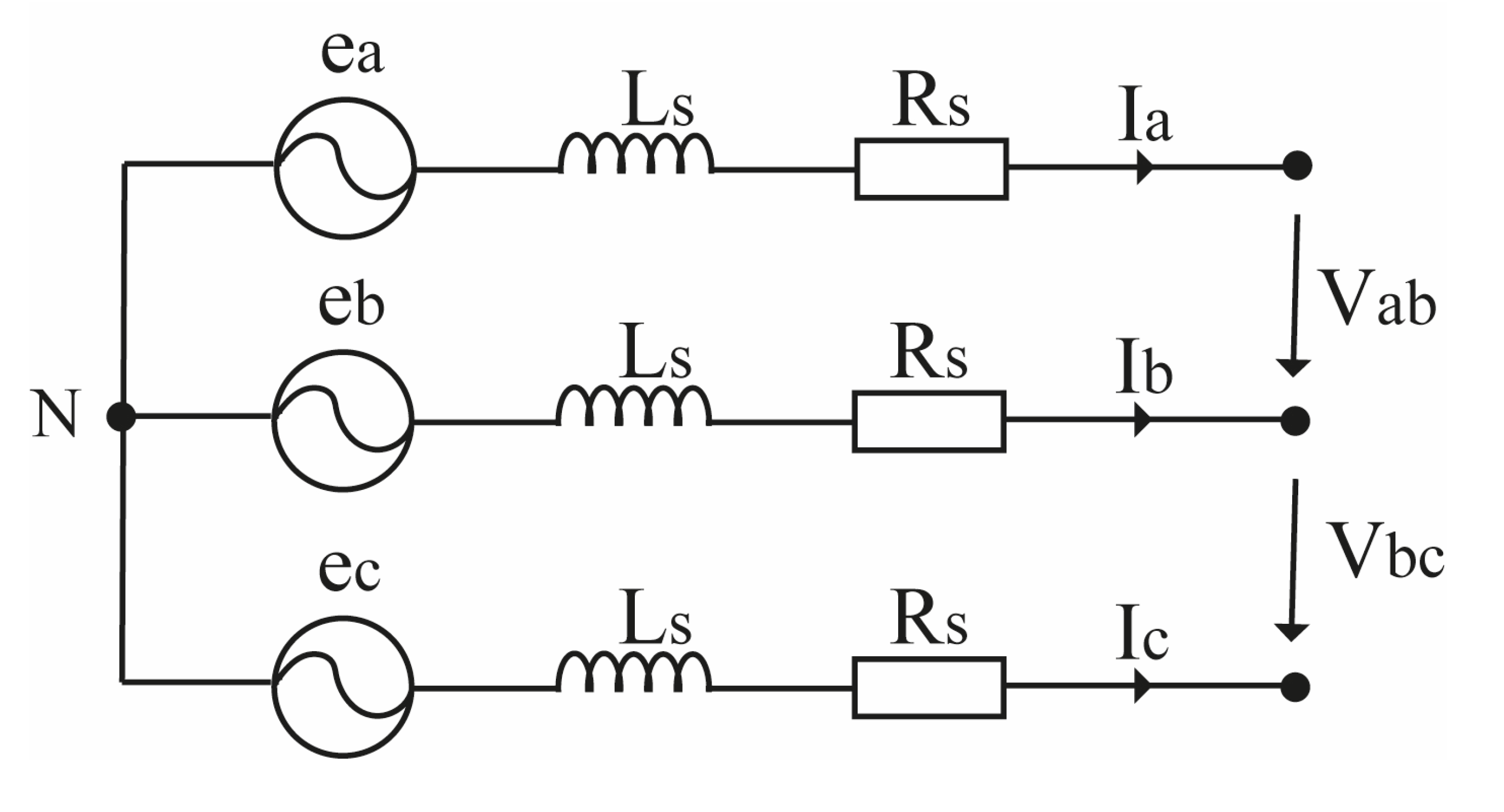
2.1. PMSG and Vienna Rectifier Models
2.2. Vienna Rectifier Operation Principle
2.3. Control Strategy
3. Simulations Conditions and Results
3.1. Simulations Conditions
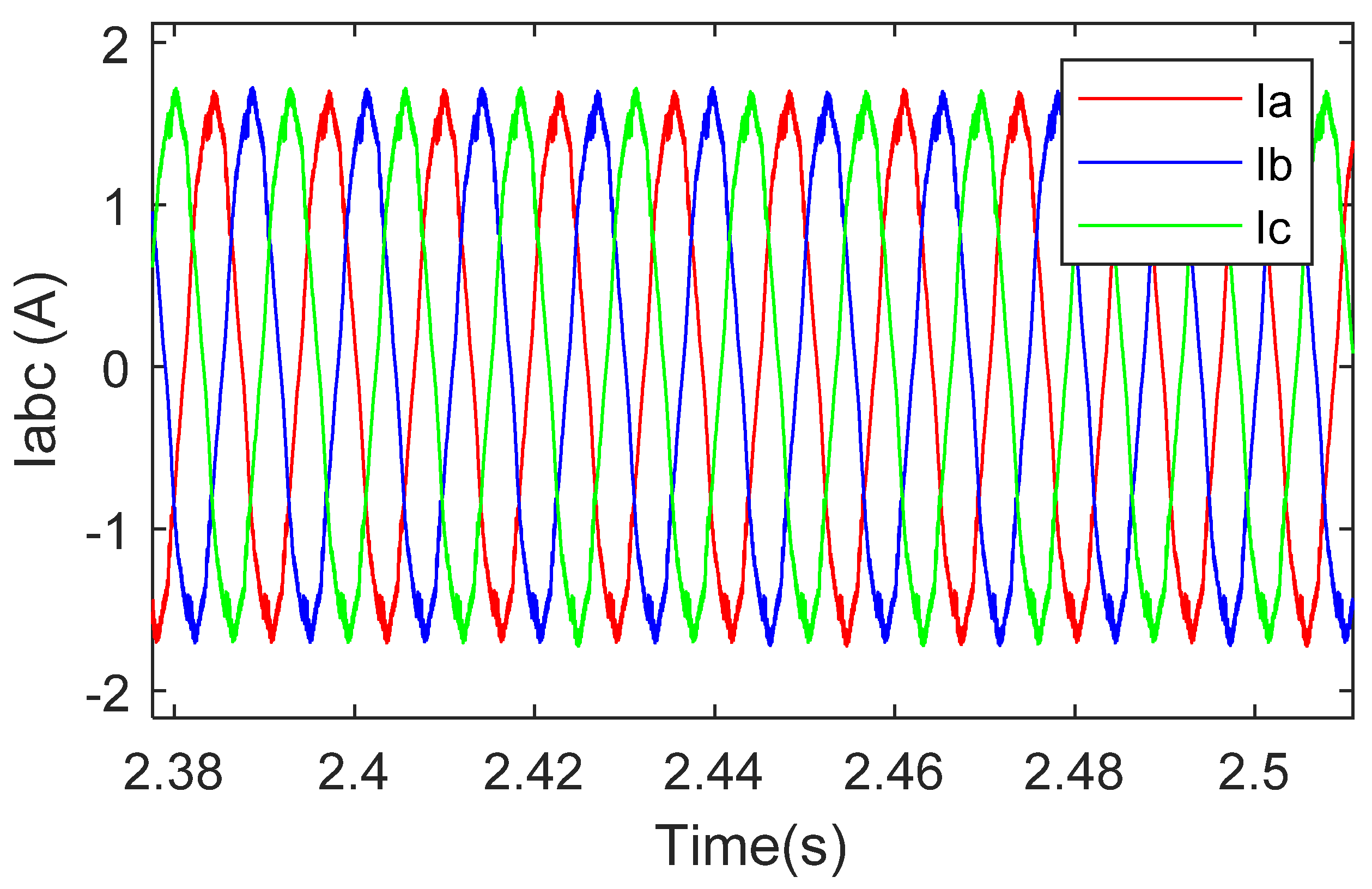
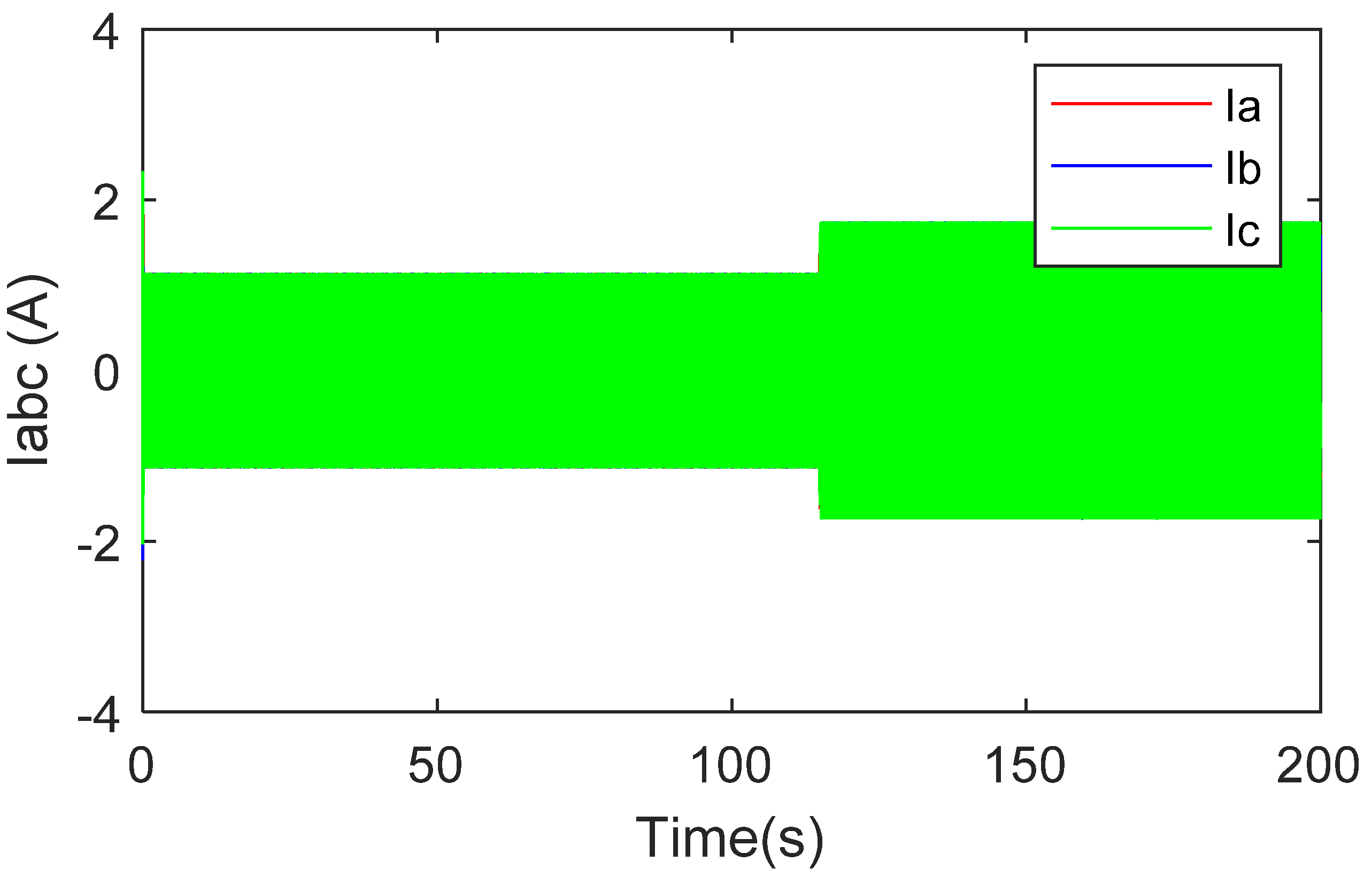
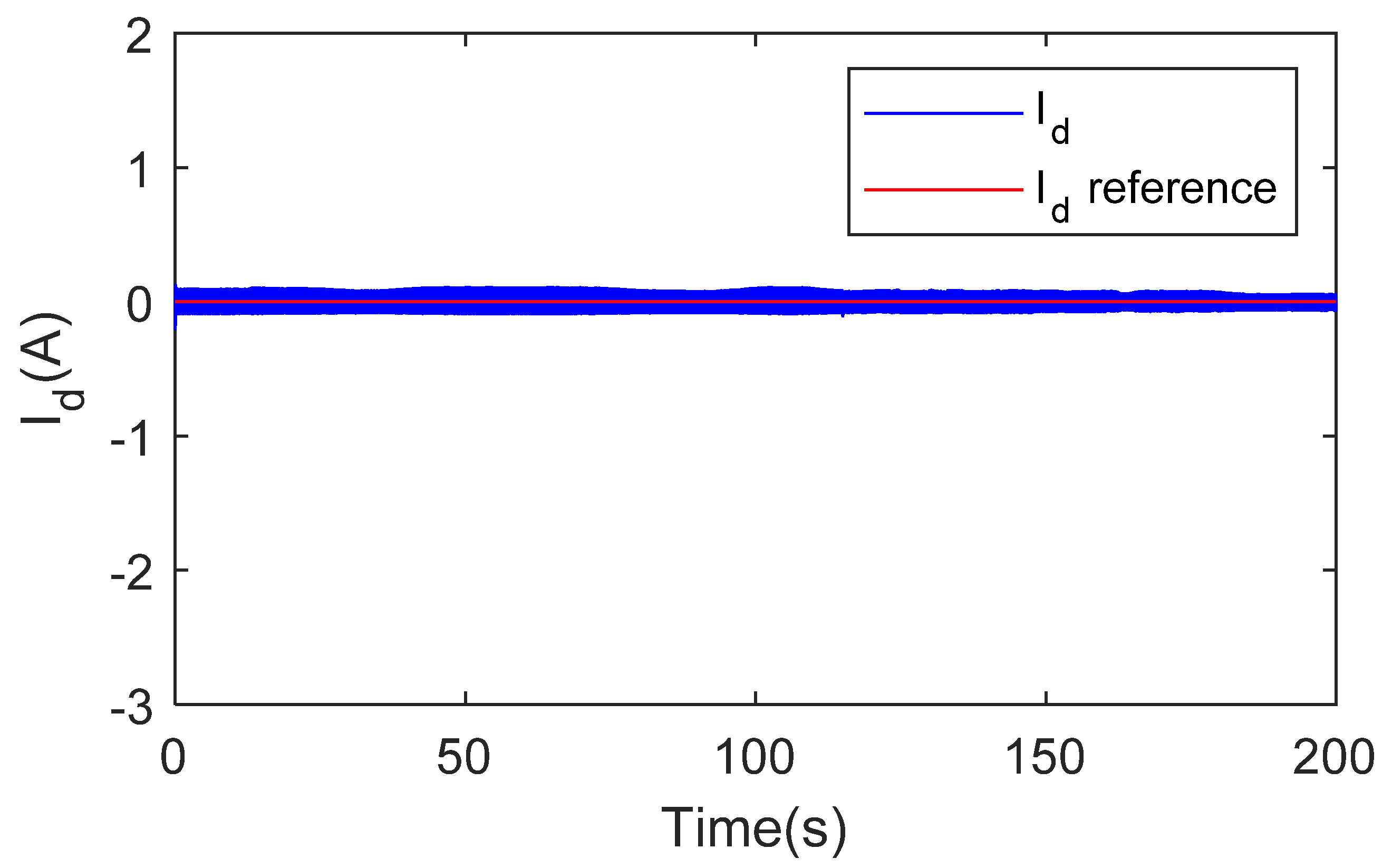
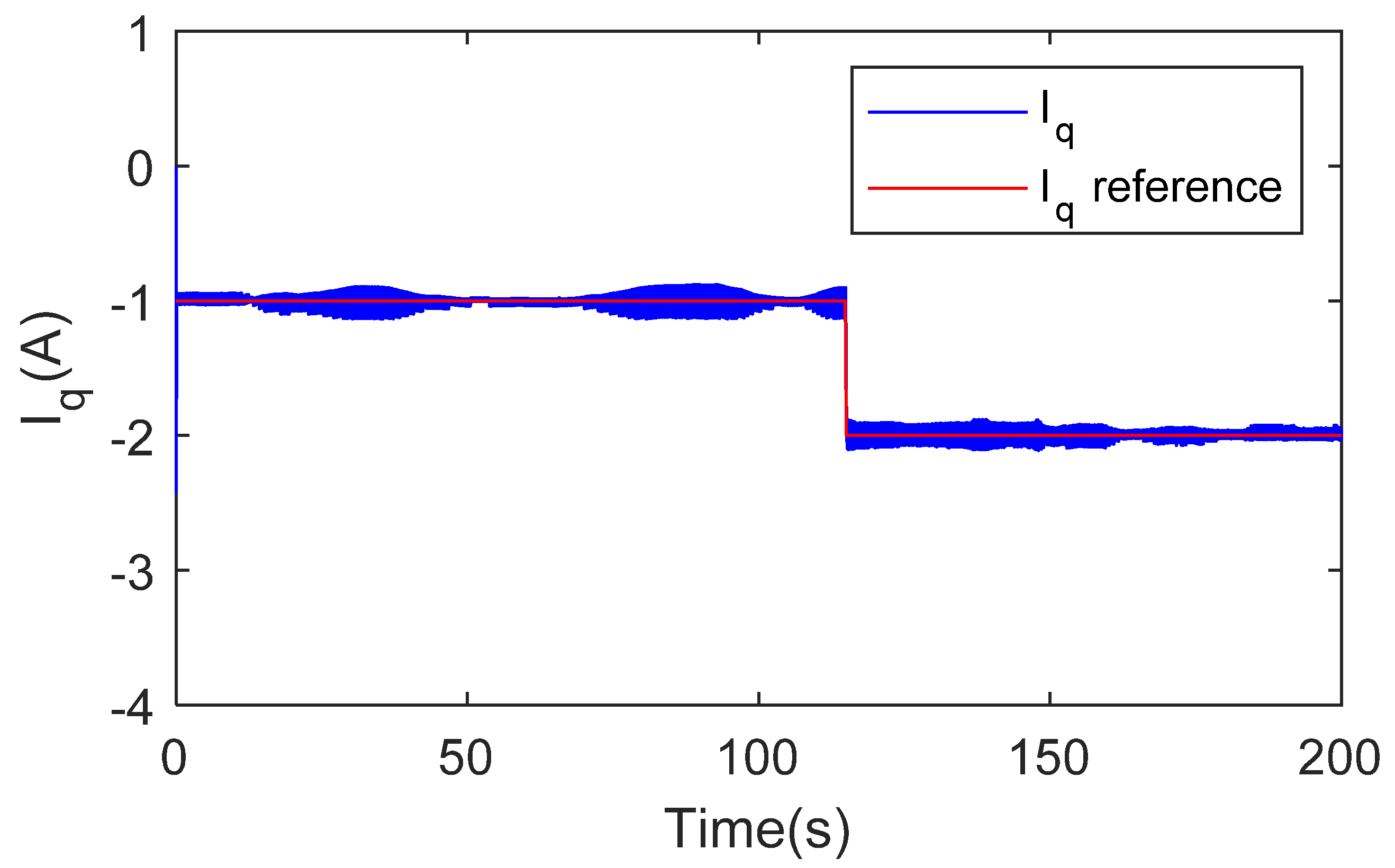
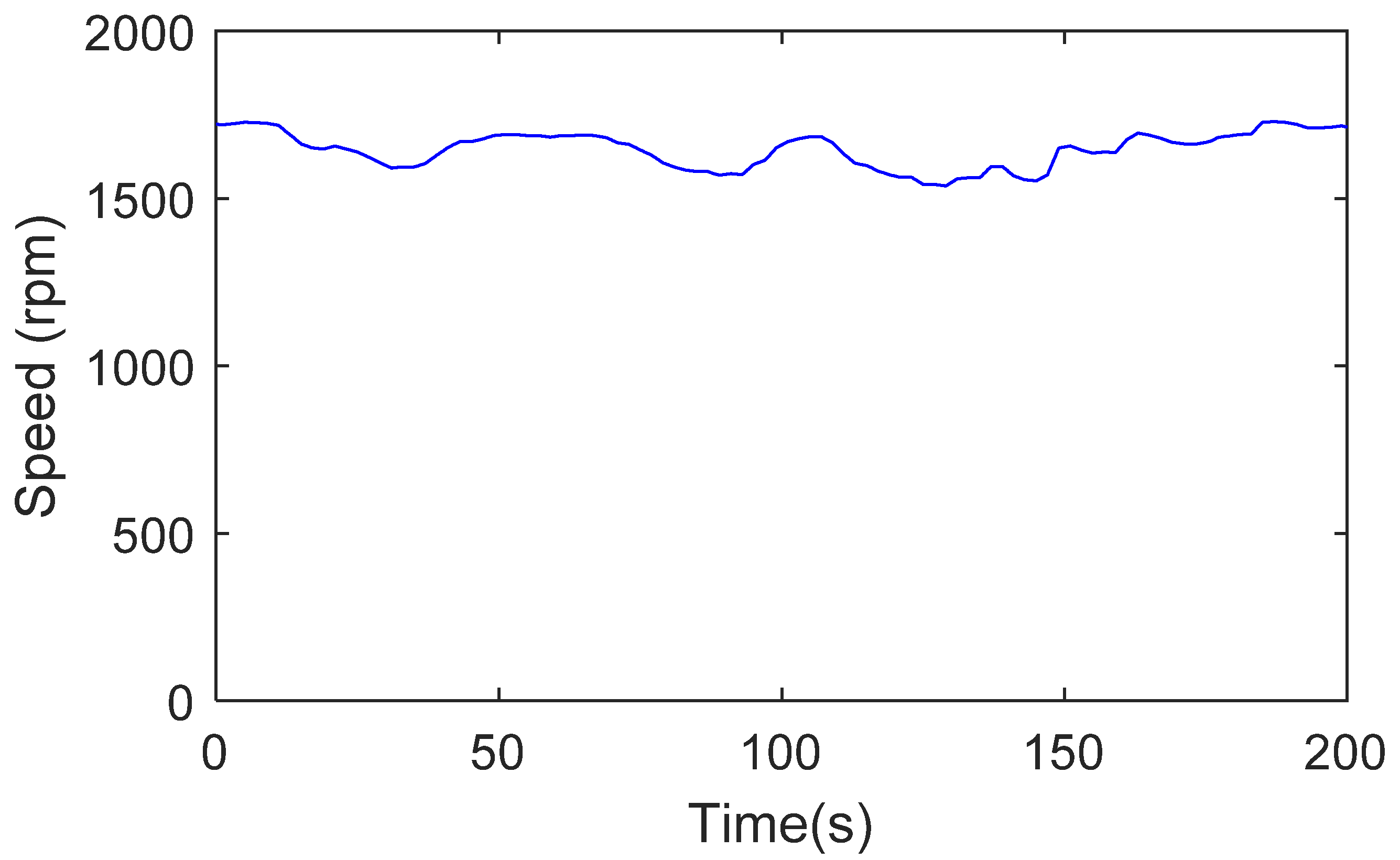
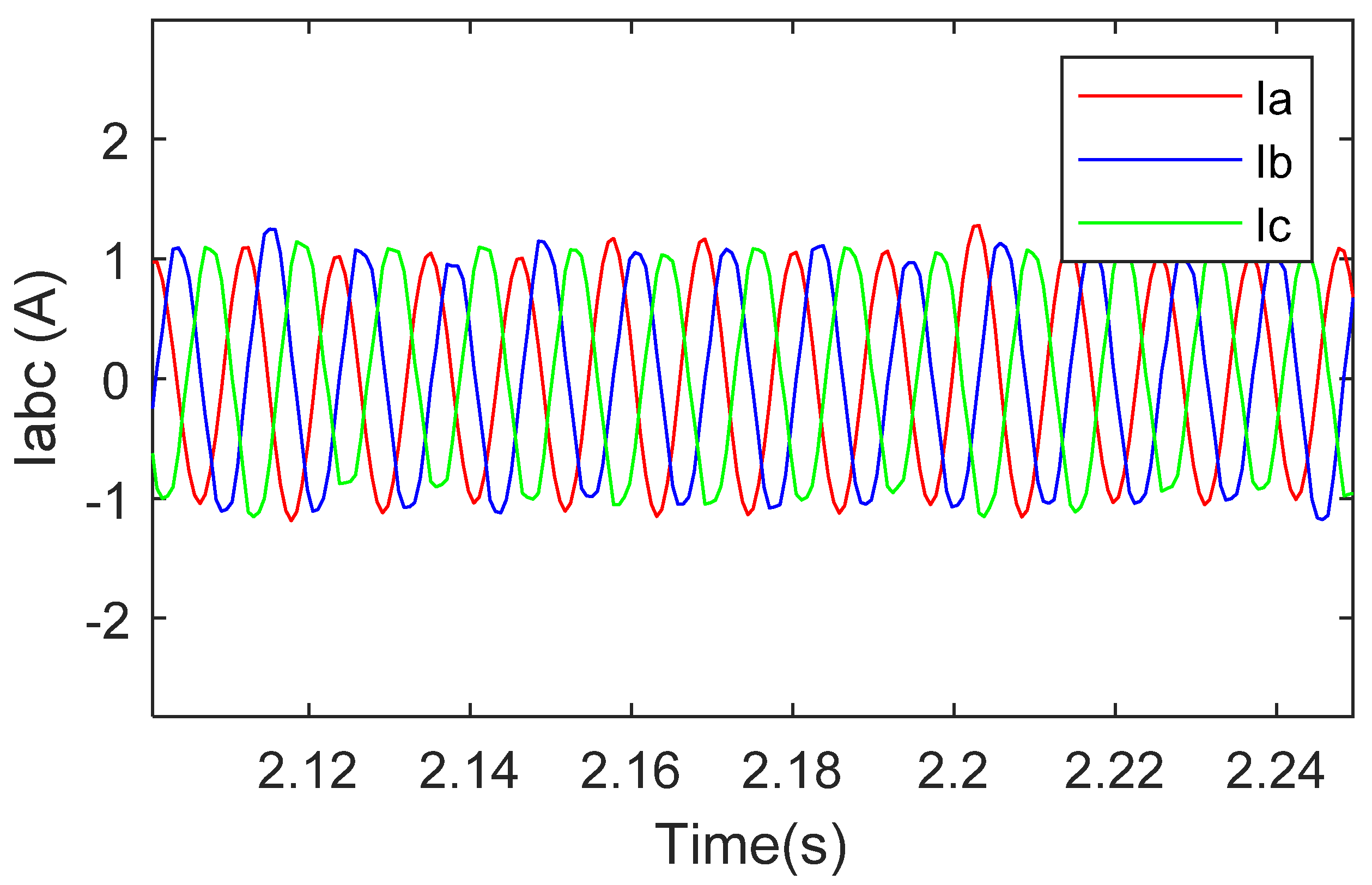
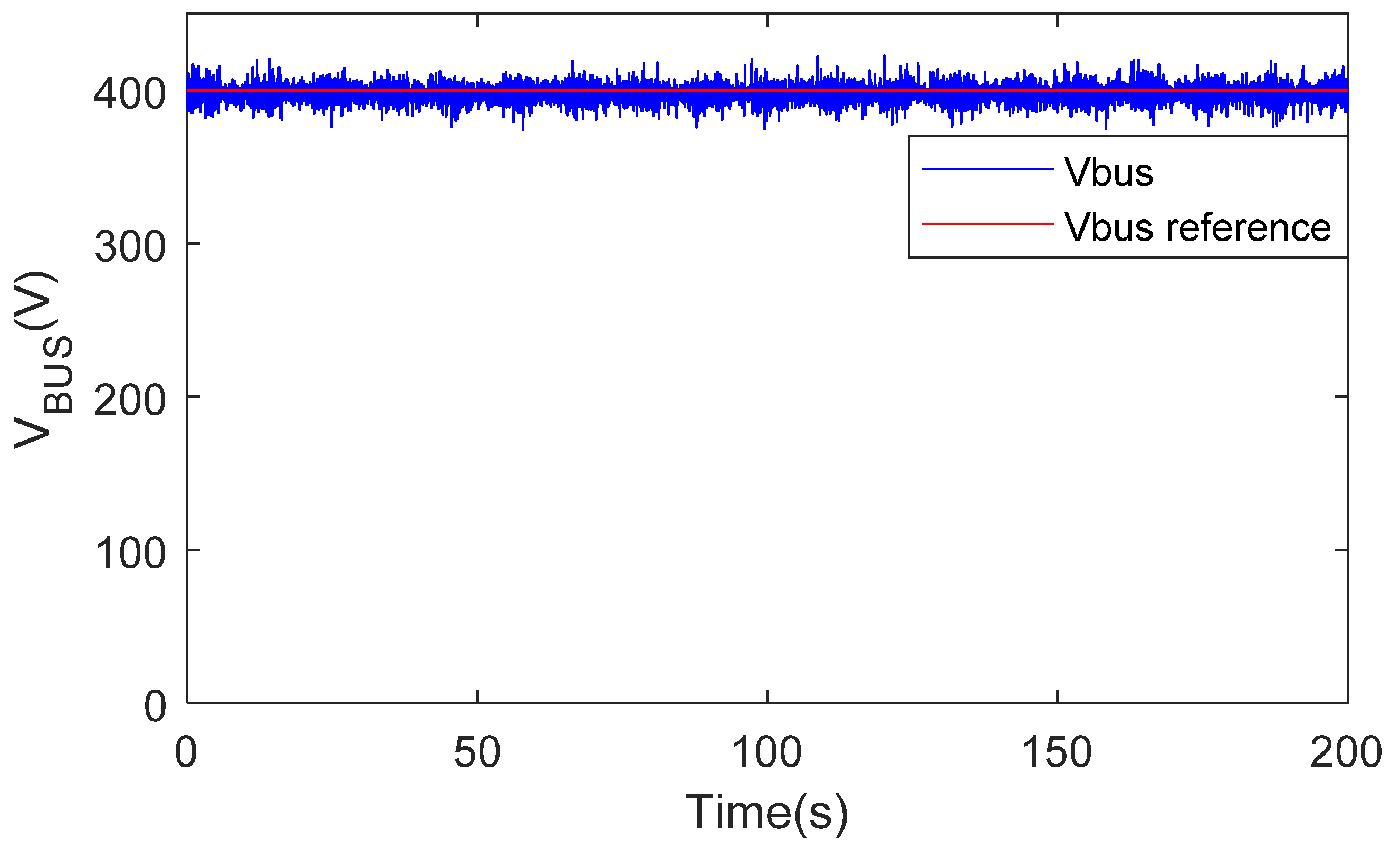
3.2. Simulations Results
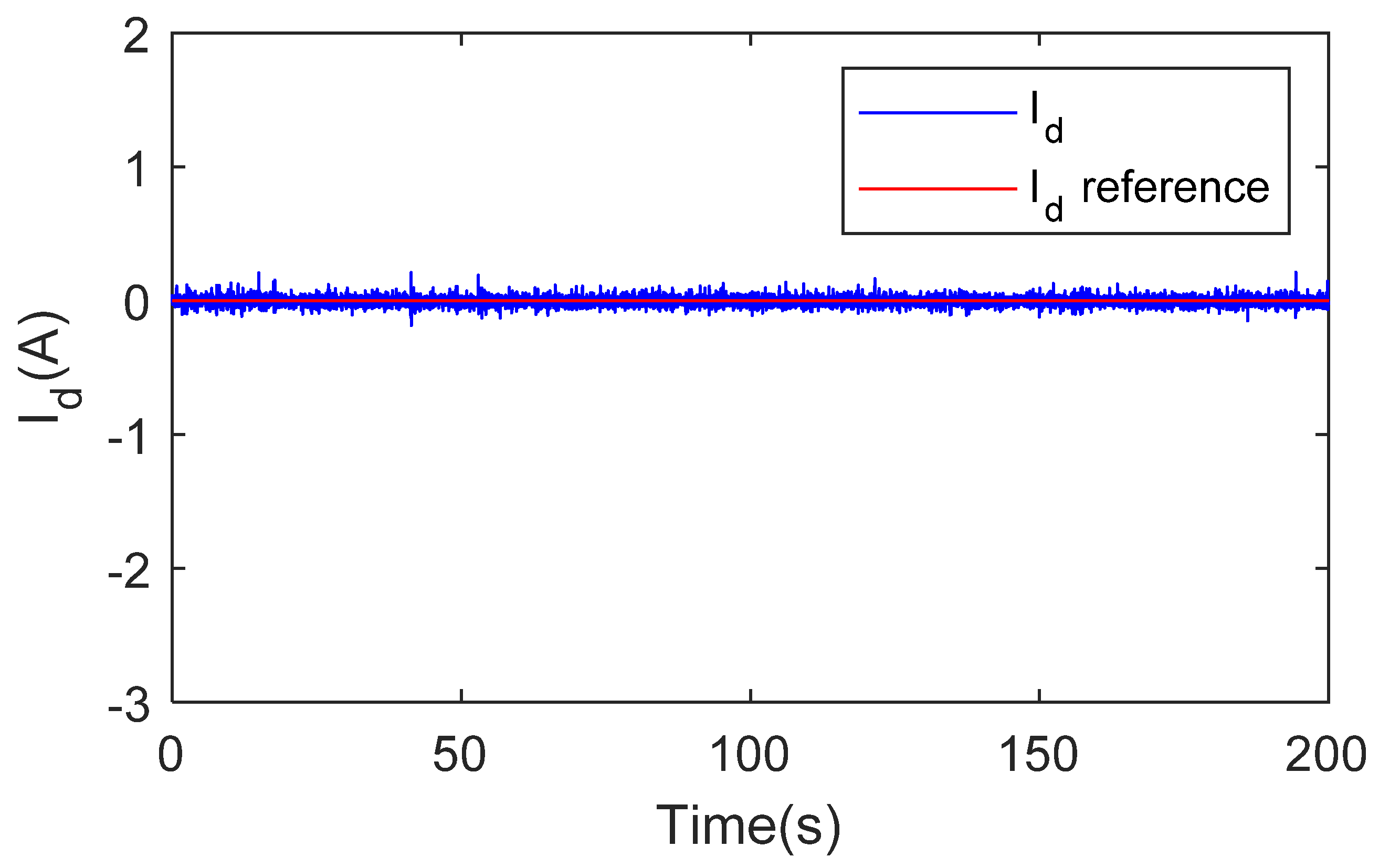
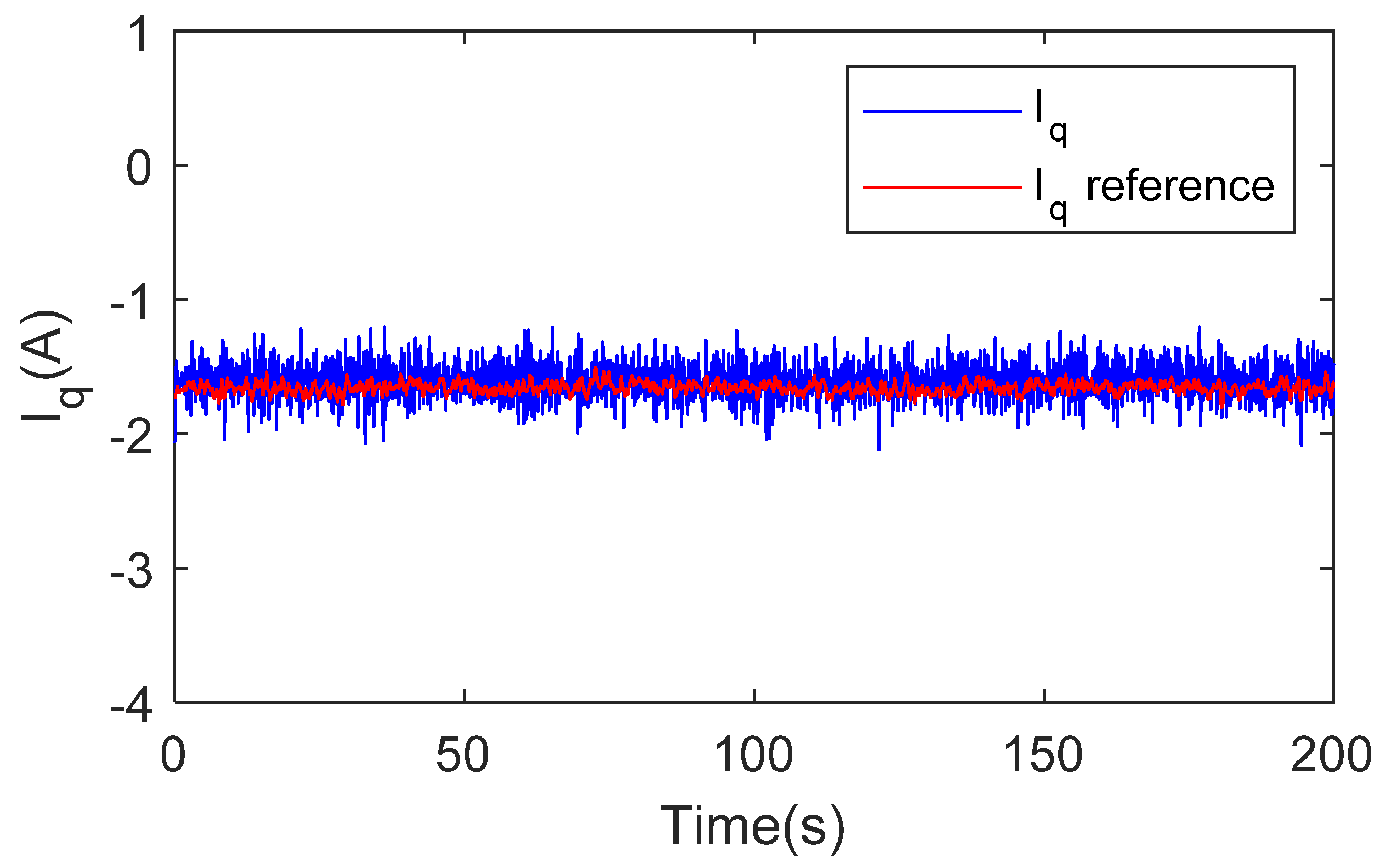
4. Experimental Tests and Results
4.1. Experimental Setup
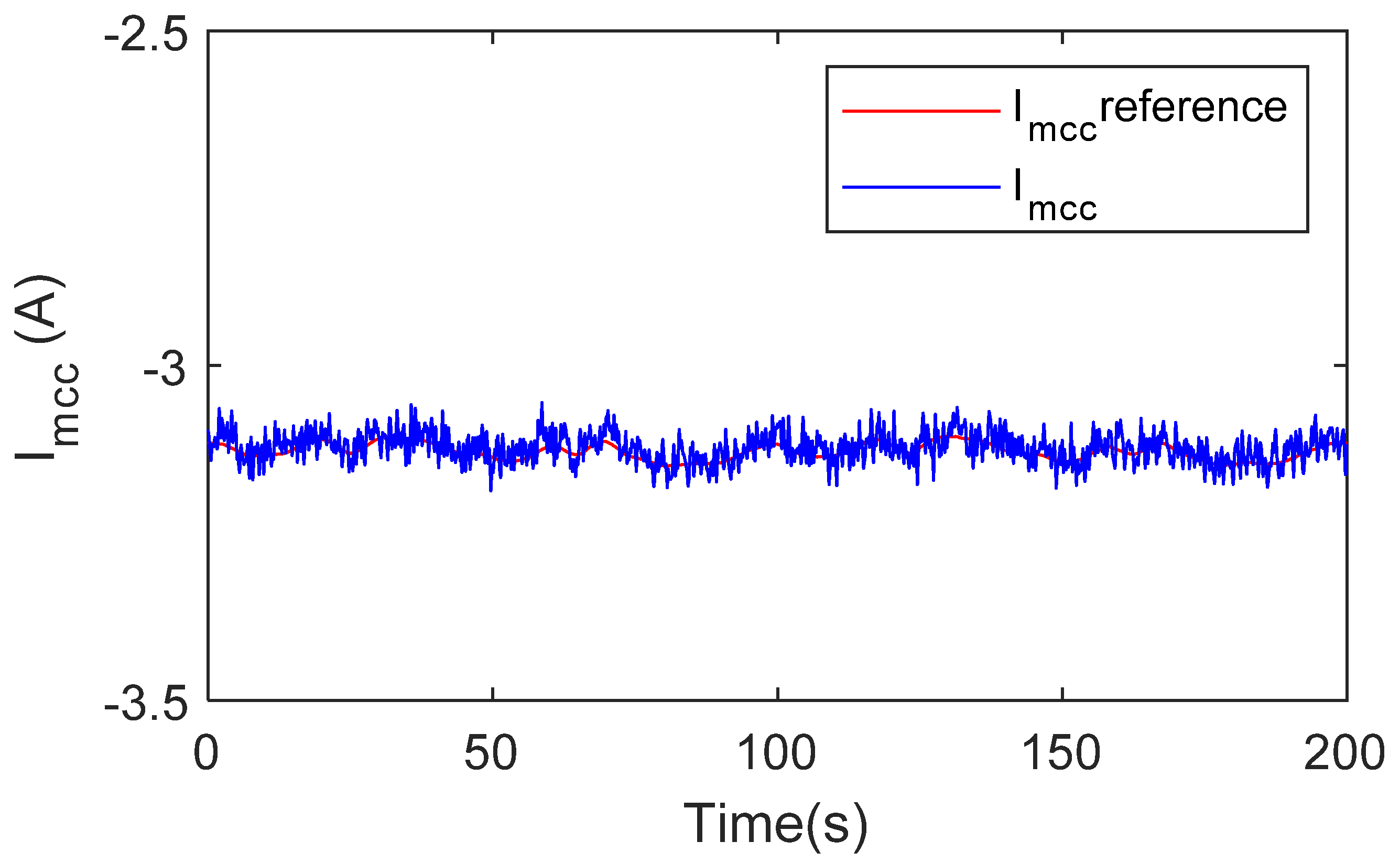
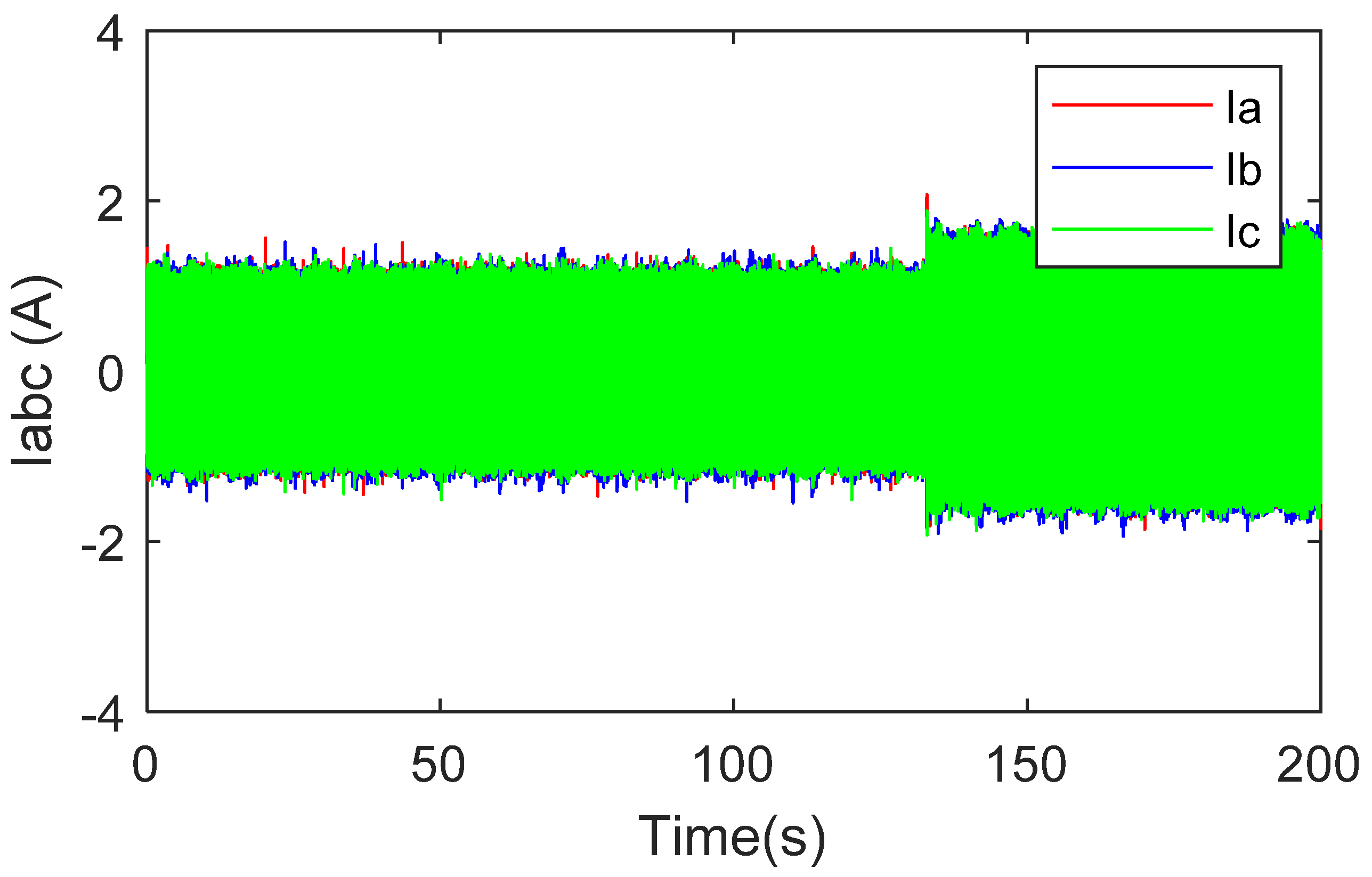
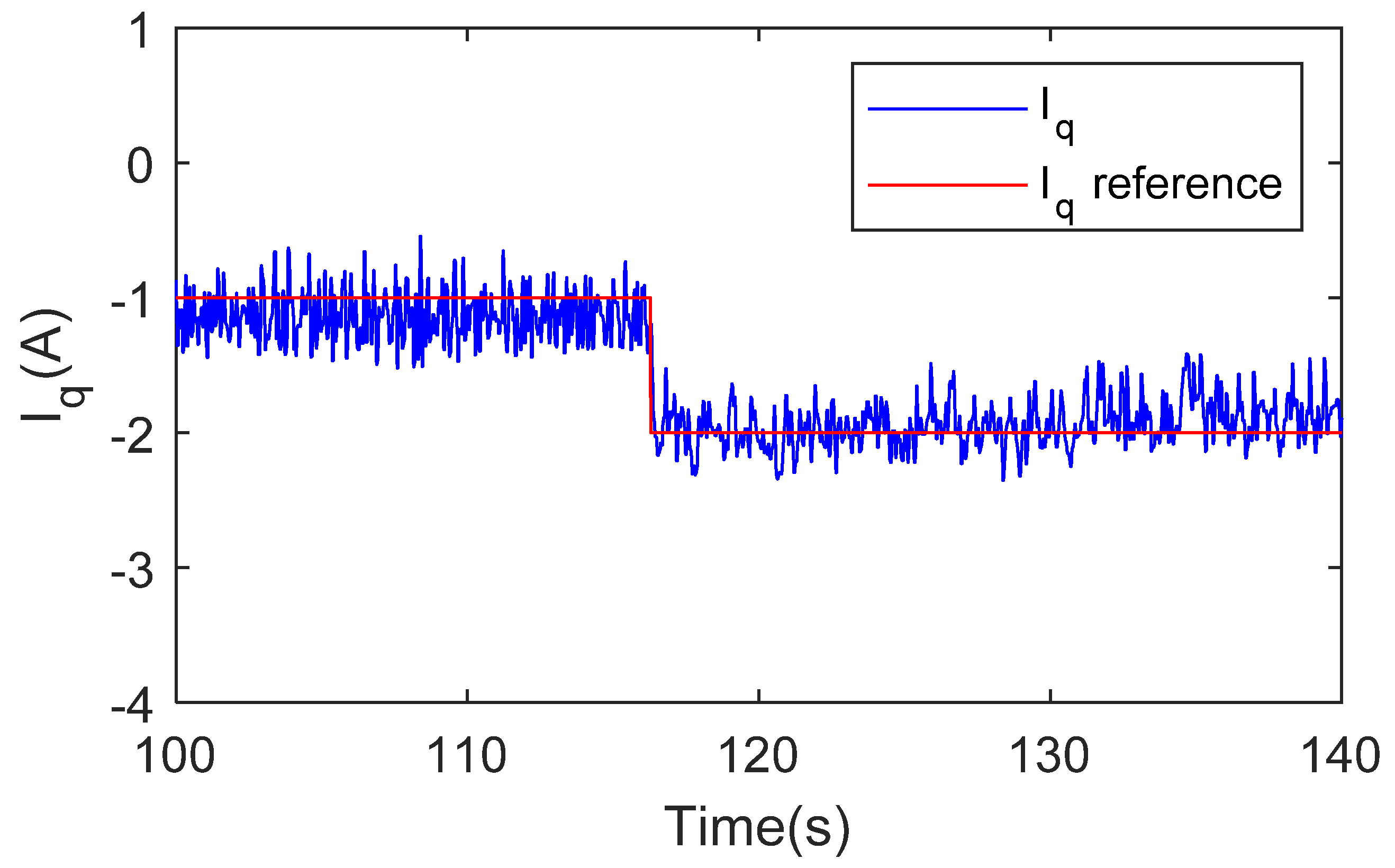
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Pn | PMSG rated power |
| Pw | The power captured by wind turbine |
| Rt | Radius of the wind turbine |
| Rs | PMSG resistance |
| Ls | Inductance of the PMSG |
| The mutual inductance of the stator windings | |
| The number of the PMSG pole pairs | |
| J = Jg + Jt | Moment of inertia of the PMSG and turbine (DC motor) |
| Air density | |
| Rotor swept area | |
| Wind speed | |
| Vbus | DC-bus voltage |
| d-q voltages | |
| , | d-q currents |
| Dynamic of the current loop | |
| C1, C2 | DC-bus capacitor |
| Magnetic induced flux |
References
- Alili, A.; Camara, M.B.; Dakyo, B.; Raharijaona, J. Power Electronic Converters Review for Wind Turbine Applications: State of Art, Reliability and Trends. In Proceedings of the GREEN 2020 Conference, IARIA, Valencia, Spain, 21–25 November 2020; pp. 12–18. Available online: https://www.thinkmind.org/index.php?view=article&articleid=green_2020_1_30_80025 (accessed on 15 February 2022).
- Gao, Z.; Liu, X. An Overview on Fault Diagnosis, Prognosis and Resilient Control for Wind Turbine Systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Jiang, Y.; Jin, X.; Wang, H.; Fu, Y.; Ge, W.; Yang, B.; Yu, T. Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation. Processes 2019, 7, 490. [Google Scholar] [CrossRef] [Green Version]
- Minibock, J.; Stogerer, F.; Kolar, J. A novel concept for mains voltage proportional input current shaping of a vienna rectifier eliminating controller multipliers. i. basic theoretical considerations and experimental verification. In Applied Power Electronics Conference and Exposition 2001, APEC 2001. Sixt. Annu. IEEE 2001, 1, 582–586. [Google Scholar] [CrossRef]
- Soeiro, T.; Kolar, J. Analysis of high-efficiency three-phase two- and three-level unidirectional hybrid rectifiers. IEEE Trans. Ind. Electron. 2013, 60, 3589–3601. [Google Scholar] [CrossRef]
- Kolar, J.; Zach, F.C. A novel three-phase utility interface minimizing line current harmonics of high-power telecommunications rectifier modules. IEEE Trans. Ind. Electron. 1997, 44, 456–467. [Google Scholar] [CrossRef] [Green Version]
- Friedli, T.; Hartmann, M.; Kolar, J. The essence of three-phase pfc rectifier systems 2014; part ii. IEEE Trans. Ind. Electron. 2014, 29, 543–560. [Google Scholar] [CrossRef]
- Bel Haj Youssef, N.; Al-Haddad, K.; Kanaan, H. Large-signal modeling and steady-state analysis of a 1.5-kw three-phase/switch/level (vienna) rectifier with experimental validation. IEEE Trans. Ind. Electron. 2008, 55, 1213–1224. [Google Scholar] [CrossRef]
- Ide, P.; Schafmeister, F.; Frohleke, N.; Grotstollen, H. Enhanced control scheme for three-phase three-level rectifiers at partial load. IEEE Trans. Ind. Electron. 2005, 52, 719–726. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, T.Q.; Li, Y.; Du, J.; Shi, P. Control and Analysis of Vienna Rectifier Used as the Generator-Side Converter of PMSG-based Wind Power Generation Systems. J. Power Electron. 2017, 17, 212–221. [Google Scholar] [CrossRef] [Green Version]
- Dalessandro, L.; Round, S.D.; Drofenik, U.; Kolar, J.W. Discontinuous Space-Vector Modulation for Three-Level PWM Rectifiers. IEEE Trans. Power Electron. 2008, 23, 530–542. [Google Scholar] [CrossRef]
- Hang, L.; Li, B.; Zhang, M.; Wang, Y.; Tolbert, L.M. Equivalence of SVM and Carrier-Based PWM in Three-Phase/Wire/Level Vienna Rectifier and Capability of Unbalanced-Load Control. IEEE Trans. Ind. Electron. 2014, 61, 20–28. [Google Scholar] [CrossRef]
- Rajaei, A.; Mohamadian, M.; Varjani, A.Y. Vienna-Rectifier-Based Direct Torque Control of PMSG for Wind Energy Application. IEEE Trans. Ind. Electron. 2013, 60, 2919–2929. [Google Scholar] [CrossRef]
- Lee, J.; Bak, Y.; Lee, K.; Blaabjerg, F. MPC-SVM method for Vienna rectifier with PMSG used in Wind Turbine Systems. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3416–3421. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.B. Predictive control of Vienna rectifiers for PMSG systems. IEEE Trans. Ind. Electron. 2017, 64, 2580–2591. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, C.; Duan, S. Model predictive control with improved discrete space vector modulation for three-level Vienna rectifier. IEEE Trans. Power Electron. 2019, 12, 1998–2004. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.B.; Blaabjerg, F. Predictive control with discrete space-vector modulation of Vienna rectifier for driving PMSG of wind turbine systems. IEEE Trans. Power Electron. 2019, 34, 12368–12383. [Google Scholar] [CrossRef]
- Yu, F.; Liu, X.; Zhang, X.; Zhu, Z. Model Predictive Virtual-Flux Control of Three-Phase Vienna Rectifier Without Voltage Sensors. IEEE Access 2019, 7, 169338–169349. [Google Scholar] [CrossRef]
- Nikouei, M. Design and Evaluation of the Vienna Rectifier for a 5 MW Wind Turbine System. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2013. Available online: https://publications.lib.chalmers.se/records/fulltext/184817/184817.pdf (accessed on 15 February 2022).
- Rajaei, A.; Mohamadian, M.; Dehghan, S.M.; Yazdian, A. PMSG-based variable speed wind energy conversion system using Vienna rectifier. Eur. Trans. Electr. Power 2011, 21, 954–972. [Google Scholar] [CrossRef]
- Yip, S.Y.; Che, H.S.; Tan, C.P.; Chong, W.T. A Lookup Table Model Predictive Direct Torque Control of Permanent-Magnet Synchronous Generator Based on Vienna Rectifier. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1208–1222. [Google Scholar] [CrossRef]
- Pan, L.; Zhu, Z.; Xiong, Y.; Shao, J. Integral Sliding Mode Control for Maximum Power Point Tracking in DFIG Based Floating Offshore Wind Turbine and Power to Gas. Processes 2021, 9, 1016. [Google Scholar] [CrossRef]
- Oukkacha, I.; Sarr, C.T.; Camara, M.B.; Dakyo, B.; Parédé, J.Y. Energetic Performances Booster for Electric Vehicle Applications Using Transient Power Control and Supercapacitors-Batteries/Fuel Cell. Energies 2021, 14, 2251. [Google Scholar] [CrossRef]
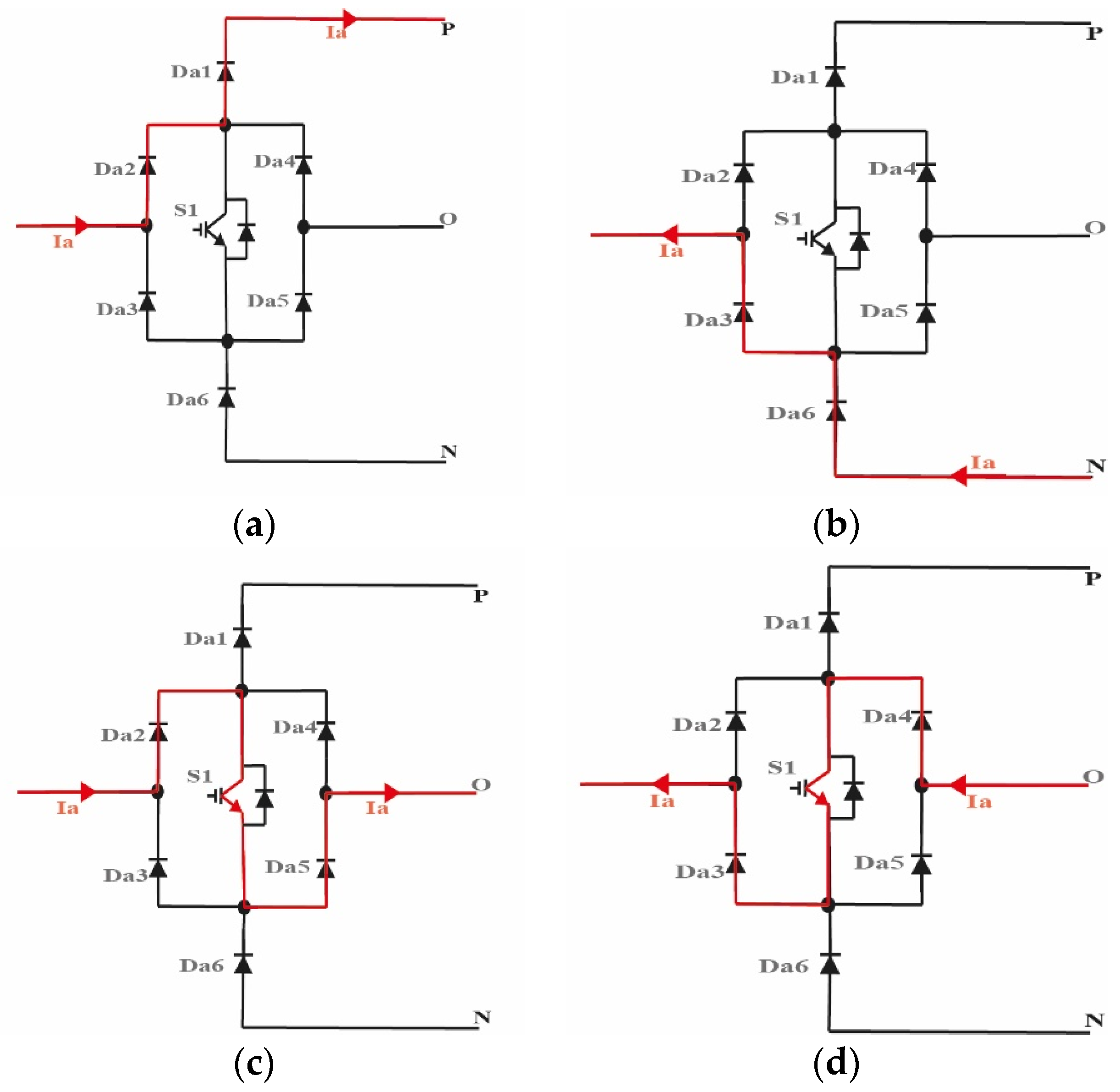



| Switching States | Semiconductors Switching States | Output Voltage | ||
|---|---|---|---|---|
| S1 | S2 | S3 | ||
| P | OFF | OFF | OFF | Vdc/2 |
| O | ON | ON | ON | 0 |
| N | OFF | OFF | OFF | −Vdc/2 |
| Parameters | Values |
| PMSG resistance | Rs = 1.870 Ω |
| PMSG inductance | Ls = 15.37 mH |
| Nominal power | Pn = 1790 W |
| Flux | = 0.015 Wb |
| Moment of inertia | Jg = 9.3 × 10−4 kg/m2 |
| Number of pole pairs | P = 3 |
| Nominal speed | 2000 rpm |
| DC-bus capacitors | 400 µF |
| Current smoothing inductances | 1 mH |
| Max. current for Vienna IGBT | 300 A |
| Sampling period | 150 A |
| Switching frequency | 10 kHz |
| Fuel cell nominal voltage | 200 V |
| 1.225 kg/m3 | |
| Rt | 1.2 m |
| Kp | 9.58 |
| Ki | 4178 |
| Parameters | Values |
|---|---|
| Motor resistance | R = 2.35 Ω |
| DC motor inductance | Ls = 57 mH |
| Nominal power | Pn = 1.7 kW |
| Rated torque | C = 5.9 Nm |
| Moment of inertia | Jt = 6 × 10−3 kg/m2 |
| Nominal speed | 2300 rpm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alili, A.; Camara, M.B.; Dakyo, B. Vienna Rectifier-Based Control of a PMSG Wind Turbine Generator. Processes 2022, 10, 413. https://doi.org/10.3390/pr10020413
Alili A, Camara MB, Dakyo B. Vienna Rectifier-Based Control of a PMSG Wind Turbine Generator. Processes. 2022; 10(2):413. https://doi.org/10.3390/pr10020413
Chicago/Turabian StyleAlili, Aimad, Mamadou Baïlo Camara, and Brayima Dakyo. 2022. "Vienna Rectifier-Based Control of a PMSG Wind Turbine Generator" Processes 10, no. 2: 413. https://doi.org/10.3390/pr10020413
APA StyleAlili, A., Camara, M. B., & Dakyo, B. (2022). Vienna Rectifier-Based Control of a PMSG Wind Turbine Generator. Processes, 10(2), 413. https://doi.org/10.3390/pr10020413








